Как найти работу реального газа

1. Лекция 5в. Реальный газ и его работа

Курс физики для студентов 1-2 курса БГТУ
Заочный факультет
для специальностей ЛИД, ТДП, ТДПС, МОЛК, МОЛКС
Кафедра физики БГТУ
доцент Крылов Андрей Борисович
Часть II.
ОСНОВНЫЕ ЗАКОНЫ
термодинамики и
молекулярной
физики
Лекция 5в.
Реальный газ и его работа
Движение молекул газа в
поле сил тяжести
2015
1
+

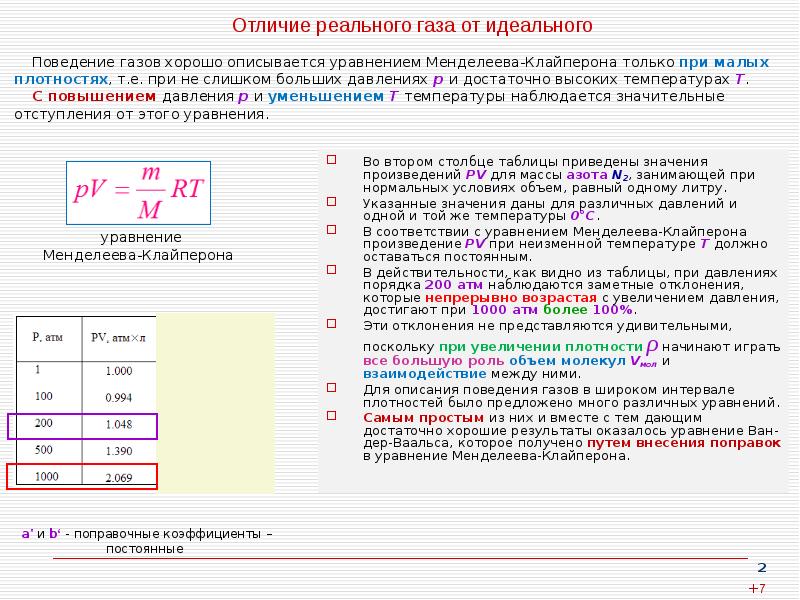
2. Отличие реального газа от идеального

Поведение газов хорошо описывается уравнением Менделеева-Клайперона только при малых
плотностях, т.е. при не слишком больших давлениях р и достаточно высоких температурах Т.
С повышением давления р и уменьшением Т температуры наблюдается значительные
отступления от этого уравнения.
уравнение
Менделеева-Клайперона
а’ и b‘ — поправочные коэффициенты –
постоянные
Во втором столбце таблицы приведены значения
произведений PV для массы азота N2, занимающей
при нормальных условиях объем, равный одному
литру.
Указанные значения даны для различных давлений и
одной и той же температуры 0°С.
В соответствии с уравнением МенделееваКлайперона произведение PV при неизменной
температуре Т должно оставаться постоянным.
В действительности, как видно из таблицы, при
давлениях порядка 200 атм наблюдаются заметные
отклонения, которые непрерывно возрастая с
увеличением давления, достигают при 1000 атм
более 100%.
Эти отклонения не представляются удивительными,
ρ
поскольку при увеличении плотности
начинают
играть все большую роль объем молекул Vмол и
взаимодействие между ними.
Для описания поведения газов в широком интервале
плотностей было предложено много различных
уравнений.
Самым простым из них и вместе с тем дающим
достаточно хорошие результаты оказалось уравнение
Ван-дер-Ваальса, которое получено путем внесения
поправок в уравнение Менделеева-Клайперона.
2
+7

3. Вывод уравнения Ван-дер-Ваальса

Вывод: наличие сил притяжения и отталкивания приводит к тому, что при больших давлениях р
(когда расстояние между молекулами уменьшается) поведение реального газа будет отличаться от
модели идеального газа.
Силы отталкивания противодействуют проникновению данной частицы в ту область объема сосуда,
которая занята другими молекулами.
Собственный объем V0, занятый частицей, можно представить представляется как объем шара с
некоторым эффективным диаметром dэфф (диаметром молекулярного действия).
Вследствие того, что молекулы обладают конечным объемом, пространство, доступное для движения
молекул. Поэтому «свободный объем» V*, в котором могут свободно (как в идеальном газе) двигаться
молекулы реального газа, будет на некоторую величину меньше, чем объем сосуда V, занимаемый
газом:
где b — поправочный коэффициент (поправочный объем)
для одного моля газа в м3/моль.
На расстоянии от стенки меньше некоторого эффективного радиуса
межмолекулярного взаимодействия rэфф =dэфф /2 на выделенную молекулу
действует некоторая равнодействующая сила, направленная от стенки и
стремящаяся уменьшить кинетическую энергию молекулы.
Величина работы этой силы А зависит от количества молекул в сфере
эффективного взаимодействия, т.е. от концентрации молекул в сосуде n.
Тогда следует ввести поправочное давление pi , которое зависит линейно от концентрации
обратно пропорционально молярному объему VM:
nи
где а — коэффициент пропорциональности, зависящий от природы
молекул.
Если давление р выражено в паскалях, а объем V в м3, то константа a
измеряется в [Па×м6/моль2], а константа b – в м3/моль.
3
+8

4. Вывод уравнения Ван-дер-Ваальса-2

Умножим обе части уравнения на объем газа
Для реального газа закон
Менделеева- Клапейрона:
Но:
где
V* :
Nа — число Авогадро,
ν – количество молей газа,
R – универсальная газовая постоянная.
где
уравнение состояния Ван-дер-Ваальса для реального
газа
лучше согласуется с опытными данными, чем уравнение Клапейрона-Менделеева, особенно при
высоких давлениях.
4
+10

5. Изотермы Ван-дер-Ваальса

Обсудим уравнения Ван-дер-Ваальса.
Изотермы Ван-дер-Ваальса – графический вид
зависимости давления реального газа p от объема V
при постоянной температуре для разных значений
температуры (Т1 > Т2 > Тк >Т3 > Т4).
Эти изотермы:
при низких температурах они имеют
волнообразные участки (максимумы и минимумы),
при некоторой температуре Тк на изотерме имеется
только точка перегиба К,
при высоких температурах изотермы Ван-дерВаальса похожи на изотермы идеального газа.
Если привести уравнение Ван-дер-Ваальса к нормальному
виду, то оно окажется кубическим уравнением
относительно объема V.
Кубическое уравнение может иметь:
либо три вещественных корня,
либо один вещественный корень и два мнимых.
Очевидно, что:
первому случаю соответствуют изотермы при
низких температурах (три значения объема газа V
отвечают одному значению давления p),
второму случаю — изотермы при высоких
температурах (одно значение объема V отвечает
одному значению давления р).
5
+7

6. Экспериментальные изотермы реального газа. Кривая фазового перехода

Эндрюс Томас
1813-1885
Томас Эндрюс в 1866 г. экспериментально исследовал зависимость
молярного
объема
VМ
углекислого
газ
от
давления
p
при
изотермическом сжатии.
Рассмотрим результаты этих опытов (смотри рисунок) в виде
графических зависимостей в координатах «давление — молярный
объем» (p-VМ), причем:
(Т1 <Т< Т2 <Tкр <T3).
Выводы:
1.
При температурах ниже Ткр = 340 К на каждой изотерме наблюдается
горизонтальный участок ВС, вдоль которого давление постоянно
р=рB , а молярный объем принимает любые значения от VВ до VС.
2.
Разность объемов (VВ — VС) в конечных точках горизонтальных
участков изотерм возрастает с понижением температуры Т.
3.
Видно, что эта разность объемов стремится к нулю по мере приближения к
температуре Ткр , которую называют критической температурой.
На изотерме при температуре Т = Ткр (критическая изотерма), точки
В и С сливаются в одну точку Кр, называемую критической точкой.
Соответствующие ей значения давления ркр и молярного объема Vкр называют
критическими.
На участке СD углекислота находится в газообразном состоянии,
а на участке АВ — в жидком.
На участке ВС углекислота одновременно находится в двух
агрегатных состояниях — жидком и газообразном (2-хфазная
система).
Точка С соответствует началу конденсации СО2 при
изотермическом сжатии, а точка В — концу конденсации.
Наоборот, при изотермическом расширении жидкой углекислоты
точка В соответствует началу кипения, а точка С — его концу.
Следовательно, точка В соответствует состоянию кипящей
жидкости, а точка С — состоянию так называемого сухого
6
насыщенного пара.
+9

7. Обобщим изотермы реального газа 

Обобщим изотермы реального газа
Линии
Синие — изотермы при температуре
ниже критической.
Красная — критическая изотерма.
Голубые — сверхкритические изотермы
Характерные точки
K — критическая точка.
F — точка кипения.
G — точка росы.
Участки на них
Зелёные участки на синих линиях —
метастабильные состояния.
Участок левее точки F — нормальная
жидкость.
Прямая FG — равновесие жидкой и
газообразной фазы.
Участок FA — перегретая жидкость
Участок F′A — растянутая
жидкость (p<0).
Участок AC — аналитическое
продолжение изотермы, физически
невозможен.
Участок CG — переохлаждённый пар.
Участок правее точки G — нормальный
газ.
Площади фигуры FAB и GCB равны.
7
+7

8. Критические параметры

Критические параметры — изотерма реального газа, соответствующая критической
температуре Ткр, точка перегиба К и соответствующее ей состояние вещества, объем
и давление, соответствующие критическому состоянию (координаты точки К).
Параметры критического состояния вещества были определены для многих газов и
газовых смесей.
Сравнивая изотермы Эндрюса и Ван-дер-Ваальса можно выразить критические
параметры через постоянные Ван-дер-Ваальса a и b.
— выражение для критического давления
— выражение для критического объема
— выражение для критической температуры
8
+10

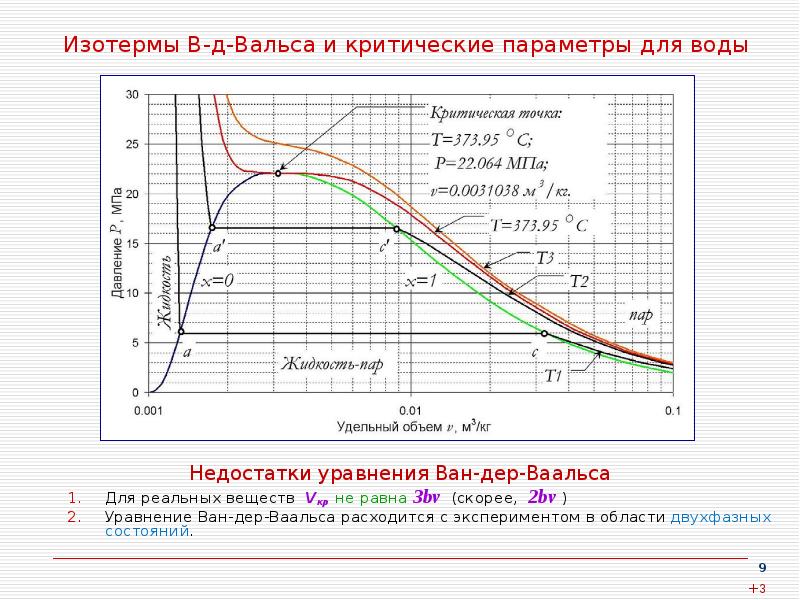
9. Изотермы В-д-Вальса и критические параметры для воды

1.
2.
Недостатки уравнения Ван-дер-Ваальса
Для реальных веществ Vкр не равна 3bν (скорее, 2bν )
Уравнение Ван-дер-Ваальса расходится с экспериментом в области двухфазных
состояний.
9
+3

10. Внутренняя энергия реального газа

Внутренняя энергия
Uреал
реального газа равна сумме кинетической энергии
хаотического движения молекул и их взаимной потенциальной энергии
Eкин
Eпот:
Uреал= Eкин + Eпот
Кинетическая энергия Eкин теплового движения молекул реального газа так же, как и
молекул идеального газа, зависит только от абсолютной температуры Т и молярной
теплоемкости газа при постоянном объеме СV:
где
Среднее значение потенциальной энергии газа Ван-дер-Ваальса равно работе А, которую
нужно затратить против сил притяжения, чтобы разнести все молекулы на бесконечно большие
расстояния. Действие сил притяжения учитывается поправкой на внутреннее давление pi.
Поэтому потенциальная энергия
Eпот взаимодействия равна:
Полная внутренняя энергия газа Ван-дер-Ваальса:
Вывод: из формулы видно, что внутренняя энергия
температуры Т, но и от объема V.
Uреал
реального газа зависит не только от
10
+6

11. Спасибо за внимание!

Курс физики для студентов 1 курса БГТУ
Кафедра физики БГТУ
доцент Крылов Андрей Борисович
Часть II.
ОСНОВНЫЕ ЗАКОНЫ
термодинамики и
молекулярной
физики
Спасибо за внимание!
Снежинка под микроскопом
11
+3

17

Лекция
8

6.1. Силы межмолекулярного взаимодействия
в газах

6.2. Газ Ван-дер-Ваальса

6.3. Изотермы реальных газов.

6.4. Внутренняя энергия реального газа.

6.5. Эффект Джоуля-Томсона

6.1. Силы межмолекулярного взаимодействия в газах

Модель идеального газа, используемая
в молекулярно – кинетической теории
газов, позволяет довольно хорошо
описывать поведение разреженных реальных
газов.

Свойства не сильно разреженных газов
отличаются от свойств идеальных газов,
подчиняющихся уравнению Клапейрона —
Менделеева.

Из этого уравнения следует, что отношение

называемое фактором сжимаемости, для
идеальных газов всегда равно единице.

Однако опыты показывают, что

• факторы сжимаемости для всех газов
  зависят от давления и температуры. При
  достаточно высоких давлениях все
  реальные газы независимо от их температуры
  менее сжимаемы, чем идеальные.

• экспериментальные исследования удельной
  теплоемкости, вязкости и других свойств
  газов показали, что эти свойства
  тоже более или менее значительно
  отличаются от соответствующих свойств
  идеальных газов. Более того, приближенная
  теория, основанная на законах идеальных
  газов, часто не в состоянии объяснить
  даже качественно характер зависимости
  свойств газов от их параметров состояния.

Причина этих трудностей кроется в
том, что поведение молекул реальных
газов отлично от того, какое приписывается
частицам идеальных газов.

Во всех телах (твердых, жидких и
газообразных) молекулы взаимодействуют
друг с другом. Тот факт, что свойства
разреженных газов близки к свойствам
идеальных газов, свидетельствует о том,
что силы взаимодействия между
молекулами в сильной степени зависят
от расстояния между ними. Эти силы
имеют электромагнитную, а также особую
квантовую природу.

Опыты показывают, что при расстояниях
более 10^-7 см межмолекулярным
взаимодействием можно пренебречь.

• Своеобразные свойства поверхностного
  слоя жидкостей, а также способность
  твердых тел сопротивляться растяжению
  приводят к выводу о том, что между
  молекулами вещества в любом агрегатном
  состоянии действуют силы
  взаимного притяжения.
  

• Относительно малая сжимаемость
  сильно уплотненных газов, а также
  способность жидких и твердых тел
  сопротивляться сжатию указывают
  на то, что между молекулами действуют
  также и силы взаимного отталкивания.
  

Существенно, что

1. эти силы действуют одновременно.
   В противном случае тела не были бы
   устойчивы: образующие их частицы
   разлетались бы в разные стороны или
   «слипались» бы.

2. зависимость сил взаимного притяжения
   и отталкивания от расстояния r
   между молекулами должна быть различной:

— на очень близких расстояниях преобладают
силы отталкивания

,

— на более далеких — силы взаимного
притяжения

,

Причем

,

где —

радиус-вектор,
проведенный в точку нахождения
рассматриваемой молекулы из той точки,
в которой находится другая молекула,
действующая на первую с силами

и

.

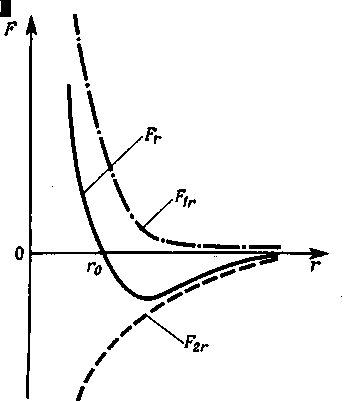
Проекции F_1r
и F_2r
сил

и

на направление вектора

зависят от расстояния r
между взаимодействующими молекулами.

Примерный
характер этих зависимостей показан
на рис. 6.1.

Результирующая сила

Причем

Характер зависимости F_r
от r также
показан на рис. 6.1.

• При r = r₀
  силы

  и

  взаимно уравновешиваются и результирующая
  сила F = 0.

• если r > r₀
  — преобладают силы
  взаимного притяжения (отрицательные)

• если r
  < r₀
  — преобладают силы отталкивания
  (положительные).

Таким образом, r₀—
это то равновесное расстояние между
молекулами, на котором они находились
бы при отсутствии теплового движения,
нарушающего это равновесие.

Рассмотрим
взаимную потенциальную
энергию W_n
двух
молекул.

Подсчитаем элементарную работу

,
совершаемую результирующей потенциальной
силой

межмолекулярного взаимодействия
при увеличении расстояния между
молекулами на dr:

(6.1)

С другой стороны, эта работа совершается
за счет уменьшения
взаимной потенциальной энергии
молекул:

(6.1^/)

Из уравнений (6.1) и (6.1^/) следует

(6.3)

Интегрируя выражение (6.3) по r
от r до ∞, получаем

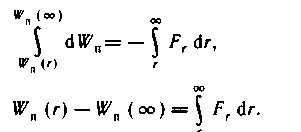
На бесконечно большом расстоянии друг
от друга молекулы не взаимодействуют.

П
оэтому
взаимную потенциальную энергию
W_n
(∞) двух
бесконечно удаленных
друг от друга молекул удобно принять
равной нулю.

Окончательно,
(6.4)

Интеграл, стоящий справа, можно найти
графически, если задана зависимость
силы F_r
, от r
(рис.6.1).

Он пропорционален площади,
ограниченной кривой F_r
= F_r(r),
осью r
и вертикалью (r
= const)
соответствующей
тому значению r,
для которого
нужно найти W_n.

Из рис. 6.1 видно,
что

• r > r₀
  при взаимная
  потенциальная энергия отрицательна,
  так как F_r<0.
  

• П
  ри
  r = r₀,
  как видно из (6.3),

,
(6.5)

т. е. W_n
достигает
минимума

Типичная кривая
зависимости энергии взаимодействия
Uвз от
расстояния r
между их центрами приведена на рисунке
6.2.

• При сближении молекул до расстояния
  r₀ их

— взаимная потенциальная энергия
уменьшается,

— а кинетическая — увеличивается.

Это происходит за
счет положительной работы, совершаемой
результирующей силой взаимного
притяжения молекул (при
r > r₀
F_r<0).

• Дальнейшее уменьшение расстояния
  между молекулами
  сопряжено
  с совершением ими работы против
  результирующей силы F
  взаимного отталкивания молекул
  (при r<r₀
  F_r>0).
  Соответственно
  взаимная потенциальная энергия
  молекул начинает расти с уменьшением
  r.

• Если молекулы находятся достаточно
  далеко друг
  от друга,
  то их взаимная потенциальная энергия
  равна нулю, а полная энергия W
  этой консервативной системы равна
  их кинетической энергии W_K.

• К
  моменту максимального
  сближения молекул (r
  = r₀)

—
вся их кинетическая
энергия
оказывается полностью израсходованной
на совершение работы против сил
отталкивания

— а их взаимная
потенциальная
энергия W_n
(r_x)
= W.

При
прочих равных условиях
расстояние r₁
тем меньше, чем выше температура
газа

зависимость W_n
от r в области
положительных значений Wn
настолько «крутая», что даже значительные
изменения температуры газа приводят к
сравнительно небольшим изменениям
величины r1.
Поэтому в первом приближении можно
считать, что r,
зависит только от химической природы
газа и представляет собой не что иное,
как эффективный диаметр d
молекул.

Из сказанного ясно, что возможность
представления молекул газа в виде
твердых шариков диаметра d
связана с очень быстрым увеличением
сил взаимного отталкивания молекул
реального газа при уменьшении расстояния
между ними.

Зависимость взаимной потенциальной
энергии W_n
двух молекул реального газа от
расстояния г между ними неплохо
описывается формулой Ленарда-Джонса
(1924):

(6.6)

где а₁ и а₂— постоянные
положительные коэффициенты, зависящие
от химической природы газа.

Дифференцируя выражение(6.6)
по r, находим зависимость
от r проекции Fr
результирующей силы F
взаимодействия двух молекул реального
газа:

,
(6.7)

где

и

Анализ формулы:

Первый член в правой части
формулы (6.7) соответствует силам
межмолекулярного притяжения, которые
часто называют ван-дер-ваальсовыми
силами по имени нидерландского физика
Я. Д. Ван-дер-Ваальса, который впервые
начал учитывать межмолекулярное
взаимодействие в газах.

Различают три типа сил межмолекулярного
притяжения:

• Ориентационные
  — между полярными молекулами

• индукционные — между полярной
  и неполярной молекулами

• дисперсионные — между неполярными
  молекулами, а также между любыми другими
  парами молекул.

Все они имеют электрическую природу и
зависят от расстояния r
между молекулами по закону const/r⁷.,
,

Второй член в правой части
формулы (6.7) соответствует силам
взаимного отталкивания молекул. Эти
силы обратно пропорциональны r¹³,
т. е. играют определяющую роль на малых
расстояниях, соответствующих перекрытию
электронных оболочек молекул. Существование
сил взаимного отталкивания молекул при
их очень сильном сближении удалось
объяснить только в квантовой механике,
основываясь на квантовом принципе
запрета Паули.

6.2.
Газ Ван-дер-Ваальса

Модели идеального газа,
подчиняющегося уравнению Менделеева
– Клапейрона

.

Однако с ростом давления при постоянной
температуре оказывается, что

.

При р = 1000 атм. величина

становится вдвое больше, чем предписывает
модель идеального газа (газ не «сжимается»).

Причин
этому две:

1) собственный размер молекул; он и
уменьшает объем, доступный для движения
молекул, при нормальных условиях он
составляет ~0,07 % объема сосуда с газом,
а при 100 атм. уже ~70% ;

2) сложный характер взаимодействия
между молекулами.

Эти причины можно учесть путем
введения поправок в уравнение состояния
идеальных газов, что и сделал
Ван-дер-Ваальс.

B
первом приближении молекулы реального
газа можно уподобить абсолютно твердым
шарикам с диаметром d,
между которыми действуют только силы
взаимного
притяжения. Учитывая
конечные размеры молекул, мы приближенно
принимаем во внимание действие сил
взаимного отталкивания между ними.
Такая
модель газа, принятая Ван-дер-Ваальсом,
позволила ему получить
уравнение состояния реального газа
более совершенное, чем уравнение
Клапейрона — Менделеева.

1. Поправка b.

— связана с собственным объемом
молекул,

— ее размерность м

/моль.

Каждая молекула реального газа имеет
объем

.

Поэтому молекулы газа движутся в сосуде
менее свободно, чем «точечные» молекулы
идеального газа.

Ван-дер-Ваальс учел собственный
объем молекул газа путем замены в
уравнении Клапейрона — Менделеева

полного
объема

сосуда, занимаемого молем газа, на
«свободный» объем:

,

(6.8)

где b —
поправка Ван-дер-Ваальса, зависящая
от собственного объема


молекулы – определяет ту часть
объема , которая недоступна для движения
молекул вследствие их конечных размеров.

Эта константа равна учетверенному
объему молекул.

Докажем, что поправка b
в 4 раза больше собственного
объема всех N_А молекул
одного моля газа:

(6.9)

Для
доказательства рассмотрим
сферу радиуса
d,
центр которой
совпадает с центром произвольной
молекулы.

• Внутри этой сферы
  не могут находиться центры других
  молекул.

• Объем
  этой сферы является «запрещенным»
  объемом
  
  
  для центров
  всех молекул, соударяющихся с данной.

• Поскольку
  молекулы сталкиваются попарно
  (вероятность столкновений трех и более
  молекул мала), приведенное рассуждение
  справедливо для любой пары молекул.
  Таким образом, в расчете на каждую из
  молекул газа недоступным будет объем,
  равный четырем объёмам одной молекулы,
  а для всех молекул – объем равный
  учетверенному суммарному объему
  молекул. Он в восемь раз больше
  собственного объема молекулы.

Поправка Ван-дер-Ваальса b
представляет собой «запрещенный»
объем, приходящийся на все N_A
молекул, т.е.

,

что и требовалось доказать.

Из формулы (6.9) следует: значение
b зависит от
эффективного диаметра молекул, т. е. от
химической природы газа.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

  08.03.2015550.91 Кб49.doc