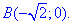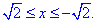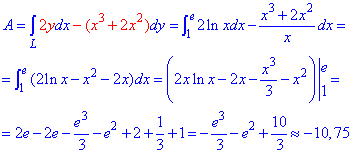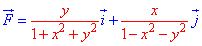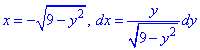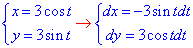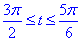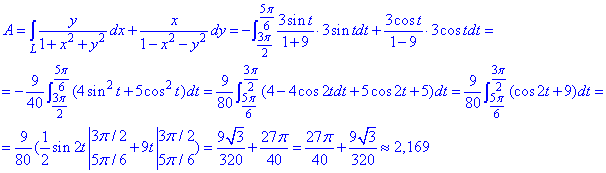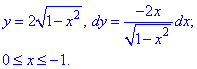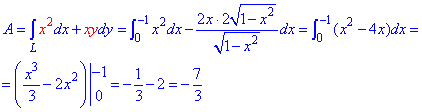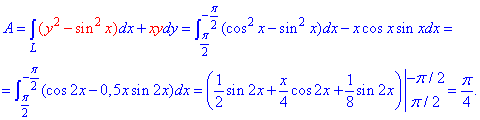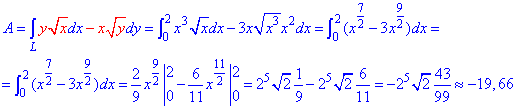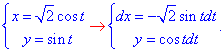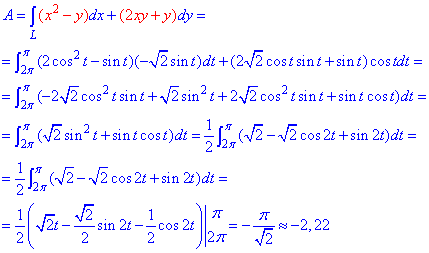Как найти работу по перемещению материальной точки - AvtoShod.ru

Продолжаем предыдущий урок на тему «Применение криволинейных интегралов 2 рода».
Готовые ответы задач на работу силового поля помогут студентам выучить тему, и научат быстро находить нужные интегралы.

Пример 4.2 Найти работу силы F (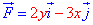) при перемещении точки вдоль кривой C:
x²/4+y²/9=1 от точки A(- 2;0) к точке B(0;3).
Решение: Запишем уравнение заданного эллипса в параметрическом виде: x=2*cos(t), y=3*sin(t).

Наведем графически траекторию материальной точки вдоль эллипса.

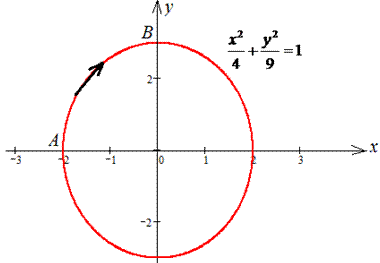
Тогда дифференциал переменных по параметру будет равен dx=-2*sin(t)dt, dy=3*cos(t)dt .
При этом пределы интегрирования ограничатся точками Pi и Pi/2.
Найдем работу силы F по кривой C через криволинейный интеграл ІІ рода :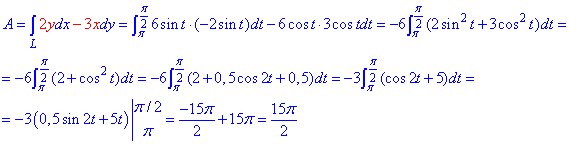
Пересмотрите внимательно формулы интегрирования синуса и косинуса, и понижения степени для таких функций.

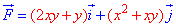
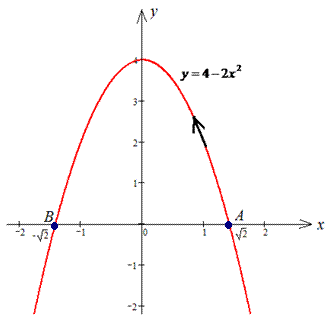
Пример 4.4 Найти работу силы по перемещению точки вдоль кривой C:
y=4-2x^2 от точки 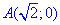к точке
Решение: Построим траекторию движения материальной точки вдоль параболы L: y=4-2x².

Вычисляем дифференциал дуги y=4-2x², dy=-4x*dx и из условия выписиваем пределы интегрирования
Работа силы F находим с помощью криволинейного интеграла второго рода

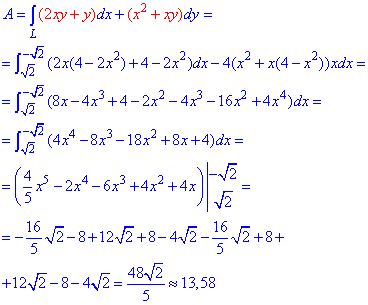
Интегрирование занимает не мало времени и при превращениях можно допустить ошибку, поэтому будьте внимательные в этих местах.

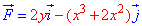
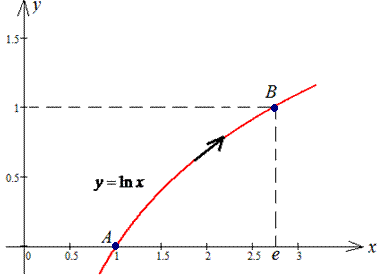
Пример 4.11 Найти работу силы при перемещении вдоль кривой C:
y=ln(x) от точки A(1;0) к точке B(e;1).
Решение: Траектория материальной точки вдоль логарифма имеет вид
Находим дифференциал логарифма y=ln (x), dy=dx/x.
Пределы интегрирования изменяются от единицы к экспоненте.
Работа силы F с помощью криволинейного интеграла ІІ рода примет значение:

Здесь для логарифма применили правило интегрирования частями (u*dv).

Пример 4.13 Найти работу силы F при перемещении вдоль кривой C:
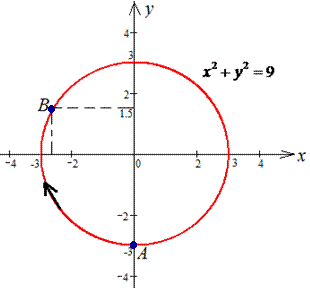
x²+y²=9 от точки A (0;-3) к точке 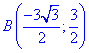, где F задана формулой

Решение: Построим траекторию движения материальной точки вдоль круга радиусом 3.

Чтобы не выражать две функции (верхняя и нижняя кривая круга) запишем зависимость x(y) и вычислим дифференциал дуги

При этом ордината изменяется от — 3 до 3/2.
Применяя криволинейный интеграл ІІ рода находим роботу силы F при перемещении вдоль круга:

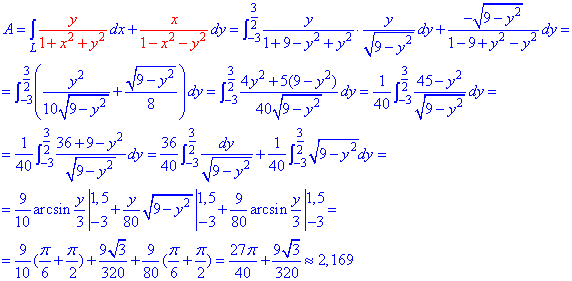
Бороться с корнями во время интегрирования непросто, о чем свидетельствует приведенные вычисления.
Намного проще вычислять интеграл при переходе к полярной системе координат.
Дальше наведем методику интегрирования:

ІІ — способ:
Параметризуэм заданный круг:

Учитывая, что во время движения от точки A(0;-3) к точке 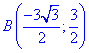угол изменяется от

Вычисляем искомый криволинейный интеграл ІІ рода :
В плане вычислений второй метод более легкий, поэтому для круговых и эллиптических форм кривой при симметричном вхождении x, y в уравнение силы рекомендуем переходить к полярной системе координат.

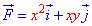
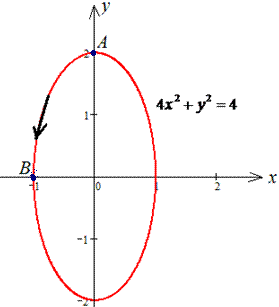
Пример 4.15 Найти работу силы при перемещении вдоль кривой C:
4x²+y²=4 от точки A(0;2) к точке B (-1;0).
Решение: Траектория движения материальной точки по эллипсу приведена ниже

Записываем верхнюю дугу эллипса и ее производную.

Пределы интегрирования изменяются от 0 к -1
Работа силы F через криволинейный интеграл второга рода выражается зависимостью:

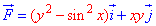
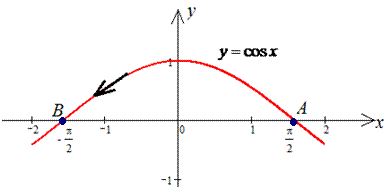
Пример 4.18 Найти работу силы по перемещению материальной точки вдоль кривой C:
y=cos(x) от точки A(Pi/2;0) к точке B(-Pi/2;0).
Решение: Изобразим траекторию материальной точки вдоль косинуса

Построим дифференциал кривой y=cos(x), dy=-sin(x)*dx.
Он нужен для возведения криволинейного интегралу ІІ рода к определенному.
Находим работу силы F по перемещении вдоль контура интегрированием

Для понижения под интегралом степеней косинуса и синуса применили известные тригонометрические формулы.

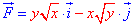
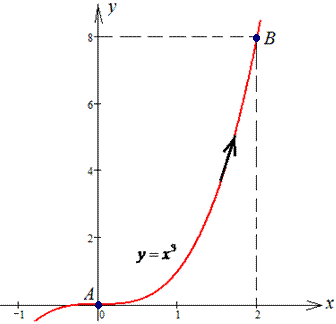
Пример 4.21 Найти работу силы при перемещении вдоль кривой C:
y=x³ от точки A(0;0) к точке B(2;8).
Решение: Построим траекторию материальной точки вдоль кривой y=x³.

Вычисляем дифференциал дуги dy=3x²dx.
Пределы интегрирования приведены на рисунку и в условии.
Работа силы F находим с помощью криволинейного интегралу ІІ рода:

Превращаем все к показательной форме и интегрируем.

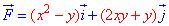
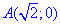
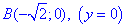
Пример 4.23 Найти работу силы при перемещении вдоль кривой C: x²+2y²=2 от точки к точке
Решение: За инструкцией строим траекторию материальной точки вдоль эллипса: x²+2y²=2.

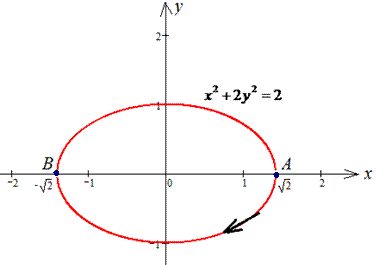
Для простоты вычислений криволинейного интеграла ІІ рода параметризуэм эллипс:

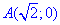
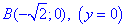
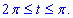
Учитывая, что от точки к точке угол изменяется в пределах переходим к интегрированию

Понижаем степени и интегрируем.

Пример 4.24 Найти работу силы 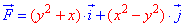при перемещении вдоль кривой C:
y=1-|x| от точки A(-1;0) к точке B(2;- 1).
Решение: Наведем траекторию материальной точки вдоль модуль функции.

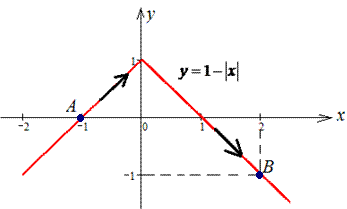
Как ни хотелось встретить задания с разбитием кривой на два интервала, однако одно Пример содержит такое условие. Разделим на две части: y=1+x, тогда пределы равны [-1;0] и дифференциал dy=dx;
На втором участке y=1-x имеем [0;2] и dy=-dx.
Вычисляем работу силы F, потраченную на перемещении точки вдоль модуль функции:

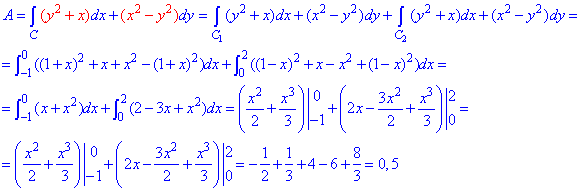
На этом ознакомление из такого сорта примерами завершено.
Больше готовых ответов из курса высшей математики ищите на страницах сайта.

Источник

Назначение. Онлайн калькулятор предназначен для нахождения работы силы F при перемещении вдоль дуги линии L.

Решение онлайн
Видеоинструкция

Криволинейные и поверхностные интегралы второго рода

Рассмотрим многообразие σ. Пусть τ(x,y,z)— единичный вектор касательной к σ, если σ — кривая, а n(x,y,z)— единичный вектор нормали к σ, если σ — поверхность в R³. Введём векторы dl=τ·dl и dS=n·dS, где dl и dS — длина и площадь соответствующего участка кривой или поверхности. Будем считать, что dσ=dl, если σ — кривая, и dσ=dS, если σ — поверхность. Назовём dσ ориентированной мерой соответствующего участка кривой или поверхности.

Определение. Пусть заданы ориентированное непрерывное кусочно-гладкое многообразие σ и на σ – вектор-функция F(x,y,z)=P(x,y,z)i+Q(x,y,z)+R(x,y,z). Разобьем многообразие на части многообразиями меньшей размерности (кривую – точками, поверхность –кривыми), внутри каждого полученного элементарного многообразия выберем по точке M₀(x₀,y₀,z₀), M₁(x₁,y₁,z₁), … ,M_n(x_n,y_n,z_n). Посчитаем значения F(x_i,y_i,z_i), i=1,2,…,n вектор-функции в этих точках,умножим скалярно эти значения на ориентированную меру dσ_i данного элементарного многообразия (ориентированные длину или площадь соответствующего участка многообразия) и просуммируем. Предел полученных сумм если онсуществует, не зависит от способа разбиения многообразия на части и выбора точек внутри каждого элементарного многообразия, при условии, что диаметр элементарного участка стремится к нулю, называется интегралом по многообразию (криволинейным интегралом, если σ -кривая и поверхностным, если σ — поверхность) второго рода, интеграломвдоль ориентированного многообразия, или интегралом от вектора F вдоль σ, и обозначается в общем случае, в случаях криволинейного и поверхностного интегралов соответственно.

Заметим, что если F(x,y,z) — сила, то — работа этой силы по перемещению материальной точки вдоль кривой, если F(x,y,z) — стационарное (не зависящее от времени) поле скоростей текущей жидкости, то — количество жидкости, протекающей через поверхность S в единицу времени (поток вектора через поверхность).

Если кривая задана параметрически или, что то же самое, в векторной форме,

то

и для криволинейного интеграла второго рода имеем

Так как dS=n·dS=(cosα, cosβ, cosγ), где cosα, cosβ, cosγ — направляющие косинусы единичного вектора нормали n и cosαdS=dydz, cosβdS=dxdz, cosγdS=dxdy, то для поверхностного интеграла второго рода получаем

Если поверхность задана параметрически или, что тоже самое, в векторной форме

r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k, (u,v)∈D

то

где — якобианы (определители матриц Якоби, или, что то же самое, матриц производных) вектор-функций соответственно.

Если поверхность S может быть задана одновременно уравнениями то поверхностный интеграл второго рода вычисляется по формуле

где D₁, D₂, D₃ — проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно и знак “+” берётся, если угол между вектором нормали и осью, вдоль которой ведётся проектирование, острый, а знак “–“, если этот угол тупой.

Свойства криволинейного и поверхностного интегралов второго рода

Отметим некоторые свойства криволинейного и поверхностного интегралов второго рода.

Теорема 1. Криволинейный и поверхностный интегралы 2-го рода зависят от ориентации кривой и поверхности, точнее

.

Теорема 2. Пусть σ=σ₁∪σ₂ и размерность пересечения dlim(σ₁∩σ₂)=n-1. Тогда

Доказательство. Включив в число многообразий разбиения в определении интеграла по многообразию второго рода общую границу σ₁ с σ₂ получаем требуемое.

Пример №1. Найти работу силы F при перемещении вдоль дуги линии L от точки M₀ до точки M₁.

F=x²yi+yj;, L: отрезок M₀M₁

M₀(-1;3), M₀(0;1)

Решение.

Находим уравнение прямой вдоль отрезка M₀M₁.

или y=-2x+1

dy=-2dx

Пределы изменения x: [-1; 0]

Пример №2. Вычислить вдоль кривой , если t∈[0;π]

Имеем

Пример №3. Вычислить поток вектора f(x,y,z)=(yz,xz,xy)^T через часть плоскости x+y+z=a лежащую в первом октанте.

Поток вектора через поверхность равен поверхностному интегралу второго рода Поверхность однозначно проектируется на все три координатные плоскости. Поэтому интеграл может быть вычислен с помощью проектирования на них. Тогда

где S₁, S₂, S₃ — проекции поверхности S на координатные плоскости Y0Z, X0Z, X0Y соответственно. Посчитаем первый из них. Имеем Остальные два интеграла считаются аналогично и также равны Поэтому поток вектора через поверхность равен Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями. Поэтому поток вектора через поверхность равен Знаки плюс перед интегралами взяты потому, что вектор нормали к поверхности составляет острые углы со всеми координатными осями.

Источник

— 9
—

Механическая работа и мощность

Если на тело
действует сила, то эта сила совершает
работу по перемещению этого тела. Прежде
чем дать определение работе при
криволинейном движении материальной
точки, рассмотрим частные случаи:

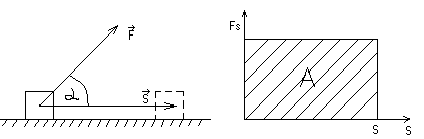
Сила
постоянная
,
движение прямолинейное.

В этом случае
механическая работа A
равна:

A =
F s cos=,

или
A
= Fcos×
s = F_S×
s ,

где F_S– проекция
силы

на перемещение. В данном случае
F_s=const,
и геометрический смысл работы A
– это площадь прямоугольника,
построенного в координатах F_S,
,
s .

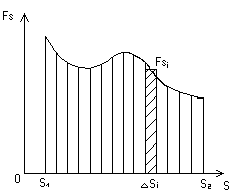
Движение
прямолинейное, сила переменная, т.е.
F_Sconst.

Построим график
проекции силы на направление перемещения
F_S
как функции перемещения s.
Полное перемещение представим как сумму
n
малых перемещений
.
Для малого i
-ого
перемещения

работа равна

или площади заштрихованной трапеции
на рисунке.

Полная
механическая работа по перемещению из
точки 1
в точку 2
будет равна:

Величина, стоящая
под интегралом будет представлять
элементарную работу по бесконечно
малому перемещению
:

– элементарная
работа.

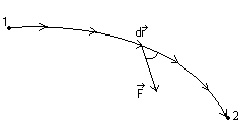
Движение
криволинейное, сила

переменная.

Разбиваем
траекторию движения материальной точки
на бесконечно малые перемещения

и работу силы

по перемещению материальной точки из
точки 1
в точку 2
определяем как криволинейный интеграл:

–работа при
криволинейном движении.

Пример 1: Работа
силы тяжести

при криволинейном движении материальной
точки.

Далее

как постоянную величину можно вынести
за знак интеграла, а интеграл
согласно
рисунку будет представлять полное
перемещение
.

Если обозначить
высоту точки 1
от поверхности Земли через
,
а высоту точки 2
через
,
то

Мы видим, что в
данном случае работа определяется
положением материальной точки в начальный
и конечный момент времени и не зависит
от формы траектории или пути. Работа
силы тяжести по замкнутому пути равна
нулю:
.

Силы, работа
которых на замкнутом пути равна нулю,
называется
консервативными.

Пример 2:
Работа силы трения.

Это пример
неконсервативной силы. Чтобы показать
это достаточно рассмотреть элементарную
работу силы трения:

т.е. работа силы
трения всегда отрицательная величина
и на замкнутом пути не может быть равной
нулю. Работа, совершаемая в единицу
времени, называется мощностью.
Если за время

совершается работа
,
то мощность равна

–механическая
мощность.

Взяв

в виде

получим для
мощности выражение:

В СИ единицей
работы является джоуль:
=
1 Дж = 1 Н1
м, а единицей мощности является ватт: 1
Вт = 1 Дж/с.

Механическая энергия.

Энергия является
общей количественной мерой движения
взаимодействия всех видов материи.
Энергия не исчезает и не возникает из
нечего: она лишь может переходить из
одной формы в другую. Понятие энергии
связывает воедино все явления в природе.
В соответствии с различными формами
движения материи рассматривают разные
виды энергии – механическую, внутреннюю,
электромагнитную, ядерную и др.

Понятия энергии
и работы тесно связаны друг с другом.
Известно, что работа совершается за
счет запаса энергии и, наоборот, совершая
работу, можно увеличить запас энергии
в каком-либо устройстве. Другими словами
работа – это количественная мера
изменения энергии:

Энергия также как
и работа в СИ измеряется в джоулях: [E]=1
Дж.

Механическая
энергия бывает двух видов – кинетическая
и потенциальная.

Кинетическая
энергия
(или энергия
движения) определяется массами и
скоростями рассматриваемых тел.
Рассмотрим материальную точку, движущуюся
под действием силы
.
Работа этой силы увеличивает кинетическую
энергию материальной точки
.
Вычислим в этом случае малое приращение
(дифференциал) кинетической энергии:

При вычислении

использован
второй закон Ньютона
,
а также

— модуль скорости материальной точки.
Тогда

можно представить в виде:

—

— кинетическая
энергия движущейся материальной точки.

Умножив и разделив
это выражение на
,
и учитывая, что
,
получим

—

— связь
между импульсом и кинетической энергией
движущейся материальной точки.

Потенциальная
энергия
(или
энергия положения тел) определяется
действием на тело консервативных сил
и зависит только от положения тела.

Мы видели, что
работу силы тяжести

при криволинейном движении материальной
точки

можно представить в виде разности
значений функции
,
взятых в точке 1
и в точке
2:

Оказывается, что
всегда, когда силы консервативны, работу
этих сил на пути 12
можно представить в виде:

Функция
,
которая
зависит только от положения тела –
называется потенциальной энергией.

Тогда для
элементарной работы получим

–работа равна
убыли потенциальной энергии.

Иначе можно
сказать, что работа совершается за счёт
запаса потенциальной энергии.

Величину
,
равную сумме кинетической и потенциальной
энергий частицы, называют полной
механической энергией тела:

–полная
механическая энергия тела.

В заключении
заметим, что используя второй закон
Ньютона
,
дифференциал кинетической энергии

можно представить в виде:

Дифференциал
потенциальной энергии
,
как указывали выше, равен:

Таким образом,
если сила

– консервативная сила и отсутствуют
другие внешние силы, то
,
т.е. в этом случае полная механическая
энергия тела сохраняется.

Соседние файлы в папке Лекции. html

Источник

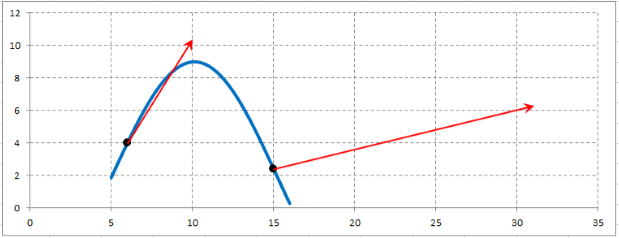
На материальную точку $Tleft(x,yright)$ действует переменная сила $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$. Под действием этой силы материальная точка перемещается на отрезке $left[6;15right]$ от точки $M$ до точки $N$ вдоль синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$. Найти работу переменной силы $overline{F}$ на криволинейном пути от точки $M$ до точки $N$. Построить графическое изображение пути от точки $M$ до точки $N$, а также векторы переменной сили $overline{F}$ в этих точках.

Выполняем графическое изображение синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$ на отрезке $left[6;15right]$.

Находим значения синусоиды в точках $x_{M} =6$ и $x_{N} =15$:

$y_{M} =7cdot sin left(0,31cdot 6-1,57right)+2approx 4$;
$y_{N} =7cdot sin left(0,31cdot 15-1,57right)+2approx 2,43$.

Выполняем графические изображения векторов переменной силы $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$, значения которого в точках $M$ и $N$ соответственно равны $overline{F}_{M} =left(3cdot 6-2cdot 4right)cdot overline{i}+4cdot 4cdot overline{j}=10cdot overline{i}+16cdot overline{j}$ и $bar{F}_{N} =left(3cdot 15-2cdot 2,43right)cdot overline{i}+4cdot 2,43cdot overline{j}=40,14cdot overline{i}+9,72cdot overline{j}$.

Работу данной силы на данном участке кривой $MN$ вычисляем по формуле $A=int limits _{a}^{b}Pleft(x,yleft(xright)right)cdot dx +int limits _{a}^{b}Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.

Здесь участок кривой $MN$ задан на отрезке $left[x_{M} ,; x_{N} right]$, поэтому формула для работы приобретает вид: $A=int limits _{x_{M} }^{x_{N} }Pleft(x,yleft(xright)right)cdot dx +int limits _{x_{M} }^{x_{N} }Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.

В этой формуле первый интеграл дает значение работы силы $F$ вдоль оси $Ox$, второй интеграл — вдоль оси $Oy$.

Находим работу силы вдоль оси $Ox$: $A_{x} =int limits _{6}^{15}Pleft(x,yleft(xright)right)cdot dx $.

Согласно условию задачи имеем:

[Pleft(x,yright)=3cdot x-2cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2.]

Поэтому:

[Pleft(x,yleft(xright)right)=3cdot x-2cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=]

[=3cdot x-14cdot sin left(0,31cdot x-1,57right)-4.]

Далее получаем:

[A_{x} =int limits _{6}^{15}left(3cdot x-14cdot sin left(0,31cdot x-1,57right)-4right)cdot dx =]

[=int limits _{6}^{15}3cdot xcdot dx +int limits _{6}^{15}left(-14cdot sin left(0,31cdot x-1,57right)right)cdot dx +int limits _{6}^{15}left(-4right)cdot dx =]

[=3cdot int limits _{6}^{15}xcdot dx -14cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dx -4cdot int limits _{6}^{15}dx =]

[=3cdot left[frac{x^{2} }{2} right]_{6}^{15} -14cdot left[-frac{1}{0,31} cdot cos left(0,31cdot x-1,57right)right]_{6}^{15} -4cdot left[xright]_{6}^{15} =]

[=1,5cdot left(15^{2} -6^{2} right)+frac{14}{0,31} cdot left(cos left(0,31cdot 15-1,57right)-cos left(0,31cdot 6-1,57right)right)-]

[-4cdot left(15-6right)=135,15.]

Находим работу силы вдоль оси $Oy$: $A_{y} =int limits _{6}^{15}Qleft(x,yleft(xright)right)cdot y’cdot dx $.

Согласно условию задачи имеем:

[Qleft(x,yright)=4cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2. ]

Поэтому:

[Qleft(x,yleft(xright)right)=4cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=28cdot sin left(0,31cdot x-1,57right)+8;]

[y’=7cdot 0,31cdot cos left(0,31cdot x-1,57right)=2,17cdot cos left(0,31cdot x-1,57right).]

Далее получаем:

[A_{y} =int limits _{6}^{15}left(28cdot sin left(0,31cdot x-1,57right)+8right)cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]

[=int limits _{6}^{15}28cdot 2,17cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]

[+int limits _{6}^{15}8cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]

[=int limits _{6}^{15}60,76cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]

[+int limits _{6}^{15}17,36cdot cos left(0,31cdot x-1,57right)cdot dx .]

Вычисляем первый интеграл $I_{1} $:

[I_{1} =60,76cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx =]

[=60,76cdot frac{1}{0,31} cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dleft(sin left(0,31cdot x-1,57right)right) =]

[=196cdot left[frac{sin ^{2} left(0,31cdot x-1,57right)}{2} right]_{6}^{15} =]

[=98cdot left(sin ^{2} left(0,31cdot 15-1,57right)-sin ^{2} left(0,31cdot 6-1,57right)right)approx -7,64.]

Вычисляем второй интеграл $I_{2} $:

[I_{2} =17,36cdot int limits _{6}^{15}cos left(0,31cdot x-1,57right)cdot dx =]

[=17,36cdot frac{1}{0,31} cdot left[sin left(0,31cdot x-1,57right)right]_{6}^{15} =]

[=56cdot left(sin left(0,31cdot 15-1,57right)-sin left(0,31cdot 6-1,57right)right)approx -12,57.]

Работа силы вдоль оси $Oy$:

[A_{y} =I_{1} +I_{2} =-7,64-12,57=-20,21.]

Общая работа силы при перемещении вдоль кривой:

[A=A_{x} +A_{y} =135,15-20,21=114,94.]

Источник

Сразу хочу сказать, что здесь никакой воды про работа, и только нужная информация. Для того чтобы лучше понимать что такое
работа, механическая работа , настоятельно рекомендую прочитать все из категории Физические основы механики.

Изменение механического движения и энергии тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы, совершаемой силой.

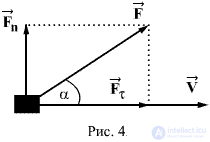
Механическая
работа — это физическая величина — скалярная количественная мера действия силы (равнодействующей сил) на тело или сил на систему тел. Зависит от численной величины и направления силы (сил) и от перемещения тела (системы тел).

При постоянной силе и прямолинейном движении материальной точки, работа рассчитывается как произведение величины силы на перемещение и на косинус угла между векторами перемещения и силы: . В более сложных случаях (непостоянная сила, криволинейное движение) это соотношение применимо к малому промежутку времени, а для вычисления полной работы необходимо суммирование по всем таким промежуткам.

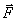
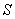
Если рассматриваемая сила постоянна,а тело, к которому она приложена, движется поступательно и прямолинейно, то работой, совершаемой силой при прохождении телом пути , называют величину

(4.1)

где а — угол между силой 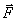и направлением движения тела.

Работа — скалярная величина. Если вектор силы и вектор перемещений образуют острый угол т.е. , то, если , то , т.е. сила, действующая перпендикулярно к перемещению тела, работы не совершает.

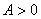
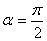
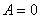
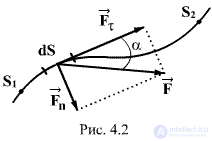
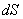
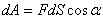В общем случае тело может двигаться произвольным, достаточно сложным образом (рис.4.2). Выделим элементарный участок пути , на котором силу можно считать постоянной и перемещение прямолинейным. Элементарная работа на этом участке равна

(4.2)

Полная работа на пути определяется интегралом

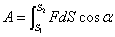(4.3)

Определение работы

По определению, «элементарная» (совершаемая за бесконечно малое время) работа — скалярное произведение действующей на материальную точку силы на перемещение , то есть

Работа за конечный промежуток времени — интеграл элементарной работы:

Если имеется система материальных точек, выполняется суммирование по всем точкам. При наличии нескольких сил их работа определяется как работа равнодействующей (векторной суммы) этих сил.

Обозначения, размерность

Работа обычно обозначается заглавной буквой (от нем. Arbeit — работа, труд) или заглавной буквой (от англ. work — работа, труд).

Единицей измерения (размерностью) работы в Международной системе единиц (СИ) является джоуль, в СГС — эрг. При этом

1 Дж = 1 кг·м²/с² = 1 Н·м;

1 эрг = 1 г·см²/с² = 1 дин·см;

1 эрг = 10⁻⁷ Дж.

Вычисление работы

Случай одной материальной точки

При прямолинейном движении материальной точки и постоянном значении приложенной к ней силы, работа (этой силы) равна произведению проекции вектора силы на направление движения и длины вектора перемещения, совершенного точкой:

Здесь «» обозначает скалярное произведение, — вектор перемещения.

Если направление приложенной силы ортогонально перемещению тела или перемещение равно нулю, то работа этой силы равна нулю.

В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки:

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из перемещений , если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат, интеграл определяется следующим образом:

где и — радиус-векторы начального и конечного положения тела . Об этом говорит сайт https://intellect.icu . Например, если движение происходит в плоскости , а и (, — орты), то последний интеграл обретет вид , где производная берется для кривой , по которой движется точка.

Если сила является консервативной (потенциальной), результат вычисления работы будет зависеть только от начального и финального положения точки, но не от траектории, по которой она перемещалась.

Случай системы точек или тела[править | править код]

Работа сил по перемещению системы из материальных точек определяется как сумма работ этих сил по перемещению каждой точки (работы, совершенные над каждой точкой системы, суммируются в работу этих сил над системой):

Если тело не является системой дискретных точек, его можно разбить (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых можно считать материальной точкой, и вычислить работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл:

где — работа по перемещению бесконечно малого фрагмента объема тела , локализованного около координаты (в системе отсчета тела), от начального до финального положения, (Н/м³) — плотность действующей силы, а интегрирование проводится по всему объему тела.

Эти формулы могут быть использованы как для вычисления работы конкретной силы или класса сил, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Работа и кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

С использованием второго закона Ньютона, позволяющего выразить силу через ускорение как (где — масса материальной точки), а также соотношений и , элементарная работа может быть переписана как

При интегрировании от начального до финального момента получится

где — кинетическая энергия. Для материальной точки она определяется как половина произведения массы этой точки на квадрат ее скорости и выражается как . Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Работа и потенциальная энергия

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая, что

Здесь — оператор набла. Если все силы, действующие на частицу, консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий, соответствующих каждой силе, то

Данный результат известен как закон сохранения механической энергии и утверждает, что полная механическая энергия

в замкнутой системе, в которой действуют консервативные силы, является постоянной во времени. Этот закон широко используется при решении задач классической механики.

Работа силы в теоретической механике

Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, , и на нее действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее).

Величина , называется элементарной работой силы на участке и принимается за приближенное значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .

Таким образом, если обозначить эту работу буквой , то, в силу данного определения,

Если положение точки на траектории ее движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из последней формулы получится

Вау!! 😲 Ты еще не читал? Это зря!

Закон сохранения энергии
Механическая энергия
Теорема о кинетической энергии системы
Механические приложения криволинейных интегралов
Работа в термодинамике

Статью про работа я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое работа, механическая работа
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Физические основы механики

Источник

Криволинейные и поверхностные интегралы второго рода

Свойства криволинейного и поверхностного интегралов второго рода

Механическая работа и мощность

Механическая энергия.

Определение работы

Обозначения, размерность

Вычисление работы

Случай одной материальной точки

Случай системы точек или тела[править | править код]

Работа и кинетическая энергия

Работа и потенциальная энергия

Работа силы в теоретической механике

Вау!! 😲 Ты еще не читал? Это зря!

Не пропустите также: