Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
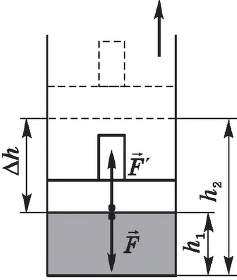
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
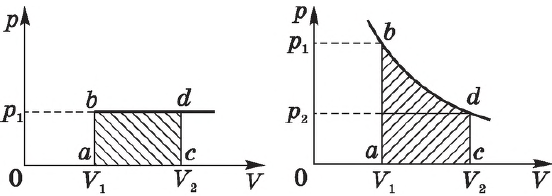
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
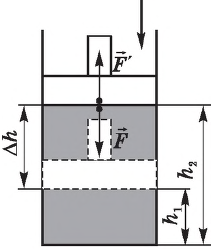
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
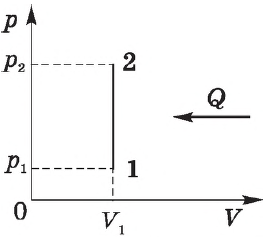
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
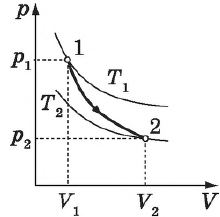
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
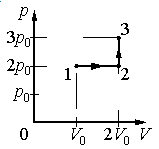
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.1k
Как найти работу газа
Работа газа осуществляется при изменении его объема. Именно при изменении объема газа приходят в движение узлы тепловых двигателей, будь то двигатель внутреннего сгорания или пуля в стволе ружья. При различных процессах работа газа вычисляется по-разному.

Вам понадобится
- — манометр;
- — термометр.
Инструкция
Если работа газа осуществляется при изобарном процессе (при постоянном давлении), то для того чтобы найти работу газа с помощью манометра, измерьте давление газа. После этого замерьте его объем перед выполнением работы и после. Найдите изменение объема газа, отняв от конечного значения начальное. После этого найдите произведение давления газа на изменение его объема. Это и будет работа газа при постоянном давлении A=p•ΔV.
Для идеального газа вычислить работу при постоянном давлении можно, применив уравнение Клапейрона-Менделеева. Найдите работу газа, умножив его массу на число 8,31 (универсальную газовую постоянную) и изменение температуры при выполнении работы. Результат поделите на молярную массу газа A=m•R•ΔT/M. При расчетах учитывайте то, что если работа выполняется газом (он расширяется), то она положительна. Если же работа выполняется над газом (его сжимают сторонние силы), то работа отрицательна.
Если работа выполняет при изотермическом расширении (когда температура постоянна), узнайте изменение объема газа и значение его температуры. Для того чтобы найти работу газа, умножьте его массу на число 8,31 (универсальную газовую постоянную) и температуру при выполнении работы. Результат поделите на молярную массу газа. Получившееся число умножьте на логарифм натуральный из отношения конечного и начального объемов газа A=m•R•T•ln(V2/V1)/M.
В общем случае, чтобы найти работу газа возьмите интеграл из функции давления по объему. Границы интеграла – от начального до конечного объема ∫pdV. Если есть график газового процесса в координатах (V,p), как правило, он представляет собой прямую линию, найдите площадь трапеции ограниченной по бокам линиями перпендикулярными оси Vв точках V1 и V2, снизу осью V, а сверху графиком функции. В более сложных случаях ищется площадь криволинейной трапеции.
Полезный совет
Если объем газа не изменяется, работа им не выполняется.
Источники:
- как изменяется объем газа
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Работа идеального газа при различных процессах.
Применение
1-го начала термодинамики к изопроцессам
и адиабатическому процессу.
Среди равновесных
процессов, происходящих с
термодинамическими системами, выделяются
изопроцессы, при которых один из основных
параметров состояния сохраняется
постоянным.
Изохорный процесс
(V=const)
При таком процессе
газ не совершает работы над внешними
телами, т.е A=pdV=0.
Тогда, из 1-го начала
термодинамики следует, что вся теплота,
переданная телу, идет на увеличение его
внутренней энергии: Q=dU.
Зная, что dUm=CvdT.
Тогда для произвольной
массы газа получим Q=
dU=mM*
CvdT.
Изобарный процесс
(p=const).
При
этом процессе работа газа при увеличении
объема от V1
до V2
равна A=
pdV(от
V1
до V2)=p(V2-V1)
и определяется площадью фигуры,
ограниченной осью абсцисс, кривой p=f(V)
и значениями V1,V2.
Если вспомнить ур-е Менделеева-Клапейрона
для выбранных нами 2-х состояний, то
pV1=mM*RT1,
pV2=mM*RT2,
откуда
V1—
V2=
mM*Rp(T2—
T1).
Тогда
выражение для работы изобарного
расширения примет вид A=
mM*R(T2—
T1)(1.1).
При
изобарном процессе при сообщении газу
массой m
количества теплоты
Q=mM*CpdT
его внутренняя энергия возрастает на
величину dU=mM*CvdT.
При этом газ совершает работу, определяемую
выражением (1.1).
Изотермический
процесс (T=const).
Этот
процесс описывается законом Бойля-Мариотта:
pV=const.
Найдем
работу изотермического расширения
газа: A=
pdV(от
V1
до V2)=
m/M*RTln(V2/V1)=m/M*RTln(p1/p2).
Т.к
при Т=const
внутренняя энергия идеального газа не
изменяется: dU=m/M*
CvdT=0,
то из 1-го начала термодинамики (Q=dU+A)
следует, что для изотермического процесса
Q=A,
т.е все количество теплоты, сообщаемое
газу, расходуется на совершение им
работы против внешних сил:
Q=A=m/M*RTln(p1/p2)=m/M*RTln(V2
/V1).
Следовательно,
чтобы при расширении газа температура
не понижалась, к газу в течение
изотермического процесса необходимо
подводить количество теплоты, эквивалентное
внешней работе расширения.
Адиабатический
процесс.
АП
— это процесс, при котором отсутствует
теплообмен (Q=0)
между системой и окружающей средой. К
адиабатическим можно отнести все
быстропротекающие процессы. Из 1-го
начала термодинамики (Q=dU+A)
для адиабатического процесса следует,
что A=
-dU,
т.е внешняя работа совершается за счет
изменения внутренней энергии системы.
Т.о, pdV=
— m/M*
CvdT(1).
Продифференцировав
ур-е состояния для идеального газа
,pV=m/M*RT,
получим
PdV
+ Vdp=m/M*RdT.(2)
Исключим из ур-я
(1) и (2) температуру T:
(pdV+Vdp)/(pdV)=
— R/Cv=
-( Cp-Cv)/
Cv.
Разделив переменные
и учитывая, что Cp/Cv=,
найдем dp/p=
— dV/V.
Интегрируя
это ур-е в пределах от p1
до p2
и соответственно от V1
до V2,
а затем, потенцируя, придем к выражению
p2/p1=(V1/V2),
или p1(V1)
= p2(V2).Так
как состояния 1 и 2 выбраны произвольно,
то можно записать
pV=const(ур-е
адиабатического процесса или ур-е
Пуассона).Здесь
— показатель адиабаты (или коэффициент
Пуассона), =(i+2)/i.
Вычислим
работу, совершаемую газом в адиабатическом
процессе: A=
-m/M*
CvdT.
Если
газ адиабатически расширяется от объема
V1
до V2,
то его температура уменьшается от T1
до T2
и работа расширения идеального газа
A=
— m/M*CvdT=m/M*
Cv(T1-T2).
Изохорный,
изобарный, изотермический и адиабатический
процессы имеют одну особенность – они
происходят при постоянной теплоемкости.
Эквиваленты
теплоты и работы.
Обмен
энергией между термодинамической
системой и внешними телами может
осуществляться 2мя качественно различными
способами: путем совершения работы и
путем теплообмена. В отсутствии внешних
полей работа совершается при изменении
объема или формы системы. Работа A’,
совершаемая внешнми телами над системой
численно равна и противоположна по
знаку работе, совершаемой самой системой
Удельной
теплоемкостью вещества
– величина, равная количеству теплоты,
необходимого для нагревания вещества
массой 1кг на 1К
(Дж/кгК):
c
= d’Q/mdT
d’Q = cmdT.
Молярная
теплоемкость
– величина, равная количеству теплоты,
необходимому для нагревания 1 моль
вещества на 1К:
C
= d’Q/dT,
C = c.
Она
определяется лишь числом степеней
свободы и не зависит от температуры.
Это утверждение справедливо для широкого
диапазона температур лишь для одноатомных
газов. Уже для двухатомных газов начинает
проявляться зависимость теплоемкости
от температуры путем уменьшения числа
степеней свободы. Различают теплоемкости
при постоянном давлении и постоянном
объеме. Запишем выражение первого начала
термодинамики для одного моля газа с
учетом теплоемкости:
CmdT
= dUm + pdVm
Если
газ нагревается при постоянном объеме,
то работа внешних сил будет равна 0.
Поэтому сообщаемая теплота идет только
на увеличение внутренней энергии тела,
т.е. молярная теплоемкость при постоянном
объеме равна изменению его температуры
на 1К.
Энергия
– универсальная мера различных форм
движения и взаимодействия. С различными
Фомами движения материи связывают
различные формы энергии: механическую,
тепловую, электромагнитную, ядерную и
др. В одних явлениях форма движения
материи не изменяется (например, горячее
тело нагревает холодное), в других –
переходит в иную форму (например, в
результате трения механическое движение
превращается в тепловое). Однако
существенно, что во всех случаях энергия,
отданная одним телом другому телу, равна
энергии, полученной последним телом
Второе начало
термодинамики. Обратимые и необратимые
процессы. Энтропия и ее вязь с вероятностью
состояния. Циклические процессы. Тепловые
машины и холодильники. Цикл Карно и КПД
тепловых машин. Термодинамические
потенциалы. Границы применимости второго
начала термодинамики
Второй
закон термодинамики.
Количество теплоты, полученное от
нагревателя, не может быть целиком
преобразовано в механическую работу
циклически действующей тепловой машиной.
Это и есть 2ой закон: в циклически
действующей тепловой машине невозможен
процесс, единственным результатом
которого было бы преобразование в
механическую работу всего количества
теплоты, полученного от источника
энергии – нагревателя. (by Кельвин
Copyright 1851). Второй закон связан с
необратимостью
процессов
в природе. Возможна другая формулировка:
невозможен процесс, единственным
результатом которого была бы передача
энергии путем теплообмена от холодного
тела к горячему. Второй закон имеет
вероятный характер. В отличие от закона
сохранения энергии, второй закон
применим лишь к системам, состоящим из
очень большого числа частиц. Для таких
систем необратимость
процессов
объясняется тем, что обратный переход
должен был бы привести систему в состояние
ничтожно малой вероятностью, практически
не отличимой от невозможности.
Самопроизвольные
процессы в изолированной системе всегда
проходят в направлении перехода от
маловероятного состояния в более
вероятное.
Обратимым
называется процесс, который может
осуществляться как в прямом, так и в
обратном направлении и при переходе в
начальное состояние состояние макросистемы
и внешней среды не меняется, в противном
случае называется необратимым. Все
реальные процессы являются необратимыми
и эта необратимость описывается еще
одним параметром, который называется
энтропией.
Энтропия.
Помимо внутренней энергии, которая
является только функциональной
составляющей термодинамической системы,
в термодинамике используется еще ряд
других функций, описывающих состояние
термодинамической системы. Особое место
среди них занимает энтропия. Пусть Q –
теплота, полученная термодинамической
системой в изотермическом процессе, а
T – температура, при которой произошла
эта передача теплоты. Величина Q/ T
называется приведенной теплотой.
Приведенное количество теплоты,
сообщаемое термодинамической системе
на бесконечно малом участке процесса
будет равно dQ / T. В термодинамике
доказывается, что в любом обратимом
процессе сумма приведенных количеств
теплоты, передаваемая системе на
бесконечно малых участках процесса
равна нулю. Математически это означает,
что dQ/T – есть полный дифференциал
некоторой функции, которая определяется
только состоянием системы и не зависит
от того, каким путем перешла система в
такое состояние. Функция, полученный
дифференциал которой равен dS= dQ/ T –
называется энтропией. Энтропия
определяется только состоянием
термодинамической системы и не зависит
от способа перехода системы в это
состояние. S – энтропия. Для обратимых
процессов delta S = 0. Для необратимых delta S
> 0 – неравенство Клаудио. Неравенство
Клаудио справедливо только для замкнутой
системы. Только в замкнутой системе
процессы идут так, что энтропия возрастает.
Если система незамкнута и может
обмениваться теплотой с окружающей
средой, ее энтропия может вести себя
любым образом ; dQ = T dS ; При равновестном
переходе системы из одного состояния
в другое dQ = dU + dA ; delta S = (интеграл 1 – 2)
dQ / T = (интеграл) (dU + dA) / T. Физический смысл
имеет не сама энтропия, а разность
энтропий при переходе системы из одного
состояния в другое.
Связь
энтропии с вероятностью состояния
системы.
Более глубокий смысл энтропии скрывается
в статической физике. Энтропия связывается
с термодинамической вероятностью
состояния системы. Термодинамическая
вероятность состояния системы – это
число способов, которыми может быть
реализовано данное состояние
макроскопической системы. Иными словами
W – это число микросостояний, которые
реализовывают данные макросостояния.
Больцман
методами статистической физики показал,
что энтропия S системы и термодинамическая
вероятность связаны соотношением: S= k
ln (W) ; где k – постоянная Больцмана.
Термодинамическая вероятность W не
имеет с математической вероятностью
ничего общего. Из этого соотношения
видно, что энтропия может рассматриваться
как мера вероятности состояния
термодинамической системы, энтропия
является мерой неупорядоченной системы.
Чем больше число микросостояний,
реализующих данное макросостояние, тем
больше ее энтропия.
Понятие
энтропии введено Клазиусом.
Для выяснения физического смысла этого
понятия рассматривают отношение теплоты
Q, полученной телом в изотермическом
процессе, к температуре T теплоотдающего
тела, называемое приведенным количеством
теплоты, равное в любом обратимом
круговом процессе 0. Выглядит так:
Q/T
= 0.
Функция
состояния, дифференциалом которой
является Q/T,
называется энтропией и обозначается
S. Из формулы следует, что для обратимых
процессов изменение энтропии S
= 0. Энтропия системы, совершающей
необратимый цикл, возрастает S
> 0. Это относится к замкнутым системам.
Если же система обменивается теплотой
с внешней средой, то ее энтропия может
вести себя любым образом. Предыдущие
соотношения можно представить в виде
неравенства Клаузиуса: S
0, т.е. энтропия замкнутой системы может
либо возрастать (в случае необратимости
процессов), либо оставаться постоянной
(в случае обратимых процеесов).
Используя
понятие энтропии и неравенство Клазиуса,
второе начало термодинамики можно
сформулировать как закон возрастания
энтропии замкнутой системы при необратимых
процессах: любой
необратимый процесс в замкнутой системе
происходит так, что энтропия системы
при этом возрастает. И более кратко: в
процессах, происходящих в замкнутой
системе, энтропия не убывает. Есть еще
две формулировки закона:
1.
(по Кельвину): невозможен круговой
процесс, единственным результатом
которого является превращение теплоты,
полученной от нагревателя, в эквивалентную
ей работу;
2.
(по Клазиусу): невозможен круговой
процесс, единственным результатом
которого является передача теплоты от
менее нагретого тела к более нагретого.
Цикл Карно.
Для
создания тепловой машины недостаточно
просто иметь нагретое тело (нагреватель),
требуется еще 2-е тело – холодильник.
Т.о, рабочее тело передает теплоту от
нагревателя к холодильнику и попутно
совершает полезную работу.
В
качестве рабочего тела Сади Карно выбрал
идеальный газ. Он рассмотрел следующий
процесс:
Кривые
1-2, 3-4 – изотермы, кривые 2-3,4-1 – адиабаты.
На
участке 1-2
газ получает теплоту Q1
от нагревателя и, расширяясь, совершает
работу (т.е расходует полученное Q1
на совершение работы). Q1=∆U+A1,
∆U=0,
т.к. T=const.
Q1=A1.
На участке 2-3:
газ совершает работу А2, которая равна
убыли внутренней энергии; температура
понижается. А2= — ∆U2
(температура понижается от Т1 до Т2).
На участке 3-4:
V
уменьшается, Т2=const.
Внешние силы совершают работу по сжатию
газа A3:
Q2=
-A3,
Q2=A′.
От системы отводится количество теплоты
Q2:
|Q2|=A3.
На участке 4-1:
V
уменьшается, T
увеличивается. A’4=∆U,
Q=∆U+A,
0= ∆U4
+ A4
=∆U4-A’4,
A’4=∆U
(внешние силы совершили работу, которая
пошла на увеличение внутренней энергии.
Для
изотерм
A=A1+A3=Q4-|Q2|.
Площадь под изотермой
3-4 меньше, чем под изотермой 1-2
|A’3|<|A1|,
Q1>Q2
газ получает от нагревателя больше
теплоты, чем отдает холодильнику.
За полный цикл:
∆U=0,
А=А1 – А’3 — ∆U2(=A2)
+ A’4,
∆U2=3/2*m
/ M*R(T2-T1).
A=Q1-|Q2| — 3/2*m/M*R(T2-T1) +
(-3/2*m/M*R(T1-T2))=Q1-|Q2|.
Коэффициентом
полезного действия тепловой машины
называется отношение полезной работы,
совершаемой за цикл, к количеству
теплоты, полученной системой. Выражается
в процентах. =(Q1-|Q2|)/Q1
* 100% (1), или =A/Q1
*100% (2). Эти формулы можно использовать
для любой тепловой машины.
Теорема Карно:
Q1/T1=|Q2|/T2
(для машины Карно). =(T1-T2)/T1
*100%.
КПД, определяемый
формулами (1) и (2) – наибольший возможный.
В реальных тепловых машинах КПД меньше.
Основываясь
на втором начале термодинамики, Карно
вывел теорему: из всех периодически
действующих тепловых машин, имеющих
одинаковые температуры нагревателей
(Т1) и холодильников (Т2), наибольшим КПД
обладают обратимые машины; при этом КПД
обратимых машин, работающих при одинаковых
температурах нагревателей (Т1) и
холодильников (Т2), равны друг другу и
не зависят от природы рабочего тела, а
определяются только температурами
нагревателя и холодильника.
Карно
теоретически проанализировал обратимый
наиболее экономичный цикл, состоящий
из двух изотерм и двух адиабат. Его
называют циклом Карно.
Порядок
цикла 1-2-3-4 по отношению к работе выглядит
так:
A12
= m/M RT1 lnV2/V1 = Q1
A23
= — m/M Cv(T2 – T1)
A34
= m/M RT2 lnV4/V3 = — Q2
A41
= — m/M Cv(T1 – T2) = — A23
Термический
КПД цикла Карно определяется так:
=
(Q1 – Q2)/Q1 или
= (T1 – T2)/T1.
Круговой
процесс (цикл) – процесс, при котором
система, пройдя через ряд состояний,
возвращается в исходное. На диаграмме
процессов цикл изображается замкнутой
прямой. Если за цикл совершается
положительная работа A =
pdV > 0, то он прямой, а если отрицательная
работа, то он обратный.
Цикл
применяется в тепловых двигателях –
периодически действующих двигателях,
совершающих работу за счет полученной
извне теплоты. Обратный цикл используется
в холодильных машинах – периодически
действующих установках, в которых за
счет работы внешних сил теплота
переносится к телу с более высокой
температурой. По 1-му началу термодинамики:
Q
= U
+ A = A;
= A/Q = 1 – Q2/Q1 (термич. КПД)
Реальные газы и
жидкости. Силы взаимодействия между
атомами и молекулами. Уравнение состояния
реальных газов Ван-дер-Ваальса.
Молекулярные силы в жидкостях. Поверхностно
натяжение. Капиллярные явления.
Реальные
газы. При
движении молекулы вдали от стенок
сосуда, в котором заключен газ, на нее
действуют силы притяжения соседних
молекул, но равнодействующая всех этих
сил в среднем равна нулю, т.к. молекулу
со всех сторон окружает в среднем
одинаковое число соседей. При приближении
некоторой молекулы к стенке сосуда все
остальные молекулы газа оказываются
по одну сторону от нее и равнодействующая
всех сил притяжения оказывается
направленной от стенки сосуда внутрь
газа. Это приводит к тому, что уменьшается
импульс, передаваемый молекулой стенке
сосуда. В результате давление газа на
стенки сосуда уменьшается по сравнению
с тем, каким оно было бы в отсутствие
сил притяжения между молекулами: p = p
идеального + delta p. Вместо уравнения
идеального газа получаем p + delta p = nkT ;
delta p = a/V(ст.2);
Где
a – постоянная, зависящая от вида газа.
Для одного моля газа получаем p+a/V(ст.2)
= R T / V ; Поправка: при любых давлениях,
объем газа не может стать равным нулю.
Уравнение Ван-дер-Ваальса:
(p
+ a / V (ст.2)) (V — b) = RT, где b – так называемый
“запрещенный объем”
Для
объяснения закономерностей поведения
реальных газов Ван дер Вальс предложил
модель,
более близкую к действительности, чем
модель идеального газа. Согласно этой
модели молекулы реального газа
уподобляются абсолютно упругим шарикам
с эффективным диаметром d, между молекулами
действуют силы взаимного притяжения.
Учет конечных размеров молекул приводит
к выводу, что они движутся в газе менее
свободно, чем в случае идеального газа.
Минимальный объем, до которого теоретически
можно сжать реальный газ, не может быть
меньше суммарного собственного объема
молекул. Собственно объем Vc, доступный
для движения молекул, тоже не равен
объему сосуда, в который заключен газ,
и его можно записать для одного моля
газа в виде: Vc = V0 – b, где b – поправка
Ван дер Вальса на собственный объем
молекул моля газа (м3/моль). С учетом всех
поправок Ван дер Вальс предложил
следующее уравнение состояния для моля
газа: (p + a/V02)(V0 – b) = RT.
В
классической статистической физике
выводится закон Больцмана о равномерном
распределении энергии по степеням
свободы молекул: для статической системы,
находящейся в состоянии термодинамического
равновесия, на каждую поступательную
и вращательную степени свободы
производится в среднем кинетическая
энергия, равная kT/2, а на каждую колебательную
степень своды – в среднем энергия,
равная kT. Колебательная степень обладает
вдвое большей энергией потому, что на
нее приходится не только кинетическая
энергия (как в случае поступательного
и вращательного движений), но и
потенциальная, причем средние значения
кинетической и потенциальной энергий
одинаковы. Таким образом, средняя энергия
молекулы:
= i/2kT, где i – сумма числа поступательных,
числа вращательных и удвоенного числа
колебательных степеней свободы молекулы:
i = iпост + iвращ + 2iколеб
При
высоких температурах изотерма реального
газа отличается от изотермы идеального
газа некоторым искажением ее формы,
оставаясь монотонно спадающей кривой.
При некоторой температуре Tк на изотерме
имеется лишь одна точка перегиба К. Эта
изотерма называется критической,
соответствующая ей температура Тк –
критической температурой. Точка перегиба
называется критической точкой.
Соответствующие этой точке объем и
давление также называются критическими.
Состояние с критическими параметрами
(p, V, T) называется также критическим
состоянием. При температурах, выше
критической, вещество существует только
в газообразном состоянии, и его нельзя
перевести в жидкое изотермическим
сжатием. Критическая точка характерна
тем, что при приближении к ней исчезает
различие между жидким и газообразным
состоянием вещества. В этом состоянии
молярные объемы жидкости и газа равны,
а поверхностное
натяжение жидкости исчезает.
Уравнение
Бернулли выглядит следующим образом:
v2/2
+ gh
+ p = const, где
p
– статическое давление (давление
жидкости на поверхность обтекаемого
ею тела); v2/2
– динамическое давление; gh
– гидростатическое давление.
Как
видно, выражение закона сохранения
энергии применительно к установившемуся
течению идеальной жидкости. Оно хорошо
выполняется и для реальных жидкостей,
внутреннее трение которых не очень
велико. Для горизонтальной трубки тока
уравнение будет иным: v2/2
+ p = const (полное давление).
Так
как динамическое давление связано со
скоростью движения жидкости (газа), то
уравнение Бернулли позволяет измерять
скорость потока жидкости.
Вязкость
– это свойство реальных жидкостей
оказывать сопротивление перемещению
одной части жидкости относительно
другой. При перемещении одних слоев
относительно других возникают силы
внутреннего трения, направленные по
касательной к поверхности слоев. Сила
внутреннего трения тем больше, чем
больше поверхность рассматриваемого
слоя и зависит от того, как быстро
меняется скорость жидкости от одного
слоя к другому. F =
|v/x|
S, где
— динамическая вязкость.
Единица
вязкости Н/м2сек.
Чем больше вязкость, тем больше силы
внутреннего трения в ней. Вязкость
зависти от температуры. Зависимость у
жидкостей и газов различна. Для жидкости
с увеличением температуры
уменьшается. У газов наоборот.
Существует
два режима течение жидкости.
Ламинарное
(слоистое) течение
– если вдоль потока каждый выделенный
тонкий слой скользит относительно
потока, не перемешиваясь с другими
слоями.
Турбулентное
(вихревое) течение
– если вдоль потока происходит интенсивное
вихреобразование и перемешивание слоев
жидкости. Таким образом, особенностью
ламинарного течения является его
регулярность. Оно наблюдается при
небольших скоростях движения жидкости.
Внешние слои жидкости из-за сил
молекулярного сцепления прилегают к
трубе и остаются неподвижными. Скорость
последующих слоев тем больше, чем больше
их расстояние до поверхности трубы и
наибольшей скоростью обладает слой,
движущийся вдоль оси трубы.
При
турбулентном течении частицы жидкости
приобретают составляющую скорости,
перпендикулярные течению. В результате,
они могут переходить из одного слоя в
другой. Скорость частиц в жидкости
быстро возрастает по мере удаления от
поверхности трубы. Затем изменяется
скорость движения жидкости.
Фазовые переходы
и фазовые диаграммы. Критическое
состояние и его параметры. Скрытые
теплоты фазовых превращений. Уравнение
Клайперона-Клаузиса. Кристаллическое
и аморфное состояние вещества. Способы
определения и описания кристаллических
структур.
Фазовые
равновесия и фазовые превращения.
Фаза
— это равновесное
состояние вещества, отличающееся по
своим физическим свойствам от других
состояний того же вещества.
Переход
вещества из одной фазы в другую называется
фазовым
переходом.
При таких переходах меняются механические,
тепловые, электрические и магнитные
свойства вещества.
Тройная
точка.
Кривые
плавления и парообразования в пересекаются
в точке A. Эту точку называют тройной
точкой, т.к. если при давлении p тр. и
температуре Tтр некоторые количества
вещества в твердом, жидком и газообразном
состояниях находятся в контакте, то без
подведения или отвода тепла количество
вещества, находящегося в каждом из 3х
состояний, не изменяется
Из
диаграммы состояний видно, что переход
вещества при нагревании из твердого
состояния в газообразное может
совершиться, минуя жидкое состояние.
Переход кристалл-жидкость-газ при
нормальном атмосферном давлении
происходит лишь у тех веществ, у которых
давление в тройной точке ниже этого
давления. Те же вещества, которых давление
в тройной точке превышает атмосферное,
в результате нагревания при атмосферном
давлении не плавятся, а переходят в
газообразное состояние.
Поскольку
тройной точке соответствует вполне
определенная температура, она может
служить опорной точкой термодинамической
шкалы.
Работа в термодинамике
В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.
Рассмотрим работу газа при изобарическом расширении.
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:
$A’=F’∆h=pS∆h=p∆V$
Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V < 0$, поскольку $∆h < 0$.
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:
$A=-A’=-p∆V$
Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.
Первый закон термодинамики
Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.
Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).
Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.
Первый закон термодинамики формулируется так:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
$∆U=A+Q$
где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.
Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.
При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.
Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:
$Q=∆U+A’$
где $А’$ — работа, совершаемая системой ($А’=-А$).
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.
Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.
Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.
Применение первого закона термодинамики к различным процессам
Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.
Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.
При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,
$∆U=Q$
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.
Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q < 0$ и $∆U < 0$, внутренняя энергия уменьшается.
Изотермический процесс графически изображается изотермой.
Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.
Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:
$Q=A’$
При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q < 0$ и $А’ < 0$. В этом случае над газом совершается работа внешними силами. Для внешних сил работа положительна. Геометрически работа при изотермическом процессе определяется площадью под кривой $р(V)$.
Изобарный процесс на термодинамической диаграмме изображается изобарой.
Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.
Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.
При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:
$Q=∆U+A’$
Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).
Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.
Адиабатический процесс
Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).
Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.
Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе
$∆U=A$
где $А$ — работа внешних сил.
При адиабатном расширении газа $А < 0$.
Следовательно,
$∆U={i}/{2}·{m}/{M}R∆T < 0,$
что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.
На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.
Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.
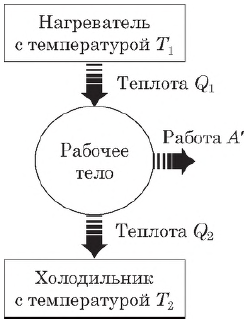
Принцип действия тепловых двигателей
Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.
Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.
Таким образом, основными элементами любого теплового двигателя являются:
- рабочее тело (газ или пар), совершающее работу;
- нагреватель, сообщающий энергию рабочему телу;
- холодильник, поглощающий часть энергии от рабочего тела.
Коэффициент полезного действия теплового двигателя
Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:
$A’=|Q_1|-|Q_2|$
где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.
Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:
$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$
Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η < 1$.
КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 — T_2=0$ двигатель не может работать.
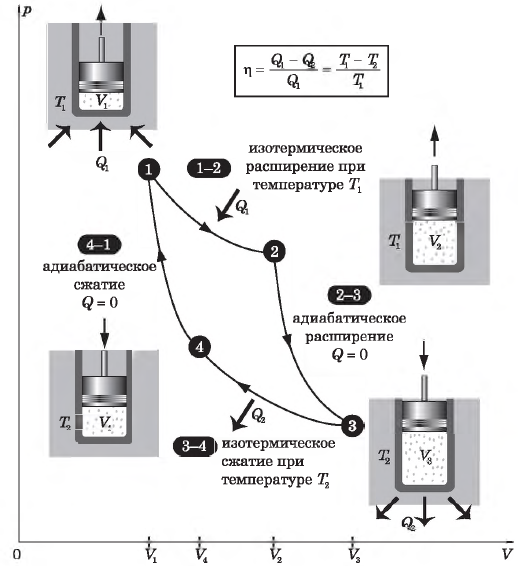
Цикл Карно
Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.
Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.
Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.
Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:
$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
$A_{23}=-∆U_{23}$
Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2 < Т_1$. В процессе ($3-4$) газ изотермически сжимается, передавая холодильнику количество теплоты $Q_2$:
$A_{34}=Q_2,$
Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.
Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:
$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$
Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.