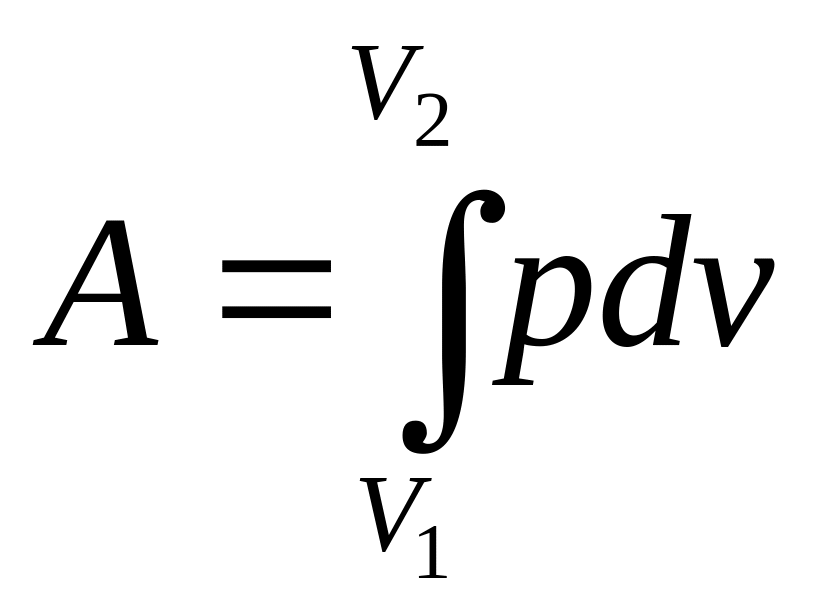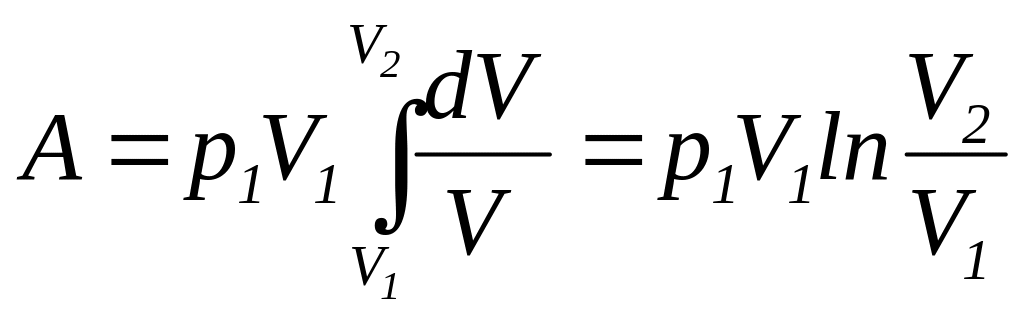Как найти работу газа при изотермическом процессе - AvtoShod.ru

Изменение
объема газа, т.е. его расширение или
сжатие, можно произвести так, чтобы
температура газа оставалась постоянной.
Такой процесс изменения состояния газа
или другой системы, который проходит
при постоянной температуре, называется
изотермическим. Для того чтобы процесс
в системе мог протекать изотермически,
она должна быть помещена в среду с
постоянной температурой, к примеру, в
термостат — аппарат, в котором специальное
устройство — терморегулятор —
автоматически поддерживает температуру
постоянной. Расширяясь в термостате,
т.е. при T=const,
система производит некоторую работу,
которая по первому началу термодинамики
равна:

(109)

где

― количество теплоты, поглощенной
системой от термостата, а

― изменение ее внутренней энергии.

В
случае идеального газа внутренняя
энергия зависит только от температуры
и не зависит от занимаемого им объема.
Поэтому при изотермическом расширении
или сжатии идеального газа его внутренняя
энергия остается неизменной при

и

.
Первое начало термодинамики (109) в этом
случае принимает вид:

(110)

(111)

A=Q

Это
равенство показывает, что при изотермическом
расширении объема идеального газа
работа

может производится только за счет
поглощаемого им тепла

.
Если газ изотермически расширяется
(
),
то он совершает положительную работу
(
)
и согласно равенству (110) получает извне
(от среды термостата) такое же количество
тепла (
).
Если же внешние силы совершают над газом
работу при его изотермическом сжатии
(
,
),
то он отдает такое же количество тепла
(
).
Таким образом, в случае изотермического
расширения газ полностью преобразует
подводимое к нему тепло в совершаемую
работу. Наоборот, при изотермическом
сжатии работа, затраченная на сжатие,
полностью преобразуется в отдаваемое
газом внешней среде (среде термостата)
тепло. Именно по этой причине внутренняя
энергия и температура газа остаются
неизменными. Газ при изотермическом
процессе ведет себя как тело с бесконечно
большой теплоемкостью. Математически
это следует из общего определения
теплоемкости; обозначив изотермическую
теплоемкость через С_Т,
получаем

,
т. к.

,

Из
сказанного выше ясно, что для того, чтобы
расширение газа могло происходить
изотермически, ему необходимо непрерывно
передавать тепло извне. Наоборот, чтобы
сжатие газа протекало изотермически,
от него необходимо непрерывно отбирать
тепло. Изотермический процесс,
следовательно, возможен лишь при идеально
хорошем обмене теплом между газом и
внешней средой (средой термостата).
Практически приблизиться к изотермическому
процессу можно, заставляя протекать
его настолько медленно, чтобы температура
газа все время успевала выравниваться
с температурой окружающей среды.

Вычислим
работу, совершаемую идеальным газом
при изотермическом изменении его объема
от V₁
до V₂.
Работа, производимая любой системой
при изменении ее объема, как мы видели,
определяется интегралом

(112)

Чтобы
произвести интегрирование, нужно знать,
как при рассматриваемом процессе
давление p
связано с объемом V,
т.е. необходимо знать уравнение процесса
в переменных p,
V.
Уравнение изотермического процесса
для идеального газа получается
непосредственно из его уравнения
состояния

(113)

Так
как при изотермическом процессе T=const,
то для данной массы газа

и, следовательно,

(114)

где
p₁
и V₁
― значения давления и объема газа в
начальном состоянии. Таким образом, при
изотермическом процессе давление и
объем идеального газа связаны между
собой законом Бойля-Мариотта. Выражая
из (114) давление газа через объем и
значение параметров в начальном состоянии

(115)

и
подставляя полученное выражение в
(112), находим

(116)

Так
как

,
то формулу для работы идеального газа
при изотермическом изменении его объема
можно представить в виде

(117)

Из
(116) и (117) видно, что работа идеального
газа при изотермическом процессе
изменения объема зависит не от разности
объемов как для изобарического процесса,
между которыми происходит расширение
или сжатие, а от их отношения (т. е. степени
расширения или сжатия газа).

Так
как при изотермическом процессе работа
A
производится идеальным газом за счет
передаваемого ему извне тепла, то
полученные выше формулы могут в равной
мере служить как для определения
совершаемой газом изотермической
работы, так и для расчета количества
теплоты Q,
необходимой для его изотермического
расширения или сжатия

(118)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как определить работу при изотермическом процессе

При изотермическом процессе, который протекает при постоянной температуре, газ выполняет работу за счет расширения. Расширение газа характеризуется его объемом, который изменяется в зависимости от изменения давления газа, обусловленного внешними воздействиями.

Вам понадобится

— герметичный сосуд с поршнем;
— весы;
— термометр;
— линейка.

Инструкция

Рассчитайте работу газа при постоянной температуре. Для этого определите, какой газ выполняет работу, и рассчитайте его молярную массу. С помощью периодической таблицы найдите молекулярную массу, которая численно равна молярной массе, измеренной в г/моль.

Найдите массу газа. Для этого откачайте воздух из герметичного сосуда и взвесьте его на весах. После этого закачайте газ, работа которого определяется, и снова взвесьте сосуд. Разность масс пустого и заполненного сосудов и будет равна массе газа. Измеряйте ее в граммах.

Измерьте при помощи термометра температуру газа. При изотермическом процессе она будет постоянна. Если измерение производится при комнатной температуре, достаточно измерить температуру окружающего воздуха. Измерения произведите в Кельвинах. Для этого к температуре, измеренной в градусах Цельсия, прибавьте число 273.

Определите начальный и конечный объем газа при выполнении работы. Для этого сосуд берите с подвижным поршнем, и, вычисляя уровень его подъема, рассчитайте первичный и вторичный объем геометрическими методами. Для этого используйте формулу для объема цилиндра V=π•R²•h, где π≈3,14, R – радиус цилиндра, h его высота.

Рассчитайте работу газа при изотермическом процессе. Для этого поделите массу газа m на его молярную массу M. Полеченный результат умножьте на универсальную газовую постоянную R=8,31 и значение температуры Т в Кельвинах. Полученный результат умножьте на натуральный логарифм из отношения конечного и начального объемов V2 и V1, A = m/M•R•T•ln(V2/V1).

В том случае, когда известно количество теплоты Q, которое получило тело при изотермическом процессе, используйте второе начало термодинамики Q = ∆U + A. Где A – работа газа, а ΔU – изменение его внутренней энергии. Поскольку изменение внутренней энергии зависит от температуры, а при изотермическом процессе она остается постоянной, то ΔU=0. В этом случае работа газа равна теплоте, переданной ему Q = A.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Для изотермического процесса характерен определенный процесс, который происходит с газовым веществом, который в свою очередь имеет неизменную массу и постоянную неизменяемую температуру вещества.

Изотермический процесс для температуры газа, основные формулы и величины

Формулы

Изотермический процесс характеризует состояние газа и данное состояние записывается следующими формулами:

[p_{1} V_{1}=v R T]

[p_{2} V_{2}=v R T]

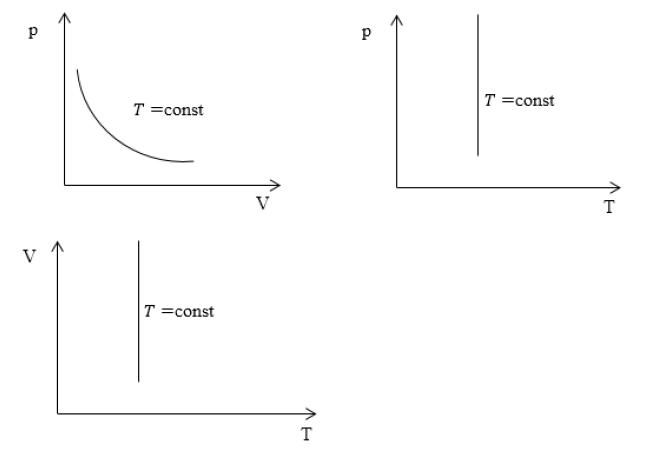
Изотермический процесс для системы координат

Характерные изотермические процессы зачастую отражают на термодинамических графиках и диаграммах.

Если рассмотреть подробно график можно увидеть линию, именно ее и принято называть изотермой. Она непосредственно является основной характеристикой процесса.

Изотермический процесс — закон Бойля-Мариотта

Разделим уравнение для второго состояния газа на выражение первого состояния и получим основное уравнение изотермического процесса.

[frac{p_{2} V_{2}}{p_{1} V_{1}}=1] или [p V=mathrm{const}] (постоянное значение)

Полученное уравнение и будет называться законом Бойля-Мариотта.

Данный процесс осуществляется с использованием тепловой энергии.

В случае, когда объем увеличивается, или отводится, для его уменьшения.

Составим первое значение термодинамики.

Затем постепенно получим уравнение для определения работы.

А также вычисления внутренней энергии и количества теплоты тела при изотермическом процессе.

[delta Q=d cup+d A=frac{i}{2} v R d T+p d V]

Температура является неизменной, поэтому, изменение значения внутренней энергии будет равняться нулевому значению. [(d cup=0)].

Из этого следует, что для изотермического процесса все подводимое тепло направлено на работу, которую совершает газ:

[
Delta Q=int_{V_{1}}^{V_{2}} d A
]

где:

[delta Q] — тепло элементарного характера, которое подводится ко всей системе;
dA — работа элементарного типа, совершаемая газом в изотермическом процессе;
i — количество свободных степеней газовых молекул;
R — газовое значение постоянной;
d — значение молей для газа;
V₁— первоначальное значение объема газа;
V₂— окончательное значение объема газа.

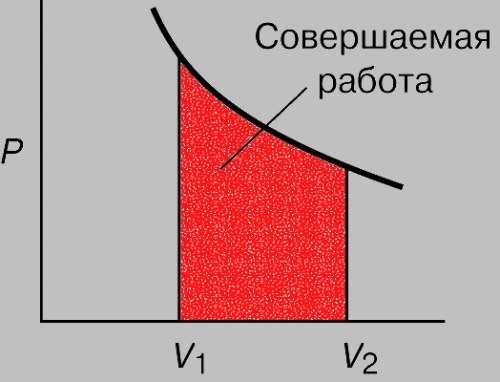
[A=int_{V_{1}}^{V_{2}} p d V]

Давление газа, которое зависит от уравнения газа в идеальном состоянии.

[p V=v R T rightarrow p=frac{v R T}{V}]

Подставим вышеуказанное выражение в подынтегральное выражение:

[A=int_{V_{1}}^{V_{2}} frac{v R T}{V}=v R T int_{V_{1}}^{V_{2}} frac{d V}{V}=mathrm{u} R T ln left(frac{V_{2}}{V_{1}}right)]

Составленное уравнение необходимо определения значения работы, которую совершает газ в изотермическом процессе.

[
A=v R T ln left(frac{p_{1}}{p_{2}}right)
]

[
Delta Q=A
]

Нет времени решать самому?

Наши эксперты помогут!

Как найти изотермический процесс — примеры решения задач

Пример №1

Основное содержание задания: газ идеального состояния, имеет способность расширяется, имея постоянную температуру, от объема.

[V_{1}=0.2 mathrm{~m}^{3}]

[V_{2}=0.6 mathrm{~m}^{3}]

Известно сила давления во втором состоянии и оно равняется [p_{2}=1 cdot 10^{5} mathrm{Pi a}].

Определить:

Величину изменения внутренней энергии газа;
Значение работы, которую совершает газовое вещество в данном процессе;
Какое необходимое количество теплоты получает газ в процессе работы.

Методика решения:

Внутренняя энергия газа неизменна, так как процесс который рассматривается в задаче, является изотермическим:

[Delta mathrm{U}=0]

Из основного закона термодинамики можно определить:

[Delta cup=A]

[A=v R T ln left(frac{V_{2}}{V_{1}}right)]

Составим и запишем уравнение, которое отражает окончательное (конечное) состояние газа:

[p_{2} V_{2}=v R T rightarrow T=frac{p_{2} V_{2}}{v R}]

Подставим в уравнение для температуры вышеизложенные формулы и получим решение:

[A=v R frac{p_{2} V_{2}}{v R} ln left(frac{V_{2}}{V_{1}}right)=p_{2} V_{2} ln left(frac{V_{2}}{V_{1}}right) .]

Следовательно, все величины расположены в международной системе единиц (СИ), можно провести вычисления и определить неизвестные значения:

[A=0.6 cdot 10^{5} ln left(frac{0.6}{0.2}right)=0.6 cdot 10^{5} cdot 1.1=6.6 cdot 10^{4} text { (Дж) }]

Ответ задачи:

значение изменения внутренней энергии газа в рассматриваемой процессе равно нулевому значению.
работа, которая совершается в процессе газовым веществом равняется [6,6 cdot 10^{4} text { Дж }].
Необходимое количество тепловой энергии равно: [6,6 cdot 10^{4} text { Дж }].

Пример №2

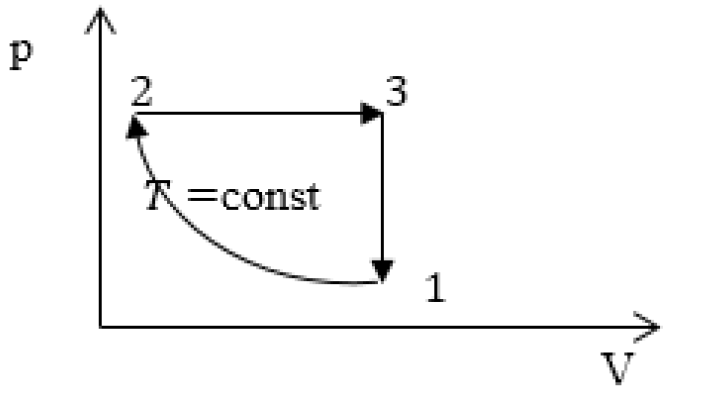
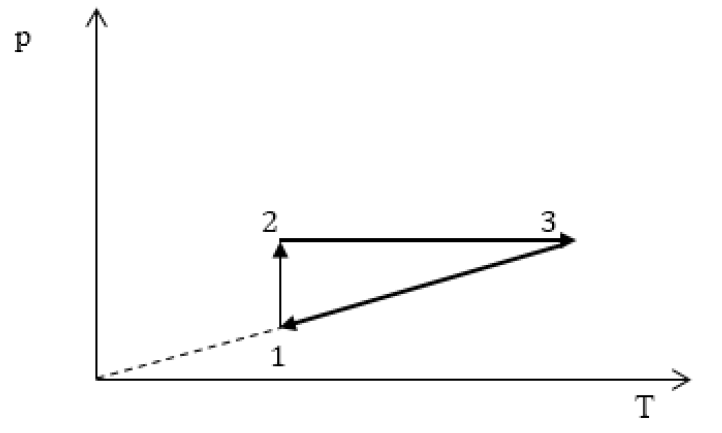
Задание: изображен график, где изменяется идеальное состояние массы газа равное m в координатных осях p (V).

Нужно перенесите данный процесс на координатные оси в p(T).

На данном графике изображен круговой процесс.

Где:

Прямая 1-2 является изотермическим процессом с константой [(T=text { cons } t)]. Следовательно значение объема будет уменьшается [(mathrm{V} downarrow)], а давления соответственно расти [(p uparrow)].
Прямая 2-3 отражает изобарический процесс [(p=text { const })]

const). Для данного процесса характерно увеличение объема [mathrm{V} uparrow] и применяя закон Гей-Люссака, увеличение [Т uparrow]

Прямая (отрезок) 3-1 является изохорным процессом объем будет постоянной величиной [(mathrm{V}=text { const })], а [p downarrow],а исходя из закона Шарля [T downarrow].

Все перечисленные процессы изобразим на координатных осях p(T).

Источник

Стенки сосуда, в котором находится газ, подвергаются беспрестанной хаотичной «бомбардировке» молекулами, из которых он состоит. Скорости молекул велики, время соударения мало, молекул много, так что эта «молекулярная барабанная дробь» воспринимается стенкой как постоянное давление. Обусловленная давлением сила направлена по нормали к поверхности вовне, а величина силы, действующей на маленький элемент стенки площадью δSδS есть p⋅δSpcdot δS, где рр – давление газа. Далее мы рассматриваем квазистационарные («медленные») процессы, при которых давление р и температура ТТ одинаковы во всех точках сосуда, содержащего газ.

Квазистационарные процессы

Пусть вся поверхность сосуда, занимаемого газом, или её часть под действием давления газа — или внешних сил — перемешается (деформируется). Выбрав очень маленькие элементы поверхности δS, настолько маленькие, что их можно рассматривать как материальные точки, сосчитаем для каждого из них работу «местной силы давления»:

δА=(р⋅δS)⋅δх⋅cos⁡α=p⋅δS⋅δn=p⋅δVδА = (р cdot δS)cdot δх cdot cosα = p cdot δS cdot δn = p cdotδV,

где δхδх – путь, пройденный элементом поверхности,

αα — угол между направлением перемещения элемента и направлением нормали к нему,

δnδn – смещение элемента δSδS вдоль нормали, направленной вовне,

δVδV – приращение объёма сосуда в месте расположения элемента δSδS;

δVδV – положительно, если объём увеличивается.

Выполнив суммирование по всем элементарным площадкам, получаем, что при очень маленьком изменении объёма газа dVdV, при котором давление почти постоянно, элементарная работа сил давления газа или кратко – элементарная работа газа dАdА есть произведение давления газа рр на изменение dVdV его объёма.

Первое начало

Основным энергетическим соотношением термодинамики является Квазистационарные процессы, которое выражается формулой Q=A+ΔUQ = A + ΔU со следующим правилом знаков:

если газ получает тепло или теплоту – так в термодинамике называется переданная энергия — то её величина QQ положительна;
QQ отрицательна, если газ отдаёт теплоту. АА – это результирующая работа газа при переходе из начального состояния в конечное, она является суммой элементарных работ, подсчитанных так, как описано выше;
ΔUΔU – разность внутренних энергий газа в конечном и начальном состояниях, т.е. ΔU=νсvΔTΔU = νсvΔT (описание обозначений – в конце статьи).

Изопроцессы

А вот теперь рассмотрим несколько типовых процессов в газах и определим для них величину работы.

Когда объём газа не меняется – а это изохорический процесс – то на всех его этапах dV=0dV = 0, dА=0dА = 0, следовательно, и результирующая работа газа равна нулю.

Когда давление газа неизменно – а это изобарический процесс – то при сложении элементарных работ постоянное давление можно вынести за скобку, а в скобке в итоге окажется разность конечного и начального объёмов газа, следовательно результирующая работа А=р(Vк−Vн)А = р(V_к — V_н).

Когда температура газа постоянна – а это изотермический процесс – то производя сложение элементарных работ и выразив давление согласно уравнению Менделеева-Клапейрона, получим следующую формулу для результирующей работы: А=∑dАi=∑pidVi=νRT∑dVi/Vi=νRTln(Vк/Vн)А = ∑dА_i = ∑p_idV_i = νRT∑dV_i/V_i = νRTln(V_к/V_н), воспользовавшись помощью математики при подсчёте суммы.

Когда процесс происходит в теплоизолированном сосуде – а это адиабатный процесс, при котором Q=0Q = 0 – в таком случае, согласно первому началу термодинамики, работа А=−ΔU=−νсvΔT=νсv(Tн–Тк)А = — ΔU = — νсvΔT = νсv(T_н – Т_к).

Таким образом, резюмируем

адиабатный процесс: А=νсv(Tн–Тк)А = νсv(T_н – Т_к);
изобарический процесс: А=р(Vк−Vн)А = р(V_к — V_н);
изотермический процесс: А=νRTln(Vк/Vн)А = νRTln(V_к /V_н);
изохорический процесс: А=0А = 0,

где VV – объём газа, рр – давление, ТТ – температура, νν – число молей, сvсv – молярная теплоёмкость при постоянном объёме, RR — универсальная газовая постоянная, индексы нн и кк указывают на начальное и конечное состояния.