Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
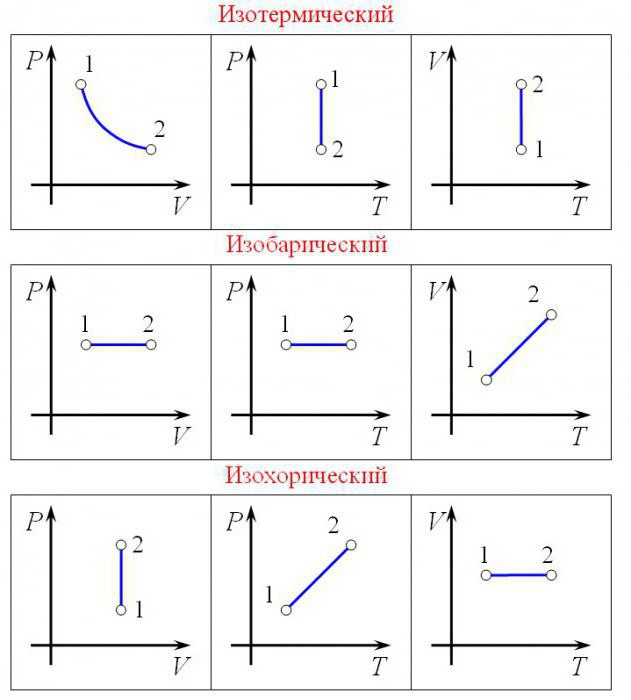
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
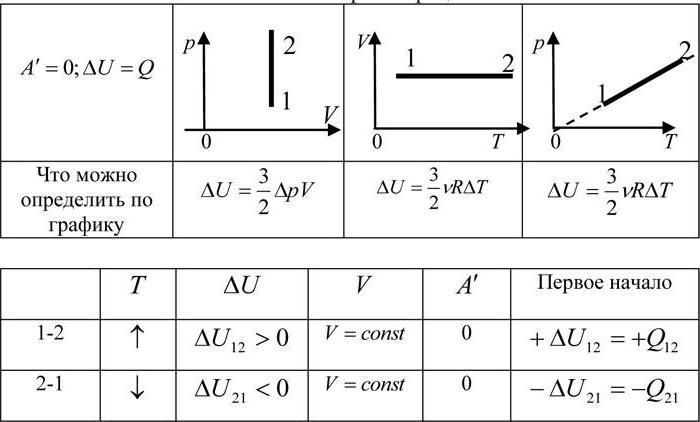
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
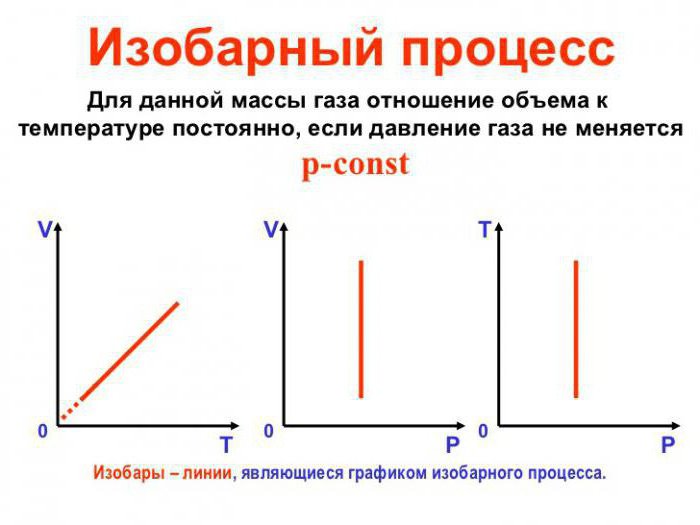
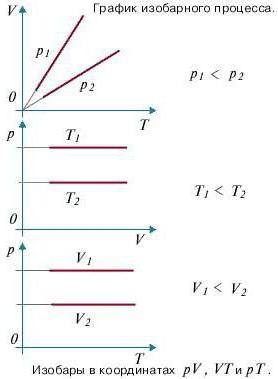
Изобарный процесс (также называемый изобарическим процессом) является одним из термодинамических процессов, которые происходят при постоянном показателе давления. Масса газа системы при этом также остается постоянной. Наглядное представление о графике, демонстрирующем изобарный процесс, дает термодинамическая диаграмма в соответствующей системе координат.
Примеры
Наиболее простым примером изобарического процесса можно назвать нагревание некоторого объема воды в открытом сосуде. В качестве еще одного примера можно привести расширение идеального газа в цилиндрическом объеме, где поршень имеет свободный ход. В каждом из этих случаев давление будет постоянным. Оно равно обыкновенному атмосферному давлению, что вполне очевидно.
Обратимость
Изобарный процесс можно считать обратимым в том случае, если давление в системе совпадает с внешним давлением и равно во все моменты времени процесса (то есть оно постоянно по своему значению), а температура изменяется очень медленно. Таким образом, термодинамическое равновесие в системе сохраняется в каждый момент времени. Именно совокупность вышеперечисленных факторов дает нам возможность считать изобарный процесс обратимым.
Чтобы осуществить в системе изобарический процесс, теплоту к ней нужно или подводить, или отводить. При этом теплота должна расходоваться на работу расширения идеального газа и на изменение его внутренней энергии. Формулу, демонстрирующую зависимость величин друг от друга при изобарном процессе, называют законом Гей-Люссака. Она показывает, что объем пропорционален температуре. Давайте выведем эту формулу на основании поверхностных знаний.
Вывод закона Гей-Люссака (первичное понимание)
Человек, хотя бы немного разбирающийся в молекулярной физике, знает, что многие задачи связаны с определенными параметрами. Имя им – давление газа, объем газа и температура газа. В тех или иных случаях в ход идут молекулярная и молярная масса, количество вещества, универсальная газовая постоянная и другие показатели. И здесь есть определенная связь. Давайте поговорим об универсальной газовой постоянной подробнее. На тот случай, если кто-то не знает, каким образом ее получили.
Получение универсальной газовой постоянной
Эту константу (постоянное число с определенной размерностью) принято также называть постоянной Менделеева. Она присутствует также в уравнении Менделеева-Клапейрона для идеального газа. Как же получил наш знаменитый физик эту константу?
Как мы знаем, уравнение идеального газа имеет следующую форму: PV/T (что озвучивается так: “произведение давления на объем, деленное на температуру”). По отношению к универсальной газовой постоянной применим так называемый закон Авогадро. Он гласит о том, что если мы возьмем любой газ, то одинаковое его количество молей при одинаковой температуре и одинаковом давлении займет одинаковый объем.
По сути дела, это есть словесная формулировка уравнения состояния идеального газа, которое было записано в виде формулы немного ранее. Если мы возьмем нормальные условия (а это когда температура газа равна 273,15 Кельвинов, давление равно 1 атмосфере, соответственно, 101325 Паскалей, а объем моля газа равен 22,4 литра) и подставим их в уравнение, все перемножим и разделим, то получим, что совокупность подобных действий дает нам численный показатель, равный 8,31. Размерность дается в Джоулях, деленных на произведение моля на Кельвин (Дж/моль*К).
Уравнение Менделеева-Клапейрона
Давайте возьмем уравнение состояния идеального газа и перепишем его в новом виде. Изначальное уравнение, напомним, имеет вид PV/T=R. А теперь умножим обе части на температурный показатель. Получим формулу PV(м)=RT. То есть произведение давления на объем равно произведению универсальной газовой постоянной на температуру.
Теперь умножим обе части уравнения на то или иное количество молей. Обозначим их количество буквой, скажем, X. Таким образом, получим следующую формулу: PV(м)X=XRT. Но ведь мы знаем, что произведение V с индексом “м” дает нам в результате просто объем V, а число молей X раскрывается в виде деления частной массы на молярную массу, то есть имеет вид m/M.
Таким образом, конечная формула будет выглядеть следующим образом: PV=MRT/m. Это и есть то самое уравнение Менделеева-Клапейрона, к которому пришли оба физика практически одновременно. Мы можем умножить правую часть уравнения (и в то же время разделить) на число Авогадро. Тогда получим: PV = XN(a)RT/N(a). Но ведь произведение количества молей на число Авогадро, то есть XN(a), дает нам не что иное, как общее число молекул газа, обозначаемое буквой N.
В то же время частное от универсальной газовой постоянной и числа Авогадро – R/N(a) даст постоянную Больцмана (обозначается k). В итоге мы получим еще одну формулу, но уже в несколько другом виде. Вот она: PV=NkT. Можно раскрыть эту формулу и получить следующий результат: NkT/V=P.
Работа газа при изобарном процессе
Как мы выяснили ранее, изобарным процессом называется термодинамический процесс, при котором давление остается величиной постоянной. А чтобы выяснить, как будет определяться работа при изобарном процессе, нам придется обратиться к первому началу термодинамики. Общая формула выглядит следующим образом: dQ = dU + dA, где dQ — это количество теплоты, dU – изменение внутренней энергии, а dA – работа, совершаемая в ходе выполнения термодинамического процесса.
Теперь рассмотрим конкретно изобарный процесс. Примем во внимание тот фактор, что давление остается постоянным. Теперь попытаемся переписать первое начало термодинамики для изобарного процесса: dQ = dU + pdV. Чтобы получить наглядное представление о процессе и работе, нужно изобразить его в системе координат. Ось абсцисс обозначим p, ось ординат V. Пускай объем будет увеличиваться. В двух отличных друг от друга точках с соответствующим значением p (конечно же, фиксированным) отметим состояния, представляющие собой V1 (первоначальный объем) и V2 (конечный объем). В этом случае график будет представлять собой прямую линию, параллельную оси абсцисс.
Найти работы в таком случае проще простого. Это будет просто площадь фигуры, ограниченная с двух сторон проекциями на ось абсцисс, а с третьей стороны – прямой линией, соединяющей точки, лежащие, соответственно, в начале и конце изобарной прямой. Попробуем вычислить значение работы при помощи интеграла.
Он будет вычисляться следующим образом: A = p (интеграл в пределах от V1 до V2) dV. Раскроем интеграл. Получим, что работа будет равна произведению давления на разность объемов. То есть выглядеть формула будет следующим образом: A = p (V2 – V1). Если мы раскроем некоторые величины, то получим еще одну формулу. Она выглядит так: A = xR (T2 – T2), где x – количество вещества.
Универсальная газовая постоянная и ее смысл
Можно сказать, что последнее выражение будет определять физический смысл R – универсальной газовой постоянной. Чтобы было понятнее, давайте обратимся к конкретным числам. Возьмем для проверки один моль какого-либо вещества. В то же время пускай температурная разница будет составлять 1 Кельвин. В этом случае легко заметить, что работа газа будет равна универсальной газовой постоянной (или же наоборот).
Заключение
Этот факт можно подать немного в другом свете, перефразировав формулировку. Например, универсальная газовая постоянная будет численно равна работе, совершаемой при изобарном расширении одним молем идеального газа, если он нагревается на один Кельвин. Вычислить работу при других изопроцессах будет несколько сложнее, но главное — при этом применять логику. Тогда все быстро встанет на свои места, и вывод формулы окажется проще, чем вы думаете.
Условие задачи:
Определить работу, которую совершает газ при изобарном нагревании на 50 °C, если он занимал при 17 °C и давлении 105 Па объем 0,75 м3.
Задача №5.4.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(Delta t=50^circ) C, (t_1=17^circ) C, (p=10^5) Па, (V_1=0,75) м3, (A-?)
Решение задачи:
Работу газа (A) при изобарном нагревании (расширении) определяют по формуле:
[A = pleft( {{V_2} – {V_1}} right)]
Раскроем скобки, тогда:
[A = p{V_2} – p{V_1};;;;(1)]
Теперь запишем дважды уравнение Клапейрона-Менделеева для начального и конечного состояния газа:
[left{ begin{gathered}
p{V_1} = nu R{T_1} ;;;;(2)hfill \
p{V_2} = nu R{T_2} hfill \
end{gathered} right.]
Учитывая эти два уравнения системы, формула (1) примет вид:
[A = nu R{T_2} – nu R{T_1}]
[A = nu Rleft( {{T_2} – {T_1}} right)]
Разность конечной (T_2) и начальной (T_1) температур есть изменение температуры (Delta T), поэтому:
[A = nu RDelta T;;;;(3)]
Отлично, осталось только выразить неизвестное количество вещества (nu) из уравнения (2) и подставить его в формулу (3):
[nu = frac{{p{V_1}}}{{R{T_1}}}]
[A = frac{{p{V_1}}}{{R{T_1}}}RDelta T = p{V_1}frac{{Delta T}}{{{T_1}}}]
Мы решили задачу в общем виде. Перед расчётом ответа нужно начальную температуру газа (t_1) перевести в Кельвины, то есть в единицы системы СИ. Интересно, но величина изменения температуры (Delta t) в различных шкалах одинакова.
[17^circ;C = 290;К]
Численно работа газа (A) равна:
[A = {10^5} cdot 0,75 cdot frac{{50}}{{290}} = 12931;Дж approx 13;кДж]
Ответ: 13 кДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.4.6 Углекислый газ массой 220 г имеет температуру 290 К. Определить работу газа
5.4.8 Газ был нагрет изобарно от 285 до 360 К. Какую работу совершил при этом газ
5.4.9 160 г гелия нагревают от 50 до 60 C. Найти работу газа при постоянном давлении
Работа газа при изобарном изменении объема.
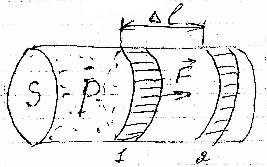
Представим
себе цилиндр с подвижным поршнем,
заполненный газом.
Пока
давление газа внутри цилиндра и
окружающего наружного воздуха одинаковы,
поршень неподвижен. Пусть при этом
температура газа и окружающей среды
равна T1,
а давление равно P.
Будем
медленно нагревать газ в цилиндре до
температуры T2.
Газ при этом начинает изобарически
расширяться и поршень переместится из
положения 1 в положение 2 на расстояние
△.
При этом газ совершает работу против
внешней силы.
F
=
P*S,
где S
– площадь сечения цилиндра.
А =
F*△*cosa
a
= 0
=> cosa = 1
A
= F*△
= P*S*△
= P*S*(2
— 1)
A
= P*
(S
*2
— S
*1)
=>
A
= P*(V2
— V1)
A
= P*△V
△V
> 0 => A > 0;
△V
< 0 => A < 0.
Физический
смысл молярной газовой постоянной:
Молярная
газовая постоянная численно равна
работе, совершаемой 1 молем идеального
газа при его изобарическом нагревании
на 1К.
Физический
смысл постоянной Больцмана:
Постоянная
Больцмана показывает сколько работы в
среднем приходится на одну молекулу
идеального газа при изобарическом
нагревании на 1К.
Изменение
внутренней энергии. Закон сохранения
энергии.
Под
внутренней
энергией тела
подразумевается сумма кинетической и
потенциальной энергий всех частиц тела
и энергии ядер его атомов.
Изменение
внутренней энергии всегда связано с
его взаимодействием с другими телами
и с окружающей средой.
Обмен
внутренней энергией между телами и
окружающей средой или между частями
тела без совершения механической работы
называется теплообменом.
Виды
теплообмена:
1.
Теплопроводность
– передача внешней энергии от одних
частей вещества к другим, обусловленная
хаотическим движением молекул и других
частиц вещества.
2.
Конвекция
– теплообмен, который происходит при
перемешивании неравномерно нагретых
слоев жидкости или газа под действием
силы тяжести.
3.
Излучение
– излучение тела, которое определяется
только его температурой.
Энергия
замкнутой системы никогда не исчезнет
и не создается из ничего. При всех
явлениях внутри системы она только
превращается из одного вида в другой
или передается от одного тела к другому,
не изменяясь количественно.
Первое
начало термодинамики.
Q
= △U
+ A
Подведенное
к системе количество теплоты частично
идет на увеличение внутренней энергии
системы и частично – на совершение этой
системой работы.
1)
Изохорический
процесс:
Q
= △U
При
изохорическом процессе все подведенное
к газу количество теплоты идет на
увеличение его внутренней энергии.
2)
Изобарический процесс:
Q
= △U
+ A
При
изобарическом процессе подведенное к
системе количество теплоты частично
идет на увеличение внутренней энергии
системы и частично – на совершение этой
системой работы.
3)
Изотермический
процесс:
Q
= A
При
изобарическом процессе все подведенное
к газу количество теплоты идет на
выполнение газом работы.
Адиабатический
процесс:
Процесс
в какой–либо системе, который происходит
без обмена теплом с окружающей средой
называется адиабатическим.
△U
+ A
= 0 =>
A = -△U
При
адиабатическом процессе система может
выполнять работу над внешними телами
только за счет внутренней энергии.
Если
газ при адиабатическом расширении
совершает работу над окружающей средой,
то его внутренняя энергия уменьшается.
Испарение
и конденсация.
Насыщенный
пар.
Кипение.
Абсолютная
и относительная влажность воздуха.
Свойства
жидкостей и твердых тел.
Свойства
жидкостей.
Характеристика
жидкого состояния вещества.
Вещество
в жидком состоянии сохраняет свой объем,
но принимает форму сосуда, в котором
она находится.
Сохранение
объема у жидкости доказывает, что между
молекулами действуют силы притяжения.
Следовательно, расстояния между
молекулами жидкости должны быть меньше
радиуса молекулярного действия.
Если
вокруг молекулы жидкости описать сферу
молекулярного действия, то внутри этой
серы окажутся центры других молекул,
которые будут взаимодействовать с этой
молекулой.
Эти
силы взаимодействия удерживают молекулу
жидкости около ее временного положения
равновесия около 10^-12с,
после чего она перескакивает в новое
временное положение равновесия.
Молекулы
жидкости между переходами совершают
колебательные движения около временного
положения равновесия.
Время
между дувумя переходами молекулы из
одного положения равновесия в другое
называется временем
оседлой жизни.
В
течение времени оседлой жизни большинство
молекул жидкости удерживаются у своего
положения равновесия, и лишь небольшая
часть их успевает за это время перейти
в новые положения равновесия. За более
длительное время уже большинство молекул
жидкости успеет переменить свое
местоположение. Поэтому жидкость
облагает текучестью и принимает форму
сосуда в котором она находится.
В
жидкости существует ближний порядок в
расположении молекул и отсутствует
дальний порядок.
Механические
свойства жидкости:
1.
сжимаемость;
2.
упругость;
3.
хрупкость;
4.
кавитация
– разрыв жидкости и образование в ней
пустот.
Поверхностный
слой жидкости.
Все
молекулы жидкости, находящиеся в
повехностном слое, толщиной , равной
радиусу молекулярного действия,
втягиваются внутрь жидкости. Но
пространство внутри жидкости занято
другими молекулами, поэтому поверхностный
слой оказывает давление на жидкость,
которое называется молекулярным
давлением.
Поскольку
молекулы жидкости, находящиеся в ее
поверхностном слое втягиваются внутрь
жидкости, их потенциальная энергия
больше, чем у молекул внутри жидкости.
Дополнительную
потенциальную энергию молекул
поверхностного слоя жидкости, называют
свободной
энергией жидкости.
Для
того, чтобы вывести молекулы, находящиеся
внутри жидкости на ее поверхность, нужно
преодолеть противодействие молекулярных
сил, то есть произвести работу, которая
будет нужна для увеличения свободной
энергии поверхностного слоя жидкости.
△П
прямо пропорциональна △S
△П
=
σ
*△S,
так как △П
= А =>
A
= σ
*△S
Эта
работа зависит от рода жидкости и от
внешних условий (t).
Величина
σ
(сигма), характеризующая зависимость
работы молекулярных сил при уменьшении
площади свободной поверхности жидкости
от рода жидкости и внешних условий,
называется коэффициент
поверхностного натяжения жидкости.
[σ]
= 1*Дж/м^2
= 1*Н/м
Коэффициент
поверхности натяжения численно равен
работе молекулярных сил при изменении
площади свободной поверхности на один
квадратный метр.
Так
как всякая система самопроизвольно
переходит в состоянии, при котором ее
потенциальная энергия ___ , то жидкость
должна самороизвольно переходить в
такое состояние, при котором площадь
ее свободной поверхности имеет наименьшее
значение. Так как при одном и том же
объеме наименьшая площадь поверхности
имеется у шара, то в состоянии невесомости
принимает форму шара.
Смачивание.
Если
молекулы жидкости притягиваются друг
к другу сильнее, чем к молекулам твердого
тела, то жидкость называется смачивающей
это тело.
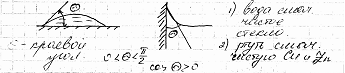
Если
молекулы жидкости притягиваются друг
к другу слабее, чем к молекулам твердого
тела, то жидкость называется не
смачивающей
это вещество

Капиллярность.
Явления,
обусловленное втягиванием смачивающих
жидкостей в капилляры и выталкивание
не смачивающих жидкостей из капилляров,
называются капиллярными
явлениями.
Вязкость.
Силы
противодействия, обусловленные движением
какого-либо тела в жидкости или
газообразной среде, называются силами
сопротивления среды.
При
движении частей жидкости относительно
друг друга возникают тормозящие это
движение силы, которые называют силами
внутреннего трения или
силами
вязкости.
РИСУНОК
Свойства
твердых тел.
Характеристика
твердого состояния вещества.
Вещество
обычно называется твердым, если оно
сохраняет свою форму и свой объем (это
внешние признаки).
При
изучении твердых веществ было обнаружено,
что многие твердые тела в природе имеют
гладкие плоские поверхности, расположенные
под определенными углами, а иногда и
форму правильных многогранников. Такие
твердые тела называют монокристаллами.
Частицы
в кристаллах имеют правильное расположение,
то есть образуют кристаллическую
решетку.
Точки
в кристаллической решетке, соответствующие
наиболее устойчивому положению равновесия
частиц твердого тела называются узлами
решетки.
Узлы
решетки имеют правильное расположение,
которое периодически повторяется внутри
кристалла.
Правильное
расположение частиц в узлах решетки
кристалла называют дальним
порядком
в расположении частиц.
В
физике под твердым
телом
подразумевают только такие вещества,
у которых имеются кристаллическое
строение.
Зависимость
каких-либо свойств кристаллов от
направления, называется анизотропией.

Анизотропией
обладают только монокристаллы.
1.
Если на поверхности кристалла кварца
нанести слой воска и коснуться концом
сильно нагретой проволоки середины
грани кристалла, то воск расплавляется
по эллипсу. Значит, теплопроводность
кристалла кварца во многом зависит от
направления.
2.
В кристаллах можно обнаружить и такие
направления, по которым те или иные
свойства оказываются одинаковыми.
Срежем верхнюю половину кристалла и
повторим предыдущий опыт При этом воск
расплавляется по окружности.
Большинство
твердых веществ имеют поликристаллическое
строение
– состоят из множества очень мелких
кристалликов, иногда различимых только
в микроскоп. Кристаллики относительно
друг друга расположены хаотически/,
твердое тело в целом является изотропным
– одинаковые свойства по всем направлениям.
Дефекты
кристаллической решетки.
1.
Нарушение правильного расположения
частиц в каждый момент времени,
обусловленное тепловым движением
частиц.
2.
Дислокация.
3.
Отсутствие частиц в отдельных узлах
кристаллической решетки или смещение
частиц в промежутках между узлами.
4.
Чужеродные атомы в отдельных узлах или
между узлами.
Виды
кристаллических структур.
1.
Ионная
кристаллическая структура
(например: поваренная соль).
В
узлах находятся положительные и
отрицательные ионы.
Силами,
удерживающими ионы в узлах решетки,
являются силы электрического притяжения
и отталкивания. Разноименно заряженные
ионы расположены ближе друг к другу,
чем одноименно заряженные. Следовательно,
силы притяжения между разноименными
ионами преобладают над силами отталкивания
одноименных ионов.
2.
Атомная
кристаллическая структура
(например: алмаз, германий, кремний).
Атомная
кристаллическая структура характеризуется
наличием нейтральных атомов в узлах
решетки, между которыми имеется
ковалентная связь.
Ковалентной
связью
называется связь, при которой каждые
два соседних атома удерживаются рядом
силами притяжения, возникающих при
взаимном обмене двумя валентными
электронами между этими атомами
(Самая
прочная кристаллическая структура.)
Ковалентная связь создает весьма прочные
кристаллы. Следовательно, такие вещества
обладают большой механической прочностью
и плавятся при высоких температурах.
3.
Молекулярная
кристаллическая структура
(например: лед, сухой лед, нафталин,
твердый азот).
В
узлах этой кристаллической решетки
находятся нейтральные молекулы вещества.
Силами,
удерживающими молекулы в узлах этой
решетки, являются силы межмолекулярного
взаимодействия.
(Самая
слабая кристаллическая решетка.) Эти
силы сравнительно слабые, поэтому
твердые тела легко разрушаются при
механическом воздействии и имеют низкую
температуру лавления.
4.
Металлическая
кристаллическая
структура (все металлы).
В
узлах этой кристаллической решетки
находятся положительно заряженные ионы
металла.
У
атомов всех металлов валентные электроны
слабо связаны с ядром атома. Это означает,
что валентные электроны отрываются от
атома и атом превращается в положительный
ион. Оторвавшиеся электроны движутся
хаотически по всему объему металла.
Совокупность
свободных электронов в металле называется
электронным
газом.
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
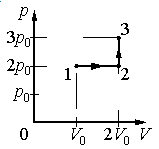
Задание EF17966
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.1k