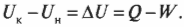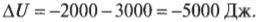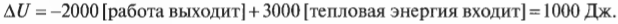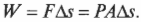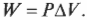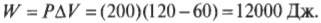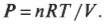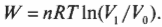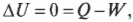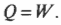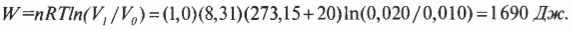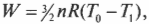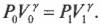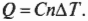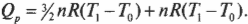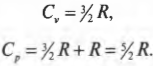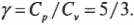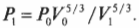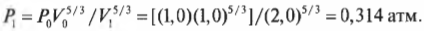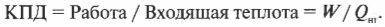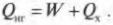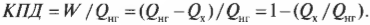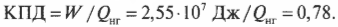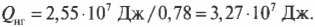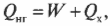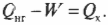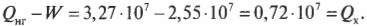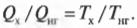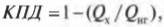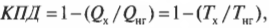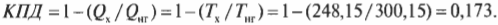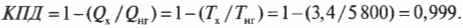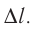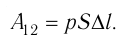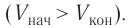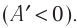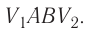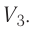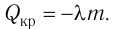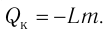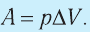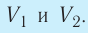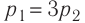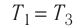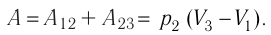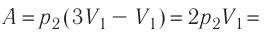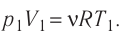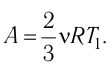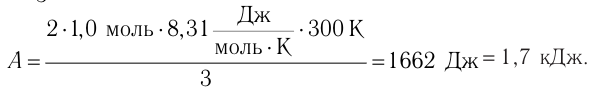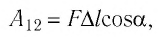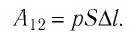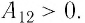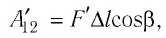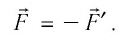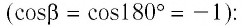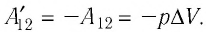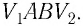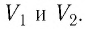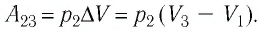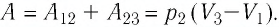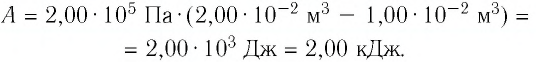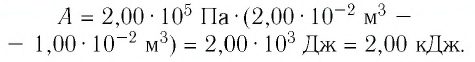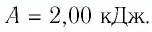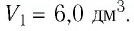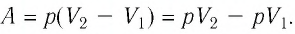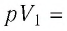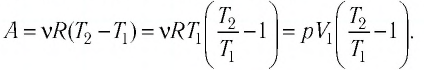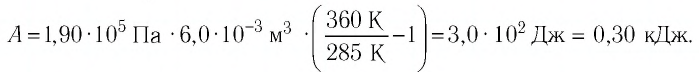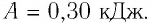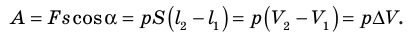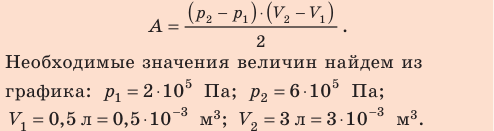Как найти работу если известно количество теплоты

Вы открыли страницу вопроса Как найти полезную работу, если известно кол — во теплоты и КПД?. Он относится к категории
Физика. Уровень сложности вопроса – для учащихся 5 — 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Физика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.

Вычисление полезной работы через КПД

Измерять КПД принято в процентах. Например, КПД 35%, означает, что почти две трети энергии пошли на ненужные траты, стали рассеянным в пустую теплом, были потрачены на истирание деталей машины, образование искр и т. п.

Важно. 35% совсем не плохой КПД. У паровозов первой половины 20 века он составлял всего 10%. Лишь одна десятая образующегося при сгорании топлива тепла шла на перемещение состава, остальное рассеивалось в атмосфере. Среднеэксплуатационный КПД у современных тепловозов 20-22%. КПД машин на бензиновом ДВС равен 25%. КПД дизеля – 33%. Хорошо на этом фоне выглядит КПД электромобилей. Он у них около 90%.

В формуле нахождения полезной работы да в физике в основном КПД обозначают буквой из греческого алфавита η (эта).

Полезная работа в физике и ненужные траты энергии

Прежде чем говорить о том, как найти полезную работу в физике, следует сказать о ней самой. Дело в том что полезная работа в физике – величина очень даже субъективная. Она напрямую связана с человеческим восприятием, с тем, чего нам нужно получить от системы. Поэтому часто, когда говорят о КПД, имеют в виду различные технические устройства, а не природные объекты.

Хотя технологии постоянно развиваются избежать значительных потерь энергии всё же не удаётся. Получается, что:

Aзатр > Aполез

Aзатр – затраченная работа, Aполез – полезная работа, та что идёт на осуществление нужного нам процесса.

Как бы мы ни пытались уменьшить ненужные потери энергии, полностью от них избавиться не получиться. Непреодолимой преградой для этого является первый закон термодинамики. Из него явственно следует, что КПД любого устройства и механизма ни при каких обстоятельствах не может быть больше единицы и даже стать равным ей.

Мощность представляет собой работу, совершённую за единицу времени. В связи с этим КПД можно посчитать как отношение входной мощности системы к выходной. Т. е.

η = Pвх/Pвых.

Как найти полезную работу в физике используя формулы для разных физических процессов

Вид формул, как найти полезную работу в физике, зависит от природы физических явлений, использующихся для преобразования затраченной энергии в нужную.

Как найти полезную работу в физике механической системы

Лучше всего это показать на конкретном примере. Допустим, нам требуется найти КПД процесса, при котором мальчик вкатывает санки весом 4 кг на горку длиной 12, высотой 2 м. Он прикладывает для этого силу, равную 15 Н.

Решение:

Напомним, что общая формула для КПД

η = (Aполез/Aзатр) * 100%

Aполез в нашем случае равна потенциальной энергии (Eп), которую нужно потратить на то, чтобы поднять санки на высоту, т. е.  Aполез = m*g*h.

Затраченная мальчиком работа равна произведению силы на перемещение, т. е. Aзатр = F*S.

Подставляем в общую формулу для КПД

η = (m*g*h*100)/(F*S)

При подстановке численных значений получаем

η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %

Из этого примера ясно, чему равна полезная работа в физике механической системы, выраженная через КПД.

Формула полезной работы в физике термодинамической системы

Именно по ней судят об эффективности тепловых машин. Допустим, нам нужно отыскать КПД тепловой машины, рабочее тело которой берёт от нагревателя 20кДж, а холодильнику отдаёт 10кДж.

Решение:

Тепловая машина работает следующим образом: нагреватель передаёт определённое количество теплоты рабочему телу, оно из-за этого расширяется, совершая тем самым механическую работу. Однако в последнюю переходит далеко не вся часть переданной тепловой энергии. Чтобы вернуть систему в исходное состояние и начать новый цикл приходится использовать холодильник.

Из выше сказанного можно сделать вывод, что Aполез равна разности энергии взятой от нагревателя и энергии, забранной холодильником, т. е.

Aполез = Qнагревателя – Qхолодильника

Затраченная работа равняется количеству той теплоты, которая была сообщена нагревателю.

Если всё это подставим в формулу для КПД, то получим

[eta=(text { Qнагревателя }-text { Qхолодильника })^{*} 100 / text { Qнагревателя }]

После подстановки численных значений будем иметь

η = (20 – 10)/20*100% = 50%

Теперь ясно, как определить полезную работу в физике термодинамической системы.

Формула полезной работы в физике электродинамической системы

Очень важный класс явлений. Каждый день все пользуются самыми разными электрическими устройствами: телевизором, компьютером, телефоном и т. д. Но мы рассмотрим случай попроще. Вычислим КПД электрического чайника. Допустим воде было передано 22176 Дж тепла за 2 мин. Напряжение в электросети стандартное 220 В. Сила тока равняется 1,4 А.

Решение:

Aполез будем считать работу, которая пошла на нагрев воды. Хотя она нам и дана из условия, формулу вспомнить всё равно не будет лишним.

• Q = cm(tконечная-tначальная)
• Q — количество теплоты [Дж]
• c — удельная теплоёмкость вещества [Дж/кг*˚C]
• m — масса [кг]
• tконечная — конечная температура [˚C]
• tначальная — начальная температура [˚C]
• Работа тока вычисляется по формуле
• A = (I^2)*Rt = (U^2)/R *t = UIt
• A — работа электрического тока [Дж]
• I — сила тока [А]
• U — напряжение [В]
• R — сопротивление [Ом]
• t — время [c]

В нашем примере она примет вид

η = Q/A *100% = Q/UIt *100%

Переводим минуты в секунды и, подставляя численные значения, получаем

η = 22176/220*1,4*120 *100% = 60%

Формула полезной работы электродинамической системы будет:

В этой главе…

• Достигаем теплового равновесия
• Сохраняем тепловую энергию при различных условиях
• Повышаем эффективность тепловых двигателей
• Падаем почти до абсолютного нуля

Каждому, кому когда-либо приходилось работать летом на открытом воздухе, хорошо известны понятия “тепло” и “работа”, связь между которыми изучает термодинамика. В данной главе, наконец-то, встречаются эти два незабвенных понятия, о которых подробно рассказывается в главе 8 (о работе) и в главе 13 (о тепле, теплоте и тепловой энергии). В термодинамике имеется три закона, а точнее начала, которые также важны для термодинамики, как и законы Ньютона для механики. Кроме того, уж в одном отношении они даже превосходят законы Ньютона, а именно в том, что в термодинамике имеется еще и нулевой закон, который чаще называют нулевым началом термодинамики. В этой главе рассказывается о термодинамическом равновесии (нулевое начало), сохранении энергии (первое начало), о тепловых потоках (второе начало) и недостижимости абсолютного нуля (третье начало). Итак, самое время обратиться к термодинамике.

Стремимся к тепловому равновесию: нулевое начало термодинамики

Основные законы термодинамики начинаются с нулевого начала. Возможно, эта нумерация покажется странной, ведь мало какой набор вещей из повседневной жизни начинается подобным образом (“Будь осторожен на нулевой ступеньке…”), но, знаете ли, физикам нравятся их традиции. Так вот, нулевое начало термодинамики гласит, что два тела находятся в тепловом равновесии, если они могут передавать друг другу теплоту, но не делают этого. (В русскоязычной научной литературе нулевое начало термодинамики называют также общим началом термодинамики. — Примеч. ред.)

Например, если у вас и у воды в плавательном бассейне, в котором вы находитесь, одна и та же температура, то никакое тепло от вас к воде или от воды к вам не передается (хотя такая передача возможна). Ваше тело и бассейн находятся в тепловом равновесии. Однако, если вы прыгнете в бассейн зимой, проломив при этом его ледяную корку, то первое время вряд ли будете в тепловом равновесии с его водой. Впрочем, вы и не захотите этого. (Не пытайтесь проделать этот физический опыт дома!)

Чтобы обнаружить тепловое равновесие (особенно в замерзших бассейнах, куда вы собираетесь прыгнуть), надо использовать термометр. Измерьте с его помощью температуру воды в бассейне, а затем — свою температуру. Если обе температуры совпадают (другими словами, наблюдается тепловое равновесие: ваше — с термометром, а термометра — с водой в бассейне), то в таком случае вы находитесь в тепловом равновесии с водой бассейна.

Использование термометра показывает: два тела, находящиеся в тепловом равновесии с третьим, также находятся в тепловом равновесии друг с другом; вот вам еще одна формулировка нулевого начала.

Кроме всего прочего, нулевое начало содержит идею, что температура — это индикатор теплового равновесия. То, что два тела, упомянутые в нулевом законе, находятся в тепловом равновесии с третьим, дает все нужное дая задания температурной шкалы, например шкалы Кельвина. Ну а с физической точки зрения нулевой закон устанавливает точку отсчета, утверждая, что между двумя телами, имеющими одинаковую температуру, тепловой поток в целом отсутствует.

Сохраняем энергию: первое начало термодинамики

Первое начало термодинамики — это, попросту говоря, закон сохранения энергии. Он утверждает, что энергия никуда не исчезает. Когда системой поглощается или высвобождается тепловая энергия ​( Q )​, а сама система выполняет над окружающими телами работу ​( W )​ (или, наоборот, окружающие тела выполняют работу над ней), то внутренняя энергия системы, имевшая начальное значение ​( U_н )​, становится равной ( U_к ) следующим образом:

В главе 8 немало говорится о сохранении механической энергии. Там показано, что общая механическая энергия (сумма потенциальной и кинетической энергии) сохраняется. Чтобы утверждать такое, надо было работать с системами, где энергия не тратится на нагревание, — например, когда отсутствует трение. Теперь все изменилось. Тепловая энергия, наконец-то, учитывается нами (как вы, вероятно, поняли из рассуждений), и теперь общую энергию системы можно рассматривать с учетом передачи тепловой энергии, проделанной работы и внутренней энергии системы.

На основании комбинации этих трех величин (тепловой энергии, работы и внутренней энергии) определяется общая энергия системы, которая в целом сохраняется. Если передать системе количество тепловой энергии, равное ( Q ), то при отсутствии работы ее количество внутренней энергии, обозначаемое как ( U ), изменится на ( Q ). Система может терять энергию, выполняя работу над окружающими телами, например, когда машина поднимает груз, висящий на конце каната. Так вот, когда система выполняет работу над окружающими телами и никакой тепловой энергии не тратит, ее внутренняя энергия ( U ) изменится на ( W ). Иначе говоря, если учитывать тепловую энергию, то с учетом всех этих трех величин (тепловой энергии, работы и внутренней энергии) общая энергия системы сохраняется.

Польза первого начала термодинамики состоит в том, что оно связывает все три основные величины: тепловую энергию, работу и внутреннюю энергию. Зная две из них, всегда можно определить третью.

Применяем закон сохранения энергии

Величина передаваемой тепловой энергии ( Q ) является положительной или отрицательной, когда система, соответственно, поглощает или высвобождает тепловую энергию. Величина работы ( W ) является положительной или отрицательной, когда работа, соответственно, выполняется системой над окружающими телами или окружающими телами над системой.

Новички часто путаются, пытаясь определить, являются ли значения каждой из величин положительными или отрицательными. Чтобы не запутаться, при работе с первым началом термодинамики рекомендуется исходить из общей идеи сохранения энергии. Допустим, что мотор выполняет над окружающими телами работу в 2000 Дж, высвобождая при этом 3000 Дж тепловой энергии. Насколько меняется его внутренняя энергия? В данном случае известно, что мотор выполняет над окружающими телами работу в 2000 Дж, поэтому ясно, что его внутренняя энергия уменьшается на 2000 Дж. Кроме того, выполняя работу, он еще высвобождает 3000 Дж тепловой энергии, так что внутренняя энергия мотора уменьшается еще на 3000 Дж.

Значения работы и передаваемой тепловой энергии следует считать отрицательными. Тогда в предыдущем примере получим такое изменение внутренней энергии:

Внутренняя энергия системы уменьшается на 5000 Дж, что определенно имеет смысл, ведь система выполняет над окружающими телами работу в 2000 Дж и высвобождает 3000 Дж тепловой энергии. С другой стороны, а что если система, выполняя над окружающими телами работу в 2000 Дж, поглощает 3000 Дж их тепловой энергии? В таком случае получилось бы 2000 Дж входящей и 3000 Дж исходящей энергии. Теперь понятно, какими должны быть знаки:

В данном случае общее изменение внутренней энергии системы равно +1000 Дж. Отрицательное значение работа принимает, когда она выполняется над системой окружающими телами. Например, система поглощает 3000 Дж, в то время как окружающие тела выполняют над ней работу в 4000 Дж. Это значит, что внутренняя энергия системы увеличивается на 3000 Дж + 4000 Дж = 7000 Дж. А если нужно все просчитать, то воспользуйтесь следующей формулой:

а затем обратите внимание, что поскольку окружающие тела выполняют работу над системой, значение ​( W )​ считается отрицательным. Таким образом, получаем:

Изучаем изобарические, изохорические, изотермические и адиабатические процессы

В этой главе рассматриваются процессы, при анализе которых приходится работать с такими параметрами, как объем, давление, температура и энергия. Причем полученные результаты очень сильно зависят от того, как эти величины меняются. Например, если газ выполняет работу, сохраняя свой объем постоянным, то этот процесс будет отличаться от того, при котором остается постоянным не объем, а давление газа.

В термодинамике обычно рассматривают четыре стандартных режима, которые отличаются постоянством одного из вышеперечисленных параметров (давление, объем, температура и энергия).

Обратите внимание, что изменения в процессах, описанных в последующих разделах, называются квазистатическими, т.е. эти изменения проходят достаточно медленно, позволяя давлению и температуре оставаться одинаковыми в любом месте системы.

Постоянное давление: изобарический процесс

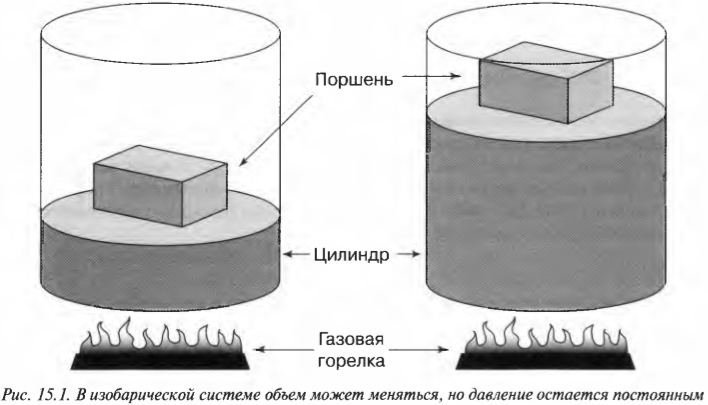
Процесс, в котором давление остается постоянным, называется изобарическим (“барический” означает “относящийся к давлению”). На рис. 15.1 показан цилиндр с поршнем, поднимаемым некоторым количеством газа, когда этот газ нагревается. Объем газа меняется, но утяжеленный поршень сохраняет давление постоянным.

Какую работу выполняет система при расширении газа? Работа равна произведению ​( F )​ на ​( s )​, означающих, соответственно, силу и перемещение. Кроме того, сила равна произведению ​( P )​ на ​( A )​, означающих, соответственно, давление и площадь. Это значит, что:

Но произведение площади ( A ) и перемещения ( s ) равно изменению объема ​( Delta!V )​. Таким образом:

Изобарический процесс можно показать в виде графика (как на рис. 15.2), на котором видно, что объем меняется, в то время как давление остается постоянным. Так как ​( W=PDelta!V )​, то работа — это площадь, ограниченная графиком.

Допустим, имеется 60 м³ идеального газа под давлением в 200 Па (см. главу 2), который нагревается до тех пор, пока он не расширится до объема в 120 м³ (​( PV= nRT )​, где ​( n )​, ​( R )​ и ​( Т )​ означают, соответственно, количество молей, универсальную газовую постоянную (8,31) и температуру; см. главу 14). Какую работу выполняет газ? Все, что вам нужно, — это подставить в формулу численные значения:

Расширяясь при постоянном давлении, газ выполняет работу в 12000 Дж.

Постоянный объем: изохорический процесс

А что если давление в системе не постоянно? В конце концов, не так уж и часто попадаются устройства с утяжеленным поршнем, как на рис. 15.1. Чаще всего приходится иметь дело с простым замкнутым сосудом, как на рис. 15.3, где показан баллончик с дезодорантом, кем-то неосторожно брошенный в огонь. В этом случае объем остается постоянным, а такой процесс называется изохорическим. По мере того как газ внутри баллончика нагревается, его давление возрастает, но объем остается постоянным (если, конечно, баллончик не взорвется).

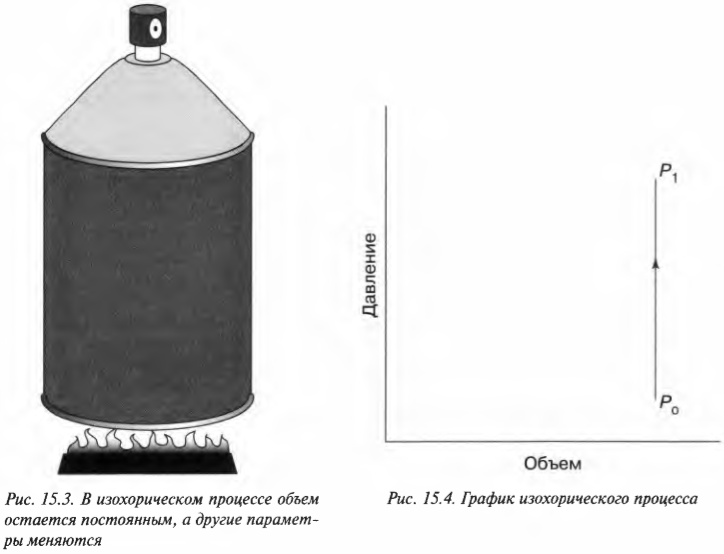
Какая работа выполняется с баллончиком распылителя? Посмотрите на график (рис. 15.4). В данном случае объем постоянный, поэтому ​( Fs )​ (произведение силы и перемещения) равно нулю. Никакая работа не выполняется — площадь под графиком равна нулю.

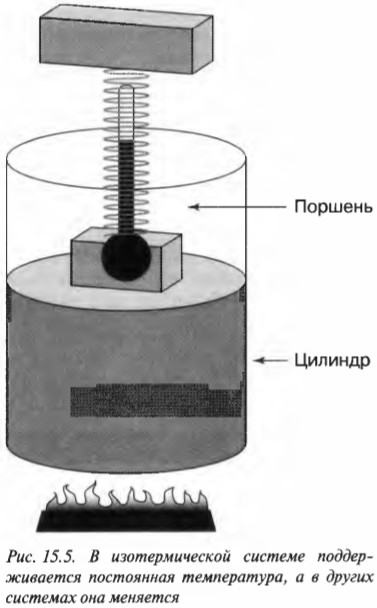
Постоянная температура: изотермический процесс

В изотермическом процессе температура остается постоянной, в то время как другие величины меняются. Посмотрите, какой замечательный аппарат показан на рис. 15.5. Этот аппарат специально предназначен для того, чтобы сохранять температуру газа постоянной, причем даже при подъеме поршня. При добавлении к системе (или отводе от системы) тепловой энергии поршень медленно поднимается (или медленно опускается) таким образом, чтобы произведение давления и объема сохранялось постоянным. Так как ( PV= nRT ) (см. главу 14), то температура также остается постоянной.

Какая работа выполняется при изменении объема? Поскольку ( PV= nRT ), то получается такое отношение между ​( P )​ и ​( V )​:

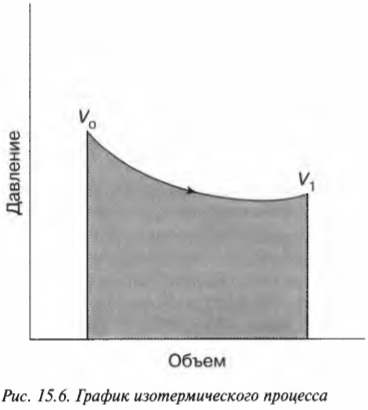
Эту формулу иллюстрирует график, показанный на рис. 15.6.

Выполненную работу “показывает” область, лежащая под графиком. Но какова же площадь этой области? Выполненная работа определяется следующей формулой, где ​( ln )​ — натуральный логарифм, ​( R )​ — газовая постоянная (8,31), ​( V_1 )​ и ​( V_0 )​ означают, соответственно, конечный и начальный объем:

Так как при изотермическом процессе температура остается постоянной, а внутренняя энергия идеального газа равна ​( (3/2)nRT )​ (см. главу 14), то эта энергия не меняется. Таким образом:

другими словами:

Итак, что произойдет, если цилиндр, показанный на рис. 15.5, погрузить в горячую ванну? В аппарат должна перейти тепловая энергия ​( Q )​, а поскольку температура газа остается постоянной, вся эта тепловая энергия должна превратиться в работу, выполненную системой. Скажем, к примеру, у вас имеется моль гелия при температуре 20°С, и, забавы ради, вы решили увеличить его объем с ​( V_0 )​ = 0,010 м³ до ( V_1 )​ = 0,020 м³. Какую работу выполнит газ при расширении? Все, что вам нужно, — это подставить в формулу численные значения:

Работа, выполняемая газом, равна 1690 Дж. Изменение его внутренней энергии равно 0 Дж, как всегда при изотермическом процессе. А так как ​( Q=W )​, то добавляемая к газу тепловая энергия также равна 1690 Дж.

Постоянная энергия: адиабатический процесс

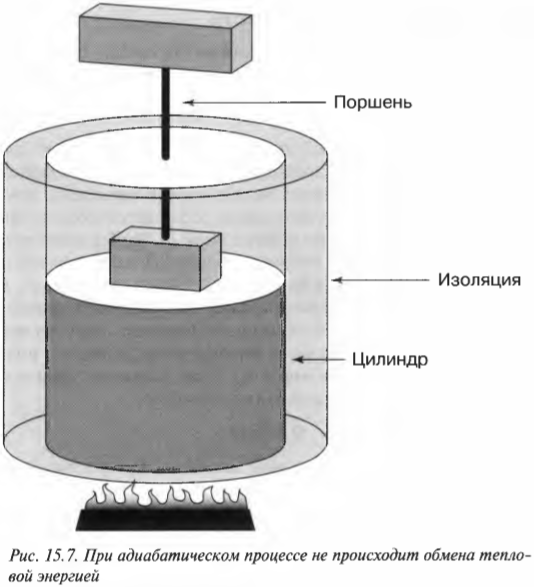
При адиабатическом процессе общая тепловая энергия системы остается постоянной. Посмотрите на рис. 15.7, где показан цилиндр, окруженный изоляционным материалом. Тепловая энергия из системы никуда не уходит, поэтому если происходит изменение, то оно является адиабатическим.

Вычисляя работу, выполняемую при адиабатическом процессе, вы можете сказать, что ​( Q )​ = 0, таким образом:

Так как внутренняя энергия ​( U )​ идеального газа равна ​( (3/2)nRT )​ (см. главу 14), то выполняется работа:

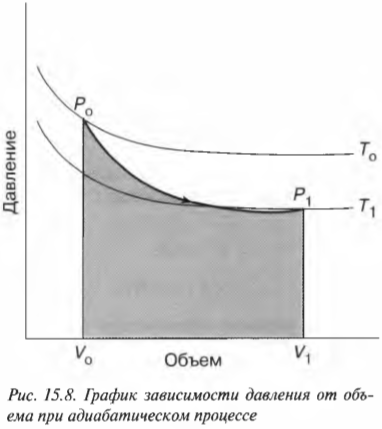
где ​( T_0 )​ и ( T_1 ) означают, соответственно, начальную и конечную температуру. Таким образом, если газ выполняет работу, то это происходит благодаря изменению температуры — при падении температуры газ выполняет работу над окружающими телами. На рис. 15.8 показан график зависимости давления от объема при адиабатическом процессе. Адиабатическая кривая, показанная на этом рисунке, так называемая адиабата, отличается от изотермических кривых, так называемых изотерм. Работа, выполненная, когда общая тепловая энергия системы постоянна, — это область под адиабатой (см. рис. 15.8).

Вычисляем удельную теплоемкость

Начальные значения давления и объема можно так связать с их конечными значениями по следующей формуле:

Что такое ​( gamma )​? Это отношение ​( C_p/C_v )​ двух удельных теплоемкостей идеального газа: в числителе — теплоемкость при постоянном давлении ​( C_p )​, а в знаменателе — теплоемкость при постоянном объеме ( C_v ). Удельной теплоемкостью называется отношение тепловой энергии, полученной телом единичной массы, к соответствующему приращению его температуры; подробнее об этом можно узнать в главе 13. Чтобы вычислить удельную теплоемкость, надо найти количество тепловой энергии ​( Q )​, необходимой для изменения температуры тела единичной массы на величину ​( Delta T )​, т.е. ​( c=Q/mDelta T )​, где ​( c )​, ​( m )​ и ( Delta T ) означают, соответственно, удельную теплоемкость, массу и изменение температуры. Впрочем, сейчас удобнее использовать молярную удельную теплоемкость, которая определяется как и удельная, но только рассчитывается не на единицу массу, а на один моль. Она обозначается символом ​( C )​ и измеряется в Дж/(моль·К). Итак, молярная удельная теплоемкость используется вместе с количеством молей ​( n )​, а не массой ​( m )​:

Как найти ​( C )​? Надо вычислить две разные величины: ​( C_mathrm{p} )​ (при постоянном давлении) и ( C_mathrm{v} ) (при постоянном объеме). Согласно первому началу термодинамики (см. предыдущий раздел этой главы), ​( Q=Delta U+W )​. Поэтому достаточно только выразить ​( Delta U )​ через ​( T )​. Выполняемая работа ​( W )​ равна ​( PDelta!V )​, тогда при постоянном объеме ​( W )​ = 0. А изменение внутренней энергии идеального газа равно ​( (3/2)nRDelta T )​ (см. главу 14), поэтому ​( Q )​ при постоянном объеме выражается следующей формулой:

При постоянном давлении работа ​( W )​ равна ( PDelta!V ). А поскольку ​( PV= nRT )​, то ​( W=P(V_1-V_0)=nR(T_1-T_0) )​. Поэтому ​( Q )​ при постоянном давлении выражается следующей формулой:

Каким образом можно получить из всего этого значения молярных удельных теплоемкостей? Как уже нам известно, ​( Q=CnDelta T )​, поэтому ( C=Q/nDelta T ). Деля предыдущие две формулы на ( nDelta T ), получаем:

Теперь вы имеете молярные удельные теплоемкости идеального газа. Нужное вам отношение ​( gamma )​ равно отношению этих двух формул:

Связать давление и объем в любых двух точках адиабаты (см. предыдущий раздел об адиабатическом процессе) можно таким образом:

Например, если сначала 1 л газа находился под давлением 1 атм, а после адиабатического изменения (когда обмена тепловой энергией нет), объем газа стал 2 л, то каким должно быть новое давление ​( P_1 )​? Путем простой алгебраической операции деления на ​( V_1^{5/3} )​ оставляем в левой части равенства только ( P_1 )​ и получаем:

Подставив в эту формулу численные значения, получим:

Итак, новое давление должно быть равно 0,314 атмосферы.

Передаем тепловую энергию: второе начало термодинамики

Формально говоря, второе начало термодинамики гласит, что тепловая энергия естественно переходит из тела с более высокой температурой в тело с более низкой температурой, но не в обратном направлении.

Это начало, конечно же, появилось в результате простых наблюдений: приходилось ли вам когда-либо видеть, чтобы тело само становилось холоднее окружающих его тел, если только другое тело не проделало над ним определенной работы? Путем определенной работы можно заставить теплоту переходить из тела, когда естественно ожидать перехода тепловой энергии в тело (вспомните холодильники или кондиционеры), но такое явление само по себе не происходит.

Заставим тепловую энергию работать: тепловые двигатели

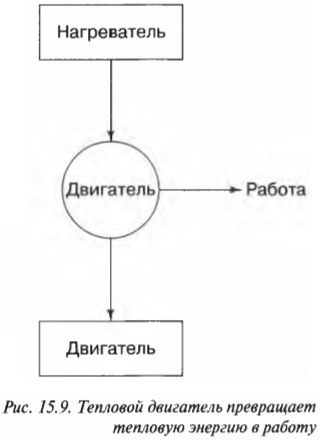
Имеется много способов заставить тепловую энергию работать. Возможно, у вас имеется, например, паровая машина с котлом и поршнями или атомный реактор, производящий перегретый пар, который может вращать турбину. Двигатели, выполняющие работу благодаря источнику тепловой энергии, называются тепловыми. Как они это делают, можно увидеть на рис. 15.9. Тепловая энергия идет от нагревателя к двигателю, который выполняет работу, а неизрасходованная тепловая энергия отправляется в холодильник. Им может быть, например, окружающий воздух или наполненный водой радиатор. Если температура холодильника меньше температуры нагревателя, то тепловой двигатель может работать — хотя бы теоретически.

Оцениваем эффективность работы: КПД теплового двигателя

Тепловая энергия, подаваемая нагревателем, обозначается как ​( Q_{нг} )​, а отправляемая в холодильник (см. предыдущий раздел) — как ​( Q_{mathrm{x}} )​. Путем некоторых вычислений можно найти коэффициент полезного действия (КПД) теплового двигателя. Он равен отношению работы ​( W )​, выполняемой двигателем, к входящей тепловой энергии — иными словами, это та доля входящей тепловой энергии, которую двигатель превращает в работу:

Когда вся входящая тепловая энергия превращается в работу, КПД равен 1. Если никакая входящая тепловая энергия не превращается в работу, КПД равен 0. Часто КПД выражается в виде процентов, поэтому только что названные значения можно представить как 100% и 0%. Поскольку общая энергия сохраняется, то тепловая энергия, входящая в двигатель, должна быть равна сумме выполняемой работы и тепловой энергии, отправляемой в холодильник, то есть:

Это значит, что для записи КПД достаточно использовать ( Q_{нг} ) и ( Q_{mathrm{x}} ):

Допустим, что имеется тепловой двигатель с КПД, равным 78%. Этот двигатель производит работу величиной 2,55·10⁷ Дж. Сколько тепловой энергии он использует, а сколько выбрасывает? Известно, что ​( W )​ = 2,55·10⁷ Дж и

Это значит, что:

Количество входящей тепловой энергии равно 3,27·10⁷ Дж. А сколько тепловой энергии ( Q_{mathrm{x}} ) остается неизрасходованной и отправляется в холодильник? Как известно:

поэтому:

Подставив в эту формулу численные значения, получим:

Количество тепловой энергии, отправляемое в холодильник, равно 0,72·10⁷ Дж.

Как сказал Карно: нельзя все тепло превратить в работу

Зная работу и КПД теплового двигателя, можно вычислить количество входящей и исходящей тепловой энергии (тут нам, конечно, поможет закон сохранения энергии, связывающий друг с другом работу, входящую и исходящую тепловую энергию; см. главу 8). А как насчет создания тепловых двигателей со 100%-ным КПД? С точки зрения производительности было бы прекрасно превращать в работу всю тепловую энергию, какая поступает в тепловой двигатель, но это невозможно. Кроме того, в реально работающих тепловых двигателях неизбежны определенные потери, например, из-за трения поршней в паровом двигателе. В XIX веке эту проблему изучал один инженер, которого звали Сади Карно, и он пришел к выводу: в сущности, лучшее, что можно сделать, — это попытаться изобрести двигатель, не имеющий таких потерь.

А если в двигателе нет потерь, то система будет возвращаться в то же состояние, что и перед началом процесса. Такой процесс называется обратимым. Например, если тепловой двигатель тратит энергию на преодоление трения, то обратимым процесс назвать нельзя, так как он не заканчивается в том же состоянии, в каком был сначала. При каких условиях работы тепловой двигатель будет иметь самый высокий КПД? Когда работа двигателя обратима (т.е. в системе нет потерь). Сегодня физики называют это принципом Карно. Итак, принцип Карно гласит, что ни у одного необратимого двигателя не будет такого же высокого КПД, как у обратимого, а все обратимые двигатели, работающие в промежутке между одинаковыми максимальными и одинаковыми минимальными температурами, имеют один и тот же КПД.

Построение двигателя Карно

Карно предложил свою идею двигателя — двигателя Карно. Этот двигатель должен работать обратимо, что не может быть ни в одном реально работающем двигателе, поэтому он представляет собой нечто идеальное. В двигателе Карно тепловая энергия идет от нагревателя, имеющего постоянную температуру ​( T_{нг} )​. А отработанная тепловая энергия уходит в холодильник, имеющий постоянную температуру ( T_{х} ). Поскольку температуры нагревателя и холодильника никогда не меняются, то можно сказать, что отношение подаваемой и отводимой тепловой энергии равно отношению их температур (в кельвинах):

А так как КПД теплового двигателя вычисляется по следующей формуле:

то получается такая формула для вычисления КПД двигателя Карно:

где температура выражается в кельвинах.

В этой формуле показан максимально возможный КПД теплового двигателя. И лучшего результата достичь нельзя. А как гласит третье начало термодинамики (в последнем разделе этой главы), абсолютного нуля достичь нельзя, т.е. ( T_{х} ) никогда не будет равна нулю, следовательно, невозможно получить тепловой двигатель со 100%-ным КПД.

Используем формулу Карно

Формулу максимально возможного КПД (см. предыдущий раздел) использовать довольно легко. Предположим, сделано потрясающее новое изобретение: машина Карно, в которой самолет совершает работу, причем земная поверхность играет роль нагревателя (с температурой примерно 27°С), а воздух на высоте 10000 м — роль холодильника (с температурой примерно -27°С). Какой максимальный КПД такой машины? Преобразуем значения температуры в кельвины и подставив их в формулу машины Карно:

Итак, КПД такой машины Карно равен всего 17,3%. Результат, скажем, не очень. А теперь представим, что в качестве нагревателя используется поверхность Солнца (примерно 5800 К), а в качестве холодильника — межзвездное пространство (примерно 3,4 К), совсем как в научно-фантастических рассказах. Тогда совсем другое дело:

Итак, в таких научно-фантастических условиях для машины Карно можно получить КПД, равный 99,9% и близкий к теоретически максимальному значению.

Охлаждаемся: третье (и абсолютно последнее) начало термодинамики

Третье начало термодинамики достаточно просто формулируется: нельзя достичь абсолютного нуля с помощью любого процесса, состоящего из конечного числа этапов, к нему можно лишь бесконечно приближаться. Иначе говоря, никогда нельзя достичь абсолютного нуля. Каждое действие по понижению температуры физического тела до абсолютного нуля может немного приблизить к цели, но достигнуть ее нельзя, если не выполнить бесконечного числа действий, что невозможно.

Странные явления вблизи абсолютного нуля

Хотя до абсолютного нуля нельзя добраться с помощью какого-либо известного конечного процесса, но к нему можно приблизиться. Причем, имея очень дорогое оборудование, вблизи абсолютного нуля можно столкнуться с множеством странных физических явлений и фактов. Один мой приятель изучает поведение жидкого гелия при очень низких температурах. Например, гелий становится таким эксцентричным, что может самостоятельно выбраться из любого сосуда, в котором он находится. За открытие и исследования этого явления сверхтекучести гелия и некоторые другие наблюдения кое-кто получил Нобелевскую премию. Везет же людям!

(Сверхтекучесть жидкого гелия-4 была открыта в 1938 году П. Л. Капицей, за что он был удостоен Нобелевской премии по физике за 1978 год. Теория сверхтекучего гелия-Н была разработана Л. Д. Ландау, за что он был удостоен Нобелевской премии по физике за 1962 год. — Примеч. ред.)

Первый закон термодинамики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

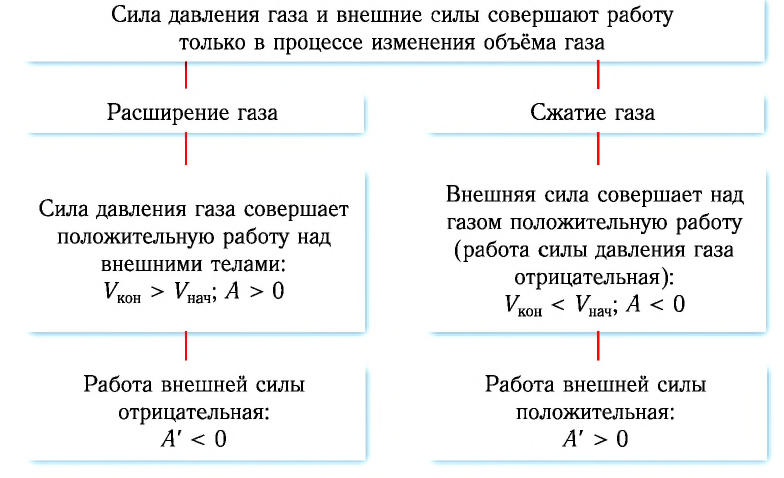
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

к оглавлению ▴

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние (рис. 1).

Рис. 1.

Работа газа равна:

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

(1)

Если и — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма до объёма . С помощью аналогичных рассуждений приходим к формуле:

Но , и снова получается формула (1).

Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

к оглавлению ▴

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу . Тогда работа газа во всём процессе найдётся суммированием этих малых работ:

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь

к оглавлению ▴

Работа, совершаемая над газом

Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу , которую поршень совершает над газом.

Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой , равной силе по модулю и противоположной по направлению: (рис. 4).

Рис. 4. Внешняя сила , действующая на газ

Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:

Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:

(2)

Нас больше всего интересует случай, когда тело является газом. Тогда (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или

(3)

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

к оглавлению ▴

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:

Всё подведённое к газу тепло идёт на совершение газом работы.

2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:

к оглавлению ▴

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе . Из первого закона термодинамики получаем: , или .

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет , поэтому : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

Содержание:

Работа в термодинамике:

В 9 классе вы узнали, что работа силы (механическая работа) связана с превращением одного вида энергии в другой, например, механической энергии во внутреннюю. Работу силы рассматривают как меру изменения энергии физической системы. А как определить работу в термодинамике? Как может быть выражена эта работа через макроскопические параметры — давление и об1

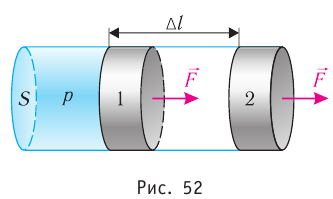
Рассмотрим газ, находящийся в цилиндрическом сосуде с площадью основания S, закрытом подвижным поршнем (рис. 52).

Взаимодействие газа с поршнем, а также со стенками сосуда можно характеризовать давлением р, которое газ оказывает на них. Допустим, что в результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние

Модуль силы давления газа, действующей на поршень, F = pS. Эта сила совершает работу по перемещению поршня

 (10.1)

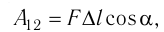
где а — угол между направлениями силы и перемещения. В рассматриваемом примере а = 0, тогда

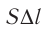
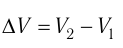
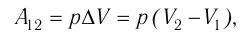
Произведение определяет приращение объёма (см. рис. 52), поэтому работа газа при его изобарном расширении

 (10.2)

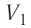
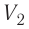
где — начальный объём газа, — объём газа в конечном состоянии.

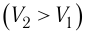
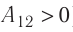
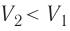
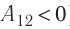
Так как давление р газа всегда величина положительная, из формулы (10.2) следует, что, если газ расширяется , работа, совершённая силой давления газа, положительная (), а в случае сжатия () работа отрицательная ().

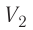
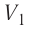
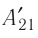
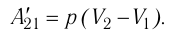
Процесс медленного изобарного сжатия газа из состояния 2 с начальным объёмом в состояние 1 с конечным объёмом можно характеризовать работой внешних сил над газом:
 (10.З)

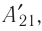
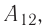
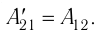
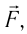
Из сравнения равенств (10.2) и (10.3) вытекает соотношение между работой у совершённой внешними силами, и работой совершённой силой давления газа:Это соотношение согласуется с третьим законом Ньютона (внешняя сила действующая на газ со стороны поршня, имеет
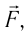
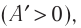
направление, противоположное силе давления действующей на поршень со стороны газа). Из формулы (10.3) видно, что работа, совершённая внешними силами, положительная если происходит сжатие газа
Если газ расширяется 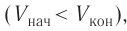), то работа, совершённая внешними силами отрицательная

Геометрическое толкование работы

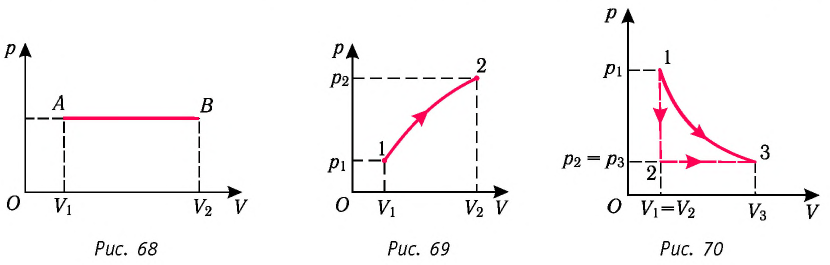
Построим график зависимости давления газа от его объёма при р = const. Как видно из рисунка 53, при изобарном расширении газа работа, совершённая силой давления газа, численно равна площади прямоугольника

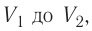
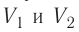
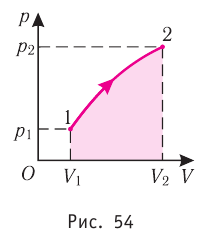
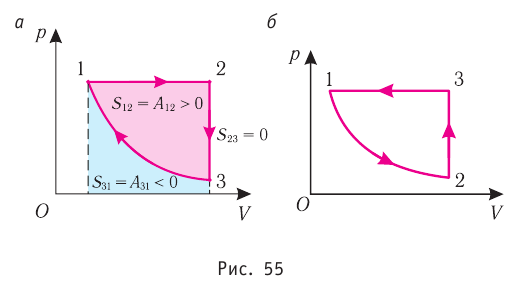
Если процесс перехода газа из начального состояния в конечное не является изобарным, то работа, совершённая силой давления газа при изменении его объёма от численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов (рис. 54).

Процесс, при котором термодинамическая система, прошедшая некоторую последовательность состояний, снова возвращается в исходное состояние, называют циклическим процессом или циклом (рис. 55). Работа, совершаемая системой при циклическом процессе, или работа цикла, равна площади фигуры, ограниченной линиями, которые изображают цикл:

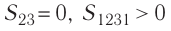
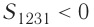
где на рисунке 55, а и на рисунке 55, б.

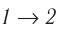
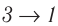
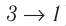
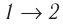
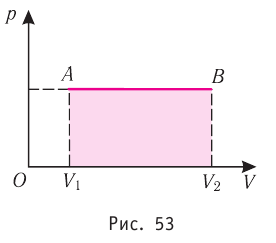
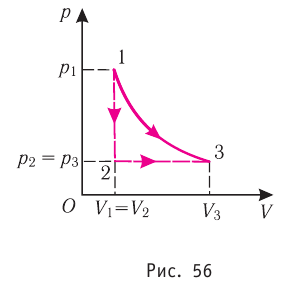
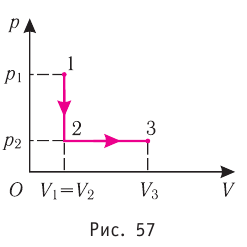
Если «кривая расширения» (изобара) (см. рис. 55, а) расположена выше «кривой сжатия» (изотерма ), то полная работа, совершённая системой за цикл (работа цикла), положительная. Если же, как изображено на рисунке 55, б, «кривая сжатия» (изобара ) расположена выше «кривой расширения» (изотерма), то работа цикла отрицательная.

Из рисунка 56 видно, что численное значение работы цикла определяется не только начальным и конечным состояниями системы, но и видом процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения, либо сначала изохорно понизив его давление до значения а затем изобарно увеличив его объём от значения до значения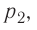

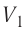
Как видно из рисунка 56, в первом случае работа, совершённая силами давления газа, больше, чем во втором. Следовательно, работа, совершаемая при переходе термодинамической системы из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.

Количество теплоты и удельная теплоёмкость

Итак, существуют два способа передачи энергии от одного тела к другому. Первый характеризуется передачей энергии в процессе механического взаимодействия тел — механическая энергия одного тела переходит в энергию хаотического движения частиц вещества другого тела или, наоборот, убыль энергии хаотического движения частиц вещества одного тела сказывается на увеличении механической энергии другого тела. Такую форму передачи энергии в термодинамике (как и в механике) называют работой. Так, например, в рассмотренной нами ранее термодинамической системе (газ в цилиндрическом сосуде под поршнем) расширение газа приводит к перемещению поршня. При этом убыль внутренней энергии газа равна работе, совершённой силой давления газа, под действием которой поршень переместился.

Второй способ передачи энергии осуществляется при непосредственном обмене энергией между хаотически движущимися частицами взаимодействующих тел. За счёт переданной при этом энергии увеличивается внутренняя энергия одного тела и уменьшается внутренняя энергия другого. Если, например, привести в соприкосновение два тела с разными температурами, то частицы более нагретого тела будут передавать часть своей энергии частицам более холодного тела. В результате внутренняя энергия первого тела уменьшается, а второго тела увеличивается. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей. Как вы уже знаете, существуют три вида теплопередачи: теплопроводность, конвекция и излучение.

Количественной мерой энергии, переданной телу в процессе теплопередачи, является количество теплоты Q. В СИ единицей количества теплоты является джоуль (Дж). Иногда для измерения количества теплоты используют внесистемную единицу — калорию (1 кал = 4,19Дж).

Если процесс теплопередачи не сопровождается изменением агрегатного состояния вещества, то
 (10,4)
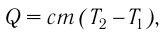
где m — масса тела, 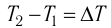— разность температур в конце и в начале процесса теплопередачи, с — удельная теплоёмкость вещества — физическая величина, численно равная количеству теплоты, которое получает или отдаёт вещество массой 1 кг при изменении его температуры на 1 К. Удельную
теплоемкость измеряют в джоулях, деленных на килограмм, кельвин
Физическая величина, равная произведению массы тела на удельную теплоёмкость вещества, носит название теплоёмкости тела. Обозначают теплоёмкость тела С и измеряют в джоулях на кельвин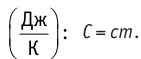Теплоёмкость, в отличие от удельной теплоёмкости, является тепловой характеристикой тела, а не вещества.
 

Удельная теплота плавления

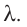
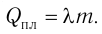
Физическую величину, численно равную количеству теплоты, необходимому для превращения кристаллического вещества массой 1 кг, взятого при температуре плавления, в жидкость той же температуры, называют удельной теплотой плавления Для плавления тела массой m, предварительно нагретого до температуры плавления, ему необходимо сообщить количество теплоты При кристаллизации тела выделяется количество теплоты

Удельная теплота парообразования

Физическую величину, численно равную количеству теплоты, которое необходимо передать жидкости массой 1 кг, находящейся при температуре кипения, для превращения её при постоянной температуре в пар, называют удельной теплотой парообразования L. Количество теплоты, необходимое для превращения жидкости массой m, предварительно нагретой до температуры кипения, в пар, определяют по формуле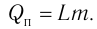Конденсация пара сопровождается выделением количества теплоты

Удельная теплота сгорания топлива

Физическую величину, численно равную количеству теплоты, выделяющемуся при полном сгорании топлива массой 1 кг, называют удельной теплотой сгорания топлива q. Количество теплоты, выделившееся при полном сгорании некоторой массы m топлива, определяют по формуле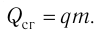Оно передаётся телам, образующим термодинамическую систему, и по отношению к ним является положительной величиной.

Отметим, что в результате теплопередачи могут изменяться как обе составляющие внутренней энергии тела, так и одна из них. При нагревании (охлаждении) изменяются кинетическая энергия хаотического движения частиц, которые составляют тело, и потенциальная энергия их взаимодействия. При плавлении (кристаллизации), кипении (конденсации) изменяется только потенциальная энергия взаимодействия частиц вещества.

При совершении работы также может изменяться как кинетическая, так и потенциальная энергия частиц вещества. Следовательно, как при теплопередаче, так и при совершении работы происходит изменение кинетической и потенциальной энергий частиц вещества, что приводит к изменению внутренней энергии тела.

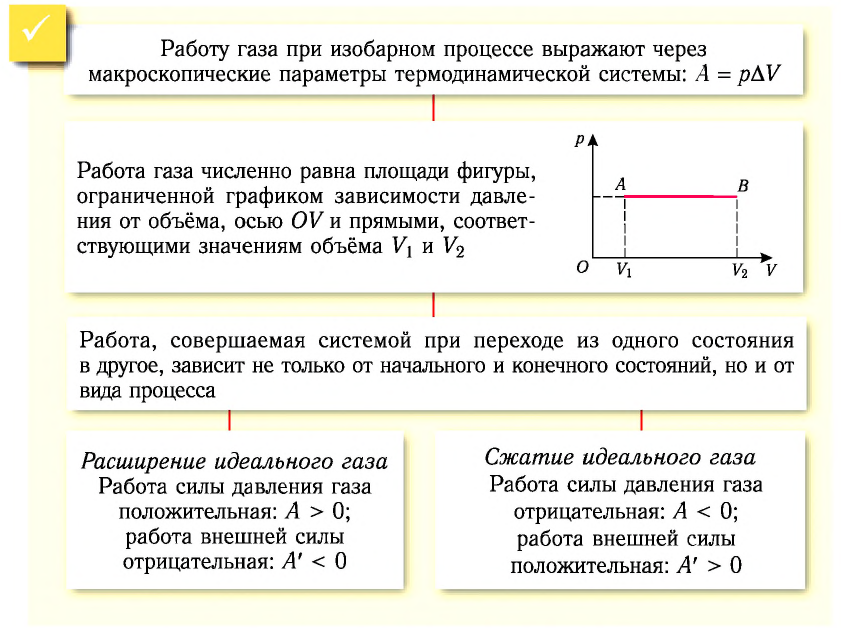
1. Работу газа при изобарном процессе выражают через макроскопические параметры термодинамической системы:

2.    Работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёмов

3.    Работа, совершаемая при переходе системы из одного состояния в другое, зависит не только от начального и конечного состояний, но и от вида процесса.

4.    Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей.

Пример №1

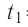
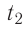
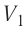
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от = 12 °С до = 87 °С, если давление газа и его начальный объём соответственно p=190кПа и = 6,Одм’5.

Дано:

Пример №2

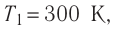
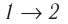
Состояние идеального газа, взятого в количестве v=l,0 моль при температуре изменяется так, как показано на рисунке 57. Определите работу газа в ходе всего процесса, если на изохоре его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.

Дано:

v = 1,0 моль

= 300 к

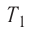
А — ?

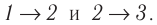
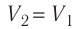
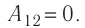
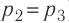
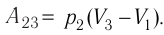
Решение. Работа Л газа в ходе всего процесса равна сумме работ на участках Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный ), то работа газа . Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным ()следовательно, работа газа Тогда
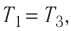
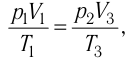
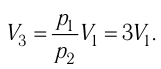
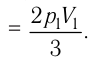
Так как по условию то воспользуемся уравнением Клапейрона (5.2):

откуда  Следовательно,
Согласно уравнению Клапейрона—Менделеева

Тогда

Ответ: А = 1,7 кДж.

Работа в термодинамике

В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.

Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.

Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.

Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.

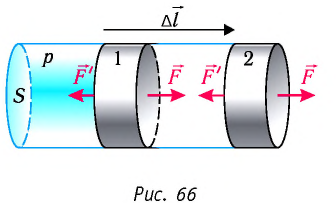
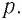
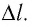
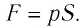
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре В результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние Модуль силы давления газа  на поршень Эта сила совершила работу по перемещению поршня, равную    

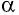
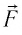
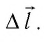
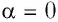
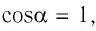
где — угол между направлениями силы  и перемещения поршня Поскольку в рассматриваемом примере и то

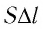
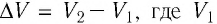
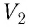
Произведение  определяет изменение объёма  — начальный объём газа; — объём газа в конечном состоянии (см. рис. 66).

Таким образом, работа силы давления газа при его изобарном расширении:

Так как давление р газа — величина положительная, то из формулы (12.1) следует, что

При изобарном расширении газа из состояния 1 в состояние 2 работа силы 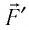(см. рис. 66):

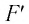
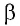
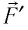
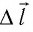
где — модуль силы, действующей на газ со стороны поршня (внешняя сила); — угол между направлениями силы и перемещения поршня.

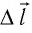
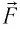
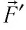
Перемещение поршня одно и то же, а сила давления газа на поршень и сила давления поршня на газ — силы, подчиняющиеся третьему закону Ньютона:

Следовательно, работы 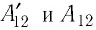отличаются только знаком

Таким образом, можно сделать следующие выводы.

Геометрическое толкование работы:

Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при 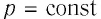(рис. 68). Если процесс перехода газа из начального состояния в конечное является изобарным (АВ — изобара), то работа силы давления газа численно равна площади прямоугольника 

Если процесс перехода газа из начального состояния в конечное не является изобарным (рис. 69), то работа силы давления газа при изменении объёма от 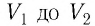численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов 

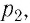
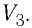
Работу газа определяют не только начальное и конечное состояния системы, но и вид процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения (рис. 70), либо сначала изохорно понизив его давление до значения а затем изобарно увеличив его объём до значения В первом случае работа газа больше, чем во втором.

Следовательно, работа, совершаемая термодинамическом системой при переходе из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.

Пример №3

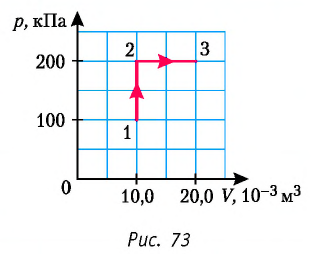
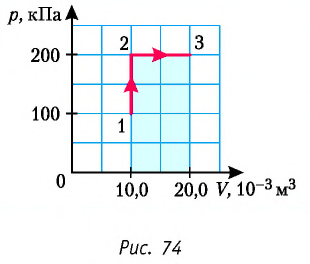
Определите работу, совершаемую силой давления идеального газа определённой 200 массы при переходе из состояния 1 в состояние 3 (рис. 73).   

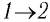
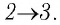
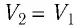
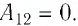
Решение. 1 способ. Работа А газа в ходе всего процесса равна сумме работ на участках и Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс ), то работа, совершаемая силой давления газа, В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу

Тогда при переходе из состояния 1 в состояние 3 работа

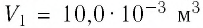
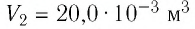
2 способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёма и (закрашенная область на рисунке 74).

Ответ:

Пример №4

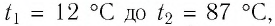
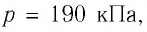
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от если давление газа а его начальный объём

Решение. Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому

Согласно уравнению Клапейрона—Менделеева,
Следовательно,

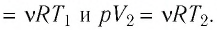
Ответ:

Как определить работу в термодинамике

В конце XVIII в. английский физик Бенджамин Томпсон (граф Румфорд) исследовал тепло, выделяющееся при сверлении бронзовых пушек. Румфорд успевал вскипятить поставленные на пушки котлы с водой за счет тепла, которое выделялось, пока лошади приводили в движение очень тупое сверло. В данном случае энергия механического движения сверла превращалась в энергию хаотического движения молекул бронзы и воды. А можно ли сделать наоборот?

Почему при изменении объема газа изменяется его внутренняя энергия

Внутренняя энергия газа может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ сжимают (газ совершает отрицательную работу) (рис. 37.1) и он при этом не отдает энергию окружающей среде, то скорость движения молекул газа, а соответственно, и внутренняя энергия, и температура газа увеличиваются. И наоборот: если газ расширяется (то есть совершает положительную работу), то скорость движения молекул, температура и внутренняя энергия газа уменьшаются.

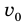
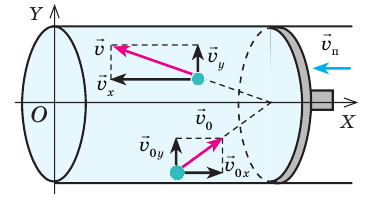
Рис. 37.1. При сжатии газа скорость его молекул после столкновения с поршнем увеличивается (v > ) — газ нагревается. (Аналогично увеличивается скорость мяча после удара волейболиста, когда его рука движется навстречу мячу.)

Как вычислить работу газа

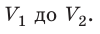
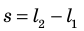
Вычислим работу, которую совершает сила давления газа при изменении его объема от По определению работы: A=Fscosα. Если газ расширяется изобарно, то сила, действующая со стороны газа на поршень, постоянна: F=pS (p — давление газа; S — площадь поршня); модуль перемещения поршня (рис. 37.2, а); α = 0.

Таким образом, работа газа при его изобарном расширении равна:

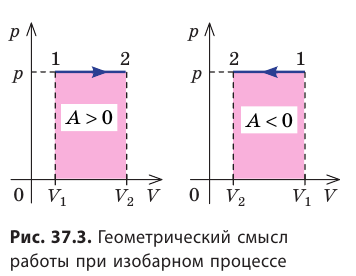
Работе газа при изобарном расширении (или сжатии) можно дать простое геометрическое толкование: работа газа численно равна площади прямоугольника под графиком зависимости p(V) (рис. 37.3).

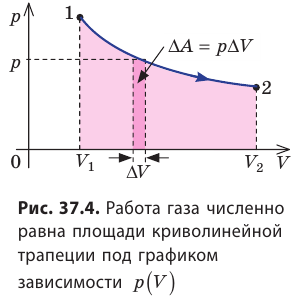
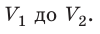
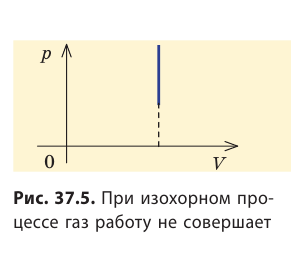
Пусть некоторый газ переходит из состояния 1 в состояние 2 (рис. 37.4). Если изменение объема газа (∆V) достаточно мало, то давление газа можно считать неизменным. Тогда работа газа численно равна площади выделенной на рисунке полосы. Полная работа при изменении объема от будет равна сумме площадей всех полос, то есть площади криволинейной трапеции под графиком зависимости p (V).

Очевидно, что при изохорном процессе (V = const) площадь фигуры под графиком зависимости p (V) равна нулю (рис. 37.5), — газ работу не совершает (A = 0) . Работа газа зависит от того, каким образом происходил переход газа из начального состояния в конечное (рис. 37.6).

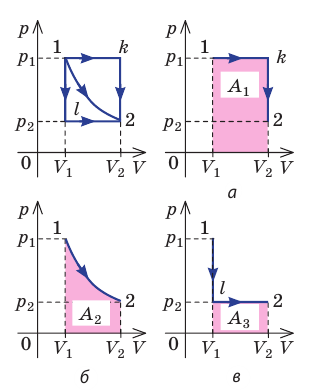
Рис. 37.6. три пути перехода газа из состояния 1 в состояние 2: а — газ изобарно расширяется (участок 1k), затем изохорно охла ждается (участок k2); б — газ изотермически расширяется; в — газ изохорно охлаждается (участок 1l), затем изобарно расширяется (участок l2). сравнив площади фигур под графиками, видим, что:

Пример №5

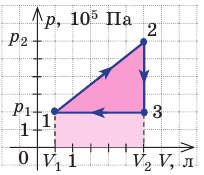
На рисунке графически изображен циклический процесс, совершаемый идеальным газом. Определите работу газа за цикл.

Решение:

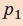
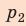
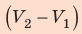
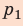
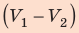
Полная работа за цикл равна сумме работ, совершенных газом в ходе каждого процесса цикла. Работа газа в ходе процесса 1–2 численно равна площади трапеции, основания которой равны и , а высота — ; объем газа увеличивается, поэтому работа газа положительна. Работа газа в ходе процесса 2–3 равна нулю, поскольку этот процесс изохорный. Работа газа в ходе процесса 3–1 численно равна площади прямоугольника со сторонами и ; объем газа уменьшается, поэтому работа отрицательна. Следовательно, для определения работы за весь цикл нужно из площади трапеции вычесть площадь прямоугольника. То есть, как видно из рисунка, работа газа за цикл численно равна площади прямоугольного треугольника 1–2–3:

Выводы:

• При отсутствии теплообмена с окружающей средой, если над газом совершают работу, внутренняя энергия газа увеличивается; если газ сам совершает работу, его внутренняя энергия уменьшается.
• Если объем газа увеличивается, то газ совершает положительную работу. Если объем газа уменьшается, то работа газа отрицательна.
• Работа газа численно равна площади фигуры под графиком зависимости p (V). При изобарном процессе работу газа можно определить по формуле A=p∆V, при изохорном процессе работа газа равна нулю: A = 0.