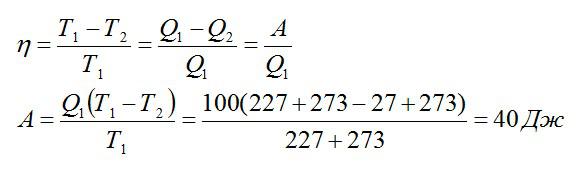Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
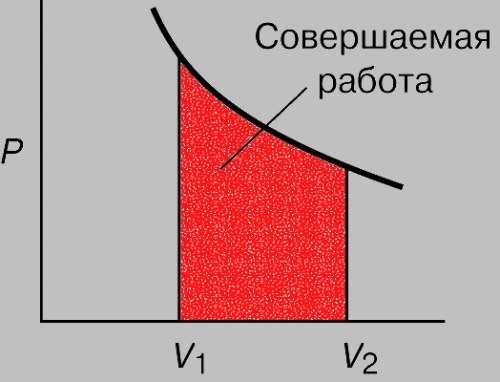
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
В этой статье рубрики «физика для чайников» рассмотрим подробное решение нескольких задач на работу в термодинамике. Тем, кто хочет научиться решать задачи, рекомендуем систематически тренироваться, предварительно ознакомившись с теорией. А еще, полезно почитать памятку по решению физических задач и держать под рукой основные физические формулы.
Чтобы не заскучать, подписывайтесь на наш телеграм-канал. Там вас ждет ежедневная рассылка, которая будет полезна всем учащимся.
Примеры решения задач на работу в термодинамике
Задача №1. Работа расширения
Условие
При адиабатическом расширении 1 кг воздуха его объем увеличился в 10 раз. Найти работу расширения, если начальное давление 1 атм, а начальная температура 15 °С.
Решение
Зная молярную массу воздуха (29 г/моль), начальный объем можно найти из уравнения Клапейрона-Менделеева:
Не забываем переводить все физические величины из условия в систему СИ.
Из условия находим конечный объем:
Работа равна:
Ответ: 751 кДж.
Задача №2. Работа в цикле Карно
Условие
Температура нагревателя идеальной тепловой машины составляет 227 °С, а охладителя — 27 °С. За один рабочий цикл тепловая машина получает количество теплоты, равное 100Дж. Какую работу совершает рабочее тело идеальной тепловой машины за один цикл?
Решение
Из формулы для КПД можно выразить искомую работу:
Ответ: 40 Дж.
Задача №3. Работа при выдувании мыльного пузыря
Условие
Определить работу, которую необходимо совершить, чтобы выдуть мыльный пузырь диаметром 10 см.
Решение
Работа, которую нужно совершить, чтобы, выдувая мыльный пузырь, увеличить площадь поверхности мыльной пленки на дельта S, равна:
Здесь сигма – коэффициент поверхностного натяжения для мыльного раствора (берется из таблицы). S – общая площадь двух сферических поверхностей пленки мыльного пузыря (внешней и внутренней). S нулевое – площадь этих поверхностей до выдувания пузыря (этой величиной можно пренебречь).
Ответ: 2,5 мДж.
Задача №4. Графическое представление работы
Условие
Газ расширяется от объёма V1 до объёма V2 один раз изотермически, другой изобарно и третий адиабатно. При каком процессе газ совершает большую работу и при каком газу передаётся большее количество теплоты?

Решение
Работа численно равна площади криволинейной трапеции. Из рисунка очевидно, что работа при изобарном процессе будет максимальной, при адиабатном минимальной, т. е.
Ответ: см. выше.
Задача №5. Работа газа
Условие
Газ совершает круговой процесс, состоящий из нескольких этапов. Сначала газ изохорно охлаждается до температуры, при которой его давление равно P2 = 105 Па. Затем он изобарно охлаждается до состояния, из которого возвращается в начальное состояние таким образом, что его давление изменяется с изменением объема по закону Р = αV (α — постоянная величина). Начальные объем и давление газа известны: V1 = 2 м3, Р1 = 4·105 Па. Нарисовать график данного кругового процесса на РV-диаграмме и найти работу, совершенную газом.
Решение
Сначала выполним рисунок:
Точки состояния газа 1 и 3 лежат на прямой, проходящей через центр координат:
C учетом этого, получаем:
Работа газа в данном случае равна площади треугольника 123:
Подставим найденное ранее значение для V3, преобразуем и подставим значения из условия:
Ответ: 2,25*10^5 Дж.
Вопросы на тему «Работа в термодинамике»
Вопрос 1. Что такое работа в термодинамике?
Ответ. Работа – одна из форм обмена энергией термодинамической системы с окружающими телами. Работа, как и энергия, измеряется в Джоулях.
Вопрос 2. Сформулируйте первое начало термодинамики.
Ответ. Первое начало термодинамики гласит:
Изменение внутренней энергии системы равно сумме совершаемой над системой работы внешних сил и количества теплоты, переданной системе.
У первого начала термодинамики исторически есть несколько формулировок. Одна из них: невозможно построить вечный двигатель первого рода.
Вопрос 3. При каком из изопроцессов работа газа равна нулю?
Ответ. При изохорном процессе объем системы остается неизменным. Следовательно, газ в данном процессе не совершает работу.
Вопрос 4. Как, совершая работу, можно изменить внутреннюю энергию?
Ответ. Если работа совершается над телом (системой), то его внутренняя энергия увеличивается, если же тело само совершает работу, это ведет к уменьшению его внутренней энергии.
Вопрос 5. Как определить работу газа геометрически?
Ответ. Величина работы газа равна площади фигуры под графиком на диаграмме pV
Нужна помощь в решении задач или в выполнении других студенческих заданий? Обращайтесь в профессиональный студенческий сервис.
Как определить работу при изотермическом процессе
При изотермическом процессе, который протекает при постоянной температуре, газ выполняет работу за счет расширения. Расширение газа характеризуется его объемом, который изменяется в зависимости от изменения давления газа, обусловленного внешними воздействиями.
Вам понадобится
- — герметичный сосуд с поршнем;
- — весы;
- — термометр;
- — линейка.
Инструкция
Рассчитайте работу газа при постоянной температуре. Для этого определите, какой газ выполняет работу, и рассчитайте его молярную массу. С помощью периодической таблицы найдите молекулярную массу, которая численно равна молярной массе, измеренной в г/моль.
Найдите массу газа. Для этого откачайте воздух из герметичного сосуда и взвесьте его на весах. После этого закачайте газ, работа которого определяется, и снова взвесьте сосуд. Разность масс пустого и заполненного сосудов и будет равна массе газа. Измеряйте ее в граммах.
Измерьте при помощи термометра температуру газа. При изотермическом процессе она будет постоянна. Если измерение производится при комнатной температуре, достаточно измерить температуру окружающего воздуха. Измерения произведите в Кельвинах. Для этого к температуре, измеренной в градусах Цельсия, прибавьте число 273.
Определите начальный и конечный объем газа при выполнении работы. Для этого сосуд берите с подвижным поршнем, и, вычисляя уровень его подъема, рассчитайте первичный и вторичный объем геометрическими методами. Для этого используйте формулу для объема цилиндра V=π•R²•h, где π≈3,14, R – радиус цилиндра, h его высота.
Рассчитайте работу газа при изотермическом процессе. Для этого поделите массу газа m на его молярную массу M. Полеченный результат умножьте на универсальную газовую постоянную R=8,31 и значение температуры Т в Кельвинах. Полученный результат умножьте на натуральный логарифм из отношения конечного и начального объемов V2 и V1, A = m/M•R•T•ln(V2/V1).
В том случае, когда известно количество теплоты Q, которое получило тело при изотермическом процессе, используйте второе начало термодинамики Q = ∆U + A. Где A – работа газа, а ΔU – изменение его внутренней энергии. Поскольку изменение внутренней энергии зависит от температуры, а при изотермическом процессе она остается постоянной, то ΔU=0. В этом случае работа газа равна теплоте, переданной ему Q = A.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Примеры решения задач
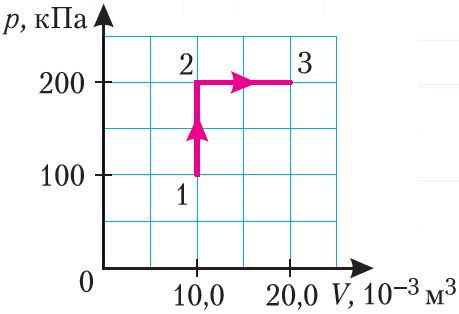
Пример 1. Определите работу, совершаемую силой давления идеального газа определённой массы при переходе из состояния 1 в состояние 3 (рис. 73).
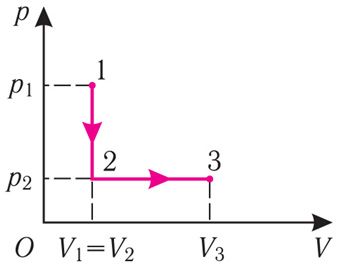
Решение. I способ. Работа А газа в ходе всего процесса равна сумме работ на участках 12 и 2
3. Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс V2 = V1), то работа, совершаемая силой давления газа, А12 = 0. В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу
A23 = p2ΔV = p2(V3 – V1).
Тогда при переходе из состояния 1 в состояние 3 работа
А = А12 + А23 = p2(V3–V1).
А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.
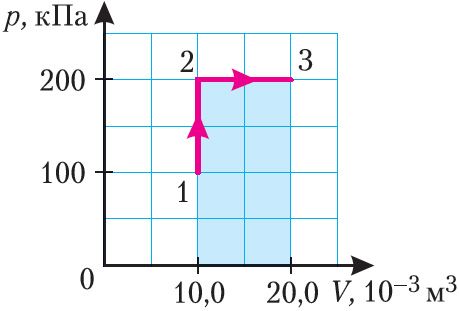
II способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью ОV и прямыми, соответствующими значениям объёма V1 = 10,0 · 10–3 м3 и V2 = 20,0 · 10–3 м3 (закрашенная область на рисунке 74).
А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.
Ответ: А = 2,00 кДж.
Пример 2. Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от t1 = 12 °С до t2 = 87 °С, если давление газа p = 190 кПа, а его начальный объём V1 = 6,0 дм3.
Дано:
Т1 = 285 К
Т2 = 360 К
p = 190 кПа = 1,90 · 105 Па
V1 = 6,0 дм3 = 6,0 · 10–3 м3
А — ?
Решение: Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому
.
Согласно уравнению Клапейрона–Менделеева, и
. Следовательно,
.
.
Ответ: .
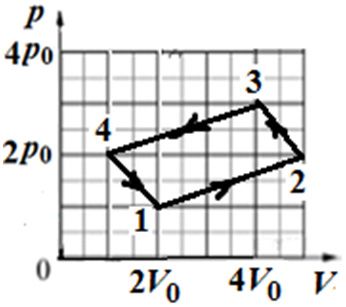
Пример 3. На рисунке 74.1 изображен процесс изменения состояния идеального газа определённой массы. На каком участке сила давления газа совершила наименьшую положительную работу? На каком участке внешняя сила совершила наибольшую положительную работу?
Решение. Работе силы давления газа соответствует площадь под графиком процесса. При расширении газа сила давления совершает положительную работу, а внешняя сила — отрицательную. При сжатии газа наоборот: сила давления совершает отрицательную работу, а внешняя сила — положительную. Анализ графика позволяет сделать вывод, что в процессе перехода из состояния 4 в состояние 1 сила давления газа совершила минимальную положительную работу (газ расширялся, а площадь под графиком минимальна). Максимальную же положительную работу внешняя сила совершает при сжатии, когда площадь под графиком максимальна (это процесс перехода из состояния 3 в состояние 4).
Пример 4. Состояние идеального газа, взятого в количестве ν = 1,0 моль при абсолютной температуре Т1 = 300 К, изменяется так, как изображено на рисунке 74.2. Определите работу газа в ходе всего процесса, если на изохоре 12 его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.
Дано:
ν = 1,0 моль
Т1 = 300 К
p1 = 3p2
Т1 = Т3
A – ?
Решение: Работа А газа в ходе всего процесса равна сумме значений работы на участках 12 и 2
3 (рис. 74.2). Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный V2 = V1), то работа газа А12 = 0. Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным (р2 = р3), следовательно, работа газа А23 = p2(V3 − V1). Тогда А = А12 + А23 = p2(V3 − V1). Так как по условию Т1 = Т3, то воспользуемся уравнением Клапейрона:
, откуда
. Следовательно,
.
Согласно уравнению Клапейрона‒Менделеева, p1V1 = νRT1. Тогда .
Ответ: А = 1,7 кДж.
На этой странице вы узнаете
- В чем прелесть фазовых переходов?
- Что лучше выбрать: Mercedes или BMW?
Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов,а именно получать тепловую энергию различными доступными способами. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне.
Тепловые машины и их КПД
Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.
Вспомним, что фазовые переходы — это переход из одного агрегатного состояния в другое. При этом может выделяться большое количество теплоты.
Именно благодаря этому они и стали такими полезными для нас. Например, в ядерных реакторах воду используют в качестве рабочего тела, то есть она нагревается вследствие энергии, полученной из ядерных реакций, доходит до температуры кипения, а затем под большим давлением уже в качестве водяного пара воздействует на ротор генератора, который вращается и дает нам электроэнергию! На этом основан принцип работы атомных электростанций.
А самый простой пример фазового перехода — образование льда на лужах в морозные ноябрьские дни. Правда о выделении тепла здесь речи не идет.
Мы не почувствуем, как испарится капелька у нас на руке, потому что это не требует много тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. А зачем мы вообще рассматриваем эти фазовые переходы? Все дело в том, что именно фазовые переходы являются ключевым звеном во всех процессах, где нас просят посчитать КПД, от них нашему рабочему телу и подводится теплота нагревателя.

Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.
Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую.
Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в автомобилях часть энергии от сгоревшего бензина идет на движение. Схематично можно изобразить так:
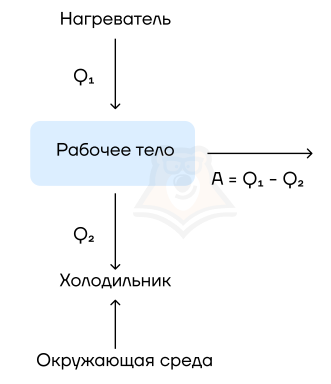
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q1, из которой A уходит на работу механизма. Остаток теплоты Q2 рабочее тело отдает холодильнику, по сути — это потеря энергии.
Физика не была бы такой загадочной, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:
Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
(eta) — КПД,
A — работа газа (Дж),
Q1 — количество теплоты, полученное от нагревателя (Дж).
Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери.
Полезную работу можно расписать как Q1 — Q2 (по закону сохранения энергии). Тогда формула примет вид:
(eta = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})
Давайте попрактикуемся в применении данной формулы на задаче номер 9 из ЕГЭ.
Задача. Тепловая машина, КПД которой равен 60%, за цикл отдает холодильнику 100 Дж. Какое количество теплоты за цикл машина получает от нагревателя? (Ответ дайте в джоулях).
Решение:
Давайте сначала вспомним нашу формулу для КПД:
(eta = frac{Q_1 — Q_2}{Q_1}),
где (Q_1) — это теплота, которую тело получает от нагревателя, (Q_2) — теплота, которая подводится к холодильнику.
Тогда отсюда можно вывести искомую теплоту нагревателя:
(eta Q_1 =Q_1-Q_2)
(eta Q_1 — Q_1= -Q_2)
(Q_1=frac{- Q_2}{eta-1}=frac{-100}{0,6-1}=250 Дж).
Ответ: 250 Дж
Цикл Карно
Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже все сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат. Рассмотрим, как этот цикл выглядит в координатах p(V).
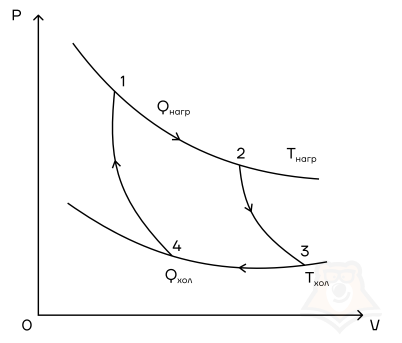
- Температура верхней изотермы 1-2 — температура нагревателя (так как теплота в данном процессе подводится).
- Температура нижней изотермы 3-4 — температура холодильника (так как теплота в данном процессе отводится).
- 2-3 и 4-1 — это адиабатические расширение и сжатие соответственно, в них газ не обменивается теплом с окружающей средой.
Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД.
Формула, по которой можно рассчитать ее КПД выражается через температуры:
T1 — температура нагревателя,
T2 — температура холодильника.
Не то круто, что красиво, а то, что по Карно работает! Поэтому присматривайте такой автомобиль, у которого высокий КПД.
Интересно, что максимальный уровень КПД двигателя внутреннего сгорания автомобилей на данный момент всего около 43%. По официальным заявлениям компания Nissan Motor с 2021 года испытывает прообраз двигателя нового поколения с планируемым КПД 50%.
Приступим к задачам
Задачи на данную тему достаточно часто встречаются в задании 27 из КИМа ЕГЭ. Давайте разберем некоторые примеры.
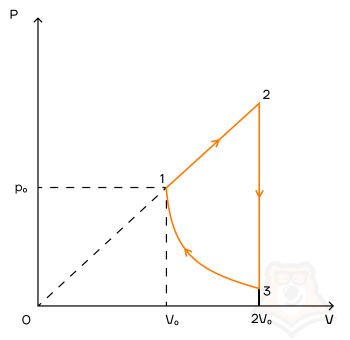
Задание 1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A12 = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Qхол| = 4780 Дж. Найдите работу газа |A13| на адиабате, если количество вещества постоянно.
Решение:
Шаг 1. Первое, с чего лучше начинать задачи по термодинамике — исследование процессов.
Посмотрим на участок 1-2 графика: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: (frac{pV}{T} = const). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем. Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.
Участок 2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: (frac{p}{T} = const). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.
Участок 3-1: адиабата по условию, то есть количество теплоты в этом переходе равна нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем.
Оформим все данные в таблицу.
Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.

Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.
Шаг 2. Первый закон термодинамики для процесса 1-2 запишется в виде:
Q12 = ΔU12 + A12.
Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции:
(A_{12} = frac{p_0 + 2p_0}{2} * V0 =frac{3p_0V_0}{2}).
Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:
(Delta U_{12} = frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = frac{9p_0V_0}{2}).
Заметим, что это в 3 раза больше работы газа на этом участке:
(Delta U_{12} = 3A_{12} rightarrow Q_{12} = 4A_{12}).
Шаг 3. Работа цикла — площадь фигуры, которую замыкает график, тогда . A = A12 — |A31|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q12 — |Q31|.
Сравним эти формулы:
Q12 -|Q31| = A12 — |A31|,
подставим выражения из предыдущего пункта:
4A12 — |Q31| = A12 — |A31| (rightarrow) |A31| = -3A12 + |Q31| = -31520 + 4780 = 220 Дж.
Ответ: 220 Дж
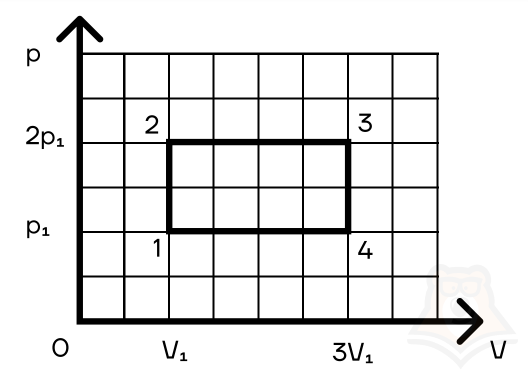
Задание 2. Найти КПД цикла для идеального одноатомного газа.
Решение:
Шаг 1. КПД цикла определим по формуле: (eta = frac{A}{Q}), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p1 — p1)(3V1 — V1) = 2p1V1.
Шаг 2. Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:
Посмотрим на участок 1-2 графика: давление растет, объем не меняется. По закону Шарля (frac{p}{T} = const) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.
2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака (frac{V}{T} = const) температура тоже растет, растет и внутренняя энергия.
3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.
4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.
Оформим данные в таблицу:
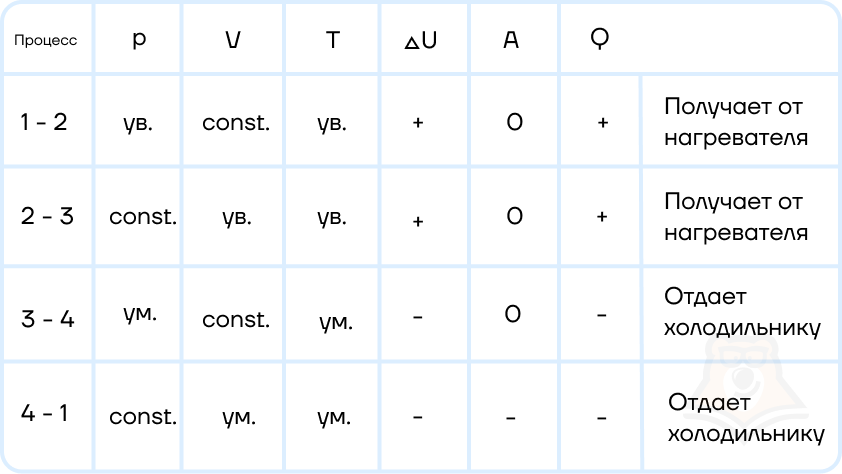
Отметим, что необходимое Q = Q12 + Q23.
Шаг 3. Запишем первый закон термодинамики для процессов 1-2 и 2-3:
(Q_{12} = U_{12} + A_{12} = Delta U_{12} = frac{3}{2}(2p_1V_1 -p_1V_1) = frac{3}{2}p_1V_1).
(Q_{23} = Delta U_{23} + A_{23}), работу газа найдем как площадь под графиком: A23 = 2p1(3V1 — V1) = 4p1V1.
(Delta U_{12} = frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1).
(Q_{23} = Delta U_{23} + A_{23} = 10p_1V_1).
Шаг 4. Мы готовы считать КПД: (eta = frac{A}{Q} = frac{A}{Q_{12} + Q_{23}} = frac{2p_1V_1}{frac{3}{2}p_1V_1 + 10p_1V_1} = frac{4}{23} approx 0,17).
Ответ: 17%
Теперь вас не должно настораживать наличие графиков в условиях задач на расчет КПД тепловых машин. Продолжить обучение решению задач экзамена вы можете в статьях «Применение законов Ньютона» и «Движение точки по окружности».
Фактчек
- Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую.
- Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
- Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
(eta = frac{A}{Q_1} = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1}) - Цикл Карно — цикл с максимально возможным КПД: (eta = frac{T_1 — T_2}{T_1} = 1 — frac{T_2}{T_1})
- Не забываем, что работа считается, как площадь фигуры под графиком.
Проверь себя
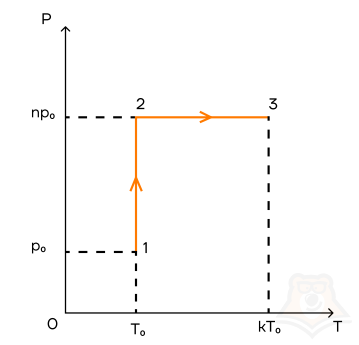
Задание 1.
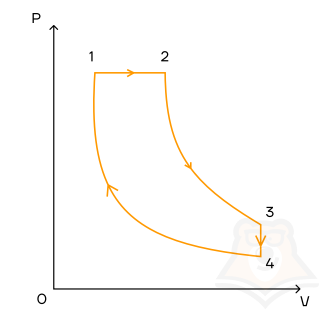
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T0 = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.
- 5672 Дж
- 4731 Дж
- 5817 Дж
- 6393 Дж
Задание 2.
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT12 к изменению его температуры ΔT34 при изохорном процессе равен 1,5. Определите КПД цикла.
- 0,6
- 0,5
- 0,8
- 1
Задание 3.
В топке паровой машины сгорело 50 кг каменного угля, удельная теплота сгорания которого равна 30 МДж/кг. При этом машиной была совершена полезная механическая работа 135 МДж. Чему равен КПД этой тепловой машины? Ответ дайте в процентах.
- 6%
- 100%
- 22%
- 9%
Задание 4.
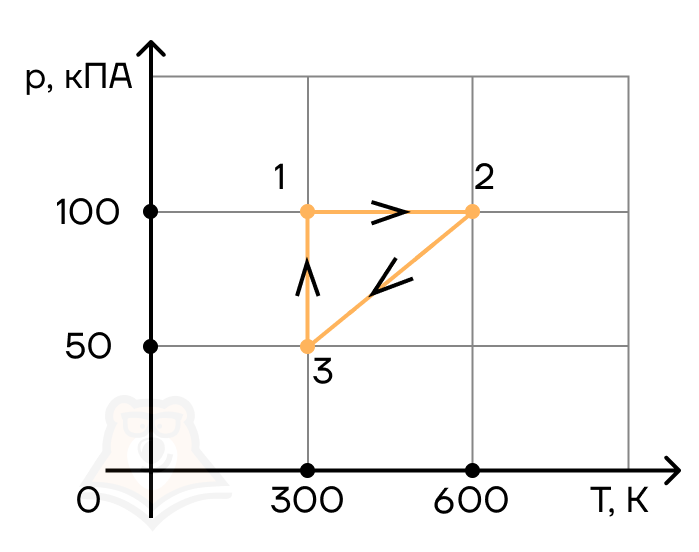
С двумя молями одноатомного идеального газа совершают циклический процесс 1–2–3–1 (см. рис.). Чему равна работа, совершаемая газом на участке 1–2 в этом циклическом процессе?
- 4444 Дж
- 2891 Дж
- 4986 Дж
- 9355 Дж
Ответы:1 — 3; 2 — 1; 3 — 4; 4 — 3.