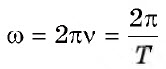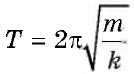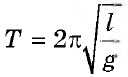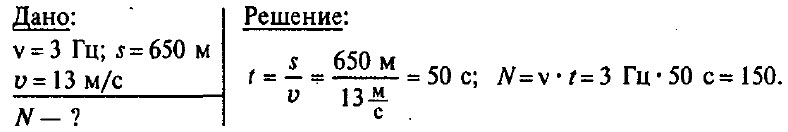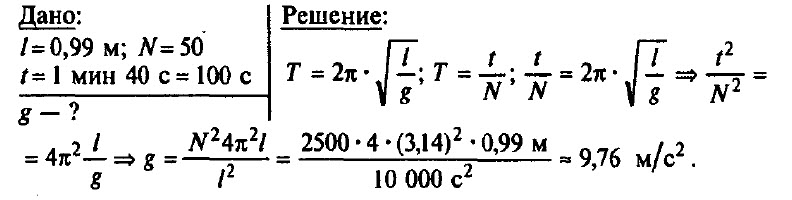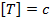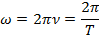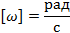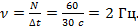Как найти путь точки струны

Ответ: 3,2 м

Объяснение:

Дано:

А = 2 мм = 0,002 м

f = 1 кГц = 10³ Гц

t = 0,4 c

———————————

s — ?

Решение:

Mы знаем что

f = N/t

Отсюда

N = ft

Где N — количество колебаний за 0,4 с

Если за 1 периуд колебаний тело проходит расстояние в 4А , тогда за время t

s = 4AN

s = 4Аft

s = 4 * 0,002 * 10³ * 0,4 = 3,2 м

Ну а так как за один период колебаний тело возвращается в точку из которой начало своё движение тогда за один период колебаний перемещение струны равно нулю

Задачи на Механические колебания с решениями

Формулы, используемые на уроках «Задачи на Механические колебания».

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2.
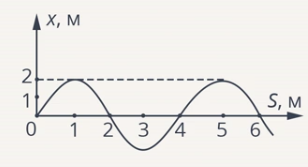
 На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

Задача № 3.
 Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

Задача № 4.
 Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

Задача № 5.
 Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с².

Задача № 6.
 Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

Задача № 7.
 Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

Задача № 8.
 Гармоническое колебание описывается уравнением 
 Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

Задача № 9.
 Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π² = 9,87.)

Задача № 10.
  ОГЭ
 Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

Задача № 11.
   ЕГЭ
 Два математических маятника за одно и то же время совершают — первый N₁ = 30, а второй — N₂ = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

Краткая теория для решения Задачи на Механические колебания.

Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на 
• Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Спрятать решение

Источник: Гельф­гат И. М. Сбор­ник задач по фи­зи­ке для 11 клас­са, Х.: «Гим­на­зия», 2004 (№ 1.6)

 Введение

Ре­ша­е­мые ниже за­да­чи яв­ля­ют­ся ти­по­вы­ми, то есть ана­ло­гич­ные им встре­ча­лись во время ЕГЭ. Для на­ча­ла вспом­ним ос­нов­ные тео­ре­ти­че­ские ха­рак­те­ри­сти­ки, ко­то­рые нам се­год­ня по­на­до­бят­ся.

1) Пе­ри­од ко­ле­ба­ний – про­ме­жу­ток вре­ме­ни, по про­ше­ствии ко­то­ро­го зна­че­ние ко­ор­ди­на­ты, ско­ро­сти, уско­ре­ния и воз­вра­ща­ю­щей силы по­вто­ря­ют­ся. За 1 пе­ри­од си­сте­ма со­вер­ша­ет одно пол­ное ко­ле­ба­ние: .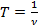

2) Ча­сто­та ко­ле­ба­ний – число пол­ных ко­ле­ба­ний, со­вер­ша­е­мых в еди­ни­цу вре­ме­ни.

, где N – ко­ли­че­ство пол­ных ко­ле­ба­ний; . Ча­сто­та и пе­ри­од свя­за­ны об­рат­ной про­пор­ци­о­наль­но­стью: .

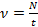
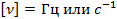
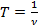
3) Уг­ло­вая ча­сто­та – ска­ляр­ная фи­зи­че­ская ве­ли­чи­на, мера ча­сто­ты вра­ща­тель­но­го или ко­ле­ба­тель­но­го дви­же­ния (см. рис. 1).

4) Ам­пли­ту­да ко­ле­ба­ний – мак­си­маль­ное от­кло­не­ние (по мо­ду­лю) ко­ор­ди­на­ты тела от по­ло­же­ния его рав­но­ве­сия: .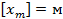

5) Ам­пли­ту­да ско­ро­сти – мак­си­маль­но зна­че­ние ско­ро­сти ко­леб­лю­ще­го­ся тела: .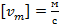

Пе­ре­хо­дим к ре­ше­нию задач.

 Задача №1

Ам­пли­ту­да ко­ле­ба­ний груза на пру­жине равна 3 см. Какой путь от по­ло­же­ния рав­но­ве­сия прой­дет груз за время, рав­ное , , , ?

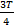
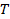
Ре­ше­ние

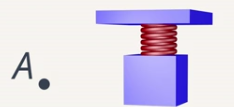
Вос­поль­зу­ем­ся ри­сун­ком и от­ме­тим на нем те точки, ко­то­рых до­стиг­нет груз через ука­зан­ный в усло­вии про­ме­жу­ток вре­ме­ни. От­ме­тим, что за пе­ри­од тело вер­ну­лось в свое на­чаль­ное по­ло­же­ние, пус­кай на ри­сун­ке это будет точка А (см. рис. 1).

Рис. 1. По­ло­же­ние груза через пе­ри­од T

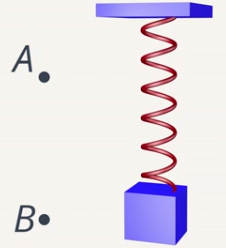
От­ме­тим, где было тело через пол­пе­ри­о­да . Ясно, что если мы рас­смат­ри­ва­ем гар­мо­ни­че­ские неза­ту­ха­ю­щие ко­ле­ба­ния, то это будет точка, мак­си­маль­но уда­лен­ная от на­чаль­ной, пус­кай это будет точка В (см. рис. 2).

Рис. 2. По­ло­же­ние груза через по­лу­пе­ри­од

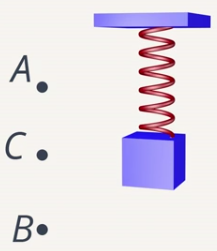
Со­от­вет­ствен­но, через чет­верть пе­ри­о­да груз будет в точке С, но эта точка яв­ля­ет­ся также точ­кой, где тело было через 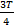 (см. рис. 3).

Рис. 3. По­ло­же­ние груза через чет­верть пе­ри­о­да и 

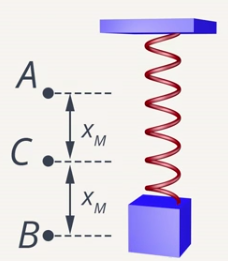
Итак, точки от­ме­че­ны, те­перь вспом­ним опре­де­ле­ние ам­пли­ту­ды – мак­си­маль­ное от­кло­не­ние от по­ло­же­ния рав­но­ве­сия. От­ме­тим это от­кло­не­ние (см. рис. 4), где рас­сто­я­ние АС = ВС.

Рис. 4. От­ме­чен­ная ам­пли­ту­да

Те­перь неслож­но найти путь – длина тра­ек­то­рии, ко­то­рый тело со­вер­шит за ука­зан­ное время. Из ри­сун­ка видно, что через чет­верть пе­ри­о­да путь будет равен длине от­рез­ка АС, то есть ам­пли­ту­де: .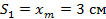

Ана­ло­гич­но мы видим, что через пол­пе­ри­о­да длина от­рез­ка ста­нет в 2 раза боль­ше, по­это­му .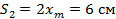

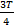
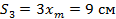
Когда груз воз­вра­ща­ет­ся в ис­ход­ную точку А, мо­дуль пе­ре­ме­ще­ния ста­но­вит­ся мень­ше, но путь на­рас­та­ет, этим он и от­ли­ча­ет­ся от пе­ре­ме­ще­ния. Итак, от точки А до В тело про­шло уже 6 см, и от В до С про­шло еще 3 см. В итоге имеем, что путь через  равен трем зна­че­ни­ям ам­пли­ту­ды: .

Тогда, воз­вра­ща­ясь в ис­ход­ную точку, пе­ре­ме­ще­ние равно 0, а вот путь будет равен че­ты­рем от­рез­кам ам­пли­ту­ды: .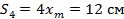

За­да­ча ре­ше­на.

Ответ: , , , .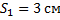

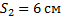
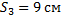
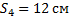
 Задача №2

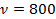
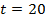
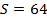
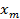
Точка стру­ны, ко­то­рая ко­леб­лет­ся с ча­сто­той  Гц, за  с про­шла путь  м. Опре­де­ли­те ам­пли­ту­ду ко­ле­ба­ний .

Ре­ше­ние

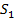
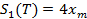
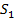
Для ре­ше­ния дан­ной за­да­чи нам по­на­до­бят­ся дан­ные из про­шлой за­да­чи. Вспом­ни­те глав­ный вывод из преды­ду­щей за­да­чи: путь, ко­то­рый точка про­хо­дит за одно пол­ное ко­ле­ба­ние, равен че­ты­рем ам­пли­ту­дам. За­пи­шем, что  – путь за одно ко­ле­ба­ние: . Это зна­чит, что для того чтоб найти ам­пли­ту­ду, нужно знать  – путь, ко­то­рый про­хо­дит стру­на за одно пол­ное ко­ле­ба­ние. Об­ра­тим вни­ма­ние на то, что мы знаем пол­ный путь, прой­ден­ный стру­ной, – это 64 м.

Чтобы по­нять, как ре­шать за­да­чу, немно­го от­вле­чем­ся и решим про­стень­кую за­дач­ку. Сколь­ко ки­ло­грамм яблок в ящике, если в 10 ящи­ках 150 кг? Ответ: 15 кг в ящике. Мы пол­ную массу яблок по­де­ли­ли на ко­ли­че­ство ящи­ков. В нашей за­да­че точно так же. Путь за одно ко­ле­ба­ние равен пол­но­му пути, де­лен­но­му на ко­ли­че­ство ко­ле­ба­ний: .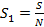

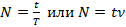
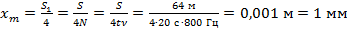
Таким об­ра­зом, за­да­ча сво­дит­ся к сле­ду­ю­щей: найти число ко­ле­ба­ний точки стру­ны, ведь пол­ный путь мы уже знаем. Для на­хож­де­ния числа ко­ле­ба­ний у нас есть все: ча­сто­та и время дви­же­ния. Можно за­пи­сать, что число ко­ле­ба­ний равно пол­но­му вре­ме­ни t по­де­лить на время од­но­го ко­ле­ба­ния T: . Тогда ко­неч­ная фор­му­ла для ам­пли­ту­ды будет иметь вид: .

Ответ: 1 мм.

А те­перь раз­бе­рем за­да­чи на тему «Ме­ха­ни­че­ские волны», но для на­ча­ла вспом­ним ос­нов­ные тео­ре­ти­че­ские све­де­ния.

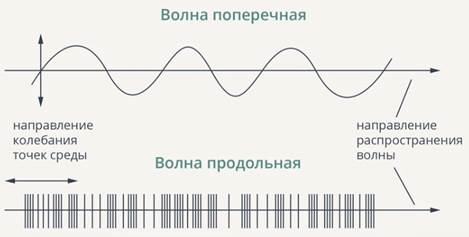
1) Волны бы­ва­ют про­доль­ны­ми и по­пе­реч­ны­ми (см. рис. 5).

Рис. 5. По­пе­реч­ные и про­доль­ные волны

От­ли­ча­ют­ся они тем, что в слу­чае про­доль­ных волн ча­сти­цы среды со­вер­ша­ют ко­ле­ба­ния в на­прав­ле­нии рас­про­стра­не­ния волны; в слу­чае по­пе­реч­ных ча­сти­цы среды со­вер­ша­ют ко­ле­ба­ния пер­пен­ди­ку­ляр­но на­прав­ле­нию рас­про­стра­не­ния волны.

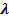
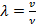
2) Ха­рак­те­ри­сти­ка волны: длина волны () – крат­чай­шее рас­сто­я­ние между точ­ка­ми, ко­леб­лю­щи­ми­ся оди­на­ко­во (в одной фазе) (см. рис. 6). Длина волны свя­за­на с её ско­ро­стью и ча­сто­той фор­му­лой .

Рис. 6. Длина волны

3) Зву­ко­вые волны яв­ля­ют­ся про­доль­ны­ми упру­ги­ми ко­ле­ба­ни­я­ми среды.

Вспом­нив все это, пе­ре­хо­дим к раз­бо­ру задач.

 Задача №3

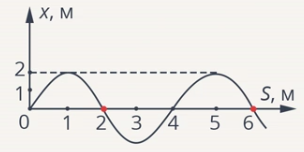
Есть мгно­вен­ная фо­то­гра­фия волны в ре­зи­но­вом шнуре (см. рис. 7).

Опре­де­ли­те: 1) длину волны; 2) ам­пли­ту­ду ко­ле­ба­ний ча­сти­чек шнура.

Рис. 7. Фо­то­гра­фия волны

Ре­ше­ние

Сна­ча­ла най­дем длину волны: 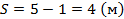. Длину волны можно также по­лу­чить, если от­ме­тить и дру­гие две точки (см. рис. 8).

Рис. 8. Опре­де­ле­ние длины волны

Зна­че­ние ам­пли­ту­ды из ри­сун­ка равно 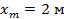. Так что длину волны и ам­пли­ту­ду мы нашли, можно за­пи­сы­вать ответ.

Ответ: , .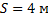

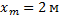
 Задача №4

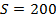
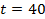
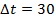
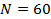
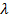
Под­вод­ная лодка всплы­ла на рас­сто­я­нии  м от бе­ре­га, вы­зва­ла волны на по­верх­но­сти воды. Волны дошли до бе­ре­га за  с, при­чем за сле­ду­ю­щие  с было  всплес­ков волн о берег. Ка­ко­во рас­сто­я­ние между греб­ня­ми со­сед­них волн ?

Ре­ше­ние

Вспом­ним фор­му­лу, ко­то­рая свя­зы­ва­ет длину волны с дру­ги­ми ха­рак­те­ри­сти­ка­ми этого вол­но­во­го дви­же­ния. Длина волны свя­за­на со ско­ро­стью и ча­сто­той, по­это­му за­да­ча раз­би­ва­ет­ся на два этапа: на на­хож­де­ние ско­ро­сти волны и на на­хож­де­ние её ча­сто­ты.

Нам из­вест­но, что пер­вая волна, как и по­сле­ду­ю­щие, про­шла рас­сто­я­ние 200 м за 40 с, по­это­му 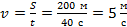. Итак, ско­рость волны най­де­на.

Ча­сто­та, если из­вест­но ко­ли­че­ство ко­ле­ба­ний, со­вер­шен­ных за опре­де­лен­ное ко­ли­че­ство вре­ме­ни, имеет вид: 

Мы знаем все для на­хож­де­ния длины волны: .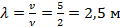

Ответ: 2,5 м.