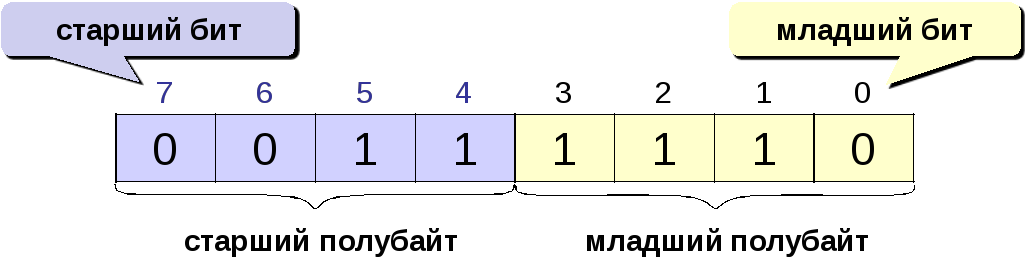
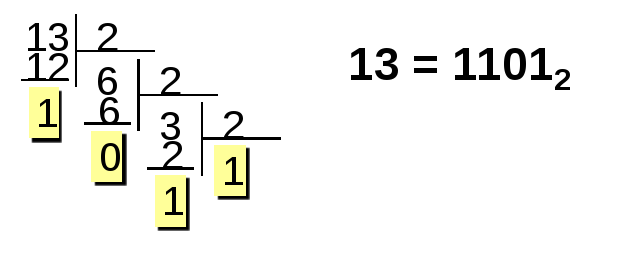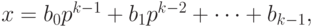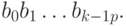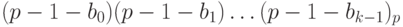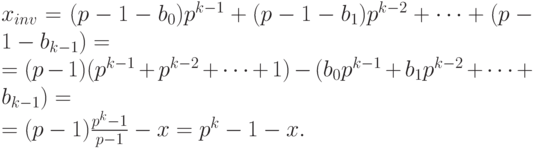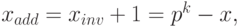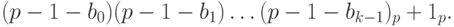Как найти прямой код десятичного числа - AvtoShod.ru

Тема 3: Представление
целых чисел в компьютере.

Представление числовой информации в
компьютере

Любая информация (числа,
текстовая, графическая и т. д.) представляется
в ЭВМ в виде двоичных кодов фиксированной
или переменной длины. Отдельные элементы
двоичного кода, имеющие значение 0 или
1, называют битами.
Двоичный код состоящий из 8 разрядов
носит название байта.

Целые числа могут
представляться в компьютере со знаком
или без знака.

Представление целых чисел без знака
в компьютере

Целые числа без знака обычно занимают
в памяти компьютера один,
два или 4 байта.

В однобайтовом формате
числа принимают значения от
00000000₂
до 11111111₂.

В двубайтовом формате —
от 00000000 00000000₂
до 11111111 11111111₂.

В четырехбайтовом — от
00000000 00000000 00000000 00000000₂
до 11111111 1111111 11111111 11111111₂

Диапазоны значений целых чисел без
знака

Формат числа в байтах	Диапазон
Запись с порядком	Обычная запись
1	0 … 2⁸–1	0 … 255
2	0 … 2¹⁶–1	0 … 65535
4	0 … 2³²–1	0…429967295

Например,
в однобайтовом формате число 62=111110₂
имеет вид:

В двубайтовом формате число 1402=10101111010₂
имеет вид:

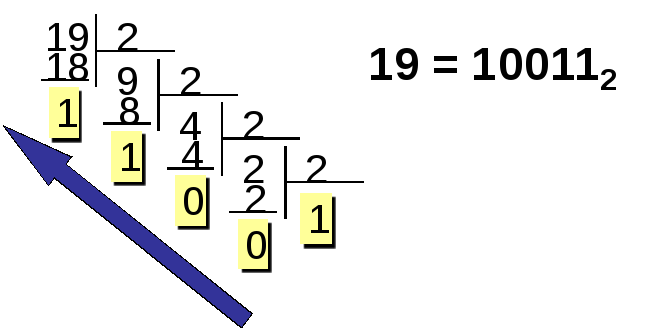
Пример 1. Для хранения целого числа
без знака используется один

байт. Записать представление числа 19 в
компьютере.

1 шаг: Переведем число 19 из десятичной
системы счисления в двоичную.

2 шаг:
Так как для представления числа в
компьютере выделен 1 байт, то код числа
должен содержать 8 знаков (8 бит). Поэтому
впереди числа дописываем 3 незначащих
нуля.

⁰

Задания.

1. Запишите числа в беззнаковом коде
(формат 1 байт):

а) 31; б)
163; в) 65; г) 128.

2. Найдите десятичные
представления чисел, записанных в
беззнаковом коде:

а) 0 1011000;
б) 1 0011011; в) 0 1101001;
г) 1 1000000.

Представление целых чисел со знаком

Так же как беззнаковые целые числа целые
со знаком обычно занимают в
памяти компьютера один, два
или 4 байта.

Диапазоны значений целых чисел со
знаком

Формат числа в байтах	Диапазон
Запись с порядком	Обычная запись
1	–2⁷ … 2⁷–1	–128 … 127
2	–2¹⁵ … 2¹⁵–1	–32768 … 32767
4	–2³¹ … 2³¹–1	–2147483648 … 2147483647

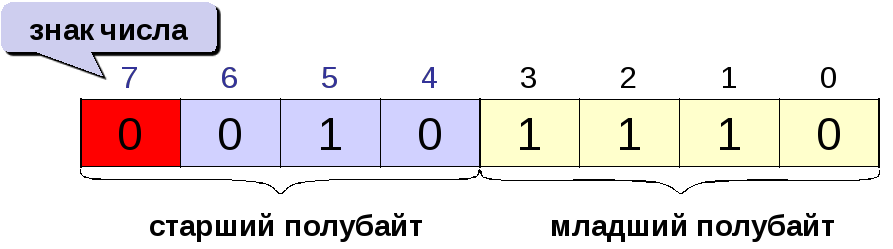
Самый левый (старший бит)
разряд определяет знак числа.
Если
он равен 0, число положительное, если 1,
то отрицательное.

Например,
в однобайтовом формате число 46=101110₂
имеет вид:

В ЭВМ в целях упрощения
выполнения арифметических операций
применяют специальные коды для
представления чисел. Использование
кодов позволяет свести операцию вычитания
чисел к арифметическому сложению кодов
этих чисел. Применяются прямой,
обратный
и дополнительный
коды чисел. Дополнительный код используется
для хранения чисел в запоминающем
устройстве ЭВМ. Обратный и дополнительный
коды используются для замены операции
вычитания операцией сложения, что
упрощает устройство арифметического
блока ЭВМ.

Прямой код.
Прямой код двоичного числа совпадает
по изображению с записью самого числа.
Значение знакового разряда для
положительных чисел равно 0, а для
отрицательных чисел 1.

Обратный код.
Обратный код для
положительного числа совпадает с прямым
кодом. Для отрицательного числа все
цифры числа заменяются на противоположные
(1 на 0, 0 на 1), а в знаковый разряд заносится
единица.

Дополнительный код.
Дополнительный код
положительного числа совпадает с прямым
кодом. Для отрицательного числа
дополнительный код образуется путем
получения обратного кода и добавлением
к младшему разряду единицы.

Например, в однобайтовом формате числа
27 и -27 имеют вид:

Число	Прямой код	Обратный код	Дополнительный код
27	00011011	00011011	00011011
-27	10011011	11100100	11100101

Пример 1. Найти прямой, обратный и
дополнительный код представления числа
13 в однобайтном формате.

1 шаг: Переведем число 13 из десятичной
системы счисления в двоичную.

2 шаг: Для представления
числа в компьютере выделен 1 байт. Старший
бит занимает знак числа – 0. Сам код
числа должен занимать 7 бит. Таким образом
прямой код числа 13

⁰

Так как для положительных чисел прямой,
обратный и дополнительный код совпадает,
то ответ 00001101.

Пример 2. Найти прямой, обратный и
дополнительный код представления числа
-23 в однобайтовом формате.

1 шаг: Переведем число -23 из десятичной
системы счисления в двоичную. Получим

-23₁₀=-10111₂

2 шаг: Прямой код числа в однобайтовом
формате, учитывая, что старший бит
занимает знак числа -1, имеет вид

⁰

3 шаг: Найдем обратный код числа -23,
заменив все цифры числа на
противоположные (1 на 0, 0 на 1), а в знаковый
разряд заносится единица. Имеем,

4 шаг: Найдем дополнительный код
числа -23, добавив 1 к младшему
разряду обратного кода.

Ответ:
прямой код – 10010111; обратный – 11101000;
дополнительный – 11101001.

Так
вот, прямой
обратный и дополнительный код — это
модели представления целых чисел,
как положительных, так и отрицательных.
Примеры записи некоторых чисел во всех
трех восьмиразрядных кодах показаны в
таблице ниже.

Число	Прямой код	Обратный код	Дополнительный код
0	00000000	00000000	00000000
1	00000001	00000001	00000001
-1	10000001	11111110	11111111
5	00000101	00000101	00000101
-5	10000101	11111010	11111011
8	00001000	00001000	00001000
-8	10001000	11110111	11111000
120	01111000	01111000	01111000
-120	11111000	10000111	10001000
127	01111111	01111111	01111111
-127	11111111	10000000	10000001

Во
всех трех кодах старший разряд указывает
на знак числа и он равен единице, если
число отрицательное и нулю в противном
случае. Остальные разряды содержат
представление модуля числа. Различие
между кодами наблюдается именно в
способах представления модуля. Для
положительного числа модуль во всех
трех кодах представляется одинаково —
это просто естественная запись двоичного
числа.
Для отрицательных чисел, в обратном
коде это просто поразрядная инверсия
прямого кода, а в дополнительном — к
обратному коду, как к числу, просто
прибавляется единица.

Распространёнными
формами представления чисел со знаками
является их представление в прямом,
обратном и дополнительном коде.
Прямой
код числа образуется кодированием знака
числа нулём, если число положительно и
единицей, если число отрицательно (для
двоичной системы)
Для общего случая
(q — 1) — если число отрицательно, и 0 — если
число положительно. q — основание системы
счисления.
Код знака записывается
перед старшей цифрой числа и отделяется
от неё точкой:
-1.01 = 1.101
Прямой, обратный
и дополнительный коды положительных
чисел совпадают между собой.
Обратный
код отрицательного числа образуется
из прямого кода, заменой его цифр на их
дополнения до величины q-1. Код знака
сохраняется без изменения.
Пример
:
+123₁₀ =
0.123_пр =
0.123_об.
-123₁₀ =
9.123_пр =
9.876_об
+3А7С00₁₆ =
0.3А7С00_пр =
0.3А7С00_об.
-3А7С00₁₆ =
F.3А7С00_пр=
F.C583FF_об.
-101₂ =
1.101_пр =
1.010_об.
Замена
цифр их дополнениями для двоичной
системы совпадает с операцией инверсии,
то есть нули заменяются единицами,
единицы — нулями. Знак принимает значение,
равное единице.
Дополнительный код
отрицательного числа образуется из
обратного увеличением на 1 его младшего
разряда. При этом перенос из знакового
разряда игнорируется.
Пример:
+236₁₀ =
0.236_пр.=
0.236_об.=
0.236_доп.
-236₁₀ =
9.236_пр.=
9.763_об.=
9.764_доп.
-101₂=
1.101_пр.=
1.010_об=
1.011_доп.
-3А7С₁₆=
F.3А7С_пр=
F.C583_об.=
F.C584_доп.
Правила
перевода из прямого кода в обратный и
из обратного в прямой, а также из прямого
в дополнительный и из дополнительного
в прямой совпадают между собой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

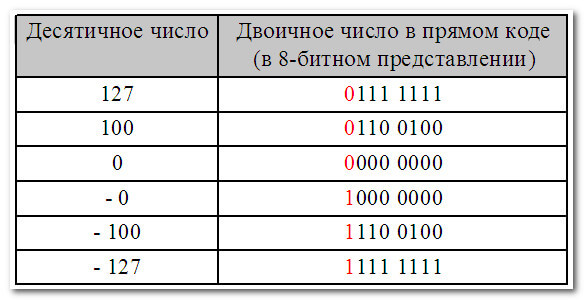
Двоичное число: прямой, обратный и дополнительный коды

Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Прямой, обратный и дополнительный коды двоичного числа — способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел

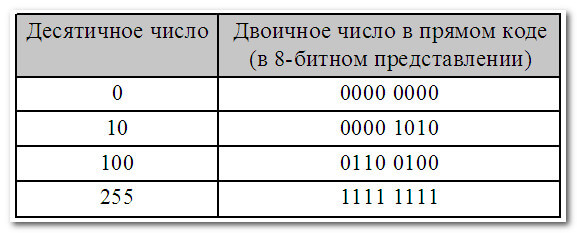
Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.

Прямой код

Прямой код — способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел

Прямой код используется в двух вариантах.
В первом (основной) — для записи только неотрицательных чисел:

В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 — от 0 до 255)

Второй вариант — для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае — восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
— знаковый разряд равен 0, то число положительное
— знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:

Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Прямой код используется главным образом для представления неотрицательных чисел.
Использование прямого кода для представления отрицательных чисел является неэффективным — очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля — положительный ноль и отрицательный ноль (чего не бывает):

Обратный код

Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 1, за которым следует инвертированное значение положительного числа.

Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.

При 8-битном двоичном числе — знаковый бит (как и в прямом коде) старший (8-й)

Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127

Арифметические операции с отрицательными числами в обратном коде:

(Арифметические операции с двоичными числами)

1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = — 0001 1001
Необходимо их сложить:
100 + (-25) = 100 — 25 = 75

1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0001 1001
-25= 1110 0110
и складываем два числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд — переполнение), = 0100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0100 1010 + 1 = 0100 1011 (знаковый бит =0, значит число положительное), что равно 75 в десятичной системе

2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = — 0000 1010
Необходимо их сложить:
5 + (-10) = 5 — 10 = -5

1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0000 1010
-10= 1111 0101
и складываем два числа:
0000 0101 (5) + 1111 0101 (-10) = 1111 1010 (знаковый бит =1, значит число отрицательное)

2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1111 1010 —-> 1000 0101
Проверяем:
1000 0101 = — 0000 0101 = -5

Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
— арифметические операции проводятся в два этапа
— как и в прямом коде два представления нуля — положительный и отрицательный

Дополнительный код

Дополнительный код — наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.

В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).

Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.

Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
— инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
— к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 —-> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 —-> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 — десятичное число -10 в дополнительном коде

2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 — 0000 1010 = 1111 0110 — десятичное число -10 в дополнительном коде

Арифметические операции с отрицательными числами в дополнительном коде

Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде

Как мы видим на этом примере — дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.

Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода

Предыдущие статьи:
1. Микроконтроллеры — первый шаг
2. Системы счисления: десятичная, двоичная и шестнадцатиричная
3. Логические операции, логические выражения, логические элементы
4. Битовые операции

(39 голосов, оценка: 4,69 из 5)

Загрузка…

Источник

Прямой, дополнительный и обратный коды

Следующий калькулятор разработан для перевода введенного вами целого числового значения в двоичный вид кода, также калькулятор показывает обратный и дополнительный код того самого числа.

Итак, давайте же разберем, что означают вышеописанные умные слова.

Прямой код — это некое вывод беззнакового двоичного числа.

Обратный код — это преобразование прямого кода (или же просто инверсный). Это простая замена нолей на единицы, и наоборот.

Дополнительный код — часто еще говорят дополнение до двойки — это тоже обратный код, плюс прибавляется единица к самому меньшему значащему разряду.

Источник

Инфоурок

›

Информатика

›Презентации›Представление чисел в компьютере. Прямой, обратный и дополнительный код

Представление чисел в компьютере. Прямой, обратный и дополнительный код

Скачать материал

Сейчас обучается 98 человек из 41 региона

Сейчас обучается 84 человека из 36 регионов

Описание презентации по отдельным слайдам:

1 слайд

Представление чисел в компьютере.
Прямой, обратный и дополнительный код
ФИО: Воронова Екатерина Николаевна
Место работы: МАОУ «Лицей №1″г. Стерлитамак
Должность: учитель информатики
2 слайд

ячейка из n разрядов
n — 1 разряд
0 разряд
Ячейка – это часть памяти компьютера, вмещающая
в себя информацию, доступную для обработки
отдельной командой процессора.
3 слайд

ячейка из n разрядов
n — 1 разряд
0 разряд
Содержимое ячейки памяти называется машинным словом.
Ячейка памяти разделяется на разряды, в каждом из которых хранится разряд числа.
4 слайд

Бит (от английского binary digit — двоичная цифра) — минимальная единица измерения информации. Каждый бит может принимать значение 0 или 1.
Битом также называют разряд ячейки памяти ЭВМ.
8 бит = 1 байт
Байт (от английского byte – слог) – часть машинного слова, состоящая из 8 бит, обрабатываемая в ЭВМ как одно целое.
7 разряд
0 разряд
ячейка из 8 разрядов
5 слайд

Знаковый разряд
Для представления чисел в памяти компьютера используются два формата: формат с фиксированной точкой и формат с плавающей точкой. В формате с фиксированной точкой представляются только целые числа, в формате с плавающей точкой – вещественные числа (целые и дробные).
Целые числа могут представляться в компьютере со знаком или без знака.
Целые числа без знака обычно занимают в памяти один или два байта.
Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» — единицей.
6 слайд

В ЭВМ в целях упрощения выполнения арифметических операций применяют
специальные коды для представления целых чисел
Прямой код числа
Обратный код числа
Дополнительный код числа
7 слайд

Прямой код – это представление числа в двоичной системе счисления, при этом первый разряд отводится под знак числа. Если число положительное, то в первом разряде находится 0, если число отрицательное, в первом разряде указывается 1.
Положительное десятичное число 24 представляется
Знак числа «+»
8 слайд

Обратный код для положительного числа в двоичной системе счисления совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Отрицательное десятичное число -24 представляется
Знак числа «-»
9 слайд

Дополнительный код используют в основном для представления в компьютере отрицательных чисел.
Алгоритм получения дополнительного кода для отрицательного числа
1. Найти прямой код числа ( перевести число в двоичную систему счисления число без знака)
2. Получить обратный код. Поменять каждый ноль на единицу, а единицу на ноль ( инвертировать число)
3. К обратному коду прибавить 1
10 слайд

Найдем дополнительный код десятичного числа — 47
1. Найдем двоичную запись числа 47 ( прямой код)
2. Инвертируем это число ( обратный код)
3. Прибавим 1 к обратному коду и получим запись этого числа в оперативной памяти
11 слайд

Задание 1. Записать внутреннее представление следующих десятичных чисел, используя 8 – разрядную ячейку:
6410
— 12010
12 слайд

Задание 2. Как запишутся в оперативной памяти компьютера следующие десятичные числа в 16-ти разрядной сетке
5710
20010
-11710
13 слайд

-20010
-11710
Задание 2. Как запишутся в оперативной памяти компьютера следующие десятичные числа в 16-ти разрядной сетке
14 слайд

Домашняя работа
Задание 1. Получить внутреннее представление целого числа 12310 в 8-разрядной ячейке памяти компьютера.

Задание 2. Получить внутреннее представление целого числа
— 12310 в 8-разрядной ячейке памяти компьютера.

Задание 3. Получить внутреннее представление целого числа — 1710 в 16 – ти разрядной ячейке памяти компьютера.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 263 482 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

18.09.2022
75
4

18.09.2022
1947
347

18.09.2022
1671
56

18.09.2022
1987
53

18.09.2022
189
7

18.09.2022
83
2

18.09.2022
376
6

Вам будут интересны эти курсы:

Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Облачные технологии в образовании»
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

Настоящий материал опубликован пользователем Айбазова Ася Васильевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 1 год и 8 месяцев
- Подписчики: 0
- Всего просмотров: 393
- Всего материалов:
  
  1

Файлы

Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….

Источник

Современные компьютеры могут обрабатывать только дискретную информацию, поэтому любой вид информации преобразуется в числовую форму, которая затем кодируется в двоичном виде.

Кодированием данных называется представление данных с помощью условных знаков. Система двоичного кодирования заключается в представлении данных произвольного типа двоичным кодом, в виде последовательности нулей и единиц.

В настоящей главе рассматриваются методы двоичного кодирования целых и действительных чисел, а также текстовой информации.

В сокращенном виде двоичный код представляется в шестнадцатеричном формате, для этого используются таблицы тетрад. Шестнадцатеричный формат обозначается hex, от hexadecimal, десятичный — dec или decimal.

Кодирование целых чисел

Рассмотрим способы кодирования целых чисел. Для кодирования используется не менее 1 байта, или 8 двоичных разрядов. Типы данных, в которых хранятся целые числа, обычно состоят из 1, 2, 4 или 8 байт.

Кодирование целых неотрицательных чисел

Рассмотрим типы данных, в которых хранятся целые неотрицательные, или беззнаковые, числа. С помощью k двоичных разрядов может быть представлено 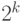2^k различных значений, с кодами от 00dots0 до 11dots1, поэтому в них хранятся целые числа в пределах от 0 до 2^k - 1 . Диапазоны целых беззнаковых чисел для таких типов данных, а также максимальные числа, которые в них представлены, показаны в табл. 2.1.

Пример 1. В четырех байтах число 33 кодируется в виде: , или 00000021 (hex).

Кодирование целых чисел со знаком

Рассмотрим типы данных, которые используются для хранения положительных и отрицательных целых чисел, или целых чисел со знаком. Диапазоны чисел для этих типов данных, которые можно закодировать с помощью 1, 2, 4 или 8 байт, а также минимальные и максимальные числа показаны в таблице 2.2. В первом столбце указывается число байт.

Если количество разрядов в типе данных равно k, то диапазон кодируемых чисел составляет от 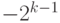$- 2^{k - 1}$ до $2^{k - 1} - 1$ . Неотрицательные числа кодируются так же, как и в случае беззнаковых чисел, коды этих чисел начинаются с 0 (см. диапазон). Соответственно, коды отрицательных чисел начинаются с 1. Множество отрицательных чисел так же, как и множество положительных, представляется множеством двоичных кодов, упорядоченных по возрастанию.

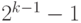
Рассмотрим, например, тип данных, в котором для кодирования целых чисел со знаком используется 2 разряда. В нем могут быть закодированы числа — 2, — 1, 0, 1 с помощью кодов 10, 11, 00, 01, соответственно. Если тип данных содержит 3 разряда, то в нем могут быть представлены числа — 4, — 3, — 2, — 1, 0, 1, 2, 3 соответственно с помощью кодов 100, 101, 110, 111, 000, 001, 010, 011.

В общем случае левая граница диапазона кодируется двоичным словом 100dots0, а правая — двоичным словом 011dots1.

Итак, если двоичный код числа начинается с 1, то он представляет отрицательное целое число, а если с 0, — то неотрицательное. Старший разряд двоичного кода называется знаковым разрядом. Код, который используется для кодирования неотрицательных целых чисел, называется прямым, а для кодирования отрицательных — дополнительным. Дополнительные коды позволяют заменить операцию вычитания операцией сложения и сделать возможной реализацию операций сложения и вычитания одинаковыми для знаковых и беззнаковых чисел (см. ниже).

Рассмотрим понятия прямого и дополнительного кода в общем случае для системы счисления с основанием p, где p — целое, p> 1.

Пусть для p-ичного кодирования , т. е. для представления целого числа в системе счисления с основанием p, используется k разрядов, и диапазон кодируемых чисел составляет от 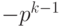$- p^{k - 1}$ до $p^{k - 1} - 1$ .

Для целого числа x, такого что 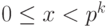, выполняется разложение

$x = b_0p^{k - 1} + b_1p^{k - 2} + dots + b_{k - 1},$

где 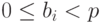, для i = 0, 1, dots, k — 1.

Прямым кодом числа x называется его представление в p-ичном виде с помощью слова длины k:

$b_0b_1 dots b_{k - 1 p}.$

Обратным кодом числа (-x) называется код

$(p - 1 - b_0)(p - 1 - b_1) dots (p - 1 - b_{k - 1})_p$

Обозначим через 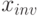$x_{inv}$ число, которое представляет этот код. Имеем:

$x_{inv} = (p - 1 - b_0)p^{k - 1} + (p - 1 - b_1)p^{k - 2} + dots + (p - 1 - b_{k - 1}) =\ = (p - 1)(p^{k - 1} + p^{k - 2} + dots + 1) - (b_0p^{k - 1} + b_1p^{k - 2} + dots + b_{k - 1}) =\ = (p-1)frac{p^k-1}{p-1}-x= p^k - 1 - x.$

Дополнительным кодом отрицательного числа (— x) называется p-ичное представление положительного числа

$x_{add} = x_{inv} + 1 = p^k - x,$

или p-ичное представление суммы

$(p - 1 - b_0)(p - 1 - b_1) dots (p - 1 - b_{k - 1})_p + 1_p.$

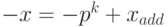
Отсюда, в частности, следует, что $x + x_{add }= p^k$ и $- x = - p^k + x_{add}$ .

Например, найдем дополнительный код числа 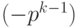$(- p^{k - 1})$ — левой границы диапазона. Прямой код числа $p^{k - 1}$ равен . Поэтому обратный код числа — $p^{k - 1}$ имеет вид: . Соответственно, дополнительный код выглядит следующим образом:

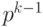
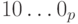
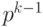
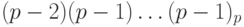
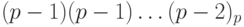
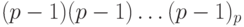
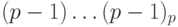
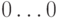
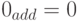
Аналогично, найдем дополнительный код числа (- 1). Число 1 имеет прямой код 00dots1, следовательно, обратный код для (- 1) имеет вид: . Поэтому дополнительным кодом числа (- 1) является . Найдем также дополнительный код числа 0. Это число имеет прямой код и, соответственно, обратный код . Следовательно, дополнительный код равен 1 0dots0 , так что $0_{add} = 0$ . Отметим, что в k-разрядной целочисленной арифметике полагают , т. е. все числа рассматриваются как остатки от деления на p^k .

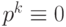
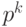
Пример 2. Найдем дополнительный код числа (- 127) при двоичном кодировании в 1 байте. Имеем:

прямой код числа 127: 01111111;

обратный код: 10000000;

дополнительный код: 10000000 + 1 = 10000001;

Пример 3. Найдем дополнительный код числа (- 12) при двоичном кодировании в 4 байтах типа данных integer. Имеем:

прямой код числа 12: 00000000 00000000 00000000 00001100;

обратный код: 11111111 11111111 11111111 11110011;

дополнительный код: 11111111 11111111 11111111 11110100,

или fffffff4 (hex).

Пример 4. Пусть p = 10. Тогда с помощью 4 разрядов можно закодировать целые числа в пределах от 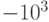- 10^3 до , т. е. от — 1000 до 999. Найдем дополнительный код при десятичном кодировании числа (- 812). Имеем:

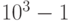
прямой код для 812: 0812;

обратный код: 9187;

дополнительный код: 9188 (= 10000 — 812).

Пример 5. Пусть p = 16. Тогда с помощью 3 разрядов можно закодировать числа в пределах от — 256 до 255. Найдем дополнительный код при 16-ричном кодировании числа (- 50). Имеем:

прямой код числа 50: 032;

обратный код: fcd;

дополнительный код: fce.

Источник

Двоичное число: прямой, обратный и дополнительный коды

Прямой код

Обратный код

Дополнительный код

Прямой, дополнительный и обратный коды

Представление чисел в компьютере. Прямой, обратный и дополнительный код

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Кодирование целых чисел

Кодирование целых неотрицательных чисел

Кодирование целых чисел со знаком

Не пропустите также: