Еще раз о поиске простых чисел
Время на прочтение
7 мин
Количество просмотров 220K

На снимке — скульптура абстрактного экспрессиониста Марка Ди Суверо «Решето Эратосфена», установленная в кампусе Стэнфорского университета
Введение
Напомним, что число называется простым, если оно имеет ровно два различных делителя: единицу и самого себя. Числа, имеющие большее число делителей, называются составными. Таким образом, если мы умеем раскладывать числа на множители, то мы умеем и проверять числа на простоту. Например, как-то так:
function isprime(n){
if(n==1) // 1 - не простое число
return false;
// перебираем возможные делители от 2 до sqrt(n)
for(d=2; d*d<=n; d++){
// если разделилось нацело, то составное
if(n%d==0)
return false;
}
// если нет нетривиальных делителей, то простое
return true;
}
(Здесь и далее, если не оговорено иное, приводится JavaScript-подобный псевдокод)
Время работы такого теста, очевидно, есть O(n½), т. е. растет экспоненциально относительно битовой длины n. Этот тест называется проверкой перебором делителей.
Довольно неожиданно, что существует ряд способов проверить простоту числа, не находя его делителей. Если полиномиальный алгоритм разложения на множители пока остается недостижимой мечтой (на чем и основана стойкость шифрования RSA), то разработанный в 2004 году тест на простоту
AKS
[1] отрабатывает за полиномиальное время. С различными эффективными тестами на простоту можно ознакомиться по [2].
Если теперь нам нужно найти все простые на достаточно широком интервале, то первым побуждением, наверное, будет протестировать каждое число из интервала индивидуально. К счастью, если у нас достаточно памяти, можно использовать более быстрые (и простые) алгоритмы решета. В этой статье мы обсудим два из них: классическое решето Эратосфена, известное еще древним грекам, и решето Аткина, наиболее совершенный современный алгоритм этого семейства.
Решето Эратосфена
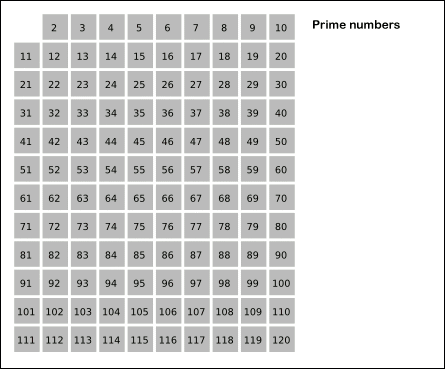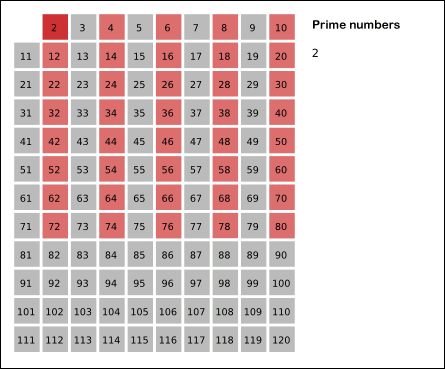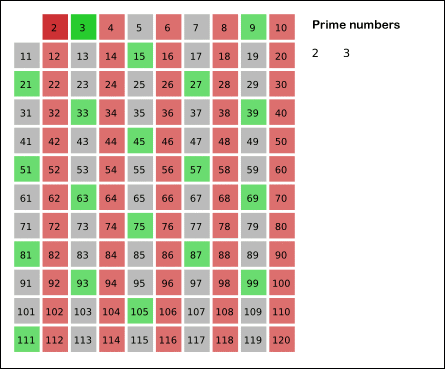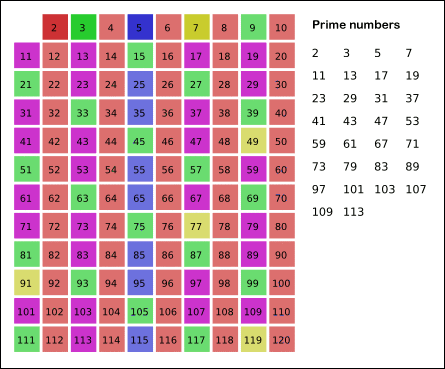
Древнегреческий математик Эратосфен предложил следующий алгоритм для нахождения всех простых, не превосходящих данного числа n. Возьмем массив S длины n и заполним его единицами (пометим как невычеркнутые). Теперь будем последовательно просматривать элементы S[k], начиная с k = 2. Если S[k] = 1, то заполним нулями (вычеркнем или высеем) все последующие ячейки, номера которых кратны k. В результате получим массив, в котором ячейки содержат 1 тогда и только тогда, когда номер ячейки — простое число.
Много времени можно сэкономить, если заметить, что, поскольку у составного числа, меньшего n, по крайней мере один из делителей не превосходит , процесс высевания достаточно закончить на
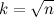
Еще немного операций можно сэкономить, если — по той же причине — начинать вычеркивать кратные k, начиная не с 2k, а с номера k2.
Реализация примет следующий вид:
function sieve(n){
S = [];
S[1] = 0; // 1 - не простое число
// заполняем решето единицами
for(k=2; k<=n; k++)
S[k]=1;
for(k=2; k*k<=n; k++){
// если k - простое (не вычеркнуто)
if(S[k]==1){
// то вычеркнем кратные k
for(l=k*k; l<=n; l+=k){
S[l]=0;
}
}
}
return S;
}
Эффективность решета Эратосфена вызвана крайней простотой внутреннего цикла: он не содержит условных переходов, а также «тяжелых» операций вроде деления и умножения.
Оценим сложность алгоритма. Первое вычеркивание требует n/2 действий, второе — n/3, третье — n/5 и т. д. По формуле Мертенса
так что для решета Эратосфена потребуется O(n log log n) операций. Потребление памяти же составит O(n).
Оптимизация и параллелизация
Первую оптимизацию решета предложил сам Эратосфен: раз из всех четных чисел простым является только 2, то давайте сэкономим половину памяти и времени и будем выписывать и высеивать только нечетные числа. Реализация такой модификации алгоритма потребует лишь косметических изменений (код).
Более развитая оптимизация (т. н. wheel factorization) опирается на то, что все простые, кроме 2, 3 и 5, лежат в одной из восьми следующих арифметических прогрессий: 30k+1, 30k+7, 30k+11, 30k+13, 30k+17, 30k+19, 30k+23 и 30k+29. Чтобы найти все простые числа до n, вычислим предварительно (опять же при помощи решета) все простые до . Теперь составим восемь решет, в каждое из которых будут входить элементы соответствующей арифметической прогрессии, меньшие n, и высеем каждое из них в отдельном потоке. Все, можно пожинать плоды: мы не только понизили потребление памяти и нагрузку на процессор (в четыре раза по сравнению с базовым алгоритмом), но и распараллелили работу алгоритма.
Наращивая шаг прогрессии и количество решет (например, при шаге прогрессии 210 нам понадобится 48 решет, что сэкономит еще 4% ресурсов) параллельно росту n, удается увеличить скорость алгоритма в log log n раз.
Сегментация
Что же делать, если, несмотря на все наши ухищрения, оперативной памяти не хватает и алгоритм безбожно «свопится»? Можно заменить одно большое решето на последовательность маленьких ситечек и высевать каждое в отдельности. Как и выше, нам придется предварительно подготовить список простых до , что займет O(n½-ε) дополнительной памяти. Простые же, найденные в процессе высевание ситечек, нам хранить не нужно — будем сразу отдавать их в выходной поток.
Не надо делать ситечки слишком маленькими, меньше тех же O(n½-ε) элементов. Так вы ничего не выиграете в асимптотике потребления памяти, но из-за накладных расходов начнете все сильнее терять в производительности.
Решето Эратосфена и однострочники
На Хабрахабре ранее публиковалась большая подборка алгоритмов Эратосфена в одну строчку на разных языках программирования (однострочники №10). Интересно, что все они на самом деле решетом Эратосфена не являются и реализуют намного более медленные алгоритмы.
Дело в том, что фильтрация множества по условию (например,
primes = primes.select { |x| x == prime || x % prime != 0 } на Ruby) или использование генераторных списков aka list comprehensions (например,
let pgen (p:xs) = p : pgen [x|x <- xs, x `mod` p > 0] на Haskell) вызывают как раз то, избежать чего призван алгоритм решета, а именно поэлементную проверку делимости. В результате сложность алгоритма возрастает по крайней мере до 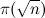
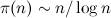
Однострочник
(n: Int) => (2 to n) |> (r => r.foldLeft(r.toSet)((ps, x) => if (ps(x)) ps -- (x * x to n by x) else ps))на Scala ближе к алгоритму Эратосфена тем, что избегает проверки на делимость. Однако сложность построения разности множеств пропорциональна размеру большего из них, так что в результате получаются те же O(n3/2-ε) операций.
Вообще решето Эратосфена тяжело эффективно реализовать в рамках функциональной парадигмы неизменяемых переменных. В случае, если функциональный язык (например, OСaml) позволяет, стоит нарушить нормы и завести изменяемый массив. В [3] обсуждается, как грамотно реализовать решето Эратосфена на Haskell при помощи техники ленивых вычеркиваний.
Решето Эратосфена и PHP
Запишем алгоритм Эратосфена на PHP. Получится примерно следующее:
define("LIMIT",1000000);
define("SQRT_LIMIT",floor(sqrt(LIMIT)));
$S = array_fill(2,LIMIT-1,true);
for($i=2;$i<=SQRT_LIMIT;$i++){
if($S[$i]===true){
for($j=$i*$i; $j<=LIMIT; $j+=$i){
$S[$j]=false;
}
}
}
Здесь есть две проблемы. Первая из них связана с системой типов данных и является характерной для многих современных языков. Дело в том, что наиболее эффективно решето Эратосфена реализуется в тех
ЯП
, где можно объявить гомогенный массив, последовательно расположенный в памяти. Тогда вычисление адреса ячейки S[i] займет всего пару команд процессора. Массив же в PHP — это на самом деле гетерогенный словарь, т. е. он индексируется произвольными строками или числами и может содержать данные различных типов. В таком случае нахождение S[i] становится куда более трудооемкой задачей.
Вторая проблема: массивы в PHP ужасны по накладным расходам памяти. У меня на 64-битной системе каждый элемент $S из кода выше съедает по 128 байт. Как обсуждалось выше, необязательно держать сразу все решето в памяти, можно обрабатывать его порционно, но все равно такие расходы дóлжно признать недопустимыми.
Для решения этих проблем достаточно выбрать более подходящий тип данных — строку!
define("LIMIT",1000000);
define("SQRT_LIMIT",floor(sqrt(LIMIT)));
$S = str_repeat("1", LIMIT+1);
for($i=2;$i<=SQRT_LIMIT;$i++){
if($S[$i]==="1"){
for($j=$i*$i; $j<=LIMIT; $j+=$i){
$S[$j]="";
}
}
}
Теперь каждый элемент занимает ровно 1 байт, а время работы уменьшилось примерно втрое. Скрипт для измерения скорости.
Решето Аткина
В 1999 году Аткин и Бернштейн предложили новый метод высеивания составных чисел, получивший название решета Аткина. Он основан на следующей теореме.
Теорема. Пусть n — натуральное число, которое не делится ни на какой полный квадрат. Тогда
- если n представимо в виде 4k+1, то оно просто тогда и только тогда, когда число натуральных решений уравнения 4x2+y2 = n нечетно.
- если n представимо в виде 6k+1, то оно просто тогда и только тогда, когда число натуральных решений уравнения 3x2+y2 = n нечетно.
- если n представимо в виде 12k-1, то оно просто тогда и только тогда, когда число натуральных решений уравнения 3x2−y2 = n, для которых x > y, нечетно.
C доказательством можно ознакомиться в [4].
Из элементарной теории чисел следует, что все простые, большие 3, имеют вид 12k+1 (случай 1), 12k+5 (снова 1), 12k+7 (случай 2) или 12k+11 (случай 3).
Для инициализации алгоритма заполним решето S нулями. Теперь для каждой пары (x, y), где 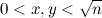
В качестве заключительного этапа пройдемся по предположительно простым номерам последовательно и вычеркнем кратные их квадратам.
Из описания видно, что сложность решета Аткина пропорциональна n, а не n log log n как у алгоритма Эратосфена.
Авторская, оптимизированная реализация на Си представлена в виде primegen, упрощенная версия — в Википедии. На Хабрахабре публиковалось решето Аткина на C#.
Как и в решете Эратосфена, при помощи wheel factorization и сегментации, можно снизить асимптотическую сложность в log log n раз, а потребление памяти — до O(n½+o(1)).
О логарифме логарифма
На самом деле множитель log log n растет крайне. медленно. Например, log log 1010000 ≈ 10. Поэтому с практической точки зрения его можно полагать константой, а сложность алгоритма Эратосфена — линейной. Если только поиск простых не является ключевой функцией в вашем проекте, можно использовать базовый вариант решета Эратосфена (разве что сэкономьте на четных числах) и не комплексовать по этому поводу. Однако при поиске простых на больших интервалах (от 232) игра стоит свеч, оптимизации и решето Аткина могут ощутимо повысить производительность.
P. S. В комментариях напомнили про решето Сундарама. К сожалению, оно является лишь математической диковинкой и всегда уступает либо решетам Эратосфена и Аткина, либо проверке перебором делителей.
Литература
[1] Agrawal M., Kayal N., Saxena N. PRIMES is in P. — Annals of Math. 160 (2), 2004. — P. 781–793.
[2] Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — М., МЦНМО, 2003. — 328 с.
[3] O’Neill M. E. The Genuine Sieve of Eratosthenes. — 2008.
[4] Atkin A. O. L., Bernstein D. J. Prime sieves using binary quadratic forms. — Math. Comp. 73 (246), 2003. — P. 1023-1030.
Решето Эратосфена — алгоритм определения простых чисел
Решето Эратосфена – это алгоритм нахождения простых чисел до заданного натурального числа путем постепенного отсеивания составных чисел. Образно говоря, через решето Эратосфена в процессе его тряски проскакивают составные числа, а простые остаются в решете.
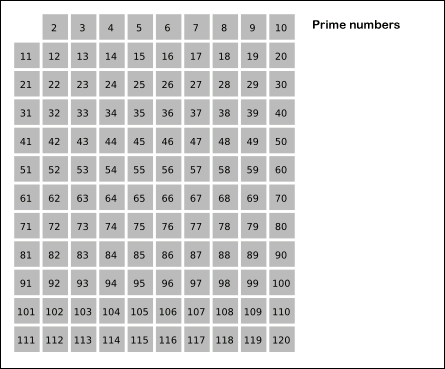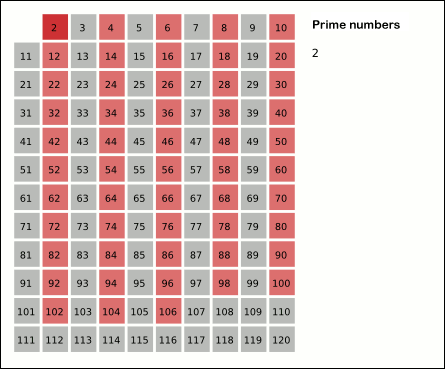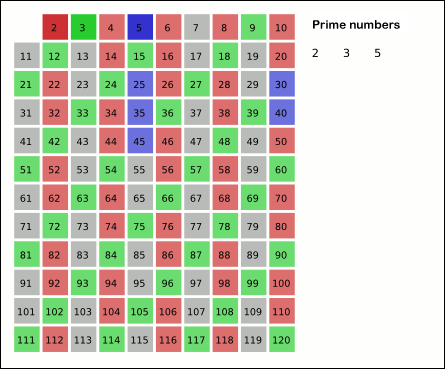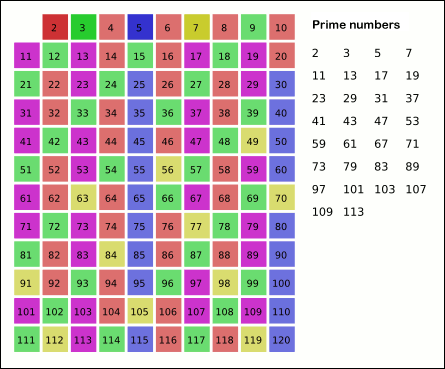
Чтобы понять данный алгоритм, вспомним, что числа являются простыми, если делятся только на единицу и самих себя. Первое простое число — это 2, второе простое число — это 3. Теперь начнем рассуждать:
- Все четные числа, кроме двойки, — составные, т. е. не являются простыми, так как делятся не только на себя и единицу, а также еще на 2.
- Все числа кратные трем, кроме самой тройки, — составные, так как делятся не только на самих себя и единицу, а также еще на 3.
- Число 4 уже выбыло из игры, так как делится на 2.
- Число 5 простое, так как его не делит ни один простой делитель, стоящий до него.
- Если число не делится ни на одно простое число, стоящее до него, значит оно не будет делиться ни на одно сложное число, стоящее до него.
Последний пункт вытекает из того, что сложные числа всегда можно представить как произведение простых. Поэтому если одно сложное число делится на другое сложное, то первое должно делиться на делители второго. Например, 12 делится на 6, делителями которого являются 2 и 3. Число 12 делится и на 2, и на 3.
Алгоритм Эратосфена как раз заключается в последовательной проверке делимости чисел на предстоящие простые числа. Сначала берется первое простое и из ряда натуральных чисел высеиваются все кратные ему. Затем берется следующее простое и отсеиваются все кратные ему и так далее.
При реализации алгоритма Эратосфена на языке программирования есть некоторая сложность. Допустим, мы помещаем натуральные числа до заданного числа N в массив. Далее в процессе выполнения алгоритма будем заменять обнаруженные сложные числа нулями. После выполнения алгоритма те ячейки массива, которые не содержат нули, содержат простые числа, которые выводятся на экран.
Однако индексация массива начинается с нуля, а простые числа начинаются с двойки. Эта проблема решаема, но добавляет сложности в код. Поскольку алгоритм Эратосфена не такой уж простой, легче пренебречь началом и взять массив от 0 до N. Здесь важнее индексы, чем значения элементов. Значениями могут быть логические True, обозначающее простое число, и False, обозначающее сложное число.
В данном примере реализации алгоритма Эратосфена на языке программирования Python список заполняется числами от 0 до N включительно так, что индексы элементов совпадают с их значениями. Далее все непростые числа заменяются нулями:
N = int(input()) # Создается список из значений от 0 до N включительно primes = [i for i in range(N + 1)] # Вторым элементом списка является единица, которую # не считают простым числом. Забиваем ее нулем primes[1] = 0 # Начинаем с 3-го элемента i = 2 while i <= N: # Если значение текущей ячейки до этого не было обнулено, # значит в этой ячейке содержится простое число if primes[i] != 0: # Первое кратное ему будет в два раза больше j = i + i while j <= N: # и это число составное, # поэтому заменяем его нулем primes[j] = 0 # переходим к следующему числу, # которое кратно i (оно на i больше) j = j + i i += 1 # Избавляемся от всех нулей в списке primes = [i for i in primes if i != 0] print(primes)
Пример выполнения:
35 [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]
Больше задач в PDF
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Решето Эратосфена
Определение. Целое положительное число называется простым, если оно имеет ровно два различных натуральных делителя — единицу и самого себя. Единица простым числом не считается.
Решето Эратосфена (англ. sieve of Eratosthenes) — алгоритм нахождения всех простых чисел от (1) до (n).
Основная идея соответствует названию алгоритма: запишем ряд чисел (1, 2,ldots, n), а затем будем вычеркивать
-
сначала числа, делящиеся на (2), кроме самого числа (2),
-
потом числа, делящиеся на (3), кроме самого числа (3),
-
с числами, делящимися на (4), ничего делать не будем — мы их уже вычёркивали,
-
потом продолжим вычеркивать числа, делящиеся на (5), кроме самого числа (5),
…и так далее.
Самая простая реализация может выглядеть так:
vector<bool> sieve(int n) {
vector<bool> is_prime(n+1, true);
for (int i = 2; i <= n; i++)
if (is_prime[i])
for (int j = 2*i; j <= n; j += i)
prime[j] = false;
return is_prime;
}Этот код сначала помечает все числа, кроме нуля и единицы, как простые, а затем начинает процесс отсеивания составных чисел. Для этого мы перебираем в цикле все числа от (2) до (n), и, если текущее число простое, то помечаем все числа, кратные ему, как составные.
Если память позволяет, то для оптимизации скорости лучше использовать не вектор bool, а вектор char — но он займёт в 8 раз больше места. Компьютер не умеет напрямую оперировать с битами, и поэтому при индексации к vector<bool> он сначала достаёт нужный байт, а затем битовыми операциями получает нужное значение, что занимает приличное количество времени.
Время работы
Довольно легко показать, что асимптотическое время работы алгоритма хотя бы не хуже, чем (O(n log n)): даже если бы мы входили в цикл вычёркиваний для каждого числа, не проверяя его сначала на простоту, суммарно итераций было бы
[
sum_k frac{n}{k} = frac{n}{2} + frac{n}{3} + frac{n}{4} + ldots + frac{n}{n} = O(n log n)
]
Здесь мы воспользовались асимптотикой гармонического ряда.
У исходного алгоритма асимптотика должна быть ещё лучше. Чтобы найти её точнее, нам понадобятся два факта про простые числа:
-
Простых чисел от (1) до (n) примерно (frac{n}{ln n}) .
-
Простые числа распределены без больших «разрывов» и «скоплений», то есть (k)-тое простое число примерно равно (k ln k).
Мы можем упрощённо считать, что число (k) является простым с «вероятностью» (frac{1}{ln n}). Тогда, время работы алгоритма можно более точнее оценить как
[
sum_k frac{1}{ln k} frac{n}{k}
approx n int frac{1}{k ln k}
= n ln ln k Big |_2^n
= O(n log log n)
]
Асимптотику алгоритма можно улучшить и дальше, до (O(n)).
Линейное решето
Основная проблема решета Эратосфена состоит в том, что некоторые числа мы будем помечать как составные несколько раз — а именно столько раз, сколько у них различных простых делителей. Чтобы достичь линейного времени работы, нам нужно придумать способ, как рассматривать все составные числа ровно один раз.
Обозначим за (d(k)) минимальный простой делитель числа (k) и заметим следующий факт: у составного числа (k) есть единственное представление (k = d(k) cdot r), и при этом у числа (r) нет простых делителей меньше (d(k)).
Идея оптимизации состоит в том, чтобы перебирать этот (r), и для каждого перебирать только нужные множители — а именно все от (2) до (d(r)) включительно.
Алгоритм
Немного обобщим задачу — теперь мы хотим посчитать для каждого числа (k) на отрезке ([2, n]) его минимальный простой делитель (d_k), а не только определить его простоту.
Изначально массив (d) заполним нулями, что означает, что все числа предполагаются простыми. В ходе работы алгортима этот массив будет постепенно заполняться. Помимо этого, будем поддерживать список (p) всех найденных на текущий момент простых чисел.
Теперь будем перебирать число (k) от (2) до (n). Если это число простое, то есть (d_k = 0), то присвоим (d_k = k) и добавим (k) в список (p).
Дальше, вне зависимости от простоты (k), начнём процесс расстановки значений в массиве (d) — переберем найденные простые числа (p_i), не превосходящие (d_k), и сделаем присвоение (d_{p_i k} = p_i).
const int n = 1e6;
int d[n+1];
vector<int> p;
for (int k = 2; k <= n; k++) {
if (p[k] == 0) {
d[k] = k;
p.push_back(k);
}
for (int x : p) {
if (x > d[k] || x * d[k] > n)
break;
d[k * x] = x;
}
}Алгоритм требует как минимум в 32 раза больше памяти, чем обычное решето, потому что требуется хранить делитель (int, 4 байта) вместо одного бита на каждое число. Линейное решето хоть и имеет лучшую асимптотику, но на практике проигрывает также и по скорости оптимизированному варианту решета Эратосфена.
Применения
Массив (d) он позволяет искать факторизацию любого числа (k) за время порядка размера этой факторизации:
[
factor(k) = {d(k)} cup factor(k / d(k))
]
Знание факторизации всех чисел — очень полезная информация для некоторых задач. Ленейное решето интересно не своим временем работы, а именно этим массивом минимальных простых делителей.
From Wikipedia, the free encyclopedia
Sieve of Eratosthenes: algorithm steps for primes below 121 (including optimization of starting from prime’s square).
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit.
It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with constant difference between them that is equal to that prime.[1] This is the sieve’s key distinction from using trial division to sequentially test each candidate number for divisibility by each prime.[2] Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes.
The earliest known reference to the sieve (Ancient Greek: κόσκινον Ἐρατοσθένους, kóskinon Eratosthénous) is in Nicomachus of Gerasa’s Introduction to Arithmetic,[3] an early 2nd cent. CE book which attributes it to Eratosthenes of Cyrene, a 3rd cent. BCE Greek mathematician, though describing the sieving by odd numbers instead of by primes.[4]
One of a number of prime number sieves, it is one of the most efficient ways to find all of the smaller primes. It may be used to find primes in arithmetic progressions.[5]
Overview[edit]
Sift the Two’s and Sift the Three’s:
The Sieve of Eratosthenes.
When the multiples sublime,
The numbers that remain are Prime.
Anonymous[6]
A prime number is a natural number that has exactly two distinct natural number divisors: the number 1 and itself.
To find all the prime numbers less than or equal to a given integer n by Eratosthenes’ method:
- Create a list of consecutive integers from 2 through n: (2, 3, 4, …, n).
- Initially, let p equal 2, the smallest prime number.
- Enumerate the multiples of p by counting in increments of p from 2p to n, and mark them in the list (these will be 2p, 3p, 4p, …; the p itself should not be marked).
- Find the smallest number in the list greater than p that is not marked. If there was no such number, stop. Otherwise, let p now equal this new number (which is the next prime), and repeat from step 3.
- When the algorithm terminates, the numbers remaining not marked in the list are all the primes below n.
The main idea here is that every value given to p will be prime, because if it were composite it would be marked as a multiple of some other, smaller prime. Note that some of the numbers may be marked more than once (e.g., 15 will be marked both for 3 and 5).
As a refinement, it is sufficient to mark the numbers in step 3 starting from p2, as all the smaller multiples of p will have already been marked at that point. This means that the algorithm is allowed to terminate in step 4 when p2 is greater than n.[1]
Another refinement is to initially list odd numbers only, (3, 5, …, n), and count in increments of 2p in step 3, thus marking only odd multiples of p. This actually appears in the original algorithm.[1][4] This can be generalized with wheel factorization, forming the initial list only from numbers coprime with the first few primes and not just from odds (i.e., numbers coprime with 2), and counting in the correspondingly adjusted increments so that only such multiples of p are generated that are coprime with those small primes, in the first place.[7]
Example[edit]
To find all the prime numbers less than or equal to 30, proceed as follows.
First, generate a list of integers from 2 to 30:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
The first number in the list is 2; cross out every 2nd number in the list after 2 by counting up from 2 in increments of 2 (these will be all the multiples of 2 in the list):
2 3456789101112131415161718192021222324252627282930
The next number in the list after 2 is 3; cross out every 3rd number in the list after 3 by counting up from 3 in increments of 3 (these will be all the multiples of 3 in the list):
2 3456789101112131415161718192021222324252627282930
The next number not yet crossed out in the list after 3 is 5; cross out every 5th number in the list after 5 by counting up from 5 in increments of 5 (i.e. all the multiples of 5):
2 3456789101112131415161718192021222324252627282930
The next number not yet crossed out in the list after 5 is 7; the next step would be to cross out every 7th number in the list after 7, but they are all already crossed out at this point, as these numbers (14, 21, 28) are also multiples of smaller primes because 7 × 7 is greater than 30. The numbers not crossed out at this point in the list are all the prime numbers below 30:
2 3 5 7 11 13 17 19 23 29
Algorithm and variants[edit]
Pseudocode[edit]
The sieve of Eratosthenes can be expressed in pseudocode, as follows:[8][9]
algorithm Sieve of Eratosthenes is
input: an integer n > 1.
output: all prime numbers from 2 through n.
let A be an array of Boolean values, indexed by integers 2 to n,
initially all set to true.
for i = 2, 3, 4, ..., not exceeding √n do
if A[i] is true
for j = i2, i2+i, i2+2i, i2+3i, ..., not exceeding n do
set A[j] := false
return all i such that A[i] is true.
This algorithm produces all primes not greater than n. It includes a common optimization, which is to start enumerating the multiples of each prime i from i2. The time complexity of this algorithm is O(n log log n),[9] provided the array update is an O(1) operation, as is usually the case.
Segmented sieve[edit]
As Sorenson notes, the problem with the sieve of Eratosthenes is not the number of operations it performs but rather its memory requirements.[9] For large n, the range of primes may not fit in memory; worse, even for moderate n, its cache use is highly suboptimal. The algorithm walks through the entire array A, exhibiting almost no locality of reference.
A solution to these problems is offered by segmented sieves, where only portions of the range are sieved at a time.[10] These have been known since the 1970s, and work as follows:[9][11]
- Divide the range 2 through n into segments of some size Δ ≤ √n.
- Find the primes in the first (i.e. the lowest) segment, using the regular sieve.
- For each of the following segments, in increasing order, with m being the segment’s topmost value, find the primes in it as follows:
- Set up a Boolean array of size Δ.
- Mark as non-prime the positions in the array corresponding to the multiples of each prime p ≤ √m found so far, by enumerating its multiples in steps of p starting from the lowest multiple of p between m — Δ and m.
- The remaining non-marked positions in the array correspond to the primes in the segment. It isn’t necessary to mark any multiples of these primes, because all of these primes are larger than √m, as for k ≥ 1, one has
.
If Δ is chosen to be √n, the space complexity of the algorithm is O(√n), while the time complexity is the same as that of the regular sieve.[9]
For ranges with upper limit n so large that the sieving primes below √n as required by the page segmented sieve of Eratosthenes cannot fit in memory, a slower but much more space-efficient sieve like the sieve of Sorenson can be used instead.[12]
Incremental sieve[edit]
An incremental formulation of the sieve[2] generates primes indefinitely (i.e., without an upper bound) by interleaving the generation of primes with the generation of their multiples (so that primes can be found in gaps between the multiples), where the multiples of each prime p are generated directly by counting up from the square of the prime in increments of p (or 2p for odd primes). The generation must be initiated only when the prime’s square is reached, to avoid adverse effects on efficiency. It can be expressed symbolically under the dataflow paradigm as
primes = [2, 3, ...] [[p², p²+p, ...] for p in primes],
using list comprehension notation with denoting set subtraction of arithmetic progressions of numbers.
Primes can also be produced by iteratively sieving out the composites through divisibility testing by sequential primes, one prime at a time. It is not the sieve of Eratosthenes but is often confused with it, even though the sieve of Eratosthenes directly generates the composites instead of testing for them. Trial division has worse theoretical complexity than that of the sieve of Eratosthenes in generating ranges of primes.[2]
When testing each prime, the optimal trial division algorithm uses all prime numbers not exceeding its square root, whereas the sieve of Eratosthenes produces each composite from its prime factors only, and gets the primes «for free», between the composites. The widely known 1975 functional sieve code by David Turner[13] is often presented as an example of the sieve of Eratosthenes[7] but is actually a sub-optimal trial division sieve.[2]
Algorithmic complexity[edit]
The sieve of Eratosthenes is a popular way to benchmark computer performance.[14] The time complexity of calculating all primes below n in the random access machine model is O(n log log n) operations, a direct consequence of the fact that the prime harmonic series asymptotically approaches log log n. It has an exponential time complexity with regard to input size, though, which makes it a pseudo-polynomial algorithm. The basic algorithm requires O(n) of memory.
The bit complexity of the algorithm is O(n (log n) (log log n)) bit operations with a memory requirement of O(n).[15]
The normally implemented page segmented version has the same operational complexity of O(n log log n) as the non-segmented version but reduces the space requirements to the very minimal size of the segment page plus the memory required to store the base primes less than the square root of the range used to cull composites from successive page segments of size O(√n/log n).
A special (rarely, if ever, implemented) segmented version of the sieve of Eratosthenes, with basic optimizations, uses O(n) operations and O(√nlog log n/log n) bits of memory.[16][17][18]
Using big O notation ignores constant factors and offsets that may be very significant for practical ranges: The sieve of Eratosthenes variation known as the Pritchard wheel sieve[16][17][18] has an O(n) performance, but its basic implementation requires either a «one large array» algorithm which limits its usable range to the amount of available memory else it needs to be page segmented to reduce memory use. When implemented with page segmentation in order to save memory, the basic algorithm still requires about O(n/log n) bits of memory (much more than the requirement of the basic page segmented sieve of Eratosthenes using O(√n/log n) bits of memory). Pritchard’s work reduced the memory requirement at the cost of a large constant factor. Although the resulting wheel sieve has O(n) performance and an acceptable memory requirement, it is not faster than a reasonably Wheel Factorized basic sieve of Eratosthenes for practical sieving ranges.
Euler’s sieve[edit]
Euler’s proof of the zeta product formula contains a version of the sieve of Eratosthenes in which each composite number is eliminated exactly once.[9] The same sieve was rediscovered and observed to take linear time by Gries & Misra (1978).[19] It, too, starts with a list of numbers from 2 to n in order. On each step the first element is identified as the next prime, is multiplied with each element of the list (thus starting with itself), and the results are marked in the list for subsequent deletion. The initial element and the marked elements are then removed from the working sequence, and the process is repeated:
[2] (3) 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 ... [3] (5) 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 ... [4] (7) 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 ... [5] (11) 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 ... [...]
Here the example is shown starting from odds, after the first step of the algorithm. Thus, on the kth step all the remaining multiples of the kth prime are removed from the list, which will thereafter contain only numbers coprime with the first k primes (cf. wheel factorization), so that the list will start with the next prime, and all the numbers in it below the square of its first element will be prime too.
Thus, when generating a bounded sequence of primes, when the next identified prime exceeds the square root of the upper limit, all the remaining numbers in the list are prime.[9] In the example given above that is achieved on identifying 11 as next prime, giving a list of all primes less than or equal to 80.
Note that numbers that will be discarded by a step are still used while marking the multiples in that step, e.g., for the multiples of 3 it is 3 × 3 = 9, 3 × 5 = 15, 3 × 7 = 21, 3 × 9 = 27, …, 3 × 15 = 45, …, so care must be taken dealing with this.[9]
See also[edit]
- Sieve of Pritchard
- Sieve of Atkin
- Sieve of Sundaram
- Sieve theory
References[edit]
- ^ a b c Horsley, Rev. Samuel, F. R. S., «Κόσκινον Ερατοσθένους or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,» Philosophical Transactions (1683–1775), Vol. 62. (1772), pp. 327–347.
- ^ a b c d O’Neill, Melissa E., «The Genuine Sieve of Eratosthenes», Journal of Functional Programming, published online by Cambridge University Press 9 October 2008 doi:10.1017/S0956796808007004, pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O’Neill and a list–based, by Richard Bird).
- ^ Hoche, Richard, ed. (1866), Nicomachi Geraseni Pythagorei Introductionis arithmeticae libri II, chapter XIII, 3, Leipzig: B.G. Teubner, p. 30
- ^ a b Nicomachus of Gerasa (1926), Introduction to Arithmetic; translated into English by Martin Luther D’Ooge ; with studies in Greek arithmetic by Frank Egleston Robbins and Louis Charles Karpinski, chapter XIII, 3, New York: The Macmillan Company, p. 204
- ^ J. C. Morehead, «Extension of the Sieve of Eratosthenes to arithmetical progressions and applications», Annals of Mathematics, Second Series 10:2 (1909), pp. 88–104.
- ^ Clocksin, William F., Christopher S. Mellish, Programming in Prolog, 1984, p. 170. ISBN 3-540-11046-1.
- ^ a b Runciman, Colin (1997). «Functional Pearl: Lazy wheel sieves and spirals of primes» (PDF). Journal of Functional Programming. 7 (2): 219–225. doi:10.1017/S0956796897002670. S2CID 2422563.
- ^ Sedgewick, Robert (1992). Algorithms in C++. Addison-Wesley. ISBN 978-0-201-51059-1., p. 16.
- ^ a b c d e f g h Jonathan Sorenson, An Introduction to Prime Number Sieves, Computer Sciences Technical Report #909, Department of Computer Sciences University of Wisconsin-Madison, January 2, 1990 (the use of optimization of starting from squares, and thus using only the numbers whose square is below the upper limit, is shown).
- ^ Crandall & Pomerance, Prime Numbers: A Computational Perspective, second edition, Springer: 2005, pp. 121–24.
- ^ Bays, Carter; Hudson, Richard H. (1977). «The segmented sieve of Eratosthenes and primes in arithmetic progressions to 1012«. BIT. 17 (2): 121–127. doi:10.1007/BF01932283. S2CID 122592488.
- ^ J. Sorenson, «The pseudosquares prime sieve», Proceedings of the 7th International Symposium on Algorithmic Number Theory. (ANTS-VII, 2006).
- ^ Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975. (
primes = sieve [2..]; sieve (p:nos) = p:sieve (remove (multsof p) nos); remove m = filter (not . m); multsof p n = rem n p==0). But see also Peter Henderson, Morris, James Jr., A Lazy Evaluator, 1976, where we find the following, attributed to P. Quarendon:primeswrt[x;l] = if car[l] mod x=0 then primeswrt[x;cdr[l]] else cons[car[l];primeswrt[x;cdr[l]]] ; primes[l] = cons[car[l];primes[primeswrt[car[l];cdr[l]]]] ; primes[integers[2]]; the priority is unclear. - ^ Peng, T. A. (Fall 1985). «One Million Primes Through the Sieve». BYTE. pp. 243–244. Retrieved 19 March 2016.
- ^ Pritchard, Paul, «Linear prime-number sieves: a family tree,» Sci. Comput. Programming 9:1 (1987), pp. 17–35.
- ^ a b Paul Pritchard, «A sublinear additive sieve for finding prime numbers», Communications of the ACM 24 (1981), 18–23. MR600730
- ^ a b Paul Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485. MR685983
- ^ a b Paul Pritchard, «Fast compact prime number sieves» (among others), Journal of Algorithms 4
(1983), 332–344. MR729229 - ^ Gries, David; Misra, Jayadev (December 1978), «A linear sieve algorithm for finding prime numbers» (PDF), Communications of the ACM, 21 (12): 999–1003, doi:10.1145/359657.359660, hdl:1813/6407, S2CID 11990373.
External links[edit]
- primesieve – Very fast highly optimized C/C++ segmented Sieve of Eratosthenes
- Eratosthenes, sieve of at Encyclopaedia of Mathematics
- Interactive JavaScript Page
- Sieve of Eratosthenes by George Beck, Wolfram Demonstrations Project.
- Sieve of Eratosthenes in Haskell
- Sieve of Eratosthenes algorithm illustrated and explained. Java and C++ implementations.
- A related sieve written in x86 assembly language
- Fast optimized highly parallel CUDA segmented Sieve of Eratosthenes in C
- SieveOfEratosthenesInManyProgrammingLanguages c2 wiki page
- The Art of Prime Sieving Sieve of Eratosthenes in C from 1998 with nice features and algorithmic tricks explained.
Содержание
- Описание алгоритма
- Реализация на массиве boolean
- Уменьшение количества проверок
- Уменьшение объёма памяти
- Финальная реализация
- Выводы
Ранее я уже приводил Алгоритм поиска простых чисел методом перебора делителей. Эта реализация хороша, если вам нужно ровно N первых простых чисел. Но если вы ищете простые числа в некотором диапазоне (скажем, не превосходящие 1 000 000), то лучше воспользоваться более быстрым алгоритмом, который называется «решето Эратосфена».
Этот алгоритм назван в честь древнегреческого учёного Эратосфена Киренского.
Алгоритм заключается в том, что изначально мы берём всё множество целых чисел в интересующем нас диапазоне, от 2 до N. Затем последовательно проходимся по этому множеству, вычёркивая каждое чётное число, т.к. оно делится на 2. После этого возвращаемся в начало и вычёркиваем все числа, делящиеся на 3, если они ещё не зачёркнуты. Затем делящиеся на следующее простое число – на 5. Затем на 7, на 11 и т. д. То есть мы «просеиваем» исходное множество целых чисел через сито. В итоге у нас останутся только простые числа.
Давайте напишем самую простую реализацию этого алгоритма. Метод getAllPrimesLessThan() на вход будет принимать размер решета sieveSize, который ограничивает сверху наш диапазон поиска. Для начала нам нужно создать массив типа boolean. Этот массив и будет нашим ситом. Если значение массива по индексу N равно true – число N простое. Если false – то нет. В начале алгоритма все элементы массива проставляем в true с помощью метода Arrays.fill(). Элементы с индексами 0 и 1 сразу ставим в false, т.к. ни 0, ни 1 не являются простыми числами.
public List<Integer> getAllPrimesLessThan(int sieveSize) {
var sieve = new boolean[sieveSize];
Arrays.fill(sieve, true);
sieve[0] = false;
sieve[1] = false;
for (int i = 2; i < sieve.length; i++) {
if (sieve[i]) {
for (int j = 2; i * j < sieve.length; j++) {
sieve[i * j] = false;
}
}
}
// …
Затем в цикле, начиная со второго элемента, проверяем значение каждого элемента. Если элемент равен true, то запускаем вложенный цикл опять же со второго элемента до тех пор, пока произведение индексов i и j не превысит размер массива. И все элементы во вложенном цикле помечаем как false, т.е. они не являются простыми.
В конце ещё раз проходимся по «решету» и собираем простые числа в список:
// …
List<Integer> primes = new ArrayList<>();
for (int i = 2; i < sieve.length; i++) {
if (sieve[i]) {
primes.add(i);
}
}
return primes;
}
Данный алгоритм работает раза в 3 быстрее, чем перебор делителей, о котором я писал в прошлой статье. Но его можно ещё ускорить.
Количество проверок можно существенно уменьшить, если проверять не все числа, а только те, квадрат которых не превосходит диапазон поиска. Действительно, если N * N больше, чем размер решета и все возможные числа уже вычеркнуты, то дальше N проверять не имеет смысла.
for (int i = 2; i * i < sieveSize; i++) {
if (sieve[i]) {
for (int j = i * i; j < sieveSize; j += i) {
sieve[j] = false;
}
}
}
Ну а вложенный цикл мы начинаем как раз с квадрата этого числа и зачёркиваем каждое число, кратное ему.
Данная оптимизация ускоряет алгоритм почти в 2 раза.
Наиболее уязвимым местом алгоритма является тот факт, что нам нужно создавать массив под весь диапазон проверяемых чисел, тогда как в методе перебора делителей мы храним только найденные простые числа. На больших диапазонах вам может просто не хватить памяти для создания такого массива.
Но мы помним, что каждый элемент массива имеет булевый тип, т.е. может принимать только 2 значения. Для хранения такой информации достаточно всего 1 бита. То есть 1 байт памяти позволит хранить 8 элементов!
Заменим наш массив на класс BitSet, который позволяет легко оперировать отдельными битами:
var sieve = new BitSet(sieveSize);
sieve.set(0, sieveSize — 1, true); // изначально все true
sieve.set(0, false);
sieve.set(1, false);
for (int i = 2; i * i < sieve.length(); i++) {
if (sieve.get(i)) {
for (int j = i * i; j < sieve.length(); j += i) {
sieve.set(j, false);
}
}
}
Данная реализация работает ещё чуть быстрее предыдущей и почти в 2 раза быстрее изначальной.
В итоге наша реализация алгоритма поиска целых чисел с помощью «решета Эратосфена» примет следующий вид:
public List<Integer> getAllPrimesLessThan(int sieveSize) {
var sieve = new BitSet(sieveSize);
sieve.set(0, sieveSize — 1, true);
sieve.set(0, false);
sieve.set(1, false);
for (int i = 2; i * i < sieve.length(); i++) {
if (sieve.get(i)) {
for (int j = i * i; j < sieve.length(); j += i) {
sieve.set(j, false);
}
}
}
List<Integer> primes = new ArrayList<>();
for (int i = 2; i < sieve.length(); i++) {
if (sieve.get(i)) {
primes.add(i);
}
}
return primes;
}
Оптимизации, которые мы применили:
- проверять не все числа, а только те, квадрат которых не выходит за диапазон поиска
- булевый массив заменили на битовые поля с помощью BitSet
«Решето Эратосфена» позволяет искать простые числа в некотором диапазоне в несколько раз быстрее, чем алгоритм перебора делителей. Однако ему требуется точно знать диапазон поиска, а также нужна дополнительная память, чтобы хранить само «решето».
В случае, если диапазон поиска заранее неизвестен или у вас не хватает памяти для хранения решета и скорость поиска при этом не столь критична – используйте метод перебора делителей.
P.S. На написание статьи меня мотивировал пользователь Nik Nikita, который выступил с конструктивной критикой алгоритма перебора делителей на моём канале на YouTube.