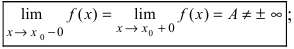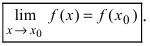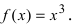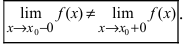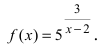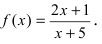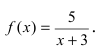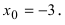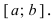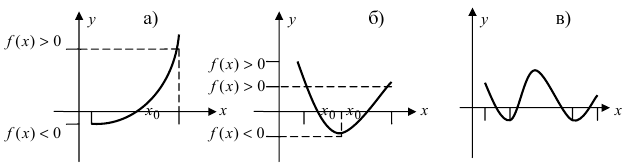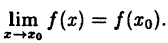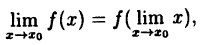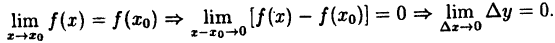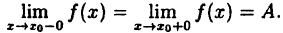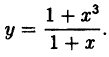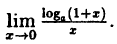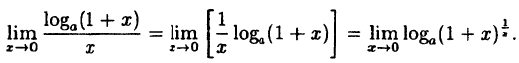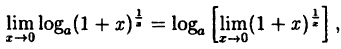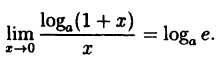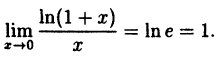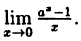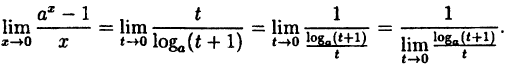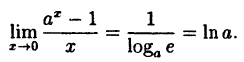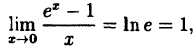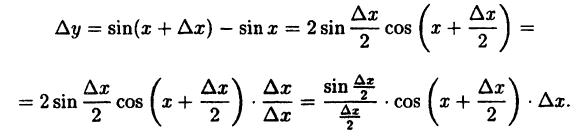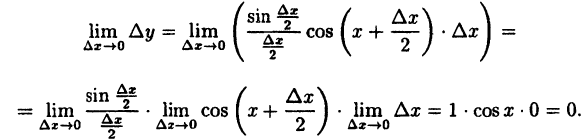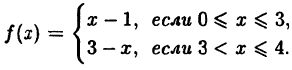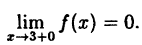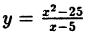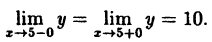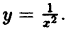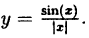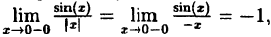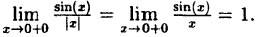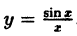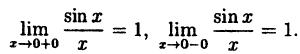Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
- — она определена в этой точке и ее некоторой
-окрестности;
- — существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
— предел функции в точке 
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 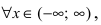
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
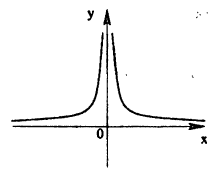
Пример:
Доказать, что функция 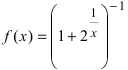
Решение:
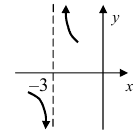
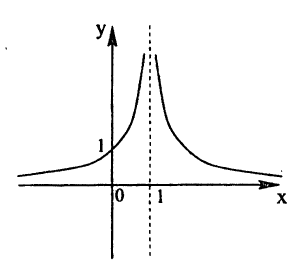
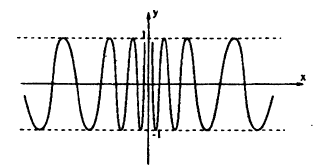
Нарисуем график функции в окрестности нуля (Рис. 64): 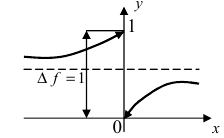
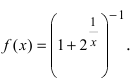
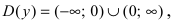
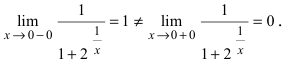
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция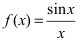
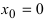
Решение:
В точке 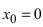
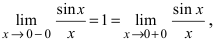
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 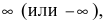
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 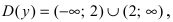
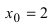
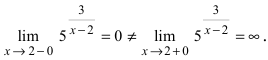
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 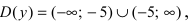
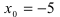
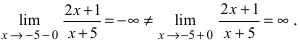
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 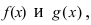
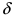
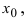
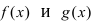
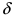
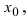
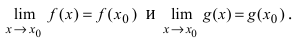
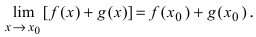
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 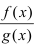
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 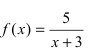
Из рисунка видно, что график функции 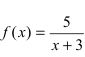
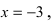
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 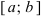
Определение: Замкнутый интервал 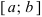
Приведем без доказательства свойства непрерывных функций на сегменте 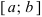
Теорема: Если функция 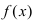
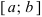
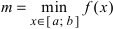
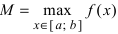
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 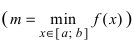
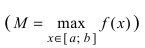
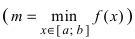
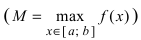
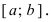
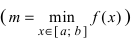
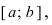
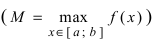
Тб. Если функция 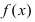
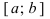
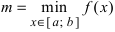
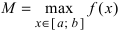
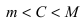
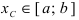
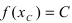
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
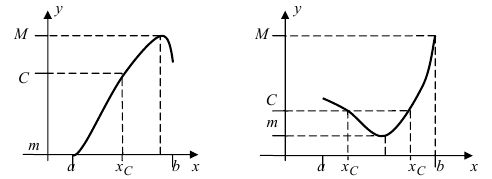
Теорема: Если функция 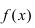
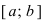
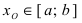
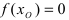
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
Непрерывность функции и точки разрыва
- Приращение аргумента и приращение функции
- Непрерывность функции в точке
- Непрерывность функции на промежутке
- Односторонние пределы
- Классификация точек разрыва
- Точки разрыва первого рода
- Точки разрыва второго рода
- Алгоритм исследования функции на непрерывность
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x= x-x_0 $$ где x — произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
 |
Пусть (y=3x-1) (x_0=1, x=1,1 ) Тогда begin{gather*} triangle x=x-x_0=0,1\ triangle y=(3x-1)-(3x_0-1)=\ =3(x-x_0 )=3triangle x=0,3 end{gather*} В данном случае приращение функции всегда в 3 три раза больше приращения аргумента. |
п.2. Непрерывность функции в точке и на промежутке
Функция (y=f(x)) непрерывна в точке (x_0), если в этой точке малому приращению аргумента (triangle x=x-x_0) соответствует малое приращение функции (triangle y=f(x)-f(x_0)): $$ lim_{triangle xrightarrow 0}triangle y=lim_{xrightarrow x_0}triangle y=0 $$
На «языке ε-δ» определение непрерывности будет следующим:
Функция (y=f(x)) непрерывна в точке (x_0), если для любого (varepsilongt 0) существует такое (delta(varepsilon)gt 0), что для любого (x, |x-x_0|ltdelta) выполняется (|f(x)-f(x_0)|ltvarepsilon:) $$ forall varepsilongt 0 existsdelta=delta(varepsilon)gt 0: forall x, |x-x_0|ltdeltaRightarrow |f(x)-a|ltvarepsilon $$
ε-δ определение непрерывности похоже на ε-δ определение предела функции, с той разницей, что модуль (|x-x_0|) может быть равен 0 для непрерывной функции, т.е. сама точка (x_0) входит в δ-окрестность.
Проанализируем предел приращения функции: begin{gather*} lim_{triangle xrightarrow 0}triangle y= lim_{triangle xrightarrow 0}left(f(x)-f(x_0)right)= lim_{triangle xrightarrow 0}f(x)-lim_{triangle xrightarrow 0}f(x_0)=\ =lim_{triangle xrightarrow 0}f(x)-f(x_0) end{gather*} т.к. (f(x_0)) — величина постоянная и от (triangle x) не зависит.
Для непрерывной функции: $$ lim_{triangle xrightarrow 0}triangle y =0 Leftrightarrow lim_{triangle xrightarrow 0}f(x)-f(x_0)=0Leftrightarrow lim_{triangle xrightarrow 0}f(x)=f(x_0) $$ Учитывая, что (triangle xrightarrow 0Leftrightarrow x-x_0rightarrow 0Leftrightarrow xrightarrow x_0)
получаем (lim{xrightarrow x_0}f(x)=f(x_0).)
Функция (y=f(x)) непрерывна в точке (x_0), если существует предел функции в этой точке и он равен значению функции в точке: $$ lim{xrightarrow x_0}f(x)=f(x_0) $$
Все три представленных определения непрерывности функции в точке эквивалентны.
Существуют и другие эквивалентные определения. Мы дадим ещё одно из них дальше, в этом же параграфе.
п.3. Непрерывность функции на промежутке
Промежуток – это интервал, отрезок, луч и т.п. (см. §16 справочника для 8 класса).
Функция (y=f(x)) непрерывна на промежутке, если она непрерывна в каждой точке этого промежутка.
График непрерывной функции – это непрерывная линия.
Кроме непрерывности, эта линия еще и «плавная», без «заломов».
При наличии заломов функция называется кусочно-непрерывной.
п.4. Односторонние пределы
Односторонний предел – это предел числовой функции при приближении к предельной точке с определенной стороны (слева или справа).
Обозначение односторонних пределов: begin{gather*} lim_{xrightarrow x_0 -0}f(x)=a — text{левый предел}\ lim_{xrightarrow x_0 +0}f(x)=b — text{правый предел} end{gather*}
Рассмотрим гиперболу (y=frac{1}{x-2}).
 |
У этой гиперболы две асимптоты (y=0) и (x=2). Точка (x_0=2) не входит в область определения. Если мы будем приближаться к (x_0=2) слева, начав, например с 1,5, мы будем постепенно опускаться по ветке гиперболы на минус бесконечность. Т.е., левый предел: $$ lim_{xrightarrow 2-0}frac{1}{x-2}=-infty $$ |
Если же мы будем приближаться к (x_0=2) справа, начав, например с 2,5, мы будем постепенно подниматься по ветке гиперболы на плюс бесконечность. Т.е., правый предел: $$ lim_{xrightarrow 2+0}frac{1}{x-2}=+infty $$ Левый и правый пределы в точке (x_0=2) для данной гиперболы не равны: $$ lim_{xrightarrow 2-0}frac{1}{x-2} ne lim_{xrightarrow 2+0}frac{1}{x-2} $$
Теперь рассмотрим параболу (y=x^2-2)
Областью определения параболы является вся числовая прямая (xinmathbb{R})
 |
В этом случае, если приближаться к (x_0=2) слева, мы получаем: $$ lim_{xrightarrow 2-0}(x^2-2)=2 $$ И если приближаться (x_0=2) справа, мы тоже получаем: $$ lim_{xrightarrow 2+0}(x^2-2)=2 $$ Левый и правый пределы равны: $$ lim_{xrightarrow 2-0}(x^2-2) =lim_{xrightarrow 2+0}(x^2-2) $$ |
Функция (y=f(x)) непрерывна в точке (x_0), если одновременно выполняются следующие три условия:
1) точка (x_0) принадлежит области определения функции (xin D);
2) левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ 3) предел функции в точке (x_0) равен значению функции в этой точке: $$ lim_{xrightarrow x_0}f(x)=f(x_0) $$
Это еще одно определение непрерывности, которым удобно пользоваться на практике.
п.5. Классификация точек разрыва
Точка (x_0) будет точкой разрыва для функции (y=f(x)), если выполняется хотя бы одно из условий:
1) точка (x_0) не принадлежит области определения функции (xnotin D);
2) левый и правый пределы в точке (x_0) не равны или бесконечны: $$ lim_{xrightarrow x_0 -0}f(x) nelim_{xrightarrow x_0 +0}f(x) text{или} lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=pminfty $$ 3) предел функции в точке (x_0) не совпадает со значением функции в этой точке: $$ lim_{xrightarrow x_0}f(x)ne f(x_0) $$
| Точки разрыва | 1-го рода Односторонние пределы существуют и конечны |
Устранимые Односторонние пределы равны между собой, но не равны (f(x_0)) |
| Неустранимые (скачок) Односторонние пределы не равны между собой |
||
| 2-го рода Хотя бы один из односторонних пределов бесконечен или не существует |
п.6. Точки разрыва первого рода
Устранимые точки разрыва 1-го рода
Левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x)=lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ НО:
либо точка (x_0) НЕ принадлежит области определения функции (xnotin D);
либо предел НЕ равен значению функции в точке (x_0): (lim_{xrightarrow x_0}f(x)ne f(x_0))
Например:
 |
(y=frac{x^2-4}{x-2}, x_0=2) Эта функция эквивалентна системе $$ y=frac{x^2-4}{x-2} Leftrightarrow begin{cases} y=x+2\ xne 2 end{cases} $$ При этом (lim_{xrightarrow 2-0}(x+2)=lim_{xrightarrow 2+0}(x+2)=4) В точке (x_0=2notin D) функция имеет устранимый разрыв. |
Разрыв можно устранить (функцию можно «склеить»), отдельно задав «гладкое» значение в особой точке: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} $$ В таком случае система станет эквивалентна всей прямой, т.е. станет непрерывной функцией: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} Leftrightarrow y=x+2 $$
Неустранимые точки разрыва 2-го рода (скачок)
Левый и правый пределы в точке (x_0) конечны, но не равны: $$ begin{cases} lim_{xrightarrow x_0 -0}f(x)=aneinfty\ lim_{xrightarrow x_0 +0}f(x)=bneinfty\ ane b end{cases} $$ Такой разрыв также называют скачком.
Величина скачка рассчитывается по формуле: $$ triangle y=lim_{xrightarrow x_0 +0}f(x)- lim_{xrightarrow x_0 -0}f(x)=b-a $$
Например:
 |
(y= begin{cases} x+1, xlt 2\ 3-x^2, xgeq 2 end{cases} , x_0=2) Односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}f(x)= lim_{xrightarrow 2-0}(x+1)=3\ lim_{xrightarrow 2+0}f(x)= lim_{xrightarrow 2+0}(3-x^2)=-1 end{gather*} Пределы не равны, но конечны. Функция в точке (x_0=2) делает скачок вниз. Величина скачка: $$ triangle y=-1-3=-4 $$ |
п.7. Точки разрыва второго рода
В точках разрыва 2-го рода хотя бы один из односторонних пределов бесконечен или не существует.
Например:
 |
(y=e^frac1x, x_0=0)
(x_0=0ne D) — точка не входит в ОДЗ Точка (x_0=0) – точка разрыва второго рода. |
На практике, при моделировании реальных процессов, разрывы 2-го рода в функциональных зависимостях встречаются довольно часто. Их положено заботливо анализировать и тщательно обходить, выбирая рабочие участки характеристических кривых, – чтобы «система не пошла в разнос».
п.8. Алгоритм исследования функции на непрерывность
На входе: функция (y=f(x))
Шаг 1. Найти ОДЗ функции, определить точки и промежутки, не принадлежащие ОДЗ.
Шаг 2. Составить множество точек, в которое входят точки и границы промежутков, не принадлежащие ОДЗ, а также – для кусочно-непрерывных функций – точки сшивания. Полученное множество состоит из точек, подозрительных на разрыв.
Шаг 3. Исследовать каждую из точек, подозрительных на разрыв, с помощью односторонних пределов. Если разрыв обнаружен, определить тип разрыва.
На выходе: список точек разрыва и тип разрыва для каждой точки.
п.9. Примеры
Пример 1. Исследуйте функцию на непрерывность:
a) ( y=frac{x+3}{x-1} )
ОДЗ: (x-1ne 0Rightarrow xne 1)
(x_0=1notin D) — точка не входит в ОДЗ, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x+3}{x-1}=frac{1-0+3}{1-0-1}=frac{4}{-0}=-infty\ lim_{xrightarrow 1+0}frac{x+3}{x-1}=frac{1+0+3}{1+0-1}=frac{4}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_0=1) — точка разрыва 2-го рода.
б) ( y=frac{x}{sqrt{x+2}-2} )
ОДЗ: ( begin{cases} x+2geq 0\ sqrt{x+2}-2ne 0 end{cases} Rightarrow begin{cases} xgeq -2\ sqrt{x+2}ne 2 end{cases} Rightarrow begin{cases} xgeq -2\ xne 2 end{cases} )
(x_0=-2) — левая граница ОДЗ
(x_1=2notin D)- точка не входит в ОДЗ
Точки (x_0) и (x_1) — подозрительные на разрыв
Исследуем (x_0=-2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} — text{предел не существует}\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{-2+0}{sqrt{-2+0+2}-2}=frac{-2}{-2}=1 end{gather*} Один из односторонних пределов не существует.
Точка (x_0=-2) — точка разрыва 2-го рода.
Исследуем (x_1=2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} =frac{2-0}{sqrt{2-0+2}-2}=frac{2}{-0}=-infty\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{2+0}{sqrt{2+0+2}-2}=frac{2}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_1=2) — точка разрыва 2-го рода.
в) ( y=frac{tgx}{3x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{tgx}{3x}=frac13lim_{xrightarrow -0}frac{tgx}{x}=frac13cdot 1=frac13\ lim_{xrightarrow +0}frac{tgx}{3x}=frac13lim_{xrightarrow +0}frac{tgx}{x}=frac13cdot 1=frac13 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
г) ( y= begin{cases} x+1, xlt 3\ x^2+3, xgeq 3 end{cases} )
ОДЗ: (xinmathbb{R})
(x_0=3)- точка сшивания, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 3-0}y=lim_{xrightarrow 3-0}(x+1)=3+1=4\ lim_{xrightarrow 3+0}y=lim_{xrightarrow 3+0}(x^2+3)=3^2+3=12 end{gather*} Односторонние пределы конечны, но неравны.
Точка (x_0=3) — точка разрыва 1-го рода, неустранимый разрыв (скачок).
Величина скачка: (lim_{xrightarrow 3+0}y-lim_{xrightarrow 3-0}y=12-4=8)
Пример 2. Доопределите функцию в точке разрыва так, чтобы она стала непрерывной в этой точке:
a) ( y=frac{2x^3-x^2}{7x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{2x^3-x^2}{7x}=frac{x^2(2x-1)}{7x}=frac{x(2x-1)}{7}) $$ y=frac{2x^3-x^2}{7x}Leftrightarrow y= begin{cases} frac{x(2x-1)}{7}\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{x(2x-1)}{7}=0, lim_{xrightarrow +0}frac{x(2x-1)}{7}=0 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=0).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{2x^3-x^2}{7x}, xne 0\ 0, x=0 end{cases} $$ б) ( y=frac{1-cos4x}{x^2} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{1-cos4x}{x^2}=frac{2sin^2 2x}{x^2}=frac{2sin^2 2x}{frac{(2x)^2}{4}}=8left(frac{sin2x}{2x}right)^2) $$ y=frac{1-cos4x}{x^2}Leftrightarrow y= begin{cases} 8left(frac{sin2x}{2x}right)^2\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8, lim_{xrightarrow +0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) — точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=8).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{1-cos4x}{x^2}, xne 0\ 8, x=0 end{cases} $$
Определение
6.4.
Функция f(x) называется непрерывной на
интервале (a,b), если
она непрерывна в каждой точке этого
интервала. Обозначают f(x)∈C(a,b).
Определение
6.5.
Функция f(x) называется непрерывной
на полуинтервале [a,b), (или (a,b]), если
она непрерывна на интервале (a,b) и
непрерывна справа в точке a (или
непрерывна слева в
точке b). Пишутf(x)∈C[a,b) (или f(x)∈C(a,b]).
Определение
6.6.
Функция f(x) называется непрерывной
на отрезке [a,b], если
она непрерывна на интервале (a,b),непрерывна
справа в точке a и
непрерывна слева в точке b. Обозначают f(x)∈C[a,b].
Теорема
6.7.
Каждая
основная элементарная функция непрерывна
в области определения.
Д
о к а з а т е л ь с т в о.
Доказательство
следует из теоремы
6.4 и определений
6.4-6.6.
■
6.4. Свойства
функций, непрерывных на отрезке
Свойство
6.1.
Функция,
непрерывная на отрезке, ограничена на
нём.
Свойство
6.2.
Функция f(x), непрерывная
на отрезке [a,b], принимает
на нем наибольшее и наименьшее значения,
т.е. существуют такие
точки ξ η отрезка [a,b], что f(ξ)=m, f(η)=M, и
для всех точек x этого
отрезка выполняются неравенства m≤f(x)≤M.
Свойство
6.3.
Если
функция f(x) непрерывна
на отрезке [a,b] и f(a)=A, f(b)=B, причем A≠B, то
для любогоC такого,
что A<C<B, найдется
точка ξ∈(a,b) такая,
что f(ξ)=C.
Как
следствие из свойства
6.3 получаем:
если функция f(x) непрерывна
на отрезке [a,b] и
принимает на его концах значения разных
знаков, то найдётся такая
точка ξ∈(a,b), что f(ξ)=0, Точка ξ в
которойf(ξ)=0, называется нулём
функции f(x).
Теорема
6.8.
Пусть
функция y=f(x) строго
монотонна (возрастает или убывает) и
непрерывна на отрезке [a,b].Тогда
обратная функция x=f−1(y) определена,
строго монотонна (возрастает или убывает)
и непрерывна на соответствующем отрезке
оси Oy.
6.5.
Точки разрыва функций и их классификация
Согласно определению
6.1 для
функции f(x), непрерывной
в точке x0, должны
выполняться три условия непрерывности:
1)
функция определена в точке x0 (∃f(x0));
2)
функция имеет конечный предел
при x→x0 (∃ конечный предел limx→x0f(x));
3)
предел функции при x→x0 равен
значению функции в самой
точке x0 (limx→x0f(x)=f(x0)).
Определение
6.7.
Точка x0 называется точкой
разрыва функции f(x), а
сама функция разрывной в
точке x0, если
она не является непрерывной в этой
точке, т.е. нарушено хотя бы одно из
указанных выше условий: либоx0∉Df, либо
не существует конечного
предела limx→x0f(x), либо limx→x0f(x)≠f(x0).
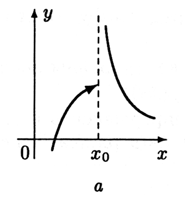
Рассмотрим
функции, заданные графически на рис.
6.5.
Для всех этих функций x0 —
точка разрыва.
Таблица
|
Рис. |
Рис. |
Рис. |
В
первом случае (рис.
6.5, а)
не выполнено условие 1, так как в
точке x0 функция
не определена.
Во
втором случае (рис.
6.5, б)
нарушено ксловие 2, так как
предел limx→x0f(x) не
существует.
В
третьем случае (рис.
6.5, в)
не выполнено условие 3, так
как limx→∞f(x)=A≠f(x0).
Определение
6.8.
Пусть x0 —
точка разрыва функции f(x). Точка x0 называется точкой
разрыва первого рода, если функция имеет
в этой точке пределы справа и слева,
т.е.
limx→x+0f(x)=f(x+0)≠∞ и limx→x−0f(x)=f(x−0)≠∞.
В
этом случае
либо f(x+0)≠f(x−0), либо f(x+0)=f(x−0)≠f(x0), причем f(x) может
быть и не определена в точке x0.
Разность f(x+0)−f(x−0) называют скачком функции f(x) в
точке x0.
Определение
6.9.
Точка
разрыва первого рода x0, в
которой f(x+0)=f(x−0), называется точкой
устранимого разрыва.
Рассмотрим
функцию f(x)=xsin1x, для
которой x=0 есть
точка разрыва, так как функция не
определена в этой точке. Односторонние
пределы функции в этой точке конечны и
равны,
посколькуf(+0)=limx→+0xsin1x=0, f(−0)=limx→−0xsin1x=0. Следовательно, x=0 —
точка устранимого разрыва.
Полагая f(0)=f(+0)=f(−0)=0, получим
функцию, непрерывную в точке x=0:
ϕ(x)=⎧⎩⎨xsin1x, 0,x≠0;x=0.
Тем
самым мы доопределили по непрерывности
данную функцию f(x).
Определение
6.10.
Точка
разрыва x0, не
являющаяся точкой разрыва первого рода,
называется точкой
разрыва второго рода. В этом случае хотя
бы один из односторонних пределов
функции в точке x0 не
существует или равен бесконечности.
Замечание
6.2.
Принимая
во внимание замечание
6.1 и определение
6.7,
подчеркнем еще раз: для того, чтобы
функция f(x) балы
непрерывной в точке x0 необходимо
и достаточно вполнение условий:
1)
функция f(x) определена
в точке x0 (∃ f(x0));
2)
cуществуют конечные односторонние
пределы функции в этой
точке(∃f(x+0)≠∞, ∃f(x−0)≠∞);
3)
односторонние пределы функции в
точке x0 равны
значению функции в этой
точке(f(x+0)=f(x−0)=f(x0)).
Поэтому
при исследовании функции на непрерывность
и определении точек разрыва функции
рекомендуется придерживаться следующей
схемы.
1
Найти область определения функции.
2
Указать промежутки области определения
функции, на которых функция непрерывна.
3
Выявить точки, в которых может быть
нарушена непрерывность функции.
4
Найти односторонние пределы функции в
каждой из указанных точек. Если функция
определена в них, то найти значения
функции в этих точках.
5
Сравнить в каждой такой точке односторонние
пределы и значение функции, если она
определена в этой точке, и установить
либо непрерывность, либо разрыв функции
в каждой из полученных точек.
6
В случае разрыва функции определить
тип точки разрыва.
6.6. Типовые
примеры
Задача
1.
Найти
односторонние пределы в точке x0=1 функции
f(x)={ x+1,3x+2,0≤x<1;1<x<3.
Р
е ш е н и е.
Найдем
правый предел f(1+0) функции f(x) в
точке x0=1, т.е.
при x→1 и x>1. Имеем
f(1+0)=limx→1+0f(x)=limx→1+0(3x+2)=5.
Для
левого предела f(1−0) в
точке x0=1 (x→1,x<1) получим
f(1−0)=limx→1−0f(x)=limx→1−0(x+1)=2.
■
Задача
2.
Найти
точки разрыва функции f(x)=∣∣x∣∣x и
определить тип каждой точки разрыва.
Р
е ш е н и е.
Точка x0=0 является
точкой разрыва функции, так как в ней
функция не определена. Найдем правый и
левый пределы функции в этой точке:
f(+0)=limx→+0|x|x=limx→+0xx=1;
f(−0)=limx→−0|x|x=limx→−0−xx=−1.
Односторонние
пределы конечны и различны, точка x0=0 —
точка разрыва первого рода. На графике
(рис. 6.6) виден конечный скачок функции
в точке x0=0, равный f(+0)−f(−0)=2.
■

Рис.
6.6

Рис.
6.7
Задача
3.
Найти
точки разрыва функции f(x)=sinxx и
определить тип каждой точки разрыва.
Р
е ш е н и е.
В
точке x0=0 функция
не определена, т.е. x0 —
точка разрыва функции. Найдем правый и
левый пределы функции в этой точке:
f(+0)=limx→+0sinxx=1;
f(−0)=limx→−0sinxx=1.
Так
как односторонние пределы конечны и
равны, т.е. f(+0)=f(−0), то x0=0 —
точка устранимого разрыва данной функции
(рис. 6.7). Если
положить f(0)=1, то
разрыв можно устранить. Тем самым
первоначальную функцию доопределим по
непрерывности в точкеx0=0. Аналитически
новую функцию ϕ(x), непрерывную
на всей числовой оси, запишем в виде
ϕ(x)=⎧⎩⎨ sinxx, 1,x≠0;x=0.
■
Задача
4.
Исследовать
на непрерывность функцию
f(x)=⎧⎩⎨⎪⎪ x3+2,2,1,x>0;x<0;x=0.
Р
е ш е н и е.
Функции y1=x3+2 и y2=2 непрерывны
при любом x. Единственной
точкой, в которой функция f(x) может
иметь разрыв, является точка x=0. Вычислим
односторонние пределы функции f(x) в
этой точке:
f(+0)=limx→+0f(x)=limx→+0(x3+2)=2;
f(−0)=limx→−0f(x)=limx→−02=2.
Так
как f(0)=1≠f(+0)=f(−0)=2, то x=0 —
точка разрыва первого рода данной
функции (рис. 6.8).
■
Задача
5.
Исследовать
на непрерывность функцию f(x)=sin1x.
Р
е ш е н и е.
Данная
функция непрерывна всюду, кроме
точки x0=0. Рассмотрим f(+0)=limx→+0sin1x. Так
как 1x→+∞ при x→+0 и
значения функции f(x) колеблются
между −1 и +1, не
приближаясь к какому-либо определенному
значению, то f(+0) не
существует. Аналогично, не существует
и f(−0). Следовательно, x=0 —
точка разрыва второго рода (рис. 3.11).
■
Задача
6.
Исследовать
на непрерывность функцию f(x)=xx2−4.
Р
е ш е н и е.
Данная
рациональная функция непрерывна всюду,
кроме точек, где знаменатель обращается
в ноль. Следовательно, функция терпит
разрыв в точках x1=2 и x2=−2. Найдем
односторонние пределы данной функции
в этих точках:
f(2+0)=limx→2+0xx2−4=+∞;
f(2−0)=limx→2−0xx2−4=−∞;
f(−2+0)=limx→−2+0xx2−4=+∞,
f(−2−0)=limx→−2−0xx2−4=−∞.
Точки x1=2 и x2=−2 —
точки разрыва второго рода (рис. 6.9).
■

Рис.
6.8

Рис.
6.9

Рис.
6.10
Задача
7.
Исследовать
на непрерывность в
точке x0=0 функцию f(x)=∣∣sinx∣∣2x.
Р
е ш е н и е.
В
точке x0=0 функция
не определена. Следовательно, x0=0 —
точка разрыва функции. Найдем односторонние
пределы функции в этой точке.
Если x→0 и x>0, то ∣∣sinx∣∣2x>0 иf(+0)=limx→+0∣∣sinx∣∣2x=12. Если x→0 и x<0, то ∣∣sinx∣∣2x<0 и f(−0)=limx→−0∣∣sinx∣∣2x=−12. Так
как односторонние пределы f(+0) и f(−0) конечны
и различны, то x0=0 —
точка разрыва первого рода, причем
скачок функции в этой точке
равен f(+0)−f(−0)=12−(−12)=1(рис.
6.10).
■
Задача
8.
Исследовать
на непрерывность функцию
f(x)={x2,2x−1,−1≤x<2;2≤x≤3.
Р
е ш е н и е.
Функция f(x) определена
всюду на [−1,3], непрерывна
на полуинтервале [−1,2) и
на отрезке[2,3]. Единственной
точкой, в которой возможен разрыв
функции f(x) является
точка x0=2.Вычислим
односторонние пределы функции f(x) в
этой точке
f(2−0)=limx→2−0x2=4,
f(2+0)=limx→2+0(2x−1)=3.
Односторонние
пределы f(2−0) и f(2+0) конечны
и различны. Следовательно, x0=2 —
точка разрыва первого рода. Скачок
функции в точке x0=2 равенf(2+0)−f(2−0)=3−4=−1 (рис.
6.11).
■

Рис.
6.11

Рис.
6.12
Задача
9.
Найти
и исследовать точки разрыва
функции f(x)=sinxx2+2x.
Р
е ш е н и е.
Точками
разрыва функции f(x) будут
точки x1=0 и x2=−2 в
которых функция f(x) не
определена (x2+2x=0). Исследуем
точку x1=0. При x→0 и x>0 функция sinx>0,sinxx(x+2)>0, f(+0)=limx→+0sinxx2+2x=limx→+0sinxx(x+2)=12. При x→0 и x<0 функция sinx<0,sinxx(x+2)>0, f(−0)=limx→−0sinxx2+2x=limx→−0sinxx(x+2)=12. Односторонние
пределы f(+0) иf(−0) в
точке x1=0 конечны
и равны. Следовательно, x1=0 —
точка устранимого разрыва. Разрыв
устраняется, если положить f(0)=12. Рассмотрим
точку x2=−2. Еслиx→−2 и x>−2, то sinx<0, x<0, x+2>0, sinxx(x+2)>0 иf(−2+0)=limx→−2+0sinxx(x+2)=+∞. Если x→−2 и x<−2, то sinx<0, x<0, x+2<0,sinxx(x+2)<0 и f(−2−0)=limx→−2−0sinxx(x+2)=−∞. Следовательно, x2=−2 —
точка разрыва второго рода (рис. 6.12).
■
Задача
10.
Исследовать
на непрерывность функцию f(x)=e1x+3.
Р
е ш е н и е.
Данная
функция непрерывна всюде, кроме
точки x0=−3. Найдем
односторонние
пределыf(−3+0) и f(−3−0) Если x→−3 и x>−3, то x+3>0, 1x+3→+∞ иf(−3+0)=limx→−3+0e1x+3=+∞ Если x→−3 и x<−3, то x+3<0, 1x+3→−∞ иf(−3−0)=limx→−3−0e1x+3=0. Следовательно,
точка x0=−3 —
точка разрыва второго рода (рис. 6.13).
■

Рис.
6.13

Рис.
6.14
Задача
11.
Исследовать
на непрерывность функцию f(x)=12−21/x.
Р
е ш е н и е.
Данная
функция непрерывна всюду, кроме
точек x1=0 и x2=1, так
как в точке x1=0 не
определена дробь 1x в
точке x2=1 знаменатель 2−21/x исходной
дроби равен нулю. Найдем односторонние
пределы данной функции в
точках x1 и x2 При x→0 и x>0 дробь 1x→+∞,21/x→+∞ и f(+0)=limx→+012−21/x=0. При x→0 и x<0 дробь 1x→−∞, 21/x→0 иf(−0)=limx→−012−21/x=12. Так
как в точке x1=0 односторонние
пределы f(+0)=0 иf(−0)=12 конечны
и различны, то x1 —
точка разрыва первого рода.
Найдем f(1+0) иf(1−0). При x→1 и x>1 дробь 1x<1, 21/x<2, разность 2−21/x→0, оставаясь
положительной.
Поэтому f(1+0)=limx→1+012−21/x=+∞. При x→1 и x<1 дробь 1x>1,21/x>2, разность 2−21/x→0, оставаясь
отрицательной,
иf(1−0)=limx→1−012−21/x=−∞. Следовательно, x2=1 —
точка разрыва второго рода (рис. 6.14).
■
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
- функция определена в точке x₀ и в некоторой ее окрестности, содержащей эту точку;
- функция имеет предел при х → x₀;
- предел функции при х → x₀ равен значению функции в точке x₀:
(10.1)
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию 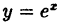
Решение:
Чтобы доказать, что функция 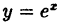
Таким образом, доказано, что функция 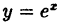
Замечание:
Формулу (10.1) можно записать в виде
(10.2)
так как 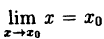
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 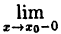
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему:
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3)
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
∆y= (x+∆x)³-x³ = x³+3x²∆x+3x∆x²+∆x³-x³ = 3x²∆x+3x∆x²+∆x³.
Используя теоремы о пределе суммы и произведения функции, получим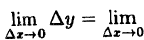
Следовательно, функция у = х³ непрерывна при — ∞< х < ∞.
Точки разрыва функции и их классификация
Определение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
Так, например, функция 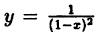
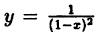
Определение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 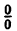
Таким образом, при x = -1 данная функция имеет устранимый разрыв.
Он будет устранен, если положить, что при x = -1 ⇒ у =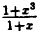
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
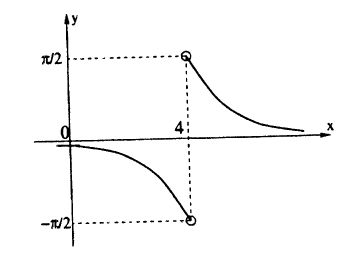
Пример:
Исследовать на непрерывность функцию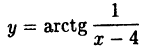
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —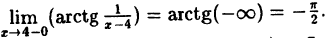
Предел справа — 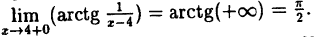
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 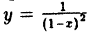
Действия над непрерывными функциями
Теорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀: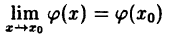
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. 
Доказательство:



Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = 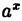
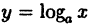
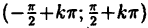
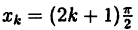
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
Без доказательства.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида 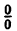
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции (

но 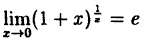
Следовательно,
(10.4)
В частности, при а = е
(10.5)
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить
Решение:
Здесь мы имеем дело с неопределенностью вида 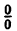
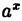
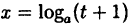
Так как на основании результата, полученного в предыдущем примере, 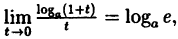
(10.6)
В частности, если а = е, имеем
т.е. у = 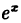
Свойства функций, непрерывных на сегменте
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
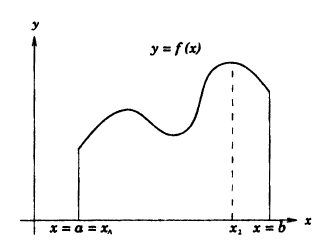
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
Теорема:
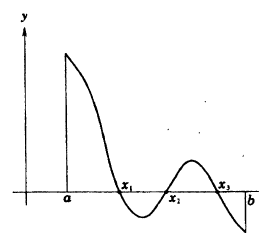
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 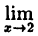
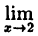
3) этот предел равен значению функции в точке х = 2
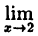
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств
Так как 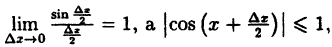
Следовательно, функция у = sin x непрерывна при -∞ < х < ∞.
Пример:
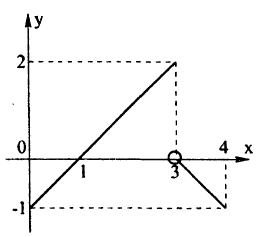
Исследовать на непрерывность функцию
Решение:
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :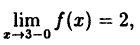
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева
предел справа
Пример:
Исследовать на непрерывность функцию 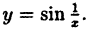
Решение:
Функция 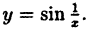
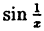
Пример:
Исследовать на непрерывность функцию
Решение:
Функция 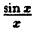
Если доопределить функцию 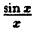
f(х) =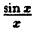
Доопределив функцию в точке х = 0, мы устранили разрыв.
Непрерывность функций
Смотрите также:
Предмет математический анализ
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Содержание:
- Точки непрерывности и точки разрыва функции
- Непрерывность элементарных функций. Свойства непрерывных функций
- Непрерывность и разрывы функций
- Определение непрерывности функции в точке. Непрерывность основных элементарных функций
- Разрывы функций и их классификация
- Непрерывность функции на промежутке. Основные теоремы о непрерывных функциях
Точки непрерывности и точки разрыва функции
Важнейшим понятием математического анализа является непрерывность функции.
Определение 1. Функция 




Определение 1 содержит четыре условия непрерывности:
1) функция 

2) должны существовать конечные односторонние пределы 

3) эти пределы должны быть одинаковы;
4) эти пределы должны быть равны 
Определение 2. Если в точке 

Например, функция 


Заметим, что разность между конечными значениями правостороннего и левостороннего пределов называют скачком функции в точке. В данном случае величина скачка равна 2.
Функция 


Непрерывность элементарных функций. Свойства непрерывных функций
Элементарные функции: степенные, показательные, логарифмические, тригонометрические и обратные им, а также их сумма, произведение, частное непрерывны при всяком 
Обратим внимание на свойства непрерывных функций.
Теорема 1. Если функции 







Теорема 2. Непрерывная функция от непрерывной функции является непрерывной функцией.
Определение 3. Функция, определенная на некотором отрезке и непрерывная в каждой его точке, называется непрерывной на отрезке.
Теорема 3. (Вейерштрасс). Всякая непрерывная на отрезке функция ограничена.
Теорема 4. (Вейерштрасс). Всякая непрерывная на отрезке функция имеет на этом отрезке как наибольшее, так и наименьшее значение.
Теорема 5. (Коши). Непрерывная на отрезке функция, принимающая какие-либо два значения, принимает и любое промежуточное.
Следствие из теоремы Коши. Если функция непрерывна на отрезке и на его концах принимает значения разного знака, то на этом отрезке существует точка, в которой функция обращается в ноль.
Заметим, что последний факт полезен при нахождении корней уравнений точно или приближенно.
Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:
Другие темы которые вам помогут понять высшую математику:
Непрерывность и разрывы функций
Непрерывная функция — функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.
Определение непрерывности функции в точке. Непрерывность основных элементарных функций
Понятие непрерывности функции тесно связано с ее пределом. Оно является характеристикой многих процессов, происходящих непрерывно: непрерывность времени, непрерывность изменения температуры, непрерывность роста дохода и др.
Пусть функция 





Рис. 14.1
Величина, на которую изменилось значение аргумента при переходе от точки 


а соответствующее изменение значения функции называют приростом функции в точке 
или
Приросты могут быть как положительными, так и отрицательными; например, на рис. 14.1 

Функция 

Заметим, что при определении непрерывности, в отличие от границы, функция в точке 
Покажем, что функция 





Найдем границу прироста функции 

Поскольку 


Аналогично можно доказать непрерывность любой из основных элементарных функций
Теорема 14.1 (о непрерывности основных элементарных функций). Основные элементарные функции непрерывные в каждой точке своей области определения.
Доказательство осуществляется для каждой функции отдельно.
Теорема 14.2 (критерий непрерывности «языком границы»). Функция 

Доказательство. Справедливость (14.4) следует из определения непрерывности и свойств предела.
Необходимость. Исходя из (14.3), имеем:
Если обозначить 


Отсюда
Следовательно,
Достаточность. Пусть функция определена в точке 
Тогда в соответствии с определением (14.4)
Таким образом, имеем два определения непрерывности функции в точке, Соответствующие формулам (14.3) и (14 .4):
Функция называется непрерывной на множестве 
Замечания. Если функция непрерывна в точке 

Например, вычислим границу 
Теорема 14.3 (критерий непрерывности «языком односторонних границ»). Функция 

Доказательство. Действительно, соотношение (14.7) базируется непосредственно на теореме существования конечного предела «языком односторонних границ» и определении непрерывности функции в точке (14.4):
Проверить в точке 
Вычислим односторонние пределы этой функции:
то есть предел слева не равен пределу справа, следовательно, функция в точке 
Рассмотрим далее две функции: 


Теорема 14.4 (о арифметические свойства непрерывных функций). Если функции 



Доказательство теоремы осуществляется на основе арифметических свойств предела. Покажем ее справедливость для доли функций.
Согласно (14.4)
Обозначим долю функций через 
Предлагаем другие выводы теоремы доказать самостоятельно.
Относительно функций, образованных из основных элементарных функций с помощью суперпозиции, возникает вопрос, какой с точки зрения «непрерывности» будет составлена функция, если ее составляющие являются непрерывными функциями.
Теорема 14.5 (о непрерывности сложной функции). Если функция 





Доказательство. Обозначим закон связи переменной 







На основании арифметических свойств непрерывных функций, непрерывности сложной функции и теоремы 14.1 (о непрерывности основных элементарных функций) делаем вывод: все элементарные функции непрерывны в каждой точке своей области существования.
Теорема 14.6 (о непрерывности обратной функции). Если функция 





Рис. 14.2
Разрывы функций и их классификация
Если функция 


Различают следующие случаи:
1. Существуют односторонние пределы (конечные), которые равны между собой 


Название разрыва «устранимый» связана с тем, что достаточно в той точке, где исследуется непрерывность функции, задать значение функции, которое бы равнялось значению односторонних границ, или изменить значение функции на значение предела в этой точке, то есть положить
Например, классический устранимый разрыв дает функция 


то есть
то для того чтобы функция была непрерывной, достаточно до определить функцию в точке 
Рис. 14.3
2. Существуют конечные односторонние пределы, но 

3. Не существует хотя бы одного из односторонних пределов, или по крайней мере один из них бесконечен, тогда точка 
Примером функции, имеющей разрыв второго рода, есть функция 
Под исследованием на непрерывность функции 

Если функция элементарная, то исследованию подлежат только точки, в которых функция не определена. При задании функции различными аналитическими выражениями на разных промежутках области существования исследование подлежат точки, которые являются пределами соответствующих промежутков.
Исследовать на непрерывность функцию
Областью определения функции является вся числовая ось, кроме 

1) односторонние границы при 
Следовательно, точка 
2) односторонние границы при
В точке 
Таким образом точка 
Исследуем на непрерывность функцию:
Имеем неэлементарную функцию, которую задано тремя формулами. На каждом из указанных промежутков функция непрерывна, как элементарная на области своего существования, следовательно, область определения этой функции 


1. Односторонние границы при 
Таким образом, функция в точке 
2. Односторонние границы при 
Поскольку f
Рис. 14.4 б
Исследовать на непрерывность функцию
Область определения функции 

Рис. 14.4 в
Непрерывность функции на промежутке. Основные теоремы о непрерывных функциях
В теоретических исследованиях и на практике применяются теоремы, которые отражают свойства непрерывных функций не в отдельно взятой точке, а на множестве точек, то есть на промежутке.
Функцию 






Сформулированные ниже теоремы примем без доказательства. Для лучшего понимания их содержания подадим в каждой теореме соответствующую геометрическую иллюстрацию, которая поможет, надеемся, осознать справедливость теорем на интуитивном уровне.
Сначала приведены определения. Если функция 









Теорема 14.7 (о наименьшем и наибольшем значении непрерывной функции). Если функция 


Если функция 


Рис.14.5
Например, функция 
Для функции 



Функция 




Функция 





Теорема 14.8 (об ограниченности непрерывной функции). Если функция 



Теорема 14.9 (о нуле непрерывной функции). Если 





Рис. 14.6
Теорема 14.10 (о промежуточных значениях функции). Если функция непрерывна на отрезке 





Заметим, что все рассмотренные вопросы непрерывности функции являются по сути применением понятия границ к исследованию функций и построения их графиков.
Лекции:
- Интервал сходимости степенного ряда
- Уравнение прямой через две точки
- Круги Эйлера фигуры, условно изображающие множества
- Тригонометрические комплексные числа
- Непрерывность функции
- Дробные рациональные выражения
- Система линейных уравнений
- Интегрирование тригонометрических функций
- Линии и поверхности уровня
- Дифференциал функции нескольких переменных

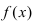
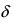 -окрестности;
-окрестности;