@guvijur
Практик, кинестетик, ретроград и консерватор
Всем привет!
Есть среди вас те, кто ещё не забыл физику? Помогите с решением задачи пожалуйста.
Дано:
Некий автомобиль разгоняется с места до 100 км/час за 11 секунд.
Можно ли вычислить расстояние, которое он проедет за это время?
-
Вопрос задан10 нояб. 2022
-
407 просмотров
Ускорение: a=v/t
Расстояние: s=at^2/2
t= 11 сек
v= 100 км/ч = 27.777(7) м/с
Подставьте сами
Пригласить эксперта
Для с̶ф̶е̶р̶и̶ч̶е̶с̶к̶о̶г̶о̶ ̶к̶о̶н̶я̶ ̶в̶ ̶в̶а̶к̶у̶у̶м̶е простейшего случая тут уже привели вычисления.
В реальности мощность двигателя зависит от оборотов, обороты связаны со скоростью и переключением передач, лобовое сопротивление растёт пропорционально квадрату скорости. В результате график ускорений выглядит как-то так:
Некий автомобиль разгоняется с места до 100 км/час за 11 секунд.
Можно ли вычислить расстояние, которое он проедет за это время?
Если движение равноускоренное, то можно.
Собственно для этого используется формула равноускоренного движения.
Если движение не равноускоренное, то там сложнее, но тоже решается — нужно просто взять функцию ускорения (или скорости) от времени и через первообразную найти пройденный путь
V = a*t ===> a = v/t ===> 0,0025 км/с^2
S = (a * t^2) / 2 ===> (0,0025 * 11^2) ===> 152 м
Вроде так. Тут обычное равноускоренное прямолинейное движение
-
Показать ещё
Загружается…
25 мая 2023, в 00:24
3000 руб./за проект
25 мая 2023, в 00:19
1000 руб./за проект
25 мая 2023, в 00:00
2500 руб./за проект
Минуточку внимания
1. Нахождение пути по графику зависимости скорости от времени
Покажем, как можно найти пройденный телом путь с помощью графика зависимости скорости от времени.
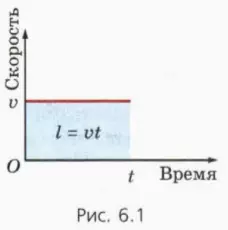
Начнем с самого простого случая – равномерного движения. На рисунке 6.1 изображен график зависимости v(t) – скорости от времени. Он представляет собой отрезок прямой, параллельной осн времени, так как при равномерном движении скорость постоянна.
Фигура, заключенная под этим графиком, – прямоугольник (он закрашен на рисунке). Его площадь численно равна произведению скорости v на время движения t. С другой стороны, произведение vt равно пути l, пройденному телом. Итак, при равномерном движении
путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени.
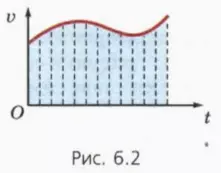
Покажем теперь, что этим замечательным свойством обладает и неравномерное движение.
Пусть, например, график зависимости скорости от времени имеет вид кривой, изображенной на рисунке 6.2.
Разобьем мысленно все время движения на столь малые промежутки, чтобы в течение каждого из них движение тела можно было считать практически равномерным (это разбиение показано штриховыми линиями на рисунке 6.2).
Тогда путь, пройденный за каждый такой промежуток, численно равен площади фигуры под соответствующим ком графика. Поэтому и весь путь равен площади фигур заключенной под всем графиком. (Использованный нами прием лежит в основе интегрального исчисления, основы которого вы будете изучать в курсе «Начала математического анализа».)
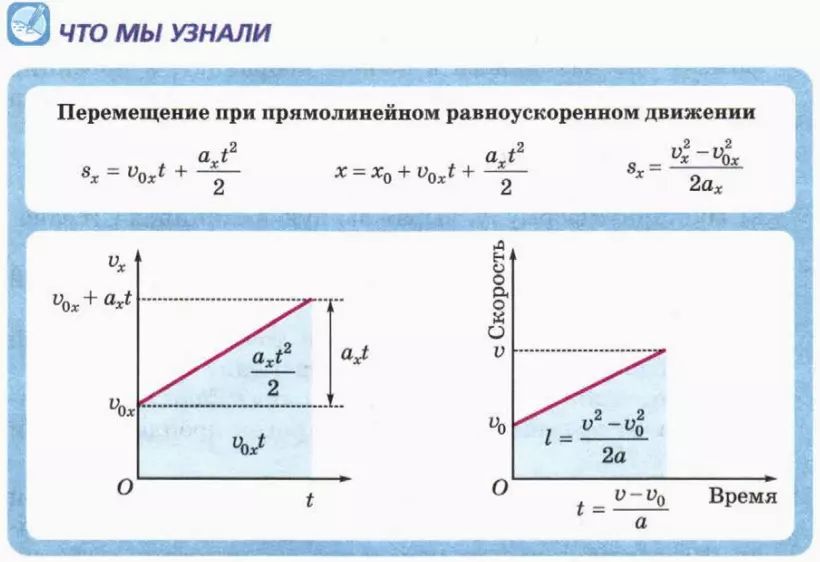
2. Путь и перемещение при прямолинейном равноускоренном движении
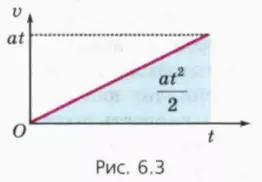
Применим теперь описанный выше способ нахождения пути к прямолинейному равноускоренному движению.
Начальная скорость тела равна нулю
Направим ось x в сторону ускорения тела. Тогда ax = a, vx = v. Следовательно,
v = at. (1)
На рисунке 6.3 изображен график зависимости v(t).
? 1. Используя рисунок 6.3, докажите, что при прямолинейном равноускоренном движении без начальной скорости путь l выражается через модуль ускорения a и время движения t формулой
l = at2/2. (2)
Главный вывод:
при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату времени движения.
Этим равноускоренное движение существенно отличается от равномерного.
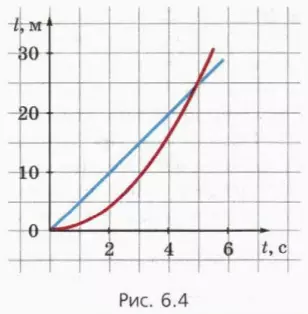
На рисунке 6.4 приведены графики зависимости пути от времени для двух тел, одно из которых движется равномерно, а другое – равноускоренно без начальной скорости.
? 2. Рассмотрите рисунок 6.4 и ответьте на вопросы.
а) Каким цветом изображен график для тела, движущегося равноускоренно?
б) Чему равно ускорение этого тела?
в) Чему равны скорости тел в тот момент, когда они прошли одинаковый путь?
г) В какой момент времени скорости тел равны?
? 3. Тронувшись с места, автомобиль за первые 4 с проехал расстояние 20 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какое расстояние проедет автомобиль:
а) за 8 с? б) за 16 с? в) за 2 с?
Найдем теперь зависимость проекции перемещения sx от времени. В данном случае проекция ускорения на ось x положительна, поэтому sx = l, ax = a. Таким образом, из формулы (2) следует:
sx = axt2/2. (3)
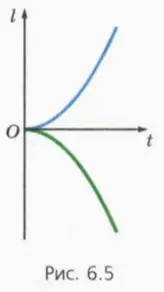
Формулы (2) и (3) очень похожи, что приводит порой к ошибкам при решении простых задач. Дело в том, что значение проекции перемещения может быть отрицательным. Так будет, если ось x направлена противоположно перемещению: тогда sx < 0. А путь отрицательным быть не может!
? 4. На рисунке 6.5 изображены графики зависимости от времени пути и проекции перемещения для некоторого тела. Какой цвет у графика проекции перемещения?
Начальная скорость тела не равна нулю
Напомним, что в таком случае зависимость проекции скорости от времени выражается формулой
vx = v0x + axt, (4)
где v0x – проекция начальной скорости на ось x.
Мы рассмотрим далее случай, когда v0x > 0, ax > 0. В этом случае снова можно воспользоваться тем, что путь численно равен площади фигуры под графиком зависимости скорости от времени. (Другие комбинации знаков проекции начальной скорости и ускорения рассмотрите самостоятельно: в результате получится та же общая формула (5).
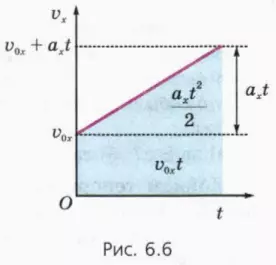
На рисунке 6.6 изображен график зависимости vx(t) при v0x > 0, ax > 0.
? 5. Используя рисунок 6.6, докажите, что при прямолинейном равноускоренном движении с начальной скоростью проекция перемещения
sx = v0x + axt2/2. (5)
Эта формула позволяет найти зависимость координаты x тела от времени. Напомним (см. формулу (6), § 2), что координата x тела связана с проекцией его перемещения sx соотношением
sx = x – x0,
где x0 — начальная координата тела. Следовательно,
x = x0 + sx, (6)
Из формул (5), (6) получаем:
x = x0 + v0xt + axt2/2. (7)
6. Зависимость координаты от времени для некоторого тела, движущегося вдоль оси x, выражается в единицах СИ формулой x = 6 – 5t + t2.
а) Чему равна начальная координата тела?
б) Чему равна проекция начальной скорости на ось x?
в) Чему равна проекция ускорения на ось x?
г) Начертите график зависимости координаты x от времени.
д) Начертите график зависимости проекции скорости от времени.
е) В какой момент скорость тела равна нулю?
ж) Вернется ли тело в начальную точку? Если да, то в какой момент (моменты) времени?
з) Пройдет ли тело через начало координат? Если да, то в какой момент (моменты) времени?
и) Начертите график зависимости проекции перемещения от времени.
к) Начертите график зависимости пути от времени.
3. Соотношение между путем и скоростью
При решении задач часто используют соотношения между путем, ускорением и скоростью (начальной v0, конечной v или ими обеими). Выведем эти соотношения. Начнем с движения без начальной скорости. Из формулы (1) получаем для времени движения:
t = v/a. (8)
Подставим это выражение в формулу (2) для пути:
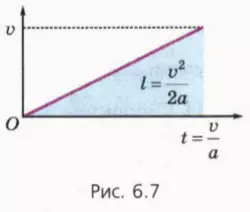
l = at2/2 = a/2(v/a)2 = v2/2a. (9)
Главный вывод:
при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату конечной скорости.
? 7. Тронувшись с места, автомобиль набрал скорость 10 м/с на пути 40 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какой путь от начала движения проехал автомобиль, когда его скорость была равна: а) 20 м/с? б) 40 м/с? в) 5 м/с?
Соотношение (9) можно получить также, вспомнив, что путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени (рис. 6.7).
Это соображение поможет вам легко справиться со следующим заданием.
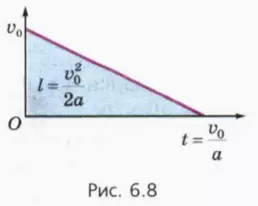
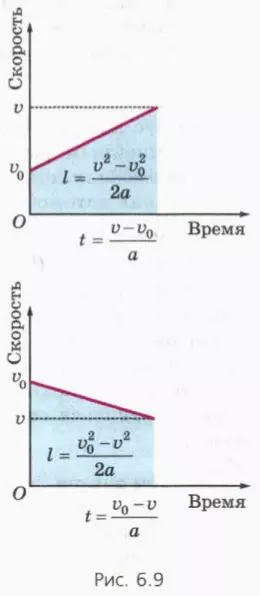
? 8. Используя рисунок 6.8, докажите, что при торможении с постоянным ускорением тело проходит до полной остановки путь lт = v02/2a, где v0 – начальная скорость тела, a – модуль ускорения.
В случае торможения транспортного средства (автомобиль, поезд) путь, пройденный до полной остановки, называют тормозным путём. Обратите внимание: тормозной путь при начальной скорости v0 и путь, пройденный при разгоне с места до скорости v0 с тем же по модулю ускорением a, одинаковы.
? 9. При экстренном торможении на сухом асфальте ускорение автомобиля равно по модулю 5 м/с2. Чему равен тормозной путь автомобиля при начальной скорости: а) 60 км/ч (максимальная разрешенная скорость в городе); б) 120 км/ч? Найдите тормозной путь при указанных скоростях во время гололеда, когда модуль ускорения равен 2 м/с2. Сравните найденные вами значения тормозного пути с длиной классной комнаты.
? 10. Используя рисунок 6.9 и формулу, выражающую площадь трапеции через ее высоту и полусумму оснований, докажите, что при прямолинейном равноускоренном движении:
а) l = (v2 – v02)/2a, если скорость тела увеличивается;
б) l = (v02 – v2)/2a, если скорость тела уменьшается.
? 11. Докажите, что проекции перемещения, начальной и конечной скорости, а также ускорения связаны соотношением
sx = (vx2 – v0x2)/2ax (10)
? 12. Автомобиль на пути 200 м разогнался от скорости 10 м/с до 30 м/с.
а) С каким ускорением двигался автомобиль?
б) За какое время автомобиль проехал указанный путь?
в) Чему равна средняя скорость автомобиля?
Лютый опыт
Дополнительные вопросы и задания
13. От движущегося поезда отцепляют последний вагон, после чего поезд движется равномерно, а вагон – с постоянным ускорением до полной остановки.
а) Изобразите на одном чертеже графики зависимости скорости от времени для поезда и вагона.
б) Во сколько раз путь, пройденный вагоном до остановки, меньше пути, пройденного поездом за то же время?
14. Отойдя от станции, электричка какое-то время ехала равноускоренно, затем в течение 1 мин – равномерно со скоростью 60 км/ч, после чего снова равноускоренно до остановки на следующей станции. Модули ускорений при разгоне и торможении были различны. Расстояние между станциями электричка прошла за 2 мин.
а) Начертите схематически график зависимости проекции скорости электрички от времени.
б) Используя этот график, найдите расстояние между станциями.
в) Какое расстояние проехала бы электричка, если бы на первом участке пути она разгонялась, а на втором – тормозила? Какова была бы при этом ее максимальная скорость?
15. Тело движется равноускоренно вдоль оси x. В начальный момент оно находилось в начале координат, а проекция его скорости была равна 8 м/с. Через 2 с координата тела стала равной 12 м.
а) Чему равна проекция ускорения тела?
б) Постройте график зависимости vx(t).
в) Напишите формулу, выражающую в единицах СИ зависимость x(t).
г) Будет ли скорость тела равна нулю? Если да, то в какой момент времени?
д) Побывает ли тело второй раз в точке с координатой 12 м? Если да, то в какой момент времени?
е) Вернется ли тело в начальную точку? Если да, то в какой момент времени, и чему будет равен пройденный при этом путь?
16. После толчка шарик вкатывается вверх по наклонной плоскости, после чего возвращается в начальную точку. На расстоянии b от начальной точки шарик побывал дважды через промежутки времени t1 и t2 после толчка. Вверх и вниз вдоль наклонной плоскости шарик двигался с одинаковым по модулю ускорением.
а) Направьте ось x вверх вдоль наклонной плоскости, выберите начало координат в точке начального положения шарика и напишите формулу, выражающую зависимость x(t), в которую входят модуль начальной скорости шарика v0 и модуль ускорения шарика a.
б) Используя эту формулу и тот факт, что на расстоянии b от начальной точки шарик побывал в моменты времени t1 и t2 составьте систему двух уравнений с двумя неизвестными v0 и a.
в) Решив эту систему уравнений, выразите v0 и a через b, t1 и t2.
г) Выразите весь пройденный шариком путь l через b, t1 и t2.
д) Найдите числовые значения v0, a и l при b = 30 см, t1 = 1с, t2 = 2 с.
е) Постройте графики зависимости vx(t), sx(t), l(t).
ж) С помощью графика зависимости sx(t) определите момент, когда модуль перемещения шарика был максимальным.
Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в (XVI) веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путём. Формула выглядит следующим образом:
, где (а) — это ускорение.
Сравним графики равномерного и равноускоренного движения.
Графики прямолинейного равномерного движения
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость (a(t)) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график (v(t)) — прямая линия, параллельная оси времени.
Правило определения пути по графику (v(t)): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График (s(t)) — наклонная линия.
Рис. (1). График зависимости скорости от времени при равномерном прямолинейном движении
Рис. (2). График зависимости пути от времени при равномерном прямолинейном движении
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график (a(t)) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. Скорость изменяется согласно линейной зависимости.
Зависимость пути от времени. При равноускоренном движении путь изменяется согласно квадратной зависимости:
s=v0t+at22
. В координатах зависимость имеет вид:
x=x0+v0xt+axt22
.
Графиком является ветка параболы.
Рис. (3). График зависимости пути от времени при равноускоренном движении
Источники:
Рис. 1. График зависимости скорости от времени при равномерном прямолинейном движении. © ЯКласс.
Рис. 2. График зависимости пути от времени при равномерном прямолинейном движении. © ЯКласс.
Рис. 3. График зависимости пути от времени при равноускоренном движении. © ЯКласс.
Время и путь разгона
Время и путь разгона
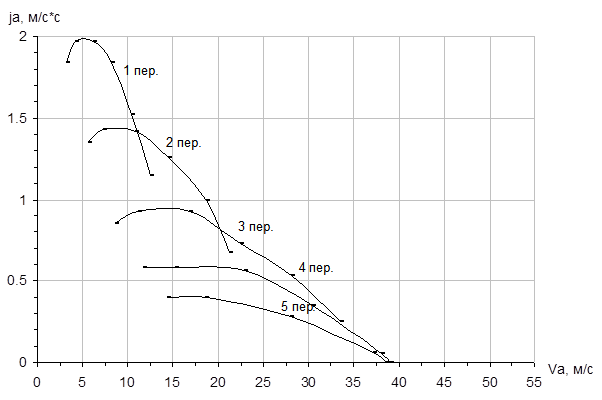
определяют следующим образом. Кривые
графика ускорений (см. рис. 3.31) разбивают
на ряд отрезков, соответствующих
определенным интервалам скоростей,
км/ч: на низшей передаче — 2…3, на
промежуточных — 5… 10 и на высшей —
10… 15. Полагают, что в каждом интервале
скоростей разгон происходит с
постоянным, средним ускорением
где
j1
и j2
— ускорения в начале и конце некоторого
интервала скоростей.
Среднее
ускорение можно также рассчитать, зная
значения скорости в начале и конце
интервала. Так, например, при изменении
скорости от
1
до
2
среднее ускорение
где
∆t
— время разгона в заданном интервале
скоростей.
Из последнего
выражения определяем время разгона в
интервале
скоростей
от
1
до
2.
(3.26)
Время
разгона автомобиля определяется в такой
последовательности (см. рис. 3.31): на
I
передаче — по кривой аб,
на
II
передаче — по кривой бв,
на
III
передаче — по кривой вг
и
на IV
передаче — по кривой де.
Скорости,
соответствующие точкам б,
в и
г, являются оптимальными для переключения
передач.
Вычислив
значение времени разгона в каждом
интервале скоростей, находим общее
время разгона на n
интервалах
от минимальной
min
до
максимальной
таx
скорости:
З
значения времени разгона в различных
интервалах скоростей, строим кривую
времени разгона (рис. 3.32). Изломы этой
кривой соответствуют моментам
переключения передач.
При переключении
передач в течение некоторого времени
(времени переключения) происходит
разъединение двигателя и ведущих колес.
При этом разрывается поток мощности и
уменьшается скорость движения автомобиля
за счет действия сил сопротивления
движению.
Время переключения
передач зависит от типа двигателя,
коробки передач и квалификации водителя.
Так, для водителей
высшей квалификации время переключения
передач составляет 0,5… 1 с при бензиновом
двигателе и 1…4 с — при дизеле.
Рис.
3.32. Графики времени и пути
разгона автомобиля:
min
— минимальная скорость автомобиля
Увеличение времени
переключения передач при дизеле
объясняется более медленным снижением
угловой скорости коленчатого вала,
чем при использовании бензинового
двигателя. У менее квалифицированных
водителей время переключения передач
на 25…40 % больше, чем у высококвалифицированных.
Уменьшение скорости,
км/ч, автомобиля при переключении
передач, зависящее от дорожных условий,
скорости движения и параметров
обтекаемости, определяется по формуле
где
tп
— время
переключения передач, с.
Для нахождения
пути разгона используют те же интервалы
скоростей, которые были выбраны при
определении времени разгона. При
этом считается, что в каждом интервале
скоростей автомобиль движется
равномерно со средней скоростью
При
разгоне от скорости
1
до
скорости
2
(см. рис. 3.31) путь разгона в этом интервале
скоростей
или с учетом
выражения (3.26)
Путь
разгона автомобиля от минимальной
min
до
максимальной
таx
скорости
Зная значения пути
разгона, соответствующие различным
интервалам скоростей, строим кривую
пути разгона (см. рис. 3.32). Изломы этой
кривой, так же, как и у кривой времени
разгона, отвечают переключению передач.
За время переключения
передач автомобиль проходит путь
где
п
— скорость
в момент начала переключения передач.
Рассмотренный
метод определения времени и пути разгона
автомобиля является приближенным.
Поэтому полученные при расчете
результаты могут несколько отличаться
от действительных.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Расчёт пути необходим для построения нагрузочной диаграммы двигателя.
Разгон двигателя постоянного тока происходит по экспоненте, но поскольку время разгона на каждой ступени мало по сравнения с механической постоянной, разгон можно считать линейным Тогда путь, пройденный при разгоне на каждой характеристике, включая естественную, может быть определен по уравнению:
( 10 ) где –начальная и конечная скорости двигателя на соответствующей характеристике, которые определяются по пусковой диаграмме рис. 2Из технического задания следует, что замедление осуществляется при включении в цепь двигателя резисторов с большим сопротивлением. Характеристика любого двигателя в этом случае может считаться линейной, а скорость вращения двигателя будет меняться практически по линейному закону.
При этих допущениях путь при замедлении рассчитывается по уравнению (10 )РАСЧЁТЫ С АСИНХРОННЫМ ДВИГАТЕЛЕМРасчёт пусковой диаграммы асинхронного двигателяПроизвести построение пусковой диаграммы для асинхронного двигателя затруднительно в силу нелинейности характеристик двигателя. Поэтому пусковая диаграмма рассчитывается аналитически.
По паспортным данным выбранного двигателя определяем его перегрузочную способность: = , где: МК – критический (максимальный) момент двигателя.
Рассчитываем номинальное и критическое скольжения двигателя: Вычисляем сопротивление обмотки ротора: где: – номинальное напряжение и ток обмотки ротора.
Введём обозначение b =М/МК – относительное значение момента двигателя.
Тогда формула Клосса может быть переписана в виде В этом уравнении за неизвестное принимаем сначала sk потом s . Решая уравнения, получаем: (11) (12)Задаёмся моментами пусковой диаграммы М1 ≤0,9 MK и М2 ≥ 1,1MC ивычисляем их относительные значения: Связываем уравнение ( 11 ) с величиной , а уравнение ( 12 )– свеличиной В правильно построенной пусковой диаграмме точки переключения должны лежать на вертикалях, соответствующих моментам М1 и М2 (смотри рис. 2 ), поэтому коэффициенты А и В в уравнениях ( 11 ) и ( 12 ) должны быть постоянными числами. Они находятся с соотношении:
=1 , ( 13 )где: –критическое скольжение на естественной характеристике.
Для расчёта диаграммы и реостата необходимо задаться числом ступеней m и каким-либо из коэффициентов.
Например, задаёмся величиной (11) коэффициент А. Далее из уравнения ( 13 ) вычисляем:
; +1).
Проверяем выполнение условия : М = МК ≥ 1,1МС Можно задаться моментом переключения М2 ≥ 1,1МС и, соответственно, коэффициентом . Тогда вычисляется по уравнению ( 12 ) коэффициент В,.
Далее вычисляются величины А и β :
B) B ; =2A Проверяется выполнение условия Полное сопротивление на первой реостатной характеристике и сопротивление первой ступени определяются как: / ; Сопротивления на остальных характеристиках рассчитываются по тем же формулам, но для каждой следующей характеристики показатель степени m уменьшается на 1.
Дальнейшие расчёты удобно свести в таблицу 4Разгон двигателя по первой реостатной характеристике начинается из точки, где М = М1, а скольжение по определению равно 1. Поэтому в соответствующей клеточке таблицы 4 записана 1. Критическое скольжение для первой характеристики вычисляется по уравнению (11) и равно А. Скольжение на этой же характеристике при М = М2 вычисляется из уравнения (12) и равно АВ. С этого скольжения начинается разгон по второй реостатной характеристике. Дальнейший ход расчёта ясен из таблицы 4.
В таблице обозначено: – скольжение на каждой характеристике при моменте М; – критическое скольжение соответствующей характеристики; – скольжение на соответствующих характеристиках при моменте М;
, – полное сопротивление роторной цепи на соответствующей характеристике исопротивление ступени реостата, ωn– частота вращения в точке переключения при скольжении .
Таблица 4
None Интеграл решается графически по графику времени разгона. Значения времени разгона tp и пути разгона Sp определяются следующим образом:
,где tp – время, соответствующее участку от 0 до v;
Δtp – приращение времени разгона на соответствующей передаче, с.
,где υ1 – начальное значение скорости, м/с;
j – ускорение, соответствующее начальному движению на 1передаче, м/с2.
,где Ftp – площадь фигуры под кривыми зависимости 1/j = f(υ), мм2;
μj – масштаб величины, обратной ускорению,μυ – масштаб скоростиПо аналогичным формулам ведется расчет пути разгона Sp ,где S – путь, соответствующий участку от 0 до t’, м,S = t2·υ;
ΔS – приращение пути разгона Sp на соответствующей скорости, м, ,где F3 – площадь участков, расположенных между tp = t(υ) и осью tp, мм2.
Найденные показатели заносятся в таблицу 5. 2. По данным таблицы 5.
2 строятся графики, примеры которых представлены на рисунках 5. 3 и 5. 4.
Таблица 5. 1.
| n | n, 1/c | υ, м/с | MКР,кНм | Pk, кН | Pw, кН | j, м/с | 1/j, c/м |
| I i δВР | |||||||
| II i δВР | |||||||
| III i δВР | |||||||
| IV i δВР | |||||||
| V i δВР | |||||||
| VI i δВР | |||||||
Таблица 5.2.
| Передача | υ, м/с | Δυ, м/с | Ft, мм | Δt, c | t разг, с | Fs, мм | ΔSp, м | Sp, м |
| I | tтм | |||||||
| II | tпер | |||||||
| III | tпер | |||||||
| IV | tпер | |||||||
| V | tпер | |||||||
| VI | tпер | |||||||
Рисунок 5.1. Пример построения графика ускорений при разгоне автомобиля.
Рисунок 5.2. Пример построения величины, обратной ускорению при разгоне автомобиля.
Рисунок 5.3. Пример графика определения времени разгона.
Рисунок 5.4. Пример графика определения пути разгона.
Лабораторная работа №6ДИНАМИЧЕСКИЙ ПАСПОРТ АВТОМОБИЛЯ
Цель работы: построение динамического паспорта автомобиля.
Задачи работы: 1. Построение графика динамического фактора полностью груженого автомобиля;
2. Построение графика динамического фактора частично груженого автомобиля; 3. Определение динамического фактора по условию сцепления ведущих колес.
Определение динамического фактора полностью груженого автомобиляСиловой баланс автомобиля определяется по уравнению:
,или баланс мощности можно записать:
,где Рк – касательная сила тяги на колесах, Н;
Рw – сила сопротивления воздуха, Н;
Рj рез – результирующая сила инерции, Н.
Из первого выражения выразим избыточную силу тяги: Из этого выражения выразим динамический фактор автомобиля:
, .
Подставляя в выражение значения Рк и Рw при различном режиме и полной загрузке автомобиля, найдем динамический фактор при полной загрузке. Результаты расчетов сведем в таблицу 6.1.
По данным таблицы 6.1 строим график зависимости D = f(υ).
Перейти к загрузке файла. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ускорение во время разгона определяется для случая движения автомобиля по горизонтальной дороге (уклон ) с твердым покрытием хорошего качества при максимальном использовании мощности двигателя и отсутствии буксования ведущих колес. Ускорение находят из выражения (1.24): None – коэффициент учета вращающихся масс; определяется по формуле (1.25): None – передаточное число коробки передач, для которой ведут расчет; – полный вес автомобиля, Н; – фактический вес автомобиля, Н. Принимаем отношение . Результаты расчета ускорения автомобиля во всем диапазоне передач представлены в таблице 1.9. Таблица 1.9 – Ускорение автомобиля.
|
Необходимо построить графики времени и пути разгона автомобиля от начала движения до максимальной скорости на первом участке перегона (характеристики первого участка перегона – см. таблицу 1. 6).
Время и путь разгона автомобиля можно определить графоаналитическим способом. С этой целью кривую ускорений разбивают на интервалы, и считают, что в каждом интервале скоростей автомобиль разгоняется с постоянным ускорением, которое определяется по формуле (1. 26):
где и – ускорения соответственно в начале и в конце интервала скоростей, м/с.
Для повышения точности расчета интервалы скоростей берут равными м/с на первой передаче, м/с на промежуточных, м/с – на высшей. В интервале скоростей – время разгона определяется по формуле (1.27):
None Общее время разгона от минимально устойчивой скорости до конечной скорости определяется из выражения (1.28):
None Во время переключения можно принимать сопротивление движению постоянным. Величину уменьшения скорости автомобиля во время переключения передач можно определить по формуле, полученной путем решения уравнения движения накатом (1.29):
None – время переключения передач, с; принимаем для автомобиля ЗАЗ-1102 с.
Падение скорости за время переключения составит:
– с первой на вторую передачу ,.
где – скорость автомобиля в момент начала переключения передач, м/c; м/с;
– со второй на третью м/с; – с третьей на четвертую м/с; Результаты расчета времени разгона автомобиля представлены в таблице 1.10.
Таблица 1.10 – Время разгона.
|
I-я передача. |
II-я передача. |
III-я передача. |
IV-я передача. |
||||
|
, м/с. |
, с. |
, м/с. |
, с. |
, м/с. |
, с. |
, м/с. |
, с. |
Page 2
Необходимо проанализировать топливную экономичность проектируемого АТС, построив топливную характеристику на первом участке перегона. Топливно-экономическая характеристика автомобиля позволяет определить расход топлива в зависимости от изменения скорости движения. Она представляет собой график зависимости путевого расхода топлива от скорости автомобиля.
Путевой расход топлива (л/100 км) определяется по формуле (1.32):
None и – коэффициенты, учитывающие соответственно изменения удельного эффективного расхода топлива от степени использования мощности И и частоты вращения двигателя Ч;
– плотность топлива, кг/л; (для бензина кг/л); – КПД трансмиссии; .
и – соответственно сила сопротивления дороги и воздуха, Н; При приближенных расчетах можно принимать и для бензиновых двигателей по формулам (1.33) и (1.34):
None Степень использования мощности двигателя можно определить из формулы (1.35):
None Степень использования частоты вращения двигателя определяется по формуле (1.36):
None Таблица 1.13 – Расчет топливно-экономической характеристики.
|
ne, об/мин |
Va, м/с |
РД, Н |
РВ, Н |
Ne, кВт |
И. |
kИ |
Ч. |
kЧ |
QS, л/100 км |
Page 3
|
Главная Техника Расчет проектируемого узла карданной передачи автомобиля ЗАЗ-1102 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Определим по условиям торможения двигателем предельный угол спуска при движении полностью груженого автомобиля на первой передаче. При этом будем исходить из условия равенства силы трения двигателя, приведенной к ведущим колесам, и составляющей силы тяжести при движении под уклон.
None МТ.ДВ.= VЛ (a1 ne – b1), (1.43)гдеVл – рабочий объем (литраж) двигателя, л ;
a и b- эмпирические коэффициенты (a=0,007, b=0,12 – для карбюраторного двигателя);
ne – частота вращения коленчатого вала двигателя, об/минМТ.ДВ.=1,3 ·(0,007·3000 – 0,12)= 27,1 НмМаксимальный угол спуска (град) определим по формуле:
б = arcsin ((Мт.дв. uдк u uг)/(rк nоб Ga); (1.44)б = arcsin ((27,1 1 2,64 3,83)/( 0,26 0,75 11221))=7,2 град .
Определение дистанции между автомобилями в колонне. Определим дистанцию между автомобилями в колонне, по условиям обеспечения безопасности движения с максимальной скоростью на первом участке перегона.
Для первого участка перегона, по графику динамического паспорта определяем максимальную скорость движения автомобиля. На данном перегоне автомобиль может двигаться на пятой передаче с максимальной скоростью 48,1м/с. Безопасная дистанция между автомобилями определяется по формуле:
(1.45)где: tР – время реакции водителя, с, ( tР=0,5 с.) tПР – время срабатывания привода, с, ( tПР=0,2 с.) tУ – время увеличения замедления, с, ( tУ=0,5 с.)Va – скорость автомобиля, м/с
Page 4
Определение предельного угла поперечного уклона дороги. Предельный угол поперечного уклона дороги (град), при котором АТС может опрокинуться при прямолинейном движении находят из уравнения статического равновесия АТС:
None Угол поперечного уклона дороги (град), при котором АТС будет скользить при прямолинейном движении определяем из выражения:
взан = arctg ( цу ), (1.47)гдецу – коэффициент сцепления колес с дорогой.
Определим предельные углы поперечного уклона дороги по условиям опрокидывания и заноса на 1-ом и 4-ом участках перегона: воп = arctg ( 1,314 / 2 0,47) = 54 град;
взан = arctg ( 0,7 ) = 35 град ;
взан = arctg ( 0,17 ) = 9,6 град.
Определение критической скорости по условиям опрокидывания. Критическая скорость движения АТС (км/ч) по условию опрокидывания :
хоп = , (1.48)гдеR – радиус кривизны полотна дороги в плане, м;
hц – высота центра тяжести, м.
Определяем критическую скорость по условиям опрокидывания для груженого автомобиля (с высотой центра тяжести hц = 0,705 м) и порожнего (hц = 0,47 м) при движении на 1-ом участке перегона по горизонтальному закруглению радиусом 50м:
хОП.Гр =
хОП.Пор. = Определение критической скорости по условиям заноса.
Критическую скорость АТС (км/ч) по условию заноса определяем по формуле:
хзан = . (1.49)Определяем критическую скорость по условиям заноса при движении на 4-ом участке перегона по горизонтальному закруглению радиусом 30м:
хзан = .
Определение зависимости критической скорости от радиуса поворота. Критическую скорость АТС по условию опрокидывания определяем для различных значений радиуса поворота и заносим в табл.4.1.
Критическую скорость АТС по условию заноса определяем для двух значений коэффициента сцепления ц = 0,4 и ц = 0,8 и различных значениях радиуса поворота и заносим в табл. 1. 16.
Таблица 1. 16 – Значения критической скорости АТС по условию заноса и опрокидывания.
|
R,м. |
|||||||
|
хзан при ц = 0,4 |
|||||||
|
хзан при ц = 0,8 |
|||||||
|
хоп |
Page 5
Дифференциалом называется механизм трансмиссии, распределяющий крутящий момент двигателя между ведущими колесами и ведущими мостами автомобиля. Дифференциал обеспечивает разную скорость вращения ведущих колес при движении автомобиля по неровным дорогам и на поворотах.
Габаритные размеры дифференциала. В связи с тем, что дифференциал обычно устанавливают внутри главной передачи, его габаритные размеры имеют важное значение. В первую очередь это относится к межколёсному дифференциалу, так как от его размеров зависят размеры ведомой шестерни главной передачи, которые строго ограничены.
От диаметра ведомой шестерни зависит высота картера ведущего моста и, следовательно, дорожный просвет и проходимость автомобиля. Наименьшие габаритные размеры имеет конический симметричный дифференциал.
Выбор прототипа дифференциала
Для данного типа АТС наиболее оптимальным является конический симметричный дифференциал.
Конический симметричный дифференциал является дифференциалом малого трения, так как имеет небольшое внутреннее трение. Конический симметричный дифференциал малого трения прост по конструкции, имеет небольшие размеры и массу, высокие КПД и надёжность, обеспечивает хорошие управляемость и устойчивость, уменьшает изнашивание шин и расход топлива. Этот дифференциал также называют простым дифференциалом.
К дифференциалу предъявляют следующие требования, в соответствие с которыми он должен: а) распределять крутящий момент между ведущими колёсами, обеспечивая автомобилю наилучшие тягово-скоростные свойства, проходимость, управляемость и устойчивость;
б) иметь минимальные габаритные размеры. При расчёте дифференциала определяют его КПД, а также рассчитывают полуосевые шестерни, сателлиты и крестовину сателлитов на прочность.
[custom_ads_shortcode1]
Выбор КПД дифференциала
Значение КПД дифференциала определяется по следующей формуле:
гдеNтр – потери мощности на трение в дифференциале;
NД – мощность на корпусе дифференциала.
[custom_ads_shortcode2]
Расчёт шестерен и сателлитов
Расчёт полуосевых шестерен и сателлитов дифференциала на прочность выполняется аналогично расчёту на прочность шестерен главной передачи. При этом различается только определение окружной силы, действующей на зубья шестерен. При расчете считают, что окружная сила распределяется поровну между всеми сателлитами и каждый сателлит передает усилие двумя зубьями.
Рис.1. Схема для расчёта конического дифференциала.
Окружная сила, действующая на один сателлит:
гдеr – радиус приложения окружной силы;
nc – число сателлитов.
ННапряжение изгиба в зубьях полуосевых шестерен и сателлитов:
гдеb – ширина шестерни – сателлита; mн – нормальный модуль;
y – коэффициент формы зуба. Допустимые напряжения изгиба [уизг] = 500…800 МПа.
Материал шестерен и сателлитов – сталь 18ХГТ, 20ХН3А и 24ХГМ.
МПа – шестерня полуоси.
МПа – сателлит.
[custom_ads_shortcode3]
Расчёт оси сателлитов
У оси рассчитывают шипы под сателлитами и в местах крепления в корпусе дифференциала. Ось под сателлитом рассчитывают на смятие и на срез:
напряжения смятия.
МПа < 60 МПа – условие выполненонапряжения среза
None l1 – длина оси под сателлитом;
d – диаметр поверхности контакта сателлита с корпусом дифференциала. Допустимые напряжения смятия [усм] = 50…60 МПа.
Допустимые напряжения среза [фср] = 100…120 МПа.
Ось в месте крепления в корпусе дифференциала рассчитывают на смятие:
МПа < 60 МПа – условие выполнено. Где.
Н – окружная сила, действующая на ось; r – радиус приложения окружной силы к оси; l – длина заделки оси в корпусе дифференциала.
Допустимые напряжения смятия [усм] = 50…60 МПа.
При расчёте дифференциала по давлению торца сателлита на корпус дифференциала в месте контакта определяют напряжения смятия:
МПа < 10 МПа – условие выполнено. где Н – осевая сила, действующая на сателлит;
б – угол зацепления; д – половина угла начального конуса сателлита;
мм – торцовая площадь сателлита.
Допустимые напряжения смятия [усм] = 10…20 МПа.
Page 6
Определив основные параметры автомобиля, и проанализировав полученные результаты, а, также сравнив их с данными автомобилей – аналогов, можно сделать вывод о том, что проектируемый автомобиль находится в промежуточном положении между своими «одноклассниками» по группе, и отвечает всем требованиям, предъявляемым к современным автомобилям. На основе анализа данных полученных в расчете можно сказать, что автомобиль обладает тягово-скоростными характеристиками, типичными для автомобилей малого класса и сопоставимыми с имеющимися данными по автомобилям – аналогам. Сравнив полученные результаты с данными контрольного расхода топлива автомобилей – аналогов, делаем вывод, о том, что топливная экономичность проектируемого АТС, приблизительно соответствует автомобилям этой же группы. В целом, автомобиль по своим характеристикам получился достаточно практичным и может эффективно использоваться в различных сферах хозяйственной жизни.
Осепчугов В. В. , Фрумкин А.
К. Автомобиль: Анализ конструкций, элементы расчета: Учебник для студентов вузов по специальности “Автомобили и автомобильное хозяйство”. – М.
: Машиностроение, 1989. – 304 с. , ил.
Литвинов А. С. , Фаробин Я.
Е. Автомобиль: Теория эксплуатационных свойств: Учебник для студентов вузов по специальности “Автомобили и автомобильное хозяйство”. – М.
: Машиностроение, 1989. – 238 с. , ил.
Иларионов В. А. Эксплуатационные свойства автомобиля.
– М. : Машиностроение, 1968. – 280 с.
Гришкевич А. И. – Проектирование трансмиссий автомобилей: справочник.
– М. : Машиностроение, 1984. – 269 с.
Вахламов В. К. – Конструкция, расчёт и эксплуатационные свойства автомобиля: учебное пособие для студ.
высш. учеб. заведений.
– М. : Издательский центр «Академия», 2007. – 560 с.
Левицкий В. С. – Машиностроительное черчение и автоматизация выполнения чертежей.
– 8-е изд. , перераб. и доп.
– М. : Высшая школа, 2007. – 435 с.
Источники:
- studopedia.net
- cyberpedia.su
- studbooks.net