|
2 / 2 / 0 Регистрация: 14.12.2013 Сообщений: 87 |
|
|
1 |
|
Как вычислять производную функции?04.02.2017, 20:54. Показов 8684. Ответов 14
Здравствуйте дорогие форумчане! Подскажите, пожалуйста, каким образом вычислять производную функции программно? То есть вводишь в форму математическую функцию например x^2-4*sin(x), а программа преобразует его в производную 2*x-4*cos(x). Есть ли библиотека vb.net для производных или готовый фрагмент кода, который позволяет преобразовывать любую функцию в производную? Добавлено через 2 часа 10 минут
0 |
|
OwenGlendower Администратор 15571 / 12545 / 4984 Регистрация: 17.03.2014 Сообщений: 25,465 Записей в блоге: 1 |
||||
|
07.02.2017, 00:51 |
2 |
|||
|
РешениеSkyls, есть! Ставим пакет MathNet.Symbolics и пишем код
9 |
|
XIST 1293 / 994 / 141 Регистрация: 01.10.2009 Сообщений: 3,169 Записей в блоге: 1 |
||||
|
07.02.2017, 12:15 |
3 |
|||
|
Не по теме: Господи, скоро совсем не нужно будет думать с этими нугетами)
0 |
|
2 / 2 / 0 Регистрация: 14.12.2013 Сообщений: 87 |
|
|
28.11.2017, 19:49 [ТС] |
4 |
|
Подскажите пожалуйста, а как с помощью этого парсера просто парсировать функцию не возводя в производную? И этот парсер с типом Decimal работает?
0 |
|
4303 / 3439 / 831 Регистрация: 02.02.2013 Сообщений: 3,334 Записей в блоге: 2 |
|
|
28.11.2017, 21:07 |
5 |
|
Skyls, не очень понятно, м.б. вы хотите просто вычислить значение производной?
0 |
|
2 / 2 / 0 Регистрация: 14.12.2013 Сообщений: 87 |
|
|
28.11.2017, 21:56 [ТС] |
6 |
|
не очень понятно, м.б. вы хотите просто вычислить значение производной? Dim result As Expression = Calculus.Differentiate(Expression.Symbol(«x»), expr) этот фрагмент кода возводит функцию в производную и выводит. А как использовать этот парсер, чтобы просто вытащить функцию из string(из textbox)? Например «sin(x)» -> sin(x).
0 |
|
ovva 4303 / 3439 / 831 Регистрация: 02.02.2013 Сообщений: 3,334 Записей в блоге: 2 |
||||
|
28.11.2017, 22:27 |
7 |
|||
|
Как понял, вы хотите в дальнейшем вычислять по полученному в виде строки выражению. Можно это выполнить так.
Ссылка на библиотеку: http://www.lundin.info/mathparser
1 |
|
2 / 2 / 0 Регистрация: 14.12.2013 Сообщений: 87 |
|
|
28.11.2017, 23:03 [ТС] |
8 |
|
ovva, lundin парсер не пойдет, потому что если тип указать decimal, то ньютон метод не находит решение. Мне надо, чтобы решение было с точностью 1e-28, lundin только 1e-15 дает. Добавлено через 10 минут
0 |
|
OwenGlendower Администратор 15571 / 12545 / 4984 Регистрация: 17.03.2014 Сообщений: 25,465 Записей в блоге: 1 |
||||
|
28.11.2017, 23:49 |
10 |
|||
|
А как использовать этот парсер, чтобы просто вытащить функцию из string(из textbox)? Если правильно понял вопрос
1 |
|
2 / 2 / 0 Регистрация: 14.12.2013 Сообщений: 87 |
|
|
29.11.2017, 10:44 [ТС] |
11 |
|
OwenGlendower, From { { «x», 1} } здесь x = 1, можно ли сделать так, чтобы к x ничего не равнялось, а просто символ «x» заменялся в функции? например так Calculus.Differentiate(Expression.Symbol(«x»), expr), только производная не нужна, нужна сама функция
0 |
|
Администратор 15571 / 12545 / 4984 Регистрация: 17.03.2014 Сообщений: 25,465 Записей в блоге: 1 |
|
|
29.11.2017, 12:27 |
12 |
|
Skyls, что значит «заменялся» и «нужна сама функция»? Нужна для чего?
0 |
|
90 / 58 / 7 Регистрация: 07.02.2010 Сообщений: 728 |
|
|
29.11.2017, 13:39 |
13 |
|
0 |
|
Skyls 2 / 2 / 0 Регистрация: 14.12.2013 Сообщений: 87 |
||||
|
29.11.2017, 16:45 [ТС] |
14 |
|||
|
OwenGlendower, lundin парсер написал таким образом:
Мне нужно чтобы парсер от MathNet.Symbolycs точно так же как lundin parser работал, именно чтобы возвращал парсированную функцию. Так вот, как нужно написать код? Дело в том, что именно для Ньютон метода парсер от lundin’a не работает с Decimal, и я надеюсь что MathNet.Symbolycs будет работать с Decimal.
0 |
|
Администратор 15571 / 12545 / 4984 Регистрация: 17.03.2014 Сообщений: 25,465 Записей в блоге: 1 |
|
|
29.11.2017, 17:41 |
15 |
|
Так вот, как нужно написать код? Я уже показал как. Переписать его в виде отдельного метода не составит никакого труда.
я надеюсь что MathNet.Symbolycs будет работать с Decimal. Я не нашел такой возможности, но я не сильно углублялся в поиски.
0 |
Понимаешь, если у тебя всегда многочлен и известна его максимальная степень, то проблем нет. Пусть, например, надо находить производные многочленов степени не выше 9. Тогда такой многочлен можно представить массивом из 10 элементов (индексы с 0), где каждый элемент — это коэффициент при соответствующей степени.
Твой многочлен y=4x^4-2x^3+3 будет представлен массивом a (0, 0, 0, 0, 0, 4, -2, 0, 0, 3)
a(0) = 3, a(1)=0, a(2)=0, a(3)=-2, a(4)=4
Тогда результат — это тоже массив, назовем его b. Его элементы будут вычисляться как b(i) = a(i+1)*(i+1)
Проверяем:
b(0) = a(1)*1 = 0
b(1) = a(2)*2 = 0
b(2) = a(3)*3 = -6
b(3) = a(4)*4 = 16
остальные 0
А если функция неизвестна — ну, то есть там всякие sin, cos, ln встречаются, то придется тебе разбирать строку, складывать встречающиеся компоненты в массив… А не дай бог там еще сложные функции встретятся (типа sin(2^x))… Тоже, в принципе, можно, наверно разобрать. Только тогда лучше дерево строить…
GSerg писал(а):Маткадом восхищаюсь… Даже не знаю, как начать думать о том, каким образом там производятся символьные вычисления.
Это точно! Но было бы интересно, как это они все-таки сделали. И если для вычисления производной я еще могу себе представить хоть как-то, то вот интегралы…
GSerg писал(а):А expression, может, и можно переделать в derivative, надо попробовать
Это ты о чем? — не поняла…
3. Последними выполняются логические операции в таком порядке, как они представлены в таблице 2.3.
Таблица 2.3. Приоритет логических операций
|
Описание операции |
Обозначение в VВА |
|
Логическое отрицание |
Not |
|
Логическое «И» |
And |
|
Логическое «ИЛИ» |
Or |
Если выражение содержит несколько операций одинакового приоритета, то порядок их выполнения слева направо. Чтобы изменить порядок действий в выражении используются круглые скобки.
Выражения бывают арифметические, отношения и логические.
Арифметические выражения записываются с помощью операндов числовых типов и арифметических операций, а результатом является числовое значение. В арифметическом выражении можно использовать стандартные математические функции, которые приведены в таблице 2.4.
Таблица 2.4. Стандартные математические функции VBA
|
Математическая запись |
Имя функции в VBA |
Описание |
|
½Х½ |
Abs(число) |
Возвращает значение, тип которого совпадает с типом переданного аргумента, равное абсолютному значению указанного числа. |
|
arctg X |
Atn(число) |
Возвращает значение типа Double, содержащее арктангенс числа. |
|
cos X |
Cos(число) |
Возвращает значение типа Double, содержащее косинус угла. |
|
]X[ |
Int(число) |
Возвращает значение типа, совпадающего с типом аргумента, которое содержит целую часть числа. |
|
ln X |
Log(число) |
Возвращает значение типа Double, содержащее натуральный логарифм числа. |
|
eX |
Exp(число) |
Возвращает значение типа Double, содержащее результат возведения числа e (основание натуральных логарифмов) в указанную степень. |
|
Sign X |
Sgn(число) |
Возвращает значение типа Variant (Integer), соответствующее знаку указанного числа. |
|
sin X |
Sin(число) |
Возвращает значение типа Double, содержащее синус угла. |
|
Sqr(число) |
Возвращает значение типа Double, содержащее квадратный корень указанного числа. |
|
|
tg X |
Tan(число) |
Возвращает значение типа Double, содержащее тангенс угла. |
Выражения отношения определяют истинность или ложность результата при сравнении двух операндов. Сравнивать можно данные любого одинакового типа. Результат операции отношения только логический: True — «истина» или False — «ложь».
Логические выражения. Результатом логического выражения является логическое значение True или False. Простейшими видами логических выражений являются: логическая константа, логическая переменная, логическая функция, выражение отношения. Логические операции выполняются только над операндами логического типа.
Пример. Записать 1£Х£5 и определить значение выражения при Х=3.1
Выражение в VВА будет выглядеть так:
X>=1 And X<=5
Результатом выражения будет True.
Чтобы получить перечень всех математических функций, достаточно набрать имя любой известной математической функции (например, SIN), а затем нажать клавишу F1 и ниже описания выбранной функции выбрать ссылку на Математические функции. В полученном перечне можно получить справку о назначении любой из встроенных математических функций и ее аргументе.
Чтобы получить перечень всех производных математических функций и правила их формирования, достаточно набрать имя любой известной математической функции (например, SIN), а затем нажать клавишу F1 и ниже описания выбранной функции выбрать ссылку на Производные математические функции.
Ниже, в таблице 2.5, приведен список функций, которые могут быть получены с помощью встроенных математических функций.
Таблица 2.5. Производные математические функции
|
Математическая запись |
Название функции |
Комбинация встроенных функций |
|
sc X |
Секанс |
1/Cos(X) |
|
csc X |
Косеканс |
1/Sin(X) |
|
ctg X |
Котангенс |
1/Tan(X) |
|
arcsin X |
Арксинус |
Atn(X/Sqr(-X*X+1)) |
|
arccos X |
Арккосинус |
Atn(-X/Sqr(-X*X+1))+2*Atn(1) |
|
arcsc X |
Арксеканс |
Atn(X/Sqr(X*X-1))+Sgn((X)-1)*2*Atn(1) |
|
arccsc X |
Арккосеканс |
Atn(X/Sqr(X*X-1))+(Sgn(X)-1)*2*Atn(1) |
|
arcctg X |
Арккотангенс |
Atn(X)+2*Atn(1) |
|
sh X |
Гиперболический синус |
(Exp(X)-Exp(-X))/2 |
|
ch X |
Гиперболический косинус |
(Exp(X)+Exp(-X))/2 |
|
th X |
Гиперболический тангенс |
(Exp(X)-Exp(-X))/(Exp(X)+Exp(-X)) |
|
sch X |
Гиперболический секанс |
2/(Exp(X)+Exp(-X)) |
|
csch X |
Гиперболический косеканс |
2/(Exp(X)-Exp(-X)) |
|
сth X |
Гиперболический котангенс |
(Exp(X)+Exp(-X))/(Exp(X)-Exp(-X)) |
|
arsh X |
Гиперболический арксинус |
Log(X+Sqr(X*X+1)) |
|
arch X |
Гиперболический арккосинус |
Log(X+Sqr(X*X-1)) |
|
arth X |
Гиперболический арктангенс |
Log((1+X)/(1-X))/2 |
|
arsch X |
Гиперболический арксеканс |
Log((Sqr(-X*X+1)+1)/X) |
|
arcsch X |
Гиперболический арккосеканс |
Log((Sgn(X)*Sqr(X*X+1)+1)/X) |
|
arcth X |
Гиперболический арккотангенс |
Log((X+1)/(X-1))/2 |
|
lognX |
Логарифм по основанию N |
Log(X)/Log(N) |
Основные операторы языка VBA
3.1. Правила записи операторов
При записи операторов необходимо придерживаться следующих правил:
— Каждый новый оператор записывается с новой строки.
— Чтобы записать несколько операторов на одной строке, их разделяют между собой двоеточием (:).
— Если оператор не помещается в одной строке, то необходимо поставить в конце строки пробел и знак подчеркивания ( _), а затем продолжить не поместившуюся часть на следующей строке.
3.2. Оператор присваивания
Оператор присваивания используется, если какой-то переменной нужно присвоить новое значение. Он имеет следующий синтаксис:
ИМЯ_ПЕРЕМЕННОЙ = ВЫРАЖЕНИЕ
Сначала вычисляется выражение в правой части, а затем результат присваивается переменной, стоящей в левой части.
Например. Записать с помощью оператора присваивания следующее математическое выражение:
На VВА это выражение можно записать в виде следующего оператора:
Y = a^(1/3)+(a^2+Exp(-b))/(Sin(a)^2-Log(b))
3.3. Операторы ввода-вывода
3.3.1. Оператор и функция MsgBox
Оператор MsgBox осуществляет вывод информации в диалоговом окне и устанавливает режим ожидания нажатия кнопки пользователем.
Он имеет следующий синтаксис:
MsgBox Сообщение[,Кнопки][, Заголовок]
Аргументы:
Сообщение — обязательный аргумент, задающий в окне выводимое информационное сообщение. Может состоять из нескольких текстовых строк, объединенных знаком &. Использование в этом аргументе Chr(13) приводит к переходу на новую строку при выводе информации.
Кнопки — значение этого аргумента определяет категории появляющихся в окне кнопок. От значения аргумента кнопки зависит также, появляется ли в окне какой-либо значок. Если не указано, какие кнопки необходимо отображать в окне сообщений, то используется значение по умолчанию, соответствующее кнопке ОК. В табл. 3.1 приведены возможные комбинации кнопок и значков в окне сообщений.
Заголовок — задает заголовок окна.
Функция MsgBox возвращает значение типа Integer, указывающее, какая кнопка была нажата в диалоговом окне.
Таблица 3.1. Допустимые значения переменной кнопки
|
Отображение |
Аргумент |
|
Кнопка ОК |
VbOKOnly |
|
Кнопки ОК и Отмена |
VbOKCancel |
|
Кнопки Да и Нет |
VbYesNo |
|
Кнопки Да, Нет и Отмена |
VbYesNoCancel |
|
Кнопки Прекратить, Повторить и Игнорировать |
VbAbortRetryIgnore |
|
Кнопки Повторить и Отмена. |
VbRetryCancel |
|
Информационный знак |
VbInformation |
|
Знак |
VbCritical |
|
Знак вопроса |
VbQuestion |
|
Знак восклицания |
VbExclamation |
Например. Вывести сообщение о текущей дате.
Для этого можно использовать следующий оператор:
MsgBox «Сегодня на календаре» & Date, , «Внимание»
В результате будет выведено следующее окно (рис.3.1).
Рис. 3.1
После щелчка по кнопке ОК окно сообщения закроется, и выполнение программы возобновится с оператора, стоящего непосредственно за вызовом MsgBox.
3.3.2. Функция InputBox
Функция InputBox осуществляет ввод значений переменных с помощью окна ввода и имеет следующий синтаксис:
Имя_Переменной = InputBox( Сообщение[, Заголовок])
Аргументы:
Сообщение — обязательный аргумент. Задает в окне информационное сообщение, обычно поясняющее смысл вводимой величины
Заголовок — задает заголовок окна.
Например, Ввести значение переменной N с клавиатуры, предусмотрев значение по умолчанию равное 10.
Для этого можно использовать следующий оператор:
N = InputBox(«Введите N», «Ввод исходных данных»,10)
В результате будет выведено следующее окно для ввода значения переменной N (рис.3.2).
Если значение по умолчанию подходит пользователю, то после щелчка кнопки ОК окно ввода закроется, переменной N присвоится значение 10 и выполнение программы возобновится с оператора, стоящего непосредственно за вызовом InputBox.
Если же значение по умолчанию не подходит пользователю, то перед щелчком по кнопке ОК необходимо ввести нужное значение переменной N.
3.4. Условный оператор IF
Для реализации разветвляющегося вычислительного процесса в VBA используется оператор If…Then…Else, который представляет собой простейшую форму проверки условий. Он имеет следующий синтаксис:
If УСЛОВИЕ Then ОПЕРАТОР_1 Else ОПЕРАТОР_2
ОПЕРАТОР_1 выполняется, если УСЛОВИЕ истинно, в противном случае выполняется ОПЕРАТОР_2. При этом оператор If…Then…Else записывается в одну строку.
УСЛОВИЕ – это выражение логического типа. Результат выражения всегда имеет булевский тип. Выражение может быть простым и сложным. При записи простых условий могут использоваться все возможные операции отношения, указанные в табл. 3.2.
Таблица 3.2. Логические отношения
|
Операция |
Название |
Выражение |
Результат |
|
= |
Равно |
A = В |
True, если А равно В |
|
<> |
Не равно |
A<>В |
True, если А не равно В |
|
> |
Больше |
А>B |
True, если А, больше В |
|
< |
Меньше |
A<B |
True, если А меньше В |
|
>= |
Больше или равно |
A>=B |
True, если А больше или равно В |
|
<= |
Меньше или равно |
A<=B |
True, если А меньше или равно В |
Сложные условия образуются из простых путем применения логических операций и круглых скобок. Список логических операций приведен в табл. 3.3.
Таблица 3.3. Логические операции
|
Название |
Выражение |
А |
В |
Результат |
|
|
Not |
Логическое |
Not A |
False True |
True False |
|
|
And |
Логическое И |
A And B |
True True False False |
True False True False |
True False False False |
|
Or |
Логическое ИЛИ |
A Or B |
True True False False |
True False True False |
True True True False |
В условном операторе допустимо использование блока операторов вместо любого из операторов. В этом случае условный оператор имеет вид:
If УСЛОВИЕ Then
БЛОК_ОПЕРАТОРОВ_1
Else
БЛОК_ОПЕРАТОРОВ_2
End If
В условном операторе может проверяться несколько условий. В этом случае условный оператор имеет вид:
If УСЛОВИЕ_1 Then
БЛОК_ОПЕРАТОРОВ_1
ElseIf УСЛОВИЕ_2 Then
БЛОК_ОПЕРАТОРОВ_2
Else
….
End If
Пример 1. Написать часть программы для алгоритма на рис. 3.3.
Пример 2. Написать часть программы для алгоритма на рис. 3.4.
3.5. Оператор выбора Select Case
Оператор Select Case удобно использовать, когда в зависимости от значения некоторого выражения, имеющего конечное множество допустимых значений, необходимо выполнить разные действия. Он также относится к условным операторам, но имеет другой вид:
Select Case ПРОВЕРЯЕМОЕ_ВЫРАЖЕНИЕ
Case ЗНАЧЕНИЯ_1
ОПЕРАТОРЫ_1
Case ЗНАЧЕНИЯ_2
ОПЕРАТОРЫ_2
. . .
Case ЗНАЧЕНИЯ_N
ОПЕРАТОРЫ_N
[Case Else
ИНАЧЕ_ОПЕРАТОРЫ]
End Select
ПРОВЕРЯЕМОЕ_ВЫРАЖЕНИЕ может иметь любой скалярный тип, кроме вещественного. ЗНАЧЕНИЯ состоят из произвольного количества значений или диапазонов, отделенных друг от друга запятыми.
Тип ЗНАЧЕНИЙ должен совпадать с типом ПРОВЕРЯЕМОГО_ВЫРАЖЕНИЯ.
Сначала вычисляется ПРОВЕРЯЕМОЕ_ВЫРАЖЕНИЕ. Если его значение совпадает с одним из значений ЗНАЧЕНИЯ_I, то выполнятся ОПЕРАТОРЫ_I и управление передается оператору, стоящему после End Select. Если его значение не совпадает ни с одним из значений ЗНАЧЕНИЯ_I, то выполнятся ИНАЧЕ_ОПЕРАТОРЫ и управление передается оператору, стоящему после End Select
Например. Написать часть программы для алгоритма на рис. 3.5, определяющего значение переменной S в зависимости от значения переменной n.
3.6. Операторы цикла
Для реализации циклического вычислительного процесса, т. е. многократного выполнения одного или нескольких операторов, служит оператор цикла For…Next, который имеет следующий синтаксис:
For СЧЕТЧИК=НАЧ_ЗНАЧЕНИЕ Тo КОН_ЗНАЧЕНИЕ Step ШАГ
БЛОК_ОПЕРАТОРОВ
[Exit For]
БЛОК_ОПЕРАТОРОВ
Next СЧЕТЧИК
Цикл For…Next перебирает значения переменной СЧЕТЧИК, которая является параметром цикла, от начального до конечного значения с указанным шагом изменения. При этом обеспечивается выполнение блока операторов тела цикла при каждом новом значении счетчика. Если Step ШАГ в конструкции отсутствует, то по умолчанию считается, что шаг равен 1. По оператору Exit For можно выйти из оператора цикла до того, как СЧЕТЧИК достигнет последнего значения.*
Для перебора объектов из группы подобных объектов, например, ячеек из диапазона или элементов массива, удобно использовать оператор цикла For… Each…Next.
For Each Элемент In Группа
БЛОК_ОПЕРАТОРОВ
[Exit For]
БЛОК_ОПЕРАТОРОВ
Next Элемент
В VBA для организации циклов с неизвестным заранее числом повторений используются и другие операторы цикла:
циклы с предусловием – Do While … Loop,
Do Until … Loop;
циклы с постусловием – Do … Loop While,
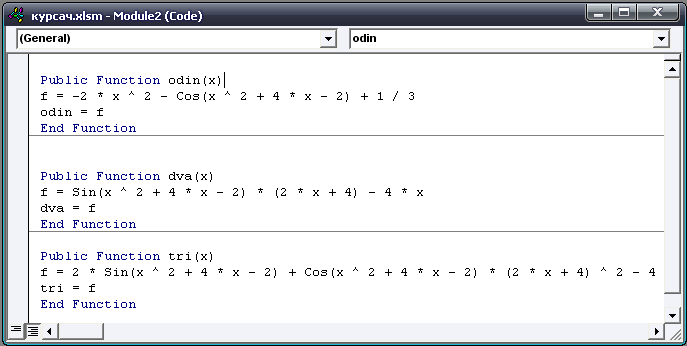
1. В ЭТ Excel+VBA
создаем
пользовательские функции (Function)
для f
(x),
f
(x),
f
(x).
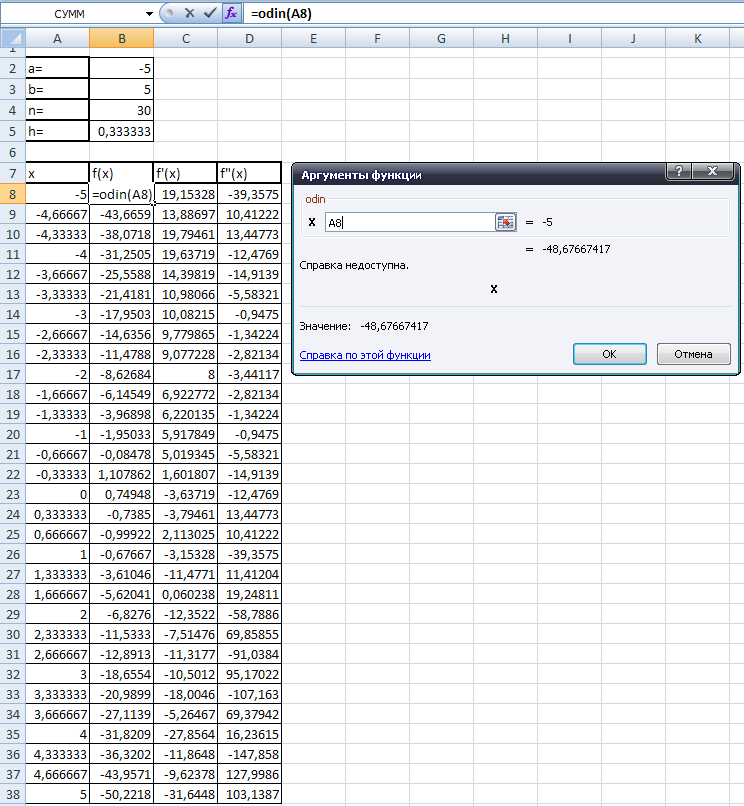
2. С
помощью
созданных процедур
строим
таблицу значений функций f
(x),
f
(x),
f
(x)
на отрезке [a, b]
с шагом h = (b – a) / n,
где n=30.
Для этого в ячейки
ЭТ Exсel
вставляем пользовательские функции
(Формулы → Вставить функцию → Определенные
пользователем) для f
(x),
f
(x),
f
(x)
и выбираем аргумент функции.
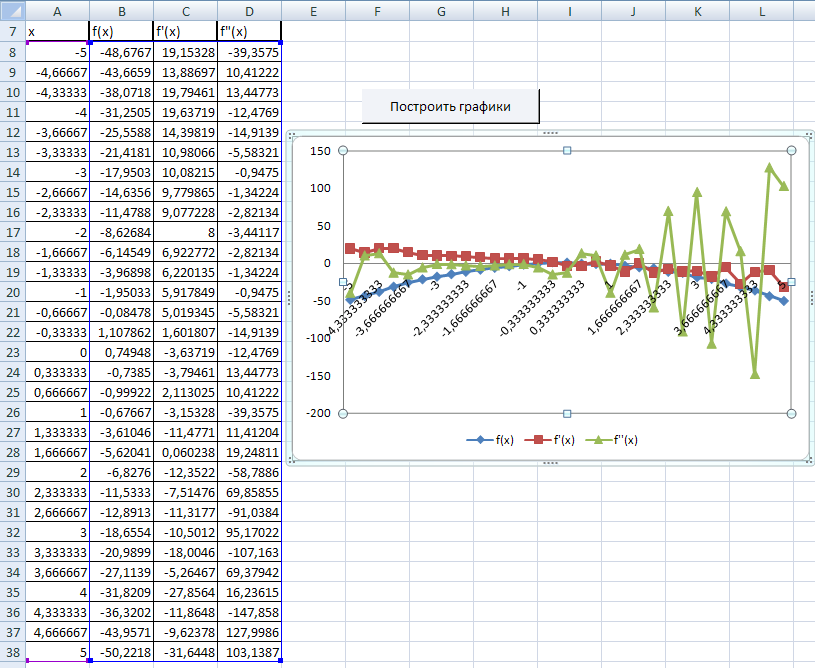
3. С помощью
макрорекордера создаём макрос для
построения на одной диаграмме графиков
функций f
(x),
f
(x),
f
(x).
Тип диаграммы – «график» с маркерами,
помечающими точки данных; легенду
размещаем внизу посередине.
Вставляем кнопку
(элемент управления формы) и назначаем
макрос объекту.
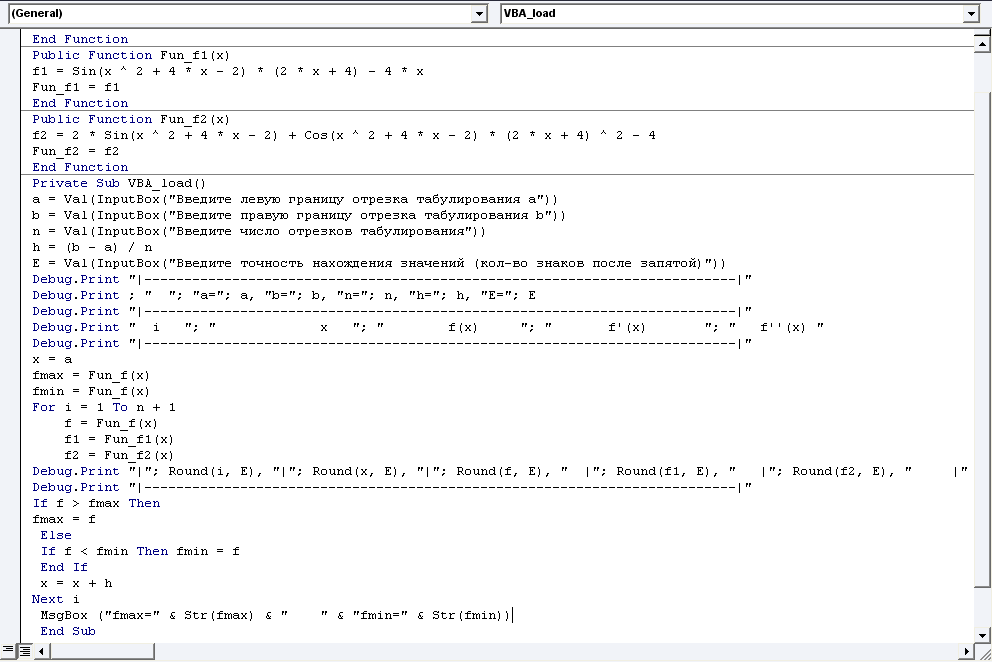
4. Составляем
процедуру (Sub)
для построения таблицы значений функций
f(x),
f
(x)
f
(x)
на отрезке [a, b]
с шагом h = (b – a) / n,
где n=30.
Начало и
конец отрезка,
а также количество разбиений отрезка
вводим с клавиатуры, используя функцию
InputBox.
Вывод результата организовываем в окно
Immediate
в виде
таблицы.
В процедуре организовываем вызов
пользовательских функций, созданных
выше. Добавляем в процедуру (Sub)
поиск глобального максимума, глобального
минимума функции. Результат выводим с
помощью окна MsgBox.
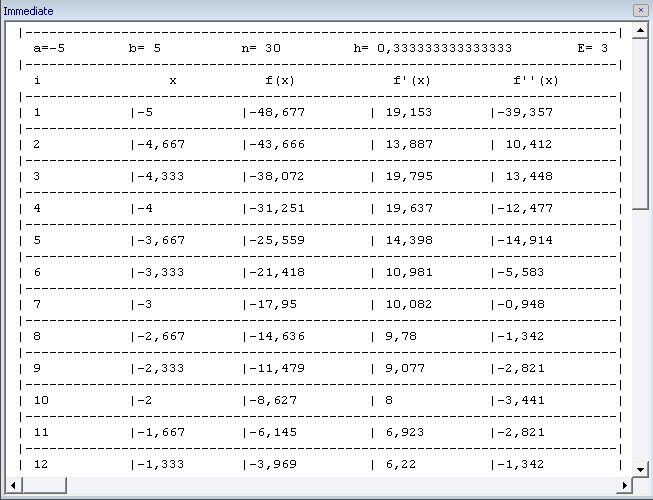
Вывод значений
функций f(x),
f
(x)
f
(x)
в окно Immediate:
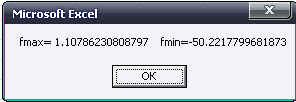
Вывод глобального
максимума, глобального минимума функции
с помощью окна MsgBox:
Глава 4. Реализация в MathCad
Mathcad —это популярная
система компьютерной математики,
предназначенная для автоматизации
решения массовых математических задач
в самых различных областях науки, техники
и образования.
В ходе решения
поставленной задачи были использованы
следующие функции: Maximize
(f,
x)
для нахождения максимума, Minimize
(f,
x)
для нахождения минимума, sin(x)
для нахождения синуса в радианах, cos(x)
для нахождения косинуса в радианах.
Также для нахождения корня были
использованы блоки Given,
в данных блоках располагаются условия,
а также функция Find(x)
для непосредственного поиска корня.
1. Порядок выполнения работы в скм MathCad:
-
Определяем функцию,
находим производную, строим графики
соответствующих функций.
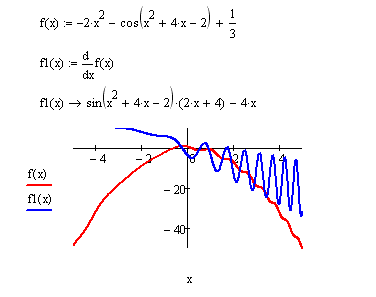
-
Находим
локальные экстремумы функции двумя
способами:
Способ 1:
С помощью блока
Given…Maximize
(Minimize);

Локальные экстремумы
в точках xmin
= 0.537, xmax
= -0.232.
Способ 2:
С помощью производной.
Здесь же определяем тип экстремумов
(максимум/минимум), используя вычисления
производной первого порядка. Для проверки
вычисляем значения производной в
найденных точках и их окрестностях.

-
Находим нули
производной, решаем уравнение f’(x)=0
(используя символьные вычисления:
выделяем переменную х
в полученной функции производной и
выбираем команду «Вычислить»
(Solve)
пункта «Переменные»
(Variable)
в меню «Символы»
(Symbolic)).

-
Решаем те же задачи
в MathCAD
на базе встроенной функции root(),
которая позволяет отыскивать корни
при данном начальном приближении.
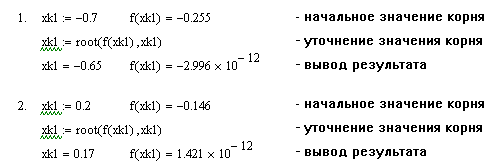
В нашем случае
корень функции xk1
= -0.65, xk2
= 0.17.
Полученные корни
полностью соответствуют корням,
полученным в ЭТ Excel.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
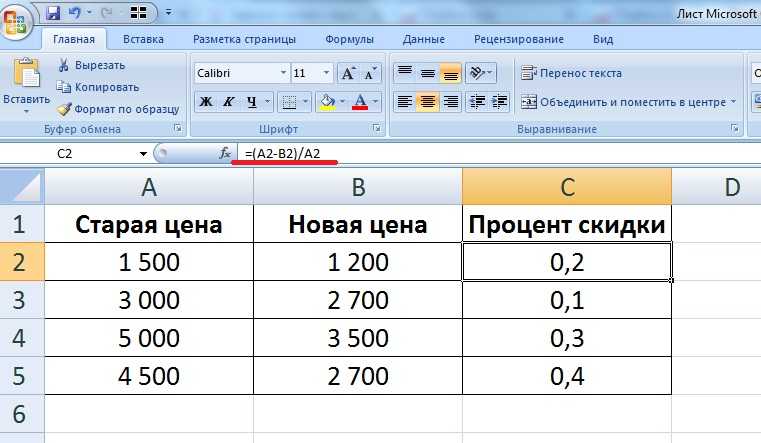
Вычислить производную в Excel по таблицам данных
Несколько недель назад я писал о вычислении интеграла данных в Excel. На этой неделе я хочу изменить направление и показать, как вычислить производную в Excel. Как и при численном интегрировании, есть два способа выполнить это вычисление в Excel:
- Производные табличных данных на листе
- Производные от Функция с использованием VBA (или Visual Basic для приложений)
В этом посте я собираюсь сосредоточиться на вычислении производных табличных данных с сообщением о вычислении того же с использованием VBA более поздняя дата.
Это вид вычисления производной, который обычно выполняется на экспериментальных данных. Это может быть особенно полезно, когда вы не могли напрямую измерить интересующее количество, но смогли измерить его интегральную функцию.
[Примечание: хотите узнать больше о расширенных Методы Excel? Смотрите мое бесплатное обучение только для инженеров. В серии видео из трех частей я покажу вам, как легко решать инженерные задачи в Excel.
Нажмите здесь, чтобы начать.]
Классическим примером, конечно же, являются положение и скорость:
Скажем, например, вы провели некоторый эксперимент, в котором было трудно получить скорость напрямую. Итак, вместо этого вы измеряли позицию в разное время, t . Вы можете импортировать данные в Excel и рассчитать скорость как производную от положения по времени.
Для выполнения этого вычисления в Excel используется метод конечных разностей.
Чтобы использовать метод конечных разностей в Excel, мы вычисляем изменение «y» между двумя точками данных и делим на изменение «x» между теми же самыми точками данных:
Это называется односторонней оценкой, потому что она учитывает только наклон данных на одном сторона точки интереса.
Более точной оценкой было бы вычисление среднего уклона в точке интереса путем усреднения наклона непосредственно до и после этой точки.
Итак, если мы хотим найти наклон в y 2 (z), мы могли бы использовать этот расчет:
Давайте посмотрим, как вычислить производную в Excel на примере.
Чтобы упростить задачу, я спрятал старые данные об ускорении и скорости. В конце мы посмотрим, как они сравниваются.
Сначала я вычисляю скорость, используя уравнение конечных разностей выше. Поскольку нам нужны y3 и y1, я начинаю вычисление в ячейке E5 и заполняю ее.
[Примечание. Хотите узнать еще больше о передовых методах работы с Excel? Посмотрите мое бесплатное обучение только для инженеров. В серии из трех видео я покажу вам как легко решать инженерные задачи в Excel. Нажмите здесь, чтобы начать.]
Затем, используя вычисленную скорость, я могу рассчитать ускорение тем же методом. На этот раз расчет начинается в строке 6.
Теоретически, если мы дифференцируем данные, полученные путем интегрирования, тогда мы должны вернуться к исходным данным.
Но насколько велика ошибка? Давайте сравним .
В этом случае мы видим небольшие отличия между исходными данными об ускорении и данными, полученными путем дифференцирования. Есть также некоторые незначительные различия в двух наборах данных о скорости. К счастью, ошибка численного дифференцирования n не является кумулятивным, в отличие от численного интегрирования.
Таблицы данных – не идеальный способ изучить эти данные, поэтому давайте посмотрим на графики:
Трудно увидеть, потому что две линии расположены друг над другом, но для всех практических целей скорости идентичны.
Как насчет разгона?
Здесь мы можем видеть, что во время периодов неуклонного увеличения или постоянного ускорения два набора данных очень похожи. Однако, когда в данных ускорения наблюдается разрыв (например, время 0,1, 0,45, 0,5, 0,7 и 0,75 с), ускорение, полученное дифференцированием (оранжевый), не соответствует исходным данным ускорения (синий).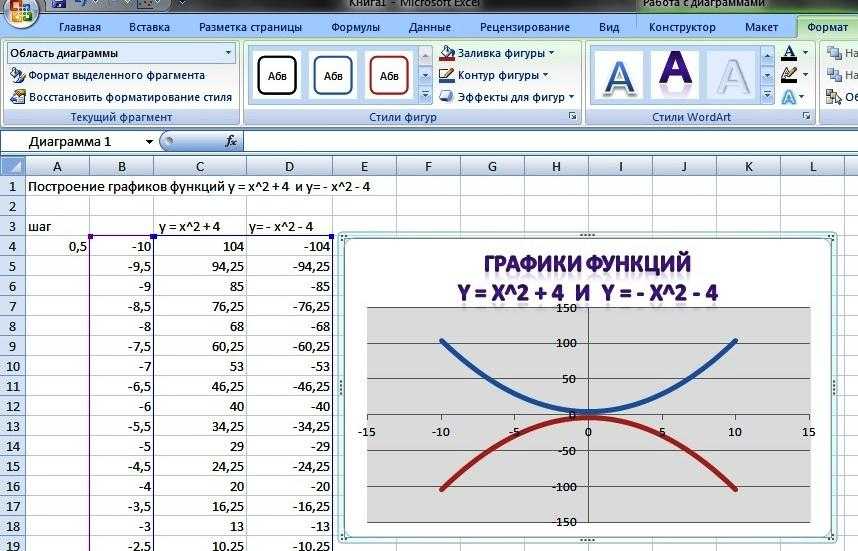
Это связано с уравнением, которое мы использовали для выполнения дифференцирования. Помните, как мы получили производную в точке путем усреднения наклона по обе стороны от этой точки? Мы видим результаты здесь.
Если вы следовали инструкциям, поздравляем! Вы только что выполнили численное дифференцирование в Excel. Конечно, вычислить производную в Excel не так сложно, если вы знаете, как это сделать.
Использовали ли вы этот метод для некоторых данных? Расскажите мне об этом в комментариях ниже.
[Примечание: Хотите узнать еще больше о продвинутых методах Excel? Смотрите мое бесплатное обучение только для инженеров. В серии видео из трех частей я покажу вам, как легко решать инженерные задачи в Excel. Щелкните здесь, чтобы начать.]
RDF> ->
6.3.3.Численное вычисление производной функции одного переменного
Известно,
что численными приближенными методами
производная функции в заданной точке
может быть вычислена с использованием
формулы конечных разностей.
для вычисления производной функции
одного переменной в точке xk,
записанное в конечных разностях, имеет
вид:
,
где Δx – очень
малая конечная величина.
При
достаточно малых значениях Δх, можно с
приемлемой точностью получить величину
производной функции в точке. Для
вычисления производной в MS Excel будем
использовать приведенную зависимость.
Рассмотрим технологию вычисления
производной на примере.
Найти производную
функции Y= 2x3 + x2в точкеx=3. Заметим, что производная
приведенной функции в точкеx=3 .
Напомним, что производная приведенной
функции, вычисленная аналитическим
методом, равна 60 – это значение нам
понадобится для проверки результата,
полученного путем вычисления численным
методом в электронной таблице.
Решим задачу двумя
способами.
Способ 1
Введем в ячейку
рабочего листа формулу правой части
заданной функциональной зависимости,
например в ячейку В2, как показано на
рис.
2))/B2.
После нажатия
клавиши Enter получим
результат вычисления 60,0000.
Как видим, результат
получен такой же, как и при первом
способе. Приведенный второй способ
является более предпочтительным в
случаях, когда нужно построить таблицу
значений производной функции для
заданных значений аргумента.
Используя приведенную
технологию численного вычисления
производной функции в заданной точке,
проверим, является ли найденная точка
x= -0,5 точкой экстремума
функцииY= X2+X +2 .
Решение приведено на рис. 6.11
Рис. 6.11
Как видно, производная
в найденной точке равна нулю, следовательно,
найденное в примере значение функции
является ее экстремальным значением.
Известно,
что чем ниже цена (p),
тем больше спрос (D)
при постоянной покупательной способности
населения.
Обычно зависимость спроса
от цены в графическом представлении
имеет вид ниспадающей линии, чаще всего
приближающейся к прямой. В свою очередь,
предложение растет с увеличением цены
на товар и в графическом представлении
имеет восходящей линии.
В
экономике представляет интерес условие
равновесия спроса и предложения.
Если
зависимость спроса от цены определяется
функцией D=f(p),
а зависимость предложения от цены –
S=φ(p),
то условие равновесия определяется
уравнением:
f(p)=
φ(p)
и
соответствует точке пересечения кривых
D
и S.
Цена Р0,
при которой выполняется это условие,
называется равновесной.
Рассмотрим
технологию решения задачи определения
точки равновесия на примере.
Зависимость спроса
yна некоторый товар от ценыx
выражается уравнением f1(x) =2/x-y + 2, а зависимость предложения от
цены – уравнениемf2(x)
= x2 — y + 1.
систему уравнений, найти точку равновесия
в диапазонес точностью 0,001.
Решение
Приведем исходные
уравнения к системе следующего вида:
Создадим
последовательность значений xс шагом 0,2.
Рассчитаем значения
функций спроса f(x)
и предложения φ(x) для
сформированной последовательности
значенийx(рис. 33).
Построим графики
функций по данным таблицы.
Подведем указатель
мыши к точке пересечения кривых –
отобразятся приближенные координаты
точки равновесия. В данном случае цена
хв точке равновесия равна 1,6,
предложение и спрос характеризуются
величиной 3,6 (рис. 6.12).
Рис. 6.12
Применяя приведенную
выше технологию, уточним решение.
Результат уточнения приведен на рис.
6.13.
Рис. 6.13
Таким образом,
равновесное значение цены составляет
1,521, а спрос и предложение находятся в
равновесии и выражаются величиной
3,315.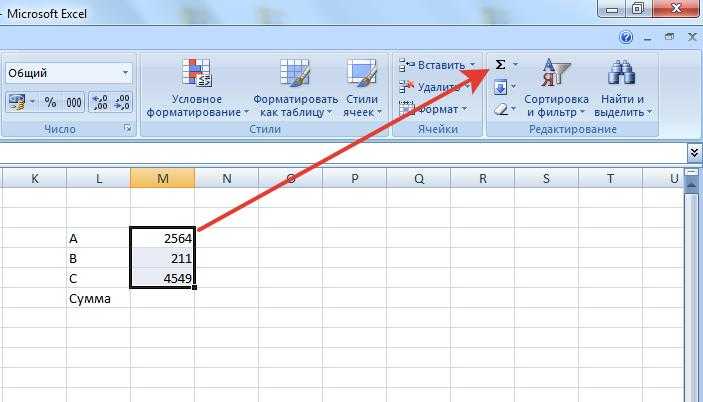
В
экономических задачах одни экономические
показатели являются функциями Y=f(x)
каких — либо других показателей или
величин. Иначе говоря, существует
зависимость одних показателей от других
–Y=f(x).
Так,
например, себестоимость продукции
зависит от производимого объема C=f(Q),
издержки производства – зависят от
количества выпускаемой продукции и
т.п.
Предельные
экономические показатели характеризуют
величину прироста величины функции ΔY
от прироста ее аргумента Δx:
Так,
например, предельная себестоимость
характеризует себестоимость ΔС прироста
продукции ΔQ:
Если
зависимость ΔY
от Δx
непрерывна, то приведенное разностное
уравнение можно заменить производной
.
Пусть зависимость
издержек производства от объема
выпускаемой продукции в денежных
единицах выражается формулой C=20Q –
0,05Q3
Требуется определить
предельные издержки производства при
объеме выпускаемой продукции 10 ден.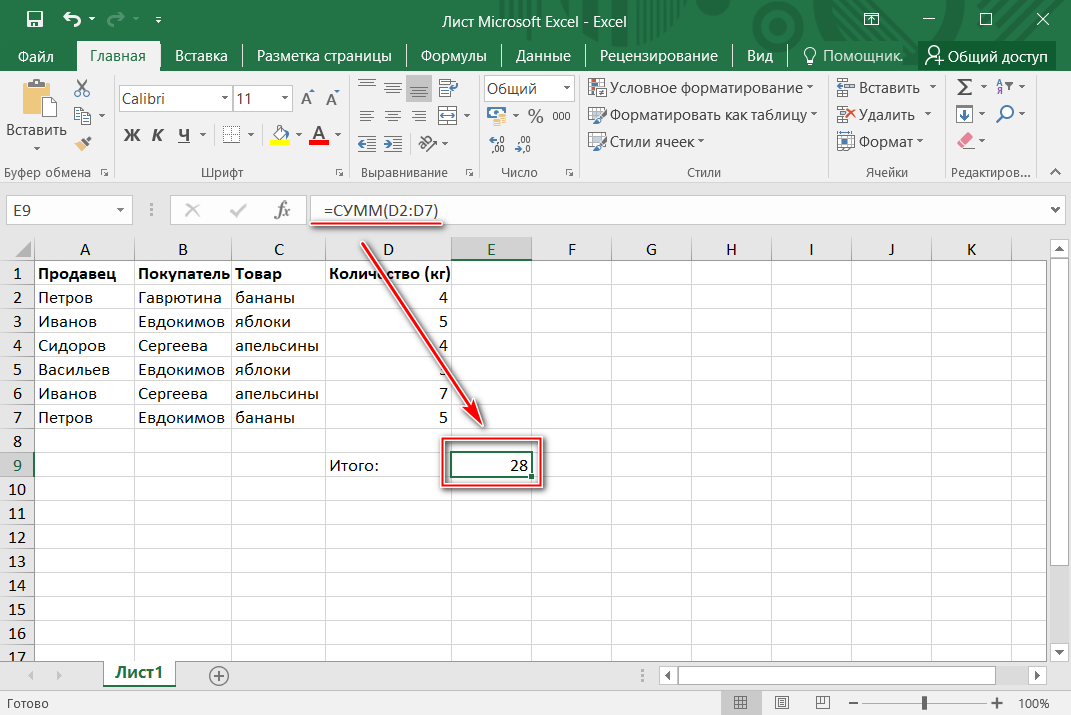
Скопируем введенную
формулу в ячейку В3 (рис.6.14).
В ячейку С3 введем
формулу вычисления производной:
=(B3-B2)/(A3-A2). В ячейки А2 и А3 введем значения
Qдля левой и правой
окрестности, соответственно (рис. 6.14).
Рис. 6.14
После выполнения
приведенных выше операций в ячейке С2
будет получен результат (рис. 6.15).
Рис. 6.15
Таким образом,
предельные издержки производства при
объеме выпускаемой продукции 10 ден.ед.
составляют примерно 4,99999 ден. ед.
Зависимость затрат от объема производства
задана приведенной ниже таблицей.
Требуется найти предельные издержки
производства при объеме выпуска х=1,9.
Указания: в данной
задаче функция зависимости затрат от
объема производства задана не аналитически,
а таблично. Поэтому, нужно прежде всего
получить аналитическую зависимость в
виде интерполяционной функции и используя
ее решить задачу в соответствии с
приведенной в примере технологией.
|
Объем |
Затраты |
|
1 |
2,7 |
|
1,2 |
3,2 |
|
1,4 |
3,7 |
|
1,6 |
4,1 |
|
1,8 |
4,7 |
|
2 |
5,1 |
|
2,2 |
5,6 |
|
2,4 |
5,8 |
Как вычислить производную от точек данных (x,y) в Excel
В этом примере мы сэмплируем функцию
f(x)=x⁢sin(x2)+1
затем вычислите его производную из выборочных точек данных, используя DERIVXY , и сравните результат с аналитическими производными, заданными формулой
f'(x)=sin(x2)+2⁢x2⁢cos(x2)
Решение
Используя формулы, показанные в таблице 1, мы генерируем с помощью автозаполнения значения данных (x, y) и аналитические производные для значений x .
показано в Таблице 2 ниже:
| А | В | С | |
| 3 92) | |||
| 6 | ⇓ Перетащите вниз до строки 20 |
⇓
| A | B | C | |
| 3 | x_data | y_data | Analytic der |
| 4 | 0 | 1 | 0 |
| 5 | 0.25 | 1.015615 | 0.1872153 |
| 6 | 0.5 | 1.123702 | 0.7318602 |
| 7 | 0.75 | 1.399977 | 1.4849677 |
| 8 | 1 | 1.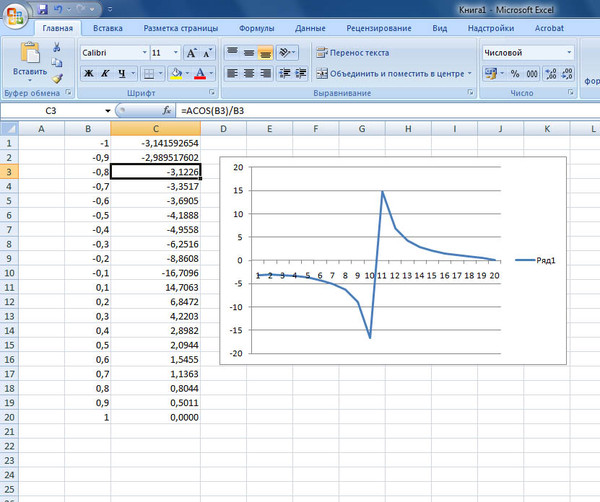 841471 841471 |
1.9220756 |
| 9 | 1.25 | 2.249957 | 1.0258913 |
| 10 | 1.5 | 2.16711 | -2.0487081 |
| 11 | 1.75 | 1.138268 | -6.0268418 |
| 12 | 2 | -0.5136 | -5.9859515 |
| 13 | 2.25 | -1.1135 | 2.5335616 |
| 14 | 2.5 | 0.917052 | 12.459939 |
| 15 | 2.75 | 3.634003 | 5.3043158 |
| 16 | 3 | 2.236355 | -15.988226 |
| 17 | 3.25 | -1.94996 | -9.773066 |
| 18 | 3.5 | -0.08892 | 22.972966 |
| 19 | 3.75 | 4.739551 | 3.0952707 |
| 20 | 4 | -0,15161 | -30,933007 |
Используя формулы DERIVXY , показанные в таблице 3, мы генерируем с помощью автозаполнения числовые производные на x -значения и вычислить относительную ошибку по отношению к
аналитические производные.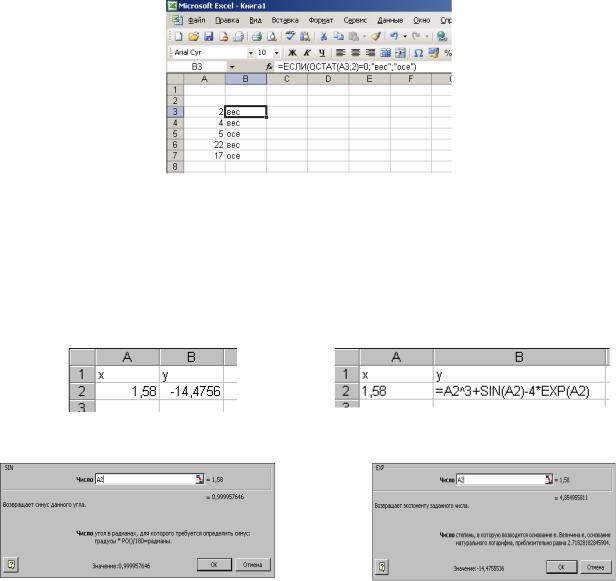
Обратите внимание, что мы передали определенные имена
x_data и y_data для столбцов A4:A20 и B4:B20 соответственно. Это один из способов заблокировать данные, поэтому автозаполнение
игнорирует эти аргументы и увеличивает только третий аргумент. В качестве альтернативы мы могли бы использовать знак доллара, $, чтобы заблокировать первые два аргумента во время автозаполнения с помощью
формула =ПРОИЗВОДНЫЙXY($A$4:$A$20, $B$4:$B$20, A4) .
| E | F | |
| 3 | Numerical Derivatives | % Errors |
| 4 | =DERIVXY(x_data,y_data,A4) | 1 |
| 5 | =DERIVXY(x_data ,y_data,A5) | =ABS((E5-C5)/C5) |
| ⇓ Перетащите вниз до строки 20 |
⇓
| E | F | |
| 3 | Numerical Derivatives | % Errors |
| 4 | -0. 006256108 006256108 |
100.00% |
| 5 | 0.189289352 | 1.11% |
| 6 | 0.733522457 | 0.23% |
| 7 | 1.488966928 | 0.27% |
| 8 | 1.923837894 | 0.09% |
| 9 | 1.015441218 | 1.02% |
| 10 | -2.07793704 | 1.43% |
| 11 | -6.043962293 | 0.28% |
| 12 | -5.914791221 | 1.19% |
| 13 | 2.68187738 | 5.85% |
| 14 | 12.35516509 | 0.84% |
| 15 | 4.867529358 | 8.23% |
| 16 | -15.99364056 | 0.03% |
| 17 | -7. | 19.16% |
| 18 | 19.69241868 | 14.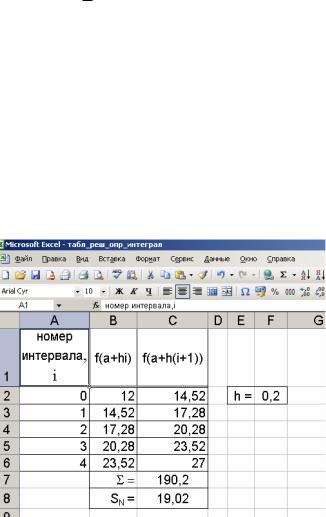 28% 28% |
| 19 | 9.404971886 | 203.85% |
| 20 | -58,06465252 | 87,71% |
4125
Обратите внимание, что ошибки максимальны вблизи конечных точек данных, поскольку сплайн по умолчанию
не ограничивает производные в конечной точке. Но в этом примере мы знаем точное
производные в концевых точках от аналитической формулы. Мы можем повысить точность, поставив
эти данные с помощью ключей ISLOPE и
ESLOPE в дополнительном элементе управления
аргумент за ПРОИЗВОДНАЯ .
Мы называем диапазон K1:L2 end_slopes и определяем следующие пары ключ/значение для начального и конечного наклона.
с использованием вычисленных значений аналитических производных в C4 и C20 из Таблицы 2 выше.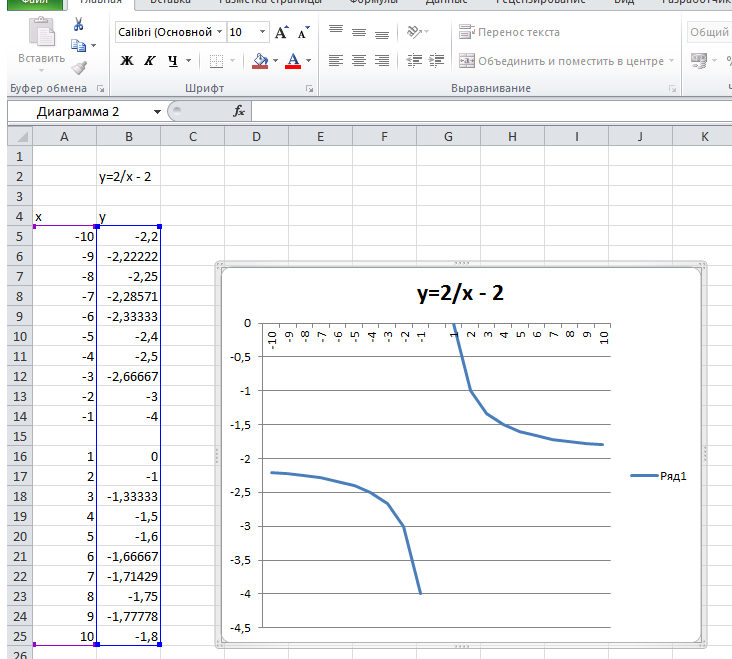
6
| К | Л | ||||
| 1 | ISLOPE |
0 |
0020 2 | ЭСЛОПА |
-30,933 |
Мы регенерируем новые производные и ошибки в столбцах h5:h30 и I4:I20 из расширенных формул DERIVXY в таблице 5.
Числовые значения, полученные с помощью автозаполнения, показаны в Таблице 6 ниже.
| H | I | ||
| 3 | НЕМЕРИЧЕСКОЙ ПРОИЗВОДИТЕЛЬНЫЙ ПРОИЗВОДИТЕЛЬНЫЙ 5 | =DERIVXY(x_data,y_data,A5,1,end_slopes) | =ABS((H5-C5)/C5) |
| ⇓ Drag down to row 20 |
⇓
| H | I | |||||
| 3 | Кол.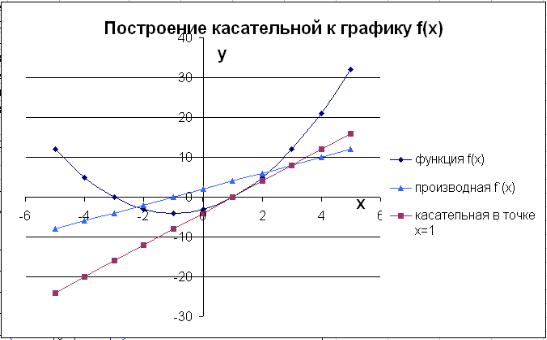 Дер. with end slopes Дер. with end slopes |
% Errors | ||||
| 4 | 0 | 0.00% | ||||
| 5 | 0.187612966 | 0.21% | ||||
| 6 | 0.733971891 | 0.29% | ||||
| 7 | 1,488845578 | 0,26% | ||||
| 8 | 1.923873859 | 0.09% | ||||
| 9 | 1.015418708 | 1.02% | ||||
| 10 | -2.077882964 | 1.42% | ||||
| 11 | -6.044156087 | 0.29% | ||||
| 12 | -5.91407012 | 1,20% | ||||
| 13 | 2,679186771 | 5,75% | ||||
| 14 | 12.36520643 18 | 12.36520643 10 | 4.830054635 | 8.94% | ||
| 16 | -15.853783 | 0.84% | ||||
| 17 | -8.422469647 | 13. 82% 82% |
||||
| 18 | 21.64038321 | 5.80% | ||||
| 19 | 2,135069296 | 31,02% | ||||
| 20 | -30,93300669 | 0,00% |
.0020 15
УВЕДОМЛЕНИЕ УВЕДОМЛЕНИЕ В ОТВЕРИТЕЛЬНЫМ ОЧЕСТИ С ЗОНА. Имейте в виду, что мы работаем с относительно небольшим размером выборки. Для получения каких-либо дальнейших улучшений потребуется более точная выборка.
Как сделать дифференцирование в Excel (с помощью простых шагов)
Дифференцирование является одним из важных элементов в области исчисления . Это процесс нахождения производных функции. Microsoft Excel упростил нам дифференциацию для многочисленных функций вместо рукописных вычислений. В этой статье мы узнаем, как сделать дифференцирование в Excel с помощью нескольких простых шагов. Посмотрим, как это работает.
Скачать рабочую тетрадь
Определение дифференциации
Дифференциал против производной
Правила дифференциации
Пошаговые процедуры для дифференциации в Excel
Шаг 1: Вставьте значения горизонтальной оси
Шаг 2: Найдите значения вертикальной оси
Шаг 3: Рассчитать дифференциацию
Шаг 4: Подготовьте диаграмму дифференциации
Пример: расчет скорости с дифференцированием в Excel
То, что нужно запомнить
Заключение
Статьи по Теме
Скачать рабочую тетрадь
Получите образец файла для самостоятельной практики.
Определение дифференциации
В общем, термин дифференцирование означает скорость изменения между двумя отдельными величинами или значениями. Отношение небольшого изменения одного значения зависит от первого значения, заданного в функции. Основная формула дифференцирования dy/dx , где y=f(x) .
Дифференциал против производной
Дифференциал и Производная — два тесно связанных термина в исчислении. Термин производная означает скорость изменения одной переменной по отношению к другой. Здесь переменных являются изменяющимися объектами.
С другой стороны, уравнение, определяющее связь между переменными и производными, называется дифференциальное уравнение . Это в основном фактическое изменение функции.
Подробнее: Как рассчитать производную от точек данных в Excel
Правила дифференциации
Когда точка дифференцирования равна 0 , функция остается непрерывной. В противном случае для каждого интервала позиции задается новый продукт, относящийся к значениям. Для этого существуют определенные правила дифференциации, которые приведены ниже: 92
5. Цепное правило : d/dx[f(g(x))]=f’(g(x))g’(x)
Пошаговые процедуры для выполнения дифференцирования в Excel
Для иллюстрации применим степенное правило дифференцирования в Excel. Давайте пройдем следующую пошаговую процедуру.
Шаг 1: Вставьте значения горизонтальной оси
Сначала мы вставим значения по оси x . Вы можете вставить любое другое значение по своему усмотрению.
- Сначала вставьте значение x в диапазон ячеек B5:B13 .
- Обязательно укажите начальную точку 0 .
- Вместе с ним вставьте значение n .
Шаг 2. Найдите значения вертикальной оси
Теперь мы вычислим значение y для каждого значения x . Здесь мы будем использовать эту функцию для расчета:
- Сначала вставьте эту формулу в 9$Е$5
- Затем нажмите Введите .
- Здесь вы увидите первый вывод и .
- Затем используйте инструмент AutoFill , чтобы вставить эту формулу в диапазон ячеек C6:C13 .
Шаг 3. Вычисление дифференциации
Наконец, на этом этапе мы проведем расчет дифференцирования. Выполните следующие действия:
- Сначала вставьте эту формулу в ячейку D5 .
=(C6-C5)/(B6-B5)Здесь dy означает разницу между последним значением и непосредственно предыдущим значением столбца y . Аналогичная функция есть и у dx .
- Затем нажмите Введите .
- Вот и все, вы провели первую дифференциацию.
- Наконец, примените аналогичную процедуру для каждого набора значений, и вы получите окончательный результат.
Подробнее: Как вычислить вторую производную в Excel (2 подходящих примера)
Шаг 4. Подготовьте диаграмму дифференцирования
Чтобы визуально представить данные, мы сейчас создадим график. Выполните следующие действия:
- В начале выберите диапазон ячеек B4:B13 и D4:D13 .
- После этого перейдите на вкладку Вставка и щелкните диаграмму Scatter в группе Диаграммы .
- Далее выберите тип диаграммы Scatter with Smooth Lines and Markers из вариантов.
- Вот и все, у вас есть исходный график, основанный на дифференциальном значении и значении x .
- После некоторых изменений конечный результат выглядит так:
Подробнее: Как сделать первую производную диаграмму в Excel (с помощью простых шагов)
Пример. Расчет скорости с дифференцированием в Excel
Давайте посмотрим на пример дифференцирования. Здесь мы будем рассчитывать скорость на основе определенных значений времени и расстояния. Выполните следующие действия:
- В начале вставьте значение время и расстояние в столбцах В и С соответственно.
- Затем вставьте эту формулу в ячейку D6 , чтобы вычислить дельту t .
=B6-B5- Затем нажмите Введите .
- Затем перетащите нижний угол ячейки D7 до ячейки D13 , чтобы найти все значения сразу.
- Затем вставьте эту формулу в ячейку E6 .
=C6-C5- Затем нажмите Введите .
- Затем с помощью инструмента AutoFill перетащите эту формулу в диапазон ячеек E7:E13 .
- Наконец, вставьте эту формулу в ячейку F6 .
=E6/D6- Как указано выше, примените эту формулу ко всей ячейке F7:F13 .
- Наконец, у нас есть значения скорости с вычислением дифференцирования.
- Вместе с ним можно построить такой график:
Что нужно помнить
- Постоянное значение дифференцирования всегда равно 0 в степенном правиле .


 Сообщение было отмечено Skyls как решение
Сообщение было отмечено Skyls как решение