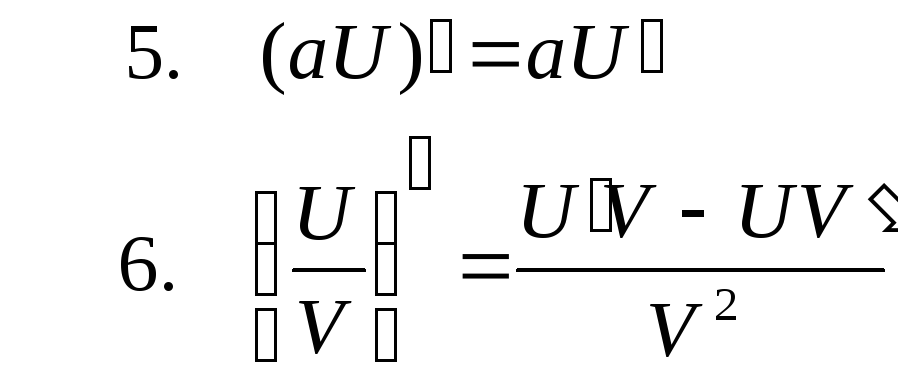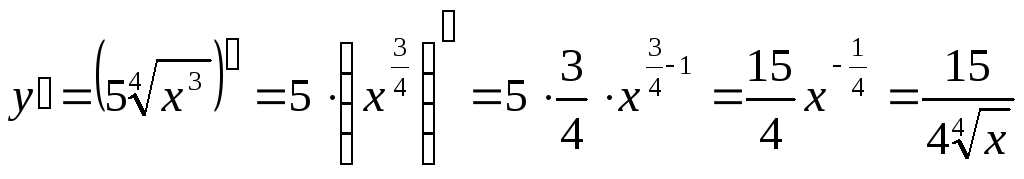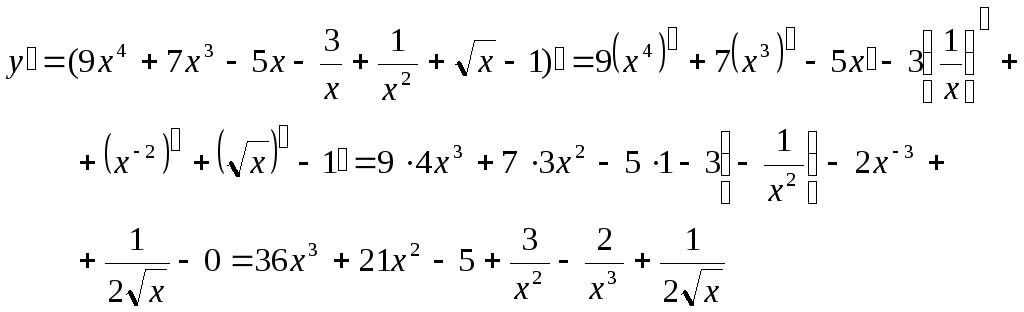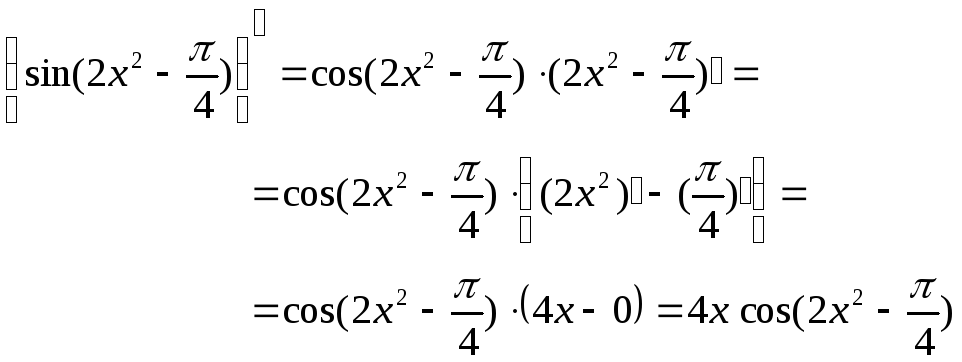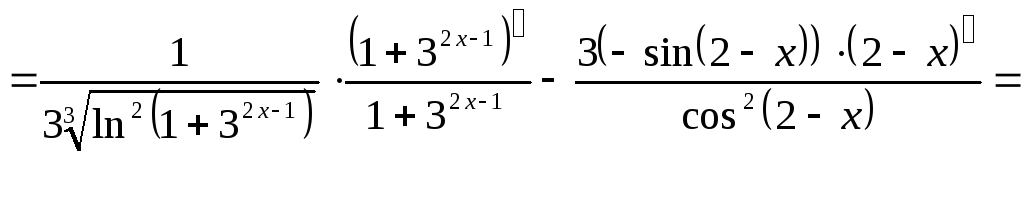Как найти производную с отрицательной степенью

Производная степени встречается в большинстве примеров на дифференцирование. Само правило нахождения производной степени простое. При дифференцировании степени с натуральным показателем проблем, как правило, не возникает. А вот найти производную степени с отрицательным или дробным показателями несколько сложнее. Легче всего понять, как найти производную степени, на примерах.

Открываем таблицу производных и правила дифференцирования.

Основная формула, по которой  может быть найдена производная любой степени —

Примеры. Найти производную степени:

Поскольку при дифференцировании число выносится за знак производной, то множитель, стоящий перед степенью, при нахождении производной просто переписываем:

Нахождение производной степени, стоящей в знаменателе дроби, немного сложнее. Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель. Получившуюся в результате вычислений степень с отрицательным показателем снова преобразовываем.

Производная степени используется и для дифференцирования корней. Предварительно корень приводится к степени, а в найденной производной снова возвращаемся к корню.

Например,

Если корень в знаменателе, сначала преобразовываем его в степень, затем — поднимаем наверх с отрицательным показателем, а  далее — как обычно, производная степени.

Например,

Примеры для самопроверки. Найти производную степени:

Показать решение

В данной публикации мы рассмотрим, чему равна производная степенной функций (в т.ч. сложной), а также разберем примеры решения задач для закрепления изложенного материала.

Формула производной степенной функции

Для функции f(x) = x ⁿ, где n – действительное число, справедливо следующее выражение:

f ‘(x) = (x ⁿ)‘ = nx ^n-1

Т.е. производная степенной функции равняется произведению показателя степени на основание в степени, уменьшенной на единицу.

n – может быть как положительным, так и отрицательным числом (в т.ч. дробным):

Производная сложной степенной функции

В сложной функции вместо x представлено более сложное выражение. Производная такой функции определяется по формуле:

(y ⁿ)‘ = ny ^n-1 ⋅ y ‘

Примеры задач

Задание 1:
Вычислите производную функцию f(x) = x³/5.

Решение:
Согласно правилам дифференцирования константу в виде дроби можно вынести за знак производной:

Применив формулу производной, рассмотренную выше, получаем:

Задание 2:
Найдите производную функции f(x) = x² + √x – 6.

Решение:
Первоначальный вид производной функции:
f ‘(x) = (x² + √x – 6)‘.

С учетом правила дифференцирования суммы получаем:
f ‘(x) = (x²)‘ + (√x)‘ – (6)‘.

Остается только вычислить производные по отдельности:

(x²)‘ = 2x^2-1 = 2x

(-6)‘ = 0 (производная константы равна нулю)

Таким образом получаем:

Дифференцирование фунций

Правила дифференцирования

Формулы дифференцирования

Рассмотрим
примеры.

Найти производные
следующих функций:

Пример1.
у= 3х⁴

Решение.

Используя правило
5 и формулу 5 – дифференцирования
степенной функции, имеем: у’=3(х⁴)’=3
4x^4-1=12x³

Пример 2.

Решение.

По определению
степени с отрицательным показателем:

.
Преобразуем данную функцию и найдем
производную аналогично решению примера
1:

Пример 3.

Решение.

По определению
степени с рациональным показателем:
,
отсюда:

Пример 4.

Решение.

Для нахождения
производной используем правила
дифференцирования 3; 5; 2, определение
отрицательной степени и формул 5; 6 и 7:

Пример 5.

Решение.

В данной функции
последним действием является произведение,
поэтому в первую очередь надо использовать
правило 4 – производная произведения,
а затем правило 5, определение степени
с рациональным показателем и формулы
дифференцирования 5 и 9:

Пример 6.

Решение.

Последнее действие
– деление, поэтому сначала применяем
правило 6 – производной частного, затем
формулы 3 и 10:

Рассмотрим
несколько примеров нахождения производных
сложных функций,
при этом будем использовать формулы
второго столбца формул дифференцирования.

Сложную функцию
обычно
обозначают в виде формулы y=f(g(x)),
где функцию у=f(u)
– называют
основной.
Ее вид соответствует последнему действию
в выражении, задающем функцию. Функцию
u=g(x)
– называют
промежуточной.

Чтобы найти
производную сложной функции надо,
производную основной функции умножить
на производную промежуточной.

Первоначальный
выбор формулы дифференцирования сложной
функции зависит от вида основной функции.

Рассмотрим
примеры.

Найти производные
следующих сложных функций:

Пример 7.
y=cos⁶x

Решение.

Основная функция
является степенной y=u⁶
, а промежуточная u=cosx
–
тригонометрической, поэтому сначала
находим производную по формуле 5 –
степенной (сложной) функции и умножаем
на производную косинуса (элементарной
функции) – формула 9.

.

Пример 8. y=
sin(2x²—)

Решение.

Основная функция
является тригонометрической y=sin
u
а промежуточная –
—
квадратичной.. Применяем формулу 8 для
сложной функции, а для нахождения
производной квадратичной функции
используем правила 3; 5; 2 и формулу 5.

Пример 9. y=log₃

Решение.

Основная функция
логарифмическая, а промежуточная
дробно-рациональная. Сначала используется
формула 3 сложной логарифмической
функции, а затем правила 6; 3; 4; 1 и 2.

Пример 10.

Решение.

Последнее действие
— сложение, поэтому используем правило
3, первое слагаемое представим в виде
степенной функции и применим формулу
5 (для сложной функции), во втором слагаемом
применим правило 5 и формулу 6 (для сложной
функции):

далее в первом
слагаемом преобразуем степенную функцию
и находим производную сложной
логарифмической функции по формуле 4,
во втором слагаемом в числителе используем
сложную формулу 9, получим:

для нахождения
оставшихся производных используем
правила 3; 1; 2 и формулу 1 для сложной
функции:

Соседние файлы в папке Учебники и пособия

• #
• #
• #
• #

Remember how fractions work when you’re dealing with numbers:

For example: $frac{6+4}{2} = frac{6}{2}+frac{4}{2} = 3+2 = 5$

What you’re saying is $frac{6+4}{2} = 6+4+1/2 = 10.5$ which is clearly incorrect.

As I said in the comments, $f(t)=frac{t^2+t^3-1}{t^4} = (t^2+t^3-1)(t^{-4})$

Another way to do it is to split up the numerator into its separate parts first:

$$f(t)=frac{t^2+t^3-1}{t^4} = frac{t^2}{t^4} + frac{t^3}{t^4} — frac{1}{t^4}$$

Then exponent laws say that if you are dividing with a common base, you subtract the exponents. So you get:

$$begin{align*}f(t)&= frac{t^2}{t^4} + frac{t^3}{t^4} — frac{1}{t^4} = t^{2-4} + t^{3-4} — t^{-4}\ &= t^{-2}+t^{-1}-t^{-4} \ end{align*}$$

Then differentiate with power rule (which you did correctly, you just took the derivative of the wrong function originally).

Содержание:

• Формула
• Примеры вычисления производной степенной функции

Формула

Производная степенной функции равна произведению показателя степени и основания в степени на единицу меньше.

Заметим, что в качестве степени 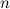может быть как
натуральное число,
то есть 1, 2, 3, …; так и любое отрицательное число: — 1, — 2 и т.д., а также и любое дробное, например, 2,34; — 4,1 или $frac{3}{4}$ , $-frac{5}{6}$ .

Заметим, что если аргумент у степенной функции есть сложная функция (то есть там стоит более сложное выражение, чем просто $x$, то производную нужно находить по следующей формуле:

$$left(u^{n}right)^{prime}=n u^{n-1} cdot u^{prime}$$

Примеры вычисления производной степенной функции

Читать дальше: производная обратной функции (1/x)’.