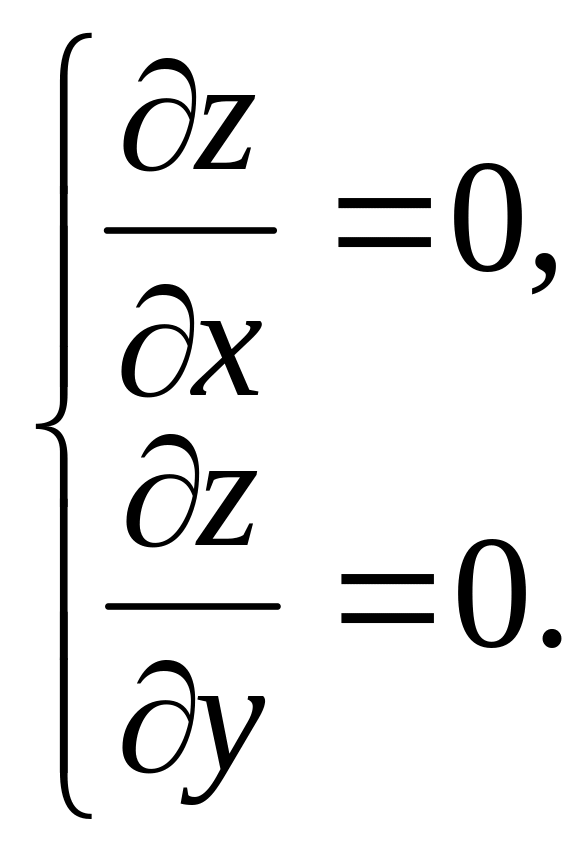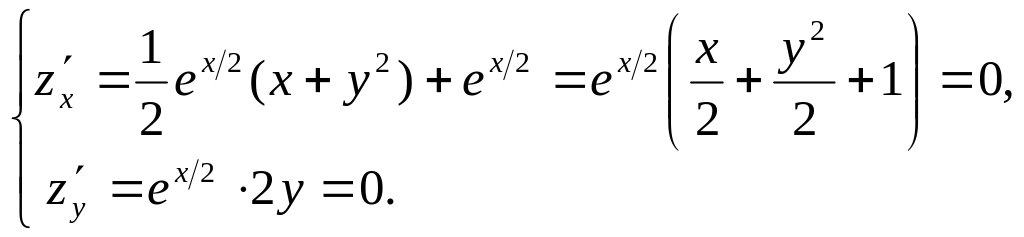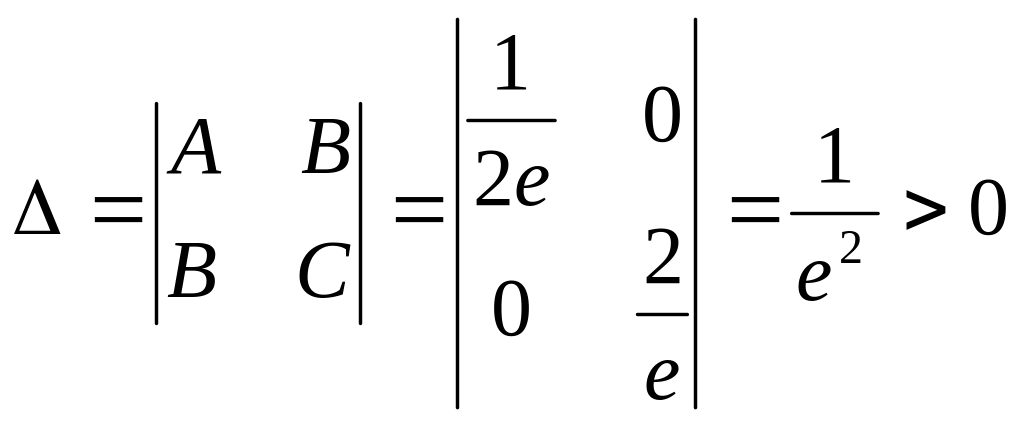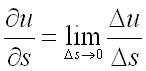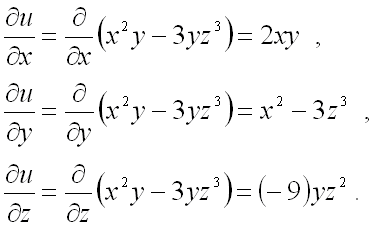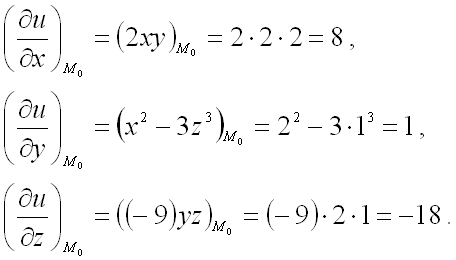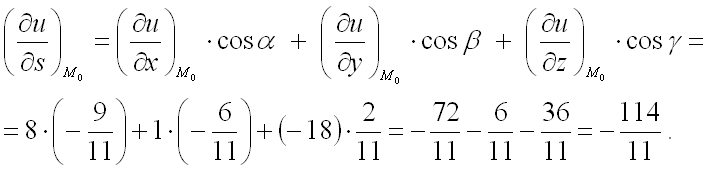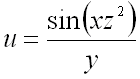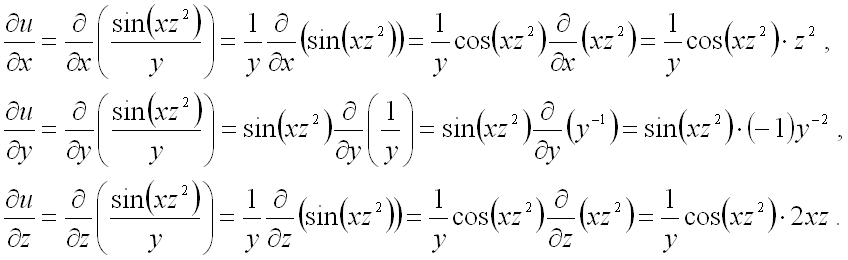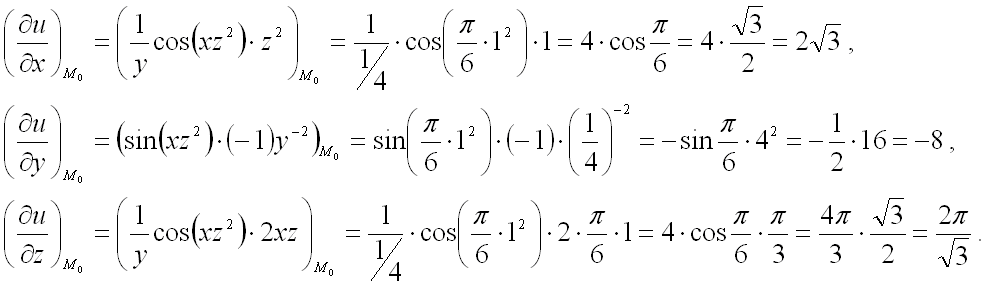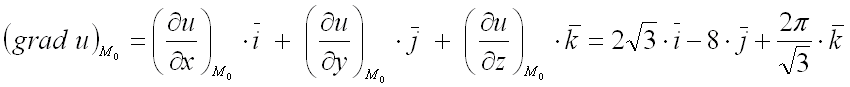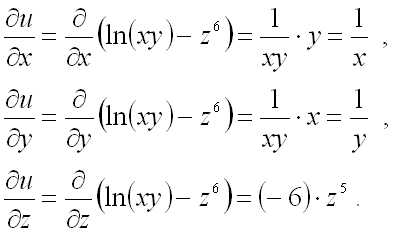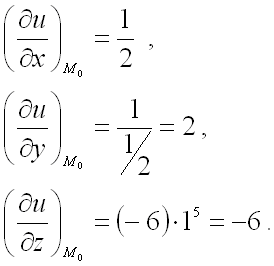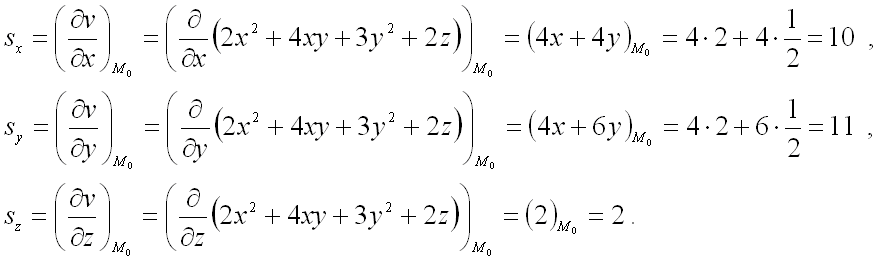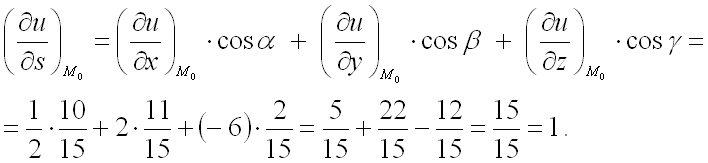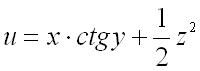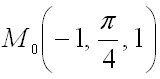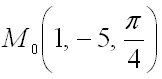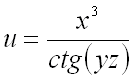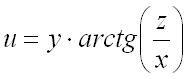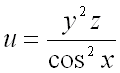Частные производные функции нескольких
переменных, по своему смыслу, характеризуют
скорость изменения функции по направлениям
осей координат. Вполне естественно
выяснить с какой скоростью изменяется
функция в данной точке
в фиксированном направлении, задаваемом
вектором
.
Ответ на этот вопрос дает понятие
производной в точке
по
направлению вектора
.
Опуская точное определение такой
производной, которая естественно
является пределом отношения приращения
функции к приращению аргумента,
вычисленному в заданном направлении,
приведем формулы для её вычисления.
Для дифференцируемой функции трех
переменных
,
производная в направлении вектора
:
,
где
— направляющие косинусы вектора
,
которые вычисляются по формулам
,
,
и являются координатами единичного
вектора
того же направления:
.
Для дифференцируемой функции двух
переменных
формулы аналогичны, только будет
отсутствовать третья координата.
Определение. Градиентом функции
называется
вектор
,
координаты которого равны соответственно
частным производным
и
в точке
,
то есть
.
Для функции трех переменных
имеем
.
Используя определение градиента,
формулы для вычисления производной по
направлению можно записать в виде
скалярного произведения двух векторов:
или
Из этих формул, с учетом определения
скалярного произведения,
,
следуют основные свойства градиента:
-
градиент
это вектор, направленный в сторону
максимального роста функции
,
то есть производная по направлению в
данной точке принимает максимальное
значение в направлении её градиента
в этой точке; -
модуль
градиента равен максимальной производной
по направлению. -
градиент
перпендикулярен линии (поверхности)
уровня функции;
Пример 1. Найти градиент функции
и
его модуль в точке
,
и вычислить производную по направлению
вектора
.
Решение.1)Вычисляем
.
Подставляя координаты точки
,
получим
.
Модуль, полученного вектора
.
2) Вычисляем единичный вектор заданного
направления
.
Производная по направлению равна
=
.
Пример 2. Найти вектор нормальный
к линиям уровня функции
.
Решение. Поскольку градиент функции
перпендикулярен линиям уровня этой
функции в произвольной точке, получим
,
значит, вектор
— нормальный вектор к линиям уровня
,
которые образовывают множество
параллельных прямых, перпендикулярных
вектору
.
7.7. Экстремум функции двух переменных
Определение. Точка
является точкой максимума (минимума)
функции
,
если существует окрестность этой точки
такая, что для всех точек
из
этой окрестности
(
).
Максимум или минимум, как и ранее,
называют экстремумом. Далее, в силу
простоты и наглядности, исследование
на экстремум проведем для функций двух
переменных
,
тем более, что идеи и последовательность
действий такие же, как и для функции
одной переменной.
Прежде всего, находим стационарные
точки, то есть точки в которых
обращаются в нуль обе частные производные
– необходимое условие экстремума,
то есть решаем систему уравнений:
Пусть, например, точка
является решением этой системы, то
есть – стационарная точка. Для
того, чтобы выяснить будет ли в этой
точке экстремум, используем следующие
достаточные условия существования
экстремума в стационарной точке.
1) Находим частные производные второго
порядка исследуемой функции и вычисляем
их значения в точке
,
обозначая:
;
;
.
2) Составим определитель
.
3) Если
,
то в точке
будет экстремум:
-
максимум,
если
-
минимум,
если
4) Если
,
то в точке
нет экстремума.
5) Если
,
то требуется дальнейшее исследование.
Пример. Исследовать на экстремум
функцию
Решение. 1) Ищем стационарные точки:
Из второго уравнения системы получим
,
подставляя это значение в первое
уравнение, после очевидных вычислений
имеем
.
Таким образом далее предстоит исследовать
единственную стационарную точку
.
2) Находим производные второго порядка
данной функции:
;
;
.
3) Вычисляем значения вторых производных
в стационарной точке:
;
;
.
4) Составляем определитель
,
т.к.
,
то в точке
есть экстремум, а так как
,
это минимум.
5) Находим
.
Замечание. Исследование на наибольшее
и наименьшее значение функции нескольких
переменных непрерывной в замкнутой
ограниченной области подобно исследованию
функции одной переменной на замкнутом
промежутке
.
Сначала ищутся критические точки внутри
области и вычисляются значения функции
в этих критических точках. Затем находят
наибольшее и наименьшее значения
функции на границе области. И в заключение,
из всех полученных значений выбирают
наибольшее и наименьшее, которые и
являются решением задачи.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть F(x,y,z)F(x,y,z) – функция трех переменных, (x,y,z)(x,y,z) – декартовы координаты.
Градиентом функции F(x,y,z)F(x,y,z) называется векторное поле
∇F(x,y,z)=∂F∂xi+∂F∂yj+∂F∂zk,
nabla F(x,y,z)=frac{partial F}{partial x}mathbf{i}+frac{partial F}{partial y}mathbf{j}+frac{partial F}{partial z}mathbf{k},
где ∂F∂xfrac{partial F}{partial x}, ∂F∂yfrac{partial F}{partial y} и ∂F∂zfrac{partial F}{partial z} – частные производные функции F(x,y,z)F(x,y,z), а imathbf{i}, jmathbf{j} и kmathbf{k} – базис декартовой системы координат (x,y,z)(x,y,z).
Иногда градиент обозначается так: gradF(x,y,z)operatorname{grad} F(x,y,z).
Градиент функции в данной точке показывает направление наибольшего роста функции.
Пример 1
Найти градиент функции F(x,y,z)=ln(x2+y2+z2)F(x,y,z)=ln(x^2+y^2+z^2) в точке M(1,2,3)M(1,2,3).
Вычислим частные производные:
∂F∂x=∂∂xln(x2+y2+z2)=2xx2+y2+z2,
frac{partial F}{partial x}=frac{partial }{partial x}ln(x^2+y^2+z^2)=frac{2x}{x^2+y^2+z^2},
∂F∂y=∂∂yln(x2+y2+z2)=2yx2+y2+z2,
frac{partial F}{partial y}=frac{partial }{partial y}ln(x^2+y^2+z^2)=frac{2y}{x^2+y^2+z^2},
∂F∂z=∂∂zln(x2+y2+z2)=2zx2+y2+z2.
frac{partial F}{partial z}=frac{partial }{partial z}ln(x^2+y^2+z^2)=frac{2z}{x^2+y^2+z^2}.
Градиент в точке M(1,2,3)M(1,2,3) (подставляем в формулы для частных производных значения x=1x=1, y=2y=2, z=3z=3):
∇F(M)=17 i+27 j+37 k=17 OM→.
nabla F(M)=frac{1}{7},,mathbf{i}+frac{2}{7},,mathbf{j}+frac{3}{7},,mathbf{k}=frac{1}{7},,overrightarrow{OM}.
Производная по направлению
Пусть FF – функция на плоскости или в пространстве.
Производной функции FF по направлению вектора amathbf{a} в точке MM называется число
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0,
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0},
если производная в правой части существует.
Пример 2
Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1).
Вычисляем значение функции в точке M+εaM+varepsilon mathbf{a} с координатами (−1+ε,−2ε,1+2ε)(-1+varepsilon,-2varepsilon,1+2varepsilon):
F(M+εa)=(−1+ε)2(−2ε)−(−2ε)2(1+2ε)+(1+2ε)2(−1+ε)=−6ε3−5ε−1.
Fleft(M+varepsilon mathbf{a}right)=(-1+varepsilon)^2(-2varepsilon)-(-2varepsilon)^2(1+2varepsilon)+(1+2varepsilon)^2(-1+varepsilon)=-6{varepsilon^{3}}-5varepsilon-1.
Длина вектора amathbf{a}:
∥a∥=a12+a22+a32=12+(−2)2+22=9=3.
|mathbf{a}|=sqrt{a_1^2+a_2^2+a_3^2}=sqrt{1^2+(-2)^2+2^2}=sqrt{9}=3.
Производная по направлению:
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0=13ddε(−6ε3−5ε−1)∣ε=0=−53
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=frac{1}{3}left.frac{d}{dvarepsilon}left(-6{varepsilon^{3}}-5varepsilon-1right)right|_{varepsilon=0}=-frac{5}{3}
Выражение производной по направлению через градиент
Используя формулу Тейлора для функций нескольких переменных, легко получить выражение производной по направлению через градиент. Действительно, из равенства
F(M+εa)=F(M)+ε(∇F(M),a)+o(ε2)Fleft(M+varepsilon mathbf{a}right)=F(M)+varepsilonleft(nabla F(M),mathbf{a}right)+oleft(varepsilon^2right)
следует, что
ddεF(M+εa)∣ε=0=(∇F(M),a).
left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=left(nabla F(M),mathbf{a}right).
Таким образом,
∂F∂a(M)=(∇F(M),a)∥a∥.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}.
Пример 2′2′
Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1) используя градиент.
Частные производные:
∂F∂x(M)=2xy+z2∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial x}(M)=left.2xy+z^2right|_{(x,y,z)=(-1,0,1)}=1,
∂F∂y(M)=x2−2yz∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial y}(M)=left.x^2-2yzright|_{(x,y,z)=(-1,0,1)}=1,
∂F∂z(M)=−y2+2zx∣(x,y,z)=(−1,0,1)=−2.
frac{partial F}{partial z}(M)=left.-y^2+2zxright|_{(x,y,z)=(-1,0,1)}=-2.
Градиент:
∇F(M)=i+j−2k.
nabla F(M)=mathbf{i}+mathbf{j}-2mathbf{k}.
Скалярное произведение:
(∇F(M),a)=(i+j−2k,i−2j+2k)=1−2−4=−5.
left(nabla F(M),mathbf{a}right)=left(mathbf{i}+mathbf{j}-2mathbf{k},mathbf{i}-2mathbf{j}+2mathbf{k}right)=1-2-4=-5.
Производная по направлению:
∂F∂a(M)=(∇F(M),a)∥a∥=−53.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}=-frac{5}{3}.
Тест по теме “Градиент функции. Производная по направлению”
Заказать задачи по любым предметам можно здесь от 10 минут
Производная функции по направлению
Как найти?
Постановка задачи
Найти производную функции $ u(x,y,z) $ в точке $ M (x_1,y_1,z_1) $ по направлению вектора $ overline{l} = (l_x,l_y,l_z) $
План решения
Если для функции $ u(x,y,z) $ существует производная в точке $ M(x_1,y_1,z_1) $, то значит в этой точке существует производная по любому направлению $ overline{l} $ и находится по формуле:
$$ frac{partial u}{partial l} = frac{partial u}{partial x} bigg |_M cdot cos alpha + frac{partial u}{partial y} bigg |_M cdot cos beta + frac{partial u}{partial z} bigg |_M cdot cos gamma $$
- Находим частные производные первого порядка:
$$ frac{partial u}{partial x}; frac{partial u}{partial y}; frac{partial u}{partial z} $$ - Вычисляем полученные производные в точке $ M(x_1,y_1,z_1) $:
$$ frac{partial u}{partial x} bigg |_{M(x_1,y_1,z_1)}; frac{partial u}{partial y} bigg |_{M(x_1,y_1,z_1)}; frac{partial u}{partial z} bigg |_{M(x_1,y_1,z_1)} $$ - Получаем направляющие косинусы по формулам:
$$ cos alpha = frac{l_x}{|overline{l}|}; cos beta = frac{l_y}{|overline{l}|}; cos gamma = frac{l_z}{|overline{l}|} $$ - Подставляем все полученные данные в формулу и записываем ответ
Примеры решений
| Пример 1 |
| Найти производную функции $ u = x+ln(z^2+y^2) $ в точке $ M (2,1,1) $ по направлению вектора $ overline{l} = (-2,1,-1) $ |
| Решение |
|
Находим частные производные первого порядка и вычисляем их начение в точке $ M $: $$ frac{partial u}{partial x} = 1; frac{partial u}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial u}{partial y} = frac{2y}{z^2+y^2}; frac{partial u}{partial y} bigg |_{M(2,1,1)}=1 $$ $$ frac{partial u}{partial z} = frac{2z}{z^2+y^2}; frac{partial u}{partial z} bigg |_{M(2,1,1)} = 1 $$ Вычисляем направляющие косинусы: $$ cos alpha = frac{-2}{sqrt{(-2)^2+1^2+(-1)^2}} = frac{-2}{sqrt{6}} $$ $$ cos beta = frac{1}{sqrt{(-2)^2+1^2+(-1)^2}} = frac{1}{sqrt{6}} $$ $$ cos gamma = frac{-1}{sqrt{(-2)^2+1^2+(-1)^2}} = — frac{1}{sqrt{6}} $$ Подставляем полученные частные производные в точке $ M $ и направляющие косинусы в формулу: $$ frac{partial u}{partial l} = 1 cdot (-frac{2}{sqrt{6}}) + 1 cdot frac{1}{sqrt{6}} + 1 cdot (-frac{1}{sqrt{6}}) = -frac{2}{sqrt{6}} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ frac{partial u}{partial l} = -frac{2}{sqrt{6}} $$ |
| Пример 2 |
| Найти производную $ u = xy — frac{x}{z} $ в точке $ M(-4,3,-1) $ по направлению вектора $ overline{l} = (5,1,-1) $ |
| Решение |
|
Берем частные производные первого порядка от функции в точке $ M(-4,3,-1) $: $$ frac{partial u}{partial x} = y — frac{1}{z}; frac{partial u}{partial x} bigg |_{M(-4,3,-1)} = 4 $$ $$ frac{partial u}{partial y} = x; frac{partial u}{partial y} bigg |_{M(-4,3,-1)} = -4 $$ $$ frac{partial u}{partial z} = frac{x}{z^2}; frac{partial u}{partial z} bigg |_{M(-4,3,-1)} = -4 $$ Вычисляем направляющие косинусы: $$ cos alpha = frac{5}{sqrt{5^2+1^2+(-1)^2}} = frac{5}{sqrt{27}} $$ $$ cos beta = frac{1}{sqrt{5^2+1^2+(-1)^2}} = frac{1}{sqrt{27}} $$ $$ cos gamma = frac{-1}{sqrt{5^2+1^2+(-1)^2}} = frac{-1}{sqrt{27}} $$ По формуле производной по направлению получаем ответ: $$ frac{partial u}{partial l} = 4 cdot frac{5}{sqrt{27}} + (-4) cdot frac{1}{sqrt{27}} + (-4) cdot frac{-1}{sqrt{27}} = frac{20}{sqrt{27}} $$ |
| Ответ |
| $$ frac{partial u}{partial l} = frac{20}{sqrt{27}} $$ |
Производная
по направлению. Градиент
Пусть в некоторой области
задана функция
и точка .
Проведем из точки
вектор ,
направляющие косинусы которого .
На векторе ,
на расстоянии
от его начала рассмотрим точку ,
т.е. 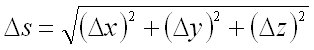
Будем предполагать, что функция
и ее частные производные первого порядка непрерывны в области .
Предел отношения
при называется
производной от функции
в точке по
направлению вектора
и обозначается ,
т.е.
.
Для нахождения производной от функции
в заданной точке по
направлению вектора
используют формулу: 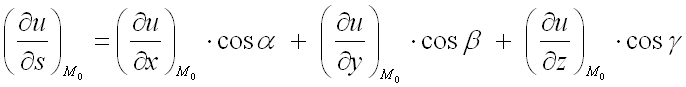
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
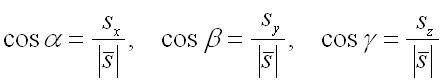
Пусть в каждой точке некоторой
области
задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных
этой функции в соответствующей точке, называется градиентом функции
и обозначается
или
(читается «набла у»): 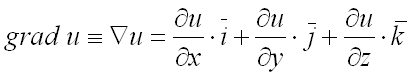
При этом говорят, что в области
определено векторное поле градиентов.
Для нахождения градиента функции
в заданной точке
используют формулу:
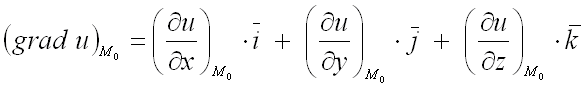
Свойства
градиента
1. Производная
в данной точке по направлению вектора
имеет наибольшее значение, если направление вектора
совпадает с направлением градиента. Это наибольшее значение производной равно
.
2. Производная
по направлению вектора, перпендикулярного к вектору ,
равна нулю.
Примеры
решения задач
Пример 1.
Найти производную от функции
в точке
по направлению вектора .
Решение.
Для решения задачи воспользуемся
формулой для нахождения производной от функции
в заданной точке
по направлению вектора :
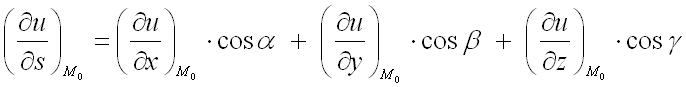
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
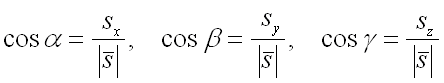
По условию задачи вектор
имеет координаты .
Тогда его длина равна:
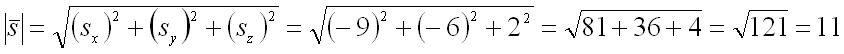
Следовательно, для направляющих косинусов вектора получим следующие значения:
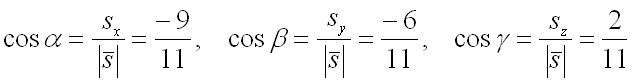
Далее для решения задачи необходимо найти все частные производные первого порядка
от функции :
Вычислим значения этих частных производных первого порядка в точке :
В заключении подставим полученные значения для направляющих косинусов вектора
и значения частных производных первого порядка от функции в
точке
в формулу для нахождения производной по направлению в заданной точке:
Ответ: производная от функции
в точке
по направлению вектора
равна 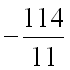
Пример 2.
Найти градиент функции
в точке 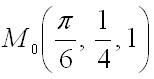
Решение.
Поскольку градиентом функции
называется вектор, проекциями которого на оси координат являются значения частных
производных этой функции в соответствующей точке, то для решения задачи сначала
найдем все частные производные первого порядка от заданной функции:
Далее вычислим значения этих частных производных первого порядка в точке 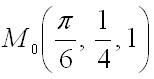
Подставим полученные значения в формулу градиента функции
в заданной точке :
.
Ответ: градиент функции
в точке
равен 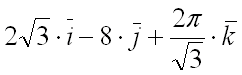
Пример 3.
Найти производную функции
в точке
по направлению градиента функции
в той же точке.
Решение.
Для нахождения производной
от функции
в заданной точке
по направлению вектора
используют формулу:
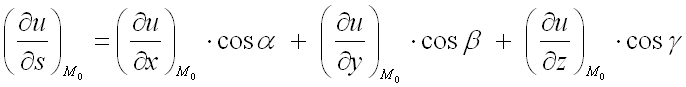
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
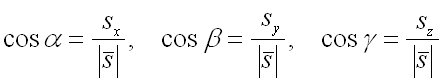
В данном случае вектор совпадает
с градиентом функции
в точке 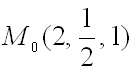
.
Следовательно, для решения задачи необходимо найти значения всех частных производных
первого порядка от функции
в точке ,
а также координаты и длину градиента функции
в той же точке.
Вычислим значения частных производных первого порядка от функции
в точке :
Для нахождения координат вектора ,
равного градиенту функции
в заданной точке ,
вычислим значения частных производных первого порядка от функции
в этой точке:
Длина вектора равна: 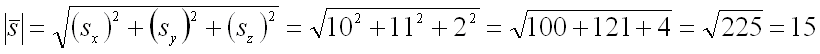
Найдем направляющие косинусы вектор по формулам:
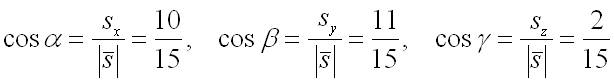
Подставим полученные значения в формулу для нахождения производной от функции
в заданной точке
по направлению вектора :
Ответ: производная функции
в точке 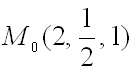
направлению градиента функции
в той же точке равна 1.
Задания
для самостоятельной работы
1.
Найти производную функции
в точке
по направлению вектора .
Ответ: .
2. Найти производную функции
в точке
по направлению вектора .
Ответ: .
3. Найти производную функции
в точке
по направлению вектора .
Ответ: .
4. Найти градиент функции
в точке 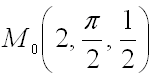
Ответ: .
5. Найти градиент функции
в точке .
Ответ: 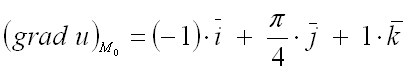
6. Найти градиент функции
в точке 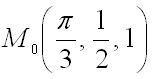
Ответ:
.