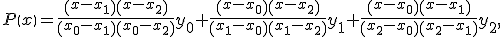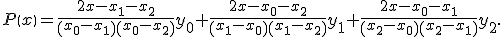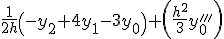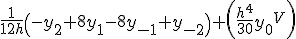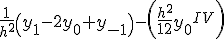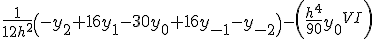Дифференцирование таблично заданной
функции
Один из широко применяемых методов дифференцирования таблично
заданной функции состоит в том, что по узловым (табличным) точкам
строится интерполяционный многочлен, а затем вычисляется производная
этого многочлена. Например, формулы численного дифференцирования могут
быть получены их интерполяционного многочлена Лагранжа. Для многочлена
второго порядка, построенного по трем точкам (xi,
yi), i = 0, 1, 2,
легко получить производную
Если это выражение вычислить при x=x0, то
получим значение производной по правым разностям, при x=x1
– по центральным разностям, а при x=x2
– по левым разностям.
Для того чтобы получить более точные значения производной используют
интерполяционные многочлены высоких порядков.
Расчетные формулы сильно упрощаются в случае, если шаг табулирования
функции постоянен (xi+1 – xi
= h = const).
В таблицах приведены наиболее часто используемые формулы вычисления
первой и второй производных таблично заданной функции. Приводятся также
значения погрешностей (главная часть) указанных формул.
Приближенные формулы дифференцирования правых разностей
| Производные | Вторые разности | Третьи разности |
|
|
|
|
|
|
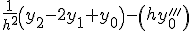 |
Приближенные формулы дифференцирования центральных разностей
| Производные | Третьи разности | Пятые разности |
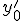 |
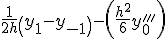 |
|
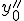 |
|
|
Приближенные формулы дифференцирования левых разностей
В общем случае вопросы численного дифференцирования имеют два аспекта. Во-первых, данную операцию приходится выполнять в тех случаях, когда информация об исследуемой функции задана в табличной форме или в виде набора результатов экспериментальных исследований. К численному дифференцированию прибегают также и в случае, когда задан явный аналитический вид функции, но выражение для производной оказывается достаточно сложным и желательно его заменить более простым. Во-вторых, своеобразное численное дифференцирование осуществляется при построении дискретного аналога обыкновенных дифференциальных уравнений или уравнений в частных производных, которые не могут быть решены аналитически вследствие нелинейности или сложной геометрии исследуемой области. Эти аспекты имеют в своей основе много общего, однако и различие между ними весьма существенно. В данной главе рассмотрим приближенное вычисление производных таблично заданной функции.
Таким образом, задача численного дифференцирования состоит в при-
ближенном вычислении значения производной функции y = f (x) в некото-
рой точке x* по заданным в конечном числе точек (узлах сетки) значениям этой функции yi = f (xi) .
4.1. Применение интерполяционных многочленов для численного дифференцирования
При численном дифференцировании функцию y = f (x) аппроксимируют легко вычисляемой функцией ϕ(x) и приближённо полагают
y(m) ≈ϕ(m)(x) . При этом можно использовать различные подходы. В ка-
честве аппроксимирующей функции обычно выбирают интерполяционный многочлен. Если узлы интеpполирования расположены неравномерно, то таким многочленом могут быть полиномы Лагранжа или Лежандра, а если равномерно, то лучше использовать полином Ньютона, так как он дает меньшую вычислительную погрешность по сравнению с другими. Сейчас мы рассмотрим простейший случай – аппроксимацию интерполяционным многочленом Ньютона, т.е.
f (m) (x) ≈ Nn(m) (x), 0 ≤ m ≤ n.
Вывод формул упрощается, если ввести вспомогательную переменную ξi = x −xi . Запишем этот многочлен и продифференцируем его почленно:
107

Nn (x) = y(x0 ) +ξ0 y(x0, x1) +ξ0ξ1y(x0, x1, x2 ) +ξ0ξξ1 2 y(x0, x1, x2, x3) +…,
|
N(1) |
(x) = y(x , x ) +(ξ +ξ )y(x , x , x ) +(ξ ξ +ξ ξ +ξξ )y(x , x , x , x ) +…, |
||||||||||||||||||
|
n |
0 |
1 |
0 |
1 |
0 |
1 |
2 |
0 |
1 |
0 |
2 |
1 |
2 |
0 |
1 |
2 |
3 |
||
|
N(2) |
(x) =2y(x , x , x ) +2(ξ +ξ +ξ )y(x , x , x , x ) +… |
||||||||||||||||||
|
n |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
3 |
Общая формула имеет, таким образом, вид:
|
, x1 |
k |
y(x0 , x1 ,K, xk +1 )+ |
(4.1) |
|||
|
Nn(k ) (x) = k ! y(x0 |
,K, xk ) + |
∑ξi |
||||
|
i=0 |
|
i=k +1 |
|||
|
+ |
∑ξi ξ j y(x0 |
, x1 ,K, xk +2 ) |
|
|
i > j≥0 |
|
i=k +2 |
||||
|
+ |
, x1,K, xk +3 ) |
|||
|
∑ξi ξ j ξl y(x0 |
||||
|
i > j >l≥0 |
+K .
Обрывая ряд на некотором числе слагаемых, получим приближённое выражение для соответствующей производной. Наиболее простые выражения соответствуют случаю, когда в формуле (4.1) оставляется только первое слагаемое:
|
y‘(x) ≈ y(x |
0 |
, x ) = |
y(x0 ) − y(x1 ) |
, |
|||||||||||
|
1 |
x0 − x1 |
||||||||||||||
|
1 |
1 |
||||||||||||||
|
y»(x) ≈ y(x0 , x1, x2 ) = |
y0 − y1 |
||||||||||||||
|
2 |
x |
0 |
− x |
2 |
x |
0 |
− x |
||||||||
|
1 |
|||||||||||||||
|
1 |
k |
k |
|||||||||||||
|
y(k ) (x) ≈ y(x0 , x1,K, xk ) = ∑y p ∏(x |
|||||||||||||||
|
k! |
|||||||||||||||
|
p=0 |
i=0 |
||||||||||||||
|
i≠p |
|
y1 |
− y2 |
|||
|
− |
||||
|
x1 |
− x2 |
, |
(4.2) |
|
p − xi )−1.
Заметим, что формулы (4.1) и (4.2) справедливы для произвольной неравномерной сетки.
Исследование точности полученных выражений при численных расчётах удобно делать при помощи апостериорной оценки, т.е. по скорости убывания слагаемых ряда (4.1). Если шаг сетки табличных значений достаточно мал, то погрешность близка к первому отброшенному слагаемому ряда.
Пусть мы используем узлы xi , i = 0,1,…n . Тогда первое отброшенное слагаемое содержит разделённую разность y(x0 , x1 ,K, xn+1 ) , которая согласно (4.2) примерно равна y(n + 1)/(n +1)!. Перед ней стоит сумма произведений различных множителей ξi ; каждое произведение содержит n + 1 – k множителей, а
вся сумма состоит из Сnk+1 слагаемых. Отсюда следует оценка погрешности формулы (4.1) с n + 1 узлами:
|
Rn(k ) ≤ |
M n+1 |
max |
ξi |
n+1−k , M n+1 = max |
y(n+1) |
(4.3) |
|||||
|
, |
|||||||||||
|
(n +1 − k)! 123 |
|||||||||||
|
i |
|||||||||||
|
108 |

[a,b]
[a,b]
В частности, если сетка равномерная, то max|ξi| < nh, откуда
|
Rn(k ) < M n+1 |
en |
n+1−k |
= O(hn+1−k ). |
||
|
h |
(4.4) |
||||
|
n +1 − k |
Эти оценки можно несколько улучшить за счёт более детального рассмотрения множителей ξi . Заметим, что строгое априорное исследование по-
грешности формулы (4.1) для произвольного расположения узлов приводит к той же оценке (4.3).
Таким образом, порядок точности формулы (4.1) по отношению к шагу сетки равен числу оставленных в ней слагаемых, или, что то же самое, он равен числу узлов интерполяции минус порядок производной. Поэтому минимальное число узлов, необходимое для вычисления k-той производной, равно k + 1; оно приводит к формулам (4.2) и обеспечивает первый порядок точности. Эти выводы соответствуют общему принципу: при почленном дифференцировании ряда скорость его сходимости уменьшается.
Если учесть ухудшение сходимости ряда при дифференцировании, то можно сделать вывод: даже если функция задана хорошо составленной таблицей на довольно подробной сетке, то практически численным дифференцированием можно хорошо определить первую и вторую производные, а третью и четвёртую – лишь удовлетворительно. Более высокие производные редко удаётся вычислить с приемлемой точностью.
4.2. Вывод простейших формул численного дифференцирования
Предположим, что функция f (x) определена и непрерывна на и обладает необходимой гладкостью (т.е. производные требуемого порядка у этой функции существуют). Рассмотрим равномерную сетку на отрезке
|
где h =b−a |
xi =a +ih , i= |
0,n |
, |
(4.5) |
|
— шаг сетки. |
||||
|
n |
Запишем интерполяционный многочлен Ньютона в начале таблицы, исполь-
зуя конечные разности ∆k y0 :
|
N |
(x)=y +∆y0 |
(x−x )+∆2y0 |
(x−x )(x−x )+K+ |
∆n y0 (x−x )(x−x )…(x−x |
) |
||||||
|
n |
0 |
h |
0 |
2!h2 |
0 |
1 |
n!hn |
0 |
1 |
n−1 |
|
Вывод формул упрощается, если ввести вспомогательную переменную
q=x−hx0 :
109

|
N (x |
+qh) = y |
+q∆y |
q(q−1) |
2 |
y |
q(q−1)…(q−n+1) |
n |
y |
||||||||||||||||||||||||||||||||||
|
+ |
∆ |
0 |
+…+ |
∆ |
0 |
(4.6) |
||||||||||||||||||||||||||||||||||||
|
2! |
n! |
|||||||||||||||||||||||||||||||||||||||||
|
n |
0 |
0 |
0 |
|||||||||||||||||||||||||||||||||||||||
|
Продифференцируем выражение (4.6) |
и получим конечноразностную фор- |
|||||||||||||||||||||||||||||||||||||||||
|
мулу численного дифференцирования: |
||||||||||||||||||||||||||||||||||||||||||
|
′ |
′ |
0 |
+qh) |
′ |
= |
1 |
0 |
0 |
+ |
q2 −q |
∆ |
2 |
0 |
+ |
q3 |
−3q2 |
+2q |
3 |
0 |
+ |
||||||||||||||||||||||
|
f (x) |
≈qx |
Nn(x |
h |
( y |
+q∆y |
2 |
y |
6 |
∆ |
y |
||||||||||||||||||||||||||||||||
|
q |
||||||||||||||||||||||||||||||||||||||||||
|
+ |
q4 −6q3 +11q2 −6q |
∆4 y0 +…)′q |
||||||||||||||||||||||||||||||||||||||||
|
т.е. |
24 |
|||||||||||||||||||||||||||||||||||||||||
|
′ |
1 |
0 |
+ |
2q−1 |
2 |
0 |
+ |
3q2 |
−6q+2 |
3 |
0 |
+ |
4q3 |
−18q2 +22q−6 |
4 |
0 |
+…) |
|||||||||||||||||||||||||
|
f (x) |
≈ h(∆y |
2 |
∆ |
y |
6 |
∆ |
y |
24 |
∆ |
y |
(4.7)
Дальнейшее дифференцирование приводит к приближенным формулам для вычисления второй и третьей производных:
|
1 |
2 |
3 |
∆4 y0 (6q2 −18q+11) |
||||||||||||||||||||||||
|
′′ |
|||||||||||||||||||||||||||
|
f |
(x) |
2 |
∆ y0 +∆ y0 (q−1)+ |
12 |
+… |
, |
|||||||||||||||||||||
|
h |
|||||||||||||||||||||||||||
|
f ′′′(x) ≈ |
1 |
3 |
y0+(q− |
3 |
4 |
y0 |
|||||||||||||||||||||
|
∆ |
2 |
)∆ |
+… . |
(4.8) |
|||||||||||||||||||||||
|
h |
3 |
||||||||||||||||||||||||||
|
Здесь учитывалось, что |
df ′(x) |
df ′(x) |
|||||||||||||||||||||||||
|
df ′(x) |
= |
dq |
= |
1 |
|||||||||||||||||||||||
|
dx |
dq |
dx |
h |
dq |
Аналогично можно определить и следующие производные функции f (x) . Но при вычислении производных более высоких порядков следует
учитывать большее количество членов ряда Ньютона для обеспечения точности результата. При использовании формул (4.7)-(4.8) для приближенного
вычисления производных в заданной точке x*, принадлежащей некоторой окрестности точки x0 , следует найти соответствующее значение q% пере-
менной q = x*h−x0 и подставить его в формулы.
Если производные функции f (x) надо определить в узлах интерполяции, т.е. x = xi , то тогда формулы (4.7)-(4.8) для первой и второй производных заметно упрощаются, так как в этом случае q ≡ 0 .
110
Простейшие формулы численного дифференцирования. Рассмотрим не-
сколько частных случаев интерполяционных многочленов степени n =1,2,3. На основе линейной интерполяции получим формулу
|
′ |
∆y0 |
0 |
1 |
(4.9) |
||||||||||||||
|
h |
||||||||||||||||||
|
f (x)≈ |
для x (x |
−δ,x +δ) , |
||||||||||||||||
|
на основе квадратичной интерполяции — |
||||||||||||||||||
|
′ |
1 |
0 |
+ |
2q−1 |
2 |
0 |
0 |
2 |
+δ) |
|||||||||
|
f |
(x) ≈ h(∆y |
2 |
∆ |
y )для |
(x |
−δ,x |
(4.10) |
|||||||||||
|
на основе кубической интерполяции: |
||||||||||||||||||
|
′ |
1 |
0 |
+ |
2q−1 |
2 |
0 |
+ |
3q2 −6q+2 |
3 |
0 |
0 |
3 |
+δ) (4.11) |
|||||
|
2 |
||||||||||||||||||
|
f (x) ≈ h |
(∆y |
∆ |
y |
6 |
∆ |
y ), для (x |
−δ,x |
и т.д. В дальнейшем особый интерес представляют частные случаи формул (4.9) – (4.11), связывающие приближенные значения производной функции
f ‘(x) в узлах x0,x1,x2,x3 с узловыми значениями самой функции. При n=1 из (4.9) получаем
|
′ |
0 |
0 |
= |
y1−y0 |
|||||||||||||||||||||||||||||||||||||
|
и |
f (x ) ≈ y‘ |
h |
(4.12) |
||||||||||||||||||||||||||||||||||||||
|
′ |
′1 |
y1−y0 |
|||||||||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||||||||||
|
f (x ) ≈ y |
= |
. |
(4.13) |
||||||||||||||||||||||||||||||||||||||
|
h |
|||||||||||||||||||||||||||||||||||||||||
|
Соотношение (4.12) называется правой разностной производной функции |
|||||||||||||||||||||||||||||||||||||||||
|
f (x) в точке x0 , а соотношение (4.13) — левой разностной производной |
|||||||||||||||||||||||||||||||||||||||||
|
функции f (x) в точке |
x1 . |
||||||||||||||||||||||||||||||||||||||||
|
При |
n=2 из (4.11) получаем три формулы: |
||||||||||||||||||||||||||||||||||||||||
|
1 |
(x |
0− |
− |
1 |
1 |
||||||||||||||||||||||||||||||||||||
|
′ |
′0 |
0 |
|||||||||||||||||||||||||||||||||||||||
|
0 |
= |
(y1 |
− y0 |
+ |
x ) 1 |
2 |
− |
1 |
0 |
1 |
0 |
− |
2 |
1 |
0 |
= |
|||||||||||||||||||||||||
|
f (x ) ≈ y |
h |
2 |
(y |
2y + y )) = |
y |
−y |
2 |
(y |
−2y |
+y ) |
|||||||||||||||||||||||||||||||
|
1 |
1 |
h |
|||||||||||||||||||||||||||||||||||||||
|
= |
(2y1−2y0−y2+2y1−y0 )= |
(−3y0+4y1−y2 ) , |
(4.14) |
||||||||||||||||||||||||||||||||||||||
|
2h |
x1−x0 |
2h |
|||||||||||||||||||||||||||||||||||||||
|
2 |
−1 |
||||||||||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||||||||||
|
′1 |
h |
||||||||||||||||||||||||||||||||||||||||
|
f (x )≈y |
= |
y |
−y |
+ |
( y |
−2y |
+y ) = |
||||||||||||||||||||||||||||||||||
|
′ |
1 |
1 |
0 |
2 |
1 |
0 |
|||||||||||||||||||||||||||||||||||
|
h |
2 |
||||||||||||||||||||||||||||||||||||||||
111
|
1 |
1 |
1 |
(2y1−2y0+y2−2y1+y0 )= |
1 |
(−y0 |
+y2 ) |
||||||||||||
|
= |
y1−y0+ |
( y2 |
−2y1+y0) = |
|||||||||||||||
|
2 |
2h |
2h |
||||||||||||||||
|
h |
(4.15) |
|||||||||||||||||
|
′ |
2 |
′2 |
= |
1 |
1 |
0 |
+ |
2(x2−x0)−1 |
2 |
1 |
0 |
|||||||
|
f (x )≈y |
y |
−y |
2 |
( y |
−2y |
+y ) = |
||||||||||||
|
h |
|
= |
1 |
(2y −2y0 +3y2 −6y1 +3y0) = = |
1 |
(y0+4y1+3y2). |
(4.16) |
|
|
2h |
1 |
2h |
||||
|
Соотношение (4.15) называется центральной разностной производной |
||||||
|
функции f (x) в точке |
x1 , т.к. для вычисления использует значения функ- |
|||||
|
ции в узлах слева и справа — y0 и y2 . |
||||||
|
При n=3 из (4.11) получаем четыре формулы для вычисления первой |
||||||
|
производной |
|
′ |
0 |
′0 |
= |
||||||||||||||||||||||||||||||||||||||||||
|
f (x )≈y |
|||||||||||||||||||||||||||||||||||||||||||||
|
2(x0−x0) −1 |
x0 |
−x0 2 |
x0−x0 |
||||||||||||||||||||||||||||||||||||||||||
|
3 |
−6 |
+2 |
|||||||||||||||||||||||||||||||||||||||||||
|
1 |
h |
h |
|||||||||||||||||||||||||||||||||||||||||||
|
h |
|||||||||||||||||||||||||||||||||||||||||||||
|
= |
y1−y0+ |
( y2−2y1+y0)+ |
( y3 |
−3y2 |
+3y1−y0) |
= |
|||||||||||||||||||||||||||||||||||||||
|
h |
2 |
6 |
|||||||||||||||||||||||||||||||||||||||||||
|
= |
1 |
1 |
( y2−2y1+y0)+ |
1 |
( y3−3y2 |
+3y1−y0) |
|||||||||||||||||||||||||||||||||||||||
|
h |
y1−y0− |
2 |
3 |
= |
|||||||||||||||||||||||||||||||||||||||||
|
= |
1 |
(6y1−6y0−3y2−6y1−3y0+2y3−6y2+6y1−2y0))= |
|||||||||||||||||||||||||||||||||||||||||||
|
6h |
+18y |
−9y |
+2y |
) |
|||||||||||||||||||||||||||||||||||||||||
|
=6h(−11y |
|||||||||||||||||||||||||||||||||||||||||||||
|
1 |
0 |
1 |
2 |
3 |
(4.17) |
||||||||||||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||||||||||||||
|
′ |
1 |
′1 |
= |
(−2y |
0 |
1 |
+6y |
2 |
3 |
) |
|||||||||||||||||||||||||||||||||||
|
6h |
|||||||||||||||||||||||||||||||||||||||||||||
|
f (x )≈y |
−3y |
−y |
|||||||||||||||||||||||||||||||||||||||||||
|
′ |
2 |
′2 |
1 |
0 |
1 |
2 |
3 |
) |
|||||||||||||||||||||||||||||||||||||
|
f (x )≈y |
=6h(y |
−6y |
+3y |
+2y |
|||||||||||||||||||||||||||||||||||||||||
|
′ |
′ |
= |
1 |
0 |
1 |
2 |
3 |
). |
|||||||||||||||||||||||||||||||||||||
|
f (x3) ≈ y |
3 |
6h |
(2y |
−9y |
+18y |
+−11y |
|||||||||||||||||||||||||||||||||||||||
112

Наиболее часто используется в приближениях простейшая аппроксимация
|
второй производной с помощью конечной разности второго порядка |
∆2 y0 |
|||||
|
h2 |
||||||
|
на промежутке (x0−δ,x2+δ) , получающаяся из (4.8) при n=2 . |
||||||
|
В частности, в точке x1 |
имеем приближенное равенство |
|||||
|
′′ |
1 |
′′1 |
y0−2y1+y2 |
|||
|
f (x )≈y |
= |
. |
(4.18) |
|||
|
h2 |
||||||
Эта формула вместе с формулами (4.12) — (4.17) широко используются при построении конечноразностных методов решения краевых задач для обыкновенных дифференциальных уравнений второго порядка.
Погрешность простейших формул численного дифференцирования.
При замене дифференциального выражения разностным возникает погрешность, выражение для которой нетрудно получить, используя формулу Тейлора:
f (x) = f (x0)+ f ′(x0)(x −x0)+12 f ′′(x0)(x−x0)2 +3!1 f ′′′(x0)(x−x0)3 +…rn (x)
Будем предполагать, что f (x) обладает дос-
таточной гладкостью для выведения оценок погрешности простейших формул численного дифференцирования.
Кроме того, будем использовать формулу Тейлора в i-ом узле сетки xi , т.е. считать, что исходная информация о функции соответствует рисунку и речь идет об аппроксимации производных в i-ом узле сетки (или в отстоящих от него на расстоянии h узлах xi −1 и xi +1 ).
Простейшая несимметричная (левая или правая) разностная производная.
Запишем представление функции f (x) по формулам Тейлора в окрестности точки xi :
|
′ |
i |
f |
′′ |
|||
|
f (x)= f (xi)+ |
f (x ) |
(x−xi)+ |
(ξ) |
(x−xi)2 |
||
|
1! |
2! |
|||||
|
′ |
||||||
|
i |
имеем: |
|||||
|
Выразив отсюда f (x ) , |
113
|
i |
f |
′′ |
||||
|
′ i |
f (x)− f (x ) |
− |
(ξ) |
i |
(4.19) |
|
|
(x−xi) |
2 |
|||||
|
f (x )= |
(x−x ) |
Первый член правой части – разностное отношение, аппроксимирующее производную вблизи xi , а второй – остаточный член, характеризующий точность такой аппроксимации.
Если зафиксировать в (4.19) x=xi −1 , то приходим к формуле левой разностной производной с остаточным членом:
|
′ i |
y |
−y |
f |
(ξ |
) |
||||
|
f (x )= |
i |
i −1 |
+ |
′′ |
i −1 |
h |
, |
(4.20) |
|
|
h |
2 |
где одновременно зафиксируется и неизвестная точка ξ=ξi −1 (xi −1, xi).
Аналогично при x = xi + 1 из (4.19) получаем формулу правой разностной производной с остаточным членом:
|
′ i |
y |
−y |
f |
(ξ |
) |
|||||||
|
f (x )= |
i +1 |
i |
− |
′′ |
i +1 |
h |
(4.21) |
|||||
|
h |
2 |
yi |
||||||||||
|
′ |
i |
yi +1− |
при i=0 узнаём выведенное |
|||||||||
|
В приближенном равенстве |
f (x )≈ |
|||||||||||
|
h |
ранее соотношение (4.12). Остаточные члены в (4.20) и (4.21) указывают на то, что, пользуясь аппроксимацией производной первого разностными производными
|
′ i |
yi −yi −1 |
и f |
′ i |
yi +1−yi |
||
|
h |
h |
|||||
|
f (x ) ≈ |
(x ) ≈ |
, |
мы совершаем ошибку O(h) , т.е. эти формулы численного дифференцирования имеют первый порядок точности.
Простейшая симметричная разностная производная. Запишем представ-
|
ление функции |
f (x) по формулам Тейлора в окрестности точки xi : |
|||||||||||||||||||
|
f (x)= f |
i |
′ |
i |
i |
1 |
′′ |
i |
i |
2 |
+ |
1 |
f |
′′′ |
i |
3 |
|||||
|
(x )+ f |
(x )(x−x )+ |
2 |
f (x )(x−x ) |
6 |
(ξ)(x−x ) |
|||||||||||||||
|
Из этого разложения при x=xi −1 и x=xi +1 получаем соответственно: |
||||||||||||||||||||
|
i +1 |
i |
′ |
i |
1 |
′′ |
i |
2 |
1 |
′′′ |
i +1 |
3 |
|||||||||
|
f (x )= f (x )+ f (x )h+ |
2 f |
(x )h |
+6 |
f (ξ |
)h |
и
114

f (xi −1)= f (xi)− f ′(xi)h+12 f ′′(xi)h2 −16 f ′′′(ξi −1)h3 .
Выполнив почленное вычитание этих равенств, получаем
yi +1−yi =2hf ′(xi)+h63 ( f ′′′(ξi +1)+ f ′′′(ξi −1)) ,
откуда с помощью теоремы о среднем, примененной к сумме третьих производных в квадратных скобках, приходим к формуле симметричной аппрок-
симации f ′(xi) с остаточным членом:
|
′ |
i |
yi +1−yi |
h2 |
′′′ |
i |
||||||
|
f |
2h |
− |
6 f |
) |
, |
(4.22) |
|||||
|
(x )= |
(ξ |
где ξi — некоторая точка из интервала (xi −1, xi +1) .
Эта формула означает, что аппроксимация первой производной функции симметричной разностной производной
f ′(xi)≈ yi +21h−yi
имеет второй порядок точности относительно шага h — O(h2) .
4.3. Некорректность операции численного дифференцирования
В формулах численного дифференцирования с постоянным шагом значения функции yi делятся на hm , где m – порядок вычисляемой производ-
ной. Поэтому при малом h неустранимые погрешности в значениях функции оказывают сильное влияние на результат численного дифференцирования. Поэтому операцию вычисления разностных отношений называют некорректной. Оказывается, что погрешность, возникающая при вычислении разностных отношений, намного превышает погрешность в задании значений
функции и даже может неограниченно возрастать при стремлении шага h сетки к нулю.
|
Пусть значения |
yi = f (xi ) |
заданы с погрешностью, т.е. вместо точного |
|
значения yi = f (xi ) |
% |
= yi +δi и граница абсолютной погрешно- |
|
имеем yi |
сти и функции в каждой точке удовлетворяет неравенству δi ≤ ∆. Если в
некоторой окрестности точки x0 производные, через которые выражаются
остаточные члены в формулах (4.20), (4.22), непрерывны и удовлетворяют неравенствам
115

|
f ′′′(x) |
≤ |
3, |
f (4)(x) |
≤ |
4 , |
(4.23) |
|||||
|
M |
M |
||||||||||
где M 3, M 4 — некоторые числа. Тогда полная погрешность формул
(4.20) — (4.22) (без учета погрешностей округления) не превосходит соответственно величин
|
∆ |
+ |
∆ |
h2 |
|||||||||||||||||||||||||||||||
|
ε |
= |
+ |
M 3 , |
|||||||||||||||||||||||||||||||
|
1 |
2h |
6 |
||||||||||||||||||||||||||||||||
|
∆ |
+ 2 |
∆ |
+ |
∆ |
h2 |
|||||||||||||||||||||||||||||
|
ε2 |
= |
+ |
M 4 |
|||||||||||||||||||||||||||||||
|
h2 |
12 |
|||||||||||||||||||||||||||||||||
|
Минимизация по h этих величин приводит к следующим значениям h: |
||||||||||||||||||||||||||||||||||
|
h |
3∆ |
13 |
, |
h |
3∆ |
14 |
, |
(4.24) |
||||||||||||||||||||||||||
|
= |
= 2 |
|||||||||||||||||||||||||||||||||
|
при этом |
1 |
M 3 |
2 |
M 4 |
||||||||||||||||||||||||||||||
|
13 |
||||||||||||||||||||||||||||||||||
|
ε1 |
= |
3 |
M 3∆−2 |
ε2 |
M 4 ∆ 12 |
. |
(4.25) |
|||||||||||||||||||||||||||
|
2 |
3 |
, |
= 2 |
3 |
||||||||||||||||||||||||||||||
|
Если при выбранном |
для какой-либо из формул (4.20) — (4.22) значении |
|||||||||||||||||||||||||||||||||
|
h отрезок [x− |
, x |
] |
не выходит за пределы окрестности точки |
x0 , в ко- |
||||||||||||||||||||||||||||||
|
1 |
1 |
торой выполняется соответствующее неравенство (4.23), то найденное h является оптимальным и полная погрешность численного дифференцирования оценивается соответствующей величиной (4.25).
116
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
Введение ……………………………………………………………………….3
Глава 1. Численные методы дифференцирования ………………………7
1.1. Понятие численного
дифференцирования ……………………………7
1.2. Двухточечный метод …………………….…………………………….
8 1.3. Трехточечный метод ………………………………………………… 10
1.4. Пятиточечный метод …………………………………………………
11
1.5. Методы численного
сглаживания и интерполяции функции ………14
Глава 2. Реализация численных методов…………………………………16
2.1. Модельная функция
(реализация методов в среде EXCEL) ……….16
2.2. Задача о нахождении
КОТР ………………………………………….23
Заключение ………………………………………………………………….30
Литература …………………………………………………………………..31
Введение
В настоящее время в отечественном образовании наблюдается
серьёзный спад качества математического образования [6]. Причём приходится
говорить не только об учащихся школ, но и о студентах – будущих специалистах,
обучающихся в вузах и колледжах и изучающих математику в качестве профильной
дисциплины [2, 7]. Несомненно, одной из причин данной ситуации послужил низкий
уровень познавательного интереса обучающихся, прежде всего, на школьном уровне,
где многие школьники причисляют себя к гуманитариям на основании неуспешности в
математике [15]. Формированием познавательного интереса к математике, в большей
степени, занимается учитель. Для формирования познавательного интереса к
математике (среди прочих средств) используется новизна материала, возможность
применить знания на практике, общение между учащимися и учителями, встречи
обучающихся со специалистами различных отраслей; совместная работа обучающихся
и учителей над исследовательскими проектами, требующими построения
математической модели исследуемого процесса или явления.
В современных науке и технике важную роль играет
математическое моделирование, заменяющее эксперименты с реальными объектами
экспериментами с их математическими моделями. Разумеется, получение точного
решения математической модели в виде конкретных функциональных соотношений
предпочтительнее, однако при решении практических задач далеко не всегда
удается найти аналитическое решение уравнений, составляющих математическую
модель явления. Поэтому приходится применять численные методы. Важным классом
прикладных задач являются оптимизационные задачи, в которых с использованием
численного дифференцирования требуется найти наибольшее (наименьшее) значение
целевой функции.
Численное решение прикладных задач составляет одну из
важнейших целей прикладной математики. Изучение соответствующих прикладных
разделов математики особенно важно при подготовке будущих инженерных и
исследовательских кадров для промышленно и технологически насыщенного
Уральского региона. Изучение этих разделов математики следует начинать на
посильном для школьников (7-9 класс) уровне гораздо раньше, чем они приступят к
изучению понятия производной и ее приложений в регулярном курсе «Алгебры и
начал анализа» (10 класс). Формирование предпонятий теории оптимизационных
задач можно осуществлять у мотивированных школьников в рамках внеклассной
учебноисследовательской и проектной деятельности.
Численное дифференцирование необходимо использовать тогда,
когда функция, подлежащая дифференцированию, представляет собой результаты
проведения экспериментов или наблюдений и не может быть найдена в явном виде
как аналитическая зависимость y = f(x). Например,
актуальная для городских служб управления движением задача о средней скорости
движения общественного автотранспорта по улицам города (в зависимости от
времени и локации) фактически может быть решена лишь численно путем наблюдения
за фактическими перемещениями некоторого количества машин разных маршрутов с
определением скорости v(t) путем численного дифференцирования
временной зависимости пройденного пути s(t): v = Δs/Δt.
Полученная зависимость v(t) позволит правильно выбрать
количество машин на городских маршрутах,
оптимизировать их количество, оптимизировать работу светофоров в течение дня,
улучшить схемы движения транспорта по городу и проч.
В качестве еще одного примера приведем весьма актуальную
для аэрокосмических и др. приложений задачу определения объемного коэффициента
теплового расширения (ОКТР) β(T) тел в широком диапазоне температур T.
Методы прямого измерения КТР с помощью дилатометров обычно охватывают область
низких и средних температур. В области же высоких температур по ослаблению
интенсивности проходящего через образец пучка γ-квантов, созданного
радиоактивным источником γизлучения, может быть непосредственно определена плотность тела ρ(T), а КТР
определяется затем путем численного дифференцирования как β(T) = (1/ρ)(dρ/dT).
С учетом сказанного, укажем объект и предмет исследования,
сформулируем цель и задачи исследования.
Объект исследования: Освоение элементов прикладной и
численной математики в основной общей школе.
Предмет исследования: Численное дифференцирование
таблично заданных функций и его приложения.
Цель исследования: Освоить методы численного
дифференцирования таблично заданных функций при решении практикоориентированных
задач в рамках учебно-исследовательской и проектной деятельности наиболее подготовленных
и мотивированных школьников 7-9 классов основной общей школы.
Задачи исследования:
1) Провести
литературный обзор существующих методов численного дифференцирования таблично
(не аналитически) заданных функций и особенностей современной реализации этих
методов.
2) Выбрать
наиболее оптимальные, с точки зрения возможности применения в школьной образовательной
практике, методы численного дифференцирования таблично заданных функций, и
разработать реализацию данных методов в среде MS Excel.
3) Провести
численные эксперименты для определения устойчивости методов численного
дифференцирования к случайным погрешностям значений таблично заданных функций.
4) Провести
выборочную апробацию избранных методов численного дифференцирования для решения
практикоориентированных задач (на примере
определения объемного коэффициента теплового расширения β(T) свинца по
табличным данным по температурной зависимости его молярного объема V(T)
от T = 0 вплоть до точки плавления металла). Предварительно провести
литературный поиск данных экспериментов по измерению молярного объема V(T)
свинца.
Глава 1. Численные методы дифференцирования
1.1. Понятие численного дифференцирования
В «Численных методах» А.В. Зенкова понятие численные методы
раскрывается следующим образом: «численные методы (вычислительные методы,
методы вычислений) – раздел вычислительной математики, изучающий приближенные
способы решения типовых математических задач, которые либо не решаются, либо
трудно решаются точными аналитическими методами» [10, c. 4].
При задании функции аналитически, производную функции можно
найти с помощью таблиц производных – как композицию простейших функций.
Существуют, однако, достаточно много ситуаций, когда функцию невозможно
представить в явном виде – например, когда функция – это результат некого
исследования, или опроса, и задана в виде таблицы (т.е. «неизвестна явная связь
между аргументом х и значением у, и невозможно записать эту связь
в виде некоторой зависимости у = f(x)» [22, c. 31]). При
данном способе задания функции также
существуют способы найти производную, однако расчеты будут неизбежно содержать
погрешность, так как функция f(x) точно не известна.
В «Введении в численные методы» А.А. Самарского говорится,
что «численные методы дают приближённое решение задачи. Это значит, что вместо
точного решения u (функции или функционала) некоторой задачи мы находим
решение y другой задачи, близкое в некотором смысле к искомому». [20, с.
16].
К методам численного дифференцирования таблично заданной
функции относятся: дифференцирование интерполяционных формул (Ньютона,
Лагранжа, Бесселя и т.д.), графическое дифференцирование, разностные методы.
Говоря о разностных методах, которые и рассматриваются в данной работе (в силу
своей относительной простоты), важно отметить, что построение формулы зависит
от количества используемых узлов. Так можно построить формулу для двух, трех,
четырех и более узлов.
Решение многих практикориентированных задач невозможно без
применения численных методов, поскольку математические модели реальных
процессов или явлений оказываются слишком сложными для получения аналитического
решения (что предпочтительно) [3, 4, 8, 10, 12– 14, 16–20, 22, 23].
1.2. Двухточечные методы
В данной работе будем использовать методы численного
дифференцирования, применяемые для равноотстоящих узлов (хотя существуют
методы дифференцирования и для неравноотстоящих узлов), по причине их большей
универсальности и относительной простоты применения, что более приемлемо для
школьников. В данной работе будем рассматривать только получение первой
производной таблично заданной функции f(x), что наиболее
востребовано на практике. Вторая производная, если необходимо, может быть
вычислена как производная первой производной таблично заданной функции.
Производной функции y = f(x) называется
предел отношения приращения функции ∆yк приращению аргумента ∆x при
стремлении ∆x к нулю:
y,
∆y = f (x + ∆x) – f (x).
(1)
Чем меньше приращение аргумента, тем точнее численное
значение производной (при прочих равных условиях).
Производная аналитически заданной функции легко вычисляется
с помощью таблицы производных, но когда функция задана таблицей, аналитическое
дифференцирование невозможно. Тогда прибегают к выр.
(1).
Далее фиксируют шаг ∆x, равный некоторому малому
конечному числу и получают приближённое равенство [3, c. 364]:
y.
(2).
Формула (2) называется аппроксимацией (приближением)
производной с помощью отношений конечных разностей [3, c. 366].
Предположим, что функция f(х) дифференцируема
в окрестности точки х достаточное количество раз. Используя классическое
определение производной, f′(x) = , получаем две
простейшие приближенные
формулы численного
дифференцирования:
(метод
1)
(метод
2)
где h – малый
параметр (шаг дифференцирования).
Эти формулы называются двухточечными формулами численного
дифференцирования с правой (разность вперед) и левой разностными производными
(разность назад).
Оценка погрешностей данных формул производится по следующей
формуле [3, стр. 365]:
,
где
,
и где либо 𝜉
– точка, принадлежащая промежутку , либо 𝜉
– точка, принадлежащая промежутку . Выбор
формулы зависит от того, по каким краям
отрезков, при разбиении, удобно принимать значения 𝑓(𝑥𝑖).
В двухточечном методе используются
значения функции в двух узлах. Формула «разность вперед» может быть
использована в начале таблицы, а формула «разность назад», – в конце таблицы.
Данные формулы применимы и в других узлах (а не только в начальном и конечном),
но для вычисления производных в них существуют более точные методы.
1.3. Трехточечный метод
Рассмотрим еще один метод численного дифференцирования,
когда берутся значения таблично заданной функции на трех точках сетки [3, 4, 8,
10, 18, 20].
Метод 3 (шаг в обе
стороны)
При этом всегда существует
такое с = с(х) ∈
[a; b], что
y Еусеч(f, h),
где индекс «усеч» указывает на ошибку
усечения. Член Еусеч(f, h)
называется ошибкой усечения [18, стр.347]:
Еусеч
Рис. 1 отражает смысл описанных методов
численного
дифференцирования. Значение тангенса угла , образованного
касательной к графику y(x) и осью абсцисс, показывает точное
значение производной – это вытекает из геометрического смысла производной.
Тангенсы углов 1,
2,
3
соответствуют приближенным значениям производных, определенными методами 1, 2,
3.

Рис. 1 Геометрическая интерпретация двух- и трёхточечных методов
численного дифференцирования.
Формулу для метода 3 также называют центральной разностной
производной.
Для оценки погрешности в производной, найденной по методу
3, используют следующую формулу [3, стр.366]:
,
где
.
«Центральная разность» может быть использована для
вычисления производной в точке, слева и справа от которой есть узлы с
фиксированным шагом. Соответственно данный метод можно использовать во второй и
предпоследней точке таблицы. Для центральных точек есть более точный метод.
1.4. Пятиточечный метод
Формула для вычисления производной по пяти точкам (два шага
назад и два шага вперед) [3, cтр.367]:
.
При этом всегда существует
такое с = с(х) ∈
[a; b], что
y Еусеч(f, h),
где
Еусеч.
Для оценки погрешности в производной, найденной по
пятиточечному методу, можно использовать следующую формулу:
,
где
.

𝛼
x-2h
x-h x x+h x+2h X
Рис. 2 Геометрическая интерпретация
пятиточечного метода численного дифференцирования
Рис. 2 отражает смысл пятиточечного метода численного
дифференцирования. Тангенс угла 4
соответствует приближенному значению производной, определенной методом по пяти
точкам. В практической части настоящей работы убедимся, что данный метод –
наиболее точный из приведенных выше.
Назначение многоточечных методов заключается в том, чтобы
повысить точность численного дифференцирования в данной точке, нивелируя,
насколько возможно, колебания функции, обусловленные её случайными
экспериментальными погрешностями.
Погрешность аппроксимации (ошибка усечения) с уменьшением
шага h, как правило, также уменьшается. Но существуют и другие источники
погрешности, такие как неточные значения yi в узлах и
погрешности, получившиеся при округлении результатов вычисления. Погрешности,
обусловленные указанными источниками, наоборот возрастают при уменьшении шага.
Поэтому «суммарная погрешность численного дифференцирования может убывать при
уменьшении шага лишь до некоторого предельного значения, после чего дальнейшее
уменьшение шага не повысит точности результатов» [22]. Потерю точности можно
минимизировать с помощью процедуры регуляризации. Один из способов – это
предварительное сглаживание табличных значений функции (данный способ будет
описан и применен ниже).
Чтобы получить аппроксимацию производных n-го
порядка точности, необходимо использовать значения функции в n+1 узле.
Поэтому при росте порядка точности растет количество используемых в формуле
узлов.
Как будет видно из результатов
практической части работы, погрешность численного дифференцирования быстро
возрастает с ростом случайных погрешностей дифференцируемой таблично заданной
функции даже при использовании многоточечных формул дифференцирования. Поэтому
перед процедурой собственно численного дифференцирования нередко приходится
прибегать к процедуре численного сглаживания таблично заданной функции, а также
к интерполяционным процедурам для получения равноотстоящих по аргументу
значений функции f(xi). Краткое описание этих
процедур приведено в следующем параграфе.
1.5
Методы численного сглаживания и интерполяции функции.
Значения функции в таблице, полученной в результате
вычислений или измерений, как правило, содержат случайные ошибки. Процедура
численного сглаживания позволяет «сгладить» значения исходной функции в узлах
сетки. Предварительное сглаживание позволяет существенно уменьшить случайные
ошибки при выполнении численного дифференцирования таблично заданной функции.
Пусть получена таблица значений функции f(t)
в равноотстоящих узлах t0, t1, … . Для
сглаживания данной функции строится аппроксимирующая функция F(t).
Как правило, в качестве F(t) выбирается среднеквадратичное
наилучшее приближение функции f(t). Например, если функция F(t)
строится по пяти соседним значениям исходной функции f(t) с
помощью полиномов Pj,4(t) (j = 0,
1, 2, 3, 4), то сглаженные значения F(tj) =
Fj для
пятерки узлов tj, j = 0, 1, 2, 3, 4, возможно найти с помощью
формул
[1]:
F),
F,
F,
F),
F.
Для проведения вышеуказанной процедуры
необходимо, чтобы узлы были равноотстоящие. Но обычно в ходе эксперимента
расстояние между полученными узлами может быть не одинаковым. Тогда сначала
следует прибегнуть к процедуре интерполяции, которая дает возможность получить
промежуточные значения, а затем провести сглаживание функции уже для
равноотстоящих узлов.
Пусть получена таблица экспериментальных
данных функции y(x)
(табл. 1):
Таблица 1 Вид
таблицы экспериментальных данных
|
x0 |
x1 |
x2 |
… |
xn—1 |
xn |
|
y0 |
y1 |
y2 |
… |
yn-1 |
yn |
Чтобы получить какое-либо промежуточное значение аргумента xi,
не совпадающее ни с одним из значений в табл. 1, но при этом принадлежащее
интервалу [x0, …, xn], применяется тот или
иной метод интерполяции функции [1, 4, 8, 10, 13, 20].
Простейший и часто используемый вид интерполяции – это
линейная интерполяция. Она состоит в том, что заданные точки с координатами xi,
yi (i = 0, 1, 2, …, n) соединяются
прямолинейными отрезками, а функцию y(x) можно приближенно
представить в виде ломаной. Уравнения каждого отрезка ломаной всегда разные. В
частности, для i-го интервала уравнение прямой, проходящей через точки (xi,
yi) и (xi+1, yi+1), можно записать
в виде
.
Отсюда y = ai x + bi, xi
≤ x ≤ xi+1.
ai
,
bi = yi – ai xi.
(3)
С помощью формул (3) находят приближенное
значение функции в точке из интервала [x0, …, xn].
Глава 2. Реализация численных методов
2.1. Модельная функция
(реализация методов в среде EXCEL)
Для демонстрации методов численного дифференцирования будем
использовать двух-, трёх- и пятиточечные методы. Для проведения модельных
расчетов используем пакет MS Excel, который не требует
дополнительной установки и
присутствует, как правило, на каждом ПК.
Согласно [17] погрешность метода аппроксимации функции f(x)
можно оценивать по величине среднеквадратичного (стандартного) отклонения (СКО)
расчетных значений функции fрасч(xi) от
точных fточн(xi) в каждой табличной точке xi,
– когда точные значения fточн(xi) известны
(при проведении модельных численных экспериментов). СКО является мерой
рассеяния расчетных значений функции и определяется выражением:
S , (4)
где n – число «расчетных» узлов xi.
Чем меньше СКО S, тем качественнее приближение.
В качестве модельной функции выберем функцию y = sin
x на промежутке 0 ≤ x ≤ 3,1 ~𝜋
с шагом h = 0,1 (всего 32 значения). Вычислим её
точную производную (для сравнения со
значениями, полученными численным дифференцированием разными методами). Как
известно, точное значение производной y′(х) = cos x.
В табл. 2 для модельной функции y = sin
x проведем вычисление ее производной, точное и используя 2-х, 3-х
и 5-ти точечные методы численного дифференцирования, – в узлах xi
(i = 0; 0,1; 0,2; …; 3; 3,1).
В столбце D вычислим точное значение производной.
Для этого введем в ячейку D2 команду =COS(B2) и скопируем
данную формулу до ячейки D33 (включительно).
В столбце Е вычислим производную численным методом
по двум точкам. Для этого введем в ячейку E2 команду =(C3-C2)/0,1,
соответствующую формуле правой разности, и скопируем её до Е17
(включительно), таким образом получив значения производных в шестнадцати первых
узлах. В Е18 вставим команду =(C18-C17)/0,1,
соответствующую формуле левой разности, и скопируем её до Е33, получив
при этом значения производных в остальных шестнадцати узлах.
В столбwе F вычислим производную численным методом
по трем точкам. Для этого введем в ячейку F3 команду =(C4–C2)*(2*0,1)
и скопируем данную формулу до F32.
В столбце G вычислим производную численным методом
по пяти точкам. Для этого введем в ячейку I4 команду = (C2 – 8*C3
+ 8*C5 – C6)/(12*0,1) и скопируем данную формулу до I31.
Таблица 2
Сравнение численных методов
дифференцирования функции y = sin x. Столбец A – порядковый
номер; столбец B – значения xi; столбец С – значение yi = sin(xi), столбец D
– точное значение производной yi′
= cos(xi) в узле xi; столбец E – значение производной, вычисленное
по двум точкам; столбец F – значение производной, вычисленное по трем
точкам; столбец G – значение производной, вычисленное по пяти точкам.
|
A |
B |
C |
D |
E |
F |
G |
|
№ п/п |
xi |
yi = sin(xi) |
yi′ = cos(xi) |
2-х точечн. |
3-х точечн. |
5-ти точечн. |
|
1 |
0 |
0 |
1 |
0,998 |
||
|
2 |
0,1 |
0,100 |
0,995 |
0,988 |
0,993 |
|
|
3 |
0,2 |
0,199 |
0,980 |
0,969 |
0,978 |
0,980 |
|
4 |
0,3 |
0,296 |
0,955 |
0,939 |
0,954 |
0,955 |
|
5 |
0,4 |
0,389 |
0,921 |
0,900 |
0,920 |
0,921 |
|
6 |
0,5 |
0,479 |
0,878 |
0,852 |
0,876 |
0,878 |
|
7 |
0,6 |
0,565 |
0,825 |
0,796 |
0,824 |
0,825 |
|
8 |
0,7 |
0,644 |
0,765 |
0,731 |
0,764 |
0,765 |
Продолжение таблицы 2
|
9 |
0,8 |
0,717 |
0,697 |
0,660 |
0,696 |
0,697 |
|
10 |
0,9 |
0,783 |
0,622 |
0,581 |
0,621 |
0,622 |
|
11 |
1 |
0,841 |
0,540 |
0,497 |
0,539 |
0,540 |
|
12 |
1,1 |
0,891 |
0,454 |
0,408 |
0,453 |
0,454 |
|
13 |
1,2 |
0,932 |
0,362 |
0,315 |
0,362 |
0,362 |
|
14 |
1,3 |
0,964 |
0,267 |
0,219 |
0,267 |
0,267 |
|
15 |
1,4 |
0,985 |
0,170 |
0,120 |
0,170 |
0,170 |
|
16 |
1,5 |
0,997 |
0,071 |
0,021 |
0,071 |
0,071 |
|
17 |
1,6 |
1,000 |
-0,029 |
0,021 |
-0,029 |
-0,029 |
|
18 |
1,7 |
0,992 |
-0,129 |
-0,079 |
-0,129 |
-0,129 |
|
19 |
1,8 |
0,974 |
-0,227 |
-0,178 |
-0,227 |
-0,227 |
|
20 |
1,9 |
0,946 |
-0,323 |
-0,275 |
-0,323 |
-0,323 |
|
21 |
2 |
0,909 |
-0,416 |
-0,370 |
-0,415 |
-0,416 |
|
22 |
2,1 |
0,863 |
-0,505 |
-0,461 |
-0,504 |
-0,505 |
|
23 |
2,2 |
0,808 |
-0,589 |
-0,547 |
-0,588 |
-0,588 |
|
24 |
2,3 |
0,746 |
-0,666 |
-0,628 |
-0,665 |
-0,666 |
|
25 |
2,4 |
0,675 |
-0,737 |
-0,702 |
-0,736 |
-0,737 |
|
26 |
2,5 |
0,598 |
-0,801 |
-0,770 |
-0,800 |
-0,801 |
|
27 |
2,6 |
0,516 |
-0,857 |
-0,830 |
-0,855 |
-0,857 |
|
28 |
2,7 |
0,427 |
-0,904 |
-0,881 |
-0,903 |
-0,904 |
|
29 |
2,8 |
0,335 |
-0,942 |
-0,924 |
-0,941 |
-0,942 |
|
30 |
2,9 |
0,239 |
-0,971 |
-0,957 |
-0,969 |
-0,971 |
|
31 |
3 |
0,141 |
-0,990 |
-0,981 |
-0,988 |
|
|
32 |
3,1 |
0,042 |
-0,999 |
-0,995 |
||
|
СКО |
22,832103 |
0,73103 |
0,00008103 |
Среднее СКО для двухточечного метода составило 22,832103, но не
превосходило 35,345103.
Среднее СКО для трехточечного метода составило 0,73103, но не превосходило 1,172103.
Среднее СКО для трехточечного метода составило 0,00008103, но не превосходило 0,00231103. Далее
и будем использовать пятиточечный метод.
Покажем, как изменяется значение производной при
искусственно введённой погрешности. Добавим с помощью случайной функции СЛЧИС()
MS Excel к каждому точному
значению yi(xi) возмущение
δyi = 0,04*(2*СЛЧИС()-1).
(5)
Очевидно, в каждом узле xi
погрешности δyi принимают случайные значения из промежутка
[–0,04; +0,04]. Результат вычислений возмущенных значений функции yi
+ δyi представлен в столбце D табл. 3. В столбце Е
показано вычисление производной (численным методом дифференцирования по пяти
точкам) функции yi + δyi с искусственно
введенной погрешностью. В столбце F вычислены сглаженные значения
возмущенной функции из столбца Е с помощью формул, представленных в п.
1.5. В столбце G вычислена производная возмущенной и затем сглаженной
функции. Наконец, столбец Н показывает для сравнения точное значение
производной yi′ = cos(xi).
Таблица 3
Значения модельной функции y =
sin x с искусственно введенной случайной ошибкой и ее
производная (5-ти точечная схема численного дифференцирования). Столбец A
– номер по порядку; столбец B – значения xi; столбец C – точные значения функции yi = sin(xi); столбец D – возмущенные значения yi = sin(xi) + δyi функции
со случайной ошибкой δyi;
столбец E – производная функции yi = sin(xi) + δyi
с введенной ошибкой (до сглаживания); столбец F – сглаженная возмущенная
функция yi = sin(xi) + δyi;
столбец G – производная возмущенной и сглаженной функции yi = sin(xi) + δyi;
столбец H – точное значение производной модельной функции yi′ = cos(xi).
|
A |
B |
C |
D |
E |
F |
G |
H |
|
№ п/п |
xi |
yi = sin(xi) |
yi |
пр-я ф-ции yi + δyi |
yi + δyi сглаж. |
пр-я сглаж. ф-ции yi + δyi. |
yi′ = cos(xi) |
|
1 |
0 |
0 |
0,003 |
— |
— |
— |
1,000 |
|
2 |
0,1 |
0,100 |
0,129 |
— |
— |
— |
0,995 |
|
3 |
0,2 |
0,199 |
0,177 |
0,969 |
0,207 |
0,938 |
0,980 |
|
4 |
0,3 |
0,296 |
0,324 |
1,171 |
0,301 |
1,054 |
0,957 |
|
5 |
0,4 |
0,389 |
0,400 |
0,884 |
0,414 |
1,033 |
0,921 |
|
6 |
0,5 |
0,479 |
0,508 |
0,987 |
0,503 |
0,822 |
0,878 |
|
7 |
0,6 |
0,565 |
0,588 |
0,618 |
0,583 |
0,791 |
0,825 |
|
8 |
0,7 |
0,644 |
0,644 |
0,837 |
0,661 |
0,740 |
0,765 |
|
9 |
0,8 |
0,717 |
0,747 |
0,681 |
0,729 |
0,616 |
0,697 |
|
10 |
0,9 |
0,783 |
0,776 |
0,317 |
0,784 |
0,476 |
0,622 |
|
11 |
1 |
0,841 |
0,827 |
0,669 |
0,831 |
0,646 |
0,540 |
|
12 |
1,1 |
0,891 |
0,904 |
0,808 |
0,908 |
0,612 |
0,454 |
|
13 |
1,2 |
0,932 |
0,968 |
0,068 |
0,945 |
0,233 |
0,362 |
|
14 |
1,3 |
0,964 |
0,935 |
0,074 |
0,962 |
0,183 |
0,267 |
Продолжение таблицы 3
|
15 |
1,4 |
0,985 |
0,993 |
0,522 |
0,984 |
0,216 |
0,170 |
|
16 |
1,5 |
0,997 |
1,015 |
-0,154 |
1,002 |
0,093 |
0,071 |
|
17 |
1,6 |
1,000 |
0,981 |
0,048 |
1,004 |
0,063 |
-0,029 |
|
18 |
1,7 |
0,992 |
1,024 |
0,249 |
1,013 |
-0,008 |
-0,129 |
|
19 |
1,8 |
0,974 |
1,007 |
-0,601 |
0,995 |
-0,369 |
-0,227 |
|
20 |
1,9 |
0,946 |
0,924 |
-0,549 |
0,943 |
-0,548 |
-0,323 |
|
21 |
2 |
0,909 |
0,902 |
-0,343 |
0,892 |
-0,524 |
-0,416 |
|
22 |
2,1 |
0,863 |
0,843 |
-0,740 |
0,839 |
-0,525 |
-0,505 |
|
23 |
2,2 |
0,808 |
0,770 |
-0,388 |
0,787 |
-0,472 |
-0,589 |
|
24 |
2,3 |
0,746 |
0,756 |
-0,434 |
0,740 |
-0,590 |
-0,666 |
|
25 |
2,4 |
0,675 |
0,671 |
-1,043 |
0,668 |
-0,775 |
-0,737 |
|
26 |
2,5 |
0,598 |
0,572 |
-0,559 |
0,593 |
-0,640 |
-0,801 |
|
27 |
2,6 |
0,516 |
0,550 |
-0,458 |
0,536 |
-0,667 |
-0,857 |
|
28 |
2,7 |
0,427 |
0,459 |
-1,275 |
0,451 |
-1,028 |
-0,904 |
|
29 |
2,8 |
0,335 |
0,317 |
-1,114 |
0,335 |
-1,182 |
-0,942 |
|
30 |
2,9 |
0,239 |
0,238 |
-0,968 |
0,223 |
-1,057 |
-0,971 |
|
31 |
3 |
0,141 |
0,119 |
— |
— |
-0,990 |
|
|
32 |
3,1 |
0,042 |
0,037 |
— |
— |
-0,999 |
|
|
СКО |
0,104 |
0,073 |
Среднее СКО для производной функции с введенной случайной
погрешностью составило 0,104, но не превзошло 0,216. Среднее СКО для
производной функции с введенной погрешностью, сглаженной составило 0,073, но не
превзошло 0,17.
По данным табл. 3 построим график производной функции y(x)
= sin(x). На этом же графике построим график производной
возмущенной функции yi + δyi (до
сглаживания функции) и производной возмущенной функции yi + δyi
(после сглаживания функции). Графики представлены на рис. 2. Там же показаны
отклонения расчетных значений производной возмущенной функции (до и после
сглаживания) от точных значений производной yi′ = cos(xi).
Рис. 3. График производной y′ = cos x, график
производной y′ = cos x c ошибкой и y′ = cos x c
ошибкой (сглаженные значения), графики разностных зависимостей: а) y′ (=
cos x) – y′ (с ошибкой без сглаживания); б) y′ (= cos x)
– y′ (с ошибкой и со сглаживанием).
По данным табл. 3 и рис. 3 видим, что погрешность
численного дифференцирования быстро возрастает с ростом случайных погрешностей
дифференцируемой таблично заданной функции.
Как видно по графику (рис. 3) и табл. 3, вычислять
производную таблично заданной функции со случайными погрешностями следует после
ее тщательного сглаживания.
Как было указано в п. 1.4, для проведения процедуры
сглаживания необходимо, чтобы узлы были равноотстоящие. Для демонстрации
возможностей метода линейной интерполяции (с целью получения равноотстоящих узлов)
введем возмущение δxi в значения xi. Далее
с помощью формул (3) п. 1.5 вычислим коэффициенты a и b, и далее
– yi(xi).
Результат в табл. 4.
В столбец С введем возмущение для xi
из столбца B с помощью команды B2 + (0,2*(2*СЛЧИС()-1)). Т.е. в
каждом узле xi погрешности δxi принимают
случайные значения из промежутка [–0,2; +0,2].
В столбце D вычислим yi от xi
с возмущением. В столбце E вычислим коэффициент a с помощью
команды (D4–D2)/(C4-C2), копируя формулу до строки
32. В столбце F вычислим коэффициент b с помощью команды D2–
E3*C2, копируя формулу до строки 33. В столбце G вычислим yi
для хi из столбца B c помощью команды E3*B3
+ F3, копируя до строки 32. В строке 1 линейная интерполяция не
применима, т.к. отсутствует предыдущий узел; в строке 33 линейная интерполяция
также неприменима ввиду отсутствия последующего узла. Таким образом, мы
получили приближенные значения yi для шага h
= 0,1.
Таблица 4
Приведение таблично заданной функции
с неравноотстоящими узлами xi
+ δxi к таблице с равноотстоящими узлами xi путем линейной интерполяции. Столбец A – номер
по порядку; столбец B – значения xi; столбец C – значение xi + δxi;
столбец D – значение yi = sin(xi + δxi);
столбец E – коэффициент a (выр. (3)); столбец F –
коэффициент b (выр. (3)); столбец G – yi, интерп = sin(xi) c применением линейной интерполяции. Столбец H
– точные значения функции yi = sin(xi). Последняя строка — среднее СКО между yi, интерп = sin(xi) и yi = sin(xi).
|
A |
B |
C |
D |
E |
F |
G |
H |
|
№ п/п |
xi |
xi + δxi |
yi |
a |
b |
y(xi) интерп. |
yi′ = cos(xi) |
|
1 |
0 |
-0,150 |
-0,150 |
— |
— |
— |
— |
|
2 |
0,1 |
0,006 |
0,006 |
0,989 |
-0,001 |
0,098 |
0,100 |
|
3 |
0,2 |
0,290 |
0,286 |
0,995 |
0,000 |
0,199 |
0,199 |
|
4 |
0,3 |
0,179 |
0,178 |
0,932 |
0,016 |
0,295 |
0,296 |
|
5 |
0,4 |
0,444 |
0,429 |
0,935 |
0,011 |
0,385 |
0,389 |
|
6 |
0,5 |
0,519 |
0,496 |
0,885 |
0,037 |
0,479 |
0,479 |
|
7 |
0,6 |
0,525 |
0,501 |
0,766 |
0,099 |
0,558 |
0,565 |
|
8 |
0,7 |
0,866 |
0,762 |
0,721 |
0,122 |
0,627 |
0,644 |
|
9 |
0,8 |
0,987 |
0,834 |
0,648 |
0,201 |
0,719 |
0,717 |
|
10 |
0,9 |
0,866 |
0,762 |
0,503 |
0,338 |
0,791 |
0,783 |
|
11 |
1 |
1,100 |
0,891 |
0,534 |
0,299 |
0,833 |
0,841 |
|
12 |
1,1 |
1,144 |
0,910 |
0,398 |
0,453 |
0,891 |
0,891 |
Продолжение таблицы 4
|
13 |
1,2 |
1,222 |
0,940 |
0,339 |
0,522 |
0,929 |
0,932 |
|
14 |
1,3 |
1,304 |
0,965 |
0,183 |
0,716 |
0,954 |
0,964 |
|
15 |
1,4 |
1,551 |
1,000 |
0,175 |
0,736 |
0,981 |
0,985 |
|
16 |
1,5 |
1,485 |
0,996 |
-0,072 |
1,111 |
1,003 |
0,997 |
|
17 |
1,6 |
1,735 |
0,987 |
0,002 |
0,994 |
0,997 |
1,000 |
|
18 |
1,7 |
1,653 |
0,997 |
-0,251 |
1,423 |
0,995 |
0,992 |
|
19 |
1,8 |
1,916 |
0,941 |
-0,254 |
1,416 |
0,959 |
0,974 |
|
20 |
1,9 |
2,005 |
0,907 |
-0,288 |
1,493 |
0,946 |
0,946 |
|
21 |
2 |
1,811 |
0,971 |
-0,393 |
1,696 |
0,909 |
0,909 |
|
22 |
2,1 |
1,946 |
0,931 |
-0,479 |
1,839 |
0,833 |
0,863 |
|
23 |
2,2 |
2,343 |
0,716 |
-0,437 |
1,781 |
0,819 |
0,808 |
|
24 |
2,3 |
2,102 |
0,862 |
-0,763 |
2,503 |
0,749 |
0,746 |
|
25 |
2,4 |
2,537 |
0,568 |
-0,600 |
2,123 |
0,683 |
0,675 |
|
26 |
2,5 |
2,330 |
0,726 |
-0,848 |
2,720 |
0,600 |
0,598 |
|
27 |
2,6 |
2,631 |
0,489 |
-0,753 |
2,479 |
0,522 |
0,516 |
|
28 |
2,7 |
2,520 |
0,583 |
-0,920 |
2,909 |
0,425 |
0,427 |
|
29 |
2,8 |
2,856 |
0,282 |
-0,884 |
2,809 |
0,335 |
0,335 |
|
30 |
2,9 |
2,801 |
0,334 |
-0,957 |
3,016 |
0,240 |
0,239 |
|
31 |
3 |
2,842 |
0,295 |
-0,986 |
3,095 |
0,138 |
0,141 |
|
32 |
3,1 |
3,292 |
-0,150 |
— |
— |
— |
— |
|
СКО |
0,004 |
Среднее СКО между yi,
интерп = sin(xi) и yi = sin(xi),
равное 0,004, но не превосходящее 0,021, позволяет сделать вывод об
эффективности применения метода линейной интерполяции (на примере
рассматриваемой функции).
2.2. Задача о нахождении КОТР
Обратимся к реальной задаче вычисления коэффициента
теплового расширения по данным измерений молярного объема V(T).
По данным измерений разных авторов [5, 9, 11, 21, 24–34]
получена температурная зависимость молярного объема свинца (Pb) V(T).
Вычислить коэффициент объемного теплового расширения (КОТР) β(T) по
формуле . По данным измерений был построен график
(рис. 4) (также с использованием MS Excel) температурной зависимости молярного
объёма свинца (температура плавления Tm = 600,61 К).
Рис. 4 Температурная зависимость молярного объема V(T)
свинца. Символы – литературные данные: 1 – [26]; 2 – [27]; 3
– [28]; 4 – [29]; 5 – [30]; 6 – [31]; 7 – [33]; 8
– [32]; 9 – [34]; 10 – [24]; 11 – [9]; 12 – [11]; 13
– [25]; 14 – [21]; Сплошная линия – сглаживающий тренд Vtrend(T).
Очевидно явное несоответствие данных работы [26] и общего
тренда V(T) для Pb, поэтому источник [26] исключен из
рассмотрения при дальнейших вычислениях. Данные V(T) из [26]
оставлены на рис. 4 лишь для сравнения. Прочие данные приняты во внимание при
расчетах.
Скомпонуем остальные источники в одну таблицу, где в первой
колонке представлены значения xi, а во второй –
соответствующие им значения yi. С помощью команды
«сортировать по возрастанию», выделив при этом весь список, получим следующую
таблицу (табл. 5).
Таблица 5
Упорядоченные первичные данные измерений молярного объема V(T)
свинца в твердом состоянии [5, 9, 11, 21, 24–34].
|
T, |
V, cm3 |
T, |
V, cm3 |
T, |
V, cm3 |
T, |
V, cm3 |
Продолжение таблицы 5
|
0,01 |
17,87098 |
127,95 |
18,00794 |
255,73 |
18,19801 |
386 |
18,40427 |
|
0,01 |
17,878 |
129,65 |
18,00437 |
255,75 |
18,19214 |
386 |
18,40427 |
|
5 |
17,87098 |
133,62 |
18,01608 |
260 |
18,20347 |
390 |
18,41143 |
|
5 |
17,87098 |
134,15 |
18,00991 |
260,65 |
18,19886 |
395 |
18,41749 |
|
5 |
17,878 |
138,15 |
18,01821 |
264,15 |
18,20557 |
400 |
18,41749 |
|
10 |
17,87152 |
140 |
18,02422 |
268,65 |
18,21228 |
400 |
18,423 |
|
16,873 |
17,87476 |
140,77 |
18,0264 |
269,86 |
18,21988 |
400 |
18,43017 |
|
20 |
17,8753 |
143,65 |
18,02487 |
273 |
18,22425 |
400 |
18,43397 |
|
20,96 |
17,87692 |
147,03 |
18,03563 |
273,15 |
18,219 |
400 |
18,438 |
|
24,91 |
17,87962 |
148,15 |
18,03154 |
273,15 |
18,233 |
401 |
18,42906 |
|
25 |
17,87854 |
151,84 |
18,04269 |
277,35 |
18,22572 |
409 |
18,4456 |
|
25 |
17,886 |
152,55 |
18,03822 |
278,32 |
18,23301 |
412 |
18,44615 |
|
28,59 |
17,88286 |
154,68 |
18,0465 |
280 |
18,2352 |
415 |
18,44285 |
|
30 |
17,88286 |
158,15 |
18,04489 |
282,05 |
18,23244 |
417 |
18,44229 |
|
32,04 |
17,88556 |
160 |
18,05302 |
285,35 |
18,23916 |
419 |
18,45939 |
|
35,3 |
17,88881 |
162,62 |
18,05846 |
290,15 |
18,24588 |
426 |
18,4627 |
|
38,98 |
17,89259 |
162,95 |
18,05128 |
292,12 |
18,25436 |
427 |
18,47264 |
|
40 |
17,89313 |
164,24 |
18,06063 |
293 |
18,256 |
429 |
18,47098 |
|
43,5 |
17,89745 |
170,15 |
18,06218 |
293 |
18,256 |
433 |
18,48368 |
|
48,89 |
17,9034 |
173,413 |
18,07423 |
293 |
18,256 |
437 |
18,47816 |
|
50 |
17,90448 |
174,15 |
18,06819 |
293 |
18,256 |
441 |
18,49915 |
|
50 |
17,90394 |
175,15 |
18,07165 |
293 |
18,256 |
451 |
18,51407 |
|
50 |
17,911 |
180 |
18,08239 |
293 |
18,27149 |
452 |
18,50744 |
|
55,32 |
17,91043 |
180,65 |
18,07812 |
293 |
18,25218 |
458 |
18,5207 |
|
60 |
17,91638 |
184,895 |
18,0911 |
293,15 |
18,28599 |
460 |
18,53564 |
|
61,091 |
17,91746 |
185,15 |
18,08476 |
293,15 |
18,264 |
466 |
18,54228 |
|
68,14 |
17,92611 |
189,95 |
18,09166 |
294,35 |
18,25261 |
478 |
18,55445 |
|
70 |
17,92882 |
193,65 |
18,09818 |
296 |
18,26467 |
480 |
18,56553 |
|
76,05 |
17,93694 |
195 |
18,10684 |
298 |
18,2731 |
490 |
18,58437 |
|
80 |
17,94181 |
197,52 |
18,11016 |
298 |
18,27358 |
491 |
18,5755 |
|
82,817 |
17,9456 |
197,95 |
18,10537 |
298 |
18,27358 |
494 |
18,57993 |
|
83,67 |
17,94668 |
200 |
18,11234 |
298,15 |
18,25934 |
499 |
18,58603 |
|
85,15 |
17,94493 |
200 |
18,11343 |
298,15 |
18,27793 |
500 |
18,60266 |
|
90 |
17,95535 |
200 |
18,12768 |
298,15 |
18,27954 |
500 |
18,60765 |
|
90,62 |
17,95643 |
200 |
18,121 |
298,15 |
18,272 |
500 |
18,5877 |
|
92,15 |
17,95219 |
203,45 |
18,11172 |
300 |
18,26696 |
500 |
18,615 |
|
92,47 |
17,95914 |
207,15 |
18,11841 |
300 |
18,27954 |
511 |
18,62541 |
|
95,65 |
17,95759 |
211,15 |
18,12461 |
312 |
18,28778 |
514 |
18,61598 |
|
99,87 |
17,96889 |
213,157 |
18,13305 |
313 |
18,28833 |
523 |
18,63096 |
|
100 |
17,96835 |
215,12 |
18,13632 |
313 |
18,27149 |
525 |
18,65707 |
|
100 |
17,96943 |
216,15 |
18,13181 |
321 |
18,30095 |
532 |
18,64873 |
|
100 |
17,97676 |
220 |
18,14232 |
323 |
18,30204 |
534 |
18,66929 |
|
100 |
17,977 |
220,65 |
18,13851 |
329 |
18,31302 |
545 |
18,67652 |
|
100,15 |
17,96491 |
222,1 |
18,14668 |
338 |
18,32729 |
551 |
18,68375 |
|
102,78 |
17,97323 |
225,05 |
18,1452 |
339 |
18,32015 |
555 |
18,7099 |
Продолжение таблицы 5
|
104,65 |
17,97164 |
229,55 |
18,1519 |
341 |
18,33004 |
559 |
18,70211 |
|
109,65 |
17,97739 |
234,07 |
18,16469 |
347 |
18,33992 |
572 |
18,73552 |
|
109,99 |
17,98298 |
234,15 |
18,15861 |
349 |
18,35806 |
574 |
18,75169 |
|
115,02 |
17,99003 |
238,55 |
18,16531 |
355 |
18,35586 |
592 |
18,78739 |
|
115,65 |
17,98434 |
240 |
18,17288 |
360 |
18,36026 |
600 |
18,80247 |
|
120 |
17,996 |
243,15 |
18,17201 |
361 |
18,36521 |
600 |
18,74401 |
|
120,15 |
17,99138 |
247,35 |
18,17872 |
368 |
18,3685 |
600 |
18,81 |
|
120,88 |
17,99817 |
247,9 |
18,18599 |
368 |
18,37565 |
600,6 |
18,811 |
|
123,65 |
17,99817 |
252,15 |
18,18543 |
378 |
18,39051 |
600,652 |
18,7457 |
Далее формируем новый список xi c
шагом 10 К. При совпадении значения температуры из разных источников, для
указания соответствующего объема, находим среднее арифметическое значение
данных объема с помощью команды СРЗНАЧ.
При этом замечаем, что в списке присутствуют не все
значения T, кратные 10 К. Для их получения воспользуемся процедурой
линейной интерполяции, описанной выше. Результат представлен в табл. 6, при
этом узлы, полученные с помощью линейной интерполяции, выделены цветом.
Таблица 6
Равноотстоящие по температуре (с шагом h = 10 K) данные
измерений молярного объема V(T) для Pb
|
T, |
V, cm3 |
T, K |
V, cm3 |
T, K |
V, cm3 |
T, K |
V, cm3 |
|
10 |
17,87152 |
160 |
18,05302 |
310 |
18,28775 |
460 |
18,53564 |
|
20 |
17,87538 |
170 |
18,06771 |
320 |
18,30225 |
470 |
18,55058 |
|
30 |
17,88286 |
180 |
18,08239 |
330 |
18,31675 |
480 |
18,56553 |
|
40 |
17,89313 |
190 |
18,10050 |
340 |
18,33125 |
490 |
18,58437 |
|
50 |
17,90647 |
200 |
18,11861 |
350 |
18,34576 |
500 |
18,60325 |
|
60 |
17,91638 |
210 |
18,13047 |
360 |
18,36026 |
510 |
18,62148 |
|
70 |
17,92882 |
220 |
18,14232 |
370 |
18,37732 |
520 |
18,63970 |
|
80 |
17,94181 |
230 |
18,15760 |
380 |
18,39437 |
530 |
18,65793 |
|
90 |
17,95535 |
240 |
18,17288 |
390 |
18,41143 |
540 |
18,67615 |
|
100 |
17,97289 |
250 |
18,18818 |
400 |
18,42853 |
550 |
18,69437 |
|
110 |
17,98444 |
260 |
18,20347 |
410 |
18,44638 |
560 |
18,71260 |
|
120 |
17,99600 |
270 |
18,21933 |
420 |
18,46423 |
570 |
18,73082 |
|
130 |
18,01011 |
280 |
18,23520 |
430 |
18,48208 |
580 |
18,74905 |
|
140 |
18,02422 |
290 |
18,25422 |
440 |
18,49993 |
590 |
18,76727 |
Продолжение таблицы 6
|
150 |
18,03862 |
300 |
18,27325 |
450 |
18,51779 |
600 |
18,78549 |
Следующий шаг – это сглаживание первичных равноотстоящих
данных V(T) (процедура описана выше). Результат представлен в
табл. 7.
Таблица 7
Сглаженные данные V(T) для Pb
|
T, |
V, cm3 |
T, |
V, cm3 |
T, |
V, cm3 |
T, |
V, cm3 |
|
10 |
17,87155 |
160 |
18,05291 |
310 |
18,28805 |
460 |
18,53490 |
|
20 |
17,87527 |
170 |
18,06743 |
320 |
18,30245 |
470 |
18,55052 |
|
30 |
17,88303 |
180 |
18,08333 |
330 |
18,31674 |
480 |
18,56645 |
|
40 |
17,89353 |
190 |
18,10070 |
340 |
18,33114 |
490 |
18,58416 |
|
50 |
17,90534 |
200 |
18,11708 |
350 |
18,34560 |
500 |
18,60295 |
|
60 |
17,91694 |
210 |
18,13066 |
360 |
18,36076 |
510 |
18,62154 |
|
70 |
17,92869 |
220 |
18,14327 |
370 |
18,37716 |
520 |
18,63973 |
|
80 |
17,94176 |
230 |
18,15735 |
380 |
18,39423 |
530 |
18,65792 |
|
90 |
17,95648 |
240 |
18,17271 |
390 |
18,41141 |
540 |
18,67615 |
|
100 |
17,97134 |
250 |
18,18819 |
400 |
18,42867 |
550 |
18,69437 |
|
110 |
17,98448 |
260 |
18,20344 |
410 |
18,44633 |
560 |
18,71260 |
|
120 |
17,99678 |
270 |
18,21907 |
420 |
18,46420 |
570 |
18,73082 |
|
130 |
18,00990 |
280 |
18,23599 |
430 |
18,48207 |
580 |
18,74905 |
|
140 |
18,02415 |
290 |
18,25431 |
440 |
18,50006 |
590 |
18,76727 |
|
150 |
18,03863 |
300 |
18,27222 |
450 |
18,51799 |
600 |
18,78549 |
Далее, пользуясь численным методом дифференцирования по
пяти точкам и применяя результат в формуле для вычисления ОКТР, получаем
следующие данные (табл. 8). При этом для шагов 10 K воспользуемся формулой
правой разности, 20 К и 590 К – формулой центральной разности, 600 К – формулой
левой разности. Важно отметить, что расчеты температурной производной проведены
через каждые 10 К, но в таблице 8, из соображений компактности выше 300 К шаг
по температуре увеличен до 50 К.
Таблица 8
Значения ОКТР β(T) для Pb, полученные численным
дифференцированием температурной зависимости молярного объема V(T).
|
T, K |
dV(T)/dT |
ОКТР |
T, K |
dV(T)/dT |
ОКТР |
T, K |
dV(T)/dT |
ОКТР |
|
10 |
0,00037 |
20,754 |
130 |
0,00136 |
75,686 |
250 |
0,00154 |
84,544 |
|
20 |
0,00057 |
32,143 |
140 |
0,00144 |
79,744 |
260 |
0,00154 |
84,580 |
|
30 |
0,00094 |
52,473 |
150 |
0,00144 |
79,654 |
270 |
0,00163 |
89,519 |
|
40 |
0,00113 |
63,095 |
160 |
0,00144 |
79,519 |
280 |
0,00177 |
97,175 |
|
50 |
0,00117 |
65,587 |
170 |
0,00153 |
84,623 |
290 |
0,00182 |
99,558 |
|
60 |
0,00117 |
65,259 |
180 |
0,00168 |
92,655 |
300 |
0,00169 |
92,662 |
|
70 |
0,00124 |
69,284 |
190 |
0,00169 |
93,325 |
350 |
0,00148 |
80,764 |
|
80 |
0,00140 |
77,897 |
200 |
0,00150 |
82,694 |
400 |
0,00175 |
94,792 |
|
90 |
0,00148 |
82,522 |
210 |
0,00131 |
72,154 |
450 |
0,00174 |
93,804 |
|
100 |
0,00140 |
78,030 |
220 |
0,00132 |
72,886 |
500 |
0,00188 |
100,855 |
|
110 |
0,00127 |
70,828 |
230 |
0,00146 |
80,617 |
550 |
0,00182 |
97,500 |
|
120 |
0,00126 |
70,248 |
240 |
0,00155 |
85,067 |
600 |
0,00182 |
97,011 |
Ниже в табл. 9 представлены значения ОКТР, полученные в
данной работе и ОКТР из источника [5].
Таблица 9 Сравнение расчетных значений ОКТР β(T)
для Pb с данными работы [5]
|
T, K |
ОКТР |
ОКТР [5] |
T, K |
ОКТР |
ОКТР [5] |
T, K |
ОКТР |
ОКТР [5] |
|
10 |
20,75 |
8,57 |
130 |
75,69 |
78,25 |
250 |
84,54 |
84,39 |
|
20 |
32,14 |
33,30 |
140 |
79,74 |
78,82 |
260 |
84,58 |
84,86 |
|
30 |
52,47 |
50,07 |
150 |
79,65 |
79,44 |
270 |
89,52 |
85,45 |
|
40 |
63,10 |
60,02 |
160 |
79,52 |
80,03 |
280 |
97,17 |
85,95 |
|
50 |
65,59 |
65,80 |
170 |
84,62 |
80,63 |
290 |
99,56 |
86,35 |
|
60 |
65,26 |
69,31 |
180 |
92,65 |
81,22 |
300 |
92,66 |
86,94 |
|
70 |
69,28 |
71,74 |
190 |
93,33 |
81,61 |
350 |
80,76 |
88,59 |
|
80 |
77,90 |
73,78 |
200 |
82,69 |
82,01 |
400 |
94,79 |
90,94 |
|
90 |
82,52 |
75,23 |
210 |
72,15 |
82,44 |
450 |
93,80 |
94,28 |
|
100 |
78,03 |
76,48 |
220 |
72,89 |
82,98 |
500 |
100,85 |
98,95 |
|
110 |
70,83 |
77,07 |
230 |
80,62 |
83,43 |
550 |
97,50 |
103,90 |
|
120 |
70,25 |
77,59 |
240 |
85,07 |
83,90 |
600 |
97,01 |
109,66 |
На основе табл. 9 построим графики температурной
зависимости ОКТР свинца (рис. 5), а также покажем разностную диаграмму ошибки
δβ(T) = β(T) – β[5](T).
Рис. 5. Температурная зависимость ОКТР β(T) = (1/V)(dV/dT)
свинца. Символы – результат численного дифференцирования зависимости Vtrend(T); сплошная линия – справочные значения βtrend(T) из обзорной работы [5]; символы со сплошной
линией – разностная диаграмма ошибки δβ(T) = β(T) – β[5](T)
Заключение
Проведенные исследования показали, что использование
численных методов для занятий в 7–9 классах основной общей школы позволит на
доступном уровне познакомить школьников с численными методами анализа на
концептуальном, логическом, математическом и алгоритмическом уровнях. Это, в
свою очередь, позволит им при продолжении обучения на более высоких ступенях
образования анализировать социально-экономические проблемы и процессы с
применением методов системного анализа и математического моделирования.
Численные методы – это увлекательное и чрезвычайно важное
направление современной математики, связанное с вычислениями на компьютере и
решением сложных задач. Рассмотрение элементов вычислительной математики на
занятиях со школьниками принесет несомненную пользу для дальнейшей подготовки
инженерных кадров и позволит дать представление о методике обработки
экспериментальных данных, методике решения инженерных задач, структуризации,
алгоритмизации и решении задачи на ПК.
В данной работе был проведён сравнительный анализ методов
нахождения производной функции, установлены в каких случаях и какие ошибки в
результатах (по сравнению с результатами, полученными аналитическими методами)
дают данные методы. Эти результаты были продемонстрированы на численных
примерах.
Проведенный анализ простейших методов численного
дифференцирования позволяет утверждать, что эти методы, вполне доступны для
понимания школьниками 7–9 классов, если не углубляться в математическую теорию
вычислительных методов и пользоваться ими в готовом виде для решения
содержательных практических задач. Впрочем, элементы теоретических основ
численных методов могут быть представлены наиболее подготовленным и увлеченным
обучающимся. Реализация численных методов в среде EXCEL показала, что это так
же доступно для школьников, и может быть использовано в рамках дополнительных
(факультативных) занятий.
Задачи курсовой работы
решены, цель достигнута.
Литература
1.
Абалкин В.К., Аксенов Е.П., Гребеников Е.А., Демин В.Г., Рябов
Ю.А. Справочное руководство по небесной механике и астродинамике / Под ред.
Г.Н. Дубошина. – М.: Наука, 1976. – 864 с.
2.
Аксенова О.В., Бодряков В.Ю. Проблемы качества математической
подготовки будущих учителей информатики в контексте фундаментализации
современного образования // Педагогическое образование в России. 2016. № 7. С.
125-130.
3.
Амосов А.А., Дубинский Ю.А., Копченова Н.В.
Вычислительные методы для инженеров: Учеб.
пособие. – М.: Высш. шк., 1994. – 544 с.: ил.
4.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.:
Лаборатория Базовых знаний, 2000. 624 с.
5.
Бодряков В.Ю., Быков А.А. Особенность корреляционной зависимости
объемного коэффициента теплового расширения свинца от его теплоемкости //
Электронное научное издание «Актуальные инновационные исследования: наука и
практика». 2014. № 2. 9 с.
6.
Бодряков В.Ю., Воронина Л.В. Проблемы качества математического
образования в педагогическом вузе и пути их решения // Педагогическое
образование в России. 2018. № 2. С. 15-27.
7.
Бодряков В.Ю., Фомина Н.Г. О качестве математической подготовки
учащихся в комплексе «школа-вуз»: взгляд с позиций работника высшего
педагогического образования // Математика в школе. 2010. № 2. С. 56-61.
8.
Волков Е. А. Численные методы. М.: Наука, 1982. 256 с.
9.
Дриц М.Е., Будберг П.Б., Бурханов Г.С., Дриц А.М., Пановко В.М..
Свойства элементов. Справ. изд. Под ред. М.Е. Дрица. М.:
Металлургия, 1985. – 672
с.
10.
Зенков А.В. Численные методы: Учебное пособие.
–
Екатеринбург: Изд-во Урал.
ун-та, 2016. – 124 с.
11.
Зиновьев В.Е. Теплофизические свойства металлов при высоких
температурах. Справ. изд., М.: Металлургия, 1989, 384 С.
12.
Катаева Л.Ю., Масленников Д.А., Лощилова Н.А., Белоцерковская
И.Е., Галина Н.В., Федосеева Т.А., Ильичева М.Н. Численные методы решения
прикладных задач: учеб. пособие /Л.Ю. Катаева и [др.]; Нижегород. гос. техн.
ун-т им. Р.Е. Алексеева. – Нижний Новгород, 2014. – 283 с.
13.
Каханер Д., Моулер К., Нэш С. Численные методы и математическое
обеспечение: Пер. с англ. – М.: Мир, 1998. – 575 с., ил.
14.
Киреев В.И. Численные методы в примерах и задачах:
Учеб.пособие/В.И.Киреев, А.В.Пантелеев. – 3-е изд. стер. – М.: Высш.шк., 2008.
– 480 с.: ил.
15.
Кузовкова А.А., Мамалыга Р.Ф., Бодряков В.Ю. Формирование
познавательного интереса к математике у обучающихся в классах
гуманитарно-эстетической направленности // Математика в школе. 2018. № 2. С.
35–42.
16.
Мастяева И.Н., Семенихина О.Н.. Численные методы: Учебное
пособие/ Московский государственный университет экономики, статистики и
информатики.-М., 2001.- 71 с.
17.
Мышенков В.И., Мышенков Е.В. Численные методы. Часть первая:
Учебное пособие для студентов специальности 01.01.07. – М.:
МГУЛ, 2001. – 120 с.: ил.
18.
Мэтьюз Джон Г., Финг Куртис Д. Численные методы.
Использование MATLAB, 3-е
издание.: Пер. с англ. – М.: Издательский дом
«Вильямс», 2001. – 720 с.:
ил. – Парат. тит. англ.
19.
Пирумов У.Г. Численные методы: теория и практика: Учебное пособие
для бакалавров / У.Г. Пирумов, В.Ю. Гидаспов, И.Э. Иванов. — М.: Юрайт, 2012. —
421 c.
20.
Самарский А. А. Введение в численные методы. Учебное пособие для
вузов. 3-е изд., стер. — СПб.: Издательство «Лань», 2005. — 288 с: ил.
21.
Станкус С.В., Хайрулин Р.А.. Плотность сплавов системы
олово–свинец в твердом и жидком состояниях // ТВТ. 2006. Т. 44. Вып. 3. С.
393–400.
22.
Турчак Л.И., Плотников П.В. Основы численных методов: Учебное
пособие. – 2-е изд., перераб. и доп. – М.: ФИЗМАТЛИТ, 2002. – 304 с.
23.
Шахов Ю.Н., Деза Е.И. Численные методы. – М.: МПГУ, 2009 г.
– 141 с.
24.
Францевич И.Н., Воронов Ф.Ф., Бакута С.А.. Упругие
постоянные и модули упругости металлов и
неметаллов. Справ. Изд., Киев: Наукова Думка, 1982, 287 с.
25.
Физические величины. Справ. изд. Под ред. Григорьева И.С.,
Мейлихова Е.З. М.:
Энергоатомиздат, 1991, 1232 с.
26.
A.R. Stokes and A.J.C. Wilson. The thermal expansion of lead from
0° C to 320° C // Proc.
Phys. Soc. 1941. V. 53. N. 6. P. 658-662.
27.
F.C. Nix and D. MacNair. The Thermal Expansion of Pure Metals.
II: Molybdenum, Palladium, Silver, Tantalum, Tungsten, Platinum, and Lead //
Phys. Rev. 1942. V.61. Issue 1-2. P.74–78.
28.
Harold P. Klug. A redetermination of the lattice constant of lead
// J. Am. Chem. Soc. 1946. V. 68. Issue 8. P. 1493–1494.
29.
J.van Duijn, J. van Galen. Influence of vacancies on the thermal
expansion of lead near the melting point // Physica. 1957. V. 23. Issues 6–10.
P.
622–624.
30.
R. Feder and A.S. Nowick. Use of thermal expansion measurements
to detect lattice vacancies near the melting point of pure lead and aluminum //
Phys. Rev. 1958. V. 109. Issue 6. P. 1959–1963.
31.
Robert J. Corruccini and John J. Gnievek. Thermal expansion of
technical solids at low temperatures. A compilation from the literature.//
National Bureau of Standards Monograph NBS-29. Washington: US Government
Printing Office, 1961. 22 p.
32.
R. A. Miller and D. E. Schuele. The Pressure Derivatives of the
Elastic Constants of Lead // J. Phys. Chem. Solids. 1969. V. 30. N. 3. P.
589–600.
33.
Thor Rubin, H.L. Johnston, Howard W. Altman. The thermal
expansion of lead // J. Phys. Chem. 1962. V.66. N.2. P.266-268.
34.
Touloukian Y.S., Kirby R.K., Taylor R.E., Desai P.D.
Thermophysical Properties of Matter. V. 12. Thermal Expansion. Metallic
Elements and Alloys. NY–Washington: IFI/Plenum. 1975, 1442 p.