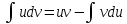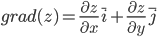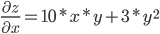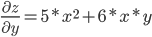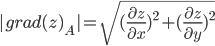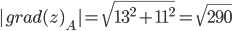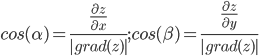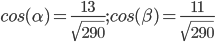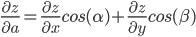Производная функции по направлению
Как найти?
Постановка задачи
Найти производную функции $ u(x,y,z) $ в точке $ M (x_1,y_1,z_1) $ по направлению вектора $ overline{l} = (l_x,l_y,l_z) $
План решения
Если для функции $ u(x,y,z) $ существует производная в точке $ M(x_1,y_1,z_1) $, то значит в этой точке существует производная по любому направлению $ overline{l} $ и находится по формуле:
$$ frac{partial u}{partial l} = frac{partial u}{partial x} bigg |_M cdot cos alpha + frac{partial u}{partial y} bigg |_M cdot cos beta + frac{partial u}{partial z} bigg |_M cdot cos gamma $$
- Находим частные производные первого порядка:
$$ frac{partial u}{partial x}; frac{partial u}{partial y}; frac{partial u}{partial z} $$ - Вычисляем полученные производные в точке $ M(x_1,y_1,z_1) $:
$$ frac{partial u}{partial x} bigg |_{M(x_1,y_1,z_1)}; frac{partial u}{partial y} bigg |_{M(x_1,y_1,z_1)}; frac{partial u}{partial z} bigg |_{M(x_1,y_1,z_1)} $$ - Получаем направляющие косинусы по формулам:
$$ cos alpha = frac{l_x}{|overline{l}|}; cos beta = frac{l_y}{|overline{l}|}; cos gamma = frac{l_z}{|overline{l}|} $$ - Подставляем все полученные данные в формулу и записываем ответ
Примеры решений
| Пример 1 |
| Найти производную функции $ u = x+ln(z^2+y^2) $ в точке $ M (2,1,1) $ по направлению вектора $ overline{l} = (-2,1,-1) $ |
| Решение |
|
Находим частные производные первого порядка и вычисляем их начение в точке $ M $: $$ frac{partial u}{partial x} = 1; frac{partial u}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial u}{partial y} = frac{2y}{z^2+y^2}; frac{partial u}{partial y} bigg |_{M(2,1,1)}=1 $$ $$ frac{partial u}{partial z} = frac{2z}{z^2+y^2}; frac{partial u}{partial z} bigg |_{M(2,1,1)} = 1 $$ Вычисляем направляющие косинусы: $$ cos alpha = frac{-2}{sqrt{(-2)^2+1^2+(-1)^2}} = frac{-2}{sqrt{6}} $$ $$ cos beta = frac{1}{sqrt{(-2)^2+1^2+(-1)^2}} = frac{1}{sqrt{6}} $$ $$ cos gamma = frac{-1}{sqrt{(-2)^2+1^2+(-1)^2}} = — frac{1}{sqrt{6}} $$ Подставляем полученные частные производные в точке $ M $ и направляющие косинусы в формулу: $$ frac{partial u}{partial l} = 1 cdot (-frac{2}{sqrt{6}}) + 1 cdot frac{1}{sqrt{6}} + 1 cdot (-frac{1}{sqrt{6}}) = -frac{2}{sqrt{6}} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ frac{partial u}{partial l} = -frac{2}{sqrt{6}} $$ |
| Пример 2 |
| Найти производную $ u = xy — frac{x}{z} $ в точке $ M(-4,3,-1) $ по направлению вектора $ overline{l} = (5,1,-1) $ |
| Решение |
|
Берем частные производные первого порядка от функции в точке $ M(-4,3,-1) $: $$ frac{partial u}{partial x} = y — frac{1}{z}; frac{partial u}{partial x} bigg |_{M(-4,3,-1)} = 4 $$ $$ frac{partial u}{partial y} = x; frac{partial u}{partial y} bigg |_{M(-4,3,-1)} = -4 $$ $$ frac{partial u}{partial z} = frac{x}{z^2}; frac{partial u}{partial z} bigg |_{M(-4,3,-1)} = -4 $$ Вычисляем направляющие косинусы: $$ cos alpha = frac{5}{sqrt{5^2+1^2+(-1)^2}} = frac{5}{sqrt{27}} $$ $$ cos beta = frac{1}{sqrt{5^2+1^2+(-1)^2}} = frac{1}{sqrt{27}} $$ $$ cos gamma = frac{-1}{sqrt{5^2+1^2+(-1)^2}} = frac{-1}{sqrt{27}} $$ По формуле производной по направлению получаем ответ: $$ frac{partial u}{partial l} = 4 cdot frac{5}{sqrt{27}} + (-4) cdot frac{1}{sqrt{27}} + (-4) cdot frac{-1}{sqrt{27}} = frac{20}{sqrt{27}} $$ |
| Ответ |
| $$ frac{partial u}{partial l} = frac{20}{sqrt{27}} $$ |
Предел
отношения при
называется производной
от функциив
точкепо
направлению вектораи
обозначается,
т.е..
Производная
по направлению характеризует скорость
изменения функции в направлении вектора.
Если то
функциявозрастает
в направлении вектора,
если,
то функцияубывает
в направлении вектора.
Механический
(физический) смысл производной по
направлению состоит в том, что она
характеризует мгновенную скорость
изменения функции в
точкевнаправлении
вектора.
Для
вычисления производной по направлению
функции двух переменных используют
формулу:
где и
направляющие
косинусы, т.е. косинусы углов, образуемых
векторомс
осями координат.
Пример..
Найти производную функции в
точкев
направлении, идущем от этой точки к
точке
Решение. Вычислим и
Найдем
значения этих производных в точке:
Найдем
координаты вектораВычислим
направляющие косинусы вектораДля
вычисления производной функциипо
направлениюподставим
полученные выражения в формулу:
9.Экстремум функции двух переменных. Условия экстремума.
Функция
имеет максимум
(минимум)
в точкеМ0, если для любой точки М,
находящейся в некоторой окрестности
точкиМ0, выполняется условие f(x0,
y0)>f(x,
y)
(f(x0,
y0)<f(x,
y)).
Максимумы
и минимумы функции называются экстремумами.
Теорема
(необходимое
условие экстремума)
Если функция-дифференцируемая функция
и достигает в точке М0 экстремума, то ее
частные производные первого порядка в
этой точке равны нулю.
Точки,
в которых частные производные первого
порядка обращаются в нуль (или не
существуют), называются критическими
или стационарными.
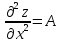

Дискриминант

Достаточное
условие экстремума в стационарной
точке:
-
–экстремум
есть, при этом, если А>0 (или С>0 при
А=0), в точке функция имеет минимум, а
если А<0 (или C<0
при А=0) – максимум -
–экстремума
нет
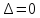
дополнительные исследования
13. Интегрирование по частям в неопред. Интеграле
12.Замена переменной в неопределенном интеграле.
Интегрирование
по частям
Замена
переменной в неопределенном интеграле
производится с помощью подстановок
двух видов:
а) ,
где –
монотонная, непрерывно дифференцируемая
функция новой переменной t. Формула
замены переменной в этом случае: ;
б) ,
где U –
новая переменная. Формула замены
переменной при такой подстановке: .
16.Интегрирование квадратичных иррациональностей.
R(x, √
a2 ± x2 ) и R(x, √ x2 − a2 )
где R —
рациональная функция.
а)
Для интегрирования выражений R(x, √
a2 − x2 ) используются подстановки
x = a ·
sin t или
x = a · cos t .
б)
Для интегрирования выражений R(x,√a2
− x2 ) dx используются подстановки
x = a ·
tg t или
x = a·sht .
в)
Для интегрирования выражений R (x,√a2
− x2 ) dx используются подстановки
x=
a/cost или
x=a·ch t .
Во
всех случаях, применив формулу замены
переменной в неопределенном интеграле,
получаем интегралы вида
∫ Rs(sin t, cos t) dt ,
где Rs —
рациональноя функция, т.е. задача сводится
к интегрированию
триглнометрических выражений.
19.Замена переменной в определенном интеграле.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Производная функции в точке в направлении вектора
Пример №1. Дана функция z=z(x,y), точка A(x0,y0) и вектор a. Найти:
1) grad z в точке A; 2) производную данной функции в точке A в направлении вектора a.
z=5x²*y+3xy²
Решение получаем, решая через калькулятор.
Градиентом функции z = f(x,y) называется вектор, координатами которого являются частные производные данной функции, т.е.:
Находим частные производные:
Тогда величина градиента равна:
grad(z)=(10xy+3y²)i+(5x²+6xy)j
Найдем градиент в точке А(1;1): grad(z)A=(10·1·1+3·1²)i+(5·1²+6·1·1)j или grad(z)A=13i+11j
Модуль grad(z):
Направление вектора-градиента задаётся его направляющими косинусами:
Найдем производную в точке А по направлению вектора а(6;-8).
Найти направление вектора — значит найти его направляющие косинусы:
Модуль вектора |a| равен:
тогда направляющие косинусы:
Для вектора a имеем:
Если ∂z/∂a > 0, то заданная функция в направлении вектора a возрастает.
Если ∂z/∂a < 0, то заданная функция в направлении вектора a убывает.
Пример №2. Даны z=f(x; y), А(х0, у0).
Найти а) градиент функции z=f(x; y) в точке А.
б) производную в точке А по направлению вектора а.
Пример №3. Найти полный дифференциал функции, градиент и производную вдоль вектора l(1;2).
z = ln(sqrt(x^2+y^2))+2^x
Решение.
Градиентом функции z = f(x,y) называется вектор, координатами которого являются частные производные данной функции, т.е.:
Находим частные производные:
Тогда величина градиента равна:
Найдем производную в точке А по направлению вектора а(1;2).
Найти направление вектора — значит найти его направляющие косинусы:
Модуль вектора |a| равен:
тогда направляющие косинусы:
Для вектора a имеем:
Если ∂z/∂a > 0, то заданная функция в направлении вектора a возрастает.
Если ∂z/∂a < 0, то заданная функция в направлении вектора a убывает.
Пример №4. Дана функция . Найти:
1) gradu в точке A(5; 3; 0);
2) производную в точке А в направлении вектора a=i-2j+k.
Решение.
1. 
Найдем частные производные функции u в точке А.
;


.
Тогда
2. Производную по направлению вектора a в точке А находим по формуле
Частные производные в точке А нами уже найдены. Для того чтобы найти cos α, cos β, cos γ, найдем единичный вектор a0 вектора a.

.
Отсюда
Пример №5. Даны функция z=f(x), точка А(х0, у0) и вектор a. Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора a.
Решение.
Находим частные производные:
Тогда величина градиента равна:
Найдем градиент в точке А(1;1)
или
Модуль grad(z):
Направление вектора-градиента задаётся его направляющими косинусами:
Найдем производную в точке А по направлению вектора а(2;-5).
Найти направление вектора — значит найти его направляющие косинусы:
Модуль вектора |a| равен:
тогда направляющие косинусы:
Для вектора a имеем:
Поскольку ∂z/∂a < 0, то заданная функция в направлении вектора a убывает.
Перейти к онлайн решению своей задачи
Градиент функции и производная по направлению вектора
Краткая теория
Градиентом называется вектор, направление которого указывает направление максимально быстрого возрастания функции f(x). Нахождение этой векторной величины связано с определением частных производных функции. Производная по направлению это скалярная величина и показывает скорость изменения функции при движении вдоль направления, заданного некоторым вектором.
Пример решения задачи
Задача
Даны функция
, точка
и вектор
. Найти:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Нахождение градиента функции
1) Найдем градиент
функции в точке
:
Искомый градиент:
Нахождение производной по направлению вектора
2) Найдем производную
в направлении вектора
:
где
-угол,
образованный вектором и осью
Искомая производная в
точке
:
Пусть F(x,y,z)F(x,y,z) – функция трех переменных, (x,y,z)(x,y,z) – декартовы координаты.
Градиентом функции F(x,y,z)F(x,y,z) называется векторное поле
∇F(x,y,z)=∂F∂xi+∂F∂yj+∂F∂zk,
nabla F(x,y,z)=frac{partial F}{partial x}mathbf{i}+frac{partial F}{partial y}mathbf{j}+frac{partial F}{partial z}mathbf{k},
где ∂F∂xfrac{partial F}{partial x}, ∂F∂yfrac{partial F}{partial y} и ∂F∂zfrac{partial F}{partial z} – частные производные функции F(x,y,z)F(x,y,z), а imathbf{i}, jmathbf{j} и kmathbf{k} – базис декартовой системы координат (x,y,z)(x,y,z).
Иногда градиент обозначается так: gradF(x,y,z)operatorname{grad} F(x,y,z).
Градиент функции в данной точке показывает направление наибольшего роста функции.
Пример 1
Найти градиент функции F(x,y,z)=ln(x2+y2+z2)F(x,y,z)=ln(x^2+y^2+z^2) в точке M(1,2,3)M(1,2,3).
Вычислим частные производные:
∂F∂x=∂∂xln(x2+y2+z2)=2xx2+y2+z2,
frac{partial F}{partial x}=frac{partial }{partial x}ln(x^2+y^2+z^2)=frac{2x}{x^2+y^2+z^2},
∂F∂y=∂∂yln(x2+y2+z2)=2yx2+y2+z2,
frac{partial F}{partial y}=frac{partial }{partial y}ln(x^2+y^2+z^2)=frac{2y}{x^2+y^2+z^2},
∂F∂z=∂∂zln(x2+y2+z2)=2zx2+y2+z2.
frac{partial F}{partial z}=frac{partial }{partial z}ln(x^2+y^2+z^2)=frac{2z}{x^2+y^2+z^2}.
Градиент в точке M(1,2,3)M(1,2,3) (подставляем в формулы для частных производных значения x=1x=1, y=2y=2, z=3z=3):
∇F(M)=17 i+27 j+37 k=17 OM→.
nabla F(M)=frac{1}{7},,mathbf{i}+frac{2}{7},,mathbf{j}+frac{3}{7},,mathbf{k}=frac{1}{7},,overrightarrow{OM}.
Производная по направлению
Пусть FF – функция на плоскости или в пространстве.
Производной функции FF по направлению вектора amathbf{a} в точке MM называется число
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0,
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0},
если производная в правой части существует.
Пример 2
Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1).
Вычисляем значение функции в точке M+εaM+varepsilon mathbf{a} с координатами (−1+ε,−2ε,1+2ε)(-1+varepsilon,-2varepsilon,1+2varepsilon):
F(M+εa)=(−1+ε)2(−2ε)−(−2ε)2(1+2ε)+(1+2ε)2(−1+ε)=−6ε3−5ε−1.
Fleft(M+varepsilon mathbf{a}right)=(-1+varepsilon)^2(-2varepsilon)-(-2varepsilon)^2(1+2varepsilon)+(1+2varepsilon)^2(-1+varepsilon)=-6{varepsilon^{3}}-5varepsilon-1.
Длина вектора amathbf{a}:
∥a∥=a12+a22+a32=12+(−2)2+22=9=3.
|mathbf{a}|=sqrt{a_1^2+a_2^2+a_3^2}=sqrt{1^2+(-2)^2+2^2}=sqrt{9}=3.
Производная по направлению:
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0=13ddε(−6ε3−5ε−1)∣ε=0=−53
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=frac{1}{3}left.frac{d}{dvarepsilon}left(-6{varepsilon^{3}}-5varepsilon-1right)right|_{varepsilon=0}=-frac{5}{3}
Выражение производной по направлению через градиент
Используя формулу Тейлора для функций нескольких переменных, легко получить выражение производной по направлению через градиент. Действительно, из равенства
F(M+εa)=F(M)+ε(∇F(M),a)+o(ε2)Fleft(M+varepsilon mathbf{a}right)=F(M)+varepsilonleft(nabla F(M),mathbf{a}right)+oleft(varepsilon^2right)
следует, что
ddεF(M+εa)∣ε=0=(∇F(M),a).
left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=left(nabla F(M),mathbf{a}right).
Таким образом,
∂F∂a(M)=(∇F(M),a)∥a∥.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}.
Пример 2′2′
Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1) используя градиент.
Частные производные:
∂F∂x(M)=2xy+z2∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial x}(M)=left.2xy+z^2right|_{(x,y,z)=(-1,0,1)}=1,
∂F∂y(M)=x2−2yz∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial y}(M)=left.x^2-2yzright|_{(x,y,z)=(-1,0,1)}=1,
∂F∂z(M)=−y2+2zx∣(x,y,z)=(−1,0,1)=−2.
frac{partial F}{partial z}(M)=left.-y^2+2zxright|_{(x,y,z)=(-1,0,1)}=-2.
Градиент:
∇F(M)=i+j−2k.
nabla F(M)=mathbf{i}+mathbf{j}-2mathbf{k}.
Скалярное произведение:
(∇F(M),a)=(i+j−2k,i−2j+2k)=1−2−4=−5.
left(nabla F(M),mathbf{a}right)=left(mathbf{i}+mathbf{j}-2mathbf{k},mathbf{i}-2mathbf{j}+2mathbf{k}right)=1-2-4=-5.
Производная по направлению:
∂F∂a(M)=(∇F(M),a)∥a∥=−53.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}=-frac{5}{3}.

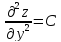
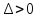 –экстремум
–экстремум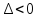 –экстремума
–экстремума