Под понятием производные различных порядков обычно понимаются производные первого или высших порядков.
Дифференцирование производной первого порядка [F^{prime}(x)] позволит вычислить производную от производной — именуемую производной второго порядка. Далее назовем определение производной.
Производная производной второго порядка именуется производной третьего порядка, в этой связи производная n-го
порядка определяется как производная от производной n-1го порядка.
Производная функции второго порядка обозначается записью [y^{prime prime}] или [F^{prime prime}(x)]. Дифференцировка функции [n] раз приводит к получению производной вида [f n(x)].
Дифференцирование второго порядка
Производные в математике всегда находятся по определенной формуле. Итак, формула дифференцирования второго порядка записывается следующим образом:
[f^{prime prime}(x)=frac{d^{2} y}{d x^{2}}=lim _{x rightarrow x_{0}}=frac{f^{prime}(x)-f^{prime}left(x_{0}right)}{x-x_{0}}=left(f^{prime}(x)right)^{prime}]
В случае, если степень меньше, чем порядок производной, производная n-го порядка будет равна нулю.
Таблица с формулами производных высших порядков
Формулы для нахождения производных высших порядков наиболее удобно представить в виде таблицы формул производных:
| Функция | Формула нахождения |
| [left(x^{p}right)^{(n)}] | [left(x^{p}right)^{(n)}=p(p-1)(p-1) ldots(p-n+1) x^{p-n}] |
| [left(a^{k x+b}right)^{(n)}] | [left(a^{k x+b}right)^{(n)}=k^{n} a^{k x+b} 1 n^{n} a] |
| [left(e^{k x+b}right)^{(n)}] | [left(e^{k x+b}right)^{(n)}=k^{n} e^{k x+b}] |
| [(sin a x)^{(n)}] | [(sin a x)^{(n)}=a^{n} sin left(a x+frac{п n}{2}right)] |
| [(cos a x)^{(n)}] | [(sin a x)^{(n)}=a^{n} cos left(a x+frac{п n}{2}right)] |
| [left((a x+b)^{p}right)^{n}] | [left((a x+b)^{p}right)^{n}=a^{n} p(p-1)(p-2) ldots(p-n+1)(a x+b)^{n-1}] |
| [left(log _{a}|x|right)^{(n)}] | [left(log _{a}|x|right)^{(n)}=frac{(-1)^{n-1}(n-1) !}{x^{n} ln a}] |
| [(ln |x|)^{n}] | [left(log _{a}|x|right)^{(n)}=frac{(-1)^{n-1}(n-1) !}{x^{n}}] |
| [(a u(x)+beta gamma(x))^{n}] | [(a u(x)+beta gamma(x))^{n}=a u^{n}(x)+beta^{n} gamma(x)] |
Нет времени решать самому?
Наши эксперты помогут!
Примеры нахождения производных
Примеры
Пример 1
Как найти производную первого порядка функции по формуле произведения:
[|f(x) cdot g(x)|^{prime}=f(x)^{prime} cdot g(x)+f(x) cdot g(x)^{prime}\y^{prime}=[x cdot ln (2
x+1)]^{prime}=x^{prime} cdot ln (2 x+1)+x cdot(ln (2 x+1))^{prime}\=1 cdot ln (2 x+1)+x cdot(ln
(2 x+1))^{prime}=y^{prime}\=ln (2 x+1)+x cdot(ln (2 x+1))^{prime}\=ln (2 x+1)+x frac{1}{2 x+1}
cdot(2 x+1)^{prime}=ln (2 x+1)+2 x cdot frac{1}{2 x+1}\=ln (2 x+1)+frac{2 x}{2 x+1}]
Как найти производную второго порядка в данном выражении:
[y^{prime prime}=left(ln (2 x+1)+frac{2 x}{2 x+1}right)^{prime}=ln (2 x+1)^{prime}+left(frac{2
x}{2 x+1}right)^{prime}\=left(frac{1}{2 x+1}right) cdot(2 x+1)^{prime}+frac{2 x^{prime} cdot(2
x+1)-2 x cdot(2 x+1)^{prime}}{(2 x+1)^{2}}\=y^{prime prime}=frac{2}{2 x+1}+frac{2(2 x+1)-2 x cdot
2}{(2 x+1)^{2}}=frac{2}{2 x+1}+frac{2((2 x+1)-2 x)}{(2 x+1)^{2}}\=frac{2}{2 x+1}+frac{2}{(2
x+1)^{2}}]
Упростим полученное решение:
[y^{prime prime}=frac{2(2 x+1)}{(2 x+1)^{2}}+frac{2}{(2 x+1)^{2}}=frac{2(2 x+1)+2}{(2 x+1)^{2}}=frac{4
x+4}{(2 x+1)^{2}}]
Пример 2
Задача на нахождение производной различных порядков на примере производной четвертого порядка:
[y=x^{5}-x^{4}+3 x^{3}]
Решение:
[y^{prime}=left(x^{5}-x^{4}+3 x^{3}right)^{prime}=5 x^{4}-4 x^{3}+3 cdot 3 x^{2}=5 x^{4}-4 x^{3}+9
x^{2}\y^{prime prime}=left(5 x^{4}-4 x^{3}+9 x^{2}right)^{prime}=20 x^{3}-12 x^{2}+18 x\y^{prime
prime prime}=left(20 x^{3}-12 x^{2}+18 xright)^{prime}=60 x^{2}-24 x+18\y^{4}=left(60 x^{2}-24
x+18right)^{prime}=120 x-24]
Пример 3
Нахождение производной различных порядков от функций на следующем частном примере:
[y=frac{x^{2}+5 x^{3}}{18}]
Ответ: решение не является сложным и не потребует онлайн-калькулятора. Наибольшая степень одной из переменных
равна 3, что меньше степени производной. Следовательно, производная четвертого порядка равна 0.
Пример 4
Необходимо найти производную 13 порядка для [y=sin x]
Решение: найдем производную первого порядка (и затем 2-4 порядков)
[y^{prime}=sin ^{prime} x=cos x=sin left(x+frac{pi}{2}right)\y^{prime prime}=cos ^{prime}
x=-sin x=sin left(x+2 frac{pi}{2}right)\y^{prime prime prime}=-sin ^{prime} x=-cos x=sin
left(x+3 frac{pi}{2}right)\y^{(4)}=-cos ^{prime} x=sin x=sin left(x+4 frac{pi}{2}right)]
Следовательно:
[y^{(n)} sin left(x+frac{n cdot pi}{2}right), n in N]
Итоговый результат:
[y^{(13)}=sin left(x+frac{13 cdot pi}{2}right)=cos x]
Пример 5
Подсчитайте производную четвертой степени функции [x^{8}]
Решение:
Используем формулу нахождения производной высшего порядка
[left(x^{p}right)^{(n)}=p(p-1)(p-1) ldots(p-n+1) x^{p-n}]
Учтем, что p=8, n=4
[left(x^{8}right)^{(4)}=8(8-1)(8-2)(8-4+1) x^{8-4}=8 cdot 7 cdot 6 cdot 5 cdot x^{4}=1680 x^{4}\left(x^{8}right)^{(4)}=1680 x^{4}]
Пример 6
Подсчитайте производную функции [y=2^{x}-operatorname{arctg} x].
Решение:
[y^{prime}=left(2^{x}-operatorname{arctg} xright)^{prime}=left(2^{x}right)^{prime}-(operatorname{arctg} x)^{prime}]
Используем формулы для обратной и тригонометрической функции [y^{prime}=2^{x} ln 2-frac{1}{1+x^{2}}]
Ответ: [y^{prime}=2^{x} ln 2-frac{1}{1+x^{2}}]
Таблица производных высших порядков
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Таблица производных высших порядков
Пример 1
Вычислить производную четвертой степени функции
[x^{8} ]
Решение.
Вычисления производим по формуле нахождения производной высшего порядка
[left(x^{p} right)^{(n)} =p(p-1)(p-2)…(p-n+1)x^{p-n} ]
где $p$ = 8, $n$ = 4
[left(x^{8} right)^{(4)} =8(8-1)(8-2)(8-4+1)x^{8-4} =8cdot 7cdot 6cdot 5cdot x^{4} =1680x^{4} ]
[left(x^{8} right)^{(4)} =1680x^{4} ]
Пример 2
Вычислить производную третей степени функции
[y=5^{2x-5} ]
Решение.
Вычисления производим по формуле нахождения производной высшего порядка
[left(a^{kx+b} right)^{(n)} =k^{n} a^{kx+b} ln ^{n} a]
Где $k$ = 2, $b$ = -5, $a$ = 5, $n$ = 3
[y^{(3)} =left(5^{2x-5} right)^{(3)} =2^{3} cdot 5^{2x-5} cdot ln ^{3} 5]
[y^{(3)} =2^{3} cdot 5^{2x-5} cdot ln ^{3} 5=frac{8cdot 25^{x} }{3125} ln ^{3} 5]
Пример 3
Вычислить производную пятой степени функции
[y=e^{2x} ]
Решение.
Вычисления производим по формуле нахождения производной высшего порядка
[left(e^{kx+b} right)^{(n)} =k^{n} e^{kx+b} ]
Где $k$ = 2, $b$ = 0, $n$ = 5
[e^{2x(5)} =2^5 e^{2x} =32e^{2x} ]
Пример 4
Вычислить четвертую производную функции
[y=sin 3x]
Решение.
Вычисления производим по формуле нахождения производной высшего порядка
[left(sin axright)^{(n)} =a^{n} sin left(ax+frac{pi n}{2} right)]
Где $а$ = 3, $n$ = 4
[left(sin 3xright)^{(4)} =3^{4} sin left(3x+frac{4pi }{2} right)]
[left(sin 3xright)^{(4)} =3^{4} sin left(3x+2pi right)=3^{4} sin 3x=81sin 3x]
«Таблица производных высших порядков» 👇
Пример 5
Вычислить восьмую производную функции
[y=cos 4x]
Решение.
Вычисления производим по формуле нахождения производной высшего порядка
[left(cos axright)^{(n)} =a^{n} cos left(ax+frac{pi n}{2} right)]
Где $а$ = 4, $n$ = 8
[left(cos 4xright)^{(8)} =4^{8} cos left(4x+frac{8pi }{2} right)=4^{8} cos 4x]
Пример 6
Вычислить производную третей степени функции
[y=(6x-10)^{3} ]
Решение.
Вычисления производим по формуле нахождения производной высшего порядка
[((ax+b)^{p} )^{(n)} =a^{n} p(p-1)(p-2)…(p-n+1)(ax+b)^{p-n} ]
Где $а$ = 6, $b$ = -10, $p$ = 3, $n$ = 3
[((6x-10)^{3} )^{(3)} =6^{3} 3(3-1)(3-3+1)(6x-10)^{3-3} ]
[((6x-10)^{3} )^{(3)} =6^{3} cdot 3cdot 2cdot 1cdot 1=1296]
Пример 7
Вычислить производную седьмой степени функции
[y=log {}_{6} x]
Решение.
Вычисления производим по формуле нахождения производной высшего порядка
[left(log _{a} left|xright|right)^{(n)} =frac{(-1)^{n-1} (n-1)!}{x^{n} ln a} ]
Где $а$ = 6, $n$ = 7
[left(log _{6} left|xright|right)^{(7)} =frac{(-1)^{7-1} (7-1)!}{x^{7} ln 6} ]
[left(log _{6} left|xright|right)^{(7)} =frac{(-1)^{7-1} (7-1)!}{x^{7} ln 6} =frac{(-1)^{6} 6!}{x^{7} ln 6} =frac{6!}{x^{7} ln 6} ]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 11.12.2022
Пусть
функция
дифференцируема в некотором интервале.
Тогда её производная
,
вообще говоря, зависит отх
, то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.
Определение.
Производная
от первой производной называется
производной
второго порядка или второй производной
и обозначается символом
или
,
то есть
.
Пример
1. Найти
вторую производную от функции
.
Решение. Найдем
первую производную функции:
.
Находим вторую
производную как производную первой
производной:
.
Определение.
Производная
от второй производной называется
производной третьего порядка или третьей
производной и обозначается символом
или
.
Определение.
Производной
n-ого
порядка функции
называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом
или
:
.
Определение.
Производные
порядка выше первого называются
высшими
производными.
Пример
2. Найти
производную четвертого порядка функции
.
Решение. Находим
последовательно первую, вторую, третью
и четвертую производные:
,
,
,
.
Пример
3.Найти
производную n-ого
порядка для функции
(k—const).
Решение. Имеем:
,
,
,
.
Пример
4. Найти
производную n-ого
порядка для функции
.
Решение. Имеем:
,
,
,
,
.
Замечание.
Аналогично можно получить формулу n-ой
производной функции
:
.
Пример
5. Найти
производную n-ого
порядка для степенной функции
, где
и
— любое вещественное число.
Решение.
Дифференцируя последовательно, получим:
,
,
,
.
В
частном случае, когда
,
гдеm
– натуральное число, получим:
,
при
.
Замечание.
При строгом выводе формулы для производной
n-ого
порядка следует применять метод
математической индукции.
Вторая
производная параметрически заданной
функции
Если
функция задана параметрически уравнениями
,
то для нахождения производной второго
порядка нужно продифференцировать
выражение для её первой производной,
как сложной функции независимой
переменной.
Так
как
,
то
,
и с учетом того,
что
,
получим
,
то есть
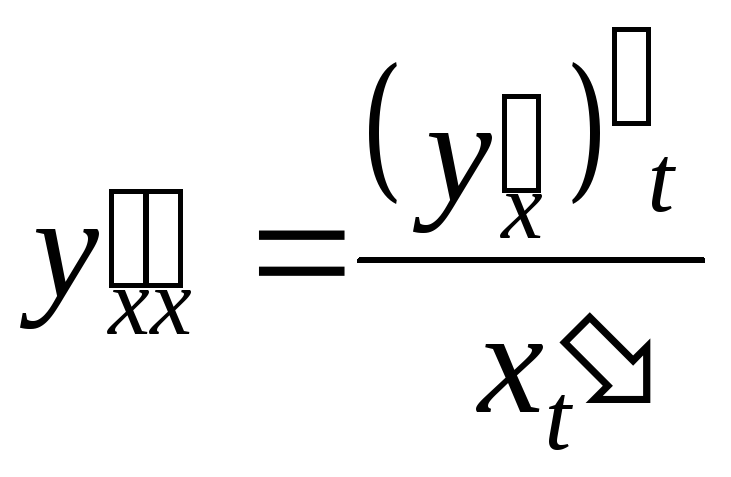
Аналогично можно найти третью
производную
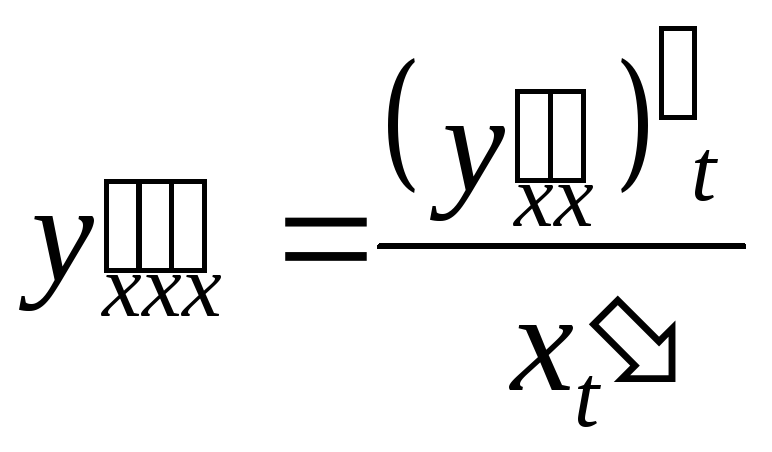
Пример
7. Найти
вторую производную параметрически
заданной функции
,
.
Решение.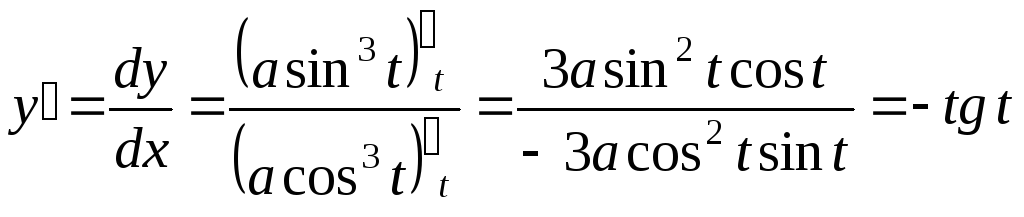
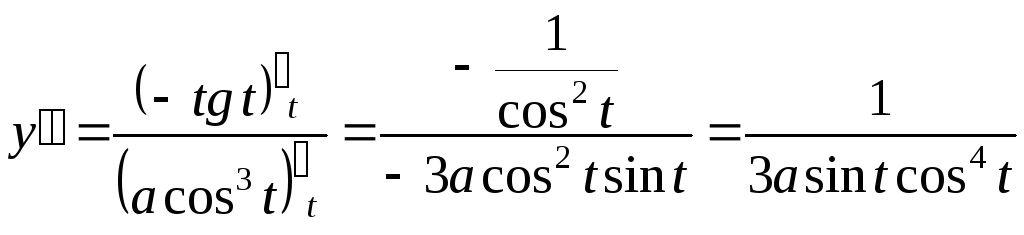
Формула Лейбница
Для
нахождения производной n-ого
порядка от произведения двух функций
большое практическое значение имеет
формула Лейбница.
Пусть
u
и
v
— некоторые
функции от переменной х,
имеющие производные любого порядка и
y=uv.
Выразим n-ую
производную
через производные функцийu
и
v.
Имеем последовательно
,
,
.
Легко подметить
аналогию между выражениями для второй
и третьей производных и разложением
бинома Ньютона соответственно во второй
и третьей степенях, но вместо показателей
степени стоят числа, определяющие
порядок производной, а сами функции
можно рассматривать как «производные
нулевого порядка». Учитывая это, получим
формулу Лейбница:
. (2)
Эту формулу
можно доказать методом математической
индукции.
Пример.
Найти пятую
производную функции
.
Решение.
Положим
и
.
Найдем,
,
,
,
;
.
Подставляя эти выражения в формулу
Лейбница при,
получим
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
урок 3. Математика ЕГЭ
Как найти производную от функции
Как считать производные?
Никто не использует определение производной, чтобы ее вычислить. Как же тогда ее посчитать?
Оказывается, существуют специальные формулы, с помощью которых производная от функции вычисляется достаточно просто.
Формулы производной
Выпишем теперь все формулы производной функции и порешаем примеры.
Производная от константы
Производная от любого числа всегда равна (0):
$$(const)^{/}=0;$$
Пример 1
$$(5)^{/}=0;$$
Производная от (x)
Производная просто от (x) равна (1):
$$x^{/}=1;$$
Производная от степени
$$(x^n)^{/}=n*x^{n-1};$$
Пример 2
$$(x^4)^{/}=4*x^{4-1}=4*x^{3};$$
$$(x^{10})^{/}=10*x^{10-1}=10*x^{9};$$
$$(x^{-3})^{/}=-3*x^{-3-1}=-3*x^{-4};$$
$$(x^{frac{1}{3}})^{/}=frac{1}{3}*x^{1-frac{1}{3}}=frac{1}{3}*x^{frac{2}{3}};$$
Производная от квадратного корня
$$(sqrt{x})^{/}=frac{1}{2sqrt{x}};$$
Тут полезно заметить, что формулу производной от квадратного корня можно не учить. Она сводится к формуле производной от степени:
$$(sqrt{x})^{/}=(x^{frac{1}{2}})^{/}=frac{1}{2}*x^{frac{1}{2}-1}=frac{1}{2}*x^{-frac{1}{2}}=frac{1}{2sqrt{x}};$$
Производная от синуса
$$sin(x)^{/}=cos(x);$$
Производная от косинуса
$$cos(x)^{/}=-sin(x);$$
Производная от тангенса
$$tg(x)^{/}=frac{1}{cos^{2}(x)};$$
Производная от котангенса
$$tg(x)^{/}=frac{-1}{sin^{2}(x)};$$
Производная от экспоненты
$$(e^x)^{/}=e^x;$$
Производная от показательной функции
$$(a^x)^{/}=a^x*ln(a);$$
Пример 3
$$(2^x)^{/}=2^{x}*ln(2);$$
Производная от натурального логарифма
$$(ln(x))^{/}=frac{1}{x};$$
Производная от логарифма
$$(log_{a}(x))^{/}=frac{1}{x*ln(a)};$$
Свойства производной
Помимо формул по вычислению производной еще есть свойства производной, их тоже надо выучить.
Вынесение константы за знак производной
$$(alpha*f(x))^{/}=alpha*(f(x))^{/};$$
Пример 4
$$(3*x^5)^{/}=3*(x^5)^{/}=3*5x^4=15x^4;$$
$$(10sin(x))^{/}==10*(sin(x))^{/}=10*cos(x);$$
Производная от суммы и разности двух функций
$$(f(x) pm g(x))^{/}=(f(x))^{/} pm (g(x))^{/};$$
Пример 5
$$(2x^4+x^3)^{/}=?$$
Тут (f(x)=2x^4), а (g(x)=x^3). Тогда по формуле производной от суммы:
$$(2x^4+x^3)^{/}=(2x^4)^{/}+(x^3)^{/}=2*(x^4)^{/}+(x^3)^{/}=2*4x^3+3x^2=8x^3+3x^2;$$
Пример 6
$$(ln(x)+cos(x))^{/}=(ln(x))^{/}+(cos(x))^{/}=frac{1}{x}-sin(x);$$
Пример 7
$$(x^6-e^x)^{/}=(x^6)^{/}-(e^x)^{/}=6x^5-e^x;$$
Производная от произведения двух функций
$$(f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/};$$
Пример 8
$$(x^2*sin(x))^{/}=?$$
$$(x^2*sin(x))^{/}=(x^2)^{/}*sin(x)+x^2*(sin(x))^{/}=2x*sin(x)+x^2*cos(x);$$
Пример 9
$$(ln(x)*e^x)^{/}=(ln(x))^{/}*e^x+ln(x)*(e^x)^{/}=frac{1}{x}*e^x+ln(x)*e^x;$$
Производная от частного двух функций
$$left(frac{f(x)}{g(x)}right)^{/}=frac{(f(x))^{/}*g(x)-f(x)*(g(x))^{/}}{(g(x))^2};$$
Пример 10
$$left(frac{x^3}{sin(x)}right)^{/}=frac{(x^3)^{/}*sin(x)-x^3*(sin(x))^{/}}{(sin(x))^2}=frac{3x^2*sin(x)-x^3*cos(x)}{(sin(x))^2};$$
Примеры нахождения производной
Рассмотрим несколько примеров нахождения производной, чтобы разобраться, как применяются свойства и формулы производной на практике.
Пример 11
$$(5x^3+2cos(x))^{/}=(5x^3)^{/}+(2cos(x))^{/}=$$
$$=5*(x^3)^{/}+2*(cos(x))^{/}=5*3*x^2+2*(-sin(x))=15x^2-2sin(x);$$
Пример 12
$$left(-frac{3x^2}{2x^4+5x}right)^{/}=-frac{(3x^2)^{/}*(2x^4+5x)-3x^2*(2x^4+5x)^{/}}{(2x^4+5x)^2}=$$
$$=-frac{6x*(2x^4+5x)-3x^2*(8x+5)}{(2x^4+5x)^2}=-frac{12x^5-24x^3+15x^2}{(2x^4+5x)^2};$$
Пример 13
$$(2xsqrt{x})^{/}=(2x)^{/}*sqrt{x}+2x*(sqrt{x})^{/}=$$
$$=2*sqrt{x}+2x*frac{1}{2sqrt{x}}=2*sqrt{x}+frac{2x}{2sqrt{x}}=2*sqrt{x}+sqrt{x}=3sqrt{x};$$
Производная сложной функции
Сложная функция — это функция не от аргумента (x), а от какой-то другой функции: (f(g(x))). Например, функция (sin(x^2)) будет сложной функцией: «внешняя» функция синуса берется от «внутренней» функции степени ((x^2)). Так как под синусом стоит аргумент не (x), а (x^2), то такая функция будет называться сложной.
Еще примеры сложных функций:
-
$$ln(3x^4);$$
Внешняя функция: натуральный логарифм; Внутренняя функция: ((3x^4)). -
$$cos(ln(x));$$
Внешняя функция: косинус; Внутренняя функция: ((ln(x))). -
$$e^{2x^2+3};$$
Внешняя функция: экспонента; Внутренняя функция: ((2x^2+3)). -
$$(sin(x))^3;$$
Внешняя функция: возведение в третью степень; Внутренняя функция: (sin(x)).
Чтобы посчитать производную от такой функции, нужно сначала найти производную внешней функции, а затем умножить результат на производную внутренней функции. В общем виде формула выглядит так:
$$f(g(x))^{/}=f^{/}(g(x))*g^{/}(x);$$
Скорее всего, выглядит непонятно, поэтому давайте разберем на примерах.
Пример 14
$$((cos(x))^4)^{/}=?$$
Внешней функцией тут будет возведение в четвертую степень, поэтому сначала считаем производную от степени по формуле ((x^n)^{/}=n*x^{n-1}). А потом умножаем результат на производную внутренней функции, у нас это функция косинуса, по формуле (cos(x)^{/}=-sin(x)):
$$((cos(x))^4)^{/}=underset{text{внешняя производная}}{underbrace{4*(cos(x))^3}}*underset{text{внутренняя производная}}{underbrace{(cos(x))^{/}}}=$$
$$=4*(cos(x))^3*(-sin(x))=-4*(cos(x))^3*sin(x);$$
Пример 15
$$(e^{2x^3+5})^{/}=?$$
Внешняя функция — это экспонента ((e^x)^{/}=e^x), а внутренняя функция — квадратный многочлен ((2x^3+5)):
$$(e^{2x^3+5})^{/}=e^{2x^3+5}*(2x^3+5)^{/}=e^{2x^3+5}*((2x^3)^{/}+5^{/})=e^{2x^3+5}*6x^2.$$
Пример 16
$$(ln((2x^2+3)^6))^{/}=?$$
Внешняя функция — это натуральной логарифм, берем производную от него по формуле ((ln(x))^{/}=frac{1}{x}), и умножаем на производную внутренней функции, у нас это шестая степень: ((x^n)^{/}=n*x^{n-1}). Но и на этом еще не все: под шестой степенью стоит не просто (x), а квадратный многочлен, значит еще нужно умножить на производную от этого квадратного многочлена:
$$ln((2x^2+3)^6)=frac{1}{(2x^2+3)^6}*((2x^2+3)^6)^{/}*(2x^2+3)^{/}=$$
$$=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*(4x+0)=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*4x=$$
$$=frac{6*(2x^2+3)^5*4x}{(2x^2+3)^6}=frac{24x*(2x^2+3)^5}{(2x^2+3)^6}=frac{24x}{(2x^2+3)^6}.$$
Вывод формул производной функции
Выведем некоторые из этих формул, чтобы было понимание, откуда они берутся. Но перед этим познакомимся с новыми обозначениями. Запись (f(x)) означает, что функция берется от аргумента (x). Например:
$$f(x)=x^3+sin(x);$$
На месте аргумента (x) может стоять все что угодно, например выражение (2x+3). Обозначение такой функции будет (f(2x+3)), а сама функция примет вид:
$$f(2x+3)=(2x+3)^3+sin(2x+3);$$
То есть, везде вместо аргумента (x) мы пишем (2x+3).
И несколько важных замечаний про (Delta f(x)) и (Delta x). Напомню, что значок (Delta) означает изменение некоторой величины. (Delta x) — изменения координаты (x) при переходе от одной точки на графике функции к другой; (Delta f(x)) — разница координат (y) между двумя точками на графике. Подробнее про это можно почитать в главе, где мы вводим понятие производной. Распишем (Delta x) для двух близких точек на графике функции (O) и (B):
$$Delta x=x_B-x_O;$$
Отсюда можно выразить (x_B):
$$x_B=x_O+Delta x;$$
Абсцисса (координата точки по оси (x)) точки (B) получается путем сложения абсциссы точки (O) и (Delta x).
Кстати, функцию (f(x)=x^3+sin(x)) от аргумента (x_B=x_O+Delta x) можно расписать:
$$f(x_B)=f(x_O+Delta x)=(x_O+Delta x)^3+sin(x_O+Delta x);$$
Рис.1. График произвольной функции
И распишем (Delta f):
$$Delta f(x)=f(x_B)-f(x_O)=f(x_O+Delta x)-f(x_O);$$
Тогда определение производной можно записать в виде:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x_O+Delta x)-f(x_O)}{Delta x} quad при quad Delta x to 0;$$
За (x_O) обычно обозначают точку, в окрестности которой берут производную. То есть, получается (x_O) — это абсцисса начальной точки, а (x_O+Delta x) — абсцисса конечной точки.
Нам это пригодится при выводе формул производной.
Производная квадратичной функции
Выведем теперь формулу производной от (f(x)=x^2), воспользовавшись определением производной:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
Распишем числитель (f(x+Delta x)-f(x)) с учетом, что (f(x)=x^2):
$$f(x+Delta x)-f(x)=(x+Delta x)^2-x^2=x^2+2xDelta x+(Delta x)^2-x^2=2xDelta x+(Delta x)^2;$$
Подставим в определение производной:
$$f^{/}(x)=frac{2xDelta x+(Delta x)^2}{Delta x}=frac{Delta x*(2x+Delta x)}{Delta x}=2x+Delta x;$$
Напоминаю, что (Delta x) это бесконечно малая величина:
$$(Delta x)^2 ll 0;$$
Поэтому этим слагаемым можно пренебречь. Вот мы и получили формулу для производной от квадратной функции:
$$f^{/}(x)=(x^2)^{/}=2x;$$
Производная от третьей степени
Аналогичные рассуждения можно провести для функции третьей степени:
$$f(x)=x^3;$$
Воспользуемся определением производной:
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
$$f(x+Delta x)-f(x)=(x+Delta x)^3-x^3=(x+Delta x-x)((x+Delta x)^2+(x+Delta x)*x+x^2)=$$
$$=Delta x*(x^2+2x*Delta x+(Delta x)^2+x^2+x*Delta x+x^2)=Delta x*(3x^2+3xDelta x);$$
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x}=frac{Delta x*(3x^2+3xDelta x)}{Delta x}=3x^2+3xDelta x;$$
Так как при умножении на бесконечно малую величину получается бесконечно малая величина, то слагаемым (3xDelta x) можно пренебречь:
$$f^{/}(x)=(x^3)^{/}=3x^2;$$
Точно таким же способом можно вывести формулы производных для любых степеней:
$$(x^4)^{/}=4x^3;$$
$$(x^5)^{/}=5x^4;$$
$$…$$
$$(x^n)^{/}=n*x^{n-1};$$
Кстати, эта формула справедлива и для дробных степеней.
Вывод остальных формул делается похожим образом, только там может понадобиться знание пределов. Вывод всех формул разбирается в университетском курсе математического анализа.
Что такое производная функции простыми словами? Для чего нужна производная? Определение производной
Как решать задания №7 из ЕГЭ по математике. Анализ графиков при помощи производной. Графики производной и графики функции
Исследуем функцию с помощью производной. Находим точки минимума и максимума, наибольшее и наименьшее значение функции. Точки экстремума. Промежутки возрастания и убывания.
Связь коэффициента наклона и тангенса угла наклона касательной к функции и производной функции в точке касания. Задание №7 в ЕГЭ по математике.
Содержание:
- Механический смысл второй производной
- Вычисления производной любого порядка, формула Лейбница
Если функция $y=f(x)$ имеет производную в каждой точке
$x$ своей области определения, то ее производная
$f^{prime}(x)$ есть функция от
$x$. Функция
$y=f^{prime}(x)$, в свою очередь, может иметь производную, которую
называют производной второго порядка функции $y=f(x)$ (или второй
производной) и обозначают символом $f^{prime prime}(x)$. Таким образом
$f^{prime prime}(x)=frac{mathrm{d}^{2} y}{mathrm{d} x^{2}}=lim _{x rightarrow x_{0}} frac{f^{prime}(x)-f^{prime}left(x_{0}right)}{x-x_{0}}=left(f^{prime}(x)right)^{prime}$
Пример
Задание. Найти вторую производную функции $y(x)=x ln (2 x+3)$
Решение. Для начала найдем первую производную:
$y^{prime}(x)=(x ln (2 x+3))^{prime}=(x)^{prime} cdot ln (2 x+3)+x cdot(ln (2 x+3))^{prime}=$
$=1 cdot ln (2 x+3)+x cdot frac{1}{2 x+3} cdot(2 x+3)^{prime}=ln (2 x+3)+$
$+frac{x}{2 x+3} cdotleft[(2 x)^{prime}+(3)^{prime}right]=ln (2 x+3)+frac{x}{2 x+3} cdotleft[2 cdot(x)^{prime}+0right]=$
$=ln (2 x+3)+frac{x}{2 x+3} cdot 2 cdot 1=ln (2 x+3)+frac{2 x}{2 x+3}$
Для нахождения второй производной продифференцируем выражение для первой производной еще раз:
$y^{prime prime}(x)=left(y^{prime}(x)right)^{prime}=left(ln (2 x+3)+frac{2 x}{2 x+3}right)^{prime}=$
$=(ln (2 x+3))^{prime}+left(frac{2 x}{2 x+3}right)^{prime}=$
$=frac{1}{2 x+3} cdot(2 x+3)^{prime}+frac{(2 x)^{prime} cdot(2 x+3)-2 x cdot(2 x+3)^{prime}}{(2 x+3)^{2}}=$
$=frac{1}{2 x+3}left[(2 x)^{prime}+(3)^{prime}right]+frac{2(x)^{prime} cdot(2 x+3)-2 x cdotleft[(2 x)^{prime}+(3)^{prime}right]}{(2 x+3)^{2}}=$
$=frac{1}{2 x+3}left[2 cdot(x)^{prime}+0right]+frac{2 cdot 1 cdot(2 x+3)-2 x cdotleft[2 cdot(x)^{prime}+0right]}{(2 x+3)^{2}}=$
$=frac{1}{2 x+3} cdot 2 cdot 1+frac{2(2 x+3)-2 x cdot 2 cdot 1}{(2 x+3)^{2}}=$
$=frac{2}{2 x+3}+frac{4 x+6-4 x}{(2 x+3)^{2}}=frac{2}{2 x+3}+frac{6}{(2 x+3)^{2}}=$
$=frac{2(2 x+3)+6}{(2 x+3)^{2}}=frac{4 x+6+6}{(2 x+3)^{2}}=frac{4 x+12}{(2 x+3)^{2}}=frac{4(x+3)}{(2 x+3)^{2}}$
Ответ. $y^{prime prime}(x)=frac{4(x+3)}{(2 x+3)^{2}}$
Производные более высоких порядков определяются аналогично. То есть производная
$n$-го порядка функции
$f(x)$ есть первая производная от производной
$(n-1)$-го порядка этой функции:
$f^{(n)}(x)=frac{mathrm{d}^{n} y}{mathrm{d} x^{n}}=left(f^{(n-1)}(x)right)^{prime}$
Замечание
Число $n$, указывающее порядок производной, заключается в скобки.
Механический смысл второй производной
Теорема
(Механический смысл второй производной)
Если точка движется прямолинейно и задан закон ее движения $s=f(t)$,
то ускорение точки равно второй производной от пути по времени:
$a(t)=s^{prime prime}(t)$
Замечание
Ускорение материального тела равно первой производной от скорости, то есть:
$a(t)=v^{prime}(t)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Материальная точка движется по закону
$s(t)=2 t^{3}+3 t$, где
$s$ измеряется в метрах, а
$t$ — в секундах. Найти значение
$t$, при котором ускорение точки равно 12.
Решение. Найдем ускорение материальной точки:
$a(t)=s^{prime prime}(t)=left(2 t^{3}+3 tright)^{prime prime}=left(left(2 t^{3}+3 tright)^{prime}right)^{prime}=left(left(2 t^{3}right)^{prime}+(3 t)^{prime}right)^{prime}=$
$=left(2 cdot 3 t^{2}+3 cdot 1right)^{prime}=left(6 t^{2}+3right)^{prime}=left(6 t^{2}right)^{prime}+(3)^{prime}=$
$=6 cdotleft(t^{2}right)^{prime}+0=6 cdot 2 t=12 t$
Искомое время $t$ найдем из уравнения:
$a(t)=12 Rightarrow 12 t=12 Rightarrow t=1 mathrm{c}$
Ответ. $t=1 c$
Вычисления производной любого порядка, формула Лейбница
Для вычисления производной любого порядка от произведения двух функций, минуя последовательное применение
формулы вычисления производной от произведения двух функций, применяется формула Лейбница:
$(u v)^{(n)}=u^{(n)} v+C_{n}^{1} u^{(n-1)} v^{prime}+C_{n}^{2} u^{(n-2)} v^{prime prime}+ldots+C_{n}^{n-1} u^{prime} v^{(n-1)}+u v^{(n)}$
где $C_{n}^{k}=frac{n !}{k !(n-k) !}$,
$n !=1 cdot 2 cdot ldots cdot n$ — факториал
натурального числа
$n$.
Пример
Задание. Найти $y^{(4)}(x)$, если
$y(x)=e^{4 x} sin 3 x$
Решение. Так как заданная функция представляет собой произведение двух функций
$u(x)=e^{4 x}$,
$v(x)=sin 3 x$, то для нахождения производной четвертого
порядка целесообразно будет применить формулу Лейбница:
$y^{(4)}(x)=left(e^{4 x}right)^{(4)} cdot sin 3 x+C_{4}^{1}left(e^{4 x}right)^{(3)} cdot(sin 3 x)^{prime}+$
$+C_{4}^{2}left(e^{4 x}right)^{prime prime} cdot(sin 3 x)^{prime prime}+C_{4}^{3}left(e^{4 x}right)^{prime} cdot(sin 3 x)^{(3)}+e^{4 x}(sin 3 x)^{(4)}$
Найдем все производные и посчитаем коэффициенты при слагаемых.
1) Посчитаем коэффициенты при слагаемых:
$C_{4}^{1}=frac{4 !}{1 ! cdot(4-1) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$
$C_{4}^{2}=frac{4 !}{2 ! cdot(4-2) !}=frac{4 !}{2 ! cdot 2 !}=frac{2 ! cdot 3 cdot 4}{2 ! cdot 2 !}=frac{3 cdot 4}{2}=6$
$C_{4}^{3}=frac{4 !}{3 ! cdot(4-3) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$
2) Найдем производные от функции $u(x)$:
$u(x)=e^{4 x}, u^{prime}(x)=left(e^{4 x}right)^{prime}=e^{4 x} cdot(4 x)^{prime}=e^{4 x} cdot 4 cdot(x)^{prime}=4 e^{4 x}$
$u^{prime prime}(x)=left(u^{prime}(x)right)^{prime}=left(4 e^{4 x}right)^{prime}=4 cdotleft(e^{4 x}right)^{prime}=16 e^{4 x}$
$u^{prime prime prime}(x)=left(u^{prime prime}(x)right)^{prime}=left(16 e^{4 x}right)^{prime}=64 e^{4 x}$
$u^{(4)}(x)=left(u^{prime prime prime}(x)right)^{prime}=left(64 e^{4 x}right)^{prime}=256 e^{4 x}$
3) Найдем производные от функции $v(x)$:
$v(x)=sin 3 x, v^{prime}(x)=(sin 3 x)^{prime}=cos 3 x cdot(3 x)^{prime}=3 cos 3 x$
$v^{prime prime}(x)=left(v^{prime}(x)right)^{prime}=(3 cos 3 x)^{prime}=3 cdot(cos 3 x)^{prime}=$
$=3 cdot(-sin 3 x) cdot(3 x)^{prime}=-9 sin 3 x$
$v^{prime prime prime}(x)=left(v^{prime prime}(x)right)^{prime}=-27 cos 3 x, v^{(4)}(x)=left(v^{prime prime prime}(x)right)^{prime}=81 sin 3 x$
Тогда
$y^{(4)}(x)=256 e^{4 x} cdot sin 3 x+4 cdot 64 e^{4 x} cdot 3 cos 3 x+$
$+6 cdot 16 e^{4 x} cdot(-9 sin 3 x)+4 cdot 4 e^{4 x} cdot(-27 cos 3 x)+e^{4 x} 81 sin 3 x=$
$=e^{4 x}(336 cos 3 x-527 sin 3 x)$
Ответ. $y^{(4)}(x)=e^{4 x}(336 cos 3 x-527 sin 3 x)$
Читать дальше: таблица производных высших порядков.



