Содержание:
- Формула
- Примеры вычисления производной арккосинуса
Формула
$$(arccos x)^{prime}=-frac{1}{sqrt{1-x^{2}}}$$
Производная арккосинуса равна минус единице, деленной на корень квадратный из разности единицы и аргумента в квадрате.
Если под арккосинусом находится сложная функция $u=u(x)$,
то производная исходной функции будет равна:
$$(arccos u)^{prime}=-frac{1}{sqrt{1-u^{2}}} cdot u^{prime}$$
Примеры вычисления производной арккосинуса
Пример
Задание. Найти производную функции $y(x)=2 arccos x$
Решение. Искомая производная
$$y^{prime}(x)=(2 arccos x)^{prime}$$
Константу вынесем за знак производной (согласно
правилам дифференцирования):
$$y^{prime}(x)=2 cdot(arccos x)^{prime}=2 cdotleft(-frac{1}{sqrt{1-x^{2}}}right)=-frac{2}{sqrt{1-x^{2}}}$$
Ответ. $y^{prime}(x)==-frac{2}{sqrt{1-x^{2}}}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить производную функции $y(x)=arccos (x-1)$
Решение. Производная заданной функции равна:
$$y^{prime}(x)=(arccos (x-1))^{prime}$$
Так как аргумент арккосинуса есть сложная функция, то производную арккосинуса умножаем еще и на производную аргумента:
$$y^{prime}(x)=-frac{1}{sqrt{1-(x-1)^{2}}}(x-1)^{prime}$$
Производная разности равна разности производных, тога получаем:
$$y^{prime}(x)=-frac{1}{sqrt{1-(x-1)^{2}}}left[(x)^{prime}-(1)^{prime}right]$$
Производная $x$ равна единице, а производная 1, как константы, равна нулю. Тогда
$$y^{prime}(x)=-frac{1}{sqrt{1-(x-1)^{2}}} cdot(1-0)=-frac{1}{sqrt{1-(x-1)^{2}}}$$
Ответ. $y^{prime}(x)=-frac{1}{sqrt{1-(x-1)^{2}}}$
Читать дальше: производная арктангенса (arctgx)’.
Производная арккосинуса считается одним из основных понятий тригонометрии. Посредством применения формулы для нахождения данной величины, можно быстро преобразовать выражения, построить соответствующие графики.
Полная таблица производных от обратных тригонометрических функций выглядит так:
Формула нахождения производной арккосинуса
Производная арккосинуса представляет собой дробь, в числителе которой стоит единица, а в знаменателе квадратный корень из разности единицы и аргумента во второй степени. Перед всем выражением ставится знак «минус».
На математическом языке запись дифференцирования имеет следующий вид:
Производная арккосинуса равна производной арксинуса, взятой со знаком минус. В этом случае выражение примет вид:
Теория по производным тригонометрических функций преподаётся в школах, а также в высших учебных заведениях для студентов. На эту тему существует немало задач. О них пойдёт речь далее.
Примеры решения задач
Задача №1
Найти производную функции y = arccos√x.
Для решения этой задачи необходимо воспользоваться формулой, представленной выше, учитывая, что это производная сложной функции:
Для получения правильного ответа, необходимо сначала найти производную арккосинуса, а затем домножить на производную корня из x:
Таким образом, получаем конечный результат:
Задача №2
Вычислить производную функции:
Данный пример аналогичен предыдущему, потому решение будет выглядеть следующим образом
Окончательный ответ:
Таким образом в данной статье мы рассмотрели основные правила нахождения производной арккосинуса.
Производная арккосинуса считается одним из основных понятий тригонометрии. Посредством применения формулы для нахождения данной величины, можно быстро преобразовать выражения, построить соответствующие графики.
Полная таблица производных от обратных тригонометрических функций выглядит так:

Содержание
- Формула нахождения производной арккосинуса
-
Примеры решения задач
- Задача №1
- Задача №2
Формула нахождения производной арккосинуса

Производная арккосинуса представляет собой дробь, в числителе которой стоит единица, а в знаменателе квадратный корень из разности единицы и аргумента во второй степени. Перед всем выражением ставится знак «минус».
На математическом языке запись дифференцирования имеет следующий вид:

Производная арккосинуса равна производной арксинуса, взятой со знаком минус. В этом случае выражение примет вид:

Теория по производным тригонометрических функций преподаётся в школах, а также в высших учебных заведениях для студентов. На эту тему существует немало задач. О них пойдёт речь далее.
Примеры решения задач
Задача №1
Найти производную функции y = arccos√x.
Для решения этой задачи необходимо воспользоваться формулой, представленной выше, учитывая, что это производная сложной функции:
Для получения правильного ответа, необходимо сначала найти производную арккосинуса, а затем домножить на производную корня из x:

Таким образом, получаем конечный результат:

Задача №2
Вычислить производную функции:
Данный пример аналогичен предыдущему, потому решение будет выглядеть следующим образом


Окончательный ответ:

Таким образом в данной статье мы рассмотрели основные правила нахождения производной арккосинуса.
Предыдущая
МатематикаСвойства вычитания — правила и примеры для 5 класса
Следующая
МатематикаДеление обыкновенных дробей — правила и примеры вычислений

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Производная арккосинуса
Как можно отметить, производная арккосинуса отличается от производной арксинуса только знаком.
Функция является обратной к функции
, но в отличии от второй является функцией общего вида.
Примеры решения задач по теме «Производная арккосинуса»
| Понравился сайт? Расскажи друзьям! | |
Вывод производных arcsin(x) и arccos(x)
Здесь мы полагаем, что нам известны производные синуса и косинуса. Далее мы выводим производные арксинуса и арккосинуса, учитывая, что они являются обратными функциями к синусу и косинусу, соответственно.
Вывод производной арксинуса
По формуле производной обратной функции
Рассмотрим функцию арксинус от переменной x:
y = arcsin x.
Здесь независимая переменная x может принимать значения от – 1 до + 1:
.
Зависимая переменная y может принимать значения от – π/2 до + π/2:
.
Функция арксинус является обратной к функции синус:
x = sin y.
Для определения производной арксинуса, применим формулу производной обратной функции:
(1) .
Производная синуса нам известна. Обычно ее записывают в следующем виде:
.
Здесь .
Поменяем местами обозначения переменных x и y. Тогда
,
где .
Подставим в формулу (1):
(2) .
Здесь
y = arcsin x;
x = sin y.
Теперь выразим правую часть формулы (2) через переменную x. Для этого заметим, что поскольку , то . Тогда
.
Подставим в формулу (2):
.
Тем самым мы вывели формулу производной арксинуса:
.
Второй способ
Поскольку арксинус и синус являются обратными функциями по отношению друг к другу, то
(3) .
Здесь .
Продифференцируем это уравнение по переменной x. То есть найдем производные левой и правой части и приравняем их друг к другу:
(4) .
Производную правой части находим из таблицы производных:
.
Производную левой части находим по формуле производной сложной функции:
.
Здесь .
Поскольку , то . Поэтому
.
Тогда
.
Подставим в (4):
.
Отсюда
.
Вывод производной арккосинуса
Используя связь между арксинусом и арккосинусом
Производную арккосинуса легко получить из производной арксинуса, если воспользоваться связью между арксинусом и арккосинусом:
.
Отсюда
.
По формуле производной обратной функции
Также производную арккосинуса можно найти по формуле производной обратной функции.
Рассмотрим функцию арккосинус:
y = arccos x.
Здесь независимая переменная x может принимать значения от – 1 до + 1:
.
Зависимая переменная y может принимать значения от 0 до π:
.
Функция арккосинус является обратной к функции косинус:
x = cos y.
Применим формулу производной обратной функции:
(1) .
Производная косинуса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x и y. Тогда
,
где .
Подставим в формулу (1):
(5) .
Здесь
y = arccos x;
x = cos y.
Теперь выразим правую часть формулы (5) через переменную x. Поскольку , то . Тогда
.
Подставим в формулу (5):
.
Таким образом, мы вывели формулу производной арккосинуса:
.
Второй способ
Поскольку арккосинус и косинус являются взаимно обратными функциями, то
(6) .
Производная Arccos – Формула, Доказательство, Примеры
Производная arccos – это дифференцирование функции арккосинуса arccos x, которая равна -1/√(1-x 2 ), где -1 < x < 1. Он записывается как производная от arccos x или производная от cos, обратная x, обозначаемая как d(arccos x)/dx = d(cos -1 x)/dx = -1/√(1-x 2 ). Производная arccos — это процесс определения скорости изменения arccos x по отношению к переменной x. Следовательно, скорость изменения arccos x под определенным углом, то есть производная arccos x, определяется выражением -1/√(1-x 2 ).
В этой статье мы выведем производную от arccos, используя различные методы, включая неявное дифференцирование и первый принцип дифференцирования. Мы также обсудим антипроизводную arccos x вместе с некоторыми примерами, использующими производную arccos.
1.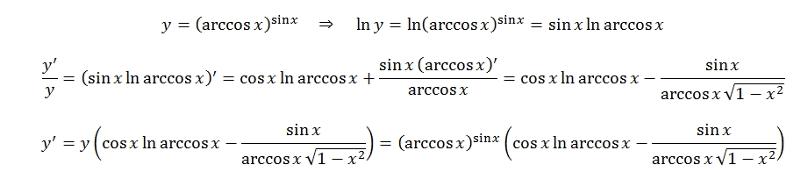 |
Что такое производное Arccos? |
| 2. | Производная от Arccos x с использованием неявного дифференцирования |
| 3. | Производная от Arccos x с использованием первого принципа дифференцирования |
| 4. | Анти-производная Arccos |
| 5. | Производная Cos, обратная x w.r.t. Инверсия греха x |
| 6. | Часто задаваемые вопросы о производной Arccos |
Что такое производное от Arccos?
Производная arccos x определяется как -1/√(1-x 2 ), где -1 < x < 1. Ее также называют производной косинуса по обратной х, то есть производной функции арккосинуса. Производные всех обратных тригонометрических функций можно вычислить методом неявного дифференцирования. Поскольку производная от arccos x равна -1/√(1-x
2 ), поэтому график производной от cos, обратного x, будет графиком -1/√(1-x 2 ).
Производная формулы Arccos
Производная функции — это наклон касательной к функции в точке касания. Следовательно, -1/√(1-x 2 ) — функция наклона касательной к графику arccos x в точке касания. Простой способ запомнить производную arccos x состоит в том, чтобы знать тот факт, что производная arccos x является отрицательной производной sin, обратной x, а производная sin, обратной x, является отрицательной производной arccos x. Теперь мы напишем производную от arccos x математически. Математическое выражение для записи дифференцирования cos -1 x:
d(arccos x)/dx = d(cos
-1 x )/ dx = -1/√(1-x 2 ), где -1 < x < 1
Производная от Arccos x с использованием неявного дифференцирования
Теперь мы докажем производную от arcos x, используя некоторые тригонометрические формулы и тождества. Предположим, что y = cos -1 x ⇒ cos y = x.
cos у = х
⇒ d(cos y)/dx = dx/dx
⇒ -sin y dy/dx = 1
⇒ dy/dx = -1/sin y —- (1)
Поскольку cos 2 y + sin 2 y = 1, мы имеем sin y = √(1 — cos 2 y) = √(1 — x 2 ) [Поскольку cos y = x]
Подставляя sin y = √( 1 — x 2 ) в (1) имеем
dy/dx = -1/√(1 — x 2 )
Поскольку x = -1, 1 составляет знаменатель √(1 — x 2 ) равно 0, и, следовательно, производная не определена при x = -1 и x = 1, поэтому x не может быть -1 и 1.
Следовательно, производная arccos x равна -1/√(1 — x 2 ), где -1 < x < 1
Производная Arccos x с использованием первого принципа дифференцирования
Теперь мы докажем производную от arccos, используя первый принцип дифференцирования. Для доказательства воспользуемся некоторыми формулами дифференцирования, обратными тригонометрическими формулами и тождествами типа:
- (f'(x)=lim_{hrightarrow 0}dfrac{f(x+h)-f( х)}{ч})
- arccos x + arcsin x = π/2 ⇒ arccos x = π/2 — arcsin x
- ( frac { mathrm {d} arcsin x} { mathrm {d} x} = lim_ {h rightarrow 0} dfrac { arcsin (x + h) — arcsin x} {h} )
Начнем доказательство производной от arccos x, используя первый принцип дифференцирования.
Таким образом, мы доказали производную от arccos, используя определение пределов, то есть первый принцип дифференцирования.
Анти-производное Arccos
Теперь, когда мы получили производную arccos, найдем первообразную arccos, то есть ∫arccos x dx = ∫cos -1 x dx, используя интегрирование по частям (ILATE).
∫cos -1 x = ∫cos -1 x · 1 dx
Используя интегрирование по частям,
∫f(x) . g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) ∫g(x) dx) dx + C
Здесь f(x) = cos -1 x и g (x) = 1.
∫cos -1 x · 1 dx = cos -1 x ∫1 dx — ∫ [d(cos -1 x)/dx ∫1 dx]dx + C
∫cos -1 x dx = cos -1 x . (x) — ∫ [-1/√(1 — x²)] x dx + C
Мы вычислим этот интеграл ∫ [-1/√(1 — x²)] x dx методом подстановки. Предположим, что 1-х 2 = u. Тогда -2x dx = du (или) x dx = -1/2 du.
∫cos -1 x dx = x cos -1 x — ∫(-1/√u) (-1/2) du + C
= x cos -1 x — 1/2 ∫u -1/2
du + C
= x cos -1 x — (1/2) (u 1/2 /(1/2)) + C
= x cos — 1 x — √u + C
= x cos -1 x — √(1 — x²) + C
Следовательно, ∫cos -1 x dx = x cos -1 x — √( 1 — x²) + С
Производная Cos, обратная x w.
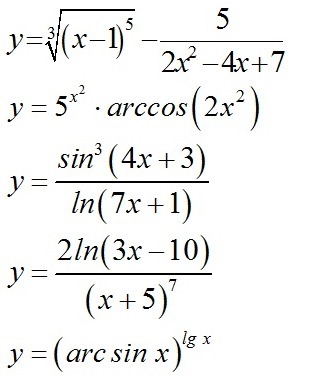
Мы знаем, что производная arccos x, т. е. cos, обратная x, равна -1/√(1 — x²), а производная sin, обратная x, равна 1/√(1 — x²). Чтобы определить производную обратного косинуса по отношению к sin inverse, мы разделим производные обеих функций.
d(cos -1 x)/dx = -1/√(1 — x²) — (1)
d(sin -1 x)/dx = 1/√(1 — x²) ) — (2)
Разделим (1) и (2), получим
[d(cos -1 x)/dx]/[d(sin -1 x)/dx] = [-1/√(1 — x²)]/[1/√(1 — x²)]
⇒ d(cos -1 x)/d(sin -1 x) = -1
Следовательно, производная cos, обратная по отношению к инверсия греха равна -1.
Важные замечания по производной Arccos
- Производная arccos x определяется как -1/√(1-x 2 ), где -1 < x < 1
- Производная обратного косинуса относительно инверсия греха равна -1.
- ∫cos -1 x dx = x cos -1 x — √(1 — x²) + C
Темы, относящиеся к производной от Arccos
- Производная от Sin, обратная x
- Обратная формула Cos
- Обратные тригонометрические формулы
Часто задаваемые вопросы о производной Arccos
Что такое производная Arccos в тригонометрии?
Производная от arccos x в тригонометрии определяется выражением -1/√(1-x 2 ), где -1 < x < 1.


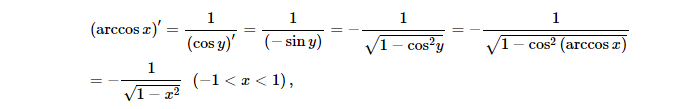

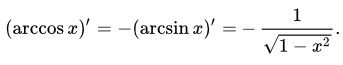
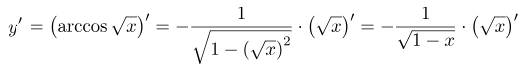
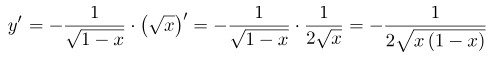
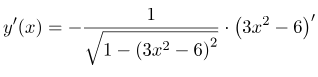


![Rendered by QuickLaTeX.com [ left( arccos x right)' = -frac{1}{sqrt{1-x^{2}}} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1d8a7b70f27da22c014f0f0e1f979351_l3.png)

