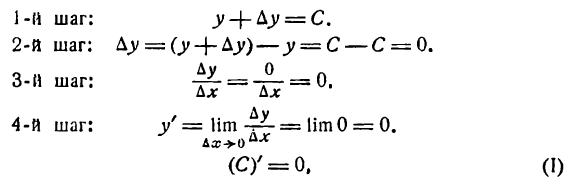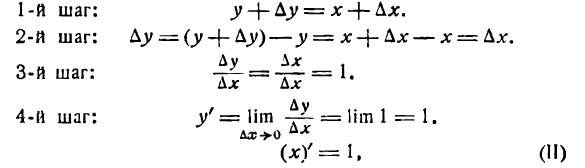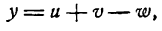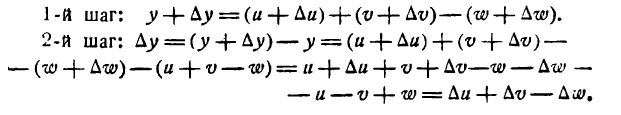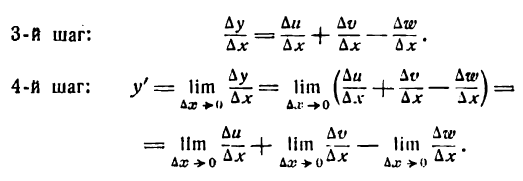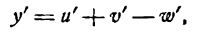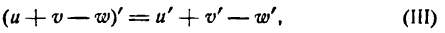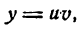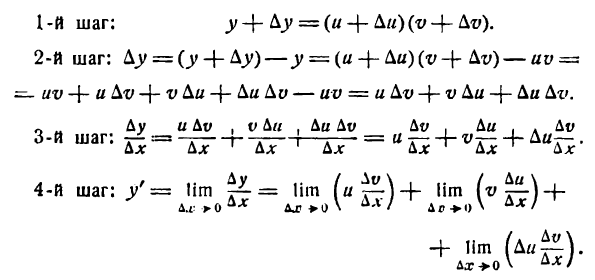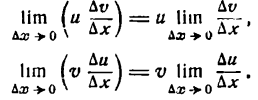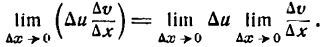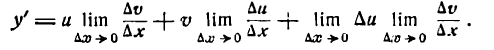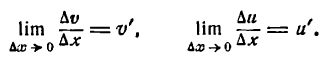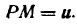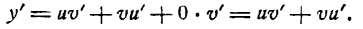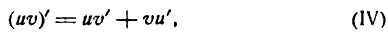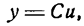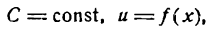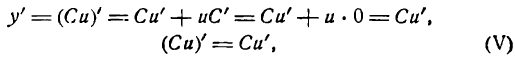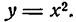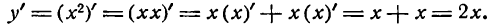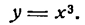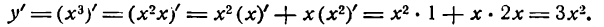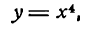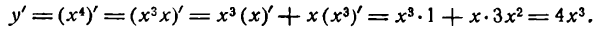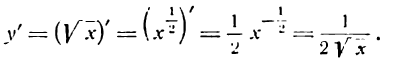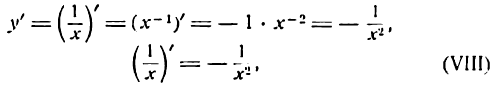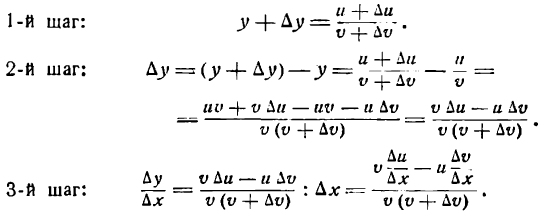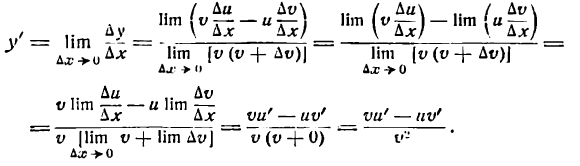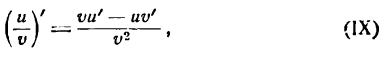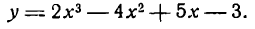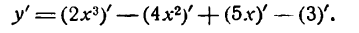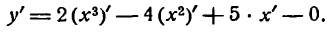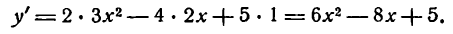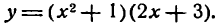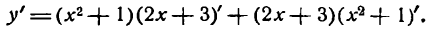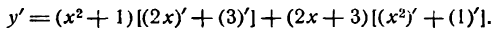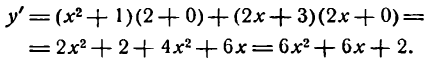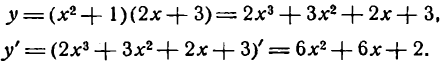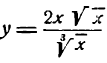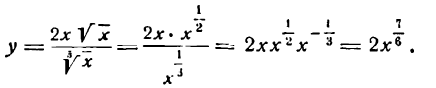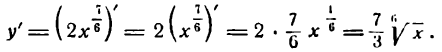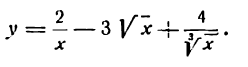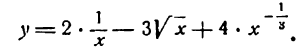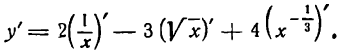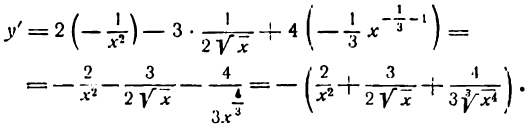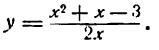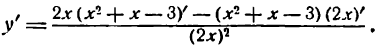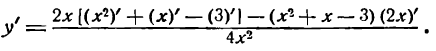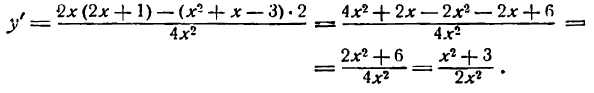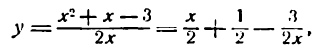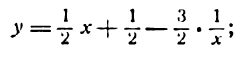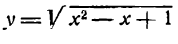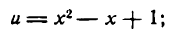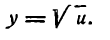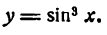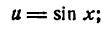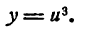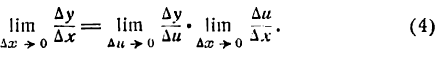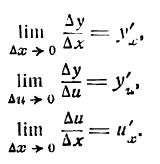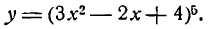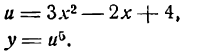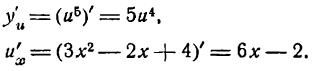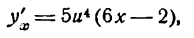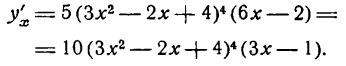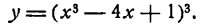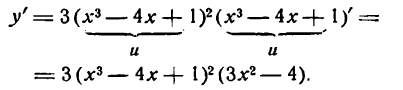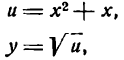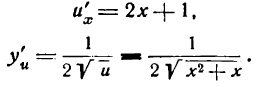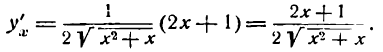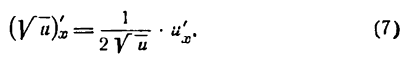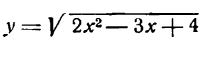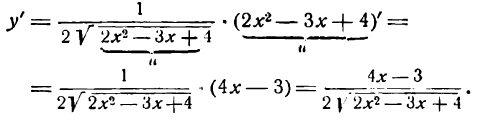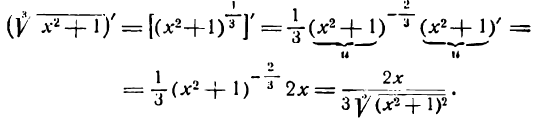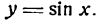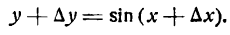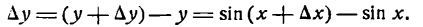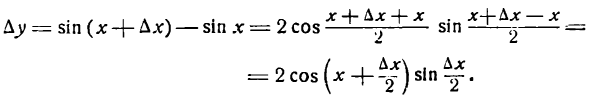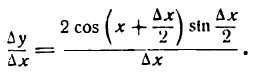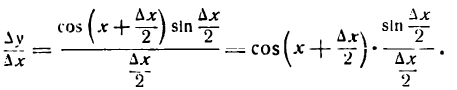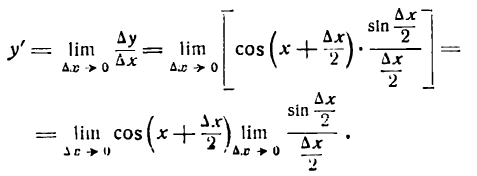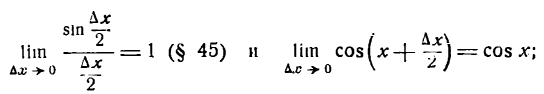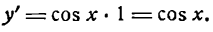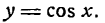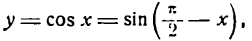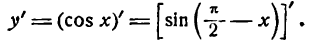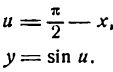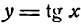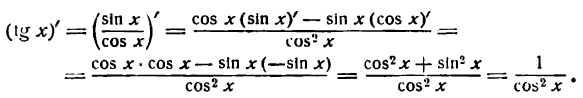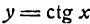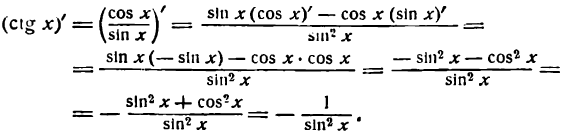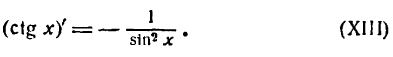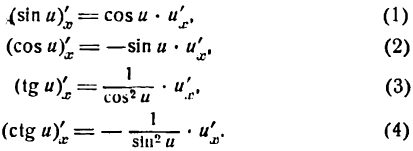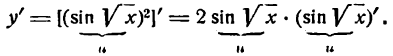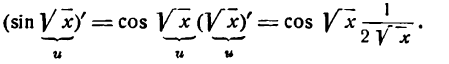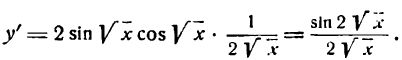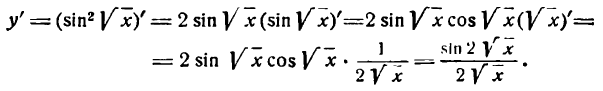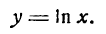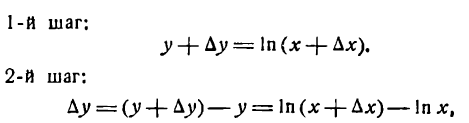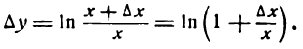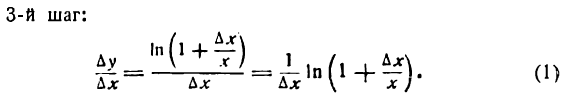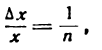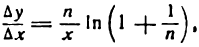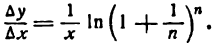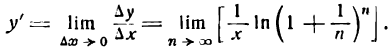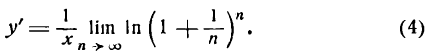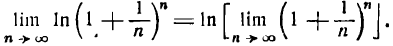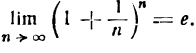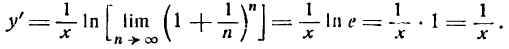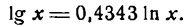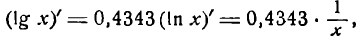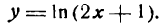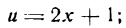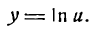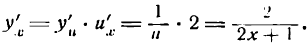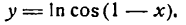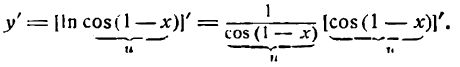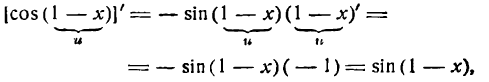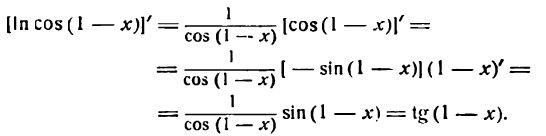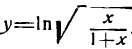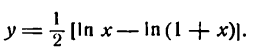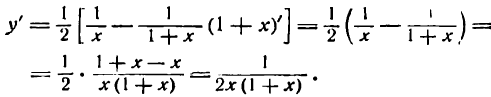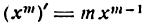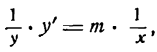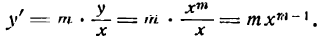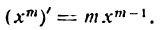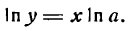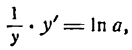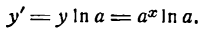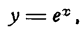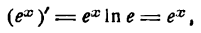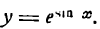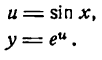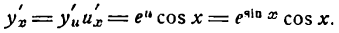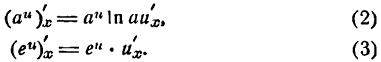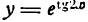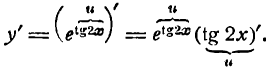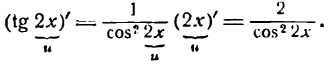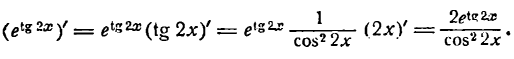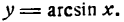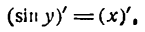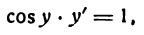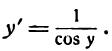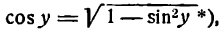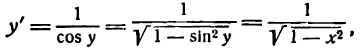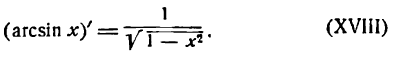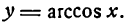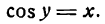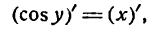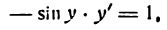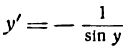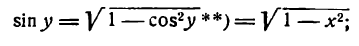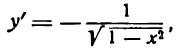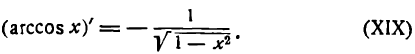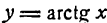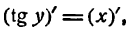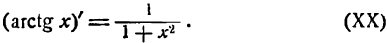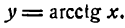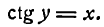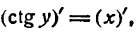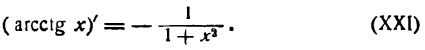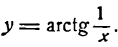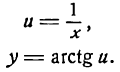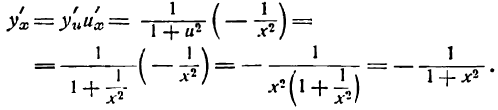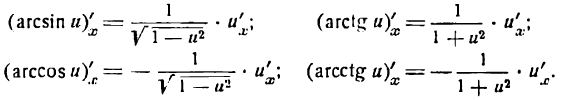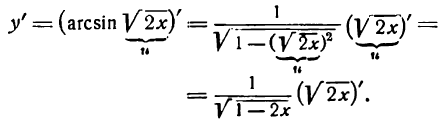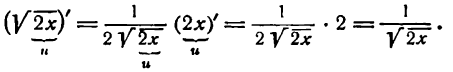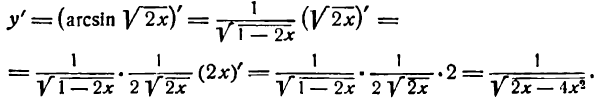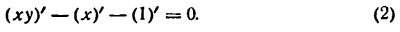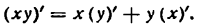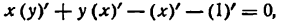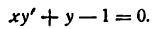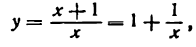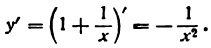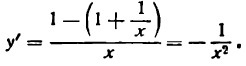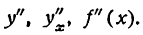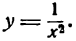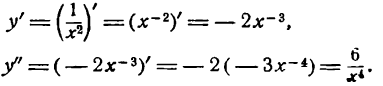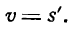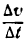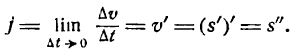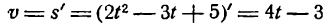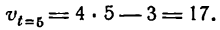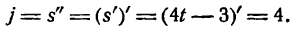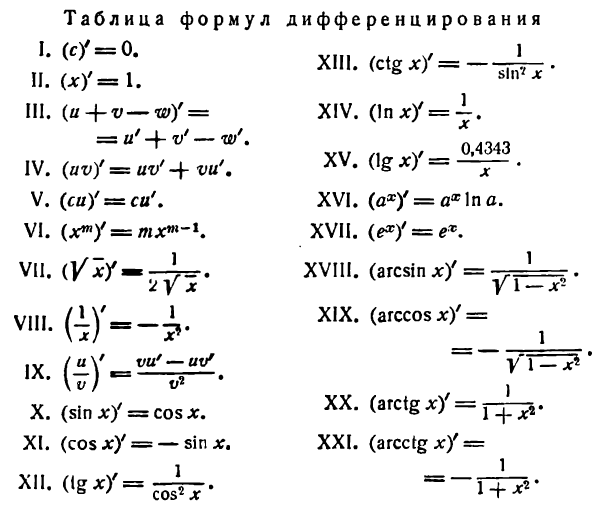Как считать производную степенной функции
3 февраля 2015
Этим видео я начинаю длинную серию уроков, посвященную производным. Этот урок состоит из нескольких частей.
В первую очередь, я расскажу вам, что вообще такое производные и как их считать, но не мудреным академическим языком, а так, как я сам это понимаю и как объясняю своим ученикам. Во-вторых, мы рассмотрим простейшее правило для решения задач, в которых будем искать производные суммы, производные разности и производные степенной функции.
Мы рассмотрим более сложные комбинированные примеры, из которых вы, в частности, узнаете, что подобные задачи, содержащие корни и даже дроби, могут быть решены при использовании формулы производной степенной функции. Кроме того, конечно, будет множество задач и примеров решений самого разного уровня сложности.
Вообще, изначально я собирался записать коротенький 5-минутный ролик, но сами видите, что из этого получилось. Поэтому хватит лирики — приступаем к делу.
Что такое производная?
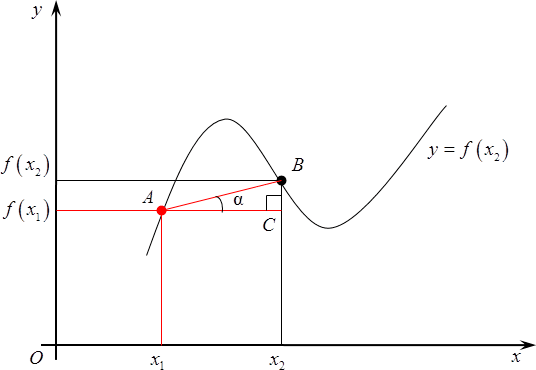
Итак, начнем издалека. Много лет назад, когда деревья были зеленее, а жизнь была веселее, математики задумались вот над чем: рассмотрим простую функцию, заданную своим графиком, назовем ее $y=fleft( x right)$. Разумеется, график существует не сам по себе, поэтому нужно провести оси $x$, а также ось $y$. А теперь давайте выберем любую точку на этом графике, абсолютно любую. Абсциссу назовем ${{x}_{1}}$, ордината, как не трудно догадаться, будет $fleft( {{x}_{1}} right)$.
Рассмотрим на том же графике еще одну точку. Не важно, какую, главное, чтобы она отличалась от первоначальной. У нее, опять же, есть абсцисса, назовем ее ${{x}_{2}}$, а также ордината — $fleft( {{x}_{2}} right)$.
Итак, мы получили две точки: у них разные абсциссы и, следовательно, разные значения функции, хотя последнее — необязательно. А вот что действительно важно, так это что, что из курса планиметрии нам известно: через две точки можно провести прямую и, причем, только одну. Вот давайте ее и проведем.
А теперь проведем через самую первую из них прямую, параллельную оси абсцисс. Получим прямоугольный треугольник. Давайте его обозначим $ABC$, прямой угол $C$. У этого треугольника возникает одно очень интересное свойство: дело в том, что угол$alpha $, на самом деле, равен углу, под которым пересекается прямая $AB$ с продолжением оси абсцисс. Судите сами:
- прямая $AC$параллельна оси $Ox$ по построению,
- прямая $AB$ пересекает $AC$ под $alpha $,
- следовательно, $AB$ пересекает $Ox$под тем же самым $alpha $.
Что мы можем сказать об $text{ }!!alpha!!text{ }$? Ничего конкретного, разве что в треугольнике $ABC$отношение катета $BC$ к катету $AC$ равно тангенсу этого самого угла. Так и запишем:
[tg=frac{BC}{AC}]
Разумеется, $AC$ в данном случае легко считается:
[AC={{x}_{2}}-{{x}_{1}}]
Точно также и $BC$:
[BC=fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)]
Другими словами, мы можем записать следующее:
[operatorname{tg}text{ }!!alpha!!text{ }=frac{fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)}{{{x}_{2}}-{{x}_{1}}}]
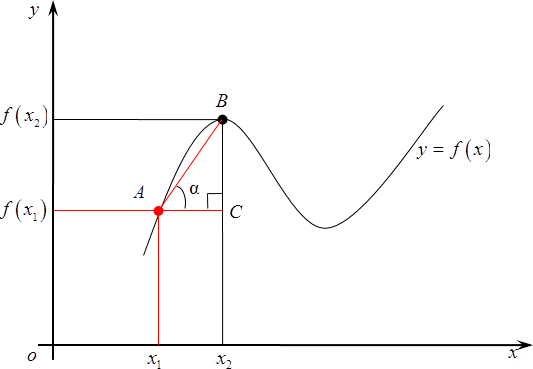
Теперь, когда мы все это выяснили, давайте вернемся к нашему графику и рассмотрим новую точку $B$. Сотрем старые значения и возьмем и возьмем $B$ где-нибудь поближе к ${{x}_{1}}$. Вновь обозначим ее абсциссу за ${{x}_{2}}$, а ординату — $fleft( {{x}_{2}} right)$.
Вновь рассмотрим наш маленький треугольник $ABC$и $text{ }!!alpha!!text{ }$ внутри него. Совершенно очевидно, что это будет уже совсем другой угол, тангенс будет также другим потому, что длины отрезков $AC$ и $BC$ существенно изменились, а формула для тангенса угла нисколько не поменялась — это по-прежнему соотношение между изменением функции и изменением аргумента.
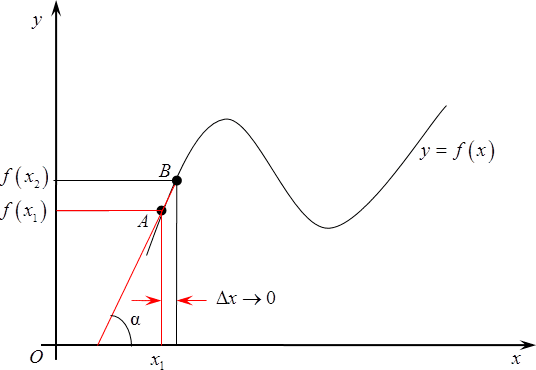
Наконец, продолжаем двигать $B$ все ближе к изначальной точке $A$, в результате треугольник еще уменьшится, а прямая, содержащая отрезок $AB$, все больше будет походить на касательную к графику функции.
В итоге, если продолжать сближение точек, т. е., уменьшать расстояние до нуля, то прямая $AB$, действительно, превратится в касательную к графику в данной точке, а $text{ }!!alpha!!text{ }$превратится из обычного элемента треугольника в угол между касательной к графику и положительным направлением оси $Ox$.
И вот тут мы плавно переходим к определению$f$, а именно, производной функции в точке ${{x}_{1}}$ называется тангенс угла $alpha $ между касательной к графику в точке ${{x}_{1}}$ и положительным направлением оси $Ox$:
[{f}’left( {{x}_{1}} right)=operatorname{tg}text{ }!!alpha!!text{ }]
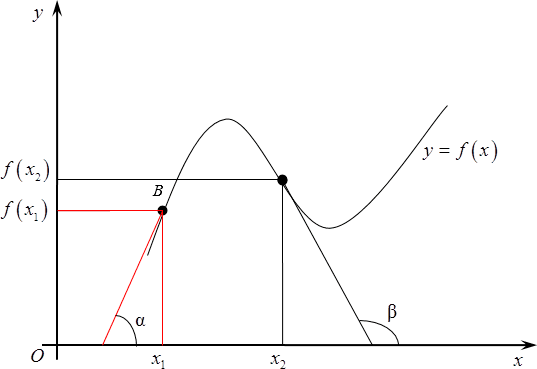
Возвращаясь к нашему графику, следует отметить, что в качестве ${{x}_{1}}$ можно выбрать любую точку на графике. Например, с тем же успехом мы могли снять штрих в точке, показанной на рисунке.
Угол между касательной и положительным направлением оси назовем $beta $. Соответственно, $f$ в ${{x}_{2}}$ будет равна тангенсу этого угла $beta $.
[{f}’left( {{x}_{2}} right)=tgtext{ }!!beta!!text{ }]
В каждой точке графика будет своя касательная, а, следовательно, свое значение функции. В каждом из этих случаев помимо точки, в которой мы ищем производную разности или суммы, или производную степенной функции, необходимо взять другую точку, находящуюся на некотором расстоянии от нее, а затем устремить эту точку к исходной и, разумеется, выяснить, как в процессе такого движения будет меняться тангенс угла наклона.
Производная степенной функции
К сожалению, подобное определение нас совершено не устраивает. Все эти формулы, картинки, углы не дают нам ни малейшего представления о том, как считать реальную производную в реальных задачах. Поэтому давайте немного отвлечемся от формального определения и рассмотрим более действенные формулы и приемы, с помощью которых уже можно решать настоящие задачи.
Начнем с самых простых конструкций, а именно, функций вида $y={{x}^{n}}$, т.е. степенных функций. В этом случае мы можем записать следующее: ${y}’=ncdot {{x}^{n-1}}$. Другими словами, степень, которая стояла в показателе, показывается в множителе спереди, а сам показатель уменьшается на единицу. Например:
[begin{align}& y={{x}^{2}} \& {y}’=2cdot {{x}^{2-1}}=2x \end{align}]
А вот другой вариант:
[begin{align}& y={{x}^{1}} \& {y}’={{left( x right)}^{prime }}=1cdot {{x}^{0}}=1cdot 1=1 \& {{left( x right)}^{prime }}=1 \end{align}]
Пользуясь этими простыми правилами, давайте попробуем снять штрих следующих примеров:
[fleft( x right)={{x}^{6}}]
Итак, мы получаем:
[{{left( {{x}^{6}} right)}^{prime }}=6cdot {{x}^{5}}=6{{x}^{5}}]
Теперь решим второе выражение:
[begin{align}& fleft( x right)={{x}^{100}} \& {{left( {{x}^{100}} right)}^{prime }}=100cdot {{x}^{99}}=100{{x}^{99}} \end{align}]
Разумеется, это были очень простые задачи. Однако реальные задачи более сложные и они не ограничиваются одними лишь степенями функции.
Итак, правило № 1 – если функция представлена в виде других двух, то производная этой суммы равна сумме производных:
[{{left( f+g right)}^{prime }}={f}’+{g}’]
Аналогично, производная разности двух функций равна разности производных:
[{{left( f-g right)}^{prime }}={f}’-{g}’]
Пример:
[{{left( {{x}^{2}}+x right)}^{prime }}={{left( {{x}^{2}} right)}^{prime }}+{{left( x right)}^{prime }}=2x+1]
Кроме того, есть еще одно важное правило: если перед некоторой $f$ стоит константа $c$, на которую эта функция умножается, то $f$ всей этой конструкции считается так:
[{{left( ccdot f right)}^{prime }}=ccdot {f}’]
Пример:
[{{left( 3{{x}^{3}} right)}^{prime }}=3{{left( {{x}^{3}} right)}^{prime }}=3cdot 3{{x}^{2}}=9{{x}^{2}}]
Наконец, еще одно очень важное правило: в задачах часто встречается отдельное слагаемое, которое вообще не содержит $x$. Например, мы можем наблюдать это в наших сегодняшних выражениях. Производная константы, т. е., числа, никак не зависящего от $x$, всегда равна нулю, причем совершенно неважно, чему равна константа $c$:
[{{left( c right)}^{prime }}=0]
Пример решения:
[{{left( 1001 right)}^{prime }}={{left( frac{1}{1000} right)}^{prime }}=0]
Еще раз ключевые моменты:
- Производная суммы двух функций всегда равна сумме производных: ${{left( f+g right)}^{prime }}={f}’+{g}’$;
- По аналогичным причинам производная разности двух функций равна разности двух производных: ${{left( f-g right)}^{prime }}={f}’-{g}’$;
- Если у функции присутствует множитель константа, то эту константу можно выносить за знак производной: ${{left( ccdot f right)}^{prime }}=ccdot {f}’$;
- Если вся функция представляет собой константу, то ее производная всегда ноль: ${{left( c right)}^{prime }}=0$.
Давайте посмотрим, как все это работает на реальных примерах. Итак:
[y={{x}^{5}}-3{{x}^{2}}+7]
Записываем:
[begin{align}& {{left( {{x}^{5}}-3{{x}^{2}}+7 right)}^{prime }}={{left( {{x}^{5}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{7}’= \& =5{{x}^{4}}-3{{left( {{x}^{2}} right)}^{prime }}+0=5{{x}^{4}}-6x \end{align}]
В этом примере мы видим и производную суммы, и производную разности. Итого, производная равна $5{{x}^{4}}-6x$.
Переходим ко второй функции:
[fleft( x right)=3{{x}^{2}}-2x+2]
Записываем решение:
[begin{align}& {{left( 3{{x}^{2}}-2x+2 right)}^{prime }}={{left( 3{{x}^{2}} right)}^{prime }}-{{left( 2x right)}^{prime }}+{2}’= \& =3{{left( {{x}^{2}} right)}^{prime }}-2{x}’+0=3cdot 2x-2cdot 1=6x-2 \end{align}]
Вот мы и нашли ответ.
Переходим к третьей функции — она уже посерьезней:
[y=2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5]
Решаем:
[begin{align}& {{left( 2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5 right)}^{prime }}={{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{{left( frac{1}{2}x right)}^{prime }}-{5}’= \& =2{{left( {{x}^{3}} right)}^{prime }}-3{{left( {{x}^{2}} right)}^{prime }}+frac{1}{2}cdot {x}’=2cdot 3{{x}^{2}}-3cdot 2x+frac{1}{2}cdot 1=6{{x}^{2}}-6x+frac{1}{2} \end{align}]
Ответ мы нашли.
Переходим к последнему выражению — самому сложному и самому длинному:
[y=6{{x}^{7}}-14{{x}^{3}}+4x+5,{{x}_{0}}=-1]
Итак, считаем:
[begin{align}& {{left( 6{{x}^{7}}-14{{x}^{3}}+4x+5 right)}^{prime }}={{left( 6{{x}^{7}} right)}^{prime }}-{{left( 14{{x}^{3}} right)}^{prime }}+{{left( 4x right)}^{prime }}+{5}’= \& =6cdot 7cdot {{x}^{6}}-14cdot 3{{x}^{2}}+4cdot 1+0=42{{x}^{6}}-42{{x}^{2}}+4 \end{align}]
Но на этом решение не заканчивается, потому что нас просят не просто снять штрих, а посчитать ее значение в конкретной точке, поэтому подставляем в выражение −1 вместо $x$:
[{y}’left( -1 right)=42cdot 1-42cdot 1+4=4]
Идем далее и переходим к еще более сложным и интересным примерам. Дело в том, что формула решения степенной производной ${{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}$ имеет еще более широкую область применения, чем обычно принято считать. С ее помощью можно решать примеры с дробями, корнями и т. д. Именно этим мы сейчас и займемся.
Для начала еще раз запишем формулу, которая поможет нам найти производную степенной функции:
[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]
А теперь внимание: до сих пор мы рассматривали в качестве $n$ лишь натуральные числа, однако ничего не мешаем рассмотреть дроби и даже отрицательные числа. Например, мы можем записать следующее:
[begin{align}& sqrt{x}={{x}^{frac{1}{2}}} \& {{left( sqrt{x} right)}^{prime }}={{left( {{x}^{frac{1}{2}}} right)}^{prime }}=frac{1}{2}cdot {{x}^{-frac{1}{2}}}=frac{1}{2}cdot frac{1}{sqrt{x}}=frac{1}{2sqrt{x}} \end{align}]
Ничего сложного, поэтому посмотрим, как эта формула поможет нам при решении более сложных задач. Итак, пример:
[y=sqrt{x}+sqrt[3]{x}+sqrt[4]{x}]
Записываем решение:
[begin{align}& left( sqrt{x}+sqrt[3]{x}+sqrt[4]{x} right)={{left( sqrt{x} right)}^{prime }}+{{left( sqrt[3]{x} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }} \& {{left( sqrt{x} right)}^{prime }}=frac{1}{2sqrt{x}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot {{x}^{-frac{2}{3}}}=frac{1}{3}cdot frac{1}{sqrt[3]{{{x}^{2}}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}{{x}^{-frac{3}{4}}}=frac{1}{4}cdot frac{1}{sqrt[4]{{{x}^{3}}}} \end{align}]
Возвращаемся к нашему примеру и записываем:
[{y}’=frac{1}{2sqrt{x}}+frac{1}{3sqrt[3]{{{x}^{2}}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}]
Вот такое сложное решение.
Переходим ко второму примеру — здесь всего два слагаемых, но каждое из них содержит как классическую степень, так и корни.
[y={{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x}]
Сейчас мы узнаем, как найти производную степенной функции, которая, кроме того, содержит и корень:
[begin{align}& {{left( {{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}}cdot sqrt[3]{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{3}}cdot {{x}^{frac{2}{3}}} right)}^{prime }}= \& ={{left( {{x}^{3+frac{2}{3}}} right)}^{prime }}={{left( {{x}^{frac{11}{3}}} right)}^{prime }}=frac{11}{3}cdot {{x}^{frac{8}{3}}}=frac{11}{3}cdot {{x}^{2frac{2}{3}}}=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}} \& {{left( {{x}^{7}}cdot sqrt[3]{x} right)}^{prime }}={{left( {{x}^{7}}cdot {{x}^{frac{1}{3}}} right)}^{prime }}={{left( {{x}^{7frac{1}{3}}} right)}^{prime }}=7frac{1}{3}cdot {{x}^{6frac{1}{3}}}=frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x} \end{align}]
Оба слагаемых посчитаны, осталось записать окончательный ответ:
[{y}’=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}}+frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x}]
Мы нашли ответ.
Производная дроби через степенную функцию
Но и на этом возможности формулы для решения производной степенной функции не заканчиваются. Дело в том, что с ее помощью можно считать не только примеры с корнями, но также и с дробями. Это как раз та редкая возможность, которая значительно упрощает решение таких примеров, но при этом зачастую игнорируется не только учениками, но и учителями.
Итак, сейчас мы попытаемся совместить сразу две формулы. С одной стороны, классическая производная степенной функции
[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]
С другой стороны мы знаем, что выражение вида $frac{1}{{{x}^{n}}}$ представимо в виде ${{x}^{-n}}$. Следовательно,
[left( frac{1}{{{x}^{n}}} right)’={{left( {{x}^{-n}} right)}^{prime }}=-ncdot {{x}^{-n-1}}=-frac{n}{{{x}^{n+1}}}]
Пример:
[{{left( frac{1}{x} right)}^{prime }}=left( {{x}^{-1}} right)=-1cdot {{x}^{-2}}=-frac{1}{{{x}^{2}}}]
Таким образом, производные простых дробей, где в числителе стоит константа, а в знаменателе — степень, также считаются с помощью классической формулы. Посмотрим, как это работает на практике.
Итак, первая функция:
[fleft( x right)=frac{1}{{{x}^{2}}}]
Считаем:
[{{left( frac{1}{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{-2}} right)}^{prime }}=-2cdot {{x}^{-3}}=-frac{2}{{{x}^{3}}}]
Первый пример решен, переходим ко второму:
[y=frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}}]
Решаем:
[begin{align}& {{left( frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}} right)}^{prime }}= \& ={{left( frac{7}{4{{x}^{4}}} right)}^{prime }}-{{left( frac{2}{3{{x}^{3}}} right)}^{prime }}+{{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{4}} right)}^{prime }} \& {{left( frac{7}{4{{x}^{4}}} right)}^{prime }}=frac{7}{4}{{left( frac{1}{{{x}^{4}}} right)}^{prime }}=frac{7}{4}cdot {{left( {{x}^{-4}} right)}^{prime }}=frac{7}{4}cdot left( -4 right)cdot {{x}^{-5}}=frac{-7}{{{x}^{5}}} \& {{left( frac{2}{3{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( frac{1}{{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( {{x}^{-3}} right)}^{prime }}=frac{2}{3}cdot left( -3 right)cdot {{x}^{-4}}=frac{-2}{{{x}^{4}}} \& {{left( frac{5}{2}{{x}^{2}} right)}^{prime }}=frac{5}{2}cdot 2x=5x \& {{left( 2{{x}^{3}} right)}^{prime }}=2cdot 3{{x}^{2}}=6{{x}^{2}} \& {{left( 3{{x}^{4}} right)}^{prime }}=3cdot 4{{x}^{3}}=12{{x}^{3}} \end{align}]…
Теперь собираем все эти слагаемые в единую формулу:
[{y}’=-frac{7}{{{x}^{5}}}+frac{2}{{{x}^{4}}}+5x+6{{x}^{2}}-12{{x}^{3}}]
Мы получили ответ.
Однако прежде чем двигаться дальше, хотел бы обратить ваше внимание на форму записи самих исходных выражений: в первом выражении мы записали $fleft( x right)=…$, во втором: $y=…$ Многие ученики теряются, когда видят разные формы записи. Чем отличаются $fleft( x right)$ и $y$? На самом деле, ничем. Это просто разные записи с одним и тем же смыслом. Просто когда мы говорим $fleft( x right)$, то речь идет, прежде всего, о функции, а когда речь идет об $y$, то чаще всего подразумевается график функции. В остальном же это одно и то же, т. е., производная в обоих случаях считается одинаково.
Сложные задачи с производными
В заключение хотелось бы рассмотреть пару сложных комбинированных задач, в которых используется сразу все то, что мы сегодня рассмотрели. В них нас ждут и корни, и дроби, и суммы. Однако сложными эти примеры будут лишь в рамках сегодняшнего видеоурока, потому что по-настоящему сложные функции производных будут ждать вас впереди.
Итак, заключительная часть сегодняшнего видеоурока, состоящая из двух комбинированных задач. Начнем с первой из них:
[y={{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x}]
Считаем:
[begin{align}& {{left( {{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}} right)}^{prime }}-{{left( frac{1}{{{x}^{3}}} right)}^{prime }}+left( sqrt[3]{x} right) \& {{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}} \& {{left( frac{1}{{{x}^{3}}} right)}^{prime }}={{left( {{x}^{-3}} right)}^{prime }}=-3cdot {{x}^{-4}}=-frac{3}{{{x}^{4}}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot frac{1}{{{x}^{frac{2}{3}}}}=frac{1}{3sqrt[3]{{{x}^{2}}}} \end{align}]
Производная функции равна:
[{y}’=3{{x}^{2}}-frac{3}{{{x}^{4}}}+frac{1}{3sqrt[3]{{{x}^{2}}}}]
Первый пример решен. Рассмотрим вторую задачу:
[y=-frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}}]
Во втором примере действуем аналогично:
[{{left( -frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( -frac{2}{{{x}^{4}}} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }}+{{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}]
Посчитаем каждое слагаемое отдельно:
[begin{align}& {{left( -frac{2}{{{x}^{4}}} right)}^{prime }}=-2cdot {{left( {{x}^{-4}} right)}^{prime }}=-2cdot left( -4 right)cdot {{x}^{-5}}=frac{8}{{{x}^{5}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}cdot {{x}^{-frac{3}{4}}}=frac{1}{4cdot {{x}^{frac{3}{4}}}}=frac{1}{4sqrt[4]{{{x}^{3}}}} \& {{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( frac{4}{xcdot {{x}^{frac{3}{4}}}} right)}^{prime }}={{left( frac{4}{{{x}^{1frac{3}{4}}}} right)}^{prime }}=4cdot {{left( {{x}^{-1frac{3}{4}}} right)}^{prime }}= \& =4cdot left( -1frac{3}{4} right)cdot {{x}^{-2frac{3}{4}}}=4cdot left( -frac{7}{4} right)cdot frac{1}{{{x}^{2frac{3}{4}}}}=frac{-7}{{{x}^{2}}cdot {{x}^{frac{3}{4}}}}=-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}} \end{align}]
Все слагаемые посчитаны. Теперь возвращаемся к исходной формуле и складываем вместе все три слагаемых. Получаем, что окончательный ответ будет таким:
[{y}’=frac{8}{{{x}^{5}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}}]
И на этом все. Это был первый наш урок. В следующих уроках мы рассмотрим более сложные конструкции, а также выясним, зачем вообще нужны производные.
Смотрите также:
- Производная произведения и частного
- Правила вычисления производных
- Теорема Виета
- Преобразование уравнений
- Тест по методу интервалов для строгих неравенств
- Тест по задачам B14: средний уровень, 2 вариант
Производная степени встречается в большинстве примеров на дифференцирование. Само правило нахождения производной степени простое. При дифференцировании степени с натуральным показателем проблем, как правило, не возникает. А вот найти производную степени с отрицательным или дробным показателями несколько сложнее. Легче всего понять, как найти производную степени, на примерах.
Открываем таблицу производных и правила дифференцирования.
Основная формула, по которой может быть найдена производная любой степени —
Примеры. Найти производную степени:
Поскольку при дифференцировании число выносится за знак производной, то множитель, стоящий перед степенью, при нахождении производной просто переписываем:
Нахождение производной степени, стоящей в знаменателе дроби, немного сложнее. Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель. Получившуюся в результате вычислений степень с отрицательным показателем снова преобразовываем.
Производная степени используется и для дифференцирования корней. Предварительно корень приводится к степени, а в найденной производной снова возвращаемся к корню.
Например,
Если корень в знаменателе, сначала преобразовываем его в степень, затем — поднимаем наверх с отрицательным показателем, а далее — как обычно, производная степени.
Например,
Примеры для самопроверки. Найти производную степени:
Показать решение

3.Дробные производные
3.1.Вычисление дробных производных
|
Дана функция f |
f(x) = x3 |
(9) |
||||||||||||||||||||||||||||||||||||
|
Необходимо вычислить дробные производные @1=2f(0), @1=2f(2), @5=2f(0). |
||||||||||||||||||||||||||||||||||||||
|
@1=2f = @x1=2x3 = |
(3 + 1 1=2)px5 = (7=2)x2px = 15p x2px = |
5 x2r |
, |
|||||||||||||||||||||||||||||||||||
|
@1=2 |
(3 + 1) |
(4) |
6 8 |
16 |
x |
|||||||||||||||||||||||||||||||||
|
15 |
||||||||||||||||||||||||||||||||||||||
|
где (4) = 6 и (7=2) = |
8p |
табличные значения. |
||||||||||||||||||||||||||||||||||||
|
@1=2f = 5 x2s |
(10) |
|||||||||||||||||||||||||||||||||||||
|
16 |
x |
|||||||||||||||||||||||||||||||||||||
|
• @1=2f(0) = 0 |
||||||||||||||||||||||||||||||||||||||
|
• @1=2f(2) = 5 22r |
10:2129 |
|||||||||||||||||||||||||||||||||||||
|
16 |
2 |
|||||||||||||||||||||||||||||||||||||
|
Очевидно, что @ |
5=2 |
= @ |
5=2 |
= @ |
2 |
@ |
1=2 |
, где @ |
1=2 |
уже вычислена ранее (10). Из этого |
||||||||||||||||||||||||||||
|
2+1=2 |
||||||||||||||||||||||||||||||||||||||
|
выражения ясно следует, что @ |
f(0) = 0. |
3.2.Вычисление дробных производных для дробной степени
|
Дана функция g |
g(x) = p |
(11) |
|||||||||||||||||
|
x |
|||||||||||||||||||
|
Необходимо вычислить дробные производные @1=2g(0), @1=2g(2). |
|||||||||||||||||||
|
@1=2 |
p |
(1=2 + 1) |
(3=2) |
= |
p |
, |
|||||||||||||
|
@1=2g = |
= |
x0 = |
|||||||||||||||||
|
x |
|||||||||||||||||||
|
(1=2 1=2 + 1) |
|||||||||||||||||||
|
1=2 |
(1) |
2 |
|||||||||||||||||
|
@xp |
|||||||||||||||||||
|
где (3=2) = |
3 |
табличное значение. Из этого выражения ясно следует, что @1=2g(0) = |
|||||||||||||||||
|
2 |
|||||||||||||||||||
|
= @1=2g(2) = |
p |
, |
|||||||||||||||||
|
2 |
10
урок 3. Математика ЕГЭ
Как найти производную от функции
Как считать производные?
Никто не использует определение производной, чтобы ее вычислить. Как же тогда ее посчитать?
Оказывается, существуют специальные формулы, с помощью которых производная от функции вычисляется достаточно просто.
Формулы производной
Выпишем теперь все формулы производной функции и порешаем примеры.
Производная от константы
Производная от любого числа всегда равна (0):
$$(const)^{/}=0;$$
Пример 1
$$(5)^{/}=0;$$
Производная от (x)
Производная просто от (x) равна (1):
$$x^{/}=1;$$
Производная от степени
$$(x^n)^{/}=n*x^{n-1};$$
Пример 2
$$(x^4)^{/}=4*x^{4-1}=4*x^{3};$$
$$(x^{10})^{/}=10*x^{10-1}=10*x^{9};$$
$$(x^{-3})^{/}=-3*x^{-3-1}=-3*x^{-4};$$
$$(x^{frac{1}{3}})^{/}=frac{1}{3}*x^{1-frac{1}{3}}=frac{1}{3}*x^{frac{2}{3}};$$
Производная от квадратного корня
$$(sqrt{x})^{/}=frac{1}{2sqrt{x}};$$
Тут полезно заметить, что формулу производной от квадратного корня можно не учить. Она сводится к формуле производной от степени:
$$(sqrt{x})^{/}=(x^{frac{1}{2}})^{/}=frac{1}{2}*x^{frac{1}{2}-1}=frac{1}{2}*x^{-frac{1}{2}}=frac{1}{2sqrt{x}};$$
Производная от синуса
$$sin(x)^{/}=cos(x);$$
Производная от косинуса
$$cos(x)^{/}=-sin(x);$$
Производная от тангенса
$$tg(x)^{/}=frac{1}{cos^{2}(x)};$$
Производная от котангенса
$$tg(x)^{/}=frac{-1}{sin^{2}(x)};$$
Производная от экспоненты
$$(e^x)^{/}=e^x;$$
Производная от показательной функции
$$(a^x)^{/}=a^x*ln(a);$$
Пример 3
$$(2^x)^{/}=2^{x}*ln(2);$$
Производная от натурального логарифма
$$(ln(x))^{/}=frac{1}{x};$$
Производная от логарифма
$$(log_{a}(x))^{/}=frac{1}{x*ln(a)};$$
Свойства производной
Помимо формул по вычислению производной еще есть свойства производной, их тоже надо выучить.
Вынесение константы за знак производной
$$(alpha*f(x))^{/}=alpha*(f(x))^{/};$$
Пример 4
$$(3*x^5)^{/}=3*(x^5)^{/}=3*5x^4=15x^4;$$
$$(10sin(x))^{/}==10*(sin(x))^{/}=10*cos(x);$$
Производная от суммы и разности двух функций
$$(f(x) pm g(x))^{/}=(f(x))^{/} pm (g(x))^{/};$$
Пример 5
$$(2x^4+x^3)^{/}=?$$
Тут (f(x)=2x^4), а (g(x)=x^3). Тогда по формуле производной от суммы:
$$(2x^4+x^3)^{/}=(2x^4)^{/}+(x^3)^{/}=2*(x^4)^{/}+(x^3)^{/}=2*4x^3+3x^2=8x^3+3x^2;$$
Пример 6
$$(ln(x)+cos(x))^{/}=(ln(x))^{/}+(cos(x))^{/}=frac{1}{x}-sin(x);$$
Пример 7
$$(x^6-e^x)^{/}=(x^6)^{/}-(e^x)^{/}=6x^5-e^x;$$
Производная от произведения двух функций
$$(f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/};$$
Пример 8
$$(x^2*sin(x))^{/}=?$$
$$(x^2*sin(x))^{/}=(x^2)^{/}*sin(x)+x^2*(sin(x))^{/}=2x*sin(x)+x^2*cos(x);$$
Пример 9
$$(ln(x)*e^x)^{/}=(ln(x))^{/}*e^x+ln(x)*(e^x)^{/}=frac{1}{x}*e^x+ln(x)*e^x;$$
Производная от частного двух функций
$$left(frac{f(x)}{g(x)}right)^{/}=frac{(f(x))^{/}*g(x)-f(x)*(g(x))^{/}}{(g(x))^2};$$
Пример 10
$$left(frac{x^3}{sin(x)}right)^{/}=frac{(x^3)^{/}*sin(x)-x^3*(sin(x))^{/}}{(sin(x))^2}=frac{3x^2*sin(x)-x^3*cos(x)}{(sin(x))^2};$$
Примеры нахождения производной
Рассмотрим несколько примеров нахождения производной, чтобы разобраться, как применяются свойства и формулы производной на практике.
Пример 11
$$(5x^3+2cos(x))^{/}=(5x^3)^{/}+(2cos(x))^{/}=$$
$$=5*(x^3)^{/}+2*(cos(x))^{/}=5*3*x^2+2*(-sin(x))=15x^2-2sin(x);$$
Пример 12
$$left(-frac{3x^2}{2x^4+5x}right)^{/}=-frac{(3x^2)^{/}*(2x^4+5x)-3x^2*(2x^4+5x)^{/}}{(2x^4+5x)^2}=$$
$$=-frac{6x*(2x^4+5x)-3x^2*(8x+5)}{(2x^4+5x)^2}=-frac{12x^5-24x^3+15x^2}{(2x^4+5x)^2};$$
Пример 13
$$(2xsqrt{x})^{/}=(2x)^{/}*sqrt{x}+2x*(sqrt{x})^{/}=$$
$$=2*sqrt{x}+2x*frac{1}{2sqrt{x}}=2*sqrt{x}+frac{2x}{2sqrt{x}}=2*sqrt{x}+sqrt{x}=3sqrt{x};$$
Производная сложной функции
Сложная функция — это функция не от аргумента (x), а от какой-то другой функции: (f(g(x))). Например, функция (sin(x^2)) будет сложной функцией: «внешняя» функция синуса берется от «внутренней» функции степени ((x^2)). Так как под синусом стоит аргумент не (x), а (x^2), то такая функция будет называться сложной.
Еще примеры сложных функций:
-
$$ln(3x^4);$$
Внешняя функция: натуральный логарифм; Внутренняя функция: ((3x^4)). -
$$cos(ln(x));$$
Внешняя функция: косинус; Внутренняя функция: ((ln(x))). -
$$e^{2x^2+3};$$
Внешняя функция: экспонента; Внутренняя функция: ((2x^2+3)). -
$$(sin(x))^3;$$
Внешняя функция: возведение в третью степень; Внутренняя функция: (sin(x)).
Чтобы посчитать производную от такой функции, нужно сначала найти производную внешней функции, а затем умножить результат на производную внутренней функции. В общем виде формула выглядит так:
$$f(g(x))^{/}=f^{/}(g(x))*g^{/}(x);$$
Скорее всего, выглядит непонятно, поэтому давайте разберем на примерах.
Пример 14
$$((cos(x))^4)^{/}=?$$
Внешней функцией тут будет возведение в четвертую степень, поэтому сначала считаем производную от степени по формуле ((x^n)^{/}=n*x^{n-1}). А потом умножаем результат на производную внутренней функции, у нас это функция косинуса, по формуле (cos(x)^{/}=-sin(x)):
$$((cos(x))^4)^{/}=underset{text{внешняя производная}}{underbrace{4*(cos(x))^3}}*underset{text{внутренняя производная}}{underbrace{(cos(x))^{/}}}=$$
$$=4*(cos(x))^3*(-sin(x))=-4*(cos(x))^3*sin(x);$$
Пример 15
$$(e^{2x^3+5})^{/}=?$$
Внешняя функция — это экспонента ((e^x)^{/}=e^x), а внутренняя функция — квадратный многочлен ((2x^3+5)):
$$(e^{2x^3+5})^{/}=e^{2x^3+5}*(2x^3+5)^{/}=e^{2x^3+5}*((2x^3)^{/}+5^{/})=e^{2x^3+5}*6x^2.$$
Пример 16
$$(ln((2x^2+3)^6))^{/}=?$$
Внешняя функция — это натуральной логарифм, берем производную от него по формуле ((ln(x))^{/}=frac{1}{x}), и умножаем на производную внутренней функции, у нас это шестая степень: ((x^n)^{/}=n*x^{n-1}). Но и на этом еще не все: под шестой степенью стоит не просто (x), а квадратный многочлен, значит еще нужно умножить на производную от этого квадратного многочлена:
$$ln((2x^2+3)^6)=frac{1}{(2x^2+3)^6}*((2x^2+3)^6)^{/}*(2x^2+3)^{/}=$$
$$=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*(4x+0)=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*4x=$$
$$=frac{6*(2x^2+3)^5*4x}{(2x^2+3)^6}=frac{24x*(2x^2+3)^5}{(2x^2+3)^6}=frac{24x}{(2x^2+3)^6}.$$
Вывод формул производной функции
Выведем некоторые из этих формул, чтобы было понимание, откуда они берутся. Но перед этим познакомимся с новыми обозначениями. Запись (f(x)) означает, что функция берется от аргумента (x). Например:
$$f(x)=x^3+sin(x);$$
На месте аргумента (x) может стоять все что угодно, например выражение (2x+3). Обозначение такой функции будет (f(2x+3)), а сама функция примет вид:
$$f(2x+3)=(2x+3)^3+sin(2x+3);$$
То есть, везде вместо аргумента (x) мы пишем (2x+3).
И несколько важных замечаний про (Delta f(x)) и (Delta x). Напомню, что значок (Delta) означает изменение некоторой величины. (Delta x) — изменения координаты (x) при переходе от одной точки на графике функции к другой; (Delta f(x)) — разница координат (y) между двумя точками на графике. Подробнее про это можно почитать в главе, где мы вводим понятие производной. Распишем (Delta x) для двух близких точек на графике функции (O) и (B):
$$Delta x=x_B-x_O;$$
Отсюда можно выразить (x_B):
$$x_B=x_O+Delta x;$$
Абсцисса (координата точки по оси (x)) точки (B) получается путем сложения абсциссы точки (O) и (Delta x).
Кстати, функцию (f(x)=x^3+sin(x)) от аргумента (x_B=x_O+Delta x) можно расписать:
$$f(x_B)=f(x_O+Delta x)=(x_O+Delta x)^3+sin(x_O+Delta x);$$
Рис.1. График произвольной функции
И распишем (Delta f):
$$Delta f(x)=f(x_B)-f(x_O)=f(x_O+Delta x)-f(x_O);$$
Тогда определение производной можно записать в виде:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x_O+Delta x)-f(x_O)}{Delta x} quad при quad Delta x to 0;$$
За (x_O) обычно обозначают точку, в окрестности которой берут производную. То есть, получается (x_O) — это абсцисса начальной точки, а (x_O+Delta x) — абсцисса конечной точки.
Нам это пригодится при выводе формул производной.
Производная квадратичной функции
Выведем теперь формулу производной от (f(x)=x^2), воспользовавшись определением производной:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
Распишем числитель (f(x+Delta x)-f(x)) с учетом, что (f(x)=x^2):
$$f(x+Delta x)-f(x)=(x+Delta x)^2-x^2=x^2+2xDelta x+(Delta x)^2-x^2=2xDelta x+(Delta x)^2;$$
Подставим в определение производной:
$$f^{/}(x)=frac{2xDelta x+(Delta x)^2}{Delta x}=frac{Delta x*(2x+Delta x)}{Delta x}=2x+Delta x;$$
Напоминаю, что (Delta x) это бесконечно малая величина:
$$(Delta x)^2 ll 0;$$
Поэтому этим слагаемым можно пренебречь. Вот мы и получили формулу для производной от квадратной функции:
$$f^{/}(x)=(x^2)^{/}=2x;$$
Производная от третьей степени
Аналогичные рассуждения можно провести для функции третьей степени:
$$f(x)=x^3;$$
Воспользуемся определением производной:
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
$$f(x+Delta x)-f(x)=(x+Delta x)^3-x^3=(x+Delta x-x)((x+Delta x)^2+(x+Delta x)*x+x^2)=$$
$$=Delta x*(x^2+2x*Delta x+(Delta x)^2+x^2+x*Delta x+x^2)=Delta x*(3x^2+3xDelta x);$$
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x}=frac{Delta x*(3x^2+3xDelta x)}{Delta x}=3x^2+3xDelta x;$$
Так как при умножении на бесконечно малую величину получается бесконечно малая величина, то слагаемым (3xDelta x) можно пренебречь:
$$f^{/}(x)=(x^3)^{/}=3x^2;$$
Точно таким же способом можно вывести формулы производных для любых степеней:
$$(x^4)^{/}=4x^3;$$
$$(x^5)^{/}=5x^4;$$
$$…$$
$$(x^n)^{/}=n*x^{n-1};$$
Кстати, эта формула справедлива и для дробных степеней.
Вывод остальных формул делается похожим образом, только там может понадобиться знание пределов. Вывод всех формул разбирается в университетском курсе математического анализа.
Что такое производная функции простыми словами? Для чего нужна производная? Определение производной
Как решать задания №7 из ЕГЭ по математике. Анализ графиков при помощи производной. Графики производной и графики функции
Исследуем функцию с помощью производной. Находим точки минимума и максимума, наибольшее и наименьшее значение функции. Точки экстремума. Промежутки возрастания и убывания.
Связь коэффициента наклона и тангенса угла наклона касательной к функции и производной функции в точке касания. Задание №7 в ЕГЭ по математике.
Формулы дифференцирования
Выгодно иметь такие правила, которые позволяли бы находить производные проще, с минимальной затратой времени. Действительно, такие правила имеются, причем они выводятся из основного правила дифференцирования.
Производная постоянной
Пусть С — постоянная величина; тогда равенство
у = С
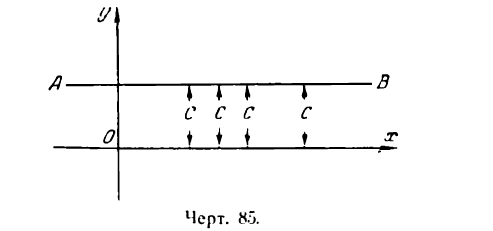
можно рассматривать как выражение функции, не меняющей своего значения с изменением аргумента. В справедливости этого можно убедиться, представив это равенство графически, т. е. в виде прямой линии АВ, параллельной оси Ох (рис. 85).
Действительно, с изменением абсциссы точек этой прямой ординаты их остаются постоянными.
Для нахождения производной функции у = С применим основное правило дифференцирования:
т. е. производная постоянной равна нулю.
Не следует производную постоянной смешивать с пределом постоянной, который, как известно, равен самой постоянной.
Производная функции у = х
Применяя основное правило дифференцирования, получим:
т. е. производная функции у = х равна единице, или: производная независимой переменной равна единице.
Производная алгебраической суммы функций
Возьмем функцию
где 
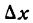
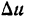
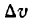
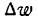
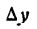
Слагаемые правой части последнего равенства являются производными функций 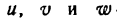
или
т. e. производная алгебраической суммы конечного числа функций равна алгебраической сумме производных каждой из них.
Производная произведения двух функций
Пусть дана функция
где и и v — функции от х имеющие производные по x. Дадим аргументу х приращение 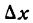
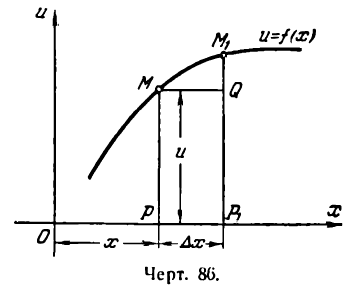
Но и и v не зависят от 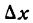
*) Это можно иллюстрировать на рис. 86. Здесь
при 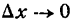
Приращение же функции 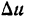
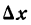
Таким образом,
Но
Далее, так как и дифференцируема, то она непрерывна, следовательно.
Если 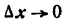
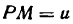
Поэтому
Итак,
т. е. производная произведения двух функций равна сумме произведений первой функции на производную второй и второй функции на производную первой.
Производная произведения постоянной на функцию
Возьмем функцию
где
причем функция и имеет производную по х. Применяя правило (IV), получим:
т. е. производная произведения постоянной на функцию равна произведению постоянной на производную функции.
Производная степени с целым положительным показателем
Возьмем сначала функцию
Представив ее в виде произведения и применяя правило (IV), получим:
Найдем производную новой функции:
Заменив ее произведением 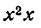
Поступив точно так же с функцией
найдем:
Если продолжать дифференцирование функций 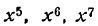
Таким образом, производная степени 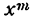
Однако выведенное правило справедливо для любого показателя т, что мы и докажем.
Производная функции 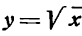
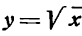
Таким образом,
т. е. производная функции 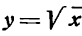
Производная функции 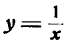
Заменив 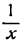
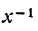
т. е. производная дроби 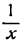
Производная частного
Возьмем функцию
где и и v — функции от х, имеющие производные по x, причем 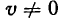
4-й шаг: применяя теоремы V, III, II и следствие 1 теоремы IV , находим:
Здесь, как и при выводе формулы (IV), нужно считать и и v не зависящими от 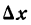
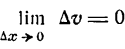
Итак,
т. е. производная частного равна дроби, знаменатель которой есть квадрат делителя, л числитель есть разность между произведением делителя на производную делимого и произведением делимого на производную делителя.
Применение формул дифференцирования
Рассмотрим несколько примеров на применение выведенных правил.
Пример:
Продифференцировать функцию
Решение:
По правилу (III) имеем:
Применяя к первым трем слагаемым правило (V), а к последнему— правило (I), получим:
Согласно правилам (VI) и (II) будем иметь:
Пример:
Продифференцировать функцию
Решение:
По правилу (IV) имеем:
По правилу (III):
По правилам (V), (II). (I) и (VI):
Этот пример можно решить иначе: сначала перемножить выражения в скобках, а затем продифференцировать полученную сумму:
Пример:
Продифференцировать функцию
Решение:
Преобразуем данную функцию следующим образом:
Применяя правила (V) и (VI), будем иметь:
Пример:
Продифференцировать функцию
Решение:
Представим данную функцию в следующем виде:
Применяя правила (III) и (V), получим:
По правилам (VIII), (VII) и (VI) имеем:
По правилам (VIII), (VII) и (VI) имеем:
Пример:
Продифференцировать функцию
Решение:
По правилу (IX) имеем:
Дифференцируя сумму по правилу (III), получим:
Наконец, по правилам (VI), (II), (I) и (V) найдем:
Можно иначе продифференцировать данную функцию, разделив в правой части данного уравнения почленно числитель на знаменатель, получим:
или
отсюда
Функция от функции (сложная функция)
Пусть нам даны две функции:
и
Если в (1) заменить и его выражением из (2), то получим:
Из уравнений (1) и (2) видно, что у есть функция от и, но и в свою очередь функция от х таким образом, функция у зависит от функции
Функцию (3) называют функцией от функции или слоэюной функцией.
Всякую сложную функцию можно представить в виде нескольких простых. Разберем примеры.
Пример:
Представить функцию
в виде двух простых.
Решение:
Положим
тогда
Мы получили две функции и и у более простого вида, чем данная.
Пример:
То же для функции
Решение:
Положим
тогда
Производная сложной функции
Возьмем функцию
причем
Пусть функция (2) имеет производную при данном х; тогда при 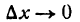
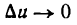
Применяя к правой части тождества (3) теорему о пределе произведения, получим:
Но, как известно,
Поэтому равенство (4) можно переписать:
Формула (5) служит для дифференцирования сложной функции, составленной из двух простых.
Пример:
Продифференцировать функцию
Решение:
Представим данную функцию в виде следующих двух:
Найдем сначала 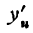
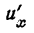
Искомая производная будет:
или, заменяя и его значением,
Как видно из формулы (5), производная сложной функции выражается произведением производных простых функций и, конечно, перестановка сомножителей не изменит результата. Однако удобней находить эти сомножители в одной определенно выбранной последовательности, которую полезно запомнить как правило. Так, например, для разобранного случая степенной функции это правило можно высказать следующим образом:
для дифференцирования сложной степенной функции*) нужно взять производную сначала от степени по основанию (принимая основание за аргумент), а потом от выражения, стоящего в основании, по независимой переменной и результаты перемножить.
*) Под сложной степенной функцией будем разуметь степень, основание которой есть функция от х.
Если 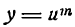
Пусть, например, требуется найти производную функции
Положив
и, применяя правило (6), будем иметь:
В дальнейшем для каждого особого случая будут даваться аналогичные правила, устанавливающие свою последовательность дифференцирования.
Разберем еще пример. Пусть требуется найти производную функции
Разбив ее на две простые функции, получим:
отсюда
Следовательно,
И здесь можно установить последовательность в нахождении производной, которая выразится следующим правилом: для дифференцирования сложной функции 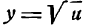
Так, например, производная функции
но вышеуказанному правилу найдется так:
Если дан корень другой степени, то его нужно предварительно преобразовать в степень с дробным показателем и применить правило для дифференцирования сложной степенной функции. Например,
Производные тригонометрических функций
По общему правилу дифференцирования находим:
1-й шаг:
2-й шаг:
Преобразуя разность синусов, будем иметь:
3-й шаг:
После деления числителя и знаменателя дроби на 2 получим:
4-й шаг:
Но
поэтому
Следовательно
2.
По формуле приведения можно написать:
отсюда
Для дифференцирования сложной функции 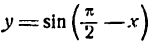
Согласно формуле (5) имеем:
Следовательно,
3.
Заменив tg x отношением 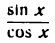
Итак, имеем:
4.
Как и в случае 3, имеем:
Таким образом,
В п. 2 настоящей лекции мы дифференцировали сложную функцию 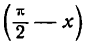
Однако эту операцию можно произвести и по следующему правилу:
для дифференцирования сложной тригонометрической функции *) нужно сначала взять производную от тригонометрической функции по выражению, стоящему под ее знаком (принимая его за аргумент), а потом от этого выражения по независимой переменной и результаты перемножить;
*) Под сложной тригонометрической функцией будем понимать тригонометрическую функцию сложного аргумента.
поэтому, считая и функцией от х, получаем:
Пользуясь правилом (1), процесс дифференцирования функции sin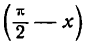
Пример:
Продифференцировать функцию
Решение:
Согласно правилу (2) настоящей лекции найдем:
Пример:
Продифференцировать функцию
Решение:
Переписав функцию в виде 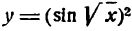
Но 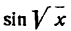
Следовательно,
Процесс дифференцирования данной функции можно записать следующим образом:
Производная логарифмической функции
Пусть дана функция
Для ее дифференцирования применим общее правило.
или
Положим
отсюда
Подставив значения 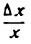
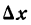
или, после потенцирования
Из равенства (2) следует, что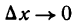
4-й шаг. Принимая во внимание условие (3), напишем:
Множитель 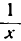
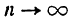
В подробных курсах анализа доказывается теорема: предел логарифма переменной величины равен логарифму предела этой же переменной величины; поэтому
Но, согласно,
Равенство (4) будет иметь вид
Следовательно,
т. е. производная натурального логарифма равна единице, деленной на аргумент.
Если дан десятичный логарифм, то его нужно предварительно выразить через натуральный. Мы знаем, что
Дифференцируя обе части последнего равенства, получим:
или
т. е. производная десятинного логарифма равна произведению производной натурального логарифма на постоянный множитель 0,4343.
Пример:
Продифференцировать функцию
Решение:
Данная функция сложная; положим
тогда
Отсюда согласно формуле (5) имеем:
Производную сложной логарифмической функции *) можно найти и по следующему правилу:
для дифференцирования сложной логарифмической функции нужно сначала взять производную от логарифма по выражению, стоящему под знаком логарифма (принимая его за аргумент), а потом от выражения, стоящего под знаком логарифма, по независимой переменной и результаты перемножить;
*) То-есть логарифмической функции сложного аргумента.
поэтому, считая и функцией х получаем:
Пример:
Продифференцировать функцию
Решение:
Согласно правилу (5) найдем:
Но cos ( 1—х) — сложная тригонометрическая функция; применяя к ней правило (2) , получим:
или
Пример:
Продифференцировать функцию
Решение:
Преобразуем сначала данную функцию, применив правила логарифмирования корня и дроби:
Продифференцировав полученную функцию [ln х по правилу (XIV), а ln (1 + x) по правилу (5)], найдем:
Производная степени при любом показателе
Мы вывели формулу
для m целого положительного. Докажем теперь справедливость этой формулы для любого показателя. Положим, что в равенстве
m имеет любое постоянное значение; логарифмируя это равенство по основанию е, получим:
Приняв во внимание, что ln у — сложная функция ( ln у зависит от у, а у зависит от x), дифференцируем обе части равенства (1) по х:
отсюда
Следовательно,
Производная показательной функции
Дана показательная функция
Прологарифмировав равенство (1) по основанию е, получим:
Дифференцируем это равенство по х, считая )ln у сложной функцией:
отсюда
Следовательно,
т. е. производная показательной функции 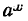
Если дана показательная функция
где е — основание натурального логарифма, то производная ее найдется по формуле (XVI):
или
т. е. производная показательной функции 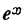
Пример:
Продифференцировать функцию
Решение:
Заменив данную сложную функцию двумя простыми, получим:
Согласно формуле (5) имеем:
Данную функцию можно дифференцировать и по следующему правилу:
для дифференцирования сложной показательной функции *) нужно сначала взять производную от показательной функции по выражению, стоящему в показателе (считая его аргументом), а потом от выражения, стоящего в показателе, по независимой переменной и результаты перемножить;
*) То-есть показательной функции сложного аргумента.
поэтому, считая и функцией от х, получаем:
Пример:
Продифференцировать функцию
Решение:
По правилу (3) настоящей лекции
Но согласно правилу (3)
Следовательно,
Производные обратных тригонометрических функций
1.
В силу определения арксинуса получаем:
Здесь sin у представляет сложную функцию (sin y зависит от у, а у зависит от х; дифференцируя обе части этого равенства по х, напишем):
или
откуда
Приняв во внимание, что
*) Здесь радикал берется с плюсом, так как значения arcsin х заключены между 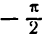
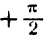
а также равенство (1), получим:
или
2.
Согласно определению арккосинуса имеем:
Дифференцируя обе части этого равенства по x, считая cos у сложной функцией, найдем:
или
отсюда
Но
**) И здесь радикал берется с плюсом, так как значения arccos х заключены между 0 и 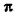
поэтому
или
*) Здесь радикал берется с плюсом, так как значения arcsin х
К . TZ
заключены между — у и +у,ав этом промежутке cos у имеет
положительные значения.
**) И здесь радикал берется с плюсом, так как значения arccos х заключены между 0 и я; в этом же промежутке sin у имеет положительные значения.
3.
Согласно определению арктангенса имеем:
Дифференцируя обе части этого равенства по х, как и в предыдущих случаях, получим:
или
отсюда
Но
Приняв во внимание равенство (2), получим:
Следовательно,
4.
Для данной функции имеем:
После дифференцирования этого равенства получим:
или
отсюда
Но
Следовательно,
т. е.
Пример:
Продифференцировать функцию
Решение:
Заменим данную сложную функцию двумя простыми:
Согласно формуле (5) имеем:
Для дифференцирования этой функции можно воспользоваться и следующим правилом:
для дифференцирования сложной обратной тригонометрической функции*) нужно сначала взять производную от обратной тригонометрической функции по выражению, стоящему под ее знаком (принимая его за аргумент), а потом от этого же выражения по независимой переменной и результаты перемножить;
*) То-есть обратной тригонометрической функции сложного аргумента.
таким образом, считая и функцией от х, получаем:
Пример:
Продифференцировать функцию 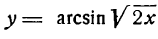
Решение:
Данная функция — обратная тригонометрическая и притом сложная; применяя вышеуказанное правило для производной аrсsin u, найдем:
Но 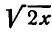
Следовательно,
Производная неявной функции
Пусть неявная функция у задана уравнением
Найдем производную у’, полагая, что она существует. Для этого дифференцируем обе части уравнения (1), применяя правило для производной алгебраической суммы, получим:
Так как ху — произведение переменных величин, то:
Таким образом, равенство (2) примет вид
или
Решая последнее уравнение относительно у’, найдем
Для дифференцирования данной функции можно было бы сначала выразить у через х, а потом уже найти производную от явной функции. В самом деле, из уравнения (1) имеем:
откуда
По внешнему виду этот результат отличается от найденного ранее, но если мы в равенстве (3) подставим значение у, то получим:
Таким образом, результаты дифференцирования в обоих случаях оказались одинаковыми. Однако переход от неявной к явной функции можно делать только в простейших случаях. Встречаются неявные функции, которые обратить в явные очень трудно и даже невозможно. Например, функцию у, заданную уравнением
ху + х = sin у, явно выразить нельзя. Поэтому приходится дифференцировать такие функции как неявные.
Разберем другой пример. Пусть требуется найти производную неявной функции у, заданной уравнением
Применяя правило дифференцирования алгебраической суммы, имеем:
Но 
Следовательно, равенство (4) примет вид
или
откуда
Производная второго порядка
Пусть функция у = f(x) имеет производную у’ = f'(x). Производная от f'(x) по x , если она существует, называется второй производной или производной второго порядка.
Вторую производную функции у = f(x) принято обозначать так:
Пример:
Найти вторую производную функции
Решение:
Механический смысл второй производной
Пусть тело движется прямолинейно по закону
Мы установили, что скорость v движения тела в данный момент t определяется как производная пути по времени, т. е.
Если тело движется неравномерно, то скорость v с течением времени
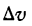
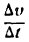

Положим, что 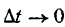
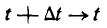
стремится к величине, которая называется ускорением в данный момент времени t. Обозначив это ускорение через j, будем иметь:
Таким образом, ускорение прямолинейного движения тела в данный момент равно второй производной пути по времени, вычисленной для данного момента.
Пример:
Точка движется прямолинейно по закону
Найти скорость и ускорение точки в момент t = 5.
Решение:
Для определения скорости нужно найти первую производную данной функции при t = 5. Таким образом:
и
Ускорение j равно второй производной функции при t = 5, т. е.
Величина ускорения оказалась постоянной для любого значения t, значит, движение точки по заданному закону происходит с постоянным ускорением.
Дополнение к формулам дифференцирования
Смотрите также:
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат