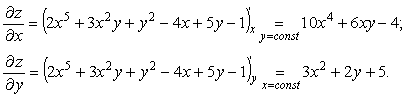Как найти производную частного в квадрате

урок 3. Математика ЕГЭ

Как найти производную от функции

Как считать производные?

Никто не использует определение производной, чтобы ее вычислить. Как же тогда ее посчитать?

Оказывается, существуют специальные формулы, с помощью которых производная от функции вычисляется достаточно просто.

Формулы производной

Выпишем теперь все формулы производной функции и порешаем примеры.

Производная от константы
Производная от любого числа всегда равна (0):
$$(const)^{/}=0;$$

Пример 1
$$(5)^{/}=0;$$

Производная от (x)
Производная просто от (x) равна (1):
$$x^{/}=1;$$

Производная от степени
$$(x^n)^{/}=n*x^{n-1};$$
Пример 2
$$(x^4)^{/}=4*x^{4-1}=4*x^{3};$$
$$(x^{10})^{/}=10*x^{10-1}=10*x^{9};$$
$$(x^{-3})^{/}=-3*x^{-3-1}=-3*x^{-4};$$
$$(x^{frac{1}{3}})^{/}=frac{1}{3}*x^{1-frac{1}{3}}=frac{1}{3}*x^{frac{2}{3}};$$

Производная от квадратного корня
$$(sqrt{x})^{/}=frac{1}{2sqrt{x}};$$
Тут полезно заметить, что формулу производной от квадратного корня можно не учить. Она сводится к формуле производной от степени:
$$(sqrt{x})^{/}=(x^{frac{1}{2}})^{/}=frac{1}{2}*x^{frac{1}{2}-1}=frac{1}{2}*x^{-frac{1}{2}}=frac{1}{2sqrt{x}};$$

Производная от синуса
$$sin(x)^{/}=cos(x);$$

Производная от косинуса
$$cos(x)^{/}=-sin(x);$$

Производная от тангенса
$$tg(x)^{/}=frac{1}{cos^{2}(x)};$$

Производная от котангенса
$$tg(x)^{/}=frac{-1}{sin^{2}(x)};$$

Производная от экспоненты
$$(e^x)^{/}=e^x;$$

Производная от показательной функции
$$(a^x)^{/}=a^x*ln(a);$$
Пример 3
$$(2^x)^{/}=2^{x}*ln(2);$$

Производная от натурального логарифма
$$(ln(x))^{/}=frac{1}{x};$$

Производная от логарифма
$$(log_{a}(x))^{/}=frac{1}{x*ln(a)};$$

Свойства производной

Помимо формул по вычислению производной еще есть свойства производной, их тоже надо выучить.

Вынесение константы за знак производной
$$(alpha*f(x))^{/}=alpha*(f(x))^{/};$$

Пример 4
$$(3*x^5)^{/}=3*(x^5)^{/}=3*5x^4=15x^4;$$
$$(10sin(x))^{/}==10*(sin(x))^{/}=10*cos(x);$$

Производная от суммы и разности двух функций
$$(f(x) pm g(x))^{/}=(f(x))^{/} pm (g(x))^{/};$$

Пример 5
$$(2x^4+x^3)^{/}=?$$
Тут (f(x)=2x^4), а (g(x)=x^3). Тогда по формуле производной от суммы:
$$(2x^4+x^3)^{/}=(2x^4)^{/}+(x^3)^{/}=2*(x^4)^{/}+(x^3)^{/}=2*4x^3+3x^2=8x^3+3x^2;$$

Пример 6
$$(ln(x)+cos(x))^{/}=(ln(x))^{/}+(cos(x))^{/}=frac{1}{x}-sin(x);$$

Пример 7
$$(x^6-e^x)^{/}=(x^6)^{/}-(e^x)^{/}=6x^5-e^x;$$

Производная от произведения двух функций
$$(f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/};$$

Пример 8
$$(x^2*sin(x))^{/}=?$$
$$(x^2*sin(x))^{/}=(x^2)^{/}*sin(x)+x^2*(sin(x))^{/}=2x*sin(x)+x^2*cos(x);$$

Пример 9
$$(ln(x)*e^x)^{/}=(ln(x))^{/}*e^x+ln(x)*(e^x)^{/}=frac{1}{x}*e^x+ln(x)*e^x;$$

Производная от частного двух функций
$$left(frac{f(x)}{g(x)}right)^{/}=frac{(f(x))^{/}*g(x)-f(x)*(g(x))^{/}}{(g(x))^2};$$

Пример 10
$$left(frac{x^3}{sin(x)}right)^{/}=frac{(x^3)^{/}*sin(x)-x^3*(sin(x))^{/}}{(sin(x))^2}=frac{3x^2*sin(x)-x^3*cos(x)}{(sin(x))^2};$$

Примеры нахождения производной

Рассмотрим несколько примеров нахождения производной, чтобы разобраться, как применяются свойства и формулы производной на практике.

Пример 11
$$(5x^3+2cos(x))^{/}=(5x^3)^{/}+(2cos(x))^{/}=$$
$$=5*(x^3)^{/}+2*(cos(x))^{/}=5*3*x^2+2*(-sin(x))=15x^2-2sin(x);$$

Пример 12
$$left(-frac{3x^2}{2x^4+5x}right)^{/}=-frac{(3x^2)^{/}*(2x^4+5x)-3x^2*(2x^4+5x)^{/}}{(2x^4+5x)^2}=$$
$$=-frac{6x*(2x^4+5x)-3x^2*(8x+5)}{(2x^4+5x)^2}=-frac{12x^5-24x^3+15x^2}{(2x^4+5x)^2};$$

Пример 13
$$(2xsqrt{x})^{/}=(2x)^{/}*sqrt{x}+2x*(sqrt{x})^{/}=$$
$$=2*sqrt{x}+2x*frac{1}{2sqrt{x}}=2*sqrt{x}+frac{2x}{2sqrt{x}}=2*sqrt{x}+sqrt{x}=3sqrt{x};$$

Производная сложной функции

Сложная функция — это функция не от аргумента (x), а от какой-то другой функции: (f(g(x))). Например, функция (sin(x^2)) будет сложной функцией: «внешняя» функция синуса берется от «внутренней» функции степени ((x^2)). Так как под синусом стоит аргумент не (x), а (x^2), то такая функция будет называться сложной.
Еще примеры сложных функций:

  • $$ln(3x^4);$$
    Внешняя функция: натуральный логарифм; Внутренняя функция: ((3x^4)).
  • $$cos(ln(x));$$
    Внешняя функция: косинус; Внутренняя функция: ((ln(x))).
  • $$e^{2x^2+3};$$
    Внешняя функция: экспонента; Внутренняя функция: ((2x^2+3)).
  • $$(sin(x))^3;$$
    Внешняя функция: возведение в третью степень; Внутренняя функция: (sin(x)).

    • Чтобы посчитать производную от такой функции, нужно сначала найти производную внешней функции, а затем умножить результат на производную внутренней функции. В общем виде формула выглядит так:
    $$f(g(x))^{/}=f^{/}(g(x))*g^{/}(x);$$
    Скорее всего, выглядит непонятно, поэтому давайте разберем на примерах.

    Пример 14
    $$((cos(x))^4)^{/}=?$$
    Внешней функцией тут будет возведение в четвертую степень, поэтому сначала считаем производную от степени по формуле ((x^n)^{/}=n*x^{n-1}). А потом умножаем результат на производную внутренней функции, у нас это функция косинуса, по формуле (cos(x)^{/}=-sin(x)):
    $$((cos(x))^4)^{/}=underset{text{внешняя производная}}{underbrace{4*(cos(x))^3}}*underset{text{внутренняя производная}}{underbrace{(cos(x))^{/}}}=$$
    $$=4*(cos(x))^3*(-sin(x))=-4*(cos(x))^3*sin(x);$$

    Пример 15
    $$(e^{2x^3+5})^{/}=?$$
    Внешняя функция — это экспонента ((e^x)^{/}=e^x), а внутренняя функция — квадратный многочлен ((2x^3+5)):
    $$(e^{2x^3+5})^{/}=e^{2x^3+5}*(2x^3+5)^{/}=e^{2x^3+5}*((2x^3)^{/}+5^{/})=e^{2x^3+5}*6x^2.$$

    Пример 16
    $$(ln((2x^2+3)^6))^{/}=?$$
    Внешняя функция — это натуральной логарифм, берем производную от него по формуле ((ln(x))^{/}=frac{1}{x}), и умножаем на производную внутренней функции, у нас это шестая степень: ((x^n)^{/}=n*x^{n-1}). Но и на этом еще не все: под шестой степенью стоит не просто (x), а квадратный многочлен, значит еще нужно умножить на производную от этого квадратного многочлена:
    $$ln((2x^2+3)^6)=frac{1}{(2x^2+3)^6}*((2x^2+3)^6)^{/}*(2x^2+3)^{/}=$$
    $$=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*(4x+0)=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*4x=$$
    $$=frac{6*(2x^2+3)^5*4x}{(2x^2+3)^6}=frac{24x*(2x^2+3)^5}{(2x^2+3)^6}=frac{24x}{(2x^2+3)^6}.$$

Вывод формул производной функции

Выведем некоторые из этих формул, чтобы было понимание, откуда они берутся. Но перед этим познакомимся с новыми обозначениями. Запись (f(x)) означает, что функция берется от аргумента (x). Например:
$$f(x)=x^3+sin(x);$$
На месте аргумента (x) может стоять все что угодно, например выражение (2x+3). Обозначение такой функции будет (f(2x+3)), а сама функция примет вид:
$$f(2x+3)=(2x+3)^3+sin(2x+3);$$
То есть, везде вместо аргумента (x) мы пишем (2x+3).

И несколько важных замечаний про (Delta f(x)) и (Delta x). Напомню, что значок (Delta) означает изменение некоторой величины. (Delta x) — изменения координаты (x) при переходе от одной точки на графике функции к другой; (Delta f(x)) — разница координат (y) между двумя точками на графике. Подробнее про это можно почитать в главе, где мы вводим понятие производной. Распишем (Delta x) для двух близких точек на графике функции (O) и (B):
$$Delta x=x_B-x_O;$$
Отсюда можно выразить (x_B):
$$x_B=x_O+Delta x;$$
Абсцисса (координата точки по оси (x)) точки (B) получается путем сложения абсциссы точки (O) и (Delta x).

Кстати, функцию (f(x)=x^3+sin(x)) от аргумента (x_B=x_O+Delta x) можно расписать:

$$f(x_B)=f(x_O+Delta x)=(x_O+Delta x)^3+sin(x_O+Delta x);$$

Определение производной

Рис.1. График произвольной функции

И распишем (Delta f):
$$Delta f(x)=f(x_B)-f(x_O)=f(x_O+Delta x)-f(x_O);$$
Тогда определение производной можно записать в виде:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x_O+Delta x)-f(x_O)}{Delta x} quad при quad Delta x to 0;$$

За (x_O) обычно обозначают точку, в окрестности которой берут производную. То есть, получается (x_O) — это абсцисса начальной точки, а (x_O+Delta x) — абсцисса конечной точки.

Нам это пригодится при выводе формул производной.

Производная квадратичной функции

Выведем теперь формулу производной от (f(x)=x^2), воспользовавшись определением производной:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
Распишем числитель (f(x+Delta x)-f(x)) с учетом, что (f(x)=x^2):
$$f(x+Delta x)-f(x)=(x+Delta x)^2-x^2=x^2+2xDelta x+(Delta x)^2-x^2=2xDelta x+(Delta x)^2;$$
Подставим в определение производной:
$$f^{/}(x)=frac{2xDelta x+(Delta x)^2}{Delta x}=frac{Delta x*(2x+Delta x)}{Delta x}=2x+Delta x;$$
Напоминаю, что (Delta x) это бесконечно малая величина:
$$(Delta x)^2 ll 0;$$
Поэтому этим слагаемым можно пренебречь. Вот мы и получили формулу для производной от квадратной функции:
$$f^{/}(x)=(x^2)^{/}=2x;$$

Производная от третьей степени

Аналогичные рассуждения можно провести для функции третьей степени:
$$f(x)=x^3;$$
Воспользуемся определением производной:
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
$$f(x+Delta x)-f(x)=(x+Delta x)^3-x^3=(x+Delta x-x)((x+Delta x)^2+(x+Delta x)*x+x^2)=$$
$$=Delta x*(x^2+2x*Delta x+(Delta x)^2+x^2+x*Delta x+x^2)=Delta x*(3x^2+3xDelta x);$$
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x}=frac{Delta x*(3x^2+3xDelta x)}{Delta x}=3x^2+3xDelta x;$$
Так как при умножении на бесконечно малую величину получается бесконечно малая величина, то слагаемым (3xDelta x) можно пренебречь:
$$f^{/}(x)=(x^3)^{/}=3x^2;$$
Точно таким же способом можно вывести формулы производных для любых степеней:
$$(x^4)^{/}=4x^3;$$
$$(x^5)^{/}=5x^4;$$
$$…$$
$$(x^n)^{/}=n*x^{n-1};$$
Кстати, эта формула справедлива и для дробных степеней.

Вывод остальных формул делается похожим образом, только там может понадобиться знание пределов. Вывод всех формул разбирается в университетском курсе математического анализа.

Что такое производная функции простыми словами? Для чего нужна производная? Определение производной

Как решать задания №7 из ЕГЭ по математике. Анализ графиков при помощи производной. Графики производной и графики функции

Исследуем функцию с помощью производной. Находим точки минимума и максимума, наибольшее и наименьшее значение функции. Точки экстремума. Промежутки возрастания и убывания.

Связь коэффициента наклона и тангенса угла наклона касательной к функции и производной функции в точке касания. Задание №7 в ЕГЭ по математике.

Источник

Простое объяснение принципов решения частных производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения частных производных

Вычисление частной производной функции из нескольких переменных осуществляется по тем же правилам, что и функций с одной переменной. Разница лишь той, что другие переменные не участвуют дифференцировании (вычислении производной).

Проще говоря, чтобы найти частную производную функции z = x^{8} + 32y^{4} по переменной x,переменную y будем считать константой (производная константы равна нулю), после чего находим производную функции по x с помощью таблицы производных элементарных функций – {z_{x}}' = 8x^{7}. Готово!

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры решения частных производных

Задача

Найти частные производные функции u = x^{2} + 3xy + 4y^{2}.

Решение

Частная производная функции по независимой переменной x:

Производная суммы равна сумме производных. Производная от x^{2} вычисляется по правилам вычислений производных функций одного аргумента, производная от слагаемого 3xy вычисляется как производная от функции двух аргументов. При этом аргумент y считается константой. Производная от слагаемого 4y^{2} вычисляется как производная от константы.

frac{partial{u}}{partial{x}} = (x^{2})' + (3xy)' + (4y^{2})' = 2x + 3y + 0 = 2x + 3y.

Частная производная функции по независимой переменной y:

Здесь вычисления также происходят по правилам вычисления производной суммы. Производная от x^{2} вычисляется как производная от константы (независимым аргументом при этом считается y). Производная от слагаемого 3xy вычисляется как производная от функции двух аргументов. При этом аргумент x считается константой, а y – независимым аргументом. Вычисление производной от слагаемого 4y^{2} осуществляется по правилам вычисления производных функций с одним аргументом.

frac{partial{u}}{partial{y}} = (x^{2})' + (3xy)' + (4y^{2})' = 0 + 3x + 8y = 3x + 8y.

Ответ

frac{partial{u}}{partial{x}} = 2x + 3y, frac{partial{u}}{partial{y}} = 3x + 8y.

Задача

Найти частные производные функции u = e^{frac{x}{y}}.

Решение

Найдём частную производную функции по независимой переменной x:

Функция e^{frac{x}{y}} является сложной. Производной показательной функции с основанием e является сама функция. Производная показателя степени вычисляется в при условии, что y является константой и равна u = frac{1}{y}. Производная функции u равна произведению e^{frac{x}{y}} и frac{1}{y}. В результате получаем:

{u_{x}}' = frac{1}{y}e^{frac{x}{y}}.

Найдём частную производную функции по независимой переменной y:

По аналогии с предыдущим случаем производная функции будет равна произведению производных от функции e^{frac{x}{y}} и показателя её степени frac{x}{y}:

Считая x постоянной величиной, находим производную по независимому аргументу y:

(e^{frac{x}{y}})' = e^{frac{x}{y}}

(frac{x}{y})' = -frac{x}{y^{2}}

{u_{y}}' = -frac{x}{y^{2}}e^{frac{x}{y}}.

Ответ

{u_{x}}' = frac{1}{y}e^{frac{x}{y}}, {u_{y}}' = -frac{x}{y^{2}}e^{frac{x}{y}}.

Задача

Найти частные производные функции z = x^{n} + y^{n}, n - натуральное число.

Решение

Частная производная функции по независимой переменной x будет равна производной от x^{n}. Производная от слагаемого y^{n} при этом будет равна нулю как производная от константы.

frac{partial{z}}{partial{x}} = nx^{n-1}

Частная производная функции по независимой переменной y находится аналогичным образом, при этом предполагается, что x является константой.

frac{partial{z}}{partial{y}} = ny^{n-1}

Ответ

frac{partial{z}}{partial{x}} = nx^{n-1}, frac{partial{z}}{partial{y}} = ny^{n-1}

Задача

Найти частные производные функции u = ysin{x} + sin{y}.

Решение

Частная производная функции u по независимой переменной x определяется слагаемым u = ysin{x}. Производная второго слагаемого – sin{y} равна нулю, как производная от константы.

frac{partial{u}}{partial{x}} = ycos{x}

В свою очередь, частная производная функции u по независимой переменной y будет определяться обоими слагаемым:

{(ysin{x})_y}' = sin{x}

{(sin{y})_y}' = cos{y}

Таким образом, окончательно получаем:

frac{partial{u}}{partial{y}} = sin{x} + cos{y}

Ответ

frac{partial{u}}{partial{x}} = ycos{x}, frac{partial{u}}{partial{y}} = sin{x} + cos{y}

Задача

Найти частные производные функции u = x^{sin{y}}, x > 0.

Решение

При нахождении производной по независимой переменной x, функцию u = x^{sin{y}} следует рассматривать как степенную. По правилу нахождения производной степенной функции получаем:

frac{partial{u}}{partial{x}} = sin{y}cdot{x^{sin{y} - 1}}

Производная по независимой переменной y находится по правилу вычисления производной показательной функции, которая, в свою очередь, определяется по правилам нахождения производных сложных функций, т.к. переменная y входит в показатель степени виде функции sin{x}.

Производная показательной функции равна:

{(x^{sin{y}})_{y}}' = x^{sin{y}}cdot{ln{x}}

Производная показателя степени равна:

{(sin{y})}' = cos{y}

В результате получаем:

frac{partial{u}}{partial{y}} = x^{sin{y}}cdot{ln{x}}cdot{cos{y}}

Ответ

frac{partial{u}}{partial{x}} = sin{y}cdot{x^{sin{y} - 1}}, frac{partial{u}}{partial{y}} = x^{sin{y}}cdot{ln{x}}cdot{cos{y}}

Задача

Найти частные производные функции z = e^{x}cos{y} - e^{y}sin{x}.

Решение

Частная производная по независимой переменной x находится как сумма слагаемых:

{(e^{x}cos{y})_{x}}' = e^{x}cos{y}

{(- e^{y}sin{x})_{x}}' = - e^{y}cos{x}

Частная производная по независимой переменной y находится как сумма слагаемых:

{(e^{x}cos{y})_{y}}' = -e^{x}sin{y}

{(- e^{y}sin{x})_{y}}' = - e^{y}sin{x}

Ответ

frac{partial{z}}{partial{x}} = e^{x}cos{y} - e^{y}cos{x}, frac{partial{z}}{partial{y}} = -e^{x}sin{y} - e^{y}sin{x}

Задача

Найти частные производные функции z = sqrt{x^{2} + y^{2}}.

Решение

По правилу нахождения производной квадратного корня получаем, рассматривая x как независимый аргумент:

{(sqrt{x^{2} + y^{2}})_{x}}' = frac{x}{sqrt{x^{2} + y^{2}}}

Т.к. функция является сложной, то результат вычисления производной от квадратного корня – frac{1}{2sqrt{x^{2} + y^{2}}} следует домножить на производную подкоренного выражения: {({x^{2} + y^{2}})_{x}}' = 2x.

Рассматривая y в качестве независимого аргумента, получаем:

{(sqrt{x^{2} + y^{2}})_{y}}' = frac{y}{sqrt{x^{2} + y^{2}}}

По аналогии с предыдущим случаем, результат вычисления производной от квадратного корня – frac{1}{2sqrt{x^{2} + y^{2}}} следует домножить на производную подкоренного выражения: {({x^{2} + y^{2}})_{y}}' = 2y.

Ответ

frac{partial{z}}{partial{x}} = frac{x}{sqrt{x^{2} + y^{2}}}, frac{partial{z}}{partial{y}} = frac{y}{sqrt{x^{2} + y^{2}}}

Задача

Найти частные производные функции z = e^{arctg {frac{y}{x}}}.

Решение

Данная функция является сложной, поэтому процесс нахождения производной данной функции целесообразно производить в несколько этапов.

Производная показательной функции с основанием e равна самой себе. Далее необходимо найти производную показателя степени: arctg {frac{y}{x}}. В свою очередь аргумент функции арктангенс в данном случае также представляет собой сложную функцию: frac{y}{x}. Результирующая производная будет равна произведению производных трёх функций: e^{arctg {frac{y}{x}}}, arctg {frac{y}{x}} и frac{y}{x}.

Нахождение частной производной функции по аргументу x:

frac{partial{z}}{partial{x}} = e^{arctg {frac{y}{x}}}cdot{(arctg {frac{y}{x}})_{x}}'cdot{({frac{y}{x}})_{x}}' = e^{arctg {frac{y}{x}}}cdot{frac{1}{1+({frac{y}{x}})^2}}cdot{frac{-y}{x^{2}}} = e^{arctg {frac{y}{x}}}cdot{frac{1}{frac{x^{2}+y^{2}}{x^{2}}}}cdot{frac{-y}{x^{2}}} = e^{arctg {frac{y}{x}}}cdot{frac{x^{2}}{x^{2}+y^{2}}}cdot{frac{-y}{x^{2}}} = - e^{arctg {frac{y}{x}}}cdot{frac{y}{x^{2} + y^{2}}}

Нахождение частной производной функции по аргументу y:

frac{partial{z}}{partial{y}} = e^{arctg {frac{y}{x}}}cdot{(arctg {frac{y}{x}})_{y}}'cdot{({frac{y}{x}})_{y}}' = e^{arctg {frac{y}{x}}}cdot{frac{1}{1+({frac{y}{x}})^2}}cdot{frac{1}{x}} = e^{arctg {frac{y}{x}}}cdot{frac{1}{frac{x^{2}+y^{2}}{x^{2}}}}cdot{frac{1}{x}} = e^{arctg {frac{y}{x}}}cdot{frac{x^{2}}{x^{2}+y^{2}}}cdot{frac{1}{x}} = e^{arctg {frac{y}{x}}}cdot{frac{x}{x^{2} + y^{2}}}

Ответ

frac{partial{z}}{partial{x}} = - e^{arctg {frac{y}{x}}}cdot{frac{y}{x^{2} + y^{2}}}, frac{partial{z}}{partial{y}} = e^{arctg {frac{y}{x}}}cdot{frac{x}{x^{2} + y^{2}}}

Задача

Найти частные производные первого и второго порядков функции z = xsin(x +y).

Решение

Найдём частную производную первого порядка по аргументу x:

frac{partial{z}}{partial{x}} = sin(x + y) + xcos(x + y)

Найдём частную производную второго порядка по аргументу x:

frac{partial^{2}{z}}{partial{x}^{2}} = cos(x + y) + cos(x + y) - xsin(x +y)

Найдём частную производную первого порядка по аргументу y:

frac{partial{z}}{partial{y}} = xcos(x + y)

Найдём частную производную второго порядка по аргументу y:

frac{partial^{2}{z}}{partial{y}^{2}} = -xsin(x +y)

Ответ

frac{partial{z}}{partial{x}} = sin(x + y) + xcos(x + y), frac{partial^{2}{z}}{partial{x}^{2}} = 2cos(x + y) - xsin(x +y), frac{partial{z}}{partial{y}} = xcos(x + y), frac{partial^{2}{z}}{partial{y}^{2}} = -xsin(x +y)

Задача

Найти частные производные первого и второго порядков функции z = (frac{x}{y})^{2}.

Решение

Найдём частную производную первого порядка по аргументу x:

frac{partial{z}}{partial{x}} = 2cdot{frac{x}{y}}cdot{frac{1}{y}}

Найдём частную производную второго порядка по аргументу x:

frac{partial^{2}{z}}{partial{x}^{2}} = frac{2}{y^{2}}

Найдём частную производную первого порядка по аргументу y:

frac{partial{z}}{partial{y}} = 2cdot{frac{x}{y}}cdot{frac{-x}{y^{2}}} = -frac{2x^{2}}{y^{3}}

Найдём частную производную второго порядка по аргументу y:

frac{partial^{2}{z}}{partial{y}^{2}} = frac{6x^{2}y^{2}}{y^{6}} = frac{6x^{2}}{y^{4}}

Ответ

frac{partial{z}}{partial{x}} = frac{2x}{y^{2}}, frac{partial^{2}{z}}{partial{x}^{2}} = frac{2}{y^{2}}, frac{partial{z}}{partial{y}} = -frac{2x^{2}}{y^{3}}, frac{partial^{2}{z}}{partial{y}^{2}} = frac{6x^{2}}{y^{4}}

Источник

Содержание:

  • Формула
  • Примеры вычисления производной частного функций

Формула

$$dleft(frac{u(x)}{v(x)}right)=frac{d u(x) v(x)-u(x) d v(x)}{v^{2}(x)}, v(x) neq 0$$

Производная частного равна производная числителя, умноженная на знаменатель, минус производная
знаменателя, умноженная на числитель, и разность делится на знаменатель в квадрате.

Примеры вычисления производной частного функций

Пример

Задание. Найти производную функции $y(x)=frac{x}{sin x}$

Решение. Заданная функция представляет частное двух функций $u(x)=x$ и $v(x)=sin x$, тогда ее производная, согласно формуле, будет равна:

$$begin{aligned} y^{prime}(x) &=left(frac{x}{sin x}right)^{prime}=frac{(x)^{prime} cdot sin x-x cdot(sin x)^{prime}}{(sin x)^{2}}=\ &=frac{1 cdot sin x-x cdot cos x}{sin ^{2} x}=frac{sin x-x cos x}{sin ^{2} x} end{aligned}$$

Ответ. $begin{aligned} y^{prime}(x) &=frac{sin x-x cos x}{sin ^{2} x} end{aligned}$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Вычислить производную функции $y(x)=frac{e^{x}}{operatorname{tg} x}$

Решение. В данном случае функции $u(x)=e^{x}, v(x)=operatorname{tg} x$ тогда, согласно формуле производной частного, имеем:

$$y^{prime}(x)=left(frac{e^{x}}{operatorname{tg} x}right)^{prime}=frac{left(e^{x}right)^{prime} cdot operatorname{tg} x-e^{x} cdot(operatorname{tg} x)^{prime}}{(operatorname{tg} x)^{2}}=$$
$$=frac{e^{x} cdot operatorname{tg} x-e^{x} cdot frac{1}{cos ^{2} x}}{operatorname{tg}^{2} x}=frac{e^{x}left(frac{sin x}{cos x}-frac{1}{cos ^{2} x}right)}{operatorname{tg}^{2} x}=$$
$$=frac{e^{x}(sin x cos x-1)}{frac{sin ^{2} x}{cos ^{2} x} cdot cos ^{2} x}=frac{e^{x}(sin x cos x-1)}{sin ^{2} x}$$

Ответ. $y^{prime}(x)=frac{e^{x}(sin x cos x-1)}{sin ^{2} x}$

Читать дальше: производная сложной функции (u(v(x))’.

Источник

Данный онлайн калькулятор предназначен для решения частных производных первого и второго порядков.
Частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Следовательно, частные производные находятся так же, как и производные функций одной переменной. Частная производная это обобщенное понятие производной, когда в функции содержится несколько переменных.

Калькулятор поможет найти частные производные функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.

Основные функции

left(a=operatorname{const} right)

  • x^{a}: x^a

модуль x: abs(x)

Производные

Для того, чтобы найти производную функции f(x)
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции f(x,y,z,...,t) напишите в окне гаджета: f[x, y, z,…,t], j, где j
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где j означает тоже, что и Выше.

Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.

Примеры
  • x*E^x, x;
  • x^3*E^x, {x,17};
  • x^3*y^2*Sin[x+y], x;
  • x^3*y^2*Sin[x+y], y,
  • x/(x+y^4), {x,6}.
Источник

Частные производные

Частной производной по x функции z = f(x,y) в точке A(x0,y0) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.

Частные производные функции z(x,y) находятся по следующим формулам: Частные производные

Вторые частные производные функции z(x,y) находятся по формулам:

Вторые частные производные

Смешанные частные производные функции z(x,y) находятся по формулам: Смешанные частные производные

Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word.

  • Решение онлайн
  • Видеоинструкция
  • Также решают

Правила ввода функции, заданной в явном виде




Примеры

x2+xy ≡ x^2+x*y.

cos2(2x+y) ≡ (cos(2*x+y))^2

≡ (x-y)^(2/3)

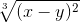
Правила ввода функции, заданной в неявном виде

  1. Все переменные выражаются через x,y,z


Примеры

≡ x^2/(z+y)

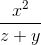
cos2(2x+zy) ≡ (cos(2*x+z*y))^2

≡ z+(x-y)^(2/3)

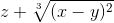
Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.

Частные производные функции нескольких переменных

Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δxz=f(x+Δx,y)-f(x,y) – это частное приращение функции z по аргументу x; Δyz=f(x,y+Δy)-f(x,y) – это частное приращение функции z по аргументу у.

Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:

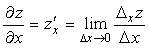
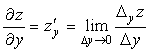
– это частная производная функции z по аргументу x;

– это частная производная функции z по аргументу у.

Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.

Пример 1. z=2x5+3x2y+y2–4x+5y-1

Пример 2. Найти частные производные функции z = f(x;y) в точке A(x0;y0).



Находим частные производные:





Найдем частные производные в точке А(1;1)





Находим вторые частные производные:



Найдем смешанные частные производные:

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти эирподс в кейсе с айфона
  • Как найти своего мужчину отзывы
  • Как найти парней ритуал
  • Как найти группу крови в карточке
  • Как исправить ошибки жесткого диска переназначенные сектора

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии