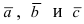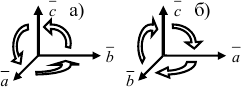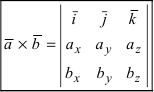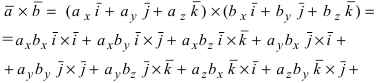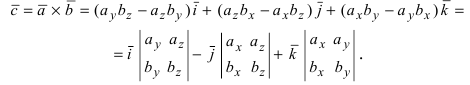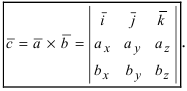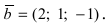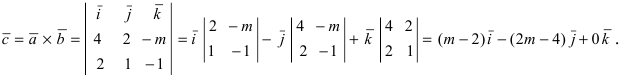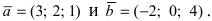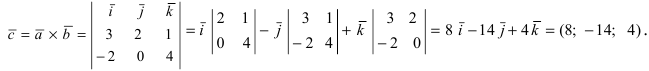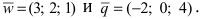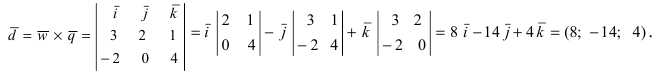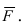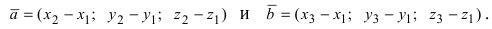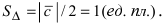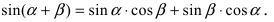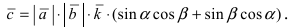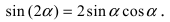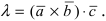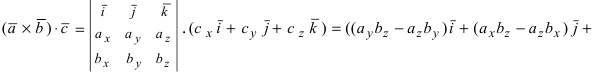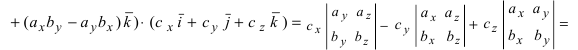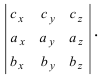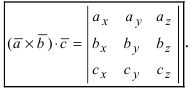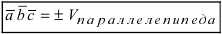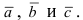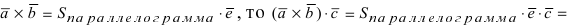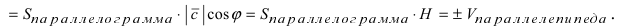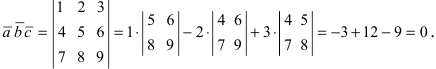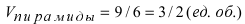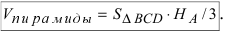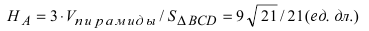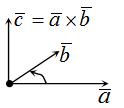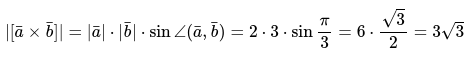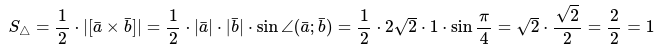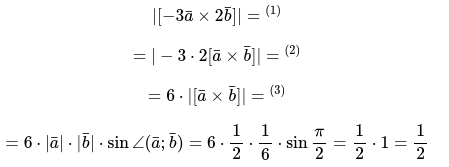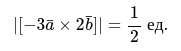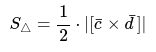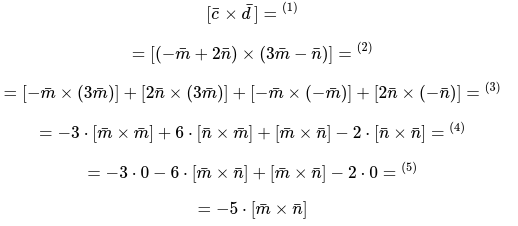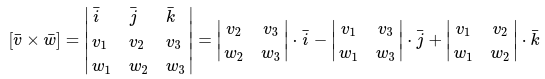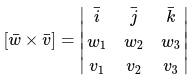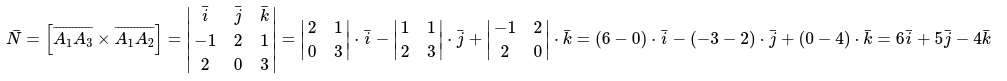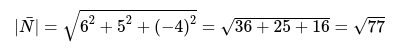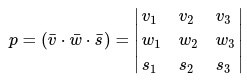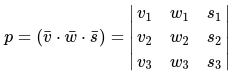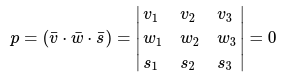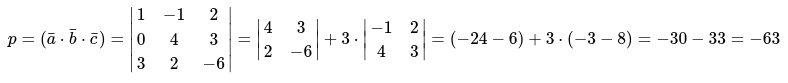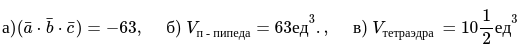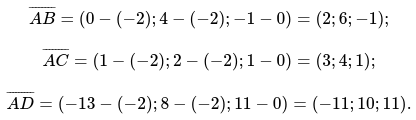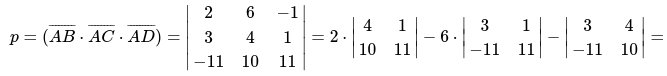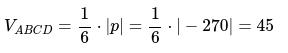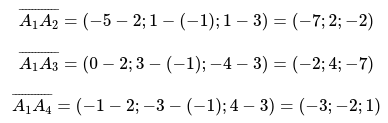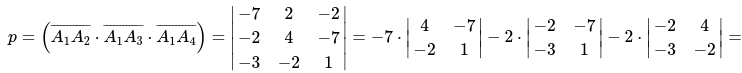В данной публикации мы рассмотрим, каким образом можно найти векторное произведение двух векторов, приведем геометрическую интерпретацию, алгебраическую формулу и свойства этого действия, а также разберем пример решения задачи.
- Геометрическая интерпретация
- Формула векторного произведения
- Свойства векторного произведения
- Пример задачи
Геометрическая интерпретация
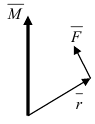
Векторное произведение двух ненулевых векторов a и b – это вектор c, который обозначается как [a, b] или a x b.
Длина вектора c равна площади параллелограмма, построенного с помощью векторов a и b.
При этом c перпендикулярен плоскости, в которой расположены a и b, и расположен так, чтобы наименьшее вращение от a к b выполнялось против часовой стрелки (с точки зрения конца вектора).
Формула векторного произведения
Произведение векторов a = {ax; ay, az} и b = {bx; by, bz} вычисляется с помощью одной из формул ниже:
Свойства векторного произведения
1. Векторное произведение двух ненулевых векторов равняется нулю тогда и только тогда, когда эти векторы являются коллинеарными.
[a, b] = 0, если
a || b
.
2. Модуль векторного произведения двух векторов равняется площади параллелограмма, образованного этими векторами.
Sпарал. = |a x b|
3. Площадь треугольника, образованного двумя векторами, равняется половине их векторного произведения.
SΔ = 1/2 · |a x b|
4. Вектор, являющийся векторным произведением двух других векторов, перпендикулярен им.
c ⟂ a, c ⟂ b.
5. a x b = –b x a
6. (m a) x a = a x (m b) = m (a x b)
7. (a + b) x c = a x c + b x c
Пример задачи
Вычислим векторное произведение a = {2; 4; 5} и b = {9; -3; 1}.
Решение:
Ответ: a x b = {19; 43; -42}.
Содержание:
Векторное и смешанное произведения векторов в векторной алгебре
Векторное произведение
Определение: Тройка векторов
Пример:
Рис. 13. Правая (а) и левая (б) тройки векторов.
Определение: Векторным произведением векторов 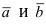
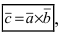
Замечание: Из определения векторного произведения следует, что направление вектора 
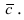
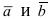
Рис. 14. Площадь параллелограмма, определяющего длину вектора 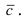
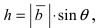
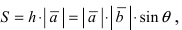
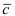
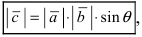
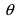
Векторное произведение векторов обладает следующими свойствами:
Замечание: Свойство 4. определяет второе условие коллинеарности векторов.
Формула для векторного произведения векторов через проекции перемножаемых векторов
Теорема: Пусть 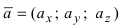
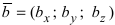
Доказательство: Запишем вектора 
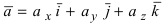
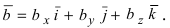
Используя эту таблицу, вычислим векторное произведение векторов
Отсюда следует, что 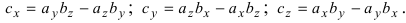
Рис. 15. Циклический переход от одной координаты к другой.
Для нахождения, например проекции 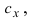
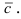
Полученное выражение представляет собой раскрытие определителя III порядка по элементам первой строки, то есть окончательно можно записать, что
Пример:
Найти, при каком значении параметра m вектор 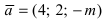
Решение:
Согласно свойству 4. для векторного произведения (пункт 1 Лекция № 6) найдем векторное произведение заданных векторов
Так как вектор 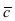
- Заказать решение задач по высшей математике
Пример:
Найти векторное произведение векторов
Решение:
Пример:
Найти векторное произведение векторов
Решение:
Приложения векторного произведения
1. Физика. Пусть точка начала вектора 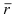
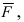
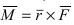
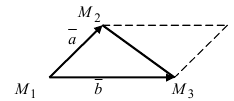
2. Геометрия. Пусть даны три разные точки 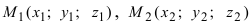
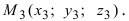
Введем в рассмотрение вектора 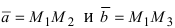
Рис. 17. Площадь треугольника
Проекции этих векторов равны:
Так как площадь треугольника составляет половину от площади параллелограмма, площадь которого равна модулю векторного произведения векторов 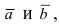
Пример:
Даны три точки 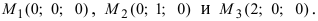
Решение:
Введем в рассмотрение вектора 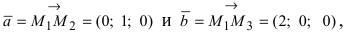
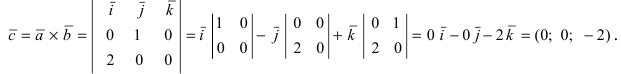
3. Тригонометрия. Выведем формулу для
Пусть в плоской декартовой системе координат даны векторы 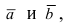
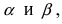
Рис. 18. Синус суммы двух углов.
Проекции векторов равны 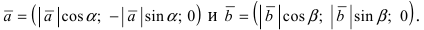
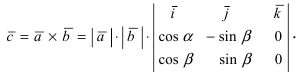
Длина этого вектора равна 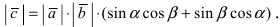
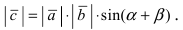
Смешанное произведение векторов
Определение: Смешанным произведением векторов 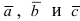
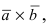
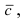
Получим формулу для вычисления смешанного произведения
Обменяв местами первую строку со второй, а затем и с третьей, получим окончательную формулу
Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства:
1. 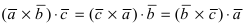
2. Смешанное произведение векторов 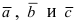
Рис. 19. Объем параллелепипеда, построенного на векторах
Так как
3. Если вектора 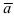
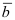
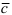
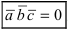
Замечание: Свойство 3. определяет условие компланарности трех векторов, т.е. если 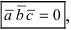
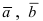
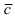
Пример:
Доказать, что вектора 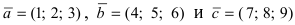
Решение:
Согласно формуле, определяющей смешанное произведение векторов, имеем
Пример:
Даны 4 точки 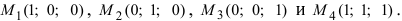
Решение:
Составим векторы 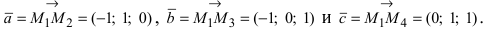
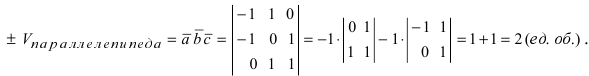
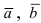
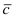
Пример:
Чему равен объём пирамиды с вершинами А, В, С и D (координаты точек А, В, С и D взять из VIII.). Найти длину высоту, которая опущена из точки А на основание BCD.
Решение:
Объём пирамиды равен 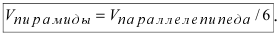
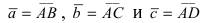
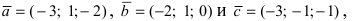
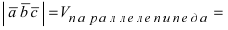
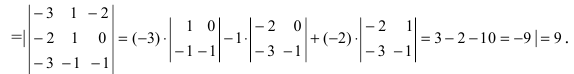
С другой стороны, её объём по формуле из средней школы равен
Вычислим площадь треугольника BCD, лежащего в основании пирамиды: 
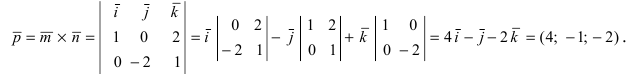
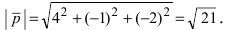
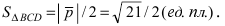
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Матричный метод
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
Векторное произведение векторов
Определение
| Определение |
|
Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $. |
Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.
Формула
| Формула 1 |
|
Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$ |
| Формула 2 |
|
В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $. |
Определитель во второй формуле можно раскрыть по первой строке:
$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 — a_3 b_2) — overline{j} (a_1 b_3 — a_3 b_1) + overline{k} (a_1 b_2 — a_2 b_1) $$
Итого вторая формула приобретает окончательный короткий вид:
$$ overline{a} times overline{b} = (a_2 b_3 — a_3 b_2; a_3 b_1 — a_1 b_3; a_1 b_2 — a_2 b_1) $$
Свойства
- При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
- Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
- $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$
Примеры решений
| Пример 1 |
|
Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$ |
| Решение |
|
Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) — overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} — overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a} times overline{b} = (5, -1, 3) $$ |
Геометрический смысл
- Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
- Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
- Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.
| Пример 2 |
| Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$ |
| Решение |
|
Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) — overline{j}(2+3) + overline{k}(4+1) = -5overline{i} — 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$ |
| Ответ |
| $$ S_Delta = 4.33 $$ |
Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом 


вектору 
обозначен 
Сформулируем ряд базовых определений.
Длиной
или модулем
вектора 
длина отрезка и обозначается 

не имеет. Вектор 
направление которого совпадает с направлением вектора 

Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.
Векторы
называются равными 
одинаковые длины.
Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.
Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через 
Выберем произвольный вектор
пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через ax, ay, az
соответственно. Тогда нетрудно показать, что

Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора 
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде

скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора
:

то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора 

свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.
Пусть в трехмерном пространстве заданы векторы 
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то
есть если

Данная
формула имеет место для произвольного конечного числа слагаемых.
Геометрически
два вектора складываются по двум правилам:
а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;
б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.
2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если 

Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.
Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства 
представлен в виде разности двух векторов, исходящих из начала координат: 


координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.
3. Умножение вектора на число λ покоординатно:
При λ>0
– вектор





4. Пусть в пространстве задана
направленная прямая (ось l), вектор 
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.
Проекцией 


знаком «+», если вектор 
знаком «–», если 
Если
в качестве оси l взять некоторый другой вектор 


Рассмотрим некоторые
основные свойства проекций:
1) проекция вектора 
вектора 
между вектором и осью, то есть 
2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;
3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.
5. Скалярным произведением 


число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол 
Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть
Теорема 2.3. Скалярное произведение двух векторов 
заданных своими координатами, равно сумме произведений их одноименных координат, то есть

С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами 

Отсюда
следует условие перпендикулярности ненулевых векторов



Нахождение проекции вектора 
заданное вектором 

С помощью скалярного произведения векторов находят
работу постоянной силы 
прямолинейном участке пути.
Предположим, что под действием постоянной силы 
положения А в положение B. Вектор силы 



равна 
Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.
Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах
Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):
Отсюда согласно формуле (2.29) получим косинус
искомого угла
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?
Таблица 2.2
Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции 
соответствующего ресурса 
Тогда 
ресурсов 
векторов 
Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей
Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix
Пример 2.11. Вычислить работу, произведенную силой 
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила 
Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала


Угол φ между 

формуле (2.29), то есть
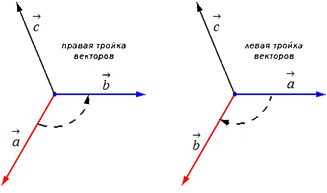
6. Три некомпланарных вектора 
тройку, если при наблюдении из конца третьего вектора 
поворот от первого вектора 
вектору 
если по часовой стрелке.
Векторным
произведением 


вектор 
– 


– имеет длину, равную 


– векторы 
тройку (рис. 2.15).

условием коллинеарности двух векторов является равенство нулю их векторного
произведения 
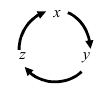
Теорема 2.5. Векторное произведение векторов 
третьего порядка вида

Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат
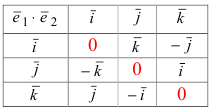
Следствие 2. Векторные произведения единичных орт равны
Следствие 3. Векторный квадрат любого вектора равен нулю
Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен 
построенного на векторах 


. Следовательно,

Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.
Пусть в точке A приложена
сила 
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы 
точки O называется вектор 
— перпендикулярен плоскости, проходящей через точки O, A, B;
— его модуль численно равен произведению силы на плечо 
— 


Следовательно,
момент силы 
точки O представляет собой векторное произведение


Линейная скорость 
угловой скоростью 
неподвижной оси, определяется формулой Эйлера 
точка оси (рис. 2.17).
Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах

Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).

произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть 

. Следовательно, искомая площадь равна 
площади)
7. Рассмотрим произведение трех векторов 

результирующий вектор – скалярно на третий. Такое произведение 
произведением трех векторов
(векторно–скалярным произведением).
Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть

Нетрудно показать, что объем параллелепипеда,
построенного на векторах 
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов 
Объем треугольной пирамиды, построенной на этих же
векторах, равен

Пример 2.13. Вершинами пирамиды служат точки 
Решение. Найдем
координаты векторов

По формуле (2.36) объем пирамиды, построенной на
векторах 


Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.
Система векторов 
линейно зависимой, если существуют такие числа 
место равенство

Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что 
получим выражение вектора 
остальные векторы
Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все


независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).
Базисом n – мерного
пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
– мерного пространства можно представить
в виде линейной комбинации векторов базиса
таким образом:
Числа

вектора 
векторов 
Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.
Например, в трехмерном пространстве
существует базис единичных орт 
линейно независимых векторов, то есть каждый вектор 
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт 

по ортам 

пространстве.
Вопросы для самопроверки
Векторное произведение
Для того чтобы дать правильное определение векторного произведения, необходимо разобраться в следующем моменте: рассмотреть вопрос, касающийся ориентации всей упорядоченной группы векторов. Для всего пространства на координатной плоскости.
Нужно отложить все три вектора от одной конкретной точки в системе. Ориентация для векторов может быть двух направлений:
- правая;
- левая.
Направление непосредственно зависит от направления самого вектора. Именно в каком направление будет осуществляться самый кратчайший поворот от двух векторов, а и b от конца третьего вектора с. При условии, что самый короткий поворот против часовой стрелки, тогда все три вектора будут именоваться – правыми.
Соответственно левыми будут называться вектора, движение которых происходит по направлению часовой стрелки.
Определение
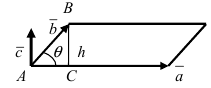
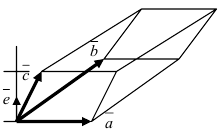
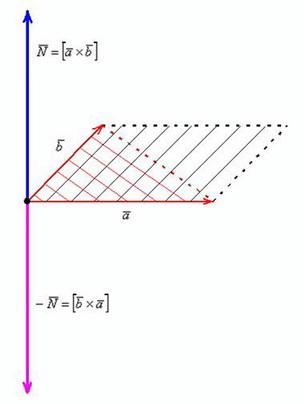
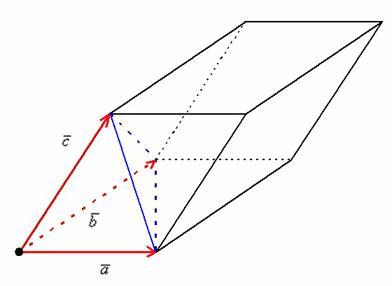
Произведение векторов неколлинеарных векторов [bar{a} text { и } bar{b} ], которые взятых в определённом порядке – это любой принятый вектор [bar{N}], у которого длина равняется площади геометрической фигуры параллелограмм. Именно он построен на основании данных векторов; вектор [bar{N}] ортогонален двум другим векторам [bar{a} text { и } bar{b} ], и направлен так, что [(bar{a} ; bar{b} ; bar{N})] являются ориентированы в правом направлении.
Следовательно, можно выделить следующие основные моменты:
1. Заданные векторы, которые обозначены линиями красного цвета, и основываясь на определение являются не коллинеарными
2. Векторы [bar{a} text { и } bar{b}] приняты в заданном порядке: произведение [[bar{a} times bar{b}]_{-}]
Окончательный результат выражен как: [bar{N}=[bar{a} times bar{b}]], обозначенный синим цветом.
Если вектора перемножить в обратном порядке, получится равный по всей длине и противоположный по направлению вектор [-bar{N}=[bar{b} times bar{a}]].
Следовательно: [[bar{a} times bar{b}]=-[bar{b} times bar{a}]]
3. Геометрический смыл векторного произведения.
Величина длины синего вектора [bar{N}=[bar{a} times bar{b}]] (следовательно это справедливо и для красного вектора [-bar{N}=[bar{b} times bar{a}]]) будет равна площади параллелограмма. Который построен на векторах [bar{a} text { и } bar{b}]. На схеме, данная фигура изображена штриховкой черного цвета. чёрным цветом.
Исходя из вышесказанного, справедливой будет формула определения длины для векторного произведения:
Данная формула отражает длину вектора а не его самого [bar{N}]. Для задач геометрии площадь параллелограмма зачастую определяют через главное понятие произведения векторов:
Выведем следующую формулу. Диагональ у параллелограмма (красная пунктирная линия) делит фигуру два равных треугольника.
Из этого следует, что площадь треугольника, который построен на векторах [bar{a} text { и } bar{b}], определяется по формуле:
4. Стоит помнить, что вектор [bar{N}] ортогонален векторам [bar{a} text { и } bar{b}], иными словами [bar{N} perp bar{a}, bar{N} perp bar{b}].
Векторное произведение коллинеарных векторов
Случаи, при которых векторы являются коллинеарными:
- когда вектора возможно расположить на одной прямой;
- параллелограмм визуально, также становится плоским относительно оси координат;
- площадь параллелограмма равна нулю [S_{text { п-грамма } }=|bar{a}| cdot|bar{b}| cdot sin angle(bar{a} ; bar{b})](синус нуля равняется или 180 градусов равняется нулю следовательно и площадь также будет нулевой).
Поэтому , если [bar{a} || bar{b} text {, то } bar{N}=[bar{a} times bar{b}]=overline{0} text{ и }|bar{N}|=|[bar{a} times bar{b}]|=0].
Нужно всегда помнить, что именно само векторное произведение равно нулю.
При решении практических задач данным моментом часто пренебрегают.
Пример частного случая [[bar{a} times bar{a}]=overline{0}].
Векторное произведение помогает определить коллинеарность векторов трехмерного типа.
Главные свойства векторного произведения
Для некоторых произвольных векторов [bar{a}, bar{b}, bar{c}] и произвольного значения числа [lambda], являются справедливыми следующие главные свойства:
- [[bar{a} times bar{a}]=overline{0}] — данное свойство обычно не выделяют. Однако именно оно является важным моментом процессе решения векторных задач.
- [[bar{a} times bar{b}]=-[bar{b} times bar{a}]] – это свойство часто называют анти коммуникативным. Иными словами, порядок векторов может иметь разное направление и значение.
- [[lambda bar{a} times bar{b}]=lambda[bar{a} times bar{b}], quad[bar{a} times(lambda bar{b})]=lambda[bar{a} times bar{b}]] – суммарные и ассоциативные законы для векторных произведений. Константа выносится за пределы векторного произведения в координатной оси.
- [[(bar{a}+bar{b}) times bar{c}]=[bar{a} times bar{c}]+[bar{b} times bar{c}], quad[bar{a} times(bar{b}+bar{c})]=[bar{a} times bar{b}]+[bar{a} times bar{c}]] – распределительные или действующие законы векторного произведения. Для решения главным моментом является умение правильно раскрывать значение в скобках.
Коллинеарные и компланарные векторы. Основные определения
Определение 1
Компланарные вектора — это вектор или несколько векторов, которые расположены на одной плоскости либо располагаются параллельно ей.
Компланарность характерна всегда двум любым, на выбор, векторам. Так как всегда можно вычистить плоскость, которой будет параллельны произвольные вектора.
Выведем основное правило признака копланарности вектора.
При условии, что два вектора a и b не характеризуются как календарные, а для вектора с свойственны только одна пара чисел x и y. c=xa+yb. Если соблюдаются данные условия, то перечисленные векторы можно назвать компланарными.
Обратное утверждение компланарности.
Когда вектора a , b , c — компланарны, при этом a , b не относятся к коллинеарным. можно вектор c разложить по двум любым векторам, только одним способом.
Определение 2
Коллинеарность векторов это — принцип соотношения параллельности векторов. Два вектора с нулевым значением, будут иметь коллинеарность, при условии, что они находятся лежат на параллельной прямой или на одной плоскости с ней.
Главные условия и класс компланарности векторов
- Если произведение трех векторов равно нулевому значению. Данные вектора можно характеризовать как компланарные.
- Когда три любых вектора независимы друг от друга, то они будут компланарными.
- Когда задано несколько векторов, выполняется условие: компланарность будет характерна, для двух любых векторов, если они линейно друг от друга зависимы.
Для более лучшего восприятия материала, необходимо применить правила компланарности и коллинеарности при решении практических задач.
Для этого решим, и подробно распишем три конкретных примера.
Пример №1:
В условии задачи даны три вектора со следующими числовыми значениями.
a(1,2,3);
b(1,1,1);
c(1,2,1).
При условии, что произведение векторов будет равняться нулевому значению, можно сделать вывод о компланарности векторов.
Определяем произведение заданных значений.
Запишем все значения в виде матрицы и решим ее, применяя правила произведения и разности чисел.
a, b, с = 1*1*1+1*2*3+2*1*1-1*1*3-2*1*1-1*2*1=2 0
Так как окончательный ответ не равен нулю, а равен значению два. Следует, что вектора не являются компланарными.
Пример №2:
Заданы три вектора с положительными и отрицательными значениями. Необходимо составить и решить матрицу чисел.
a(1,-1,2);
b(0,1,-1);
c(2,-2,4).
Для решения задачи, нужно вычислить произведение значений векторов.
a, b, с=1*1*1+0*(-2)*2+(-1)*(-1)*2-2*(-1)*1-0*(-1)=0
Выполнив все действия по вычислению произведения данных, мы видим, что ответ уравнения равен нулю.
Согласно основному правило компланарности, можно сделать вывод, что вектора ему соответствую. То есть являются компланарными между собой.
Нет времени решать самому?
Наши эксперты помогут!
Примеры решения
Для решения некоторых категорий задач, необходимо пользоваться тригонометрической таблицей. Для определения углов функций.
Пример 1:
- Необходимо определить длину векторного произведения двух векторов [bar{a} text { и } bar{b}], , если:
- Определить площадь параллелограмма, который построен на основании векторов [bar{a} text { и } bar{b}], если:
По условию задачи необходимо вычислить длину векторного произведения. По следующей формуле:
Ответ:
В ответе обязательно следует указывать единицы измерения, так как определится длина.
Из условия задачи нужно определить площадь фигуры параллелограмм, который построен на векторах [bar{a} text { и } bar{b}].
Площадь равняется значению длины векторного произведения:
Ответ:
Пример 2:
Определить площадь геометрической фигуры треугольник, который построен на векторах [bar{a} text { и } bar{b}], , если:
Для решения задачи применим соответствующую формулу и вспомним все преобразования, которые необходимы для определения площади.
Ответ:
Пример 3:
Найти:
Решение: По условию требуется определить длину векторного произведения:
Алгоритм решения:
- вынести за пределы скобок векторного произведения все константы, согласно ассоциативного закона.
- затем выносим значение константы за пределы модуля; при этом модуль изменят отрицательный знак на положительный.
Ответ:
Пример 4:
Необходимо определить значение площади треугольника.
Для этого задано в задаче следующие данные:
, если:
Алгоритм решения задачи:
Площадь треугольника определяется по уже известной формуле:
Данный алгоритм стандартный и частично имеет схожесть с другими примерами.
Решение для удобства, необходимо разделить на три этапа:
Этап 1:
Нужно правильно выразим произведение векторов: [[bar{c} times bar{d}]] через определение векторного произведения [[bar{m} times bar{n}]].
Иными словами, выражение вектора через вектор.
Для этого сформулируем и запишем следующее:
подставляем в формулу соответствующие выражения векторов [bar{c}, bar{d}].
- используя определённые законы, нужно раскрыть скобки по характерным правилам умножения числовых многочленов.
- применяя ассоциативные векторные законы, можно вынести все константы за скобки и пределы векторных произведений.
Первое и последнее выражение равно нулевому значению или нулевому вектору, исходя из принятого свойства: [[bar{a} times bar{a}]=overline{0}].
Для второго слагаемого применяется свойство анти коммутативности и выглядит следующим образом: [6 cdot[bar{n} times bar{m}]=-6 cdot[bar{m} times bar{n}]]
— приведение подобных слагаемых.
По результатам вычисления заданный вектор получился выражен через вектор. Этого и требовалось доказать:
[[bar{c} times bar{d}]=-5 cdot[bar{m} times bar{n}]]
Этап 2:
На втором этапе определяется длина заданного векторного произведения.
Приведенное действие напрямую напоминает задачу №3:
Этап 3:
Применяя все известные данные и формулы, можно определить площадь треугольника:
Ответ:
Пример 5:
Определить векторное произведение, применяя все заданные значения векторов:
[|[bar{c} times bar{d}]|], если:
Необходимо выразить вектор [[bar{c} times bar{d}]] через другой вектор [[bar{m} times bar{n}]]:
Используя все данные и алгоритм решения можно составить формулу и записать следующее выражение подставляя числа:
Окончательным действием будет определение произведения векторов, поэтапно подставляя все числовые значения:
Ответ задачи: [|[bar{c} times bar{d}]|=4 text { ед }]
Векторное произведение векторов в системе координат
Произведение векторов [bar{v}left(v_{1} ; v_{2} ; v_{3}right), bar{w}left(w_{1} ; w_{2} ; w_{3}right)], заданные в координатной системе базиса [(bar{i} ; bar{j} ; bar{k})],
характеризуются соответствующей формулой:
Формула достаточно проста и понятна для восприятия: в верхней строке определителя указываются координатные значения векторов.
Во второй и третьей строке указываются векторные координаты, при этом обозначены в строгом порядке:
- для начала координаты векторов номер 1;
- затем координаты вектора номер 2.
Когда векторы необходимо перемножить в ином порядке, то необходимо все строки поменять с друг другом местами:
Основываясь на свойства определителя, можно выделить следующее: в случае, когда в определителе две строки нужно поменять местами, то, следовательно, изменится знак
Данное значение определителя всегда отражается в первой строке, что и указано выше.
Пример 7:
Даны следующие данные векторов:
Необходимо определить произведение векторов [left[overline{A_{1} A_{3}} times overline{A_{1} A_{2}}right]] и вычислить [left|left[overline{A_{1} A_{3}} times overline{A_{1} A_{2}}right]right|]
Используя алгоритм решения выполним следующие действия:
- Сформулируем и запишем формулу для нахождения векторного произведения
- Подставим имеющиеся данные и вычислим длину векторов по следующей формуле:
Окончательный ответ:
Смешанное произведение векторов
Смешанное произведение применяется довольно редко, поэтому и примеров задач не много.
Практически вся информация сводится к следующим данным:
- главному определению;
- геометрическому смыслу;
- рабочие формулы.
Важно
Смешанным произведение нескольких векторов, будет называться произведение трёх характерных векторных значений:
[(bar{a} cdot bar{b} cdot bar{c})]
Смешанное произведение трех векторов [(bar{a} cdot bar{b} cdot bar{c})] и некомпланарных векторов [bar{a} cdot bar{b} cdot bar{c}], которые берутся в определенном порядке, будет называется объём геометрического параллелепипеда.
Данная геометрическая фигура построена на заданных векторах, которые отражены с положительным значением.
Если базисное значение векторов [(bar{a} cdot bar{b} cdot bar{c})] имеет правое направление , когда отрицательный знак, то базис векторов [(bar{a} cdot bar{b} cdot bar{c})] имеет левое направление.
Все характеристики подробно изображены на рисунке.
Смешанное произведение векторов в координатах
Для данного способа определения произведения векторов, используется сугубо алгебраический метод.
Перечень смешанных векторов: [bar {v}left(v_{1}, v_{2}, v_{3}right), bar{w}left(w_{1}, w_{2}, w_{3}right), bar{s}left(s_{1}, s_{2}, s_{3}right)], которые непосредственно заданы в координатной системе данных [(bar{i} ; bar{j} ; bar{k})] для правого направления, следует выражать характерной формулой, виде матрицы:
Определение
Ориентация базиса – это его стандартная ориентация, для которой решаются практически все задачи.
С практической точки зрения стоит отметить следующие важные моменты:
- для всего векторного произведения, координатные данные векторов следует изображать в конкретный определитель в особо строгом порядке.
- когда в любом смешанном произведении [(bar{v} cdot bar{w} cdot bar{s})] выбрать несколько векторов, затем переставить их местами, следовательно нужно переставить и все характерные строки определителя.
- при перестановке строк в количестве двух штук, соответствующие строки изменяют знак на противоположный.
- при перемене местами любых векторов, для смешанного произведения будет характерно изменение знака на противоположный.
Соответственно, все координаты векторов не всегда нужно записывать в виде строк. Также они могут изображаться как таблица: слева направо, и обязательно, в строгом порядке.
Основное значение главного определителя при этом изменяться не будет: компланарность векторов также имеет огромное значение в данном случае.
Пример 1
Даны следующие значения векторов [bar{a}(1 ;-1 ; 2), bar{b}(0 ; 4 ; 3), bar{c}(3 ; 2 ;-6)].
Необходимо определить:
- смешанное векторное произведение;
- значение объема параллелепипеда, который построен на векторах [bar{a}, bar{b}, bar{c}];
- значение объёма геометрической фигуры тетраэдра, который также построен на векторах [bar{a}, bar{b}, bar{c}].
Процесс решения заключается в следующем
1. Применяя формулу для смешанного произведения вычисляем неизвестную:
Значение определителя раскрыто по первому столбцу
2. Определение значения объёма параллелепипеда, который построен на векторах [bar{a}, bar{b}, bar{c}], равняется модулю смешанного векторного произведения:
3. Определяем значение объема тетраэдра, который построен на заданных векторах:
Ответ:
Пример 2
Определить значение объема, которое характерно для треугольной пирамиды. Применяя все известные ее вершины: A(-2 ;-2 ; 0), B(0 ; 4 ;-1), C(1 ; 2 ; 1), D(-13 ; 8 ; 11)
Решение: Для простоты выполнения, рекомендуется выполнять схематический рисунок геометрической пирамиды, это необходимо для более понятного процесса решения.
Для начал определяются значения векторов, по исходным данным:
Следующим действием произведение векторов смешанного типа.
[=2 cdot(44-10)-6 cdot(33+11)-(30+44)=68-264-74=-270]
Выполним расчет для треугольной пирамиды ABCD:
Ответ задачи: [V_{A B C D}=45 mathrm{ед}^{3}]
Пример 3
Определить объём заданной пирамиды, с известными вершинами: [A_{1}(2 ;-1 ; 3), A_{2}(-5 ; 1 ; 1), A_{3}(0 ; 3 ;-4), A_{4}(-1 ;-3 ; 4)]
Для начала определим значения векторов
Смешанное произведение определим по формуле:
[=-7 cdot(4-14)-2 cdot(-2-21)-2 cdot(4+12)=70+46-32=84]
Применяя формулу из геометрии определим объем пирамиды [A_{1} A_{2} A_{3} A_{4}]
[V_{text {пир}}=frac{1}{6} cdot|p|=frac{1}{6} cdot 84=14text{ед} .^{3}]
[V_{text {пир}}=14text{ед} .^{3}]