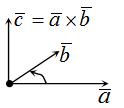Векторное произведение векторов
Определение
| Определение |
|
Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $. |
Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.
Формула
| Формула 1 |
|
Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$ |
| Формула 2 |
|
В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $. |
Определитель во второй формуле можно раскрыть по первой строке:
$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 — a_3 b_2) — overline{j} (a_1 b_3 — a_3 b_1) + overline{k} (a_1 b_2 — a_2 b_1) $$
Итого вторая формула приобретает окончательный короткий вид:
$$ overline{a} times overline{b} = (a_2 b_3 — a_3 b_2; a_3 b_1 — a_1 b_3; a_1 b_2 — a_2 b_1) $$
Свойства
- При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
- Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
- $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$
Примеры решений
| Пример 1 |
|
Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$ |
| Решение |
|
Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) — overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} — overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a} times overline{b} = (5, -1, 3) $$ |
Геометрический смысл
- Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
- Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
- Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.
| Пример 2 |
| Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$ |
| Решение |
|
Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) — overline{j}(2+3) + overline{k}(4+1) = -5overline{i} — 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$ |
| Ответ |
| $$ S_Delta = 4.33 $$ |
Любовь Петровна Гаврилюк
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Угол между векторами
Для того чтобы мы могли ввести понятие векторного произведения двух векторов, нужно сначала разобраться с таким понятие, как угол между этими векторами.
Пусть нам даны два вектора $overline{α}$ и $overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $overline{α}=overline{OA}$ и $overline{β}=overline{OB}$, тогда угол $AOB$ будет называться углом между этими векторами (рис. 1).
Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ
Причем мы будем считать, что если векторы $overline{α}$ и $overline{β}$ будут сонаправленными, или один или оба из них нулевой, то угол между этими векторами будет равен $0^circ$.
Обозначение: $∠(overline{α},overline{β})$
Понятие векторного произведения векторов и формула нахождения
Определение 1
Векторным произведением двух векторов называется вектор, перпендикулярный обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $overline{α}хoverline{β}$.
Математически это выглядит следующим образом:
- $|overline{α}хoverline{β}|=|overline{α}||overline{β}|sin∠(overline{α},overline{β})$
- $overline{α}хoverline{β}⊥overline{α}$, $overline{α}хoverline{β}⊥overline{β}$
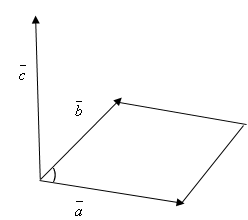
- $(overline{α}хoverline{β},overline{α},overline{β})$ и $(overline{i},overline{j},overline{k})$ одинаково ориентированы (рис. 2)
«Как найти векторное произведение векторов» 👇
Рисунок 2. Произведение векторов. Автор24 — интернет-биржа студенческих работ
Очевидно, что внешнее произведение векторов будет равняться нулевому вектору в двух случаях:
- Если длина одного или обоих векторов равняется нулю.
- Если угол между этими векторами будет равняться $180^circ$ или $0^circ$ (так как в этом случае синус равняется нулю).
Чтобы наглядно увидеть, как находится векторное произведение векторов, рассмотрим следующие примеры решения.
Пример 1
Найти длину вектора $overline{δ}$, который будет являться результатом векторного произведения векторов, с координатами $overline{α}=(0,4,0)$ и $overline{β}=(3,0,0)$.
Решение.
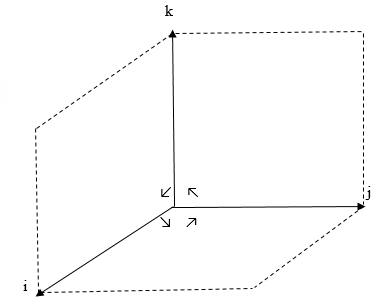
Изобразим эти векторы в декартовом координатном пространстве (рис. 3):
Рисунок 3. Векторы в декартовом координатном пространстве. Автор24 — интернет-биржа студенческих работ
Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^circ$. Найдем длины этих векторов:
$|overline{α}|=sqrt{0+16+0}=4$
$|overline{β}|=sqrt{9+0+0}=3$
Тогда, по определению 1, получим модуль $|overline{δ}|$
$|overline{δ}|=|overline{α}||overline{β}|sin90^circ=4cdot 3cdot 1=12$
Ответ: $12$.
Вычисление векторного произведения по координатам векторов
Из определения 1 сразу же вытекает и способ нахождения векторного произведения для двух векторов. Поскольку вектор кроме значения имеет еще и направление, находить его только при помощи скалярной величины невозможно. Но помимо него существует еще способ нахождения с помощью координат данных нам векторов.
Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые будут иметь координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно. Тогда вектор векторного произведения (а именно его координаты) можно найти по следующей формуле:
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$
Иначе, раскрывая определитель, получим следующие координаты
$overline{α}хoverline{β}=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
Пример 2
Найти вектор векторного произведения коллинеарных векторов $overline{α}$ и $overline{β}$ с координатами $(0,3,3)$ и $(-1,2,6)$.
Решение.
Воспользуемся формулой, приведенной выше. Получим
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\0&3&3\-1&2&6end{vmatrix}=(18-6)overline{i}-(0+3)overline{j}+(0+3)overline{k}=12overline{i}-3overline{j}+3overline{k}=(12,-3,3)$
Ответ: $(12,-3,3)$.
Свойства векторного произведения векторов
Для произвольных смешанных трех векторов $overline{α}$, $overline{β}$ и $overline{γ}$, а также $r∈R$ справедливы следующие свойства:
-
$overline{α}хoverline{β}=-(overline{β}хoverline{α})$
Верность этого свойства будет следовать из третьего пункта определения 1.
-
$(roverline{α})хoverline{β}=r(overline{α}хoverline{β})$ и $overline{α}х(roverline{β})=r(overline{α}хoverline{β})$
Из формулы для нахождения векторного произведения будем получать:
$(roverline{α})overline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\rα_1&rα_2&rα_3\β_1&β_2&β_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$
$overline{α}х(roverline{β})=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\rβ_1&rβ_2&rβ_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$
-
$overline{α}х(overline{β}+overline{γ})=overline{α}overline{β}+overline{α}overline{γ}$ и $(overline{α}+overline{β})overline{γ}=overline{α}overline{γ}+overline{β}overline{γ}$.
Данное свойство векторного произведения векторов также можно проверить с помощью формулы.
Следующее свойство называют геометрическим смыслом векторного произведения:
-
Длина вектора векторного произведения равняется площади параллелограмма, который нужно было построить между ними (рис. 4)
Рисунок 4. Длина вектора векторного произведения. Автор24 — интернет-биржа студенческих работ
Пример 3
Найдите площадь параллелограмма, вершины которого имеют координаты $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ и $(3,8,0)$.
Решение.
Вначале изобразим данный параллелограмм в координатном пространстве (рис.5):
Рисунок 5. Параллелограмм в координатном пространстве. Автор24 — интернет-биржа студенческих работ
Видим, что две стороны этого параллелограмма построены с помощью коллинеарных векторов с координатами $overline{α}=(3,0,0)$ и $overline{β}=(0,8,0)$. Используя четвертое свойство, получим:
$S=|overline{α}хoverline{β}|$
Найдем вектор $overline{α}хoverline{β}$:
$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\3&0&0\0&8&0end{vmatrix}=0overline{i}-0overline{j}+24overline{k}=(0,0,24)$
Следовательно
$S=|overline{α}хoverline{β}|=sqrt{0+0+24^2}=24$
Ответ: $24$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
- Формула
- Примеры вычисления векторного произведения векторов
Формула
Для того чтобы найти векторное произведение
$[bar{a}, bar{b}]$ двух векторов, заданных своими координатами
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и
$bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$ соответственно, необходимо
вычислить следующий определитель
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Обычно такой определитель вычисляют разложением по первой строке. Отметим также, что результатом векторного произведения является вектор.
Примеры вычисления векторного произведения векторов
Пример
Задание. Найти векторное произведение векторов
$bar{a}=(1 ; 0 ; 0)$ и $bar{b}=(0 ; 1 ; 0)$
Решение. Для вычисления векторного произведения заданных векторов воспользуемся формулой
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Подставляя координаты заданных векторов, получим:
$$[bar{a}, bar{b}]=left|begin{array}{lll}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|$$
Раскладываем определитель по первой строке:
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 1 & 0 & 0 \ 0 & 1 & 0end{array}right|=$$
$$=bar{i} cdotleft|begin{array}{cc}0 & 0 \ 1 & 0end{array}right|-bar{j} cdotleft|begin{array}{cc}1 & 0 \ 0 & 0end{array}right|+bar{k} cdotleft|begin{array}{cc}1 & 0 \ 0 & 1end{array}right|=$$
$$=0 cdot bar{i}-0 cdot bar{j}+1 cdot k$$
Первые два определителя равны нулю, так как они содержат нулевой столбец, а третий определитель вычисляем
как определитель второго порядка: от произведения элементов главной диагонали отнимаем произведение элементов побочной.
Итак, координаты искомого вектора равны коэффициентам при ортах, то есть
$$[bar{a}, bar{b}]=(0 ; 0 ; 1)$$
Ответ. $[bar{a}, bar{b}]=(0 ; 0 ; 1)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны векторы
$bar{a}=(5 ; 3 ;-4)$ и $bar{b}=(6 ; 7 ;-8)$ . Найти координаты векторного произведения
$[bar{a}, bar{b}]$
Решение. Координаты векторного произведения
$[bar{a}, bar{b}]$ вычисляются по формуле
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z}end{array}right|$$
Подставляя координаты заданных векторов, получим:
$$[bar{a}, bar{b}]=left|begin{array}{ccc}bar{i} & bar{j} & bar{k} \ 5 & 3 & -4 \ 6 & 7 & -8end{array}right|$$
Раскладываем полученный определитель по первой строке:
$$=bar{i} cdotleft|begin{array}{cc}3 & -4 \ 7 & -8end{array}right|-bar{j} cdotleft|begin{array}{cc}5 & -4 \ 6 & -8end{array}right|+bar{k} cdotleft|begin{array}{cc}5 & 3 \ 6 & 7end{array}right|=$$
$$=[3 cdot(-8)-7 cdot(-4)] cdot bar{i}-[5 cdot(-8)-6 cdot(-4)] cdot bar{j}+$$
$$+[5 cdot 7-6 cdot 3] cdot bar{k}=(-24+28) bar{i}-(-40+24) bar{j}+(35-18) bar{k}=$$
$$=4 cdot bar{i}+16 cdot bar{j}+17 cdot bar{k}$$
Тогда
$$[bar{a}, bar{b}]=(4 ; 16 ; 17)$$
Ответ. $[bar{a}, bar{b}]=(4 ; 16 ; 17)$
Читать дальше: как найти смешанное произведение векторов.
Векторное произведение двух векторов a и b – это вектор, который перпендикулярен плоскости этих же обоим исходным векторам.
Что такое векторное произведение векторов
Рис. 1
Алгебраические свойства векторного произведения
Давайте рассмотрим свойства векторного произведения.
Если – произвольные векторы, а
– произвольные число, тогда:
x
=
x
. (Векторное произведение антикоммутативно).
x
=
x
=
x
.(Векторное произведение обладает сочетательным свойством относительно скалярного множителя).
x
=
x
+
x
.
x
=
||
,
,
. (Два ненулевых вектора коллинеарны только тогда, когда их векторное произведение равно нулевому вектору).
Таблица векторного умножения ортов
x
=
,
x
=
;
x
=
,
x
=
;
x
=
,
x
=
.
x
=
x
=
x
=
.
Рис. 2
Векторное произведение одноимённых ортов равняется . При самом коротком повороте от одного орта к другому против часовой стрелки получаем третий орт, а по часовой стрелке – третий орт со знаком
.
Формулы векторного произведения в координатной форме
Формулы векторного произведения в координатной форме получаем с учётом таблицы векторного произведения ортов:
x
=
x
=
x
x
x
=
x
–
x
+
x
x
=
Примеры нахождения векторного произведения
Чтобы закрепить материал, рассмотрим на примерах, как найти векторное произведение векторов.
Найти площадь треугольника , если
.
Решение:
Сначала находим векторы:
и
и их векторное произведение:
x
=
=
.
Длина полученного вектора по определению численно равняется площади параллелограмма, построенного на данных векторах и поэтому:
пар =
x
=
=
.
А площадь треугольника составляет половину найденной площади, то есть:
тр. =
пар =
x
x
,