(Решено) как построить спектральные проекторы линейного оператора…
Вопрос от пользователя:
как построить спектральные проекторы линейного оператора
Подождите!
Не закрывайте страницу. Нейросеть пишет ответ. Он появится тут.
Этот ответ написан нейросетью.
Искуственный интеллект во многом преуспевает, но в некоторых областях может давать неточные ответы.
Если вам не понравился ответ, попробуйте задать его более развёрнуто и конкретно, используя точные параметры.
Ответ нейросети:
Спектральные проекторы линейного оператора – это проекторы на собственные подпространства этого оператора, раскладывающие пространство линейного оператора в прямую сумму этих подпространств. Для построения спектральных проекторов линейного оператора необходимо следовать следующим шагам:
Шаг 1. Найти характеристический многочлен линейного оператора. Для этого необходимо найти собственные значения линейного оператора, решив уравнение $det(lambda I — A) = 0$, где $A$ – матрица линейного оператора, $I$ – единичная матрица, $lambda$ – собственное значение.
Шаг 2. Найти собственные подпространства линейного оператора. Для этого необходимо найти собственные векторы для каждого собственного значения, решив систему уравнений $(A — lambda I)x = 0$.
Шаг 3. Построить проекторы на собственные подпространства. Для этого необходимо для каждого собственного подпространства $E_{lambda}$ построить матрицу проектора $P_{lambda}$, удовлетворяющую условию $P_{lambda}^2 = P_{lambda}$ и $P_{lambda}x = x$ для $xin E_{lambda}$, $P_{lambda}x=0$ для $xin E_{mu}$, $muneqlambda$. Матрицу проектора можно построить следующим образом: пусть $S_{lambda}$ – базис в $E_{lambda}$, тогда матрица проектора $P_{lambda}$ в базисе $S$ будет иметь вид $P_{lambda} = sum_{i=1}^{n} e_ie_i^T$, где $e_i$ – базисный вектор в $S_{lambda}$.
Шаг 4. Построить спектральный проектор линейного оператора. Для этого собственные проекторы необходимо сложить, умножив каждый проектор на соответствующее ему собственное значение: $P = sum_{i=1}^{n} lambda_i P_{lambda_i}$.
Таким образом, спектральный проектор линейного оператора позволяет разложить пространство линейного оператора в прямую сумму собственных подпространств и представить любой вектор из этого пространства в виде суммы проекций на собственные подпространства. Это является важным инструментом для решения задач линейной алгебры и теории управления.
⚠️Зарепортить пост!
Чтобы оставить комментарий, необходимо авторизоваться.
Задай любой вопрос нейросети!
она справится с любой поставленной задачей быстрее чем поиск в Яндекс.
Последние вопросы
(c) ChatGPT по русски 2023. Все права защищены. При обнаружении неправомерного контента пишите на [email protected]
Содержание
- 1 Ортогональная сумма подпространств
- 2 Ортогональный проектор
- 3 Задача о перпендикуляре
- 3.1 Способ 1(через ОРТН базис)
- 3.2 Способ 2 (через систему уравнений)
- 4 Матрица Грама
Ортогональная сумма подпространств
| Определение: |
| Пусть подпространство унитарного линейного пространства , тогда говорят, что , если |
| Определение: |
| Подпространство все называется ортогональным дополнением к в , обозначается |
| Теорема: |
| Доказательство: |
|
Шаг 1. Рассмотрим — ОРТН базис . Шаг 2. Дополним до базиса , получим . Шаг 3. Приведем этот набор к ОРТН базису (процесс Грама-Шмидта), в итоге получим — ОРТН базис, при этом (по определению и построению) ло , то есть Шаг 4. Докажем, что сумма должна быть прямой. — единственные. Докажем этот факт от противного. Пусть . (так как ) , то есть разложение единственное, теорема доказана. |
| Определение: |
| Прямая сумма взаимно перпендикулярных пп называется ортогональной суммой, обозначается как . |
NB:
| Определение: |
| Прямая сумма попарно перпендикулярных пп называется их ортогональной суммой. |
Ортогональный проектор
| Определение: |
| Пусть
называется ортогональным проектором на пп и обозначается . называется ортогональным проектором на пп и обозначается . |
| Определение: |
| называется разложением вектора в сумму ортогональной проекции на пп и ортогональной составляющей на пп . |
| Лемма: |
|
Пусть — ОРТН базис тогда |
| Доказательство: |
|
Без ограничения общности рассмотрим — ОРТН базис , где — ОРТН базис , a — ОРТН базис (на остальные вектора распространим по линейности) Шаг 1. Рассмотрим Шаг 2. Рассмотрим |
| Лемма: |
| Доказательство: |
|
по теореме Пифагора Отсюда напрямую следует утверждение леммы. |
Задача о перпендикуляре
| Определение: |
| Задачей о перпендикуляре называется задача отыскания ортогональной составляющей и проекции вектора , то есть его разложения по формуле: (где — ортогональный проектор на пп , — пп унитарного пространства , a — ортогональный проектор на пп , — ортогональное дополнение ). |
Способ 1(через ОРТН базис)
| Утверждение: |
|
1) Найти — ОРТН базис |
Способ 2 (через систему уравнений)
| Утверждение: |
|
Рассмотрим — базис (не ОРТН) Решая эту систему уравнений для неизвестных , находим коэффициенты разложения . |
Матрица Грама
| Определение: |
| Пусть — результат ортогонализации по Граму-Шмидту набора , тогда называется определителем Грама соответствующего набора векторов . |
Проекция матрицы
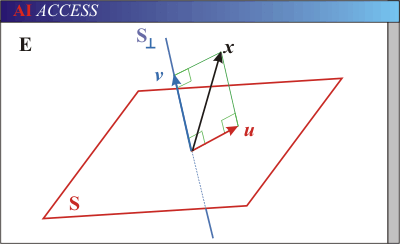
Эта
иллюстрация представляет:
*
S подпространство E векторное
пространство.
*
Вектор х и у его
ортогональное проектирование на S.
«Ортогональная
проекция на S» является линейным
оператором, поэтому может быть представлено
матрицей. Матрица представляет проектор
называется проекцией матрицы,
а это всегда симметричны.
Из-за
их важности в области статистики,
специальная запись
этого Словарь предназначен для проекции
матрицы.
Положительный (полу-) определенных матриц
Симметричная
матрица называется неотрицательно
определенной, если для любого, не
0 вектор х:
|
х |
Если
это неравенство всегда строгое, матрица
называется положительно определенной.
——
Положительно
определенные матрицы играют важную
роль в области статистики (в основном,
потому что ковариационной
матрицы неотрицательно), и
вступление
в эту Словарь предназначен для положительно
определенной матрицы.
________________________________________________________________
|
Учебник |
В
этом уроке мы переходим те свойства
симметричных матриц, которые будут
необходимы на этом сайте для установления
важных результатов о:
*
Анализ главных компонент,
*
Линейная регрессия (простых и кратных),
*
Ridge регрессии,
*
Многомерного нормального распределения,
*
Квадратичные формы в нормальных величин.
—-
Только
общими свойствами симметричных матриц
рассматриваются в этой статье.
*
Свойства матрицы проектирования решаются
здесь
.
*
Свойства положительно определенных
матриц рассматриваются здесь
.
Симметричных
матриц
|
Собственные Собственные Сопряженное Собственные Собственные Собственные Спектральное Ранг |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
