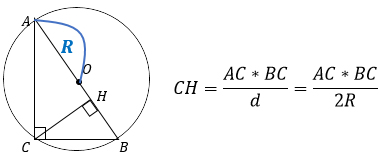
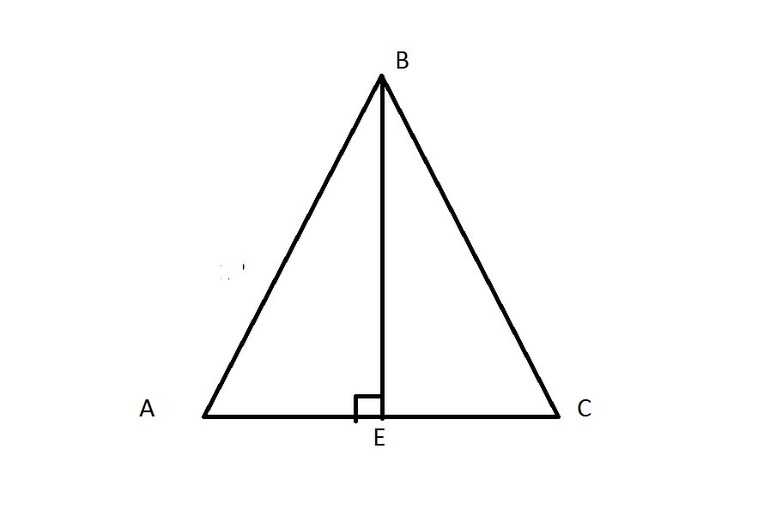
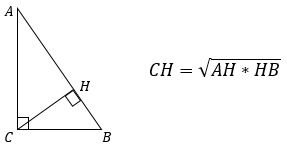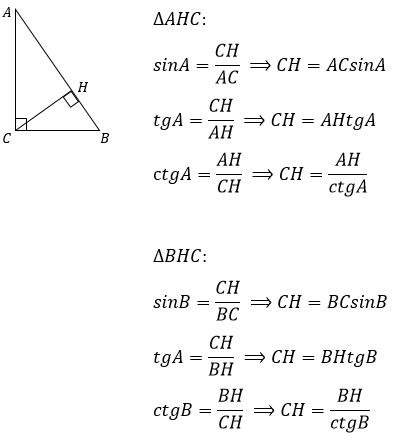Как найти проекцию высоты на гипотенузу - AvtoShod.ru

Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.

Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.

1) Свойство высоты, проведенной к гипотенузе.

Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.

или

$[C{D^2} = AD cdot BD.]$

2) Свойства катетов прямоугольного треугольника.

Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.

или

$[A{C^2} = AB cdot AD]$

$[B{C^2} = AB cdot BD.]$

Источник

Высота прямоугольного треугольника, проведенная к гипотенузе

Как и в любом треугольнике прямоугольный треугольник имеет три высоты. Две из них совпадают с катетами, а вот третья высота, проведенная к гипотенузе, постоянно будоражит наши умы.

Поэтому представляю вашему вниманию основные формулы для ее нахождения.

Начну с самой важной.

1. Высота, проведенная к гипотенузе равна корню квадратному из произведения проекций катетов на эту гипотенузу.

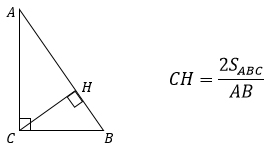
2. Высоту, проведенную к гипотенузе, можно найти, разделив удвоенную площадь прямоугольного треугольника на гипотенузу.

Такая формула получается из классический формулы нахождения площади треугольника: половина произведения основания на высоту, проведенную к этому основанию.

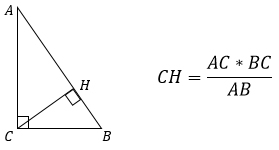
3. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.

Эта формула получится из второй если заменить площадь на половину произведения катетов.

Т.к. АВ — гипотенуза, то ее можно выразить через катеты АС и ВС, используя теорему Пифагора. Тогда формула примет другой вид:

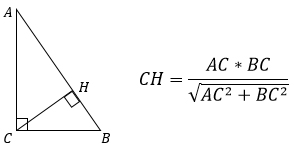
4. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на диаметр описанной вокруг треугольника окружности (или на удвоенный радиус).

Так получается потому, что центр описанной окружности лежит в середине гипотенузы, значит, гипотенуза равна 2R или d.

5. Высоту, проведенную к гипотенузе, можно найти, используя геометрические определения синуса, тангенса и котангенса.

Надеюсь, что данная статья оказалась полезной!)

Готовься к экзамену вместе с нами! Заходи на нашу страницу в ВК.

Источник

§1. Прямоугольный треугольник. Метрические соотношения.

Основные метрические сооьтношения в прямоугольном треугольнике

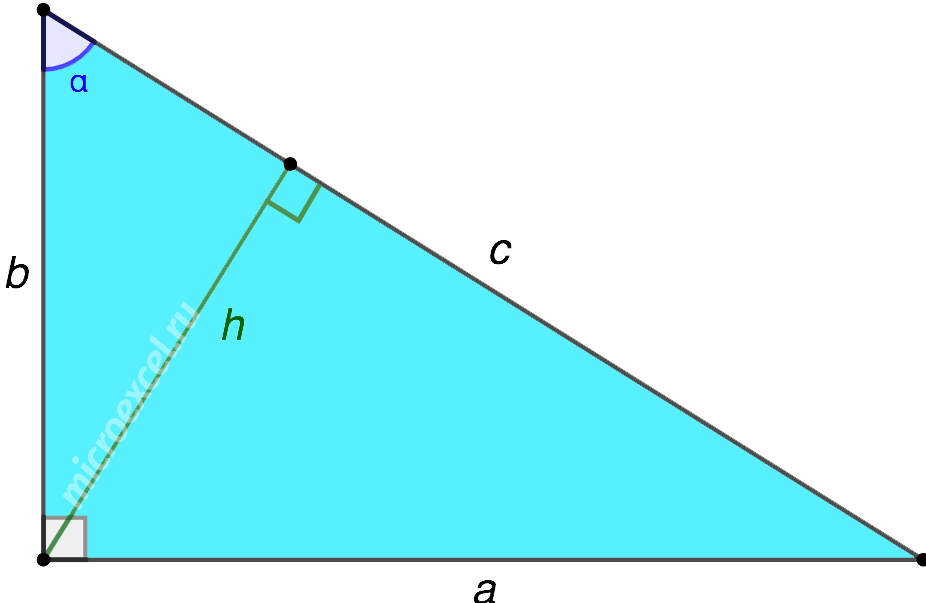
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).

Используем обычные обозначения:

`c` — гипотенуза `AB`;

`a` и `b` – катеты `BC` и `AC` (по-гречески «kathetos — катет» означает отвес, поэтому такое изображение прямоугольного треугольника нам представляется естественным);

`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;

`h` – высота `CD`, опущенная на гипотенузу;

`m_c` – медиана `CM`, проведённая к гипотенузе;

`R` – радиус описанной окружности;

`r` – радиус вписанной окружности.

Напомним, что если `alpha` — величина острого угла `A` прямоугольного треугольника `ABC` (см. рис. 1), то

`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.

Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

`c^2 = a^2 + b^2`

Доказательство теоремы повторите по учебнику.

Выведем ряд соотношений между элементами прямоугольного треугольника.

Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу

`a^2 = c * a_c`

`b^2 = c * b_c`

Если `/_ A = alpha` (см. рис. 1), то `/_ CBD = 90^@ — alpha` и `/_ BCD = alpha`. Из треугольника `ABC` `sin alpha = (BC)/(AB)`, а из треугольника `BCD` `sin alpha = (BD)/(BC)`.

Значит, `(BC)/(AB) = (BD)/(BC)`, откуда `BC^2 = AB * BD`, т. е. `a^2 = c * a_c`. Аналогично доказывается второе равенство.

Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу

`h^2 = a_c * b_c`

Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.

Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.

Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу

`a * b = c * h`

Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.

Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.

Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.

`m_c = 1/2 c`

Пусть `AM = BM`. Проведём $$ MKVert BC$$ (рис. 2), тогда по теореме Фалеса `AK = CK`

Кроме того, из того, что `BC _|_ AC` и $$ MKVert BC$$ следует `MK _|_ AC`. В прямоугольных треугольниках `CMK` и `AMK` катет `MK` общий, катеты `CK` и `AK` равны. Эти треугольники равны и `CM = AM`, т. е. `CM = 1/2 AB`.

Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.

Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы

`R = m_c = 1/2 c`

Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.

Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей

`a + b = 2(R + r)` или `a + b = c + 2r`

Пусть `O` — центр вписанной окружности и `F`, `N` и `S` — точки касания сторон треугольника `ABC` (рис. 3), тогда `OF_|_ BC`, `ON _|_ AC`, `OS _|_ AB` и `OF = ON = OS = r`. Далее, `OFCN` — квадрат со стороной `r`, поэтому `BF = BC — FC`, `AN = AC — CN`, т. е. `BF = a — r` и `AN = b — r`.

Прямоугольные треугольники `AON` и `AOS` равны (гипотенуза `AO` — общая, катеты `ON` и `OS` равны), следовательно, `AS = AN`, т. е. `AS = b — r`.

Аналогично доказывается, что `BS = a — r`, поэтому из `AB = AS + BS` следует `c = (b — r) + (a — r)`, т. е. `a + b = c + 2r`. Зная, что `c = 2R`, окончательно получаем `a + b = 2(R + r)`.

Равенства, доказанные в Свойствах 1 и 2, записываются также как:

`a = sqrt(c * a_c)`

`b = sqrt(c * b_c)`

`h = sqrt(a_c * b_c)`

и, соответственно, формулируются утверждения

Катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.

Высота, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу.

Приведём примеры применения доказанных метрических соотношений в прямоугольном треугольнике.

Проекции катетов прямоугольного треугольника на гипотенузу равны `9` и `16` . Найти радиус вписанной окружности.

1. Пусть `a_c = 9`, `b_c = 16` (рис. 4), тогда `c = a_c + b_c = 25`.

2. По Свойству 1: `a = sqrt(c * a_c) = 15`, `b = sqrt(c * b_c) = 20`.

3. По Свойству 6: находим радиус `r = 1/2 (a + b — c) = 5`.

В прямоугольном треугольнике из вершины прямого угла проведены медиана и высота (рис. 5), расстояние между их основаниями равно `1`. Найти катеты, если известно, что один из них в два раза больше другого.

1. Заметим, что `a_c = c/2 — 1`, a `b_c = c/2 + 1` (рис. 5), откуда `a^2 = c * a_c = c(c/2 — 1)` и `b^2 = c * b_c = c(c/2 + 1)`.

2. По условию `b = 2a`, значит `b^2 = 4a^2`, т. е. `c(c/2 + 1) = 4c(c/2 — 1)`.
Находим `c = (10)/3`, и `a = sqrt(c(c/2 — 1)) = 2/3 sqrt5` и `b = 2a = 4/3 sqrt5`.

Источник

Высота в прямоугольном треугольнике

Вспомним определение. Высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.

Один из типов экзаменационных задач в банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:

sin A $displaystyle = frac{a}{c}=frac{h}{b}=frac{BH}{a};$

cos A $displaystyle = frac{b}{c}=frac{h}{a}=frac{AH}{b};$

$displaystyle S_{ABC}= frac{ab}{2}=frac{ch}{2}.$

Высота проведена к гипотенузе AB. Она делит треугольник ABC на два прямоугольных треугольника — и . Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.

Мы помним, что сумма двух острых углов прямоугольного треугольника равна $90^{circ}$ . Значит, $angle AC mkern -3mu H=90^{circ}-angle C mkern -3mu AH$ , то есть угол равен углу ABC . Аналогично, угол равен углу .

Иными словами, каждый из трех углов треугольника ABC равен одному из углов треугольника (и треугольника ). Треугольники и называются подобными. Давайте нарисуем их рядом друг с другом.

Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?

Возьмем треугольники и ABC . Стороны треугольника ABC длиннее, чем стороны треугольника в раз:

$genfrac{}{}{}{0}{displaystyle AC}{displaystyle A mkern -3mu H} =genfrac{}{}{}{0}{displaystyle BC}{displaystyle C mkern -3mu H} = genfrac{}{}{}{0}{displaystyle AB}{displaystyle AC}.$

Мы доказали свойство высоты прямоугольного треугольника. Его можно сформулировать как теорему.

Теорема 1. Высота прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, делит треугольника на три подобных друг другу треугольника:

При решении задач нам пригодится равенство углов треугольников и , а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника ABC можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту. В геометрии это называется «метод площадей» и часто применяется в решении задач.

Задача 1.

В треугольнике ABC угол C равен $90^{circ},$ CH — высота, BC = 3, cos A = $genfrac{}{}{}{0}{displaystyle sqrt{35}}{displaystyle 6}.$ Найдите AH.

Решение:

Рассмотрим треугольник ABC. В нем известны косинус угла A и противолежащий катет BC. Зная синус угла A, мы могли бы найти гипотенузу AB. Так давайте найдем sin A:

sin ${}^2A$ + cos ${}^2A$ = 1.

Эта формула – основное тригонометрическое тождество. Конечно, вы его знаете:

sin ${}^2 A + genfrac{}{}{}{0}{displaystyle 35}{displaystyle 36} = 1;$

sin ${}^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle 36};$

sin A $= genfrac{}{}{}{0}{displaystyle 1}{displaystyle 6}$ (поскольку значение синуса острого угла положительно).

Тогда:

$AB=BC: sin A = 3: genfrac{}{}{}{0}{displaystyle 1}{displaystyle 6}=3 cdot 6=18.$

Рассмотрим прямоугольный треугольник , $angle H = 90^{circ}$ . Поскольку

Отсюда $H mkern -3mu B=BC cdot sin HC mkern -3mu B = 3 cdot genfrac{}{}{}{0}{displaystyle 1}{displaystyle 6}=0,5.$

Ответ: 16.

Задача 2.

В треугольнике ABC угол C равен 90 ${}^{circ},$ AB = 13, tg A $= genfrac{}{}{}{0}{displaystyle 1}{displaystyle 5}$ . К гипотенузе проведена высота CH. Найдите AH.

Решение:

Это чуть более сложная задача. Ведь вам неизвестны катеты a и b.

Запишем теорему Пифагора: (1)

Нам известно также, что:

tg A $= genfrac{}{}{}{0}{displaystyle a}{displaystyle b} = genfrac{}{}{}{0}{displaystyle 1}{displaystyle 5}.$ (2)

Решая уравнения (1) и (2), найдем:

Запишем площадь треугольника AВС двумя способами:

$S = genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2} ab = genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2} ch$

и найдем длину .

Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений, как в алгебре.

Теорема 2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, равна произведению катетов, деленному на гипотенузу.

Доказательство:

Из прямоугольного треугольника ABC с прямым углом C и гипотенузой AB:

sin $displaystyle (angle BAC)=frac{a}{c}.$

Из прямоугольного треугольника AНС с прямым углом Н и гипотенузой AС:

sin $displaystyle (angle BAC)=frac{h}{b}.$

Мы разными способами вычислили синус одного и того же угла. Приравняем полученные выражения:

$displaystyle frac{h}{b}=frac{a}{c}.$

Найдем высоту:

$displaystyle h= frac{ab}{c}.$

Что и требовалось доказать.

Задача 3. Катеты прямоугольного треугольника равны 15 и 20.
Найдите высоту, проведенную к гипотенузе.

Решение:

Воспользуемся теоремой 2 о высоте прямоугольного треугольника:

Катеты BС и AС нам известны: BC = 15, AC = 20. Найдем гипотенузу AB с помощью теоремы Пифагора:

${AB}^2={BC}^2+{AC}^2={15}^2+{20}^2={25}^2, AB=25.$

Найдем высоту, проведенную из вершины прямого угла:

$displaystyle CH=frac{15cdot 20}{25}=12.$

Ответ: 12.

Теорема 3. В прямоугольном треугольнике квадрат высоты, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу.

Сейчас мы докажем эту полезную формулу.

Вспомним, что такое проекция точки на прямую. Например, из точки С опускаем СН — перпендикуляр к прямой AВ. Точка Н и будет проекцией точки С. Тогда AН – проекция катета AВ, а BН – проекция катета BС.

Обозначим:

Доказательство проведем двумя способами.

Первый способ доказательства:

Из прямоугольного треугольника BНС с прямым углом Н и гипотенузой BС:

tg $displaystyle (angle CBH)=frac{h}{c_a}.$

Из прямоугольного треугольника AНС с прямым углом Н и гипотенузой AС:

ctg $displaystyle (angle CAH) = frac{c_b}{h}.$

Заметим, что угол CBН – это угол CBA, а угол CAН – это угол BAC. Тогда:

$displaystyle frac{h}{c_a}=frac{c_b}{h}.$

Мы воспользовались тем, что тангенс и котангенс двух разных острых углов прямоугольного треугольника равны друг другу. Это следует из определения тангенса и котангенса.

Преобразуем получившееся выражение:

$displaystyle h=frac{c_a cdot c_b}{h} Rightarrow h^2 = c_a c_b .$

Что и требовалось доказать.

Второй способ доказательства:

Воспользуемся подобием треугольников, о которых говорится в теореме 1.

Рассмотрим пару прямоугольных треугольников AНC и BНC. Как было показано выше, эти треугольники подобны по двум углам, поэтому

$displaystyle frac{h}{c_a}=frac{c_b}{h}.$

Мы получили такое же соотношение, как и в первом способе доказательства.

Далее аналогично получим, что

Что и требовалось доказать.

Задача 4. На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH = 4, BH = 16. Найдите длину CH.

Решение:

Воспользуемся теоремой 3 о высоте прямоугольного треугольника:

Подставим данные задачи.

${CH}^2=4cdot 16=64,$ CH = 8.

Ответ: 8.

Разберем решения других задач ОГЭ и ЕГЭ по теме «Свойства высоты в прямоугольном треугольнике».

Задача 5. Катеты прямоугольного треугольника относятся как 3:4, а гипотенуза равна 50. Найти высоту, проведенную из вершины прямого угла и отрезки, на которые гипотенуза делится высотой.

Решение:

Рассмотрим прямоугольный треугольник ABС с гипотенузой AB. Проведем высоту CD=h.

Учитывая отношение катетов, обозначим их длины как: BC = 3x, AC = 4x.

Тогда по теореме Пифагора получим:

$AB=sqrt{9x^2 +16 x^2} = sqrt{25 x^2}=5x.$

По условию гипотенуза AB = 50. Следовательно, х = 10, BC = 30, AC = 40.

Далее можно действовать разными способами. Например, так.

$displaystyle CD=frac{BCcdot AC}{AB}=frac{30cdot 40}{50}=24.$

где по определению косинуса:

cos A $displaystyle =frac{AC}{AB}=frac{4}{5},;$ cos B $displaystyle =frac{BC}{AB}=frac{3}{5}.$

$displaystyle AD=ACcdot frac{4}{5}=32,; BD=BCcdot frac{3}{5}=18.$

Ответ:

Задача 6. В прямоугольном треугольнике ABC высота CD делит гипотенузу на отрезки AD = 3 см и BD = 2 см. Найти катеты треугольника.

Решение:

Найдем квадрат длины высоты с помощью теоремы 3:

${CD}^2=ADcdot BD=3cdot 2=6.$

Из прямоугольного треугольника ADC по теореме Пифагора найдем

${AC}^2={AD}^2+{CD}^2=9+6=15,; AC= sqrt{15}$ см.

Из прямоугольного треугольника BDC по теореме Пифагора найдем

${BC}^2={BD}^2+{CD}^2=4+6=10,; BC= sqrt{10}$ см.

Ответ: см и см.

Задача 7. Точка D является основанием высоты, проведенной из вершины прямого угла C треугольника ABC к гипотенузе AB. Найдите AC, если AD=8, AB=32.

Указание:

Найдите отрезок BD = AB — AD, после чего задача сводится к предыдущей.

Длину высоты прямоугольного треугольника можно также найти, если известны гипотенуза и один из острых углов треугольника.

h = c sin alpha cos alpha = c sin beta cos beta.

Докажем эту формулу.

Рассмотрим прямоугольный треугольник ACD:

В то же время из треугольника AВC:

Таким образом, h = CD = AC cos⁡ alpha = AB sin alpha cos alpha = c sin alpha cos⁡ alpha.

Аналогично, из треугольника BCD получим: h = CD = BC cos beta = AB sin⁡ beta cos beta = c sin beta cos⁡ beta.

Задача 8. В прямоугольном треугольнике гипотенуза равна 10, а один из острых углов 15 градусов. Найти высоту, проведенную из вершины прямого угла.

Решение:

Воспользуемся доказанной выше формулой:

h = c sin alpha cos alpha = 10 sin ${15}^circ$ cos ${15}^circ$ = 5sin ${30}^circ$ = 2,5.

Ответ: 2,5.

Задача 9. Высота прямоугольного треугольника делит его гипотенузу на отрезки 6 см и 4 см. Найдите площадь этого треугольника.

Решение:

Гипотенуза прямоугольного треугольника равна сумме данных отрезков:

см.

Найдем высоту, проведенную из вершины прямого угла к гипотенузе: см.

Площадь треугольника:

$displaystyle S=frac{1}{2}ch=frac{1}{2}cdot 10cdot 2sqrt{6}=10sqrt{6}$ см ${}^2.$

Ответ: см ${}^2.$

Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Высота в прямоугольном треугольнике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Как построить высоту треугольника — основные способы

С применением циркуля

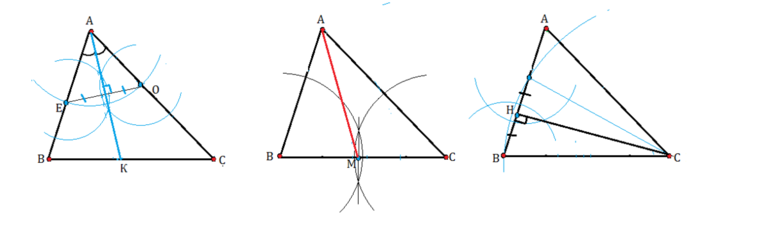
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.

Способ начертить искомый отрезок:

На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
Иглу циркуля ставят в вершине любого угла у основания.
Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
Делают пометку в месте пересечения начерченных окружностей.
Ластиком стирают лишние линии, оставляя лишь поставленную точку.
С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
Стирают линии, находящиеся под основанием.

Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.

С помощью линейки

Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.

В остроугольном треугольнике

Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.

Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.

Правильная последовательность действий:

Находят вершину, из которой хотят провести перпендикуляр.
Совмещают угольник с противоположной стороной фигуры.
Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
Простым карандашом проводят линию, которая и будет искомым отрезком.

В тупоугольной фигуре

Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.

Порядок действий:

Располагают чертёж так, чтобы тупой угол оказался у основания.
Угольник прикладывают к наибольшей стороне фигуры.
Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
Соединяют 2 точки простым карандашом, получая искомую линию.

В прямоугольном и равнобедренном

В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.

Пошаговая инструкция:

Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
Вторую сторону линейки совмещают с вершиной прямого угла.
Проводят линию, которая будет высотой.

Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.

Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:

Линейкой замеряют длину основания.
Эту величину делят на 2.
Полученное значение откладывают от вершины одного из углов при основании.
Отмечают середину стороны и соединяют её с верхней точкой фигуры.

Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.

Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.

Проекции катетов на гипотенузу

1) Свойство высоты, проведенной к гипотенузе.

2) Свойства катетов прямоугольного треугольника.

Свойства высоты прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть

Свойства высоты в прямоугольном треугольнике

Свойство 1

В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:

источники:

Проекции катетов на гипотенузу

Свойства высоты прямоугольного треугольника

Источник

Высота прямоугольного треугольника, проведенная к гипотенузе

§1. Прямоугольный треугольник. Метрические соотношения.

Высота в прямоугольном треугольнике

Как построить высоту треугольника — основные способы

С применением циркуля

С помощью линейки

В остроугольном треугольнике

В тупоугольной фигуре

В прямоугольном и равнобедренном

Проекции катетов на гипотенузу

Свойства высоты прямоугольного треугольника

Свойства высоты в прямоугольном треугольнике

Свойство 1

Свойство 2

Свойство 3

Свойство 4

Пример задачи

Не пропустите также: