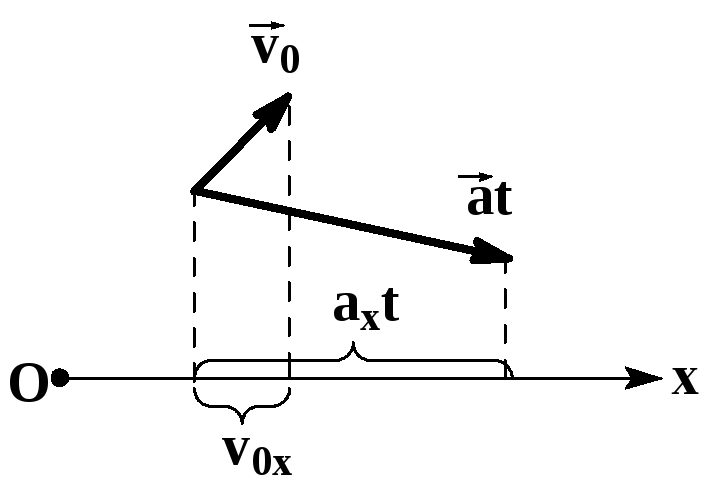
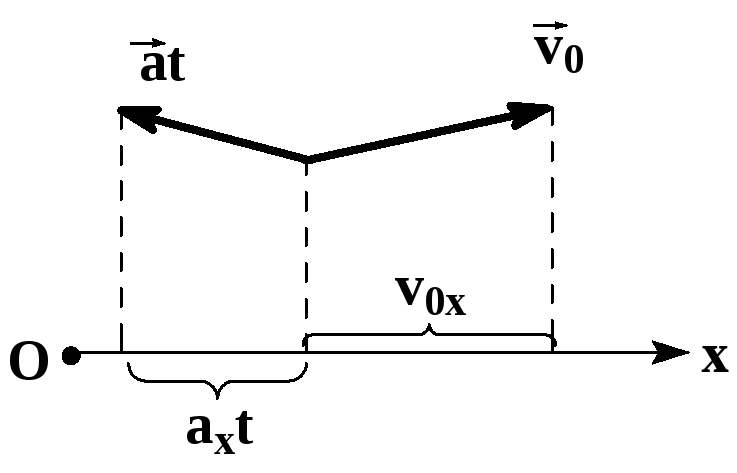
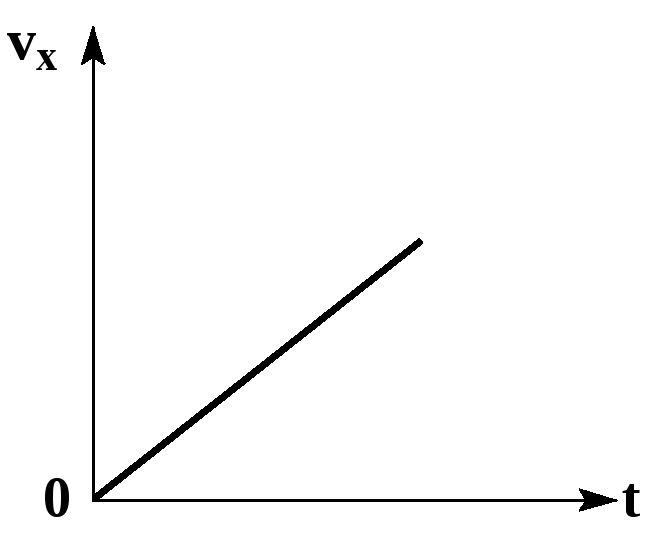
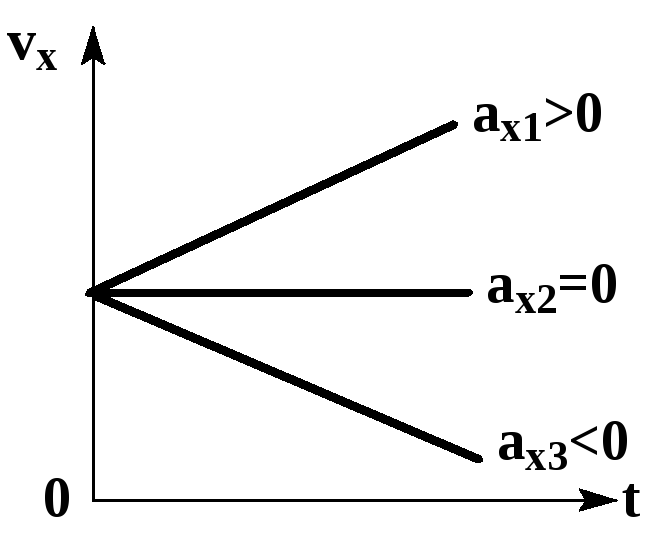
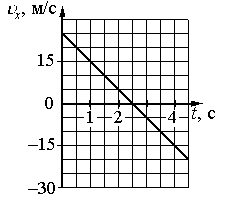Как найти проекцию вектора ускорение тела - AvtoShod.ru

Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
Единица измерения ускорения — метр в секунду в квадрате (м/с²).
Акселерометр — прибор для измерения ускорения.

Формула ускорения

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

Проекция ускорения на ось ОХ

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁= 1 и t₂= 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

В момент времени t₁= 1с ускорение a = 2 м/с². В момент времени t₂= 3 ускорение a = 0 м/с².

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

перемещение и путь;
скорость;
ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17992

Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?

Алгоритм решения

Записать исходные данные.
Записать формулу, связывающую известные из условия задачи величины.
Выразить из формулы искомую величину.
Вычислить искомую величину, подставив в формулу исходные данные.

Решение

Запишем исходные данные:

Начальная скорость v₀ = 5 м/с.
Конечная скорость v = 15 м/с.
Пройденный путь s = 40 м.

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Ответ: 2,5

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18202

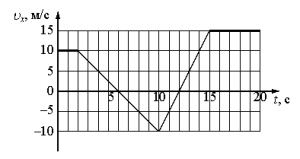
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
Вычислить ускорение движение тела на этом участке.
Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18027

На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.

Алгоритм решения

Записать формулу ускорения.
Записать формулу для вычисления модуля ускорения.
Выбрать любые 2 точки графика.
Определить для этих точек значения времени и проекции скорости (получить исходные данные).
Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 13.8k

Источник

Проекции скорости и ускорения

Для выполнения
расчетов скоростей и ускорений необходимо
переходить от записи уравнений в
векторной форме к записи уравнений в
алгебраической форме.

Векторы начальной
скорости
и ускорениямогут иметь различные направления,
поэтому переход от векторной записи
уравнений к алгебраической может
оказаться весьма трудоемким.

Известно, что
проекция суммы двух векторов на какую-либо
координатную ось равна сумме проекций
слагаемых векторов на ту же ось.

Поэтому для
нахождения проекции
вектора скоростина произвольную ось OX нужно найти
алгебраическую сумму проекций векторовина ту же ось.

Проекцию
вектора на ось считают положительной,
если от проекции начала к проекции
конца вектора нужно идти по направлению
оси, и отрицательной в противоположном
случае.

График скорости

Из уравнения
следует, что графиком зависимости
проекции скорости равноускоренного
движения от времени является прямая.
Если проекция начальной скорости на
ось OX равна нулю, то прямая проходит
через начало координат.

Основные
виды движения

а_n= 0, a_
= 0 –
прямолинейное равномерное движение;
а_n= 0, a_
= const
– прямолинейное равнопеременное
движение;
а_n= 0, a_

0 – прямолинейное
с переменным ускорением;
а_n= const,
a_
= 0 – равномерное
по окружности
а_n= const,
a_
= const
– равнопеременное по окружности
а_n
const,
a_

const
– криволинейное с переменным ускорением.

Вращательное движение твердого тела.

Вращательное
движение твердого тела относительно
неподвижной оси
– движение, при котором все точки
твердого тела описывают окружности,
центры которых лежат на одной прямой,
называемой осью
вращения.

Равномерное движение по окружности

Рассмотрим наиболее
простой вид вращательного движения, и
уделим особое внимание центростремительному
ускорению.

При равномерном
движении по окружности значение скорости
остается постоянным, а направление
вектора скорости
изменяется в процессе движения.

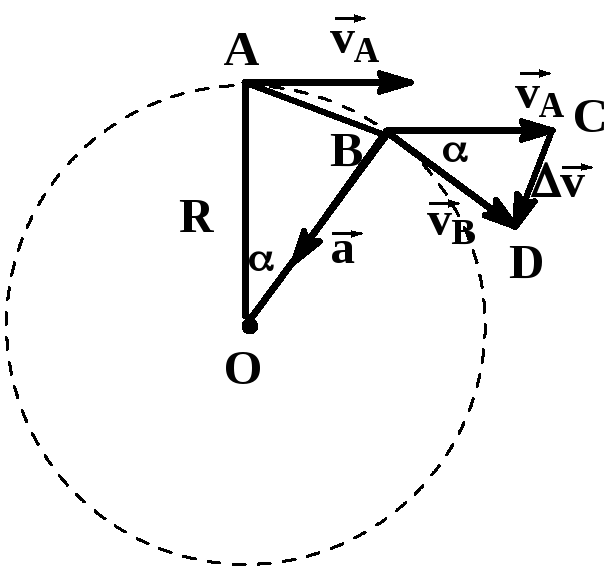
За
интервал времени ∆t
тело проходит путь
.
Этот путь равен длине дугиAB.
Векторы скоростей
ив точкахA
и B направлены
по касательным к окружности в этих
точках, а угол 
между векторами
иравен углу между радиусамиOA
и OB.
Найдем разность векторов
и определим отношение изменения
скорости к∆t:

Из подобия
треугольников OAB и BCD следует

Если интервал
времени ∆t
мал, то мал и угол .
При малых значениях угла 
длина хорды AB примерно равна длине дуги
AB, т.е.
.
Т.к.,,
то получаем

Поскольку
,
то получаем

Период и частота

Промежуток времени,
за который тело совершает полный оборот
при движении по окружности, называется
периодам
обращения
(Т).
Т.к. длина окружности равна 2R,
период обращения при равномерном
движении тела со скоростью v
по окружности радиусом R
равняется:

Величина, обратная
периоду обращения, называется частотой.
Частота показывает, сколько оборотов
по окружности совершает тело в единицу
времени:

(с^-1)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
01.06.2015304.13 Кб31KP.doc
#
#
#
#
#
#
#
#

Источник

Равноускоренное прямолинейное движение. Ускорение

Равноускоренное движение
Ускорение
Уравнение скорости и график скорости при равноускоренном прямолинейном движении
Определение пути и перемещения по графику скорости
Задачи

п.1. Равноускоренное движение

Если тело начинает двигаться из состояния покоя, оно набирает скорость не мгновенно, а в течение некоторого времени. Аналогично происходит при торможении: тело останавливается не сразу, а теряя скорость постепенно.

Движение, во время которого скорость тела за любые равные промежутки времени увеличивается на одну и ту же величину, называют равноускоренным.

Примеры равноускоренного движения:

скатывание велосипеда с горки, скатывание санок с горки;
старт и торможение автомобиля, автобуса, трамвая, поезда;
падение на землю камня, ракеты, метеорита.

Это интересно
Время разгона от 0 до 100 км/ч – одна из основных характеристик современных автомобилей.

п.2. Ускорение

Ускорение – это векторная величина, которая равна отношению изменения скорости тела к интервалу времени, за которое это изменение произошло: $$ overrightarrow{a}=frac{overrightarrow{v}-overrightarrow{v_0}} {t} $$ где (overrightarrow{v_0}) — начальная скорость тела, (overrightarrow{v}) — скорость тела в момент времени (t).

В системе СИ (см. §2 данного справочника) скорость измеряется в метрах в секунду, а время – в секундах. Поэтому:

Единицей ускорения в системе СИ является метр на секунду в квадрате (1 м/с²) – ускорение равноускоренного прямолинейного движения, при котором тело за 1 с увеличивает скорость на 1 м/с.

При описании прямолинейного движения мы переходим от векторов к проекциям на ось ОХ (см. §8 данного справочника).

Назовем проекцией вектора ускорения (overrightarrow{a}) на параллельную ему ось координат OX величину (a_x=pm|overrightarrow{a}|=pm a).
Знак проекции определяется следующим правилом:

если направление вектора (overrightarrow{a}) совпадает с направлением оси OX, то (a_x=agt 0)
если направление вектора (overrightarrow{a}) противоположно направлению оси OX, то (a_x=-alt 0)

При равноускоренном прямолинейном движении проекция ускорения равна: $$ a_x=frac{v_x-v_{0x}}{t} $$ где (v_{0x}) — проекция начальной скорости, (v_x) — проекция скорости в момент времени (t).

п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении

Для проекции скорости на ось ОХ в произвольный момент времени можем записать: $$ v_x(t)=v_{0x}+a_x t $$ Сравним полученное уравнение с уравнением прямой (y(x)=kx+b ) (см. §38 справочника по алгебре для 7 класса).
В уравнении скорости роль углового коэффициента (k) играет проекция ускорения (a_x), а роль свободного члена (b) – начальная скорость (v_{0x}).

В осях (t) и (v) график (v_x(t)=v_{0x}+a_x t) является прямой.
Эта прямая:

возрастает, если (a_xgt 0)
убывает, если (a_xlt 0)
постоянна (параллельна оси (t)), если (a_x=0)

Пример построения графика скорости
1-й участок пути. Пусть автомобиль начал движение из состояния покоя с ускорением 4 м/с². Направим ось ОХ в направлении ускорения и получим уравнение скорости: $$ v_{0x}=0, a_x=4frac{text{м}}{c^2}, v_x(t)=0+4t=4t $$ Через 5 с скорость автомобиля станет равной (v_x(5)=4cdot 5=20) м/с.
2-й участок пути. Пусть автомобиль, набрав эту скорость, проехал с ней без ускорения в течение 10 с. На этом участке уравнение скорости: $$ a_{x}=0, v_x(t)=20frac{text{м}}{c}, 5 cleq tlt 15 c $$ Скорость не меняется, автомобиль движется прямолинейно равномерно.
3-й участок пути. Наконец, на последнем участке пути, автомобиль тормозил с ускорением 5 м/с² до полной остановки. Тогда уравнение скорости на этом участке: $$ v_{0x}=20frac{text{м}}{c}, a_x=5frac{text{м}}{c^2}, v_x(t)=20-5t $$ Проекция ускорения при торможении отрицательна. Скорость станет равна 0 через 4 с после начала торможения, автомобиль остановится.

Опишем полностью движение на всех участках: $$ v_x(t)= begin{cases} 4t, 0leq tlt 5\ 20, 5leq tlt 15\ 20-5t, 15leq tleq 19 end{cases} $$ И построим график:

Участок AB соответствует разгону автомобиля от 0 до 20 м/с, участок BC — равномерному движению со скоростью 20 м/с, участок CD — торможению от 20 м/с до 0.

п.4. Определение пути и перемещения по графику скорости

В §10 данного справочника мы рассматривали неравномерное прямолинейное движение, которое можно разбить на отдельные равномерные участки. Для такого движения путь равен сумме модулей площадей участков, определенных по графику скорости. А перемещение также равно сумме площадей, но уже с учетом знака.
Этот подход можно расширить на любое прямолинейное движение.

Пусть график скорости при прямолинейном движении разбит на (n) участков, площади которых легко определить (треугольники, прямоугольники, трапеции). Тогда:
Весь пройденный путь равен сумме модулей площадей всех участков: $$ s=|s_1|+|s_2|+…+|s_n| $$ Величина перемещения по оси ОХ равна сумме площадей всех участков с учетом знака: $$ triangle x=s_1+s_2+…s_n $$ Конечная координата равна: (x_к=x_0+triangle x)

Пример определения пути и перемещения по графику скорости
Для построенного выше графика скорости автомобиля получаем следующие участки:
1) ΔABE, его площадь равна $$ s_1=frac12 AEcdot BE=frac12cdot 5cdot 20=50 (м) $$ 2) прямоугольник EBCF, его площадь равна $$ s_2=EFcdot BE=10 cdot 20=200 (м) $$ 3) ΔCFD, его площадь равна $$ s_2=frac12 FDcdot GF=frac12cdot 4cdot20=40 (м) $$ Весь пройденный путь: $$ s=s_1+s_2+s_3=50+200+40=290 (м) $$ Скорость автомобиля все время оставалась положительной (направление движения не менялось), поэтому величина перемещения равна пройденному пути: $$ triangle x=s=290 (м) $$

п.5. Задачи

Задача 1. За 1 мин автобус увеличил скорость с 28,8 км/ч до 72 км/ч. Найдите его ускорение, постройте график зависимости скорости от времени.

Дано:
(t=1 мин=60 с)
(v_0=28,8 км/ч=8 м/с)
(v=72 км/ч=20 м/с)
__________________
(a-?)
Как перевести км/ч в м/с – см. §7 данного справочника.

Направим ось ОХ по направлению движения автобуса. Автобус направления движения не меняет, и проекции ускорения и скорости все время положительны и по величине равны значениям величин: $$ a_x=a, v_x=v $$ Поэтому ускорение равно: $$ a=frac{v-v_0}{t} $$ Получаем: $$ a=frac{20-8}{60}=0,2 left(frac{м}{c^2}right) $$ Уравнение зависимости скорости от времени: begin{gather*} v(t)=v_0+at\ v(t)=8+0,2t end{gather*} График:

Ответ: 0,2 м/с²

Задача 2. Поезд двигался прямолинейно равномерно со скоростью 18 км/ч, а в процессе торможения – равноускоренно и остановился через 10 с. Найдите модуль ускорения. Постройте график зависимости скорости от ускорения, найдите пройденный поездом путь за все время торможения.

Дано:
(v_0=18 км/ч=5 м/с)
(v=0)
(t=10 с)
__________________
(a, s-?)
Направим ось ОХ по направлению скорости (v_0). Тогда проекция ускорения: $$ a_x=frac{v-v_0}{t}, a_x=frac{0-5}{10}=-0,5 (м/с^2) $$ Проекция при торможении отрицательна.
Величина (модуль) ускорения: $$ a=|a_x|=0,5 м/c^2 $$ Зависимость скорости от времени: begin{gather*} v(t)=v_0+a_x t\ v(t)=5-0,5t end{gather*} График:

Пройденный путь равен площади треугольника ΔABC: $$ s=frac12 ACcdot BC=frac12cdot 5cdot 10=25 (м) $$ Ответ: 0,5 м/с²; 25 м

Задача 3*. С каким ускорением двигался автомобиль, если его скорость выросла с 36 км/ч до 72 км/ч на пути длиной 600 м? Постройте график зависимости скорости от времени, найдите время движения и путь с помощью графика, проверьте полученное значение пути.

Дано:
(v_0=36 км/ч=10 м/с)
(v=72 км/ч=20 м/с)
(s=600 м)
__________________
(a-?, t-?)
Ускорение равно: (a=frac{v-v_0}{t}). Откуда время равно: (t=frac{v-v_0}{a})
Средняя скорость на всем пути: (v_{cp}=frac{v_0+v}{2})
Весь путь: $$ s=v_{cp}t=frac{v_0+v}{2}cdotfrac{v-v_0}{a}=frac{v^2-v_0^2}{2a} $$ Значит, ускорение равно: $$ a=frac{v^2-v_0^2}{2s} $$ Подставляем: $$ a=frac{20^2-10^2}{2cdot 600}=0,25 left(frac{м}{c^2}right) $$ Уравнение зависимости скорости от времени: begin{gather*} v(t)=v_0+at\ v(t)=10+0,25t end{gather*} График:

Скорость достигает значения (v=20 м/с) в момент времени (t=40 с).
Значит, время движения 40 с.

Путь по графику скорости равен площади четырехугольника ABCD. begin{gather*} S_{ABCD}=S_{ABE}+S_{AECD}=frac12 AEcdot EB+AEcdot AD=frac12cdot 40cdot 10+40cdot 10=200+400=600 (м)\ s=600 м end{gather*} Найденное значение пути совпадает с условием задачи. Все параметры движения найдены верно.
Ответ: 0,25 м/с²; 40 c

Источник

Как найти ускорение — определение и формулы расчета в физике

Содержание:

Что такое ускорение
- Единица измерения
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
Мгновенное ускорение
Максимальное ускорение
Среднее ускорение
Проекция ускорения

Что такое ускорение

Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.

Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.

Единица измерения

В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как рассчитать ускорение: формулы

Для прямолинейного движения

Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.

В этом случае ускорение находится по следующим формулам:

(a;=;frac{mathrm V}t)

(a;=;frac{2S}{t^2})

(a;=;frac{V^2}{2S})

Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.

Время отсчитывается от начала движения тела.

При прямолинейном равномерном движении ускорение по модулю равняется нулю.

Для равноускоренного движения

Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).

При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.

Для равнозамедленного движения

Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).

При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V₀ и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.

Нахождение ускорения через массу и силу

Принцип инерции Галилея:

Если не действовать на тело, то его скорость не будет меняться.

Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.

Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).

II закон Ньютона:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

или

(overrightarrow a=frac{overrightarrow F}m)

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.

Выражается по формуле:

( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})

Максимальное ускорение

(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.

Среднее ускорение

Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.

(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.

Проекция ускорения

Определение проекции ускорения на ось (х):

(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.

Насколько полезной была для вас статья?

Рейтинг: 1.92 (Голосов: 36)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

«Опыт — это не то, что происходит с вами; это
то, что вы делаете с тем, что происходит с вами»

Исаак
Ньютон

ДВИЖЕНИЕ С ПОСТОЯННЫМ
УСКОРЕНИЕМ

План лекции:

1.
Скорость. Ускорение

2.
Равноускоренное прямолинейное движение

3.
Перемещение, координата и путь при равноускоренном движении

4. Свободное падение

5. Падение тел в воздухе

1. Скорость. Ускорение

Скорость — привычное для каждого
понятие. Однако, когда в обыденной жизни говорят, что, например, автомобиль
движется со скоростью 60 километров в час, то с точки зрения строгой физической
терминологии совершают ошибку. Под словом «скорость» в этом утверждении
подразумевается другая физическая величина — средняя путевая скорость.

Путь не имеет направления и является скалярной
неотрицательной величиной. Поэтому и средняя путевая скорость всегда является скалярной неотрицательной
величиной. Она не имеет направления, так как не является вектором.

Кроме средней путевой скорости, в
физике вводят среднюю скорость перемещения, которую для краткости называют
средней скоростью.

Подобно перемещению, средняя скорость является вектором. Она
характеризует не только быстроту движения тела, но и направление его движения. Направление вектора средней скорости совпадает
с направлением перемещения , т. е. направление вектора скорости — это и есть направление движения тела.
Изобразить скорость можно направленным отрезком (стрелкой), длина которого в
определённом масштабе характеризует модуль
скорости.

Наблюдая за показаниями спидометра в движущемся автомобиле, мы видим,
что в каждый момент времени он показывает определённую величину, которая
изменяется с течением времени. Это означает, что средние путевые скорости,
измеренные за различные промежутки времени, отличаются друг от друга. Понятно,
что отличаются друг от друга и средние скорости автомобиля за эти промежутки
времени. Автомобиль мог поворачивать, изменяя направление движения. В этом
случае средние скорости будут отличаться не только по модулю, но и по
направлению, Таким образом, приходим к выводу, что средняя скорость автомобиля
всё время изменяется.

Чтобы охарактеризовать скорость
автомобиля, необходимо преобразовать определение средней скорости. Рассмотрим
промежуток времени , следующий сразу за
интересующим нас моментом времени , и определим среднюю
скорость тела за этот промежуток времени. Потом уменьшим промежуток времени и
вновь определим скорость за уже меньший промежуток . Будем
повторять эту процедуру, уменьшая промежуток времени до
тех пор, пока он не станет достаточно малым. Под достаточно малым подразумевают
настолько малый промежуток времени, что при его дальнейшем уменьшении
полученные новые значения средней скорости практически не изменяются.

При этом
говорят, что промежуток времени стремится к нулю . Таким образом, достаточно
малый промежуток времени — это такой промежуток, на котором движение тела
практически неотличимо от движения с постоянной скоростью. Чем быстрее
исследуемое тело изменяет свою скорость, тем меньший промежуток времени будет
удовлетворять условию достаточной малости. Именно среднюю скорость за
достаточно малый промежуток времени , начинающийся сразу
после момента времени , считают скоростью тела в
данный момент времени .

При стремлении промежутка времени к нулю
средняя скорость (отношение ) стремится к
определённому предельному значению, которое называют пределом. Это записывают
так: . Обозначение
следует читать как «предел».

Из определения мгновенной скорости
видно, что её направление совпадает с направлением вектора перемещения за достаточно малый промежуток времени.
Из этого следует, что мгновенная скорость тела всегда направлена по касательной к траектории в той её
точке, где находится тело.

На рисунке
показано движение точечного тела по криволинейной траектории. Пусть в момент
времени тело находится в точке , а в момент — в
точке . Направление вектора средней скорости совпадает с направлением вектора
перемещения . Этот вектор направлен вдоль хорды . При уменьшении длительности
рассматриваемого промежутка времени до достаточно малого
хорда «стягивается» в точку, а направление вектора стремится
к направлению касательной в точке . При этом средняя
скорость становится мгновенной скоростью .

Тело
может изменять скорость быстро или медленно. Например, мяч, катящийся по земле,
плавно снижает скорость. Если же мы бросим этот мяч в стену, то при ударе, он
изменит скорость мгновенно. Для того, чтобы описать, насколько быстро меняется
скорость тела, необходимо ввести физическую величину, которая называется ускорением.

Физическая величина,
характеризующая быстроту изменения скорости, называется ускорением

При прямолинейном равномерном движении , т. е. скорость тела не изменяется
ни по модулю, ни по направлению, поэтому . При
прямолинейном неравномерном движении скорость тела направлена вдоль прямой,
соответствующей траектории движения, т. е. направление скорости не изменяется,
а изменяется только модуль скорости. При криволинейном движении всегда
происходит изменение скорости по направлению, так как вектор скорости направлен
по касательной к траектории движения тела. С течением времени модуль скорости
может как изменяться, так и не изменяться.

Обозначим —
скорость тела в начальный момент времени, а —
скорость тела через промежуток времени . Тогда
изменение скорости за этот промежуток времени —

Поделив вектор на промежуток времени , получим вектор, направленный так же, как
и вектор изменения скорости . Этот вектор называют средним
ускорением точки за промежуток времени .

Обозначив его через , запишем:

По аналогии с определением мгновенной
скорости определяют мгновенное ускорение. При уменьшении промежутка времени вектор изменения скорости уменьшается по модулю
и меняется по направлению. Соответственно средние значения ускорения меняются
по модулю и направлению. Но при стремлении промежутка
времени к нулю отношение стремится к определённому вектору как к
своему предельному значению. В механике эту величину называют ускорением точки в данный момент времени или
просто ускорением и обозначают .

Ускорение, как и скорость, является векторной величиной. В общем
случае направление вектора не совпадает ни с
направлением ни вектора , ни вектора . Вектор направлен
в сторону вогнутости траектории движения материальной точки, его направление
совпадает с направлением вектора изменения скорости.

Значение ускорения определяют,
учитывая векторные свойства данной физической величины. В проекциях на ось формула ускорения приобретает вид . Формулу можно записать и для модуля ускорения . Единицей измерения ускорения является
метр на секунду в квадрате:

В технике ускорение измеряют с помощью специальных
приборов — акселерометров.

2. Равноускоренное
прямолинейное движение

Для
простоты дальнейших рассуждений будем рассматривать самый простой вид движения
с ускорением — равноускоренное прямолинейное движение тела, то есть
такое движение, при котором его скорость за любые равные промежутки времени
изменяется одинаково. Так же говорят, что это движение с постоянным по
модулю и направлению ускорением.

Прямолинейным равноускоренным
движением называют прямолинейное движение, при
котором скорость тела за любые равные промежутки времени изменяется на одну и
ту же величину

Следует иметь в виду, что житейское
понимание слова «ускорение» ýже его физической трактовки. В обыденной жизни движение считают
ускоренным лишь в том случае, когда скорость движения возрастает; в противном
же случае, когда скорость уменьшается, говорят о замедленном движении. Но в физике любое движение с изменяющейся скоростью называют
ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или
тормозит (скорость уменьшается!), в любом случае он движется с ускорением. Движение с неизменной по модулю, но обязательно изменяющейся по
направлению скоростью также называют ускоренным.

Основная задача кинематики состоит в том, чтобы найти положение тела в
любой момент времени. Для того, чтобы ее решить, нужно сначала суметь найти
скорость тела в любой момент времени. Для этого следует знать закон, по
которому происходит изменение мгновенной скорости от времени для
равноускоренного движения. Выразим вектор скорости из формулы определения
ускорения тела, воспользовавшись известными математическими приемами:

Полученное уравнение называется уравнением скорости для равноускоренного
движения. Если тело движется прямолинейно вдоль оси прямолинейной декартовой системы
координат, совпадающей по направлению с траекторией тела, то проекция вектора
скорости на эту ось определяется формулой:

Знак «-» (минус) перед проекцией вектора ускорения
относится к равнозамедленному движению. Аналогично записываются уравнения
проекций вектора скорости на другие оси координат.

Таким образом, зная проекцию вектора начальной
скорости и проекцию вектора ускорения, можно вычислить проекцию вектора
мгновенной скорости, которую будет иметь тело к концу любого заданного
промежутка времени.

Как и в случае равномерного прямолинейного движения
тела, зависимости кинематических величин от времени при равноускоренном
движении можно изобразить графически.

Зависимость ускорения тела от времени. Так как в случае равноускоренного движения модуль и направление вектора
ускорения не меняется , то график ускорения имеет вид
прямой, параллельной оси времени.

При этом график располагается над осью времени,
если тело движется равноускорено; под осью времени — в случае равнозамедленного
движения (то есть когда проекция ускорения на координатную ось меньше нуля); и
будет совпадать с осью времени, если тело движется прямолинейно и
равномерно.

Если мы рассмотрим конечный промежуток времени, то
получим ограниченную область, имеющую форму прямоугольника. Площадь этого
прямоугольника будет являться ничем иным, как изменением скорости.
Действительно, ведь длина одной из сторон прямоугольника — это ускорение, а
длина другой — это время.

Зависимость скорости тела от времени. Зависимость скорости от времени — это линейная функция, графиком
которой является прямая линия, наклоненная к оси времени. График зависимости скорости от времени показывает, что

Перемещение численно равно площади фигуры под
графиком.

На графике зависимости скорости тела от времени при различных
ускорениях прямые красного и коричневого цвета соответствуют движению с
положительным ускорением и некоторой начальной скоростью, прямая зелёного цвета
— движению с отрицательным ускорением и положительной начальной скоростью, а
прямая синего цвета — прямолинейному равномерному движению тела. Чем больше
угол наклона, тем большее ускорение имеет тело.

3. Перемещение,
координата и путь при равноускоренном движении

Рассмотрим,
как определить местоположение тела при равноускоренном движении, то есть как
можно определить координату тела, путь и перемещение при таком движении.

Первым, кто решил задачу о местоположении тела
в определенный момент времени при равноускоренном движении, был итальянский
учёный Галилео Галилей. Для своих опытов он использовал наклонную плоскость с
гладкой канавкой посередине, по которой скатывались латунные шары. По водным
часам он засекал определённый интервал времени и фиксировал расстояния, которые
за это время преодолевали шары. Таким образом, Галилей выяснил, что это
расстояние квадратично зависит от времени движения шаров.

Получим формулу для определения перемещения при
равноускоренном движении графическим методом. Для этого обратимся к графику
зависимости скорости тела от времени при равноускоренном движении. Поскольку
ускорение постоянно, график представляет собой прямую. Площадь под графиком равна
перемещению и представляет собой трапецию. Из геометрии известно, что площадь
трапеции равна произведению полусуммы оснований и высоты. В нашем случае,
высота трапеции — это промежуток времени, а основания — это скорости в начальный
и конечный моменты времени.

Таким образом, площадь трапеции, а значит, и проекция
перемещения на ось равна .
Учитывая, что , получим:

В случае равнозамедленного движения проекция ускорения
отрицательна и в формуле для проекции перемещения перед ускорением ставится
знак «–» (минус).

Общая формула для определения проекции перемещения:

Данное уравнение называется уравнением
перемещения при равноускоренном движении в проекциях на координатную ось.

Так как рассматриваем прямолинейное движение, то в
случае, когда скорость и ускорение направлены в одну сторону, модуль
перемещения равен пройденному пути, поэтому, когда определяется модуль
перемещения, то определяется и пройденный путь. Заменив проекции
соответствующими векторами, получим уравнение перемещения в векторном виде

Так как координата тела в любой момент времени
определяется суммой начальной координаты и проекции перемещения, то основное
кинематическое уравнение равноускоренного движения будет
выглядеть следующим образом:

Скалярное уравнения можно заменить векторным
уравнением:

Графическое изображение зависимости проекции
перемещения от времени при равноускоренном движении.

Так как проекция перемещения квадратично зависит от
времени, то графиком перемещения для равноускоренного движения является
парабола, положение вершины которой зависит от направлений начальной скорости и
ускорения тела.

Для равноускоренного движения графиком движения (то
есть графиком зависимости координаты тела от времени), является парабола,
положение вершины которой, как и в случае с перемещением, так же зависит от
направлений начальной скорости и ускорения тела.

Задача 1. Птица летит
с постоянной скоростью 8 м/с, а перпендикулярно её движению дует ветер.
Ветер сносит птицу с постоянным ускорением 0,2 м/с². Найдите
расстояние между начальным положением птицы и её положением через 30 с.

Решение. Для начала
нам нужно определиться с системой отсчета. Поскольку нас просят найти изменение
положения птицы, то логично принять начальное положение птицы за точку отсчёта.
Расположим оси координат так, чтобы скорость птицы была направлена вдоль оси х,
а дуновение ветра — вдоль оси у.

Задача 2. На рисунке представлен график зависимости проекции
вектора скорости материальной точки от времени. Постройте график зависимости
проекции ускорения от времени.

4. Свободное
падение тел

Известно, что все тела,
предоставленные самим себе, падают на Землю. Тела, брошенные вверх,
возвращаются на Землю. Мы говорим, что это падение происходит вследствие
притяжения Земли. Это всеобщее явление и уже поэтому изучение законов
свободного падения тел только под действием притяжения Земли представляет
особый интерес.

Однако повседневные наблюдения показывают, что в
обычных условиях тела падают по-разному. Тяжелый шар падает быстро, легкий лист
бумаги падает медленно и по сложной траектории.

Характер движения, скорость и ускорение падающих тел в
обычных условиях оказываются зависящими от тяжести тел, их размеров и формы. Опыты
говорят о том, что эти различия обусловлены действием воздуха на движущиеся
тела. Это сопротивление воздуха используется и практически, например, при
прыжках с парашютом. Падение парашютиста до и после раскрытия парашюта носит
разный характер. Раскрытие парашюта изменяет характер движения, меняются
скорость и ускорение парашютиста.

Понятно,
что такие движения тел нельзя называть свободным падением под действием одного
только земного притяжения. Если мы хотим изучить свободное падение тел, то
должны или полностью освободиться от действия воздуха, или хотя бы как-то
уравнять влияние формы и размеров тел на их движение.

Свободное падение тел — это падение тел на Землю в вакууме при отсутствии помех.

Движение
тела под действием силы тяжести при отсутствии сопротивления воздуха можно
считать свободным падением. Например, в свободном падении находится спортсмен,
прыгающий в воду с вышки или мяч, выпущенный из руки.

Свободное падение — это не обязательно движение вниз.
Если начальная скорость направлена вверх, то тело при свободном падении
некоторое время будет лететь вверх, уменьшая свою скорость, и лишь затем начнёт
падать.

«Наука, связывающая теорию
и эксперимент, фактически началась с работ Галилея», — говорил Эйнштейн. В 1583 году итальянский учёный Галилео Галилей установил, что при
отсутствии сопротивления воздуха все тела, независимо от их массы, падают на
землю с одинаковым ускорением , которое направлено
вертикально вниз. Это ускорение называют ускорением свободного
падения.

Из-за несовершенства измерительного оборудования того
времени свободное падение тел изучать было почти невозможно. В поисках способа
уменьшения скорости движения Галилей заменил свободное падение на качение по
наклонной поверхности, где были значительно меньшие скорости и сопротивление
воздуха. Было замечено, что со временем скорость движения растет — тела
движутся с ускорением, и сделан вывод, что скорость и ускорение не зависят ни
от массы, ни от материала шара.

Галилей проверил, что полученные им законы скатывания
качественно не зависят от угла наклона плоскости, и, следовательно, их можно
распространить на случай падения. Окончательный вывод Галилея из последней его
книги: скорость падения нарастает пропорционально времени, а путь —
пропорционально квадрату времени.

Выводы Галилея были подтверждены английским учёным
Робертом Бойлем, наблюдавшим синхронное падение различных предметов в сосуде,
из которого был откачан воздух. Воздух из сосуда откачали для того, чтобы
исключить силу сопротивления воздуха, препятствующего движению тел.

Ускорение свободного падения тел на Землю впервые
измерил Христиан Гюйгенс в 1656 г. с помощью маятниковых часов. Вблизи
поверхности Земли ускорение свободного падения м/с².

Правильность выводов Галилея и Бойля была наглядно
продемонстрирована американскими астронавтами. Наблюдения свободного падения
птичьего пера и молотка на поверхность Луны показали, что в отсутствие
атмосферы предметы падают с одной и той же высоты за одинаковый промежуток
времени, т. е. с одинаковым ускорением. Ускорение свободного падения тел
на Луне примерно в 6 раз меньше, чем на Земле. м/с²

Почему же в вакууме тела разной массы приземляются
одновременно, ведь и в вакууме, и в воздухе масса у них разная? Ответ прост.
Сила, которая заставляет тела падать (сила тяжести), вызываемая гравитационным
полем Земли у этих тел разная. У камня она больше (так как у камня больше
масса), у перышка она меньше. Но здесь нет зависимости: чем больше сила, тем
больше ускорение! Сравним, действуем с одинаковой силой на тяжелый шкаф и
легкую тумбочку. Под действием этой силы тумбочка будет перемещаться быстрее. А
для того, чтобы шкаф и тумбочка двигались одинаково, на шкаф необходимо
воздействовать сильнее, чем на тумбочку. То же самое проделывает Земля. Более
тяжелые тела она притягивает с большей силой, чем легкие. И эти силы так
распределяются между массами, что все они в результате падают в вакууме
одновременно, независимо от массы.

Свободным падением называют движение
предметов вертикально вниз или вертикально вверх. Это равноускоренное
движение, но особый его вид. Для этого движения справедливы все формулы
и законы равноускоренного движения.

Если тело летит вертикально вниз, то
оно ускоряется, в этом случае вектор скорости (направлен вертикально вниз)
совпадает с вектором ускорения. Если тело летит вертикально вверх, то оно
замедляется, в этом случае вектор скорости (направлен вверх) не совпадает с
направлением ускорения. Вектор ускорения при свободном падении всегда направлен
вертикально вниз.

Ускорение при свободном падении тел является
постоянной величиной и зависит от высоты над уровнем моря и от географической
широты места. Оно изменяется примерно от 9,83 м/с² на полюсе и до
9,78 м/с² на экваторе. На широте Москвы ускорение свободного падения
принимается равным g = 9,8 м/с². Поэтому в большинстве случаев при
решении задач по физике ускорение свободного падения принимается равным 9,8 м/с².

Различие в значении ускорения объясняется суточным
вращением Земли и формой Земли — Земля сплюснута у полюсов, поэтому полюсный
радиус Земли меньше экваториального радиуса.

Ускорение свободного падения принято
обозначать буквой, отличной от ускорения. Но ускорение свободного падения и ускорение
— это одна и та же физическая величина и имеют они одинаковый физический смысл.
Участвуют одинаково в формулах для равноускоренного движения.

Знак «+» в формулах пишем, когда тело
летит вниз (ускоряется), знак « – » — когда тело летит вверх
(замедляется).

5. Падение тел в
воздухе

В воздухе падение
тел происходит иначе, чем в вакууме. На тело, движущееся в воздухе, действует
сила сопротивления воздуха. Свободно падающее тело сначала движется как в
вакууме, с ускорением свободного падения, так как при небольшой скорости сила
сопротивления воздуха пренебрежимо мала. увеличение скорости падения тела
приводит к увеличению силы сопротивления воздуха и уменьшению ускорения тела. Когда
сила сопротивления воздуха стаёт равной силе притяжения тела к Земле, ускорение
тела оказывается равным нулю. Вблизи Земли тела, падающие с большой высоты,
имеют постоянную скорость.

Например,
скорость падения капель дождя на землю около 30 км/ч. В отсутствие
атмосферы они достигали бы Земли со скоростью пули. Впрочем, надуманность этой
ситуации очевидна: без атмосферы не было бы ни капель дождя, ни жителей Земли.

Лёгкие тела с
большой площадью поверхности (снежинки, листья) через короткий промежуток
времени начинают двигаться в воздухе равномерно с небольшой скоростью.

Скорость тяжёлых
предметов при падении в атмосфере Земли возрастает в течение нескольких первых
секунд, а затем остаётся постоянной (порядка 100 м/с). В таблице приведена
примерная конечная скорость падения различных тел с большой высоты на Землю.

При падении тел в воздухе на их движение
влияет сопротивление воздуха, поэтому ускорение тел не равно . Но когда движутся такие тела, как
камень, спортивное ядро и т. д., сопротивление воздуха влияет на их движение
незначительно. В этом случае движение тел можно рассматривать как свободное
падение. Лишь при больших скоростях (снаряд, пуля и т. д.) сопротивление
воздуха становится существенным. Для лёгких тел типа пушинки сопротивление
воздуха существенно и при малых скоростях.

Контрольные вопросы

1. Что такое ускорение?

2. В каких единицах выражают ускорение?

3. Куда направлено ускорение при прямолинейном движении точки, если модуль
скорости точки увеличивается? уменьшается?

4. Точка движется по криволинейной траектории с постоянной по модулю
скоростью. Имеет ли эта точка ускорение?

5. Может ли точка иметь ускорение, если её скорость в данный момент
времени равна нулю?

6. По какой формуле можно найти скорость тела,
движущегося с постоянным ускорением?

7. Какое понятие является наиболее общим: равноускоренное движение,
равнозамедленное, равнопеременное?

8. Чем равноускоренное движение отличается от равнозамедленного,
происходящего в том же направлении?

9. Определите направления ускорения авиалайнеров, если один ускоренно
летит на восток, а другой — замедленно на запад.

10. Как
определяется графически перемещение тела при равноускоренном движении?

11. Какая
кривая определяет зависимость координаты от времени при равноускоренном
движении?

12. Точка
движется равноускорено. Чему равен модуль изменения скорости за 5 с, если
модуль ускорения равен 0,5 м/с²?

13. Какое
движение тела называют свободным падением?

14. С
каким ускорением движутся тела при свободном падении?

15. При
каких условиях падение на землю можно считать равноускоренным движением?

16. Является
ли равноускоренным падение тел вблизи поверхности Луны?

17. Чем
отличается падение тел в воздухе от их падения в безвоздушном пространстве?

18. Почему
раскрытие парашюта существенно уменьшает скорость приземления парашютиста?

Упражнения

1.
С каким ускорением двигался мотоциклист, если его
скорость увеличилась с 5до 15 м/с за 20 с?

2.
За какое время скорость автомобиля уменьшилась с 20
до 12 м/с, если он двигался с ускорением, равным по модулю 0,2 м/с²?

3.
Проекция скорости тела, движущегося прямолинейно,
изменяется по закону (все величины выражены в
единицах СИ). Чему равна скорость тела через 10 с от начала движения?
Постройте график

4.
Зависимость координаты точки от времени (все величины в СИ). В какой момент
времени скорость точки равна м/с?

5.
Проекции скорости на оси и
изменяются согласно уравнениям , . Чему
равно ускорение, с которым движется точка?

6.
К. Э. Циолковский в книге «Вне Земли»,
описывая полёт ракеты, отмечал, что через 10 с после старта ракета
находилась на расстоянии 5 км от поверхности Земли. С каким ускорением
двигалась ракета?

7.
Зависимость координаты от времени для некоторой
точки описывается уравнением . В какой момент
времени проекция скорости точки на ось равна
нулю?

8.
С какой высоты свободно падала сосулька, если
расстояние до земли она преодолела за 4 с?( м/с²)
(Отв. 80 м)

9.
За какое время мяч, начавший движение без начальной
скорости, пройдёт путь 20 м? (Отв. с)

10.
Мяч падает с начальной скоростью 5 м/с. Какой
будет его скорость через 3 с после начала падения? (Отв. м/с)

11.
На какую максимальную высоту поднимется тело,
брошенное вертикально вверх со скоростью 40 м/с? (Отв. м)

12.
С какой начальной скоростью брошено тело
вертикально вверх, если через 1 с после начала движения скорость тела направлена
вверх и равна 10 м/с? (Отв. 20 м/с)

13.
Два поезда идут навстречу друг другу: один —
ускоренно на север, другой — замедленно на юг. Как направлены ускорения
поездов? (Отв. Одинаково на север. Потому что у первого поезда ускорение
совпадает по направлению с движением, а у второго — противоположное движению
(он замедляется)).

14.
Поезд движется равноускорено с ускорением . Известно, что к концу четвертой секунды
скорость поезда равна 6 м/с. Что можно сказать о величине пути, пройденном
за четвертую секунду? Будет ли этот путь больше, меньше или равен 6 м?
(Отв. Так как поезд движется с ускорением, то скорость его все время возрастает
. Если к концу четвертой секунды скорость
равна 6 м/с, то в начале четвертой секунды она была меньше 6 м/с.
Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6 м.)

15.
Какие из приведенных зависимостей описывают
равноускоренное движение? (Отв. 1, 3, 4 и 5)

16.
Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?
(Отв. )

17.
Автомобиль прошел за первую секунду 1 м, за
вторую секунду 2 м, за третью секунду 3 м, за четвертую секунду
4 м и т.д. Можно ли считать такое движение равноускоренным? (Отв. В
равноускоренном движении пути, проходимые в последовательные равные промежутки
времени, относятся как последовательный ряд нечетных чисел. Следовательно,
описанное движение не равноускоренное.)

Литература

1. Мякишев Г. Я., Физика 10 класс, 2016 год, стр. 34-41

2. Дмитриева В.Ф., Физика для
профессий и специальностей технического профиля, 2017 год, стр.23-31

3. Фирсов А. В., Физика для
профессий и специальностей технического и естественнонаучного профилей, стр.
15, 17-18.

4. Тихомирова С. А. Физика. 10 класс, 2012 год, стр. 19-28.

Интернет-ресурсы

1. http://fizmat.by/kursy/kinematika/ravnouskorennoe

2. http://fizmat.by/kursy/kinematika/svobodnoe_padenie

3. http://fizmat.by/kursy/kinematika/grafiki_dvizhenija

4. http://msk.edu.ua/ivk/Fizika/Internet-uroki/6_Pryamolin_ravnousk_dvig.mp4

5. http://msk.edu.ua/ivk/Fizika/Internet-uroki/7_Ur_dvig_s_post_usk.mp4

6. http://msk.edu.ua/ivk/Fizika/Internet-uroki/8_Usk_sv_padeniya.mp4

7. http://msk.edu.ua/ivk/Fizika/Internet-uroki/9_Uskorenie_Ravnousk_dvig_Zavisimost_v_ot_t.mp4

8. http://surl.li/aupew

https://www.youtube.com/watch?v=6VXvLh3AnUs&index=24&list=PL96zz4Yl-B2jSlfQcByYg_yiPQHoVcds6

https://www.youtube.com/watch?v=9u2MuzHii7Y&index=25&list=PL96zz4Yl-B2jSlfQcByYg_yiPQHoVcds6

https://www.youtube.com/watch?v=Io2Nq6f3HuQ&index=34&list=PL96zz4Yl-B2jSlfQcByYg_yiPQHoVcds6

Источник

Проекция ускорения

Направление вектора ускорения

График ускорения

Проекции скорости и ускорения

График скорости

Вращательное движение твердого тела.

Равномерное движение по окружности

Период и частота

Равноускоренное прямолинейное движение. Ускорение

п.1. Равноускоренное движение

п.2. Ускорение

п.3. Уравнение скорости и график скорости при равноускоренном прямолинейном движении

п.4. Определение пути и перемещения по графику скорости

п.5. Задачи

Как найти ускорение — определение и формулы расчета в физике

Что такое ускорение

Единица измерения

Как рассчитать ускорение: формулы

Для прямолинейного движения

Для равноускоренного движения

Для равнозамедленного движения

Нахождение ускорения через массу и силу

Мгновенное ускорение

Максимальное ускорение

Среднее ускорение

Проекция ускорения

Текст с ошибкой:

Поиск по содержимому

1. Скорость. Ускорение

2. Равноускоренное прямолинейное движение

3. Перемещение, координата и путь при равноускоренном движении

4. Свободное падение тел

5. Падение тел в воздухе

Контрольные вопросы

Упражнения

Литература

Интернет-ресурсы

Не пропустите также:

2. Равноускоренное
прямолинейное движение

3. Перемещение,
координата и путь при равноускоренном движении

4. Свободное
падение тел

5. Падение тел в
воздухе