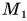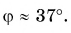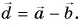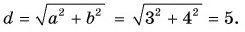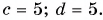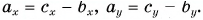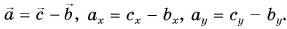Преподаватель который помогает студентам и школьникам в учёбе.
Проекция вектора на ось в физике — формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Как определяют проекцию вектора на ось
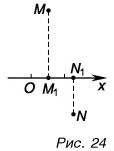
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 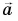
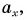
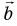
Проекция 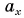
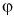
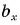
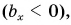
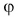
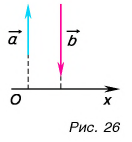
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 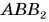
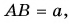
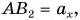
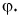
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
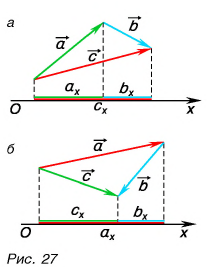
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 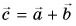
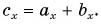
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
Рассмотрим вектор 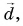
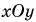
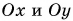
Модуль вектора 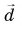
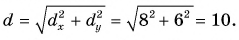
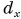
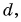
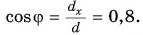
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
Вектор в пространстве определяется тремя проекциями: 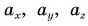
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
Пример №1
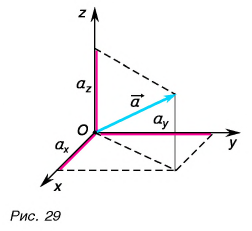
1. Определите сумму и разность взаимно перпендикулярных векторов 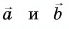
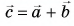
Решение
Сумму векторов 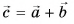
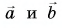
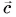
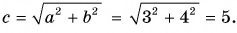
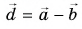
Модуль вектора 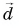
Ответ:
- Заказать решение задач по физике
Пример №2
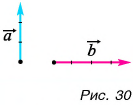
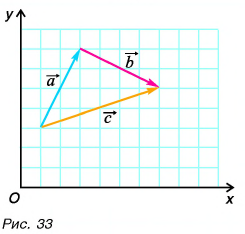
Выразите вектор 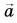
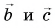
Решение
По правилу треугольника находим: 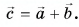
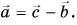
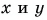
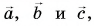
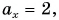
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
Векторное описание движения является полезным, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения. Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами – проекциями векторов.
Проекцией вектора на ось называют скалярную величину, равную произведению модуля проектируемого вектора на косинус угла между направлениями вектора и выбранной координатной оси.
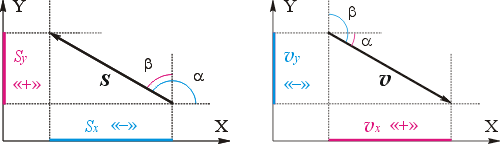
На левом чертеже показан вектор перемещения, модуль которого 50 км, а его направление образует тупой угол 150° с направлением оси X. Пользуясь определением, найдём проекцию перемещения на ось X:
sx = s · cos(α) = 50 км · cos( 150°) = –43 км
Поскольку угол между осями 90°, легко подсчитать, что направление перемещения образует с направлением оси Y острый угол 60°. Пользуясь определением, найдём проекцию перемещения на ось Y:
sy = s · cos(β) = 50 км · cos( 60°) = +25 км
Как видите, если направление вектора образует с направлением оси острый угол, проекция положительна; если направление вектора образует с направлением оси тупой угол, проекция отрицательна.
На правом чертеже показан вектор скорости, модуль которого 5 м/с, а направление образует угол 30° с направлением оси X. Найдём проекции:
υx = υ · cos(α) = 5 м/c · cos( 30°) = +4,3 м/с
υy = υ · cos(β) = 5 м/с · cos( 120°) = –2,5 м/c
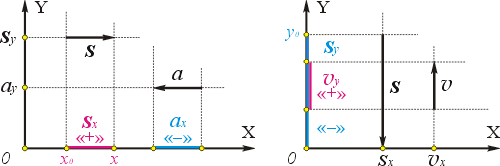
Гораздо проще находить проекции векторов на оси, если проецируемые векторы параллельны или перпендикулярны выбранным осям. Обратим внимание, что для случая параллельности возможны два варианта: вектор сонаправлен оси и вектор противонаправлен оси, а для случая перпендикулярности есть только один вариант.
Проекция вектора, перпендикулярного оси, всегда равна нулю (см. sy и ay на левом чертеже, а также sx и υx на правом чертеже). Действительно, для вектора, перпендикулярного оси, угол между ним и осью равен 90°, поэтому косинус равен нулю, значит, и проекция равна нулю.
Проекция вектора, сонаправленного с осью, положительна и равна его модулю, например, sx = +s (см. левый чертёж). Действительно, для вектора, сонаправленного с осью, угол между ним и осью равен нулю, и его косинус «+1», то есть проекция равна длине вектора: sx = x – xo = +s .
Проекция вектора, противонаправленного оси, отрицательна и равна его модулю, взятому со знаком «минус», например, sy = –s (см. правый чертёж). Действительно, для вектора, противонаправленного оси, угол между ним и осью равен 180°, и его косинус «–1», то есть проекция равна длине вектора, взятой с отрицательным знаком: sy = y – yo = –s .
На правых частях обоих чертежей показаны другие случаи, когда векторы параллельны одной из координатных осей и перпендикулярны другой. Предлагаем вам убедиться самостоятельно, что и в этих случаях тоже выполняются правила, сформулированные в предыдущих абзацах.
Проекция вектора на ось
Вектор может отбрасывать тень (проекцию) на какую-нибудь ось
Рис. 1. Векторы и их проекции на ось Ox
На рисунке 1 изображены векторы ( vec{a} ), ( vec{b} ), ( vec{c} ), ( vec{g} ) и их проекции на ось Ox.
Если:
- вектор параллелен оси, то «его проекция = его длина», пример для вектора ( vec{g} );
- вектор перпендикулярен оси, то его проекция равна нулю, пример для вектора ( vec{b} );
- проекция направлена против оси, то её записывают со знаком «-», пример для вектора ( vec{a} ).
- чем больше вектор наклоняется к оси, тем больше его проекция на эту ось. Сравните проекции векторов ( vec{c} ) и ( vec{g} ).
Примечание:
Длина вектора – это положительная величина, а проекция вектора может быть отрицательной
Как разложить вектор на проекции
Мы уже находили длину и направление вектора по его координатам.
Теперь решим обратную задачу: пользуясь длиной и направлением вектора, найдем его координаты.
На плоскости (две оси) легко разложить вектор на проекции, если известны:
- длина вектора и
- угол между вектором и какой-либо осью (угол обозначается дугой).
Алгоритм действий для разложения вектора на проекции
- Проводим прямоугольник так, чтобы вектор стал его диагональю.
- Диагональ разделит прямоугольник на треугольники. Эти два треугольника прямоугольные.
- Выберем треугольник, в котором угол отмечен дугой.
- Дуга одним своим концом всегда касается гипотенузы, а вторым концом – одного из катетов.
Важно! Вектор, который мы раскладываем, всегда является гипотенузой.
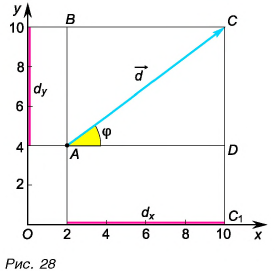
Рис. 2. Проекции вектора поможет найти угол между вектором и осью
Формулы разложения вектора на проекции
Формулы разложения легко запомнить с помощью фразы:
Гипотенузу умножаем на косинус (угла), получаем катет, который касается (дуги).
На языке математики эта фраза запишется так:
[ |vec{m}| cdot cos(alpha) = m_{x} ]
Катет ( m_{x} ) – это «x» координата вектора.
Если длину вектора умножим на синус, то получим второй катет:
[ |vec{m}| cdot sin(alpha) = m_{y} ]
Катет ( m_{y} ) – это «y» координата вектора.
Обе формулы запишем в виде системы:
[ large boxed {begin{cases} left|vec{m}right| cdot cos(alpha) = m_{x} \ left|vec{m}right| cdot sin(alpha) = m_{y} end{cases}} ]
Величина ( |vec{m}| ) — это длина вектора ( vec{m} )
Оценка статьи:
Загрузка…
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Для понятия проекции вектора на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
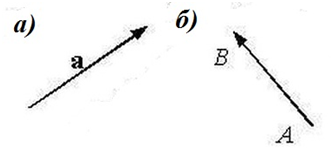
Одной маленькой буквой: $overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
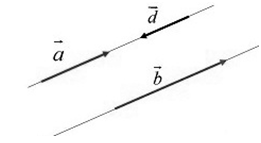
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
«Проекция вектора на ось. Как найти проекцию вектора» 👇
Определение 4
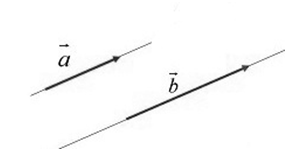
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $overline{a}↑↑overline{b}$
Определение 5
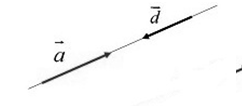
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $overline{a}↑↓overline{d}$
Определение 6
Длиной вектора $overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
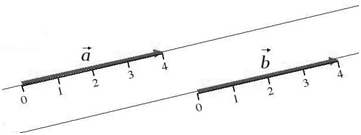
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A’$ — начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B’$ — конец искомого вектора. Вектор $overline{A’B’}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
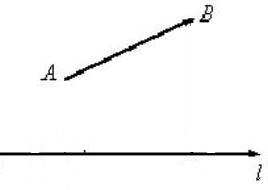
Постройте геометрическую проекцию $overline{AB}$ на ось $l$, изображенные на рисунке 6.
Решение.
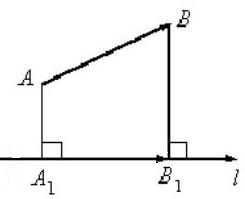
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A’$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B’$ (рис. 7).
Полученный на оси $l$ вектор $overline{A’B’}$ и будет искомой геометрической проекцией.
Замечание 1
Заметим, что если угол между вектором и осью острый, то проекция сонаправлена с осью, а если тупой, то проекция противоположно направлена с осью.
Числовая проекция
Как мы уже знаем, результатом алгебраической проекции будет неотрицательное действительное число.
Определение 9
Числовой (алгебраической) проекцией на ось будем называть неотрицательное число, равное длине вектора геометрической проекции.
Рассмотрим это понятие на примере задачи:
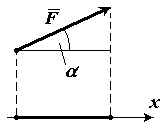
Пример 2
Найти числовую проекцию вектора $overline{F} на сонаправленную ему ось $x$, если угол между ними равняется $α$ (рис. 8). (рис. 8).
Решение.
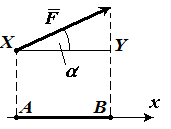
Введем на рисунке следующие обозначения:
Видим, что длина вектора геометрической проекции, равняется длине $XY$. Из определения косинуса получим, что
$XY=|overline{F}|cosα$
где $|overline{F}|$ — длина вектора $overline{F}$. Это и будет искомая алгебраическая проекция на ось.
Другие случаи можете видеть на рисунке 9.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
В математике существуют два определения:
1) геометрическая проекция вектора — вектор;
2) проекция вектора на ось — число.
Геометрическая проекция вектора — это вектор, который можно получить, если провести перпендикуляры от концов вектора до выбранной оси. Проекция начала вектора соответствует началу геометрической проекции, а проекция конца вектора соответствует концу геометрической проекции.
Ваш браузер не поддерживает HTML5 видео
Для вектора
v→
геометрическая проекция на оси (t) — это вектор
vt→
.
Для вектора
n→
геометрическая проекция на оси (y) — это вектор
ny→
.
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
ax=4bx=−3
Если длина вектора
a→
равна
a→
и
α
— это острый угол, созданный вектором и осью (x), то скалярная проекция вектора вычисляется по формуле:
ax=a→⋅cosα
.
Знак проекции вектора выбирается в зависимости от направления оси.
На рисунке видно, что эту формулу можно получить из соотношения в прямоугольном треугольнике:
.
Обрати внимание!
Если вектор и ось проекций параллельны, то скалярная проекция на этой оси — число, которое равно длине вектора, если направления вектора и оси совпадают, или число, противоположное длине вектора, если направления вектора и оси — противоположные.
Если вектор и ось проекций перпендикулярны, то проекция вектора на этой оси равна (0).
at=3bt=−5ct=0dt=0