Проекция точки на плоскость онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Проекция точки на плоскость − теория, примеры и решения
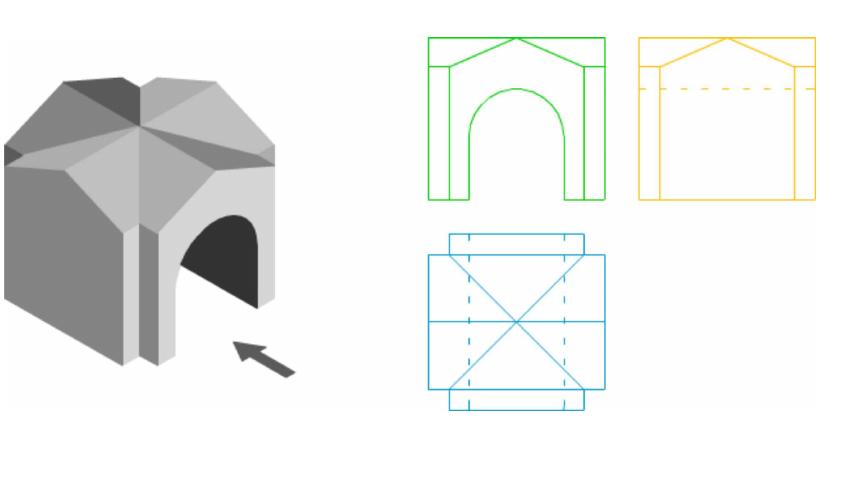
Для нахождения проекции точки M0 на плоскость α, необходимо:
- построить прямую L, проходящую через точку M0 и ортогональной плоскости α.
- найти пересечение данной плоскости α с прямой L(Рис.1).
Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M0 на плоскость (1).
Пример 1.Найти проекцию M1 точки M0(4, -3, 2) на плоскость
Решение.
Нормальный вектор плоскости имеет вид:
т.е. A=5, B=1, C=−8.
Координаты точки M0: x0=4, y0=−3, z0=2.
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
Из выражений (7) находим:
Ответ:
Проекцией точки M0(4, -3, 2) на плоскость (6) является точка:
Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.
1. Строим проекции треугольника АВС.
2. Строим проекции треугольника EDK.
3. Находим точку пересечения стороны АС с треугольником EDK
4. Находим точку пересечения стороны А B с треугольником EDK и строим линию пересечения MN
5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.
6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.
7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.
Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.
8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.
Определение видимости на чертеже.
В начертательной геометрии плоскости считаются непрозрачными, поэтому необходимо на проекциях определить видимость.
Для определения видимости на чертеже используем метод конкурирующих точек, сущность которого заключается в выборе двух скрещивающихся прямых.
Для определения видимости на фронтальной плоскости проекций V поступают так. Выбираем две скрещивающиеся прямые В²С² и М²N², фронтальные проекции которых пересекаются в точках 1 и 3. По горизонтальной проекции определяем, что проекция точки 3¢, лежащая на проекции прямой M¢N¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой В¢С¢, т. к она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на фронтальной плоскости проекций проекция М²N² будет закрывать проекцию В²С². Границей видимости является проекция точки пересечения К².
Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢С¢ и M¢N¢, горизонтальные проекции которых пересекаются в точках 4¢ и 5¢. По фронтальной проекции определяем, что проекция точки 5², лежащая на проекции прямой М²N², будет закрывать проекцию точки 4², лежащую на проекции прямой А²С², т. к. она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на горизонтальной плоскости проекций проекция M¢N¢ будет закрывать проекцию А¢С¢. Границей видимости является проекция точки пересечения К¢.
Задача 3. Построение линии пересечения двух плоскостей, одна из которых занимает частное положение.
Даны две плоскости: плоскость ∆АВС – плоскость общего положения, плоскость ∆DЕК – плоскость частного положения, которая расположена перпендикулярно фронтальной плоскости проекций (рис. 3).
Рис. 3. Построение линии пересечения двух плоскостей, одна из которых занимает
частное положение
Фронтальная проекция ∆DЕК совпадает с фронтальным следом плоскости и фронтальной проекцией линии пересечения треугольников.
(KL) ‑ линия пересечения двух треугольников. Проекции этой линии пересечения – фронтальную и горизонтальную строят исходя из свойства принадлежности точек K и L сторонам (АВ) и (ВС), соответственно. Видимость треугольников на горизонтальной плоскости проекций определяем методом конкурирующих точек, рассмотренном в задаче 2.
Задача 4. Построение линии пересечения двух плоскостей общего положения.
Даны две плоскости общего положения, заданные треугольниками АВС и DЕК. Построить линию пересечения двух треугольников, определить видимость треугольников на проекциях.
Прямая линия, получаемая при взаимном пересечении двух плоскостей, определяется двумя точками, каждая из которых одновременно принадлежит обеим плоскостям. Общие точки определяются решением основной позиционной задачи начертательной геометрии – построение точки пересечения прямой с плоскостью (см. рис. 2).
Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (проецирующие плоскости). Решение задачи приведено на рис. 4.
Алгоритм решения задачи:
1. Определяют первую точку линии пересечения двух треугольников – точку М.
1.1. Фронтально-проецирующая плоскость a проведена через сторону DК и задана на чертеже фронтальным следом aV.
1.2. Плоскость a пересекает плоскость треугольника АВС по прямой (1,2), на чертеже строят две проекции этой прямой.
1.3. Прямая (1,2) пересекает сторону DК в точке М, строят две проекции точки М² и М¢.
2. Определяют вторую точку искомой линии пересечения двух треугольников – точку N.
2.1. Горизонтально-проецирующая плоскость b проведена через сторону АВ и задана на чертеже горизонтальным следом bН.
2.2. Плоскость b пересекает плоскость треугольника DЕК по прямой (3,4), на чертеже строят две проекции этой прямой.
2.3. Прямая (3,4) пересекает АВ в точке N, строят две проекции точки N² и N¢.
Плоскости треугольников АВС и DЕК пересекаются по прямой MN.
Рис. 4. Построение линии пересечения двух треугольников
3. Видимость плоских фигур на проекциях определяют методом конкурирующих точек.
Для определения видимости на фронтальной плоскости проекций V выбираем две скрещивающиеся прямые D²K² и A²B², фронтальные проекции которых пересекаются в точках 1² и 5². По горизонтальной проекции определяем, что проекция точки 5¢, лежащая на проекции прямой D¢K¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой А¢В¢, т. к. она будет ближе к наблюдателю. Следовательно, на фронтальной плоскости проекция D²K² будет закрывать проекцию A²B². Границей видимости является проекция линии пересечения M²N².
Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢В¢ и D¢Е¢, горизонтальные проекции которых пересекаются в точках 3¢ и 6¢. По фронтальной проекции определяем, что проекция точки 3², лежащая на проекции прямой D²Е², будет закрывать проекцию точки 6², лежащую на проекции прямой A²B², т.к. она будет ближе к наблюдателю. Следовательно, на горизонтальной плоскости проекция D¢Е¢ будет закрывать проекцию А¢В¢. Границей видимости является проекция линии пересечения N¢M¢.
Задача 5. Построить две проекции линии пересечения плоскости a ‑ общего положения, заданной следами и плоскости b ‑ общего положения, заданной параллельными прямыми а и b.
Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (плоскости уровня), пересекающие заданные плоскости по прямым, недостающие проекции которых легко строятся и пересекаются в пределах чертежа.
Графическое решение задачи приведено на рис. 5.
Рис. 5. Построение линии пересечения двух плоскостей
Вспомогательная горизонтальная плоскость-посредник γ задана следом γV и пересекает плоскость a по горизонтали, проходящей через точку 3, а плоскость b по горизонтали (1, 2). Горизонтальные проекции этих горизонталей пересекаются в точке К. Строят фронтальную проекцию точки К, используя свойство принадлежности точки прямой линии. Точка К принадлежит обеим плоскостям a и b. Вторая точка N, общая для двух плоскостей a и b, определяется второй вспомогательной плоскостью-посредником частного положения δ (на чертеже задана следом δV). Искомая прямая (КN) является линией пересечения двух плоскостей a и b.
ПРИЛОЖЕНИЕ 1
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Гордон В.О., Семенцов-Огиевский М. А. Курс начертательной геометрии. Учеб. пособие. М.: Высшая школа. 2007.272 с.
2. Самохвалов Ю. И. Начертательная геометрия. Учебное пособие. Екатеринбург: Изд-во УГГУ. 2011. 121 с.
3. Самохвалов Ю. И., Шангина Е. И. Начертательная геометрия. Инженерная графика. Учебно-методическое пособие. Екатеринбург: Изд-во УГГУ. 2011. 96 с.
Определение видимости в начертательной геометрии с примерами
Определение видимости:
Точки, расположенные на одной проецирующей прямой, называются конкурирующими.
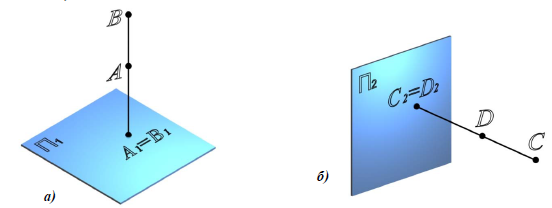
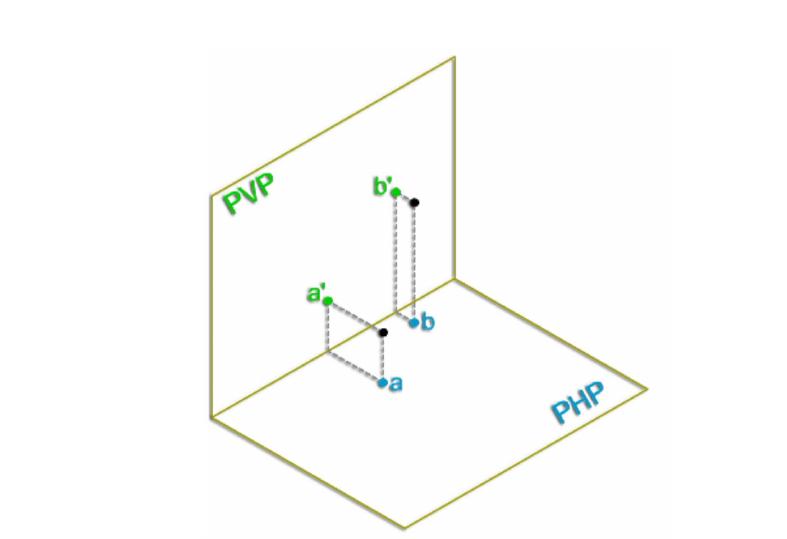
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).
Рис. 7.1. Конкурирующие точки:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D — невидима).
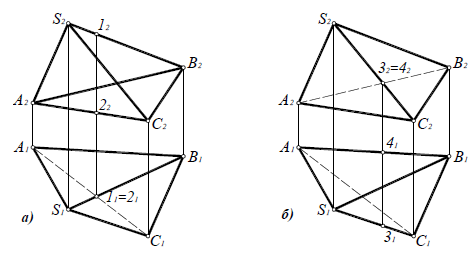
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).
Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П1, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П1.
Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П2.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Конструктивное отображение пространства
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Комплексный чертеж
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://poisk-ru.ru/s25018t12.html
http://www.evkova.org/-opredelenie-vidimosti
Проекции точек на поверхностях геометрических тел
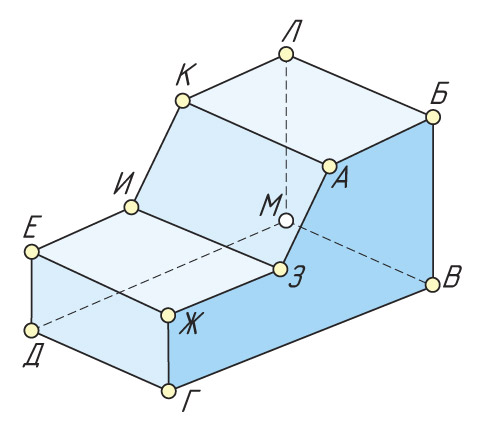
Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.
Укажите количество вершин, ребер и граней изображенного предмета.
|
Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки. |
 |
|
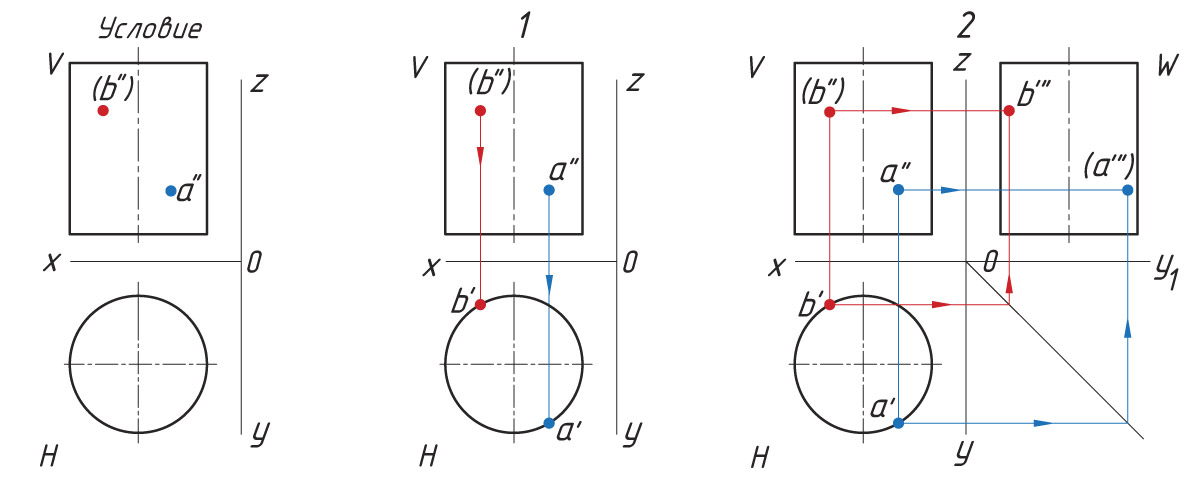
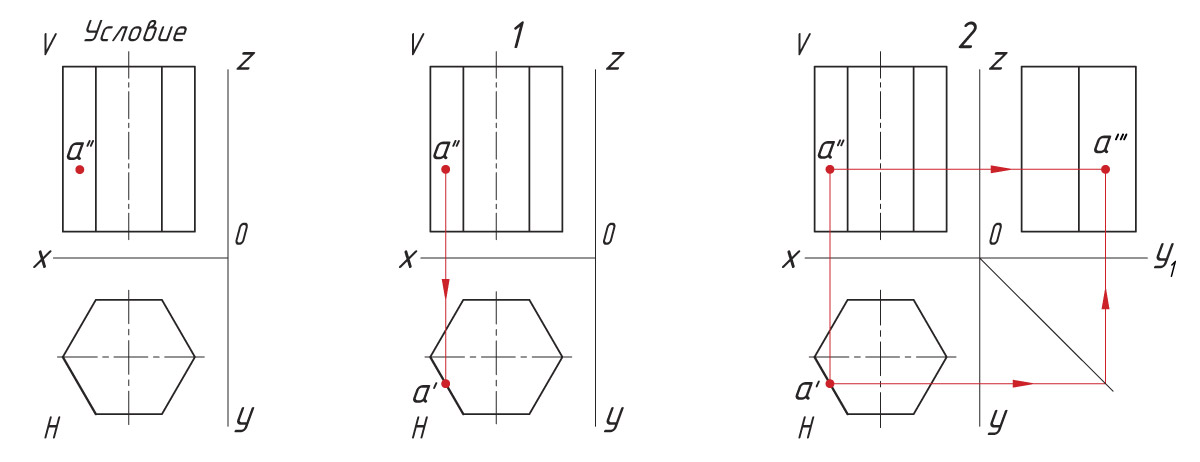
Рассмотрим проекции точки на геометрических телах. Проецирование точек на поверхности цилиндра Последовательность проецирования точек 1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью. 2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи. |
 |
Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).
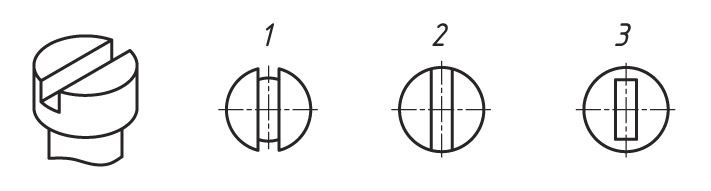
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
|
Проецирование точек на поверхности призмы Последовательность проецирования точек 1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы). 2. Проекцию точки а′″ находят на пересечении линий проекционной связи. |
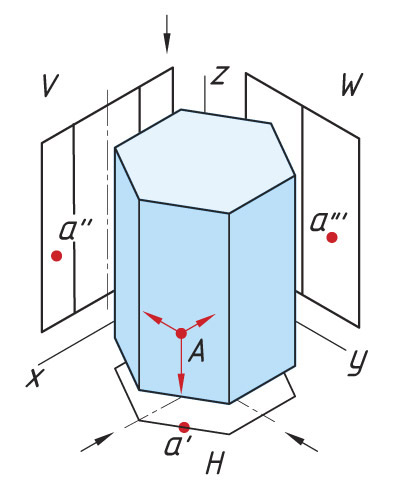 |
Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.
Проецирование точек на поверхности пирамиды
Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.
Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.
Построение проекции точки, лежащей на грани
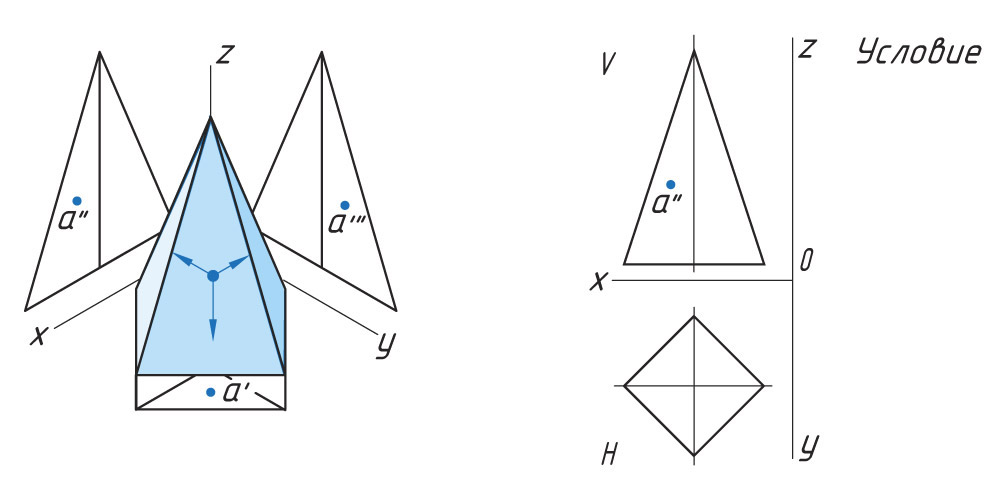
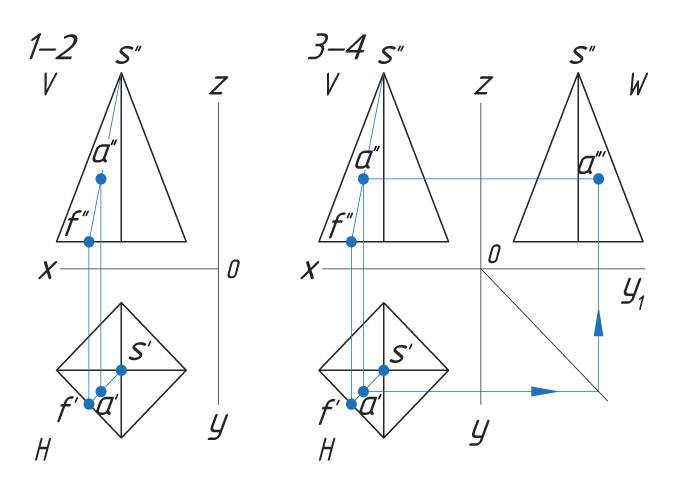
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.
Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.
|
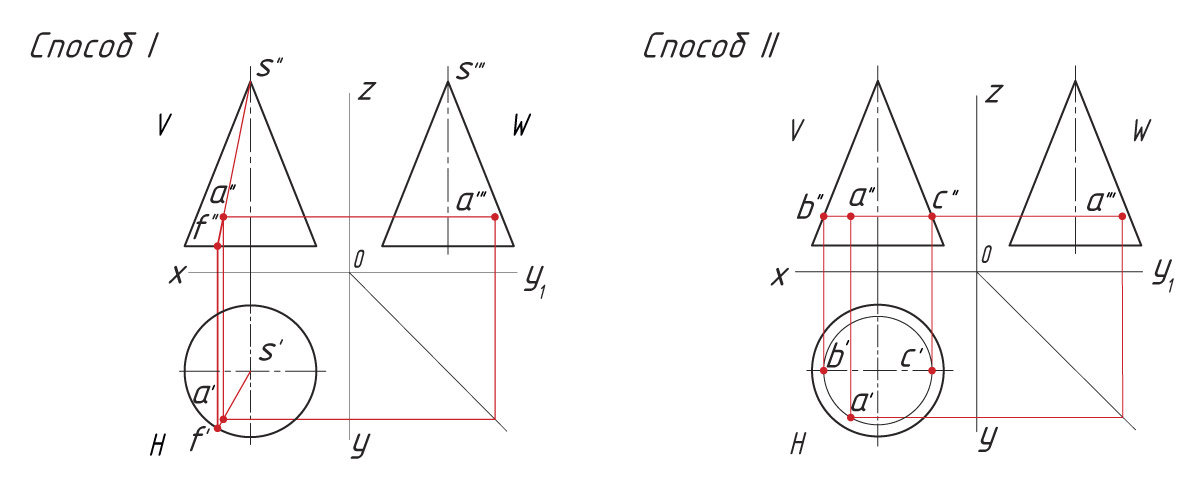
Способ I. 1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″. |
 |
|
Способ II. 1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″. |
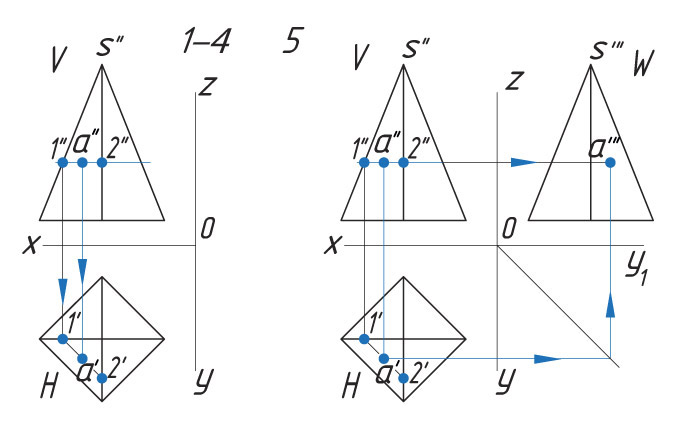 |
На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
|
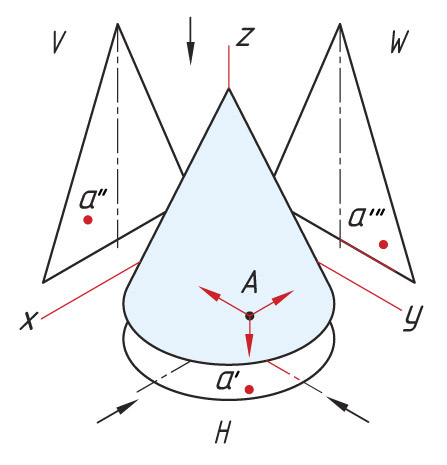
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами. Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А. |
 |
Помогите, пожалуйста, бьюсь вторую неделю и никак… все вычисления 5 раз проверила.
Задача: Найти проекцию точки А4 на грань А1А2А3. Построить график. Дано А1(4,3,1) А2 (2,7,5) А3(4,2,4) А4(2,3,5).
Что делаю:
1) Ищу нормаль n к грани А1А2А3, получаю n=(16,6,2)
2) Ищу уравнение плоскости А1А2А3, получаю 16x+6y+2z-84=0
3) Ищу уравнение прямой перпендикулярно А1А2А3, которая проходит через А4. Используя найденное в пункте 1 и 2, получаю: (x-2)/16=(y-3)/6=(z-5)/2. Ввожу переменную t, подставляю в уравнение плоскости А1А2А3, решаю (t=3/37). Нахожу координаты. Получаю x=3,3, y=3,5 z=5,2. И даже делаю проверку, все ок.
Строю график…. И тут точка (3,3;3,5;5,2) не попадает на грань А1А2А3… и даже не похоже что она лежит на перпендикуляре от А4… Что делаю не правильно? В каком месте не так? Сдавать на следующей неделе, а я застряла на этом месте…(((
При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.
Уравнение для описания плоскости
Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее — ниже.
Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:
A*x + B*y + C*z + D = 0.
Первые три коэффициента — это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.
Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.
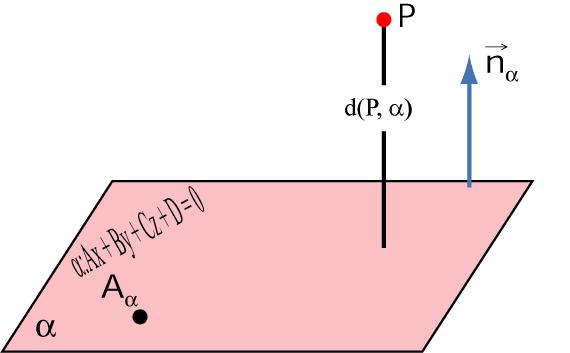
Понятие о проекции точки и ее вычисление
Предположим, что задана некоторая точка P(x1; y1; z1) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x2; y2; z2). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.
Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:
(x; y; z) = (x1; y1; z1) + λ*(A; B; C).
Где λ — действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.
После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.
Вычисление расстояния от плоскости до точки
Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:
d = |PQ¯| = √((x2 — x1)2 + (y2 — y1)2 + (z2 — z1)2).
Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.
Пример задачи
Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:
2*x — y + z + 4 = 0.
Следует найти точки проекцию на плоскость и вычислить между ними расстояние.
В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90o. Имеем:
(x; y; z) = (0; -2; 3) + λ*(2; -1; 1).
Записывая это равенство в явном виде, приходим к следующей системе уравнений:
x = 2*λ;
y = -2 — λ;
z = λ + 3;
2*x — y + z + 4 = 0.
Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:
2*(2*λ) — (-2 — λ) + λ + 3 + 4 = 0 =>
6*λ + 9 = 0 =>
λ = 9/6 = 3/2 = 1,5.
Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:
(x; y; z) = (0; -2; 3) + 1,5*(2; -1; 1) = (3; -3,5; 4,5).
Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:
d = √((3 — 0 )2 + (-3,5 + 2 )2 + (4,5 — 3 )2) = 3,674.
В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.