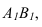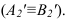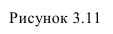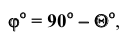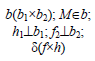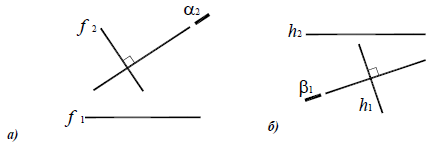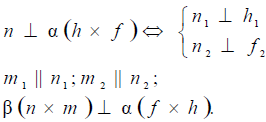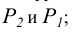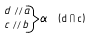Проецирование прямого угла.
Прямой
угол между двумя пресекающимися прямыми
проецируется в натуральный размер
только в том случае , когда одна из
сторон угла параллельна плоскости
проекций. Если одна сторона прямого
угла будет параллельна фронталь-
ной плоскости
проекций , то прямой угол будет
проецироваться в натуральный
размер на фронтальную
плоскость проекций.
Это имеет очень
важное значение при построениях на
комплексном чертеже
1) прямых
перпендикулярных к друг к другу;
2) прямой
перпендикулярной к плоскости ;
3) взаимно
перпендикулярных плоскостей.
И соответственно,
если ни одна из сторон прямого угла не
занимает положение
прямой уровня, то
угол не будет проектироваться в
натуральную величину.
Решить задачу
нахождения натуральной величины угла,
в таком случае можно преобразовав
комплексный чертеж.
( Подробно ”О
Свойствах проекций плоских углов”
читайте параграф 58 Н.Г.
С.А. Фролов)
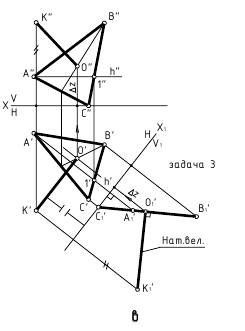
Преобразование комплексного чертежа . (Первая и вторая основные задачи преобразования чертежа).
Преобразование
чертежа используется при решении задач
связанных с измерениями геометрических
образов или их взаимным расположением.
Всего существует четыре основных задачи
преобразования чертежа, две из которых
связаны с преобразованием прямой линии
и две с преобразованием плоскости.
Сформулируем две
первые основные задачи :
1) преобразование
комплексного чертежа таким образом,
чтобы заданная на
чертеже
прямая общего
положения
стала прямой уровня.
2)
преобразование
комплексного чертежа так, чтобы заданная
на чертеже
прямая
уровня заняла
проецирующие положение.
Рассмотрим решение
первой задачи на примере преобразования
чертежа способом введения новой
плоскости проекций. Способ введения
новой плоскости проекций мы
уже применяли
когда рассматривали комплексный чертеж
точки.
Теперь рассмотрим
этот способ применительно к линиям.
Пусть мы имеем два
пересекающихся отрезка прямых общего
положения .
Проведем такую
замену плоскости проекций , чтобы одна
из прямых стала прямой уровня. Это
позволит нам судить под каким углом
(тупым, прямым или острым )
пересекаются
прямые . Причем, если этот угол не прямой,
то для его измерения не достаточно будет
одной замены плоскости проекций. В этом
случае нам
потребуется ,
чтобы обе стороны угла были параллельны
плоскости проекций.


=
В2


С 1

4 В4,С4 = В,С
А
1

1
В
4
90 град
=
А
4
Х
1,4
Введем новую
плоскость проекций П 4 , так чтобы она
была параллельна отрезку ВС. Одновременно
плоскость П 4 перпендикулярна плоскости
П 1.
Эти плоскости
образуют новую ось Х 1,4. Ось на чертеже
проводим
параллельно
горизонтальной проекции отрезка В 1С
1.
Строим новую
проекцию отрезка ВС:
1)
(В1,В4)
В 1 ; ( В 1, В4)
Х 1,4. (построить прямую В1,В4,
которая включает
точку В 1 ; прямая перпендикулярна оси
Х 1,4)
2)
В 4
( В1, В4) ; В
4, Х 1,4
=
В 2, Х 1,2
(построить точку В 4 принадлежащую прямой
В1,В4 ; расстояние от В 4 до оси Х 1,4 равно
расстоянию от В2 до оси Х 1,2.)
3)
(С1, С4)
С 1 ; ( С 1, С 4)
Х 1,4 ( построить линию С1,С4,
которой принадлежит
точка С1; линию С1,С4 провести перпендикулярно
оси Х 1,4)
4)
С 4
(С 1, С4) ;
С4, Х 1,4
=
С2, Х 1,2
(построить точку С 4 принадлежащую
прямой С1, С4; расстояние от точки С4 до
оси Х 1,4
равно расстоянию
от точки С2 до оси Х 1,2)
5)
В 4 С 4
В 4
С 4 ( построить проекцию отрезка прямой
В4,С4 включающего точки В4 и С4)
.
На этом этапе мы
построили проекцию отрезка прямой
В4,С4, которая обладает следующими
метрическими свойствами :длина проекции
отрезка равна длине
самого
отрезка . Величина угла
4 между
проекцией В4,С4 и новой осью Х 1,4
равна
углу наклона отрезка прямой В,С к
плоскости П
1.
Чтобы
закончить наши построения достаточно
:
6)
(А1,А4)
А1 ; ( А 1,А4)
Х 1,4. (построить прямую А1,А4, которая
включает точку А 1 ; прямая перпендикулярна
оси Х 1,4)
7)
А 4
( А1, А4) ; А
4, Х 1,4
=
А 2, Х 1,2
(построить точку А 4 принадлежащую прямой
А1,А4 ; расстояние от А 4 до оси Х 1,4 равно
расстоянию от А2 до оси Х 1,2.)

А
4, В 4
А 4
В 4 ( построить проекцию отрезка прямой
А4,В4 включающего точки А4 и В4).
Теперь мы построили
проекцию угла А4В4С4 на плоскость П4 ,
причем проекция
равна
натуральной величине угла АВС, так как
это прямой угол.
Соседние файлы в предмете Начертательная геометрия
- #
- #
29.03.2015366.42 Кб201ВС. С 14-30 варианты Начерт.docx
- #
29.03.20154.33 Mб52Начерт геометрия контрольная работа №2.docx
На этой странице вы узнаете
- Как мы сталкиваемся с двугранными углами, когда читаем книгу?
- Где в комнате можно найти перпендикулярные плоскости?
- Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
Углы между плоскостями
Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели.
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия.
Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла.
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке:
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.
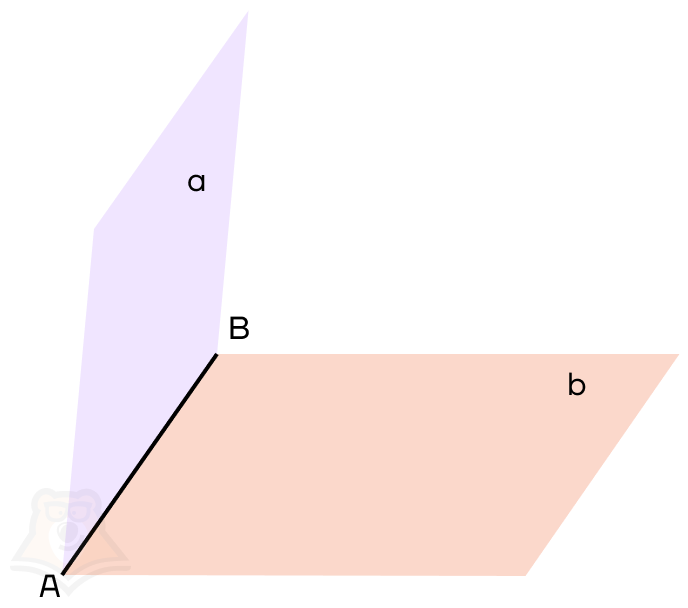
Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.
Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.
Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях.
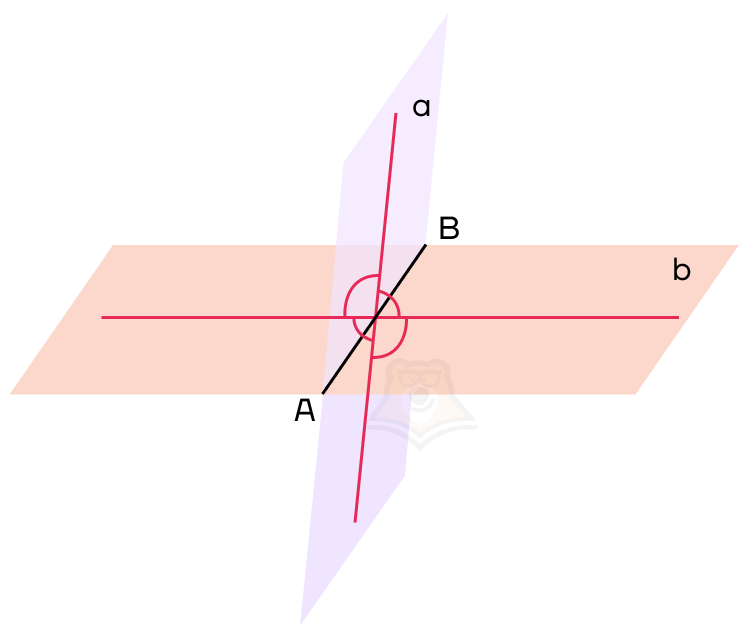
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями.
Угол COD также будет называться линейным углом двугранного угла.
Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой.
Как и обычные углы, углы между плоскостями бывают трех видов:
- Острые, то есть меньше 900
- Прямые, равные 900
- Тупые, которые больше 90и меньше 1800
Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.
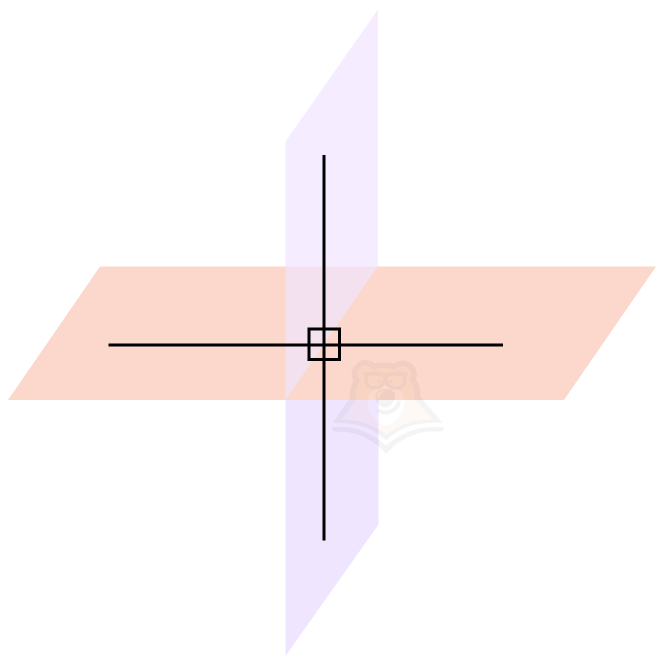
А что будет, если между плоскостями получится прямой угол?
Такие плоскости называются перпендикулярными.
Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.
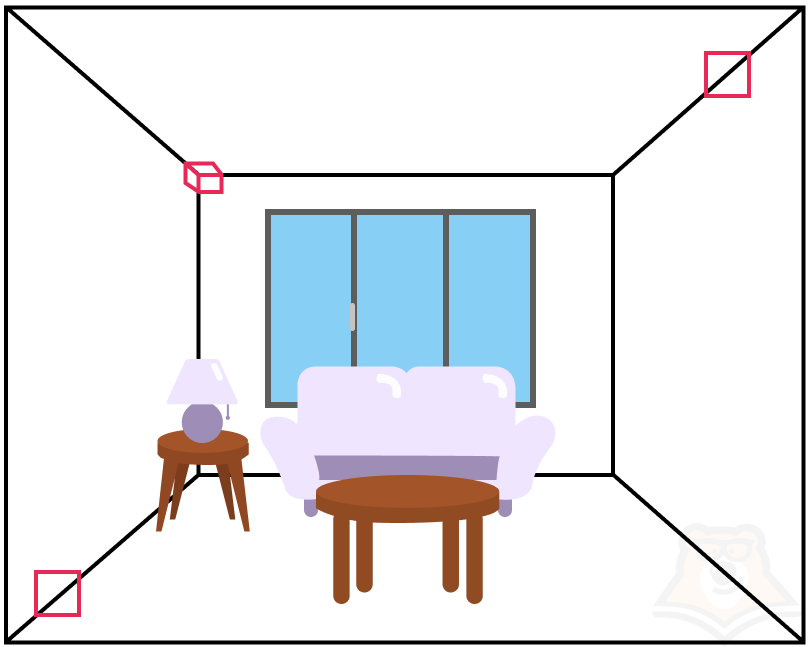
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам.
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму.
1 шаг. Найти линию пересечения плоскостей.
2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости.
3 шаг. Найти острый угол между построенными перпендикулярами.
Углы между прямой и плоскостью
Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?
И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.
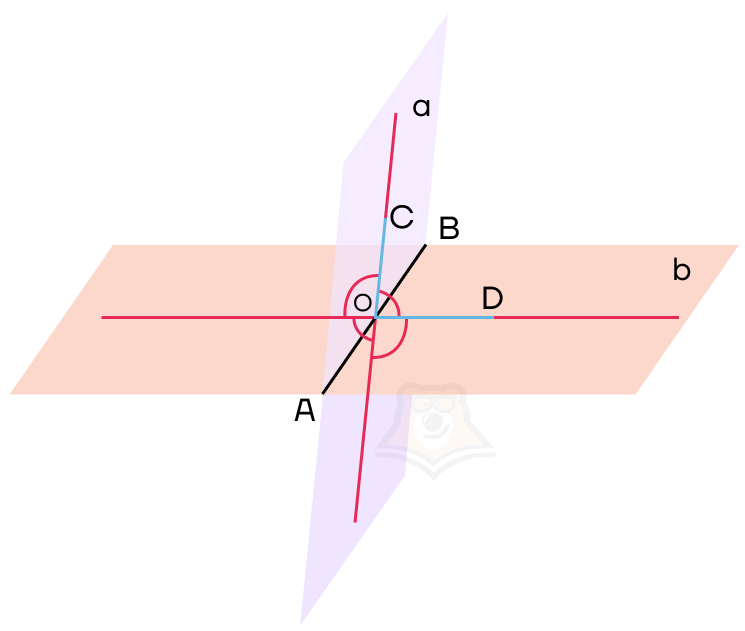
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.
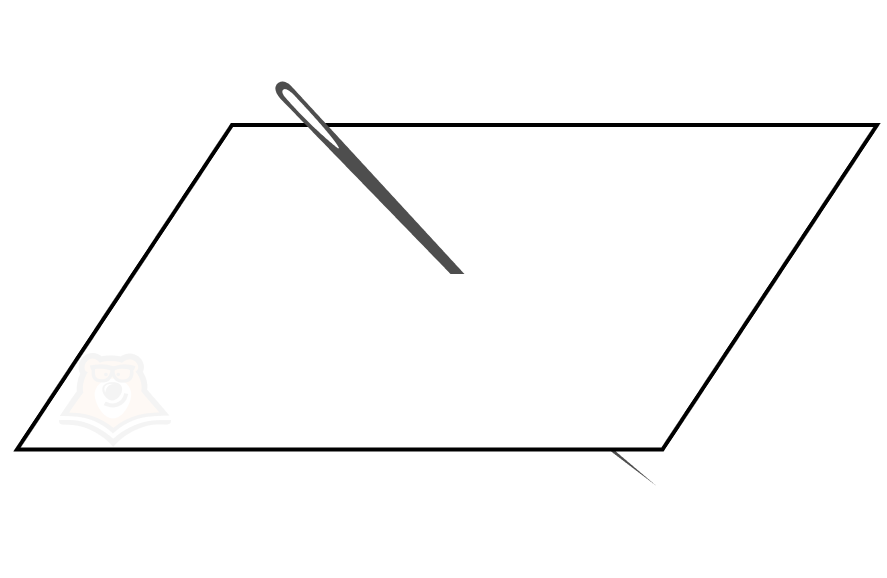
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.
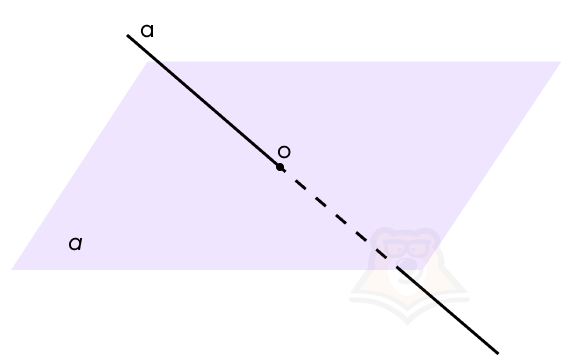
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.
Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А1.
Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.
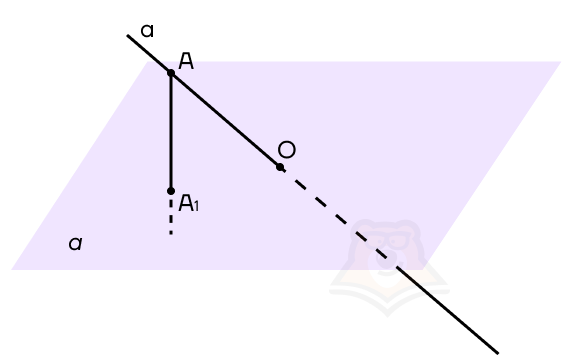
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А1О.
Проекция прямой а на плоскость — это прямая а1, образованная проекциями всех точек прямой а на плоскость.
Таким образом можно построить проекции не только прямой, но и любой фигуры.
Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А1ОА.
В этом случае мы также берем острый угол, образованный прямой и плоскостью.
Шаг 1. Построить проекцию прямой на плоскость.
Шаг 2. Найти угол между прямой и построенной проекцией.
Если прямая параллельна плоскости угол будет равен 0.
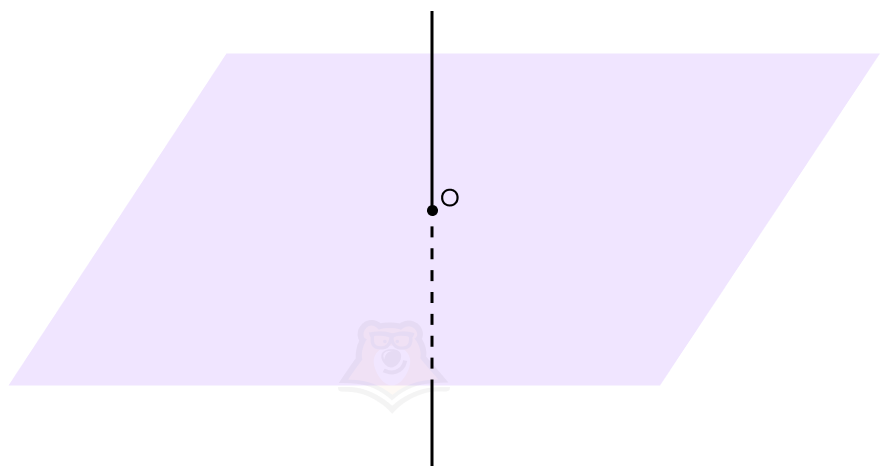
Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.
Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.
А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?
Для этого существует признак перпендикулярности прямой и плоскости:
- Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
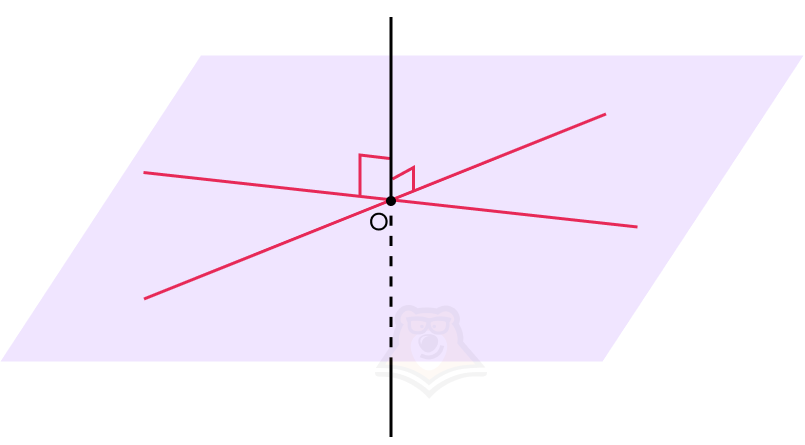
Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.
Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.
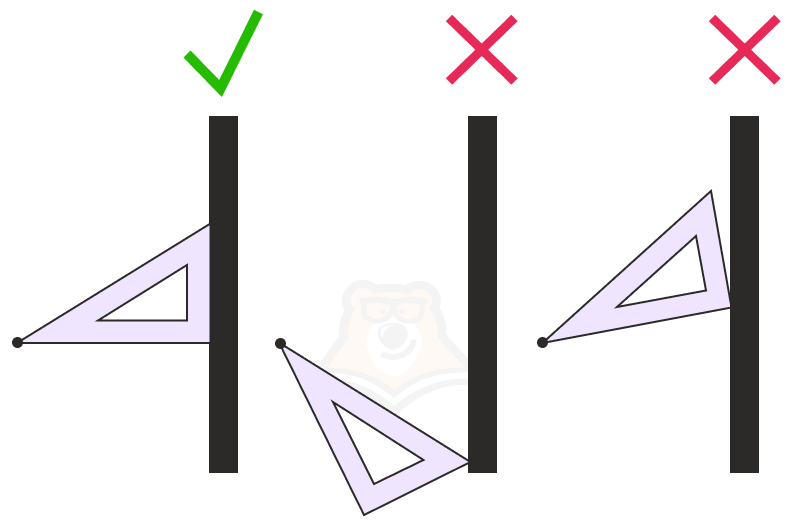
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.
Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.
Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.
Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.

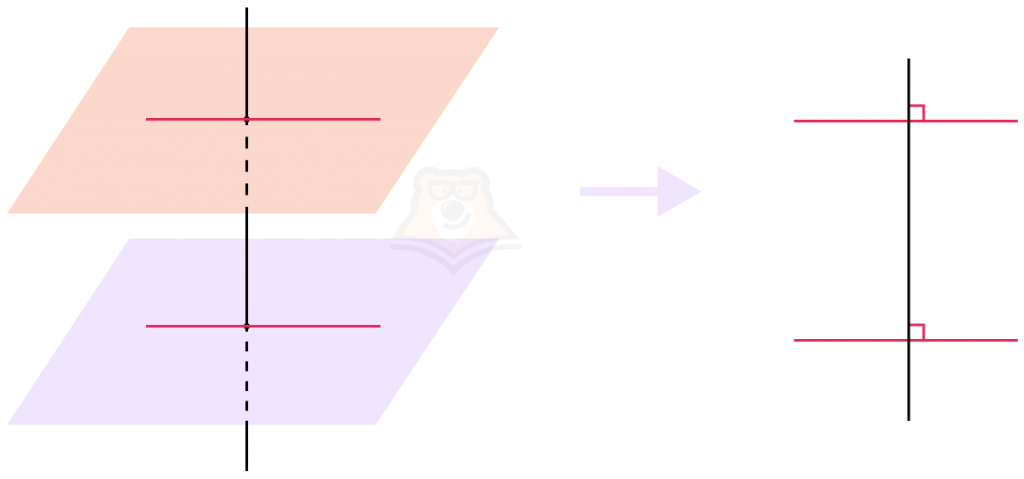
Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.
Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.
Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.
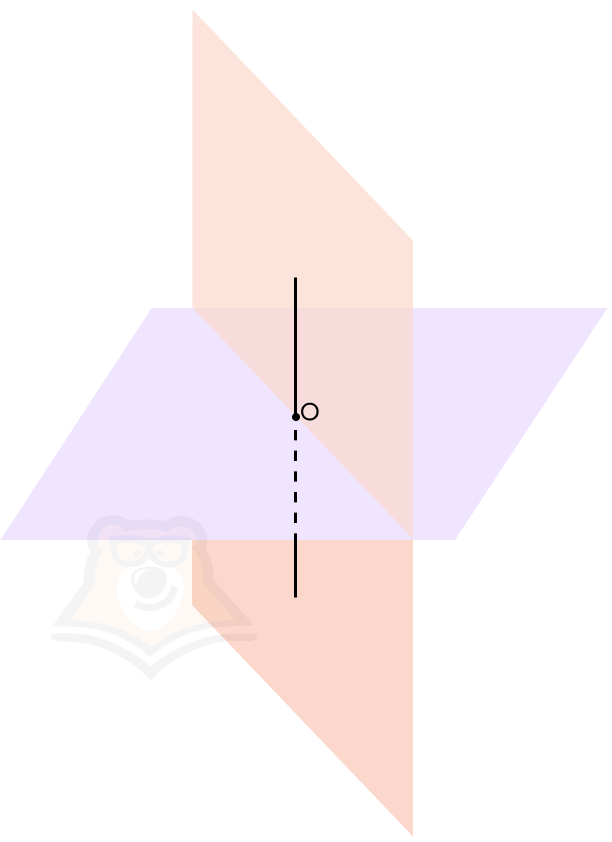
Это легко проверить, если найти любой двугранный угол между построенными плоскостями.
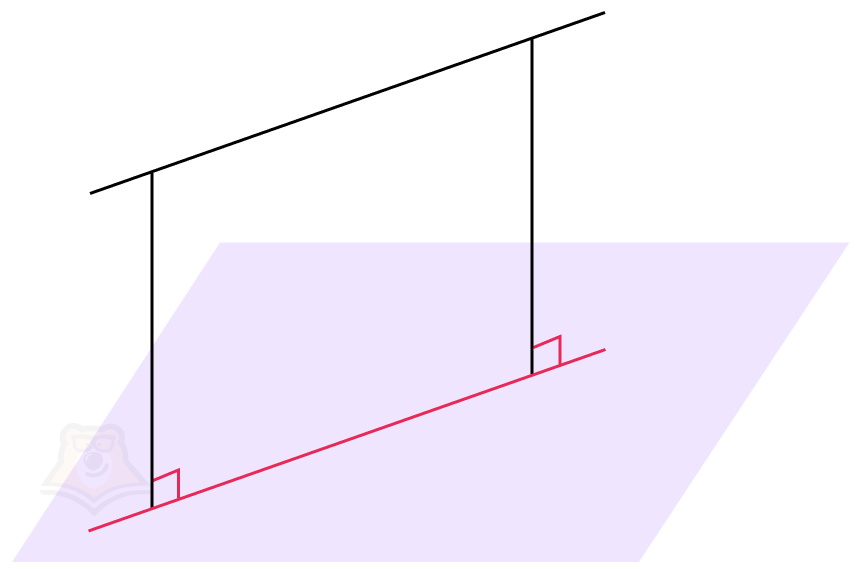
Теорема о трех перпендикулярах
Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах.
Для начала попробуем понять ее на реальных предметах.
Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Возьмем уголок и зафиксируем его строго вертикально на листе. Для удобства назовем уголок АВС, где С — прямой угол.
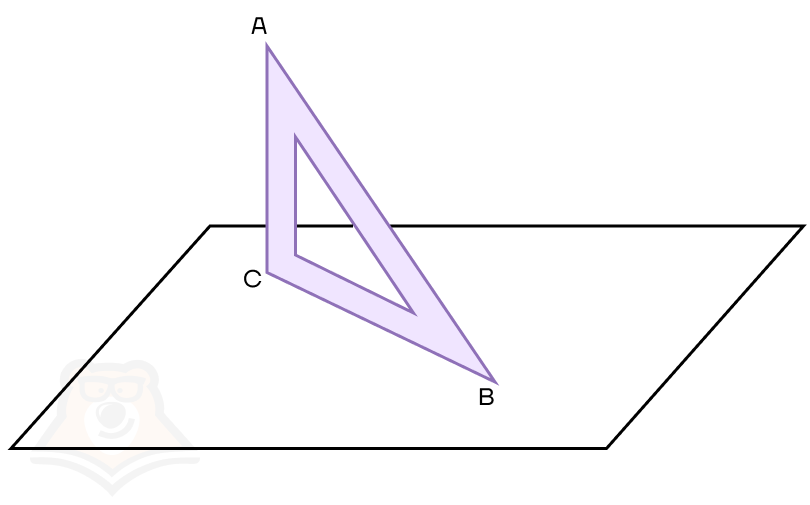
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально).
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°.
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ.
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).
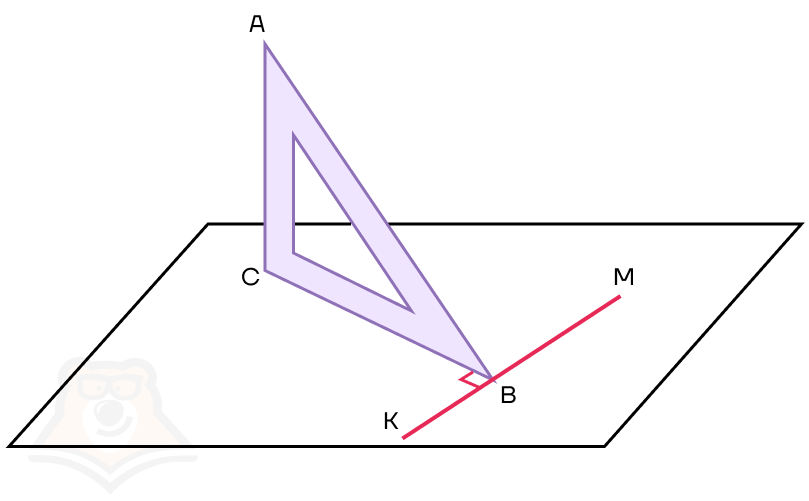
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ.
Возникнет вопрос, почему?
1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
Теперь узнаем, как этот признак выполняется в данной ситуации.
2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку.
3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости.
4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком.
Теорема о трех перпендикулярах
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.
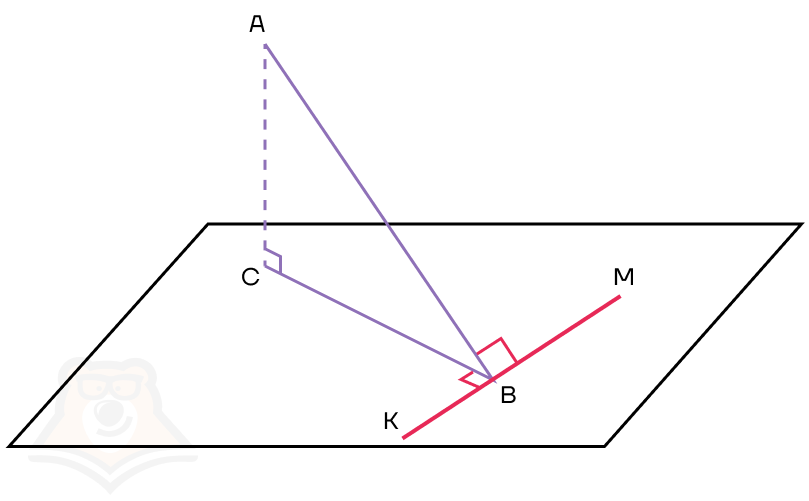
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости.
Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.
Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач.
Фактчек
- Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
- Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°.
- Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.
- Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b.
Проверь себя
Задание 1.
Выберите верное утверждение.
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
- Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
- Ребра двугранного угла — это плоскости, которые его образуют.
Задание 2.
Угол между плоскостями — это…
- Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.
Задание 3.
Что такое проекция прямой на плоскость?
- Это любая прямая, проведенная из точки пересечения прямой и плоскости;
- Это перпендикуляр, опущенный из любой точки на плоскость;
- Это всегда точка пересечения прямой и плоскости;
- Это прямая, образованная проекциями всех точек прямой на плоскость.
Задание 4.
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?
- Проекция будет равна этой прямой и параллельна ей;
- Проекция будет меньше прямой и образовывать с ней угол;
- Проекция будет точкой пересечения прямой и плоскости;
- Проекция будет больше прямой и образовывать с ней угол.
Задание 5.
Как доказать, что прямая перпендикулярна плоскости?
- Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
- Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
- Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
- Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.
Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4
Теорема о проекции прямого угла. Частное расположение прямых — перпендикулярные прямые
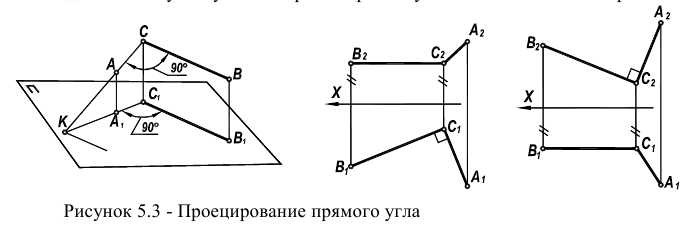
Пересекающиеся прямые в пространстве могут быть расположены под прямым углом, т.е. взаимно перпендикулярно. Прямой угол между перпендикулярными прямыми может проецироваться на чертеж в натуральную величину при определенном условии.
Теорема о проекции прямого угла :
- если одна сторона прямого угла параллельна какой-либо плоскости проекций, а вторая сторона ей не перпендикулярна, то на эту плоскость проекций угол проецируется в натуральную величину, т.е. прямым (90°).
Па рис. 4.17 дано изображение, поясняющее теорему о проекции прямого угла. Две перпендикулярные прямые 
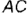
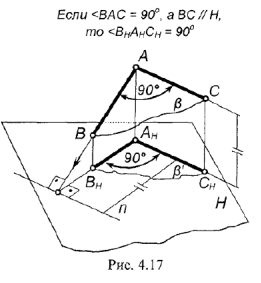
!!! Для решения многих задам начертательной геометрии требуется по условию строить проекции прямого угла.
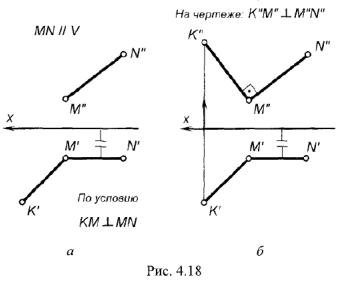
На рис. 4.18. а, б показано построение на чертеже недостающей фронтальной проекции прямого угла 
На рис. 4.18, а изображено графическое условие задачи: дана горизонтальная проекция 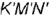
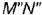
На рис. 4.18, б показано решение задачи: так как одна сторона 
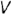
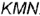
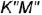
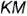
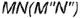
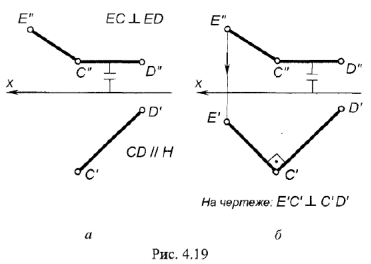
На рис. 4.19, а, 6 показано построение на чертеже недостающей горизонтальной проекции прямого угла 
На рис. 4.19, а изображено графическое условие задачи: дана фронтальная проекция 
На рис. 4.19, б показано решение задачи: так как одна сторона 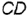
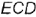
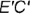
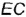
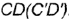
Эта теория взята со страницы задач по начертательной геометрии:
- Решение задач по начертательной геометрии
Возможно эти страницы вам будут полезны:
Содержание:
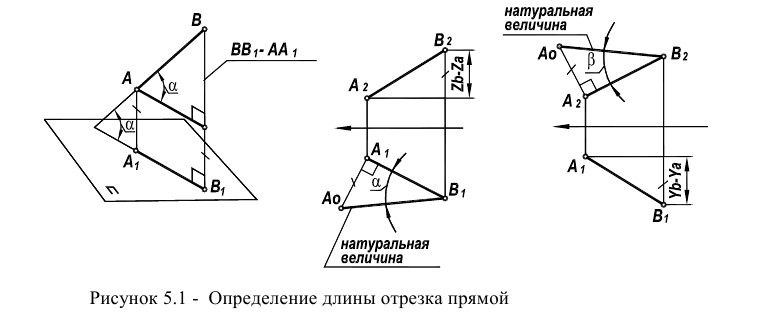
К метрическим задачам относятся задачи на определение натуральной величины отрезков, расстояний углов, площадей плоских фигур.
Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольною треугольника Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым — разность расстояний концов отрезка от той плоскости, на которой ведется построение. При этом угол между гипотенузой и катетом проекций является углом наклона отрезка к той плоскости, ряльной величины выполнено на горизонтальной проекции. Поэтому одним катетом прямоугольного треугольника, является горизонтальная проекция
Если необходимо определить угол наклона отрезка АВ к плоскости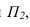
Решение метрических задач методами преобразовании проекций
Положении геометрических образов, при которых расстоянии и углы не искажаются на плоскостях проекций
Метрические характеристики объектов на чертежах не искажаются, если геометрические образы занимают частное положение относительно плоскостей проекций.
Приведем некоторые из них.
1. Прямая проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.2).
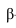
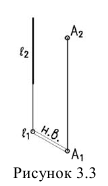
2. Расстояние от точки до прямой проецируется в натуральную величину, если прямая проецирующая (рисунок 3.3).
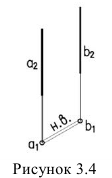
3. Расстояние между параллельными прямыми проецируется в натуральную величину, если прямые проецирующие (рисунок 3.4).
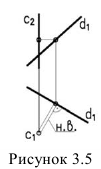
4. Расстояние между скрещивающимися прямыми проецируется в натуральную величину, если одна из прямых проецирующая (рисунок 3.5).
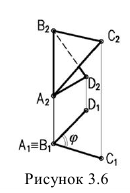
5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее (рисунок 3.6).
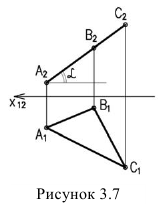
6. Угол наклона плоскости к плоскости проекций проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.7)
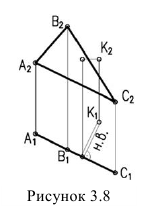
7. Расстояние от точки до плоскости проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.8)
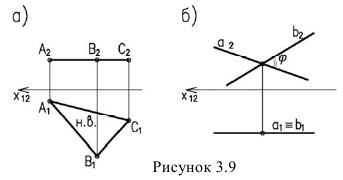
8. Любая плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.9а,б)
Таким образом, для решения метрических задач целесообразно данный объект привести в частное положение с тем, чтобы на одной из новых проекций получить более простое решение задачи.
Для такого перехода и служат способы преобразования проекций.
Существует несколько способов преобразовании проекций: способ вращения вокруг осей перпендикулярных плоскостям проекций, способ плоскопараллельного перемещения, способ замены плоскостей проекций и др.
Четыре основных задачи преобразовании проекций
Этими способами решаются четыре основные задачи:
- Задача 1. Прямую общего положения преобразуем в линию уровня (одно преобразование).
- Задача 2. Прямую общего положения преобразуем в проецирующую (два преобразования)
- Задача 3. Плоскость общего положения преобразуем в проецирующую (одно преобразование)
- Задача 4. Плоскость общего положения преобразуем в плоскость уровня (два преобразования)
Решение 1-ой и 2-ой задачи преобразовании проекций методом вращении, плоскопараллельного перемещении и замены плоскостей проекций
Способ вращения
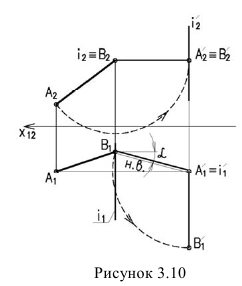
Способ вращения заключается в том, что геометрические образы вращаются вокруг осей перпендикулярных плоскостям проекций до занятия ими какого-либо частного положения относительно плоскостей проекций. При этом одна проекция точки перемещается по окружности, вторая — но прямой параллельной оси проекций.
На рисунке 3.10 вокруг оси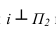
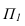
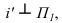
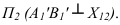
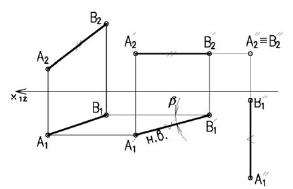
Способ плоскопараллельного перемещения
Способ плоскопараллельного перемещения является разновидностью способа вращения (вращение без закрепленных осей), т.е. положение объекта можно преобразовывать путем перемещения его параллельно одной плоскости проекций, одновременно изменяя его положение относительно другой плоскости проекций до занятия им какого-либо частного положения.
На рисунке 3.11 сначала АВ переводим из общего положения в положение горизонтальное. При этом 
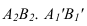
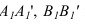
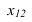
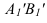
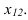
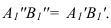
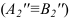
Способ замены плоскостей проекций
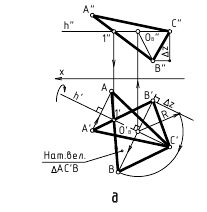
Сущность способа замены плоскостей проекций заключается в том, что старая система плоскостей проекций заменяется на новую, с таким расчетом, чтобы относительно новой системы плоскостей, геометрический образ занял какое-то частное положение. При этом нужно помнить, что линии связи будут перпендикулярны относительно новой оси проекций и расстояния от новой оси проекций до новой проекции точки равно расстоянию от старой проекции точки до старой оси.
На рисунке 3.12 произведена первая замена плоскость 
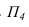
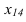
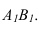
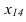
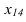
Далее прямую АВ преобразуем в проецирующую. Для этого проводим новую ось 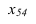
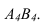
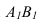
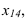
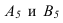
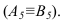
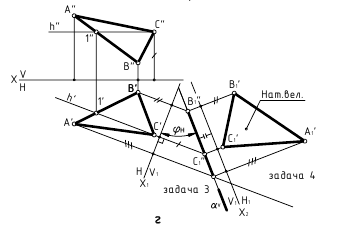
Решение 3-ой и 4-ой задачи преобразовании проекций методом плоскопараллельного перемещения и замены плоскостей проекций
Так как метод вращения является более громоздким, рассмотрим решение 3-ей и 4-ой задачи преобразования методом плоскопараллельного перемещения и методом замены плоскостей проекций.
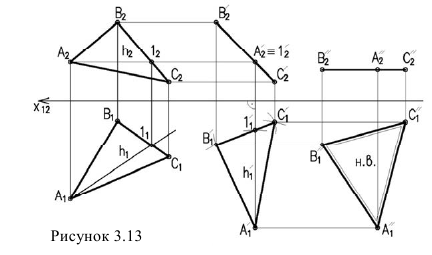
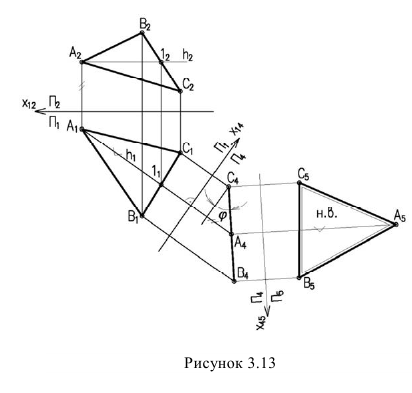
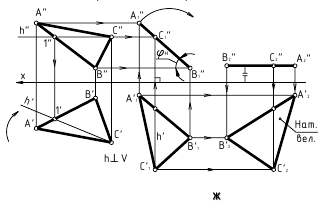
Способ плоскопараллельного перемещения
Для того чтобы плоскость из общего положения перевести в проецирующее, нужно иметь ввиду, что при этом ее горизонталь или фронталь должна быть перпендикулярна плоскости проекций. Поэтому на рисунке 3.13 проведена горизонталь 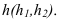
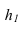
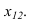
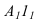
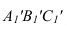
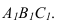
Чтобы плоскость треугольника перевести в положение плоскости уровня, достаточно полученную фронтальную проекцию 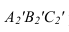
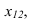
Способ замены плоскостей проекций
При решении задачи методом замены (рисунок 3.14) новую ось 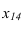
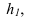
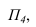
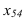
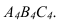
Для того, чтобы методами преобразования решить любую метрическую задачу, необходимо определить какую из четырех основных задач преобразования необходимо решать в каждом конкретном случае.
Метрические задачи
Метрические задачи — это задачи на определение линейных или угловых размеров геометрических объектов, а также расстояний и углов между ними.
Главным вопросом метрических задач является вопрос о построении перпендикуляра к прямой или плоскости. Построение взаимно перпендикулярных прямых было рассмотрено ранее.
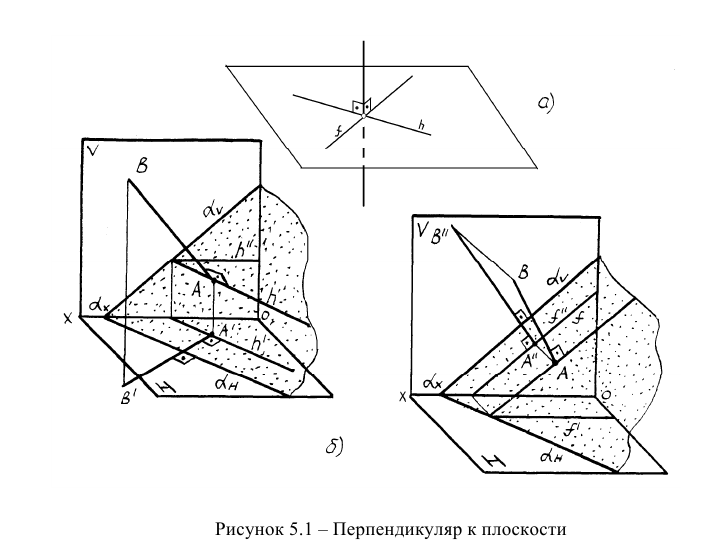
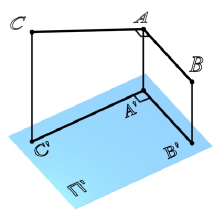
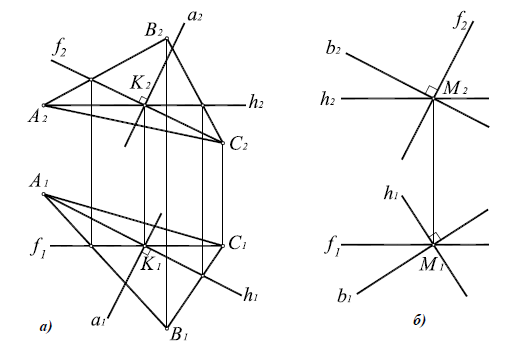
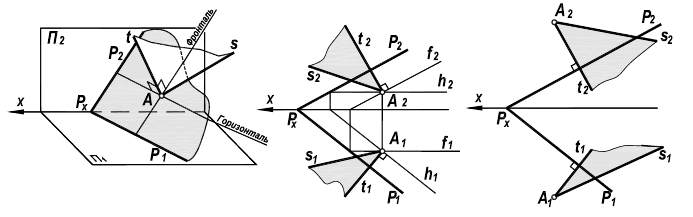
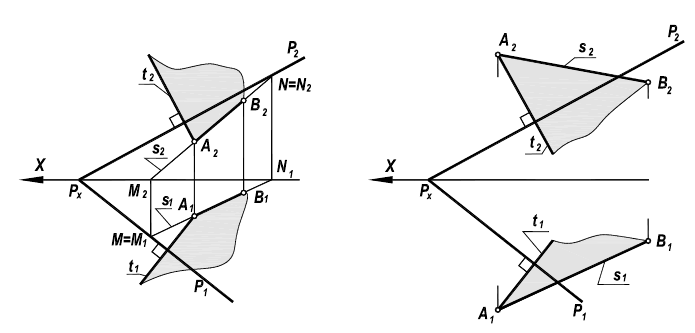
Из элементарной геометрии известно, что прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве этих пересекающихся прямых наиболее целесообразно использовать горизонталь и фронталь плоскости. Это объясняется тем, что только в этом случае прямой угол будет проецироваться в натуральную величину на соответствующие плоскости проекций. На рисунке 5.1 приведен пространственный чертеж, на котором из плоскости а (из точки А) восстановлен перпендикуляр АВ. Из приведенного изображения можно выяснить методику построения проекций перпендикуляра к плоскости: горизонтальная проекция перпендикуляра к плоскости проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу плоскости, а фронтальная проекция перпендикуляра проводится перпендикулярно фронтальной проекции фронтали или фронтальному следу плоскости. Таким образом, необходимо выполнить следующий алгоритм проведения проекций перпендикуляра к плоскости:
Построение перпендикуляра к плоскость и восстановление перпендикуляра из плоскости называется прямой задачей, а построение плоскости, перпендикулярной к прямой — обратной задачей. Обе задачи решаются по одному и тому же вышеописанному алгоритму. При этом плоскость, перпендикулярную заданной прямой, можно задать следами или пересекающимися горизонталью и фронталью.
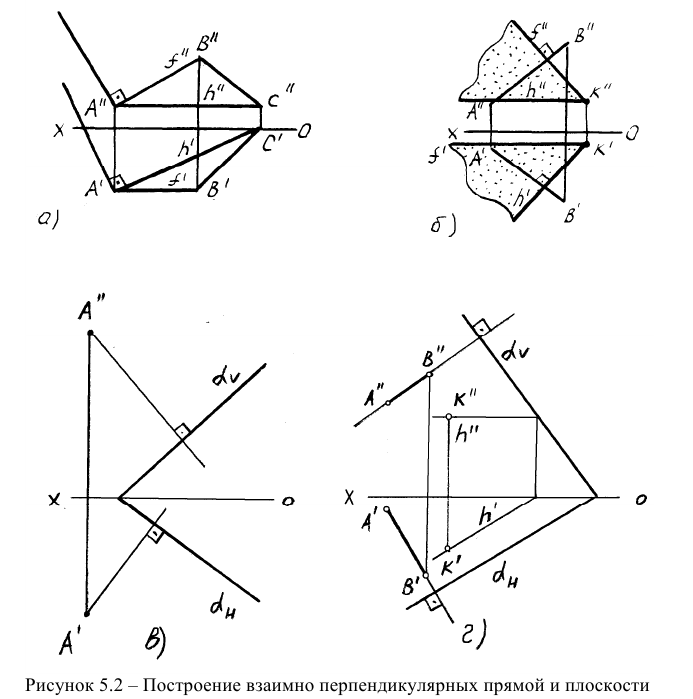
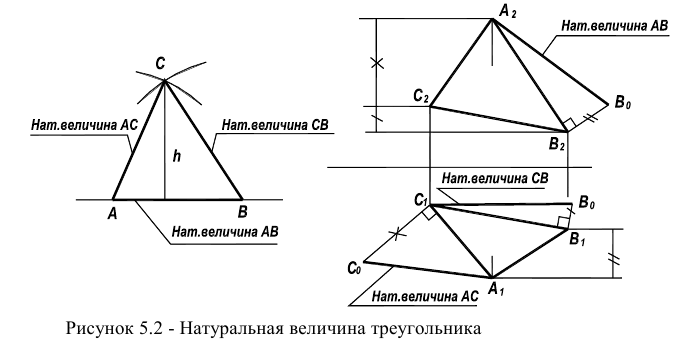
На рисунке 5.2 показано решение прямой (а) и обратной (б) задач. В прямой задаче из точки A треугольника AВС восстановлен перпендикуляр, в обратной задаче через точку К проведена плоскость, перпендикулярная прямой АВ. Плоскость задана пересекающимися горизонталью и фронталью.
Здесь же приведены примеры прямой и обратной задач, если плоскость задана следами. В прямой задаче (в) из точки Л построен перпендикуляр на плоскость, в обратной (г) — через точку К проведена плоскость перпендикулярно прямой АВ.
Определение расстояний между геометрическими объектами
Среди этих задач можно выделить следующие задачи: расстояние от точки до плоскости, расстояние от точки до прямой, расстояние между двумя параллельными прямыми, расстояние между двумя скрещивающимися прямыми, расстояние между двумя параллельными плоскостями и другие. В общем случае все задачи сводятся к определению расстояний между двумя точками.
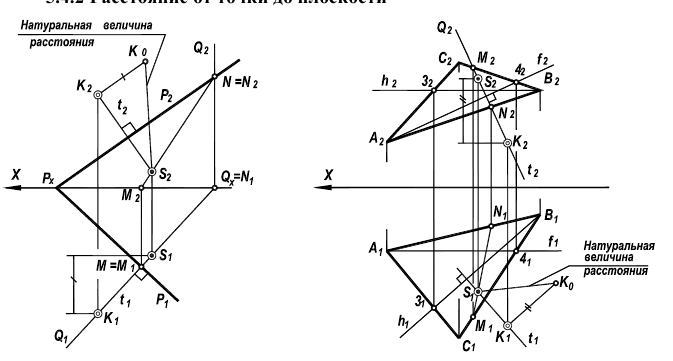
Чтобы определить расстояние от точки до плоскости, необходимо выполнить ряд логических действий:
- Из точки опустить перпендикуляр на заданную плоскость;
- Найти точку встречи перпендикуляра с плоскостью;
- Определить НВ расстояния между заданной и найденной точками.
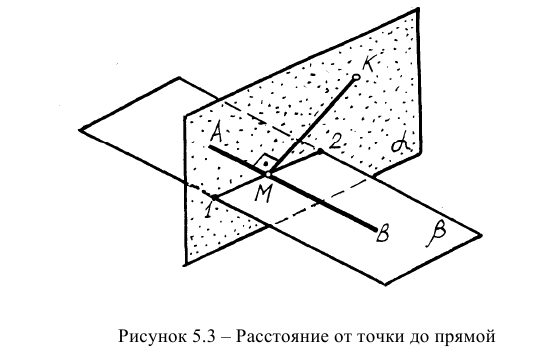
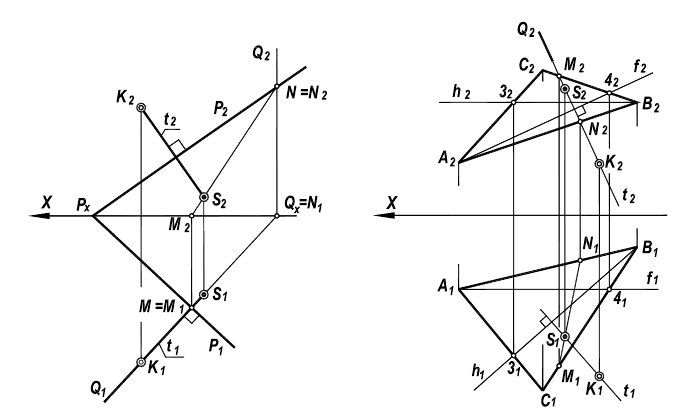
Задача на определение расстояния от точки до прямой решается по следующему плану:
- Через точку к провести плоскость, перпендикулярную заданной прямой;
- Найти точку встречи М заданной прямой с проведенной плоскостью;
- Соединить полученные точки (это будет перпендикуляр из точки на прямую);
- Определить НВ перпендикуляра.
Пространственная модель решения второй задачи представлена на рисунке 5.3. Рассмотренная задача относится также к задачам на перпендикулярность двух прямых.
Другие упомянутые задачи на определение расстояний легче решаются методами преобразования эпюра, которые будут рассмотрены в последующих разделах.
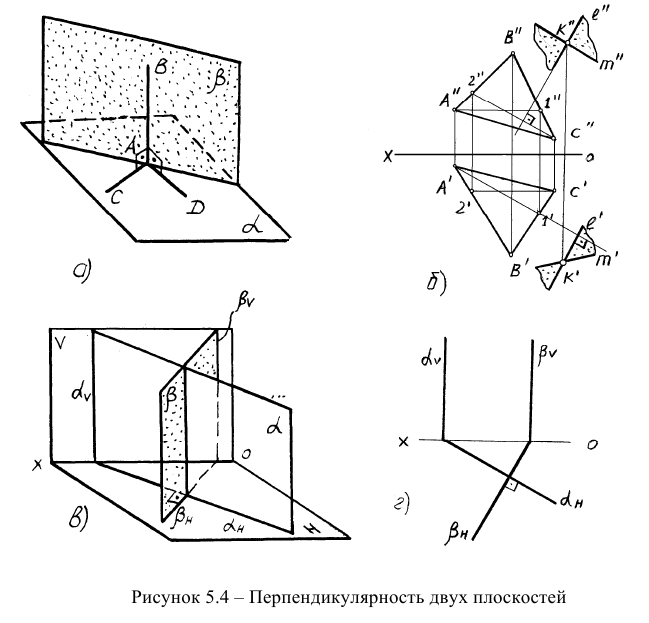
Перпендикулярность плоскостей
Плоскость перпендикулярна другой плоскости, если она содержит прямую, перпендикулярную другой плоскости (рисунок 5.4а). Таким образом, для того, чтобы провести плоскость, перпендикулярную другой, необходимо сначала провести перпендикуляр к заданной плоскости, а затем через него провести искомую плоскость. На рисунке 5.46 представлена задача: через точку К провести плоскость, перпендикулярную плоскости треугольника AВС. Искомая плоскость задана двумя пересекающимися прямыми, одна из которых перпендикулярна заданной плоскости.
Если две плоскости являются одноименными плоскостями частного положения (например, горизонтально- или фронтально-проецирующими), то при перпендикулярности плоскостей их собирательные следы будут перпендикулярны друг другу (рисунок 5.4в,г).
Если плоскости являются плоскостями общего положения, то при их перпендикулярности одноименные следы не будут взаимно перпендикулярны. Другими словами, перпендикулярность одноименных следов плоскостей общего положения не является достаточным условием для перпендикулярности самих плоскостей.
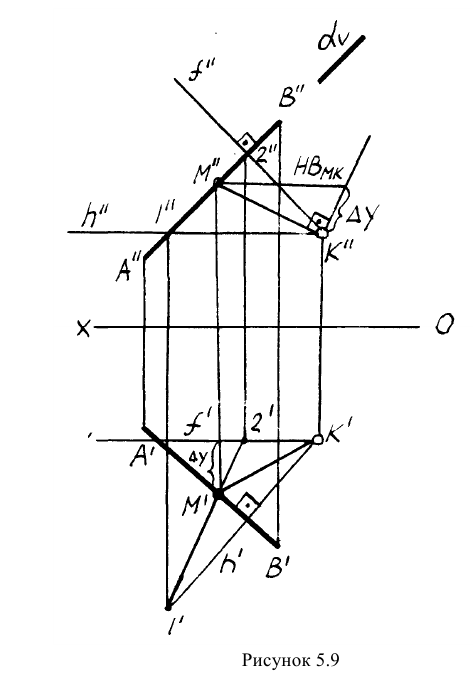
Определение углов между прямой и плоскостью и между двумя плоскостями
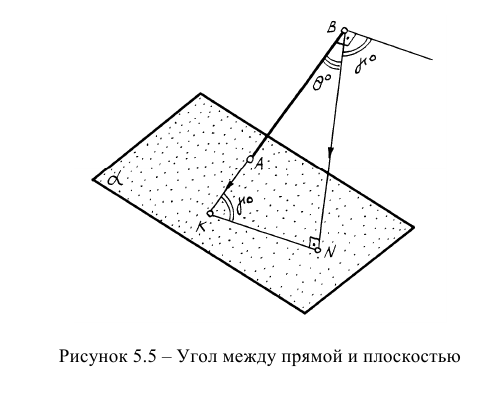
Определение углов между геометрическими объектами является трудоемкой задачей, если её решать традиционными геометрическими способами. Так, например, задачу на определение угла между прямой и плоскостью (рисунок 5.5) можно решить способом, алгоритм которого содержит следующие операции:
- Определить точку встречи прямой АВ с плоскостью а;
- Из точки В построить перпендикуляр на плоскость;
- Найти точку встречи перпендикуляра с плоскостью;
- Точки К и N соединить и определить НВ угла BKN.
Однако задача может быть значительно упрощена, если использовать способ решения задачи с помощью дополнительного угла. Дополнительным углом назовем угол между заданной прямой АВ и перпендикуляром BN, обозначенный через 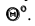
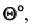
которую можно решить графически, достроив угол 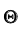
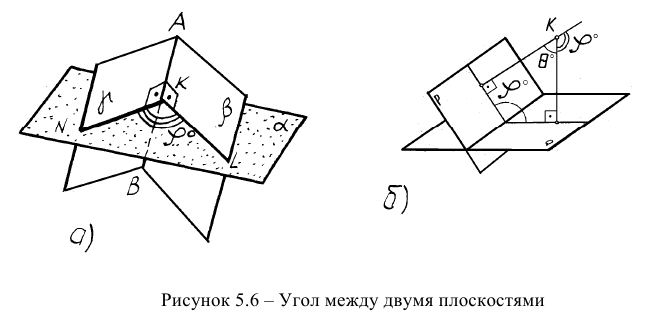
То же самое можно сказать о задаче на определение двугранного угла, то есть угла между двумя плоскостями (рисунок 5.66). Первый способ (геометрический) достаточно трудоемок. Он заключается в пересечении угла вспомогательной плоскостью а, перпендикулярной ребру АВ, построении линий пересечения KN и KL и определении натуральной величины угла NKL.
С помощью дополнительного угла задача решается следующим образом. В растворе двугранного угла (рисунок 5.6в) берут любую точку К и строят из неё перпендикуляры на обе плоскости двугранного угла, которые образуют дополнительный угол 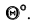
Дополненный угол будет искомым.
Натуральную величину дополнительного угла
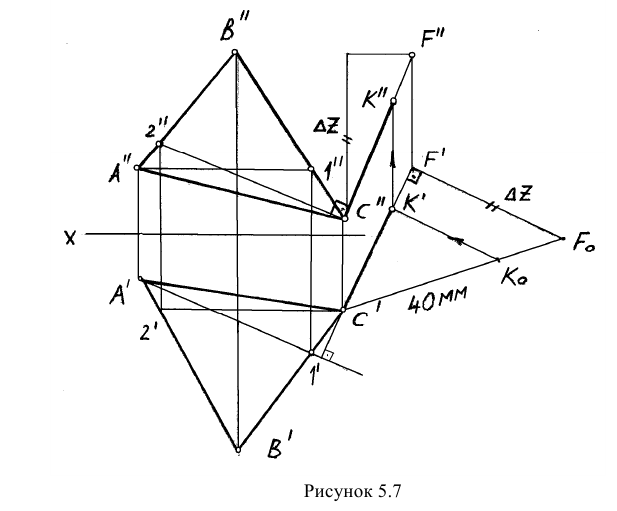
Пример: Из любой вершины треугольника АВС восстановить перпендикуляр длиной 40 мм.
Решение: Сначала необходимо в плоскости треугольника АВС провести горизонталь и фронталь для того, чтобы построить проекции восстановленного перпендикуляра. Далее из точки С проводим проекции перпендикуляра согласно рассмотренному выше алгоритму о перпендикуляре к плоскости. Для того, чтобы отложить 40 мм, необходимо определить НВ ограниченного отрезка перпендикуляра CF (точку F берем произвольно). НВ отрезка CF определяем методом прямоугольного треугольника на горизонтальной проекции CF. Полученную точку К возвращаем на проекции по теореме Фалеса. Получаем проекции перпендикуляра длиной 40 мм (рисунок. 5.7).
Пример: Найти расстояние от точки А до плоскости, заданной следами
Решение: Из точки А строим перпендикуляр на заданную плоскость. Проекции перпендикуляра проводим перпендикулярно следам. Далее находим точку встречи перпендикуляра с заданной плоскостью с помощью вспомогательной фронтально-проецирующей плоскости 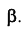
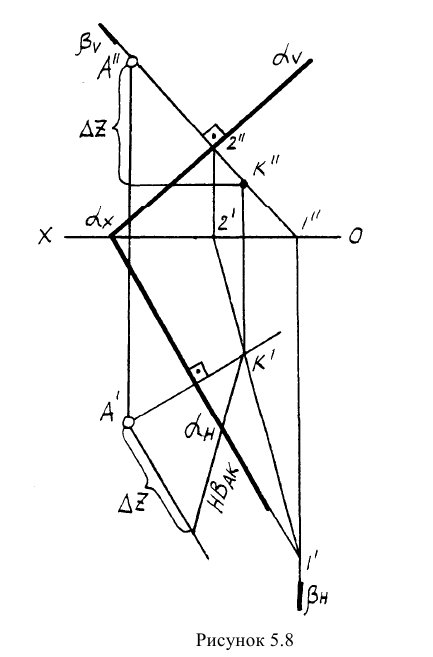
Пример: Определить расстояние от точки К до прямой AВ.
Решение: Через точку К проводим плоскость, перпендикулярную заданной прямой. Плоскость задаем пересекающимися горизонталью и фронталью. Их проекции проводим согласно алгоритму о перпендикуляре к плоскости (обратная задача). Далее находим точку встречи прямой AВ с проведенной плоскостью (точка М). Определяем натуральную величину КМ методом прямоугольного треугольника (рисунок 5.9).
Примеры метрических задач
Задачи, в которых определяются различные геометрические величины -расстояния между объектами, длины отрезков, углы, площади и т.д. называются метрическими. Решение многих метрических задач, например задач на определение кратчайших расстояний, требует построения перпендикулярных прямых и плоскостей.
Перпендикулярность является частным случаем пересечения прямых, прямой и плоскости или двух плоскостей. Необходимо установить соотношения, по которым строятся проекции перпендикулярных прямых и плоскостей.
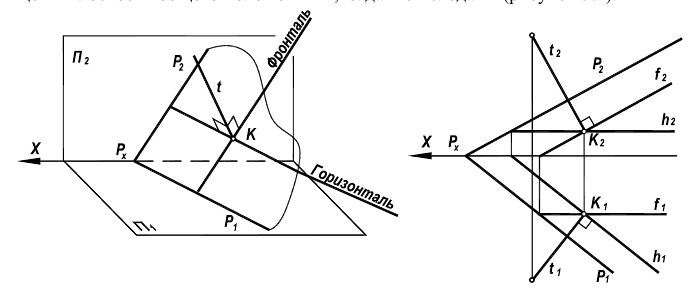
Теорема о проекциях прямого угла
Прямой угол проецируется на плоскость без искажения, если одна из его сторон параллельна этой плоскости (рис. 10.1).
Рис. 10.1. Теорема о проекциях прямого угла
Дано :
Доказать, что C’A’
Доказательство: если AB||П’, то A’B’||AB, но AA’





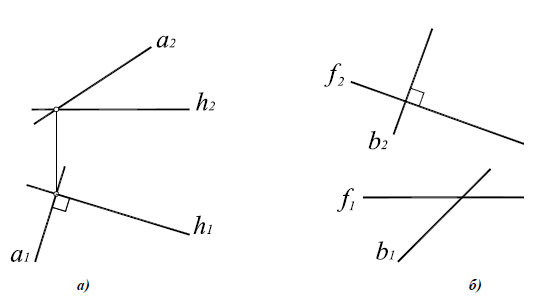
На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на П1 в виде взаимно перпендикулярных прямых, если одна из них горизонталь, на П2 — если одна из них фронталь (рис. 10.2,а).
Условие перпендикулярности скрещивающихся прямых (рис. 10.2,б) сводятся к условиям перпендикулярности пересекающихся прямых, поведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.
Рис. 10.2. Перпендикулярные прямые:
а -пересекающиеся a1 
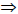

б -скрещивающиеся b2 
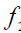
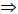

Линии наибольшего наклона плоскости
Прямые, лежащие в плоскости и перпендикулярные линиям уровня этой плоскости, называются линиями наибольшего наклона к соответствующей плоскости проекций (рис. 10.3). Так, прямая, лежащая в плоскости и перпендикулярная горизонтали плоскости, называется линией наибольшего наклона к горизонтальной плоскости проекций, а прямая, перпендикулярная фронтали — линией наибольшего наклона к фронтальной плоскости проекций.
Угол между линией наибольшего наклона и ее проекцией на соответствующую плоскость равен углу наклона плоскости к плоскости проекций (см. рис. 9.15).
Рис. 10.3. Линия наибольшего наклона плоскости а к П1:
а — плоскость общего положения; h ∈α — горизонталь плоскости а; AB 
φ = 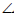
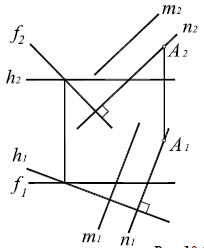
Перпендикулярность прямой и плоскости
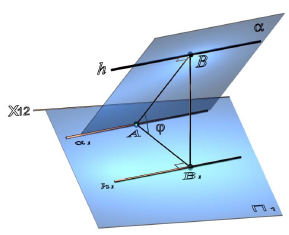
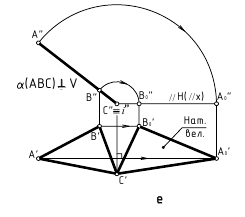
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На основании теоремы о проекциях прямого угла можно получить условие перпендикулярности прямой общего положения и плоскости общего положения:
Если прямая а перпендикулярна плоскости α(ABC), то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция — фронтальной проекции фронтали плоскости.
Например, при построении прямой а, перпендикулярной плоскости α(ABC) (рис. 10.4,а), в плоскости строятся линии уровня — горизонталь и фронталь, затем через произвольную точку в плоскости, в данном случае точку K(h×
Рис. 10.4. Перпендикулярность прямой и плоскости:
а -построение прямой, перпендикулярной плоскости:
б -построение плоскости, перпендикулярной прямой:
Аналогично решается задача о построении плоскости, перпендикулярной прямой общего положения (рис. 10.4,б)
Если плоскость проецирующая, проекции линий уровня совпадают со следом плоскости, перпендикулярность устанавливается по отношению к следу плоскости. Горизонтальная проекция перпендикуляра к горизонтально-проецирующей плоскости строится перпендикулярно горизонтальному следу плоскости (рис. 10.5,а). Прямая, перпендикулярная горизонтально-проецирующей плоскости, занимает положение горизонтальной линии уровня.
Аналогично, фронтальная проекция перпендикуляра к фронтально-проецирующей плоскости строится перпендикулярно фронтальному следу плоскости (рис. 10.5,б). Прямая, перпендикулярная фронтально-проецирующей плоскости, занимает положение фронтали.
Рис. 10.5. Перпендикулярность прямой и проецирующей плоскости:
а -построение прямой, перпендикулярной плоскости;
б -построение плоскости, перпендикулярной прямой
Взаимная перпендикулярность плоскостей
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Таким образом, построение взаимно перпендикулярных плоскостей сводится к построению перпендикулярных прямой и плоскости. Например, чтобы через произвольную точку А провести плоскость, перпендикулярную плоскости a(



Рис. 10.6. Перпендикулярность двух плоскостей
Дано: α(h × 
Построить: A ∈ β 
Решение:
A ∈ n;
Определение метрических задач
Традиционно задачи, связанные с измерением длин, углов, площадей и объемов относят к метрическим. В основе решения этих задач лежит определение длины отрезка и, как производной от этого, площади плоской фигуры.
Определение длины отрезка
Одним из наиболее распространенных методов (рисунок 5.1) является метод прямоугольного треугольника (так его называют в начертательной геометрии) или метод ортогональных дополнений (название, принятое в линейной алгебре).
Идея метода базируется на следующем. Истинная величина отрезка AВ является гипотенузой прямоугольного треугольника, один из катетов которого, является проекцией отрезка AВ на плоскость проекции 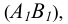
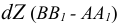
На комплексном чертеже возможно решение как на плоскости 
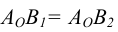
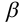
Определение площади треугольника
Определение площади треугольника и величины плоского угла можно свести к известной задаче построения треугольника по трем сторонам.
Для этого достаточно, используя рассмотренный выше способ прямоугольного треугольника, найти по порядку истинные величины сторон 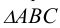
Величина плоского угла между двумя любыми сторонами этой фигуры может быть измерена на истинной величине треугольника.
Проецирование прямого угла
Решение многих задач Начертательной геометрии связано с необходимостью построения на чертеже взаимно перпендикулярных прямых и плоскостей. Базой для этого служит умение строить прямые углы на комплексном чертеже.
Известная в теории чертежа теорема (приведем ее без доказательства) утверждает, что прямой угол (в соответствии с рисунком 5.3) проецируется на
соответствующую плоскость проекций вез искажения, если одна из его сторон параллельна этой плоскости проекций, а вторая — ей не перпендикулярна.
- Заказать чертежи
Перпендикулярность прямых и плоскостей
Выше уже отмечалось, что в трехмерном Евклидовом пространстве отсутствует полная параллельность, то же самое можно сказать и о перпендикулярности. Понятие перпендикулярности так же, как и параллельности, вводится через определение.
Перпендикулярность прямой и плоскости
Считают, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся (любым) прямым этой плоскости.
При решении задачи возможны два варианта: проведение перпендикулярной прямой к плоскости из внешней точки и из точки, лежащей в плоскости.
Рассмотрим возможность проведения перпендикуляра из точки К, лежащей в плоскости общего положения Р, заданной следами (рисунок 5.4).
Рисунок 5.4 — Перпендикулярность прямой и плоскости
В плоскости Р (через точку К) проводятся горизонталь h и фронталь f. Прямые, перпендикулярные соответствующим проекциям линий уровня 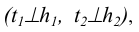
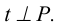
В том случае, когда точка К не лежит в плоскости Р, решение задачи аналогично (рисунок 5.5).
Поскольку положение точки пересечения искомого перпендикуляра не определено, решение соответствует следующей схеме:
а) в плоскости проводятся горизонталь h (через точку В) и фронталь f (через точку A), в случае задания плоскости следами за фронталь и горизонталь принимаются соответствующие следы плоскости
Рисунок 5.5 — Перпендикуляр к плоскости
б) из внешней точки К к соответствующим проекциям линий уровня (следам) проводятся перпендикулярные прямые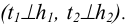
в) определяется точка S пересечения этого перпендикуляра t и плоскости.
Расстояние от точки до плоскости
Рисунок 5.6 — Расстояние от точки до плоскости
Задачу на определение расстояние от точки до плоскости (рисунок 5.6) можно свести к решению уже известных задач на построение перпендикуляра к плоскости (рисунок 5.5) и определения натуральной величины отрезка прямой (рисунок 5.1)
Перпендикулярность плоскостей
Считают, что две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.
Задача может ставиться, как проведение плоскости, перпендикулярной заданной, проходящей через точку или прямую.
При проведении искомой плоскости через точку, как и в предыдущем случае, возможны два варианта проведения плоскости перпендикулярной заданной: через точку, лежащую в плоскости и через точку вне ее (рисунок 5.7).
Точно такой же вариант возникает и при проведении перпендикулярной плоскости через прямую (лежащую в исходной плоскости или не лежащую).
Рассмотрим вариант построения плоскости, проходящей через точку. Пусть точка А лежит в плоскости Р. Линии 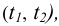
Рисунок 5.7 — Перпендикулярность плоскостей
Проведение через точку А произвольной прямой s позволяет определить плоскость Q, которая будет перпендикулярна плоскости Р.
Если точка А лежит вне плоскости Р, то решение аналогично. Проведение через точку А перпендикуляра t и произвольной прямой s определит плоскость Q, которая также, по определению, будет перпендикулярна плоскости Р.
Решение задачи на проведение плоскости через прямую аналогично решению задачи по проведению плоскости через точку. Достаточно вместо произвольной прямой s использовать заданную прямую АВ. И тогда, в соответствии с рисунком 5.8, задача сведется к проведению перпендикуляра t к плоскости Р (из точки, лежащей в плоскости или лежащей вне ее).
Рисунок 5.8 — Перпендикулярность плоскостей
Определение натуральных величин геометрических элементов
1. Определить натуральную величину отрезка общего положения:
- способом прямоугольного треугольника;
- способом замены плоскостей проекций преобразовать в прямую уровня;
- способом вращения вокруг проецирующей оси преобразовать в прямую уровня.
2. Определить натуральную величину плоскости общего положения (замкнутого отсека):
- способом замены плоскостей проекций преобразовать в плоскость уровня;
- способом вращения вокруг линии уровня преобразовать в плоскость уровня;
- способом плоскопараллельного перемещения преобразовать в плоскость уровня.
Определение расстояния между геометрическими элементами (образами)
1. Определить расстояние от точки до прямой общего положения:
- способом замены плоскостей проекций преобразовать плоскость, заданную прямой и точкой, в плоскость уровня (задачи 3 и 4 преобразования; прямую и точку рассматривать как плоскость);
- способом замены плоскостей проекций преобразовать прямую общего положения в проецирующую прямую (задачи 1 и 2 преобразования);
- способом вращения вокруг линии уровня преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
- способом плоскопараллельного перемещения преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
- способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить через заданную точку плоскость, перпендикулярную к прямой, и определить точку пересечения последней с плоскостью.
2. Определить расстояние между параллельными прямыми:
- способом замены плоскостей проекций преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня (задачи 3 и 4 преобразования);
- способом замены плоскостей проекций преобразовать две параллельные общего положения в проецирующие прямые (задачи 1 и 2 преобразования);
- способом вращения вокруг линии уровня преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня, ограничив ее замкнутым отсеком;
- способом плоскопараллельного перемещения преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня;
- способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить плоскость через любую точку, принадлежащую одной из прямых, перпендикулярную ко второй прямой, и определить точку пересечения этой плоскости со второй прямой.
3. Определить расстояние между скрещивающимися прямыми, преобразовав одну из прямых в проецирующую (задачи 1 и 2 преобразования).
4. Определить расстояние от точки до плоскости:
- по теме «Перпендикулярность» – провести перпендикуляр к плоскости, построить точку пересечения этого перпендикуляра с заданной плоскостью и найти любым способом натуральную величину построенного отрезка (см. пункт 1);
- способом замены плоскостей проекций преобразовать плоскость общего положения в плоскость проецирующую.
5. Определить расстояние от точки до поверхности вращения:
- способом замены плоскостей проекций преобразовать плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня (задача 4 преобразования);
- способом вращения вокруг проецирующей оси повернуть плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня.
Определение углов наклона геометрических элементов к плоскостям проекций H и V
1. Определить углы наклона прямой общего положения к плоскостям проекций H и V:
- способом прямоугольного треугольника построить на двух проекциях натуральные величины отрезка и определить углы наклона прямой;
- способом замены плоскостей проекций преобразовать прямую общего положения в горизонтальную, а затем во фронтальную прямую (задача 1 преобразования);
- способом вращения вокруг соответствующей проецирующей оси преобразовать прямую общего положения в горизонтальную и во фронтальную прямые.
2. Определить угол наклона прямой к заданной плоскости общего положения:
- из любой точки прямой опустить перпендикуляр к плоскости;
- способом вращения вокруг линии уровня преобразовать построенную плоскость, заданную прямой и перпендикуляром, в плоскость уровня;
- искомый угол будет дополнять построенный угол до 90°.
3. Определить величину двухгранного угла, если на чертеже есть линии пересечения плоскостей, образующих двухгранный угол (ребро):
- способом замены плоскостей проекций преобразовать ребро двухгранного угла в проецирующую прямую (задачи 1 и 2 преобразования).
4. Определить угол между двумя плоскостями общего положения, если на чертеже нет линии пересечения заданных плоскостей (ребра):
- задача решается косвенным путем, для чего из любой точки пространства следует опустить перпендикуляры к заданным плоскостям, которые, в свою очередь, задают вспомогательную плоскость, перпендикулярную к этим плоскостям;
- эту вспомогательную плоскость способом вращения вокруг линии уровня следует преобразовать в плоскость уровня, определив угол между перпендикулярами (преобразование вспомогательной плоскости в плоскость уровня возможно и другими способами – ее плоскопараллельным перемещением или заменой плоскостей проекций);
- искомый угол будет дополнять построенный угол до 180° (углом между плоскостями считают угол острый).
Структуризация материала тринадцатой лекции в рассмотренном объеме схематически представлена на рис. 13.1 (лист 1). На последующих листах 2–7 компактно приведены иллюстрации к этой схеме для визуального повторения изученного материала при его повторении (рис. 13.2–13.7).
Метрические задачи:
Определение натуральной величины геометрических элементов:
1. Определение длины отрезка
Способ прямоугольного треугольника
Способ замены плоскостей проекций (задача 1)
Способ вращения вокруг проецирующей оси
2. Определение площади замкнутого отсека
Способ замены плоскостей проекций (задачи 3 и 4)
Способ вращения вокруг прямой уровня (горизонтали)
Способ вращения вокруг проецирующей оси i(i 
Способ плоско-параллельного перемещения (переноса)
Определение расстояний:
1. Расстояние между точками — определяется величиной отрезка, соединяющего эти точки
См. рис. 13.2, а, б, в
2. Расстояние от точки до прямой — определяется величиной перпендикуляра, опущенного из точки к прямой
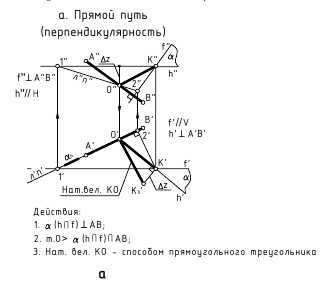
а. Прямой путь (перпендикулярность)
б. Способ замены плоскостей проекций: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис. 13.2, г)
в. Способ вращения вокруг прямой уровня: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, д)
г. Способ плоскопараллельного переноса: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, ж)
3. Расстояние между параллельными прямыми — определяется величиной перпендикуляра, проведённого из произвольной точки одной прямой к другой прямой
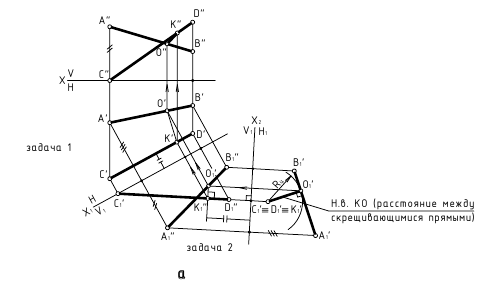
а. Способ замены плоскостей проекции (рассматриваем две прямые) — задачи 1 и 2 (преобразовать прямые общего положения AB и CD в проецирующие)
б. Способ замены плоскостей проекции (рассматриваем плоскость, которую определяют параллельные прямые) — задачи 3 и 4 (определить натуральную величину плоскости ? (AB//СВ))
4. Расстояние между скрещивающимися прямыми — определяется величиной перпендикуляра, проведённого от одной из прямых, преобразованной в точку, к другой прямой (задачи 1 и 2 замены плоскостей проекции).
Способ замены плоскостей проекций — задачи 1 и 2
5. Расстояние от точки до плоскости — определяется величиной перпендикуляра, проведённого из точки на плоскость до точки его пересечения с этой плоскостью.
а. Прямой путь (перпендикулярность)
б. Способ замены плоскостей проекций (плоскость преобразовать в проецирующую — задача 3)
6. Расстояние между прямой и параллельной ей плоскостью — определяется величиной перпендикуляра, проведённого из произвольной точки на прямой к плоскости.
См. рис. 13.4, б, в
7. Расстояние между параллельными плоскостями — определяется величиной отрезка перпендикуляра, опущенного из точки одной плоскости на другую плоскость (до точки пересечения с другой плоскостью).
См. рис. 13.4, б, в
8. Расстояние от точки до поверхности
a. Cпособ вращения вокруг проецирующей оси
б. Способ замены плоскостей проекции
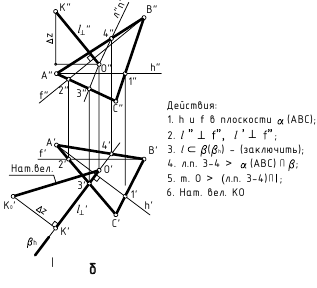
Определение величин углов:
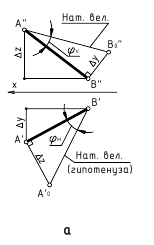
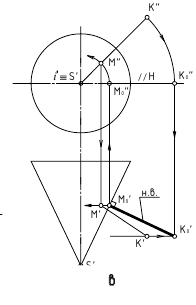
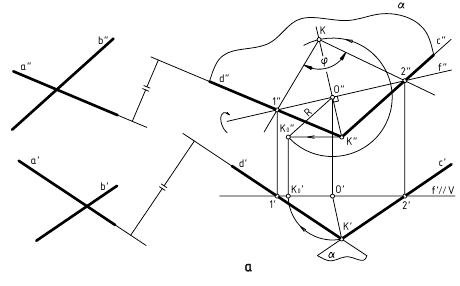
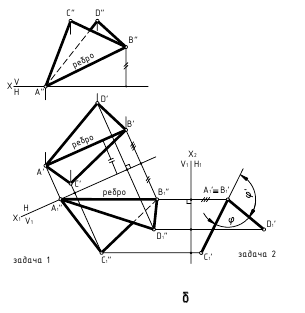
1. Угол φ между скрещивающимися прямыми — определяется плоским углом, образованным двумя пересекающимися прямыми, проведёнными из произвольной точки пространства параллельно скрещивающимся прямым (рис. 13.6, а)
Способ вращения вокруг линии уровня
Дано:
а и b — скрещивающиеся прямые
Требуется:
∠φ — ?
Решение:
1.
2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости α(d ∩с)
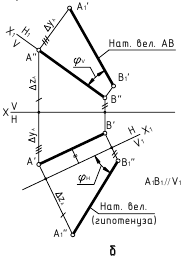
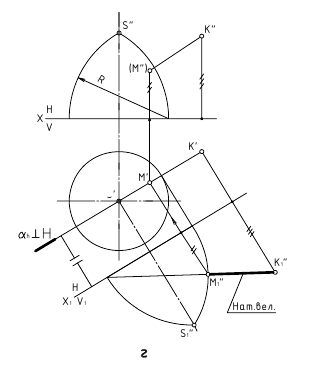
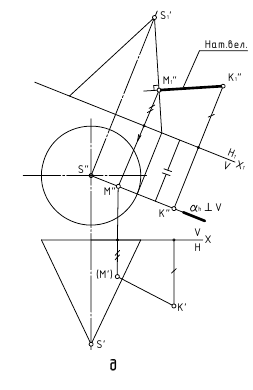
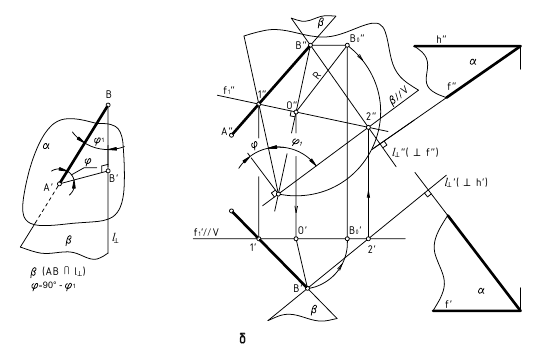
2. Угол φ между прямой и плоскостью — определяется углом между прямой и её проекцией на эту плоскость.
Дано:
α(h ∩ f);
AB — прямая общего положения
Требуется:
∠φ — ?
Решение:
1. l 
l

l

2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости β(AB∩l)
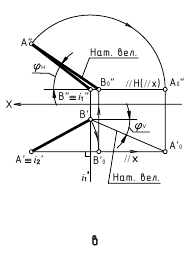
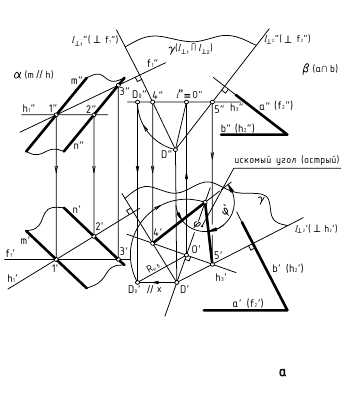
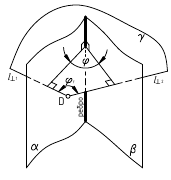
3. Угол φ между плоскостями α и β — определяется линейным углом, образованным двумя прямыми, по которым некоторая плоскость γ, перпендикулярная плоскостям (или их ребру), пересекает эти плоскости (углом между плоскостями считают острый угол).
а. Если на чертеже нет ребра (линии пересечения заданных плоскостей) — угол φ определяется способом вращения вокруг линии уровня (рис. а)
Дано:
(m // h); (а ∩ b).
Требуется:
∠φ — ?
Решение:
1. провести в заданной плоскости фронтали и горизонтали;
2. из произвольной точки пространства D (D’, D») провести перпендикуляры l1 и l2 к заданными плоскостям, которые определяют плоскость γ(l1 ∩ l2);
3. ∠φ — вращением вокруг горизонтали h3, проведённой в построенной плоскости γ(l1 ∩ l2).
б. Если на чертеже есть ребро (линия пересечения заданных плоскостей) — угол φ определяется способом замены плоскостей проекций (задачи 1 и 2, рис. б)
Решение:
ребро АВ двугранного угла преобразовать двумя заменами в проецирующую прямую.
- Тени в ортогональных проекциях
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Пересечения поверхностей с прямой и плоскостью
- Пересечение поверхности плоскостью и прямой
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости