Как найти проекцию матрицы

Проекция матрицы

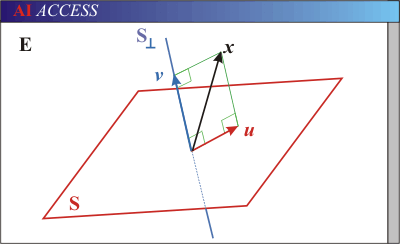
Эта
иллюстрация представляет:

*
S подпространство E векторное
пространство.

*
Вектор х и у его
ортогональное проектирование на S.

«Ортогональная
проекция на S» является линейным
оператором, поэтому может быть представлено
матрицей. Матрица представляет проектор
называется проекцией матрицы,
а это всегда симметричны.

Из-за
их важности в области статистики,
специальная запись
этого Словарь предназначен для проекции
матрицы.

Положительный (полу-) определенных матриц

Симметричная
матрица называется неотрицательно
определенной, если для любого, не
0 вектор х:

Если
это неравенство всегда строгое, матрица
называется положительно определенной.

——

Положительно
определенные матрицы играют важную
роль в области статистики (в основном,
потому что ковариационной
матрицы неотрицательно), и
вступление
в эту Словарь предназначен для положительно
определенной матрицы.

________________________________________________________________

В
этом уроке мы переходим те свойства
симметричных матриц, которые будут
необходимы на этом сайте для установления
важных результатов о:

*
Анализ главных компонент,

*
Линейная регрессия (простых и кратных),

*
Ridge регрессии,

*
Многомерного нормального распределения,

*
Квадратичные формы в нормальных величин.

—-

Только
общими свойствами симметричных матриц
рассматриваются в этой статье.

*
Свойства матрицы проектирования решаются
здесь
.

*
Свойства положительно определенных
матриц рассматриваются здесь
.

Симметричных
матриц

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Интересная задачка. На факультете прикладной математики учитесь?
Общие соображения можно здесь посмотреть:

https://ocw.mit.edu/courses/mathematics/18-06sc-li…
(Projection in higher dimensions)

https://en.wikipedia.org/wiki/Projection_matrix

Попробуйте воспользоваться элементарным разложением квадратной матрицы на сумму симметричной и кососимметричной:

( 1, 3,  3)   (1, 2, 1)   ( 0, 1,  2)
( 1, 1, -1) = (2, 1, 2) + (-1, 0, -3)
(-1, 5,  1)   (1, 2, 1)   (-2, 3,  0)

Преобразование P — это ортогональная проекция на линию m.

В линейной алгебре и функциональный анализ, проекция — это линейное преобразование P { displaystyle P}из векторного пространства самому себе так, что P 2 = P { displaystyle P ^ {2} = P}. То есть всякий раз, когда P { displaystyle P}применяется дважды к любому значению, он дает такой же результат, как если бы он был применен один раз (идемпотент ). Он оставляет свой образ неизменным. Хотя абстрактная, это определение «проекции» формализует и обобщает идею графической проекции. Можно также рассмотреть влияние проекции на геометрический объект , исследуя влияние проекции на точки в объекте.

Содержание

• 1 Определения
  • 1.1 Матрица проекции
• 2 Примеры
  • 2.1 Ортогональная проекция
  • 2.2 Наклонная проекция
• 3 Свойства и классификация
  • 3.1 Идемпотентность
  • 3.2 Комплементарность диапазон и ядро ​​
  • 3.3 Спектр
  • 3.4 Произведение проекций
  • 3.5 Ортогональные проекции
    • 3.5.1 Свойства и особые случаи
      • 3.5.1.1 Формулы
  • 3.6 Косые проекции
  • 3.7 Поиск проекции с внутренним продуктом
• 4 Канонические формы
• 5 Проекции на нормированных векторных пространствах
• 6 Приложения и дополнительные соображения
• 7 Обобщения
• 8 См. также
• 9 Примечания
• 10 Ссылки
• 11 Внешние ссылки

Определения

A проекция на векторное пространство V { displaystyle V}— линейный оператор P: V ↦ V { displaystyle P : V mapsto V}такой, что P 2 = P { displaystyle P ^ {2} = P}.

Когда V { displaystyle V}имеет внутренний продукт и является полным (т.е. когда V { displaystyle V}— это гильбертово пространство ) может использоваться концепция ортогональности. Проекция P { displaystyle P}в гильбертовом пространстве V { displaystyle V}называется ортогональной проекцией, если она удовлетворяет ⟨п Икс, Y⟩ знак равно ⟨Икс, П Y⟩ { Displaystyle langle Px, y rangle = langle x, Py rangle}для всех x, y ∈ V { displaystyle x, y in V}. Неортогональная проекция на гильбертово пространство называется наклонной проекцией .

Матрица проекции

Собственные значения матрицы проекции должно быть 0 или 1.

Примеры

Ортогональная проекция

Например, функция, отображающая точку (x, y, z) { displaystyle (x, y, z)}в трехмерном пространстве R 3 { displaystyle mathbb {R} ^ {3}}до точки (x, y, 0) { displaystyle (x, y, 0)}— ортогональная проекция на плоскость x – y. Эта функция представлена ​​матрицей

P = [1 0 0 0 1 0 0 0 0]. { displaystyle P = { begin {bmatrix} 1 0 0 \ 0 1 0 \ 0 0 0 end {bmatrix}}.}

Действие этой матрицы на произвольный вектор:

P (xyz) = (xy 0). { displaystyle P { begin {pmatrix} x \ y \ z end {pmatrix}} = { begin {pmatrix} x \ y \ 0 end {pmatrix}}.}

Чтобы увидеть что P { displaystyle P}действительно является проекцией, т.е. P = P 2 { displaystyle P = P ^ {2}}, мы вычисляем

P 2 (xyz) = P (xy 0) = (xy 0) = P (xyz) { displaystyle P ^ {2} { begin {pmatrix} x \ y \ z end {pmatrix} } = P { begin {pmatrix} x \ y \ 0 end {pmatrix}} = { begin {pmatrix} x \ y \ 0 end {pmatrix}} = P { begin {pmatrix} x \ y \ z end {pmatrix}}}.

Заметим, что PT = P { displaystyle P ^ { mathrm {T}} = P}показывает, что проекция является ортогональной проекцией.

Наклонная проекция

Простым примером неортогональной (наклонной) проекции (определение см. Ниже) является

P = [0 0 α 1]. { displaystyle P = { begin {bmatrix} 0 0 \ alpha 1 end {bmatrix}}.}

Через умножение матриц можно увидеть, что

P 2 = [0 0 α 1] [0 0 α 1] = [0 0 α 1] = P. { displaystyle P ^ {2} = { begin {bmatrix} 0 0 \ alpha 1 end {bmatrix}} { begin {bmatrix} 0 0 \ alpha 1 end {bmatrix}} = { begin { bmatrix} 0 0 \ alpha 1 end {bmatrix}} = P.}

доказывает, что P { displaystyle P}действительно является проекцией.

Проекция P { displaystyle P}ортогональна тогда и только тогда, когда α = 0 { displaystyle alpha = 0}, потому что только тогда PT = P { displaystyle P ^ { mathrm {T}} = P}.

Свойства и классификация

Преобразование T — это проекция вдоль k на m. Диапазон T равен m, а пустое пространство — k.

Идемпотентность

По определению проекция P { displaystyle P}является идемпотентной (например, P 2 = P { displaystyle P ^ {2} = P}).

Комплементарность диапазона и ядра

Пусть W { displaystyle W}будет конечномерным векторным пространством и P { displaystyle P}быть проекцией на W { displaystyle W}. Предположим, что подпространства U { displaystyle U}и V { displaystyle V}— это диапазон и ядро ​​ из P { displaystyle P}соответственно. Тогда P { displaystyle P}имеет следующие свойства:

1. P { displaystyle P}— оператор идентичности I { displaystyle I}на U { displaystyle U}

   ∀ x ∈ U: P x = x { displaystyle forall x in U: Px = x}.

2. У нас есть прямая сумма W = U ⊕ V { displaystyle W = U oplus V}. Каждый вектор x ∈ W { displaystyle x in W}может быть разложен однозначно как x = u + v { displaystyle x = u + v}с u = P x { displaystyle u = Px}и v = x — P x = (I — P) x { displaystyle v = x-Px = (IP) x}, и где u ∈ U, v ∈ V { displaystyle u in U, v in V}.

Диапазон и ядро ​​проекции дополняют друг друга, как и P { displaystyle P}и Q = I — P { displaystyle Q = IP}. Оператор Q { displaystyle Q}также является проекцией, поскольку диапазон и ядро ​​P { displaystyle P}становятся ядром, а диапазон Q { displaystyle Q}и наоборот. Мы говорим, что P { displaystyle P}— это проекция вдоль V { displaystyle V}на U { displaystyle U}(ядро / диапазон) и Q { displaystyle Q}— это проекция вдоль U { displaystyle U}на V { displaystyle V}.

Спектр

В бесконечномерных векторных пространствах спектр проекции содержится в {0, 1} { displaystyle {0,1 } }как

(λ I — P) — 1 = 1 λ I + 1 λ (λ — 1) P. { displaystyle ( lambda IP) ^ {- 1} = { frac {1} { lambda}} I + { frac {1} { lambda ( lambda -1)}} P.}

Только 0 или 1 могут быть собственным значением проекции. Это означает, что ортогональная проекция P { displaystyle P}всегда является положительной полуопределенной матрицей. В общем, соответствующие собственные подпространства являются (соответственно) ядром и диапазоном проекции. Разложение векторного пространства на прямые суммы не единственно. Следовательно, учитывая подпространство V { displaystyle V}, может быть много проекций, диапазон (или ядро) которых составляет V { displaystyle V}.

Если проекция нетривиальна он имеет минимальный многочлен x 2 — x = x (x — 1) { displaystyle x ^ {2} -x = x (x-1)}, который делится на отдельные корни, и, таким образом, P { displaystyle P}диагонализуемый.

Произведение проекций

Произведение проекций, как правило, не является проекцией, даже если они ортогональны. Если две проекции коммутируют, то их произведение является проекцией, но обратное неверно: произведение двух некоммутирующих проекций может быть проекцией.

Если две ортогональные проекции коммутируют, то их произведение является ортогональной проекцией. Если продукт двух ортогональных проекций является ортогональным проектором, то эти два ортогональных проектора коммутируют (в более общем смысле: два самосопряженных эндоморфизма коммутируют тогда и только тогда, когда их произведение самосопряжено).

Ортогональные проекции

Когда векторное пространство W { displaystyle W}имеет внутренний продукт и является полным (это гильбертово пространство ) может использоваться концепция ортогональности. Ортогональная проекция — это проекция, для которой диапазон U { displaystyle U}и пустое пространство V { displaystyle V}являются ортогональными подпространствами. Таким образом, для каждого x { displaystyle x}и y { displaystyle y}в W { displaystyle W}, ⟨P Икс, (Y — п Y)⟩ знак равно ⟨(Икс — П Икс), п Y⟩ знак равно 0 { Displaystyle langle Px, (Y-Py) rangle = langle (x-Px), Py rangle = 0}. Эквивалентно:

⟨x, P y⟩ = ⟨P x, P y P = ⟨P x, y⟩ { displaystyle langle x, Py rangle = langle Px, Py rangle = langle Px, y rangle}.

Проекция ортогональна тогда и только тогда, когда она самосопряженная. Используя самосопряженные и идемпотентные свойства P { displaystyle P}для любых x { displaystyle x}и y { displaystyle y}в W { displaystyle W}мы имеем P x ∈ U { displaystyle Px in U}, y — P y ∈ V { displaystyle y-Py in V}и

⟨P x, y — P y⟩ = ⟨P 2 x, y — P y⟩ = ⟨P x, P (I — П) y⟩ знак равно ⟨п Икс, (п — п 2) y⟩ знак равно 0 { displaystyle langle Px, y-Py rangle = langle P ^ {2} x, y-Py rangle = langle Px, P (IP) y rangle = langle Px, (PP ^ {2}) y rangle = 0 ,}

где ⟨⋅, ⋅⟩ { displaystyle langle cdot, cdot rangle}— это внутренний продукт, связанный с W { displaystyle W}. Следовательно, P x { displaystyle Px}и y — P y { displaystyle y-Py}являются ортогональными проекциями. Другое направление, а именно, что если P { displaystyle P}ортогонален, то он самосопряжен, следует из

⟨x, P y⟩ = ⟨P x, y⟩ = ⟨Икс, P * Y⟩ { Displaystyle langle x, Py rangle = langle Px, y rangle = langle x, P ^ {*} y rangle}

для каждого x { displaystyle x}и y { displaystyle y}в W { displaystyle W}; таким образом, P = P ∗ { displaystyle P = P ^ {*}}.

Доказательство существования

Пусть H { displaystyle H}будет полным метрическим пространством с внутренний продукт, и пусть U { displaystyle U}будет замкнутым линейным подпространством из H { displaystyle H}(а значит, и полный). Для каждого x { displaystyle x}следующий набор неотрицательных норм {‖ x — u ‖ | u ∈ U} { displaystyle { | xu || u in U }}имеет нижнюю границу , а из-за полноты U { displaystyle U}это минимум. Мы определяем P x { displaystyle Px}как точку в U { displaystyle U}, где достигается этот минимум. Очевидно, P x { displaystyle Px}находится в U { displaystyle U}. Осталось показать, что P x { displaystyle Px}удовлетворяет ⟨x — P x, P x⟩ = 0 { displaystyle langle x-Px, Px rangle = 0 }и что это линейно. Определим a = x — P x { displaystyle a = x-Px}. Для каждого ненулевого v { displaystyle v}в U { displaystyle U}выполняется следующее: ‖ a — ⟨a, v⟩ ‖ v ‖ 2 v ‖ 2 знак равно ‖ a ‖ 2 — ⟨a, v⟩ 2 ‖ v ‖ 2 { displaystyle | a — { frac { langle a, v rangle} { | v | ^ {2}}} v | ^ {2} = | a | ^ {2} — { frac {{ langle a, v rangle} ^ {2}} { | v | ^ { 2}}}} Определив w = P x + ⟨a, v⟩ ‖ v ‖ 2 v { displaystyle w = Px + { frac { langle a, v rangle} { | v | ^ {2}}} v}мы видим, что ‖ x — w ‖ < ‖ x − P x ‖ {displaystyle |x-w|<|x-Px|}, если ⟨a, v⟩ { displaystyle langle a, v rangle}исчезает. Поскольку P x { displaystyle Px}был выбран как минимум из вышеупомянутого набора, следует, что ⟨a, v⟩ { displaystyle langle a, v rangle}действительно исчезает. В частности, (для y = P x { displaystyle y = Px}): ⟨x — P x, P x⟩ = 0 { displaystyle langle x-Px, Px rangle = 0}. Линейность следует из исчезновения ⟨x — P x, v⟩ { displaystyle langle x-Px, v rangle}для каждого v ∈ U { displaystyle v in U}: ⟨(x + y) — P (x + y), v⟩ = 0 { displaystyle langle left (x + y right) -P left (Икс + Y справа), v rangle = 0} ⟨(x — P x) + (y — P y), v⟩ = 0 { displaystyle langle left (x-Px right) + left (y-Py right), v rangle = 0} Взяв разность между уравнениями, мы имеем ⟨P x + P y — P (x + y), v⟩ = 0 { displaystyle langle Px + Py-P left (x + y right), v rangle = 0} Но поскольку мы можем выбрать v = P x + P y — P (x + y) { displaystyle v = Px + Py-P (x + y)}(как в U { displaystyle U}) следует, что П Икс + Р Y знак равно п (Икс + Y) { Displaystyle Px + Py = P (x + y)}. Точно так же у нас есть λ п Икс = P (λ x) { displaystyle lambda Px = P ( lambda x)}для каждого scalar λ { displaystyle lambda}.

Свойства и особые случаи

Ортогональная проекция — это ограниченный оператор. Это связано с тем, что для каждого v { displaystyle v}в векторном пространстве мы имеем по неравенству Коши – Шварца :

‖ P v ‖ 2 = ⟨P v, P v ⟩ Знак равно ⟨п v, v⟩ ≤ ‖ п v ‖ ⋅ ‖ v ‖ { displaystyle | Pv | ^ {2} = langle Pv, Pv rangle = langle Pv, v rangle leq | Pv | cdot | v |}

Таким образом, ‖ P v ‖ ≤ ‖ v ‖ { displaystyle | Pv | leq | v |}.

Для конечномерных комплексных или вещественных векторных пространств стандартный внутренний продукт можно заменить на ⟨⋅, ⋅⟩ { displaystyle langle cdot, cdot rangle}.

Формулы

Простые случай возникает, когда ортогональная проекция находится на прямой. Если u { displaystyle u}является единичным вектором на линии, то проекция задается внешним произведением

P u = uu T. { displaystyle P_ {u} = uu ^ { mathrm {T}}.}

(Если u { displaystyle u}имеет комплексные значения, транспонирование в приведенном выше уравнении заменяется эрмитовым транспонированием). Этот оператор оставляет u инвариантным и аннулирует все векторы, ортогональные к u { displaystyle u}, доказывая, что это действительно ортогональная проекция на линию, содержащую u. Простой способ увидеть это — рассмотреть произвольный вектор x { displaystyle x}как сумму компонента на линии (т. Е. Проецируемого вектора, который мы ищем) и другого перпендикуляра к нему, Икс = Икс ∥ + Икс ⊥ { Displaystyle x = x _ { parallel} + x _ { perp}}. Применяя проекцию, получаем

P ux = uu T x ∥ + uu T x ⊥ = u (sign (u T x ∥) ‖ x ∥ ‖) + u ⋅ 0 = x ∥ { displaystyle P_ {u} x = uu ^ { mathrm {T}} x _ { parallel} + uu ^ { mathrm {T}} x _ { perp} = u left ( mathrm {sign} (u ^ { mathrm {T}} x _ { parallel}) | x _ { parallel} | right) + u cdot 0 = x _ { parallel}}

по свойствам точечного произведения параллельного и перпендикулярного векторов.

Эту формулу можно обобщить на ортогональные проекции на подпространство произвольной размерности. Пусть u 1,…, uk { displaystyle u_ {1}, ldots, u_ {k}}будет ортонормированным базисом подпространства U { displaystyle U}, и пусть A { displaystyle A}обозначает n × k { displaystyle n times k}матрица, столбцы которой равны u 1,…, uk { displaystyle u_ {1}, ldots, u_ {k}}, т.е. A = [u 1… uk] { displaystyle A = { begin {bmatrix} u_ {1} ldots u_ {k} end {bmatrix}}}. Тогда проекция задается следующим образом:

PA = AAT { displaystyle P_ {A} = AA ^ { mathrm {T}}}

, который можно переписать как

PA = ∑ i ⟨ui, ⋅ ⟩ Ui. { displaystyle P_ {A} = sum _ {i} langle u_ {i}, cdot rangle u_ {i}.}

Матрица AT { displaystyle A ^ { mathrm {T }}}— это частичная изометрия, которая исчезает в ортогональном дополнении U { displaystyle U}и A { displaystyle A }— изометрия, которая включает U { displaystyle U}в базовое векторное пространство. Диапазон P A { displaystyle P_ {A}}, следовательно, является последним пространством A { displaystyle A}. Также ясно, что AAT { displaystyle AA ^ { mathrm {T}}}является оператором идентичности в U { displaystyle U}.

Условие ортонормальности также может быть отброшенным. Если u 1,…, uk { displaystyle u_ {1}, ldots, u_ {k}}является базисом (не обязательно ортонормированным) и A { displaystyle A }— матрица с этими векторами в качестве столбцов, тогда проекция будет:

PA = A (ATA) — 1 AT. { displaystyle P_ {A} = A (A ^ { mathrm {T}} A) ^ {- 1} A ^ { mathrm {T}}.}

Матрица A { displaystyle A }по-прежнему встраивает U { displaystyle U}в основное векторное пространство, но больше не является изометрией в целом. Матрица (A T A) — 1 { displaystyle (A ^ { mathrm {T}} A) ^ {- 1}}— это «нормализующий коэффициент», который восстанавливает норму. Например, оператор ранга 1 uu T { displaystyle uu ^ { mathrm {T}}}не является проекцией, если ‖ u ‖ ≠ 1. { displaystyle | u | neq 1.}После деления на u T u = ‖ u ‖ 2, { displaystyle u ^ { mathrm {T}} u = | u | ^ {2},}получаем проекцию u (u T u) — 1 u T { displaystyle u (u ^ { mathrm {T}} u) ^ {- 1} u ^ { mathrm {T}}}на подпространство, охватываемое u { displaystyle u}.

В общем случае мы можем иметь произвольную положительно определенную матрицу D { displaystyle D}определение внутреннего продукта ⟨x, y⟩ D = y † D x { displaystyle langle x, y rangle _ {D} = y ^ { dagger} Dx }, а проекция PA { displaystyle P_ {A}}задается как PA x = argminy ∈ range (A) ‖ x — y ‖ D 2 { displaystyle P_ {A} x = mathrm {argmin} _ {y in mathrm {range} (A)} | xy | _ {D} ^ {2}}. Тогда

P A = A (A T D A) — 1 A T D. { displaystyle P_ {A} = A (A ^ { mathrm {T}} DA) ^ {- 1} A ^ { mathrm {T}} D.}

Когда создается пространство диапазона проекции по кадру (т. е. количество генераторов превышает его размер) формула для проекции принимает вид: PA = AA + { displaystyle P_ {A} = AA ^ {+ }}. Здесь A + { displaystyle A ^ {+}}обозначает псевдообратную матрицу Мура – ​​Пенроуза. Это лишь один из многих способов построения оператора проекции.

Если [AB] { displaystyle { begin {bmatrix} AB end {bmatrix}}}— невырожденная матрица и ATB = 0 { displaystyle A ^ { mathrm {T}} B = 0}(например, B { displaystyle B}— матрица пустого пространства из A { displaystyle A}) выполняется следующее:

I = [AB] [AB] — 1 [ATBT] — 1 [ATBT] = [AB] ([ATBT ] [AB]) — 1 [ATBT] = [AB] [ATAOOBTB] — 1 [ATBT] = A (ATA) — 1 AT + B (BTB) — 1 BT { displaystyle { begin {выровнено} I = { begin {bmatrix} AB end {bmatrix}} { begin {bmatrix} AB end {bmatrix}} ^ {- 1} { begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix}} ^ {- 1} { begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix}} = { begin {bmatrix} AB end {bmatrix}} left ({ begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix} } { begin {bmatrix} AB end {bmatrix}} right) ^ {- 1} { begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix}} \ = { begin {bmatrix} AB end {bmatrix }} { begin {bmatrix} A ^ { mathrm {T}} AO \ OB ^ { mathrm {T}} B end {bmatrix}} ^ {- 1} { begin {bmatrix} A ^ { mathrm {T}} \ B ^ { mathrm {T}} end {bmatrix}} \ [4pt] = A (A ^ { mathrm {T}} A) ^ {- 1} A ^ { mathrm {T}} + B (B ^ { mathrm {T}} B) ^ {- 1} B ^ { mathrm {T}} end {align}}}

Если условие ортогональности улучшено до ATWB = ATWTB = 0 { displaystyle A ^ { mathrm {T}} WB = A ^ { mathrm {T}} W ^ { mathrm {T}} B = 0}с W { displaystyle W}неособым числом, выполняется следующее:

I = [AB] [(ATWA) — 1 AT (BTWB) — 1 BT] W. { displaystyle I = { begin {bmatrix} AB end {bmatrix}} { begin {bmatrix} (A ^ { mathrm {T}} WA) ^ {- 1} A ^ { mathrm {T}} \ (B ^ { mathrm {T}} WB) ^ {- 1} B ^ { mathrm {T}} end {bmatrix}} W.}

Все эти формулы также верны для сложных внутренних пространств продукта при условии, что вместо транспонирования используется сопряженное транспонирование. Более подробную информацию о суммах проекторов можно найти в Banerjee and Roy (2014). Также см. Banerjee (2004) о применении сумм проекторов в основной сферической тригонометрии.

Наклонные проекции

Термин «наклонные проекции» иногда используется для обозначения неортогональных проекций. Эти проекции также используются для представления пространственных фигур на двухмерных чертежах (см. наклонная проекция ), хотя и не так часто, как ортогональные проекции. В то время как для вычисления подобранного значения регрессии обычных наименьших квадратов требуется ортогональная проекция, для вычисления подобранного значения регрессии инструментальных переменных требуется наклонная проекция.

Проекции определяются своим нулевым пространством и базисными векторами, используемыми для характеристики их диапазона (который является дополнением к нулевому пространству). Когда эти базисные векторы ортогональны нулевому пространству, тогда проекция является ортогональной проекцией. Когда эти базисные векторы не ортогональны нулевому пространству, проекция является наклонной проекцией. Пусть векторы u 1,…, uk { displaystyle u_ {1}, ldots, u_ {k}}образуют основу для диапазона проекции и объединяют эти векторы в n × k { displaystyle n times k}матрица A { displaystyle A}. Диапазон и пустое пространство являются дополнительными пространствами, поэтому нулевое пространство имеет размерность n — k { displaystyle n-k}. Отсюда следует, что ортогональное дополнение пустого пространства имеет размерность k { displaystyle k}. Пусть v 1,…, vk { displaystyle v_ {1}, ldots, v_ {k}}образуют основу для ортогонального дополнения нулевого пространства проекции, и соберите эти векторы в матрице B { displaystyle B}. Тогда проекция определяется как

P = A (B T A) — 1 B T. { displaystyle P = A (B ^ { mathrm {T}} A) ^ {- 1} B ^ { mathrm {T}}.}

Это выражение обобщает формулу для ортогональных проекций, приведенную выше.

Поиск проекции с помощью внутреннего продукта

Пусть V { displaystyle V}будет векторным пространством (в данном случае плоскостью), натянутым на ортогональные векторы u 1, u 2, ⋯, вверх { displaystyle u_ {1}, u_ {2}, cdots, u_ {p}}. Пусть y { displaystyle y}будет вектором. Можно определить проекцию y { displaystyle y}на V { displaystyle V}как

proj V ⁡ y = y ⋅ ujuj ⋅ ujuj { displaystyle operatorname {proj} _ {V} y = { frac {y cdot u ^ {j}} {u ^ {j} cdot u ^ {j}}} u ^ {j}}

, где j { displaystyle j}подразумевает нотацию суммы Эйнштейна. Вектор y { displaystyle y}может быть записан как ортогональная сумма, такая что y = proj V ⁡ y + z { displaystyle y = operatorname {proj} _ {V } y + z}. proj V ⁡ y { displaystyle operatorname {proj} _ {V} y}иногда обозначается как y ^ { displaystyle { hat {y} }}. В линейной алгебре есть теорема, согласно которой этот z { displaystyle z}является кратчайшим расстоянием от y { displaystyle y}до V { displaystyle V}и обычно используется в таких областях, как машинное обучение.

y проецируется в векторное пространство V.

Канонические формы

Любая проекция P = P 2 { displaystyle P = P ^ {2}}в векторном пространстве размерности d { displaystyle d}над полем представляет собой диагонализуемую матрицу, поскольку ее минимальный многочлен делит x 2 — x { displaystyle x ^ {2} -x}, который разбивается на отдельные линейные множители. Таким образом, существует базис, в котором P { displaystyle P}имеет форму

P = I r ⊕ 0 d — r { displaystyle P = I_ {r} oplus 0_ { dr}}

, где r { displaystyle r}— это ранг P { displaystyle P}. Здесь I r { displaystyle I_ {r}}— это единичная матрица размера r { displaystyle r}, а 0 d — r { displaystyle 0_ {dr}}— нулевая матрица размера d — r { displaystyle dr}. Если векторное пространство является сложным и снабжено скалярным произведением , то существует ортонормированный базис, в котором матрица P имеет вид

P = [1 σ 1 0 0] ⊕ ⋯ ⊕ [1 σ k 0 0] ⊕ я м ⊕ 0 s { displaystyle P = { begin {bmatrix} 1 sigma _ {1} \ 0 0 end {bmatrix}} oplus cdots oplus { begin {bmatrix} 1 sigma _ {k} \ 0 0 end {bmatrix}} oplus I_ {m} oplus 0_ {s}}.

где σ 1 ≥ σ 2 ≥… ≥ σ k>0 { displaystyle sigma _ {1} geq sigma _ {2} geq ldots geq sigma _ {k}>0}. Целые числа k, s, m { displaystyle k, s, m}и действительные числа σ i { displaystyle sigma _ {i}}определяются однозначно. Обратите внимание, что k + s + m = d { displaystyle k + s + m = d}. Фактор I m ⊕ 0 s { displaystyle I_ {m} oplus 0_ {s}}соответствует максимальному инвариантному подпространству на который P { displaystyle P}действует как ортогональная проекция (так что сама точка P ортогональна тогда и только тогда, когда k = 0 { displaystyle k = 0}) и σ i { displaystyle sigma _ {i}}-блоки соответствуют наклонным компонентам.

Проекции на нормированные векторные пространства

Когда основное векторное пространство X { displaystyle X}является (не обязательно конечномерным) нормированным В векторном пространстве необходимо рассмотреть аналитические вопросы, не относящиеся к конечномерному случаю. Предположим теперь, что X { displaystyle X}является банаховым пространством.

Многие из алгебраических результатов, обсужденных выше, переживают переход к этому контексту. Разложение заданной прямой суммы X { displaystyle X}на дополнительные подпространства по-прежнему определяет проекцию, и наоборот. Если X { displaystyle X}— прямая сумма X = U ⊕ V { displaystyle X = U oplus V}, то оператор, определяемый P (u + v) = u { displaystyle P (u + v) = u}по-прежнему является проекцией с диапазоном U { displaystyle U}и ядро ​​V { displaystyle V}. Также ясно, что P 2 = P { displaystyle P ^ {2} = P}. И наоборот, если P { displaystyle P}является проекцией на X { displaystyle X}, то есть P 2 = P { displaystyle P ^ {2} = P}, тогда легко проверить, что (1 — P) 2 = (1 — P) { displaystyle (1-P) ^ {2} = (1- P)}. Другими словами, 1 — P { displaystyle 1-P}также является проекцией. Отношение P 2 = P { displaystyle P ^ {2} = P}подразумевает 1 = P + (1 — P) { displaystyle 1 = P + (1-P) }и X { displaystyle X}— прямая сумма ran (P) ⊕ ran (1 — P) { displaystyle mathrm {ran} ( P) oplus mathrm {ran} (1-P)}.

Однако, в отличие от конечномерного случая, проекции не обязательно должны быть непрерывными в целом. Если подпространство U { displaystyle U}из X { displaystyle X}не замкнуто в топологии нормы, то проекция на U { displaystyle U}не является непрерывным. Другими словами, диапазон непрерывной проекции P { displaystyle P}должен быть замкнутым подпространством. Кроме того, ядро ​​непрерывной проекции (в общем, непрерывного линейного оператора) замкнуто. Таким образом, непрерывная проекция P { displaystyle P}дает разложение X { displaystyle X}на два дополнительных закрытых подпространства: X = ran (P) ⊕ ker (P) знак равно ker (1 — P) ⊕ ker (P) { displaystyle X = mathrm {ran} (P) oplus mathrm {ker} (P) = mathrm {ker} ( 1-P) oplus mathrm {ker} (P)}.

Обратное также верно с дополнительным предположением. Предположим, что U { displaystyle U}является замкнутым подпространством X { displaystyle X}. Если существует замкнутое подпространство V { displaystyle V}такое, что X = U ⊕ V, то проекция P { displaystyle P}с диапазоном U { displaystyle U}и ядро ​​V { displaystyle V}является непрерывным. Это следует из теоремы о замкнутом графике. Предположим, что x n → x и Px n → y. Необходимо показать, что P x = y { displaystyle Px = y}. Поскольку U { displaystyle U}замкнут и {Px n } ⊂ U, y лежит в U { displaystyle U}, т.е. Py = y. Кроме того, x n — Px n = (I — P) x n → x — y. Поскольку V { displaystyle V}закрыто и {(I — P) x n } ⊂ V, мы имеем x — y ∈ V { displaystyle xy in V}, т.е. P (x — y) = P x — P y = P x — y = 0 { displaystyle P (xy) = Px-Py = Px-y = 0}, что доказывает утверждение.

В приведенном выше аргументе используется предположение, что оба U { displaystyle U}и V { displaystyle V}закрыты. В общем случае, учитывая замкнутое подпространство U { displaystyle U}, может не существовать дополнительное замкнутое подпространство V { displaystyle V}, хотя для Гильбертовы пространства это всегда можно сделать, взяв ортогональное дополнение. Для банаховых пространств одномерное подпространство всегда имеет замкнутое дополнительное подпространство. Это непосредственное следствие теоремы Хана – Банаха. Пусть U { displaystyle U}будет линейным промежутком u { displaystyle u}. По Хану-Банаху существует ограниченный линейный функционал φ { displaystyle varphi}такой, что φ (u) = 1. Оператор P (x) = φ (x) u { displaystyle P (x) = varphi (x) u}удовлетворяет P 2 = P { displaystyle P ^ {2} = P}, т.е. это проекция. Ограниченность φ { displaystyle varphi}подразумевает непрерывность P { displaystyle P}и, следовательно, ker ⁡ (P) = ran ⁡ ( I — P) { displaystyle operatorname {ker} (P) = operatorname {ran} (IP)}— это закрытое дополнительное подпространство U { displaystyle U}.

Applications и другие соображения

Проекции (ортогональные и другие) играют важную роль в алгоритмах для некоторых задач линейной алгебры:

• QR-разложение (см. преобразование Хаусхолдера и разложение Грама – Шмидта );
• Разложение по сингулярным значениям
• Приведение к форме Хессенберга (первый шаг во многих алгоритмах собственных значений )
• Линейная регрессия
• Проективные элементы матричные алгебры используются при построении некоторых K-групп в Операторной K-теории

Как указано выше, проекции являются частным случаем идемпотентов. Аналитически ортогональные проекции являются некоммутативными обобщениями характеристики ристические функции. Идемпотенты используются при классификации, например, полупростых алгебр, тогда как теория меры начинается с рассмотрения характеристических функций измеримых множеств. Поэтому, как можно догадаться, проекции очень часто встречаются в контекстных операторных алгебрах. В частности, алгебра фон Неймана порождается ее полной решеткой проекций.

Обобщения

В более общем смысле, если дана карта между нормированными векторными пространствами T: V → W, { displaystyle T двоеточие V to W,}аналогично можно попросить, чтобы это отображение было изометрией на ортогональном дополнении ядра: (ker ⁡ T) ⊥ → W { displaystyle ( ker T) ^ { perp} to W}быть изометрией (сравните Частичная изометрия ); в частности он должен быть включен. Случай ортогональной проекции — это когда W является подпространством V. В римановой геометрии это используется в определении римановой субмерсии.

См. Также

• Центрирующая матрица, который является примером матрицы проекции.
• Ортогонализация
• Инвариантное подпространство
• Свойства трассировки
• Алгоритм проекции Дикстры для вычисления проекции на пересечение множеств

Примечания

Источники

• Банерджи, Судипто; Рой, Аниндия (2014), Линейная алгебра и матричный анализ для статистики, Тексты в статистике (1-е изд.), Чепмен и Холл / CRC, ISBN 978-1420095388
• Данфорд, Нью-Йорк.; Шварц, Дж. Т. (1958). Линейные операторы. Часть I: Общая теория. Interscience.
• Мейер, Карл Д. (2000). Матричный анализ и прикладная линейная алгебра. Общество промышленной и прикладной математики. ISBN 978-0-89871-454-8 .

Внешние ссылки

• Лекция MIT по линейной алгебре по проекционным матрицам на YouTube, из MIT OpenCourseWare
• Линейная алгебра 15d: Преобразование проекции на YouTube, автор Павел Гринфельд.
• Учебник по плоской геометрической проекции — простой в использовании учебник, объясняющий различные типы плоские геометрические проекции.

A square matrix $A$ is symmetric if $A = A^T$ . Let $S$ be the subspace of symmetric matrices, inside the vector space of all $2 × 2$ matrices. Consider the matrix X = begin{bmatrix} a & b \ c & d\ end{bmatrix} where a, b, c, d are known constants.

A) Find the orthogonal projection of X onto subspace $S$

B) Find the orthogonal projection of X onto $S^perp$

My attempt:
I’ve never really projected into a matrix vector subspace, I’ve only ever done vectors to vectors, but the steps I think are probably the same.

Finding an orthogonal basis for the subspace of symmetric matrices: $$begin{bmatrix} 1 & 0 \ 0 & 0\ end{bmatrix}, begin{bmatrix} 0 & 1 \ 1 & 0\ end{bmatrix}, begin{bmatrix} 0 & 0 \ 0 & 1\ end{bmatrix}$$

Here’s where things get confusing. I need to find how much of X is in the «direction» of each of my basis matrices, right?

So,

$$Proj(X) = begin{bmatrix} 1 & 0 \ 0 & 0\ end{bmatrix} X + begin{bmatrix} 0 & frac{1}{sqrt(2)} \ frac{1}{sqrt(2)} & 0\ end{bmatrix}X + begin{bmatrix} 0 & 0 \ 0 & 1\ end{bmatrix}X$$.

Where the second matrix is normalized so that it has «length» = 1, is this correct approach?

I actually computed it and it didn’t seem to work. In the end I got
$$proj(x) = begin{bmatrix} a + frac{c}{sqrt(2)} & b + frac{d}{sqrt(2)} \ frac{a}{sqrt(2)} + c & frac{b}{sqrt(2)}+ d\ end{bmatrix} $$

To get a symmetric matrix, I need the off diagonal terms to be equal. How can I go about finding this projection?

For part b, I’m not really sure how to go about finding $S^{perp}$. If S were spanned by a set of vectors, then I would just need to find the nullspace of S and that would be $S^{perp}$. How do I go about doing it in this situation where we have a space of matrices?