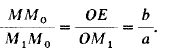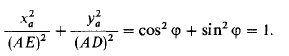Как найти проекцию диагоналей на плоскость

Пусть $%ABCD$% — ромб со стороной $%a$%. Плоскость проведена через $%AB$%, и на неё проектируется $%BC$%. Пусть $%h$% — расстояние от точки $%C$% до плоскости. По теореме Пифагора, $%h^2=a^2-b^2$%. Диагональ $%AC$% (более длинная) равна $%asqrt3$%. Квадрат длины её проекции равен $%3a^2-h^2=2a^2+b^2$%. Диагональ $%BD$% имеет длину $%a$%, и точка $%D$% находится на том же расстоянии от плоскости, что и $%C$%. Поэтому квадрат длины её проекции равен $%a^2-h^2=b^2$%. Таким образом, проекции диагоналей ромба будут равны $%sqrt{2a^2+b^2}$% и $%b$%.

Надеюсь, я трактовал условие правильно.

3.1. Способы задания плоскости на ортогональных чертежах

Положение плоскости в пространстве определяется:

• тремя точками, не лежащими на одной прямой;
• прямой и точкой, взятой вне прямой;
• двумя пересекающимися прямыми;
• двумя параллельными прямыми;
• плоской фигурой.

В соответствии с этим на эпюре плоскость может быть задана:

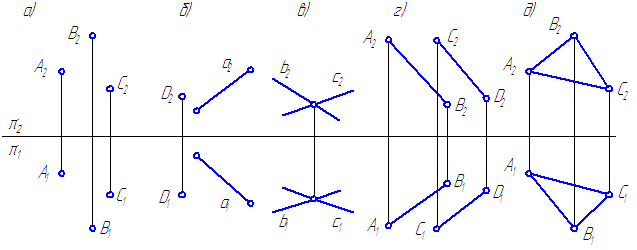
• проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
• проекциями точки и прямой (Рисунок 3.1,б);
• проекциями двух пересекающихся прямых (Рисунок 3.1,в);
• проекциями двух параллельных прямых (Рисунок 3.1,г);
• плоской фигурой (Рисунок 3.1,д);
• следами плоскости;
• линией наибольшего ската плоскости.

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

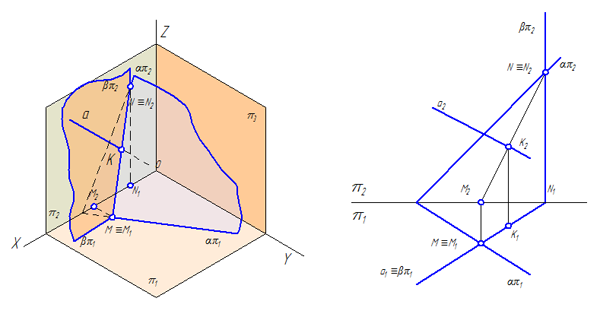
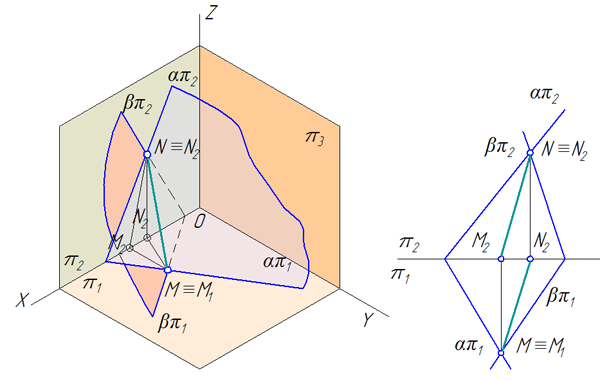
Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

α = m // n D ∈ n ⇒ D ∈ α

Рисунок 3.6 – Принадлежность прямой плоскости

left.begin{array}{l}alpha=mparallel n,\Dinalpha\Cinalpha\end{array}right} Longrightarrow CDinalpha

Упражнение

Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С.

Рисунок 3.7 – Решение задачи

Решение:

1. ABCD – плоский четырехугольник, задающий плоскость.
2. Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
3. Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A₂C₂ ∩ B₂D₂=K₂.
4. Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B₁D₁ строим К₁.
5. Через А₁К₁ проводим проекцию диагонали А₁С₁.
6. Точку С₁ получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А₁К₁.

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

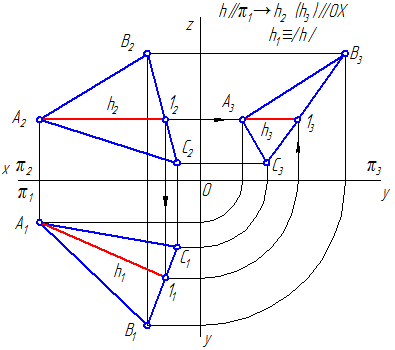
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

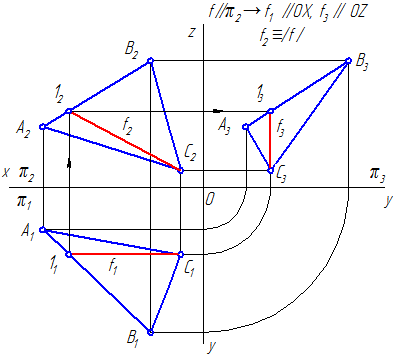
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

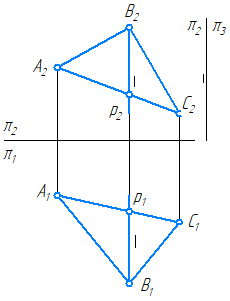
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная  прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная  прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

alpha=mcap n\left.begin{array}{l}a_2parallel m_2\a_1parallel m_1\end{array}right} Rightarrow aparallelalpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

1. Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
2. Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
3. Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

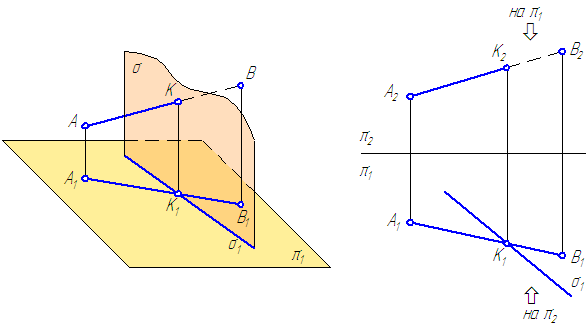
Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Решение:

1. 1. Точка К должна принадлежать прямой АВ ⇒ К₁∈А₁В и заданной плоскости σ ⇒ К₁∈σ, следовательно, К₁ находится в точке пересечения проекций А₁В₁ и σ₁;
   2. Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ₁ (горизонтальный след плоскости);
   3. Фронтальную проекцию точки К находим посредством линии проекционной связи: К₂∈А₂В₂.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы:  плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

Решение:

1. Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
2. Если α⊥π₁, то на плоскость проекций π₁ плоскость α проецируется в прямую (горизонтальный след плоскости απ₁ или α₁), совпадающую с E₁F₁;
3. Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
4. Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.

Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:

1. left.begin{array}{l}alpha perp pi_1\alphain EF\end{array}right} Longrightarrow alpha_1in E_1F_1
2. alphacapsigma=(1-2)left.begin{array}{l}|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\end{array}right.
3. (1_2-2_2)cap E_2F_2=K_2\left.begin{array}{l}Kin EF\Kin (1-2)Rightarrow Kinsigma\end{array}right}Longrightarrow K=EFcap (sigma =triangle ABC)

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и)  «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

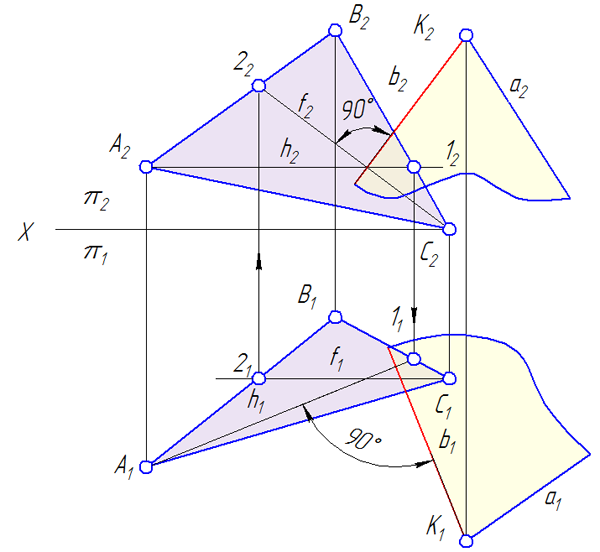
Пусть прямая p перпендикулярна плоскости σ=ΔАВС  и проходит через точку K.

1. Построим горизонталь и фронталь в плоскости σ=ΔАВС  : σ=ΔАВС : A-1∈σ; A-1//π₁; С-2∈σ; С-2//π₂.
2. Восстановим из точки K перпендикуляр к заданной плоскости: p₁⊥h₁ и p₂⊥f₂, или p₁⊥απ₁ и p₂⊥απ_2.

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей: две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

Решение: В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.

1. Через точку F проводим прямую m, параллельную, например, АВ.
2. Через точку F, или же через любую точку, принадлежащую m,  проводим прямую n, параллельную, например, ВС, причём m∩n=F.
3. β = m∩n и β//α по определению.

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Порядок построения линии пересечения плоскостей:

1. Найти точку пересечения горизонтальных следов — это точка М (её проекции М₁  и М₂, при этом М₁=М, т.к. М – точка частного положения, принадлежащая плоскости π₁).
2. Найти точку пересечения фронтальных следов — это точка N (её проекции N₁ и N₂, при этом N₂=N, т.к. N – точка частного положения, принадлежащая плоскости π₂).
3. Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М₁N₁ и М₂N₂.

МN – линия пересечения плоскостей.

Упражнение

Задана плоскость σ = ΔАВС, плоскость α – горизонтально- проецирующая (α⊥π₁) ⇒α₁ – горизонтальный след плоскости (Рисунок 3.19). Построить линию пересечения этих плоскостей.

Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K₁ и L₁ , на пересечении горизонтального следа (α₁) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А₁В₁ и A₁C₁. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K₂ и L₂ на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K₁ и L₁; K₂ и L₂. Линия пересечения заданных плоскостей построена.

Алгоритм решения задачи:

left.begin{array}{l}ABcapsigma=K\ACcapsigma=L\end{array}right} left.begin{array}{l}Rightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\end{array}right.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

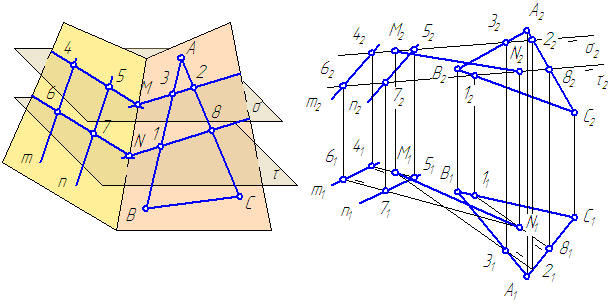
Заданы плоскости α  = m//n и плоскость σ = ΔАВС (Рисунок 3.20). Построить линию пересечения заданных плоскостей. Решение:

1. Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
2. В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π₂; τ⊥π₂.
3. Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:

— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7); — результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).

1. Прямые  (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях σ и β, то есть на прямой пересечения этих плоскостей;
2. Аналогично находим точку N, общую для плоскостей  σ и β.
3. Соединив точки M и N, построим прямую пересечения плоскостей σ и β.

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи:

left.begin{array}{l}alphacapsigma=(4-5)\betacapsigma=(3-2)\end{array}right}\left.begin{array}{l}alphacaptau=(6-7)\betacaptau=(1-8)\end{array}right}left.begin{array}{l}(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\end{array}right}rightarrow\left.begin{array}{l}M_1N_1\M_2N_2\end{array}right}Rightarrowalphacapbeta=MN

Упражнение

Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Решение.

Проведём перпендикуляр CD к плоскости  σ – C₂D₂⊥σ₂ (на основании теоремы о проецировании прямого угла).

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Задана плоскость α = ΔАВС и точка K вне плоскости α. Требуется построить плоскость β⊥α, проходящую через точку K. Алгоритм решения (Рисунок 3.23):

1. Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС;
2. Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости: если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b₂⊥f₂; b₁⊥h₁;
3. Задаём плоскость β любым способом, например, β = a∩b, таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость  α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

Рисунок 3.24

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

Рисунок 3.25

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

Рисунок 3.26

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

Рисунок 3.27

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

Рисунок 3.28

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Плоскость в
пространстве может быть задана следующими
способами:

• тремя
  точками, не лежащими на одной прямой;

• прямой
  и точкой, не лежащей на этой прямой;

• двумя
  параллельными прямыми;

• двумя
  пересекающимися прямыми;

• любой
  плоской фигурой.

Следует
отметить, что минимально необходимое
число точек для задания плоскости —
три, поэтому при любых способах задания
плоскости можно выделить эти три точки,
не лежащие на одной прямой.

Построение
проекций плоскости.
Для задания плоскости на чертеже
достаточно построить проекции точек,
прямых или фигур, определяющих данную
плоскость.

Например,
на рис. 3.1 положение плоскости в
пространстве определяют: любые три
точки (А,В,С; A,C,D; A,B,D; B,C,D А,В,Е;
В,С,Е C,D,E),
любой треугольник (ABC, ACD, ABD, BCD,
ABE, ВСЕ, CDE), две
параллельные прямые АВ
и CD,
две пересекающиеся прямые АС
и BD.

Изменение
положения в пространстве любой точки
или прямой, принадлежащей плоскости,
приведет к изменению положения в
пространстве этой плоскости.

с’

с’

Рис. 3.1

Рис. 3.2

Плоскую
фигуру можно построить из любого числа
точек, но при этом необходимо помнить,
что все диагонали плоской фигуры должны
пересекаться, а точки пересечения
проекций диаго­налей должны лежать
на одной линии связи.

Трапеция
ABCD на рис. 3.1
является плоской, так как ее диагонали
АС и BD
пересекаются в точке Е.

Подняв
точку В
выше, получим трапецию ABXCD
(рис. 3.2), которая не является плоской,
так как ее диагонали АС
и BD не
пересекаются (АС и BXD —
скрещивающиеся прямые) и точки пе­ресечения
их проекций не лежат на одной линии
связи.

Положение
плоскости относительно плоскостей
проекций. Плоскость
в пространстве может занимать
общее положение,
т. е. положение, при котором она не
параллельна и не перпендикулярна ни
одной из плоскостей проекций.

Плоскость,
перпендикулярная одной из плоскостей
проекций, называется проецирующей.

Плоскость,
параллельная одной из плоскостей
проекций, будет перпендикулярной
(проецирующей) к двум другим плоскостям
проекций, что очевидно из расположения
трех взаимно-пер­пендикулярных
плоскостей проекций системы параллельного
пря­моугольного проецирования.
Плоскости, параллельные одной из
плоскостей проекций, называются также
плоскостями уровня.

Плоскость
общего положения, как и прямая линия,
может быть восходящей и нисходящей.
Если точки плоскости поднимаются,
удаляясь от наблюдателя, плоскость
называется восходя­щей,
если же они опускаются, — нисходящей.

На
рис. 3.3, а
точки плоскости, заданной треугольником
ABC, удаляясь от наблюдателя по прямой
BD, принадлежащей
этой плоскости, от точки В
к точке D,
поднимаются вверх, следова­тельно,
данная плоскость является восходящей.
Плоскость EFH на
рис. 3.3, б — нисходящая, так как ее точки,
удаляясь от наблю­дателя по прямой
FG, опускаются
вниз.

Проецирующие
плоскости в плоскостях проекций, к
которым они перпендикулярны, вырождаются
в прямую линию.

На
рис. 3.4, а
плоскость треугольника ABC,
перпендикулярная горизонтальной
плоскости проекций, называется
горизонтально-проецирующей,
плоскость треугольника DEF
на рис. 3.4, б, перпендикулярная
фронтальной плоскости проекций, —
фронтально-проецирующей,
а плоскость треугольника KLM
на рис. 3.4, в,
перпендикулярная профильной плоскости
проекций, — профилъно-проецирующей.

Все
линии, углы между ними, а также фигуры,
лежащие в плос­кости уровня, проецируются
на плоскость проекций в натураль­ном
виде. При этом плоскости уровня могут
быть горизонтальными, фронтальными
и профильными.

Рис. 3.3

Горизонтальная
плоскость уровня, перпендикулярная
(проецирующая) фронтальной и профильной
плоскостям проекций, проецируется на
них в виде прямой линии, параллельной
осям проекций (рис. 3.5).

Фронтальная
плоскость уровня, перпендикулярная
(проецирующая) горизонтальной и профильной
плоскостям проекций, проецируется на
них в виде прямой линии, параллельной
осям проекций (рис. 3.6).

Профильная
плоскость уровня, перпендикулярная
(проецирующая) фронтальной и горизонтальной
плоскостям проекций, проецируется на
них в виде прямой линии, параллельной
осям проекций (рис. 3.7).

Рис. 3.6

Взаимное
положение точки и прямой относительно
плоскости.

Точка может
принадлежать плоскости или лежать вне
ее.

Точка принадлежит
плоскости, если находится на любой
прямой, лежащей в этой плоскости.

На
рис. 3.8 точки А, В, С, D, Ей F принадлежат
плоскости, образованной треугольником
ЛВС, так как
они лежат на прямых, образующих данный
треугольник.

Точка не принадлежит
плоскости, если не находится на любой
прямой, принадлежащей этой плоскости.

На
чертеже, приведенном на рис. 3.9, видно,
что через точку D
нельзя провести никакую прямую, которая
принадлежала бы плоскости треугольника
ЛВС.

Прямая может лежать
в плос­кости, быть параллельна
плоско­сти или пересекать плоскость
в какой-либо точке.

Прямая
принадлежит плоско­сти, если две ее
любые точки лежат в этой плоскости.

На
рис. ЗЛО прямая BD
принадлежит плоскости, образованной
треугольником
ЛВС,
так как точки
В и D
лежат в этой плоскости.

Из
множества прямых, принадлежащих
плоскости, выделяют линии, параллельные
плоскостям проекций. Эти линии,
характеризующие направление плоскости
в пространстве, называются
главными линиями плоскости: горизонталь
(параллельна горизонтальной плоскости
проекций), фронталь
(параллельна фронтальной плоскости
проекций) и профильная
прямая
(параллельна профильной плоскости
проек­ций).

В
плоскости, образованной треугольником
ABC на рис. 3.11, линия AD
— горизонталь, АЕ
— фронталь, a BF —
профильная прямая.

в»

Рис. 3.8

Прямая параллельна
плоскости, если она параллельна любой
прямой, лежащей в этой
плоскости.

Рис. 3.11

На
рис. 3.12 прямая FG
параллельна прямой DE,
лежащей в плоскости треугольника
А ВС (так как
проекция F»G»
параллельна проекции D»E»,
а проекция F’G’
параллельна проекции D’E’),
следовательно, прямая FG
параллельна плоскости ЛВС.

Прямая пересекает
плоскость, если у них имеется единственная
совместная точка.

На
рис. 3.13 прямая FG
пересекает прямую DE,
лежащую в плоскости треугольника
ЛВС, в точке
К, следовательно,
прямая

в»

FG
пересекает плоскость треугольника
ABC в точке
К, принадлежащей
плоскости ЛВС.

Взаимное
положение двух плоскостей.
Плоскости могут сливаться в пространстве,
быть параллельными или пересекаться.

Плоскости
сливаются, если
две прямые, принадлежащие одной плоскости,
одновременно принадлежат и другой
плоскости.

На
рис. 3.14 плоскости, образованные
параллелограммом ABCD
и треугольником EFG,
сливаются, так как на плоскостях проекций
видно, что любые две прямые одной
плоскости принадлежат и другой плоскости.

Плоскости
параллельны
между собой, если две пересекающиеся
прямые, лежащие в одной плоскости,
соответственно параллельны двум
пересекающимся прямым, лежащим в другой
плоскости.

На
рис. 3.15 пересекающиеся прямые А
В и ВС,
лежащие в плоскости параллелограмма
ABCD, соответственно
параллельны пересекающимся прямым
EF и FG,
лежащим в плоскости треугольника
EFG.

Плоскости
пересекаются,
если имеется единственная прямая линия,
принадлежащая и той, и другой плоскости.

На
рис. 3.16 прямая KL
принадлежит и плоскости параллелограмма
ABCD, и плоскости
треугольника проекций EFG.
При этом любые другие прямые, лежащие
в плоскости параллелограм­ма, не
принадлежат плоскости треугольника, и
наоборот.

Построение проекций плоских фигур (т. е. фигур, все точки которых лежат в одной плоскости, например, квадрата, круга, эллипса и т. д.) сводится к построению проекций ряда точек, отрезков прямых и кривых линий, образующих контуры проекций фигур. Зная координаты вершин, например, треугольника, можно построить проекции этих точек, затем проекции сторон и получить таким образом проекции фигуры.

Чертежи, содержащие проекции треугольника, уже встречались (например, рис. 110, 112 и др.). Если сравнить между собой рис. 110 и 112, то можно заметить, что на рис. 110 одна из проекций, положим фронтальная, изображает «лицевую» сторону треугольника, а горизонтальная — «тыльную». А на рис. 112 каждая из проекций изображает треугольник с одной и той же его стороны. Признаком может служить порядок обхода вершин: на рис. 110 для фронтальной проекции по часовой стрелке (считая от А» к С»), а для горизонтальной — против часовой стрелки; на рис. 112 для обеих проекций обход в одном направлении — в данном случае по часовой стрелке.

В общем случае в системе π₁, π₂, π₃ проекции какого-либо многоугольника представляют собой также многоугольники с тем же числом сторон; при этом плоскость этого многоугольника является плоскостью общего положения. Но если в системе π₁, π₂ обе проекции, например, треугольника представляют собой треугольник, то его плоскость может оказаться плоскостью общего положения или профильно-проецирующей: на рис. 112 — плоскость общего положения, а на рис. 127 — профильно-проецирующая. Определителем служит, как было сказано на с. 52 в пояснении к рис. 127, горизонталь (или фронталь): если ее проекции на π₁ и π₂ взаимно параллельны, то плоскость профильно-проецирующая (рис. 127); если же не параллельны, то плоскость общего положения (например, рис. 112, 115, слева).

Если проекция многоугольника на π₁ или на π₂ представляет собой отрезок прямой, то плоскость этого многоугольника соответственно перпендикулярна к π₁ или к я2. Например, на рис. 123 плоскость треугольника горизонтально-проецирую- щая, на рис. 125 — фронтально-проецирующая.

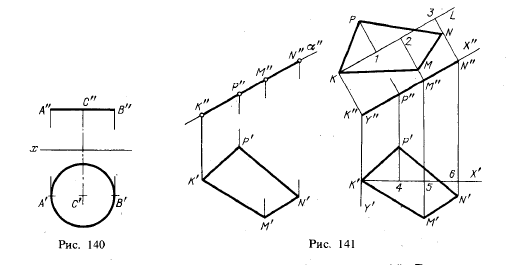
Фигура, расположенная параллельно плоскости проекций, проецируется на нее без искажения. Например, все элементы треугольника CDE, изображенного на рис. 133, проецируются на пл. π₂ без искажения; круг, изображенный на рис. 140, проецируется на пл. π₁ без искажения. —

Если же плоскость фигуры не параллельна плоскости проекций, то для определения натурального вида (т. е. без искажения) этой фигуры применяют способы, указанные далее, в главе V. Конечно, можно было бы и теперь, не зная еще этих способов, построить, например, натуральный вид треугольника, изображенного на рис. 112, определив длину каждой его стороны как длину отрезка (см. § 13) и затем построив треугольник по найденным отрезкам. Вместе с тем определились бы и углы данного треугольника. Так поступают, например, при построении развертки

боковой поверхности пирамиды, призмы и др. (см. далее § 44). Если же многоугольник расположен в проецирующей плоскости, то можно построить его натуральный вид так, как показано на рис. 141.

Положим, требуется определить натуральный вид четырехугольника KPNM, расположенного в фронтально-проецирующей пл. α. Тогда, как это показано на рис. 141 справа, можно взять в плоскости фигуры две оси прямоугольных координат с началом хотя бы в точке К; ось абсцисс {К»Х», К’Х’) параллельно пл. π₂, ось ординат перпендикулярно к π₂ (проекции этой оси K»Y», K’Y’), провести прямую KL (это можно сделать, например, параллельно К»Х») и отложить на ней К1 = = К»Р», К2 = К»М», КЗ = K»N». Затем на перпендикулярах к прямой KL в точках 1,2 и 3 отложим отрезки Р1 = Р’4, М2 = М’5 и N3 = N’6. Построенный таким образом четырехугольник KMNP представляет собой натуральный вид заданного.

При решении многих задач вопрос о том, какое положение занимает плоская фигура относительно плоскостей проекций, приобретает существенное значение. В качестве примера рассмотрим вопрос о построении четырех замечательных точек треугольника.

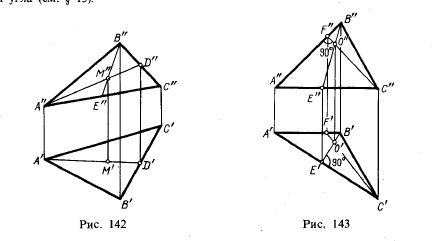
Так как делению отрезка прямой в пространстве пополам отвечает такое же деление проекций этого отрезка (см. § 12), то построение точки пересечения медиан треугольника ¹) может быть произведено на чертеже во всех случаях непосредственно. Достаточно (рис. 142) провести медианы на каждой из проекций треугольника, и точка пересечения его медиан будет определена. При этом можно ограничиться построением обеих проекций лишь одной из медиан (например, A’D’ и A»D») и одной проекции второй медианы (например, В»E»); в пересечении A»D» и В»Е’ получаем точку М», а по ней находим на A’D’ точку М’.

Можно было бы также, построив лишь одну из медиан треугольника, найти на ней точку М на основании известного из геометрии свойства этой точки (она делит каждую медиану в отношении 2 : 1).

Построение точки пересечения трех высот треугольника ²) и точки перпендикуляров к сторонам треугольника, проведенных через их середины ³), связано с проведением взаимно перпендикулярных прямых.

¹)Точка пересечения медиан есть центр тяжести треугольника.

²)Ортоцентр треугольника.

³)Центр описанной окружности.

В § 15 были указаны условия, при которых перпендикулярные отрезки в пространстве имеют своими проекциями также перпендикулярные отрезки, Если плоскость треугольника параллельна плоскости проекций (например, треугольник CDE на рис. 133), то, опустив перпендикуляры из точек С», D» и Е» на противоположные им стороны, получаем проекции высот треугольника, Но в треугольнике общего положения так поступить нельзя,

В частном случае, когда одна сторона треугольника параллельна пл. π₁; а другая параллельна пл, π₂ (рис, 143), проведя C»F» перпендикулярно к А»В» и В’Е’ перпендикулярно к А’С’, получаем в пространстве CF⊥АВ и BE⊥АС; точка пересечения высот оказалась построенной без каких-либо особых приемов.

В самом же общем случае для проведения на проекционном чертеже перпендикулярных линий приходится прибегать к особым приемам, которые будут изложены дальше.

Построение точки пересечения биссектрис треугольника¹) также может быть произведено непосредственно лишь в частных случаях расположения треугольника относительно плоскостей проекций. Это объясняется тем, что деление пополам проекции какого-либо угла отвечает его делению пополам в пространстве только в том случае, если стороны данного угла одинаково наклонены к той плоскости проекций, на которой производится деление пополам проекции угла (см. § 15).

При построении проекций какого-либо многоугольника необходимо обратить внимание на то, чтобы не нарушалось условие нахождения всех точек данной фигуры в одной плоскости

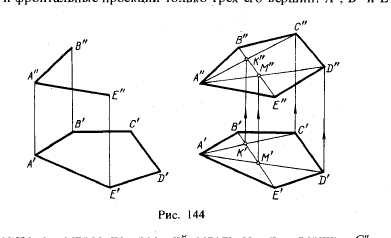
На рис. 144 даны полностью горизонтальная проекция некоторого пятиугольника ABCDE и фронтальные проекции только трех его вершин: А», В» и Е», Справа

на рис, 144 показано построение проекций остальных двух вершин, С» и D», пятиугольника, Чтобы точки С и D лежали в плоскости, определенной тремя точками А.

¹) Центр вписанной окружности.

В и Е, необходимо, чтобы они находились на прямых, лежащих в этой плоскости, Этими прямыми являются диагонали АС, AD и BE, горизонтальные проекции которых мы можем построить. На фронтальной проекции пятиугольника мы можем провести лишь В»Е», Но в плоскости пятиугольника лежат точки пересечения диагоналей К и М, горизонтальные проекции которых (К’ и М’) имеются, а фронтальные проекции получаются сразу, так как они должны лежать на В»Е». По двум точкам строятся фронтальные проекции и остальных двух диагоналей А»К» и А»М», на них должны лежать точки С» и D», которые определяются по их горизонтальным проекциям.

Круг, плоскость которого параллельна какой-либо плоскости проекций, проецируется на эту плоскость без искажения (см, рис, 140, где круг взят в горизонтальной плоскости). Если плоскость круга расположена перпендикулярно к плоскости проекций, то на эту плоскость круг проецируется в виде отрезка прямой, равного диаметру круга,

Но если круг расположен в плоскости, составляющей с плоскостью проекций какой-либо острый угол φ, то проекцией круга является фигура, называемая эллипсом.

Эллипсом называется также кривая, ограничивающая эллипс-фигуру: если эллипс-фигура является проекцией круга, то эллипс-линия является проекцией окружности. В дальнейшем изложении, говоря об эллипсе, будем подразумевать проекцию окружности.

Эллипс относится к числу кривых, называемых кривыми второго порядка. Уравнения таких кривых в декартовых координатах представляют собой уравнения второго порядка. Кривая второго порядка пересекается с прямой линией в двух точках. Далее мы встретимся еще с параболой и гиперболой, тоже кривыми второго порядка.

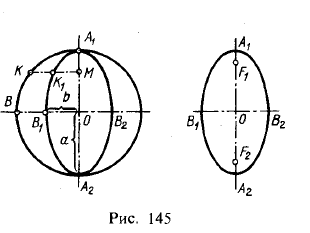
Эллипс можно рассматривать как «сжатую» окружность. Это показано на рис, 145, слева, Положим, что на радиусе ОВ отложен отрезок ОВ₁ длиной b, причем b<а (т, е, меньше радиуса окружности). Если теперь взять на окружности какую-либо точку K и, проведя из K перпендикуляр на A₁A₂, отметить на KM точ-

ку так, чтобы МК₁:МК = b:а, то эта точка K₁ будет принадлежать эллипсу. Так можно преобразовать каждую точку окружности в точку эллипса, соблюдая одно и то же отношение b:а. Окружность как бы равномерно сжимается; линия, в которую при этом преобразуется окружность, является эллипсом. Отношение b:а называется коэффициентом сжатия эллипса. Если b приближается к а, то эллипс расширяется и при b = а превращается в окружность.

Напомним (из курса черчения средней школы), что

1. отрезок A₁,A₂ = 2а называется большой осью эллипса;
2. отрезок B₁,B₂ — 2b называется малой осью эллипса;
3. большая и малая оси взаимно перпендикулярны;
4. точка пересечения осей называется центром эллипса;
5. отрезок прямой между двумя точками эллипса, проходящий через центр эллипса, называется его диаметром;
6. точки А₁, A₂, В₁, В₂ называются вершинами эллипса;
7. эллипс симметричен относительно его осей и относительно его центра;
8. эллипс есть геометрическое место точек, сумма расстояний которых до двух заданных точек F₁ и F₂ (рис, 145, справа) имеет одно и то же значение 2а (размер большой оси).

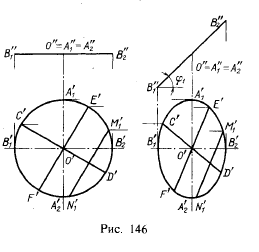
Из рассмотрения рис. 146 следует, что при повороте окружности вокруг диаметра А₁A₂ на угол φ₁ этот диаметр, параллельный пл. π₁, сохраняет в горизонтальной проекции свою величину и становится большой осью эллипса (см. рис. 146, справа). Диаметр же В₁, В₂ повернутый на угол φ₁ к пл. π₁, проецируется на нее с сокращением:

B’₁B’₂=B»₁B»₂cosφ₁

Это соответствует отношению осей эллипса, т. е. его коэффициенту сжатия.

Если в окружности провести какие-либо два взаимно перпендикулярных диаметра, то в проекции, представляющей собой эллипс (рис. 146, справа), проекции таких диаметров окружности оказываются диаметрами эллипса, называемыми сопряженными. Если в окружности (рис. 146, слева) провести, например, хорду M’₁N’₁, параллельную диаметру E’F’, то диаметр C’D’ разделит эту хорду (и все хорды, ей параллельные) пополам. Очевидно, что и в эллипсе сохранится это свойство (см. рис. 146, справа): диаметр C’D’ делит хорду M’₁N’₁, параллельную диаметру E’F’, сопряженному с CD’, пополам. Но именно такие два диаметра эллипса, из которых каждый делит пополам хорды, параллельные другому, являются сопряженными.

Сопряженные диаметры эллипса не перпендикулярны один к другому; исключение составляют оси эллипса, также являющиеся парой сопряженных диаметров.

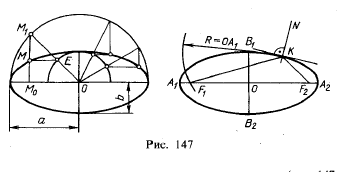
Напомним, как производится построение эллипса по его осям (рис. 147, слева). Построение выполняется при помощи двух концентрических окружностей, проведенных радиусами а (большая полуось) и b (малая полуось). Если провести какой-либо радиус ОМ₁ и прямые М₁М₀ и ЕМ, параллельные малой и большой осям эллипса, то при пересечении этих прямых получится точка М, принадлежащая эллипсу. Действительно,

Проводя ряд радиусов и повторяя указанное построение, получаем ряд точек эллипса.

Построив какую-нибудь точку эллипса, можно построить еще три точки, расположенные симметрично найденной относительно осей эллипса или его центра.

На рис. 147 справа показано построение фокусов эллипса: засекая из точки В₁ большую ось дугой радиуса, равного большой полуоси ОА₁, получаем точки F₁ и F₂ — фокусы эллипса. Построив угол F₁KF₂, где К — любая точка эллипса, проводим в нем биссектрису и перпендикулярно к ней в точке К касательную к эллипсу. Прямая KN, перпендикулярная к касательной, является нормалью ¹) к эллипсу в точке К.

¹) От normalis (лат.) — прямолинейный.

Как построить оси эллипса, если известны его сопряженные диаметры?

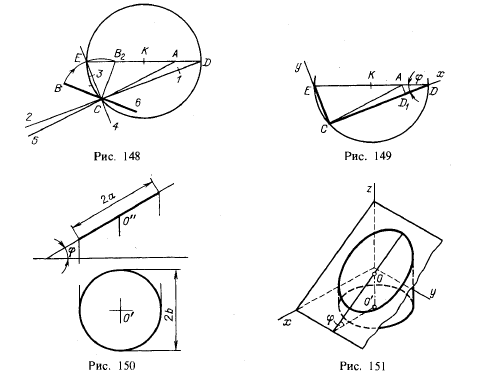
Пусть получены сопряженные полудиаметры С А и СВ (рис. 148). Для построения осей эллипса:

1. один из сопряженных полудиаметров, например СВ, поворачиваем на угол 90° по направлению к другому (до положения СВ₂);
2. проводим отрезок АВ₂ и делим его пополам;
3. из точки К проводим окружность радиусом КС;
4. прямую, определяемую отрезком АВ₂, продолжаем до пересечения с этой окружностью в точках D и Е;
5. проводим прямую DC, получаем направление большой оси эллипса;
6. проводим ЕС — направление малой оси эллипса;
7. откладываем C₁ = АЕ — большая полуось;
8. откладываем СЗ = AD — малая полуось;
9. откладываем С2=С1, С4=СЗ, С5=СА, Сб = СВ.

Эллипс может быть проведен через восемь точек 1, А, 3, В, 2, 5, 4 и 6 или построен по большой и малой осям, как показано на рис. 147.

Итак, проведя прямые CD и СЕ, мы получили направления большой и малой осей эллипса; точка А, принадлежащая эллипсу, делит диаметр ED на два отрезка, из которых один (АЕ) равен большой полуоси этого эллипса, а другой (AD) — малой полуоси. Если (рис. 149)

взять оси координат х и у соответственно по прямым CD и СЕ и из точки А провести перпендикуляр AD к прямой CD, то координаты точки А могут быть выражены следующим образом:

х_a=АЕcosφ, у_a = ADsinφ.

Отсюда

Это уравнение эллипса, у которого АЕ — большая полуось, a AD — малая полуось.

———-

На рис. 146 было показано построение горизонтальной проекции окружности, расположенной в фронтально-проецирующей плоскости, наклоненной к пл. π₁. Пусть теперь в такой плоскости лежит эллипс с полуосями а и Ь. Его проекцией иногда может оказаться окружность с диаметром, равным малой оси эллипса: это будет тогда, когда для угла между плоскостью, в которой лежит эллипс, и пл. π₁ имеет место соотношение cos? =b/a (рис. 150).
Полученная окружность будет служить проекцией ряда эллипсов, если изменять угол φ и размер a, оставляя b неизменным. Представим себе прямой круговой цилиндр с вертикальной осью (рис. 151); наклонные сечения этого цилиндра будут эллипсами, малая ось которых равна диаметру цилиндра.

Вопросы к §§20-21

1. Как изображается на чертеже фронгально-проецирующая плоскость, проведенная через прямую общего положения?
2. Как построить проекции центра тяжести в заданном чертеже треугольника?
3. Что могут представлять собой проекции круга в зависимости от положения его плоскости относительно плоскости проекций?
4. Можно ли рассматривать эллипс как «сжатую» окружность?
5. Что такое коэффициент сжатия эллипса?
6. Имеет ли эллипс: а) оси симметрии, б) центр симметрии?
7. Какие диаметры эллипса называются: а) осями, б) сопряженными диаметрами?
8. Как по заданным сопряженным диаметрам эллипса построить его оси?