Задачи на растворы, смеси и сплавы относятся к традиционным арифметическим и алгебраическим задачам, решение которых нередко вызывает трудности. Для решения таких задач нужно уметь рассуждать и уметь решать задачи на проценты и дроби, на составление уравнений и систем уравнений.
Давайте, сначала, определим, что это за задачи на смеси и сплавы. Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты, а для этого надо четко понимать, что:
— масса раствора = масса воды + масса соли;
— масса сплава равна сумме масс металлов, входящих в этот сплав;
— масса смеси равна сумме масс компонентов этой смеси.
При решении задач на смеси, растворы и сплавы, мы используем их общее свойство, которое заключается в том, что масса смеси, раствора или сплава равна сумме масс их компонентов.
Введем понятие концентрации или процентного содержания вещества в растворе (смеси, сплаве).
Концентрация соли или процентное содержание соли в растворе — это отношение массы соли к массе раствора, записанное в виде процентов:
K=(mc/M)*100%,
где mс — масса соли, M – масса всего раствора, К – концентрация (процентное содержание) соли.
Концентрация вещества или процентное содержание вещества в смеси — это отношение массы вещества к массе смеси, записанное в виде процентов: K=(mв/M)*100%, где mв — масса вещества, M – масса всей смеси, К – концентрация (процентное содержание) вещества
Концентрация вещества или процентное содержание вещества в сплаве — это отношение массы вещества к массе сплава, записанное в виде процентов : K=(mв/M)*100%, где mв — масса вещества, M – масса всего сплава, К – концентрация (процентное содержание) вещества.
Пример раствора. Возьмем 180 грамм воды и добавим в воду 20 грамм соли. Получим раствор, его масса равна 180 + 20 = 200 грамм. Определим концентрацию соли (процентное содержание соли) в растворе: К= (20/(180+20))*100%=10% . Тогда процентное содержание воды 90%. (100%-10%=90%). Процентное содержание воды можно определить и так: Кв=(180/(180+20))*100%=90%. Результаты запишем в виде таблицы.
| соль | 20гр | 10% |
| вода | 180гр | 90% |
| раствор | 200гр | 100% |
Пример смеси. Возьмем и перемешаем одно ведро цемента с тремя ведрами песка. Получим смесь цемента с песком, её масса равна 1 + 3 = 4 (единиц массы). Определим концентрацию (процентное содержание) цемента в смеси : К=(1/(1+3))*100%=25%.. Концентрация (процентное содержание) песка в смеси 100%-25%=75%.
Результаты запишем в виде таблицы.
| цемент | 1 ведро | 25% |
| песок | 3ведра | 75% |
| смесь | 4 ведра | 100% |
Пример сплава. Сплав цинка и меди массой 600 гр. содержит 270 гр.меди. Определим концентрацию (процентное содержание) меди в сплаве:
Км= (270/600)*100%= 45%.
Концентрация (процентное содержание) цинка в смеси:
100%-45%=55%. Или Кц=((600-270)/600))*100%= 55%.
Результаты запишем в виде таблицы.
| цинк | 330 | 55% |
| медь | 270 | 45% |
| сплав | 600гр | 100% |
Масса вещества в растворе, смеси, сплаве.
Из формулы K=(m/M)*100%, где m масса вещества, М — масса всего раствора ( смеси, сплава), получим, что масса вещества в растворе находится по формуле: m=(M*K)/100%.
Например: а) Имеется 200 гр 40% раствора соли. Определите массу соли.
Решение : mc = (200*40%)/100 = 80г. Ответ: 80 г
б) Сплав меди и цинка массой 900г содержит 64% меди. Определите массу цинка в сплаве.
Решение: 1 способ. 100% — 64% = 36% цинка в смеси,
mц=(900*36%)/100%=324г.
2 способ. mм= (900*64%)/100%=576г, 900 – 576 = 324 г.
Ответ: 324г.
.
Последнее изменение: Четверг, 24 июля 2014, 21:53
Формулы для расчета процентного содержания металлов в сплаве приведены под калькулятором.
Процентное содержание металлов в сплаве
Плотность первого металла
Плотность второго металла
Точность вычисления
Знаков после запятой: 2
Процентное содержание первого металла
Процентное содержание второго металла
Расчет процентного содержания металлов в сплаве двух металлов
Пусть нам известны физические характеристики сплава, масса и плотность, их можно просто померять, и плотности металлов, составляющих сплав (например, их можно узнать из справочника).
Имеем следующие очевидные соотношения:
,
где
m — масса сплава,
V — объем сплава,
m₁ — масса первого металла,
V₁ — объем первого металла,
ρ₁ — плотность первого металла,
m₂ — масса второго металла,
V₂ — объем второго металла,
ρ₂ — плотность второго металла.
m₁, V₁, m₂, V₂ — четыре неизвестных на четыре уравнения — существует единственное решение.
Выполнив подстановки, можно получить довольно громоздкие формулы для m₁ и m₂
Процентные соотношения получим, поделив массы металлов на массу сплава.
И
ПЛОТНОСТИ СПЛАВОВ
Концентрация
— величина, определяющая содержание
компонента в смеси, растворе, сплаве.
Способы выражения концентрации различные.
В
физике концентрация – n
— это количество частиц в единице объема
; [c]
= M-3
в СИ.
По
этой формуле определяют число атомов
или молекул в единице объема, а также
концентрацию электронов, дырок и др.
Долевая
(относительная) концентрация Сm
по
массе
есть отношение массы компонента mi
к
общей массе смеси
m
.
По
этой формуле чаще всего определяют
концентрацию компонента (по массе) в
сплавах. Например, в бинарном сплаве
А10В90
содержится 10масс.% компонента А и 90масс.%
компонента В.
Атомная
(молекулярная) долевая концентрация
Сат
–
это отношение содержащегося в смеси
числа атомов (молекул) Nx
компонента
к числу атомов (молекул) всех компонентов
N
.
Мольная
долевая концентрация С
— это отношение содержащегося в смеси
числа молей х
одного
из компонентов к общему числу
молей вещества
С
х/.
Концентрации Сm
,Сат
,С
выражаются в виде дроби, либо в процентах.
Относительная концентрация Сат
чаще
всего используется для нахождения
концентрации вакансий, либо атомов
примесей. В этом случае под Nx
подразумевают
число вакансий, либо инородных атомов,
а под N–
число узлов кристаллической решетки,
либо общее число позиций, которые могут
быть заняты атомами примесей (обычно
их также приравнивают к числу узлов в
кристаллической решетке).
Молярная
концентрация С
удобна для определения концентрации
компонента в смеси газов, либо в растворе
жидкости.
Моль
раствора
М
–
количество раствора, при котором число
молей каждого компонента равно его
молярной доле
,
где
—
молярная массаi-гокомпонента.
Молярность
– число молей вещества в 1 литре раствора
(моль/л или моль/м3)
.
Мольность
– число молей вещества в 1 кг растворителя
(моль/кг)
.
Титр
– масса вещества 1 мл раствора
.
Объемная
концентрация
—отношение
объема Vx,
занимаемого компонентом к общему объему
V
системы
.
Концентрация
компонента по плотности
—
отношение массы компонентаm
к объему системы V
,
.
Согласно
системе СИ к концентрации относят
только массовую Сm
и
молярную С
концентрации. Все остальные характеристики
содержания компонента не являются
концентрациями.
При
изготовлении сплавов часто возникают
практические задачи по определению
плотности
сплавов,
атомной
Са
,
массовой Сm
и
молярной С
концентраций сплавов, а также молярной
массы сплава М.
Приведем наиболее распространенные
методы вычисления этих параметров для
бинарных и тройных сплавов.
Бинарные сплавы
Задача
№1.
Определить
относительное содержание компонентов
и
по массе, если известны плотности
компонентови смеси
,
,
,
,
,
,
,
из
этой системы находим
или
, откуда
,
следовательно,
.
Тогда
.
(23.1)
Аналогично ,
(23.2)
или , (или
100%).
Например,
для сплава олово-свинец с плотностью
=102/см3
имеем
.
Задача
№ 2.
Найти
плотность
сплава, если известны массыm1,
m2
и
плотности
и
компонентов
,
,
,
,
,

. (23.3)
Например,
для сплава олова и свинца при
и
имеем
.
Задача
№ 3.
Найти
плотность
для сплава при заданных концентрациях
и
компонентов и их плотностях
и
.

.
(23.4)
Например,
для сплава олова с свинцом при
получим
.
Задача
№ 4.
Найти
массу m2
второго
компонента в сплаве при известной массе
m1
первого компонента и его массовой
концентрации
.

(23.5)
Задача
№ 5.
Найти
атомный процент
,
компонентов
сплава, если известны их массы и
молекулярные массы.
;


(23.7)
Задача
№ 6.
Найти
молярный процент
компонентов сплава, если известны их
молярные массыМ1,
М2
и
массы компонентов m1
и m2..
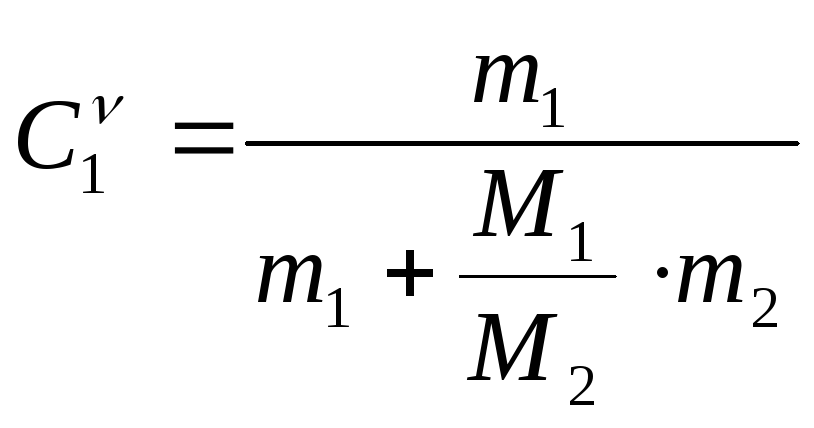

(23.9)
Задача
№ 7.
При
известных атомных концентрациях
компонентов
и
найти массовые концентрации
и
.


(23.11)
Задача
№ 8.
При
известных массовых концентрациях
и
компонентов найти атомные концентрации
компонентов.

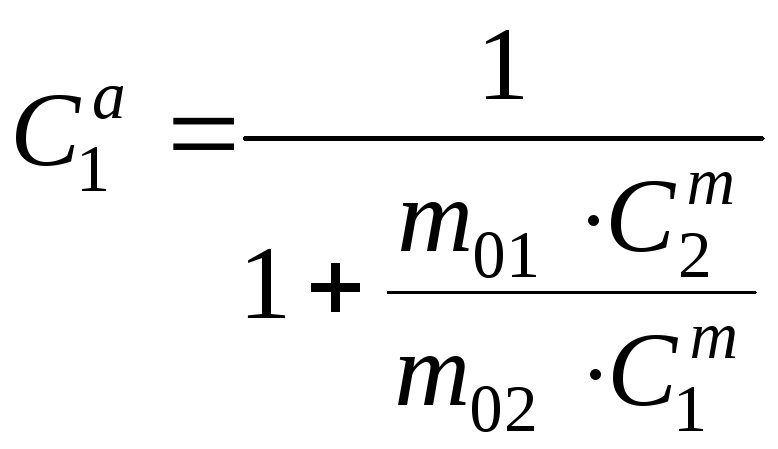

(23.13)
Задача
№ 9.
По
массовым концентрациям
и
найти молярные концентрации
и
.

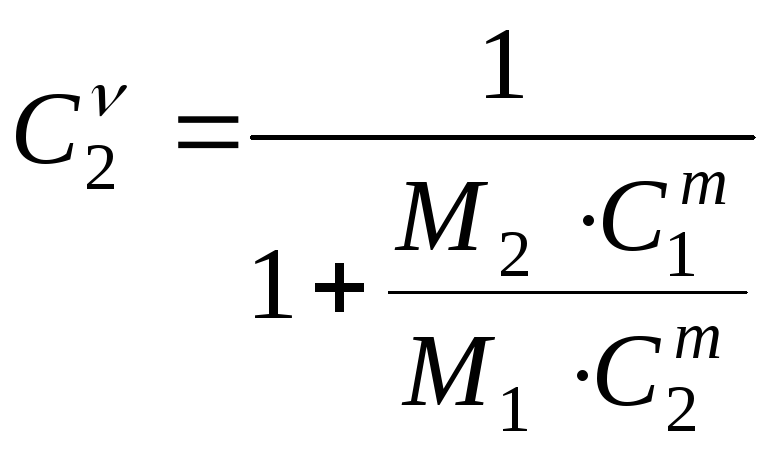
(23.15)
Задача
№ 10.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
Правило 1. Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь.
Решение задач на понятия «процентное содержание», «концентрация», «%-й раствор».
Процентное содержание. Процентный раствор.
Пример. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.
Решение.10 . 0,15 = 1,5 (кг) соли.
Ответ: 1,5 кг.
Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором, например, 15%-й раствор соли.
Пример. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение: Процентное содержание вещества в сплаве — это часть, которую составляет вес данного вещества от веса всего сплава.
1) 10 + 15 = 25 (кг) — сплав;
2) 10/25 . 100% = 40% — процентное содержание олова в сплаве;
3) 15/25 . 100% = 60% — процентное содержание цинка в сплаве;
Ответ: 40%, 60%.
Концентрация.
Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.
Пример. Концентрация серебра в сплаве 300 г составляет 87%. Это означает, что чистого серебра в сплаве 261 г.
Решение. 300 . 0,87 = 261 (г).
В этом примере концентрация вещества выражена в процентах.
Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.
Сумма концентраций всех компонент, составляющих смесь, равна 1.
Если известно процентное содержание вещества, то его концентрация находится по формуле: К=р/100% к — концентрация вещества; р — процентное содержание вещества (в процентах).
Пример. Имеется 2 сплава, в одном из которых, содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
Решение: Пусть к 20 кг первого сплава нужно добавить х кг второго сплава. Тогда получим (20 + х) кг нового сплава. В 20 кг первого сплава содержится 0,4 . 20 = 8 (кг) серебра, в х кг второго сплава содержится 0,2х кг серебра, а в (20+х) кг нового сплава содержится 0,32 . (20+х) кг серебра. Составим уравнение:
8 + 0,2х = 0,32 . (20 +х); х = 13 1/3.
Ответ: 13 1/3 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.
Пример. К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Решение. Пусть добавили х л 5%-ного раствора соли. Тогда нового раствора стало (15 + х) л, в котором содержаться 0,8 . (15 + х) л соли. В 15 л 10%-ного раствора содержится 15 . 0,1 = 1,5 (л) соли, в х л 5%-ного раствора содержится 0,05х (л) соли.
Составим уравнение.
1,5 + 0,05х = 0,08 . (15 + х);
х = 10.
Ответ: добавили 10 л 5%-ного раствора



