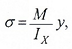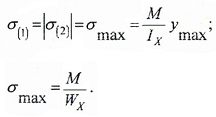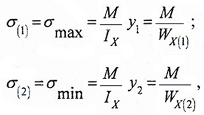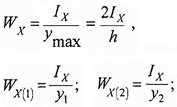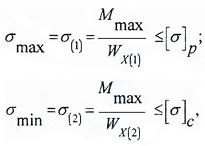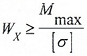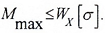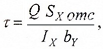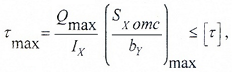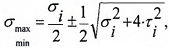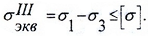
13. Изгиб бруса
В случаях, когда длина балки много больше высоты и ширины сечения ( h ), возникающие нормальные напряжения при изгибе значительно больше касательных напряжений. Вследствие этого касательными напряжениями в таких случаях можно пренебречь.
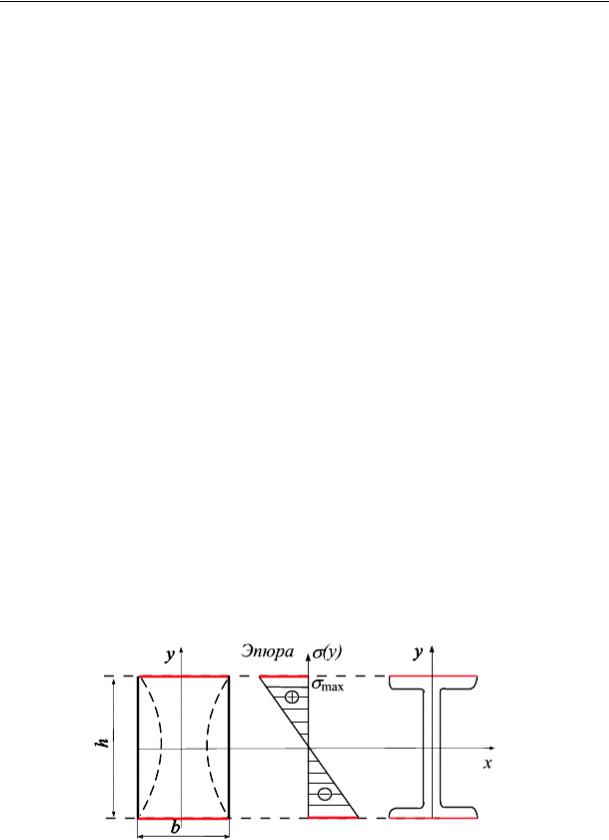
Балки из материалов, одинаково сопротивляющихся растяжению и сжатию (сталь), проектируются симметричными относительно оси x (рис. 13.10, а).
Условие прочности для балок из материалов, одинаково сопротивляющихся растяжению и сжатию (сталь), имеет вид
|
σmax = |
Mmax |
ymax = |
Mmax |
≤[σ], |
(13.13) |
|
Jx |
Wx |
где Mmax – наибольший по абсолютному значению изгибающий мо-
|
мент от нагрузок; [σ] – допускаемое напряжение; W = |
Jx |
– момент |
|
x |
ymax |
|
сопротивления поперечного сечения балки.
Характер распределения σ(y) для симметричных сечений представлен на рис. 13.10, а, б.
а б в
Рис. 13.10
285

Mmax
И. В. Богомаз. Механика
Из эпюры σ(y) видно, что материал, расположенный у нейтральной оси, нагружен очень мало (рис.13.10, б). В целях экономии и снижения веса балок следует выбирать такие формы сечения, чтобы большая часть материала была удалена от нейтральной оси (на рис. 13.10, а пунктирные линии) – рациональная форма. Двутавровое сечение более экономично, чем прямоугольное (рис. 13.10, а, в).
Возьмем две одинаковые прямоугольные балки, закрепленные одним концом в неподвижной опоре с разной геометрией (рис. 13.11) и приложим к свободным концам силу F. Возможные разрушения могут произойти в опасном сечении, совпадающем с заделкой, изгибающий момент Mx, создаваемый силой F в обеих балках, равен
= F и не зависит от закрепления.
В первом варианте (рис. 13.11, а) балка изогнется при сравнительно небольшой величине силы F. Во втором варианте (рис. 13.11, б) для достижения того же результата понадобится значительно большая сила. В первом случае деформируемые слои материала балки в сечении ближе расположены к нейтральной оси х, а во втором – дальше. Из предыдущего материала известно, что нейтральная ось (нулевая линия) – это геометрическое место точек поперечного сечения, в которых нормальные напряжения равны нулю.
Поскольку основное сопротивление изгибу оказывают наиболее удаленные от нейтральной линии слои материала, целесообразно при изгибе ориентировать сечения балки так, чтобы в плоскости изгиба лежали точки сечения, наиболее удаленные от нейтральной оси. Следовательно, сечение на рис. 13.11, б, более рационально расположено, чем сечение на рис. 13.11, а.
Рис. 13.11
286
13. Изгиб бруса
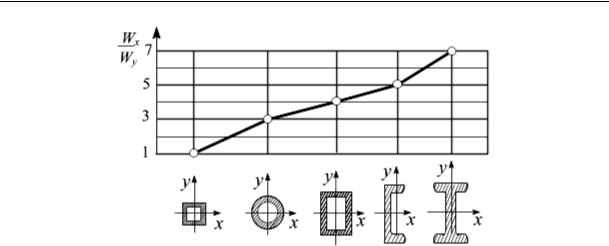
Рис.13.12
Способность поперечного сечения сопротивляться деформации изгиба характеризуется осевым моментом сопротивления изгибу Wx Величина Wx зависит от формы и размеров поперечного сечения и от его ориентации по отношению к изгибающей силе. На рис. 13.12 приведена диаграмма соотношения моментов сопротивления Wx и Wy для некоторых профилей проката, широко применяющихся в практике.
Из диаграммы видно, что отношение Wx / Wy колеблется в пределах от 1 до 7. В связи с этим для рационального использования материала в строительных конструкциях с нагрузками в плоскости zy профиль проката следует располагать рационально, т. е. так, чтобы момент сопротивления относительно плоскости изгиба yz был макси-
мальным (Wxmax ), а плоскости xy – минимальным (Wymin ). Для стан-
дартных профилей типа двутавров и швеллеров величины осевых моментов сопротивления изгибу приведены в справочниках.
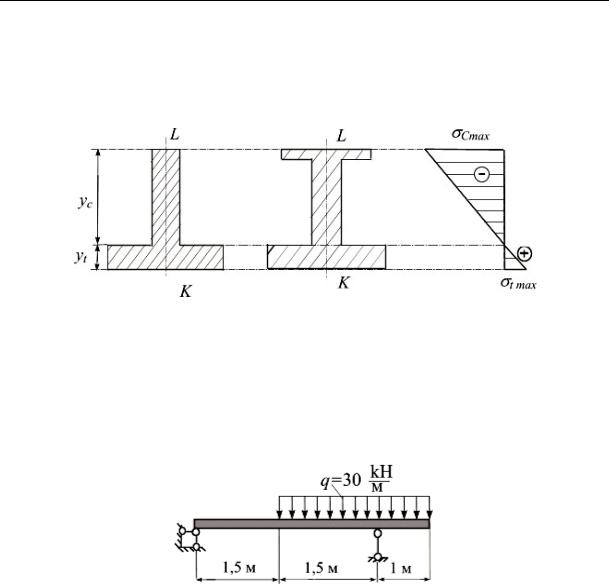
Для балок из хрупких материалов, различно сопротивляющихся растяжению и сжатию, следует применять сечения, несимметричные относительно нейтральной оси (тавровое, несимметричное двутавровое, П-образное). При этом целесообразно располагать сечение так, чтобы большаяегочастьсечениянаходиласьвсжатойзоне(рис. 13.13).
При этом приходится отдельно проверять наибольшие напряжения в растянутой и сжатой зоне. Условие прочности (13.7) распадается на два:
|
σp max = |
M x max |
; |
σc max = |
M x max |
yc ≤[σc ]. (13.14) |
|
|
Jx |
yp ≤ σp |
Jx |
||||
|
287 |
И. В. Богомаз. Механика
где yp и yc – расстояния от нейтральной оси до наиболее удаленных точек растянутой и сжатой зон; [σp] и [σc] – допускаемые напряжения на растяжение и сжатие.
Рис. 13.13
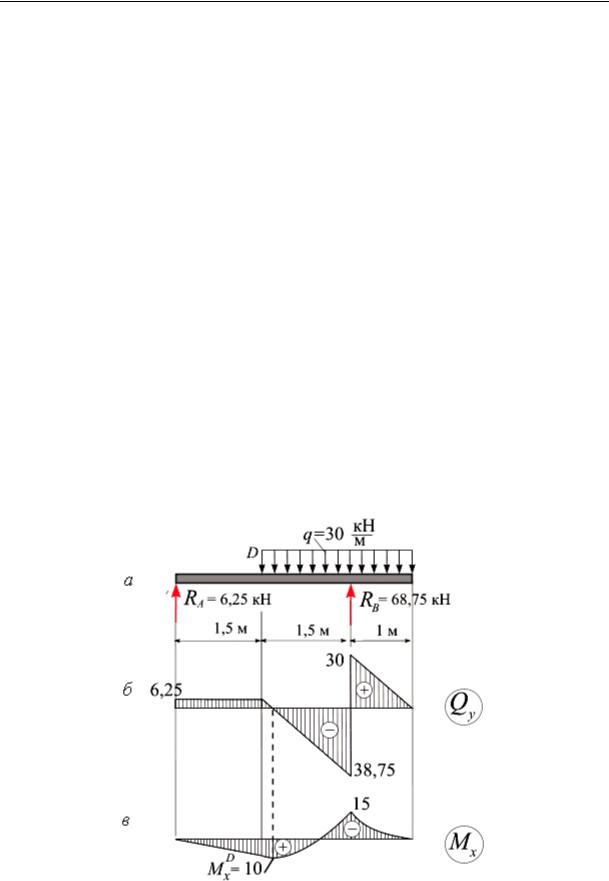
Пример 13.1. Подобрать сечение двутавровой балки (рис. 13.14), если длина пролета 1 = 3м, консоли 2 =1 м, равномерная нагрузка q = 30 кН/м, расчетное сопротивление материала изгибу R = 240 МПа.
Рис. 13.14
Решение. Вычислим реакции опор RA и RB, сделаем проверку вычисленных значений (рис.13.15, а).Запишем уравнения равновесия:
|
∑M A = 0, RB 3 −q 2,5 2,75 = 0 → RB = 30 2,5 |
2,75 |
= 68,75кH; |
|||
|
3 |
|||||
|
∑M B = 0, − RA 3 +30 2,5 0,125 = 0 → RB = |
30 2,5 |
0, 25 |
= 6, 25 кH. |
||
|
3 |
Проверка: ∑Fy = 6,25 −30 2,5 +68,75 = 0.
288
13. Изгиб бруса
Построим эпюру Mx и эпюру Qy для контроля эпюры Mx (рис. 13.15, б, в). Из эпюры изгибающего момента Mx видно, что опасное сечение балки находится в сечении В: M xB = M xmax =15 кН м.
Подберем поперечное двутавровое сечение балки. Запишем условие прочности для выявленного опасного сечения D и вычислим требуемый момент сопротивления балки:
|
M B |
|||||||
|
σmax = |
x |
≤ R , |
|||||
|
Wx |
|||||||
|
W |
≥ |
M xD |
= |
15 103 |
= 0,0625 10−3 м3 = 62,5см3 . |
||
|
x |
R γc |
240 106 |
|||||
Находим из сортамента подходящее значение момента сопро-
тивления: двутавр № 12 с Wx = 58,4 см3 . Проверим двутавр № 12 на прочность:
|
M D |
15 103 |
||||||||
|
σ |
max |
= σ |
№12 |
= |
x |
= |
= 256,8 MПа. |
||
|
W |
58, 4 10−6 |
||||||||
|
x |
Рис. 13.15
289

И. В. Богомаз. Механика
Сравниваем:
σmax = σ№12 = 256,8МПа и R = 240 МПа → σmax > R.
Вычислим возникшее перенапряжение
|
σ№12 − R |
100% = |
256,8 −240 |
100% = 6,5% > 5 %, что не допус- |
|||||
|
σ№12 |
256,8 |
|||||||
|
тимо. |
||||||||
|
Выбираем из сортамента двутавр № 14 с Wx = 81,7 см3. |
||||||||
|
Проверим двутавр № 14 на прочность: |
||||||||
|
σ′max = σ№14 |
= |
M xD |
= |
15 103 |
=183,6MПа. |
|||
|
81,7 10−6 |
||||||||
|
Wx |
Сравниваем:
σ′max = σ№14 =183,6МПа и R = 240 МПа → σ′max < R .
Прочность балки обеспечена с большим запасом. Ответ: выбираем двутавр № 14.
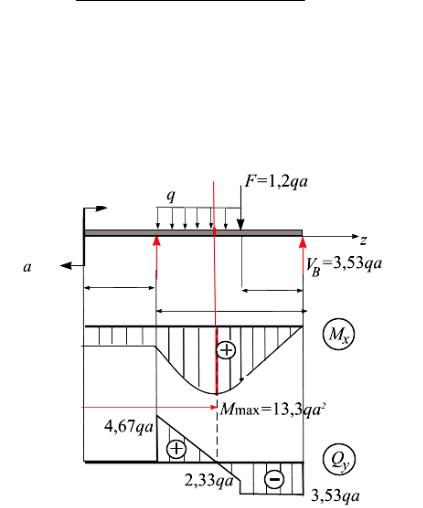
Пример 13.2. Шарнирно опертая двутавровая балка нагружена равномерно распределенной нагрузкой q, силой F = 1,2qa и моментом m = 2,4q2 (рис.13.16).
Требуется построить эпюры поперечных сил Qy и изгибающих моментов Mx и вычислить их наибольшие значения; определить несущую способность балки q из условия прочности по нормальным напряжениям; проверить прочность балки по касательным напряжениям при вычисленной нагрузке q.
Рис.13.16
290
|
13. Изгиб бруса |
|||||
|
Дано: Длина пролета балки = 6м, |
a1 |
= 3, |
a2 |
= 4 . Сечение |
|
|
a |
a |
||||
балки – двутавр № 30а. Расчетное сопротивление материала на изгиб R = 210 МПа, на срез RS = 130 МПа.
Решение. Вычерчиваем расчетную схему (рис. 13.17, а). Запишем уравнения равновесия.
∑M A = 0, VB 10a − F 7a −q 7a 3,5a −m = 0 →
= 1,2qa 7a + 24qa2 + 2,4qa2 =
VB 3,5qa. 10a
∑M B = 0, −m −VA 10a + q 7a 6,5a + F 3a = 0 →
VA = −2,4qa2 + 45,5qa2 +3,6qa2 = 4,67qa. 10a
Проверка:
∑Fy =VA −7qa −1,2qa +VB = 3,53qa −7qa −1,2qa + 4,67qa =
=8, 2qa +8, 2qa = 0.
m = 2,4q2
а
2,4qa2
б
z0
a2 = 4a VA = 4,67qa a1 = 3a l = 10a
10,6qa2
z0

И. В. Богомаз. Механика
|
Построим |
эпюру |
Mx |
и эпюру |
Qy |
для |
контроля эпюры Mx |
|||||||||||||||||
|
(рис. 13.17, б, в). Вычислим Mmax: |
|||||||||||||||||||||||
|
M (z) = −m +VA z − |
qz |
2 |
, |
||||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
Q |
(z |
o |
) |
= |
d M x (z) |
=V |
A |
−qz |
0 |
= 0 |
→ z |
0 |
= |
VA |
= 4,67a. |
||||||||
|
x |
d z |
z=zo |
q |
||||||||||||||||||||
|
qz2 |
|||||||||||||||||||||||
|
M max (z0 ) = −m +VA z0 |
− |
0 |
= |
||||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
= −2, 4qa2 + 4,67qa 4,67a − |
q(4,67a)2 |
=13,3qa2 . |
|||||||||||||||||||||
|
2 |
Вычислим несущую способность балки. Из сортамента
(ГОСТ8239–89) длядвутавра№ 30анаходим: Wx = 518 см3, Jx = 7780 см4, статическиймоментполусеченияSx = 292 см, толщинастенкиs = 6,5 мм.
Условие прочности по нормальным напряжениям имеет вид
|
M max |
13,3qa2 |
|||||||
|
σmax = |
x |
≤ R → |
≤ R, откуда |
|||||
|
Wx |
Wx |
|||||||
|
W R |
518 |
10−6 210 106 |
0,9 |
|||||
|
q ≤ |
x |
= |
= 22719 Н/м. |
|||||
|
13,3a2 |
13,3 0,62 |
|||||||
Проверим прочность балки по касательным напряжениям. Ус-
ловие прочности по касательным напряжениям имеет вид
|
τ |
= |
Qmax S |
x max ≤ R . |
|||
|
y |
||||||
|
max |
S |
|||||
|
Ix вy |
Здесь
|
τ |
max |
= |
Qymax расч Sxmax |
= |
4,67qa Sx max |
= |
|
Ix вy |
Ix вy |
|||||
|
= |
4.67 22719 0,6 292 10−6 |
= 36,7 MПa. |
||||
|
7780 10−8 6,5 10−3 |
||||||
292
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Важнейшим критерием оценки прочности балок при изгибе являются напряжения.
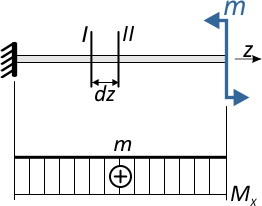
Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки
Расчет напряжений
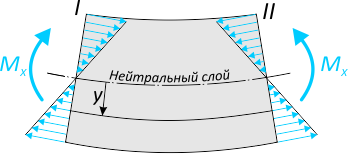
Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент Mx
представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.
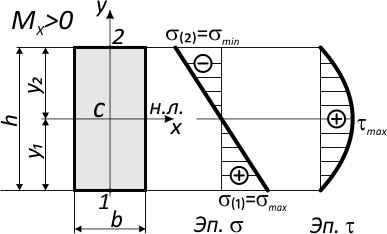
Закон распределения нормальных напряжений по высоте сечения выражается формулой:
где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
Ix — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.
Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.
По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.
Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.
Например, для симметричного относительно нейтральной оси сечения, где y1=y2=h/2:
Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.
Для несимметричного сечения
напряжения определяются отдельно для нижней точки 1 и верхней точки 2:
где:
WX — осевой момент сопротивления симметричного сечения;
WX(1) и WX(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.
Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.
Условия прочности при изгибе
Прочность по нормальным напряжениям
Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.
В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.
Здесь:
Mmax — максимальное значение изгибающего момента, определяемого по эпюре Mx;
[σ], [σ]р, [σ]с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).
Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]с>[σ]р.
В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.
При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:
- Проверка прочности
- Подбор сечений
- Определение максимально допустимой нагрузки
Прочность по касательным напряжениям
В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.
Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского
где
Sx отс — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
by — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.
Другие видео
Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Qmax:
где [τ] – допустимое значение касательных напряжений для материала балки.
Полная проверка прочности
Полную проверку прочности балки производят в следующей последовательности:
- По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
- По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
- По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда Mmax и Qmax действуют в одном и том же сечении балки).
При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид:
так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.
Другие видео
Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:
Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >
В этой статье начнем говорить об изгибе. Здесь я расскажу, что такое изгиб. Посмотрим, какие виды изгибов бывают. А также рассмотрим основные расчеты при этом виде деформации: расчеты на прочность и жесткость.
Что такое изгиб?
Изгиб – это вид деформации, при котором происходит искривление (изгиб) продольной оси стержня, а в поперечных сечениях стержня возникают изгибающие моменты, и почти всегда поперечные силы.
Поперечные силы и изгибающие моменты называют внутренними силовыми факторами (ВСФ).
Как определяют внутренние силовые факторы при изгибе?
Для определения поперечных сил и изгибающих моментов, используется метод сечений. Как обычно, стержни мысленно рассекаются на части:

Действие частей друг на друга заменяется внутренними силовыми факторами:

И рассматривая равновесие одной из частей, находятся поперечная сила и изгибающий момент в сечении:

Для стержней, работающих на изгиб, обязательно рассчитывают и строят эпюры внутренних силовых факторов. Как рассчитывать и строить эпюры поперечных сил и изгибающих моментов можно прочитать, перейдя по ссылке чуть ниже.
Виды изгибов
В зависимости от возникающих в поперечных сечениях ВСФ, принято выделять различные виды изгибов.
Поперечный (прямой) изгиб


Поперечный (прямой) изгиб – это вид деформации, при котором в поперечных сечениях стержня возникают два внутренних силовых фактора: поперечные силы и изгибающие моменты.
Чистый изгиб


При чистом же изгибе в сечениях возникают исключительно изгибающие моменты.
Другие виды изгибов
Чистый и поперечный изгиб — это наиболее простые виды изгибов, только их и будем рассматривать в этой статье. Однако, ты должен знать, что существуют и более сложные виды сопротивления: косой изгиб, изгиб с кручением, внецентренное растяжение (сжатие). Такие темы, как правило, изучаются во втором семестре.
Расчеты на прочность при изгибе
Теперь предлагаю поговорить о расчётах на прочность при поперечном изгибе. При этом виде деформации расчёты проводятся и по нормальным напряжениям и по касательным. Но так как зачастую касательные напряжения в несколько раз меньше нормальных, основным здесь является расчёт по нормальным напряжениям, а расчёт по касательным напряжениям — проверочный.
Условие прочности
Условие прочности по нормальным напряжениям такое же, как и при растяжении (сжатии):
Нормальные напряжения в сечениях при поперечном изгибе, определяются по следующей формуле:

где Mизг – изгибающий момент в сечении;
W – момент сопротивления сечения;
Моменты сопротивления сечений можно вычислить по данным формулам.
Расчет на жесткость при изгибе
В качестве примера возьмём балку, загруженную распределенной нагрузкой по всей длине. Для этой балки подберем двутавровое сечение (ГОСТ 8239-89) по сортаменту из условия прочности. Затем проверим жесткость такой балки, если допустимое перемещение равно [V] = 2 см.

Для такой балки наиболее опасным сечением будет сечение в заделке (точка A), для которого изгибающий момент будет равен:

А эпюра будет выглядеть следующим образом:

Более подробно о построении эпюры изгибающих моментов можно почитать, перейдя по указанной ссылке.
Теперь, зная значение максимального изгибающего момента, найдем минимально требуемый момент сопротивления, чтобы балка удовлетворяла условию прочности:

По сортаменту выбираем двутавр №36, у которого:

Более подробно, о прочностных расчетах при изгибе, можно узнать здесь.
Проверка балки на жесткость
Мы предварительно подобрали поперечное сечение балки, а теперь, нужно проверить, выполняется ли условие жесткости для такой балки, с таким сечением.

Нетрудно догадаться, что свободный торец балки (точка K) будет иметь наибольшее перемещение. Именно для этого сечения будем производить расчет на жесткость.

Для определения прогиба точки K можно воспользоваться шаблонной формулой, которая уже выведена конкретно для расчетной схемы, как у нас (консольной балки, загруженной по всей длине распределенной нагрузкой):

Подставим все численные значения и найдем прогиб точки K:

Таким образом, условие жесткости не выполняется:

Подбор нового сечения из условия жесткости
Подберем новое поперечное сечение! Для этого нужно найти минимально требуемый момент инерции из условия жесткости:



Выбираем следующий по списку сортамента двутавр №40, у которого:
Вычислим прогиб с учетом нового профиля:

Теперь жесткость балки обеспечена:
Таким образом, окончательно принимаем двутавр №40. Который одновременно удовлетворяет условиям прочности и жесткости.
Содержание
Предел прочности при изгибе
Предел прочности при изгибе (σ), также признанный Модуль разрыва или сила изгиба или поперечная прочность на разрыв, — это свойство материала, четко определяемое как напряжение материала непосредственно перед его деформацией при испытании на изгиб. Образец (круглое / прямоугольное поперечное сечение) сгибают до разрушения или текучести с использованием трехточечного испытания на изгиб. Прочность на изгиб означает наивысшее напряжение, приложенное в момент текучести ».
Определение прочности на изгиб
Прочность на изгиб можно определить как нормальное напряжение, возникающее в материале из-за изгиба или изгиба элемента при испытании на изгиб. Он оценивается с помощью метода трехточечного изгиба, при котором образец круглого или прямоугольного поперечного сечения деформируется до разрушения. Это максимальное напряжение, испытываемое этими материалами при пределе текучести.
Формула прочности на изгиб | Блок прочности на изгиб
Предположим, что прямоугольный образец находится под нагрузкой в установке для 3-точечного изгиба:
σ = 3WL/2bd2
Где W — сила в точке разрушения или разрушения.
L — расстояние между опорами
b — ширина балки
d — толщина балки
Единица прочности на изгиб — МПа, Па и т. Д.
Точно так же в установке 4-точечного изгиба, где длина нагрузки составляет половину пролета опоры.
σ=3Wl/4bd2
Аналогично, в установке 4-точечного изгиба, где длина нагрузки составляет 1/3 пролета опоры.
σ=WL/бд2
Испытание на прочность на изгиб
Это испытание создает растягивающее напряжение на выпуклой стороне образца и сжимающий напряжение с противоположной стороны. Отношение пролета к глубине контролируется, чтобы свести к минимуму вызванное напряжением сдвига. Для большинства материалов отношение L/d считается равным 16.
По сравнению с испытанием на изгиб при трехточечном изгибе, при испытании на изгиб при четырехточечном изгибе не наблюдаются сдвиговые силы в зоне между двумя нагружающими штифтами. Таким образом, испытание на четырехточечный изгиб наиболее подходит для хрупких материалов, которые не могут выдерживать напряжения сдвига.
Испытание на трехточечный изгиб и уравнения
Эквивалентная точечная нагрузка wL будет действовать в центре луча. т.е. при L / 2
Значение реакции в точках A и B можно рассчитать, применяя условия равновесия суммы ΣFx = 0, ΣFy=0, ΣМA = 0
Для вертикального равновесия ΣFy=0
RA+RB=В………..1
Принимая момент около A, момент по часовой стрелке положительный, а момент против часовой стрелки считается отрицательным, W * L / 2 — RB*Л = 0
RB = Вт/2
Положив значение RB в [1] получаем, RA = ВРB
RA = WW/2
RA = Вт/2
В соответствии с соглашением о знаках для ЮФО и ПРО
Сила сдвига при A, VA = RA = Вт/2
Сила сдвига при C, VC = RA – Вт/2
VC = Вт/2 – Вт/2 = 0
Сила сдвига в B, VB = RB = -Вт/2
Для Диаграмма изгибающего момента, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке воспринимается как положительный. Момент против часовой стрелки принимается как Negative.
Изгибающий момент при A = MA = 0
Изгибающий момент при С, МC = МA – В/2 * Д/2
MC = 0-WL/4
MC = -WL/4
Изгибающий момент при B = 0
В конфигурации с 3-точечным изгибом прочность на изгиб определяется выражением
σ = 3WL/2bd2
Где W — сила в точке разрушения или разрушения.
L — расстояние между опорами
b — ширина балки
d — толщина балки
Единица прочности на изгиб — МПа, Па и т. Д.
Испытание на четырехточечный изгиб и уравнения
Рассмотрим балку с простой опорой, у которой две равные нагрузки W действуют на расстоянии L / 3 от обоих концов.
Значение реакции в точках A и B можно рассчитать, применяя условия равновесия ΣFx = 0, ΣFy = 0, ΣМA = 0
Для вертикального равновесия ΣFy = 0
RA + RB = Вт……………1
Принимая момент около A, момент по часовой стрелке положительный, а момент против часовой стрелки считается отрицательным, W * L / 6 — RB*L = WL/3
RB = Вт/2
Положив значение RB в [1] получаем, RA = ВРB
RA = WW/2
RA = Вт/2
В соответствии с соглашением о знаках для ЮФО и ПРО
Сила сдвига в точке A,
VA=RA=Вт/2
Сила сдвига при C, VC = RA – Вт/2
VC = Вт/2 – Вт/2 = 0
Сила сдвига в B, VB = RB = -Вт/2
Для диаграммы изгибающего момента, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке воспринимается как положительный. Момент против часовой стрелки принимается как Negative.
Изгибающий момент при A = MA = 0
Изгибающий момент при C = [Вт / 2] * [L / 3] ………………………… [поскольку момент направлен против часовой стрелки, изгибающий момент становится отрицательным]
Изгибающий момент при C = MC = ВЛ/6
Изгибающий момент при D = MD = W/2*2L/3 – W/2*L/3
MD = ВЛ/6
Изгибающий момент при B = 0
Для прямоугольного образца под установкой 4-точечного изгиба:
Точно так же, когда пролет нагрузки составляет 1/3 пролета опоры,
σ = WL/барр2
В конфигурации с 4-точечным изгибом, где пролет нагрузки составляет половину пролета опоры, σ = 3WL/4bd2
Где W — сила в точке разрушения или разрушения.
L — расстояние между опорами
b — ширина балки
d — толщина балки
Единица прочности на изгиб — МПа, Па и т. Д.
Прочность на изгиб и модуль упругости при изгибе
Модуль упругости при изгибе — это отношение напряжения, вызванного изгибным изгибом, к деформации во время изгибной деформации. Это свойство или способность материала сопротивляться изгибу. Для сравнения, прочность на изгиб можно определить как нормальное напряжение, возникающее в материале из-за изгиба или изгиба элемента при испытании на изгиб. Он оценивается с использованием метода трехточечного изгиба, при котором образец круглого или прямоугольного поперечного сечения изгибается до разрушения или деформации. Это максимальное напряжение, испытываемое материалом при пределе текучести.
Предположим, что балка прямоугольного поперечного сечения изготовлена из изотропного материала, W — сила, приложенная к середине балки, L — длина балки, b — ширина балки, d — толщина балки. δ — прогиб балки
Для настройки 3-точечного изгиба:
Модуль изгиба может быть задан как Eизгиб = σ/ε
Eизгиб = ВЛ3/4сп3Δ
для свободно опертой балки с нагрузкой в центре прогиб балки можно определить по формуле Δ=WL3/48Эл
Прочность на изгиб против прочности на разрыв
Прочность на растяжение — это максимальное растягивающее напряжение, которое материал может выдержать при растягивающей нагрузке. Это свойство материала. Это не зависит от формы образца. На это влияет толщина материала, выемки, внутренние кристаллические структуры и т. Д.
Прочность на изгиб не является свойством материала. Это нормальное напряжение, возникающее в материале из-за изгиба или изгиба элемента при испытании на изгиб. Это зависит от размера и формы образца. Следующий пример поясняет дальнейшее:
Рассмотрим балку квадратного сечения и ромбовидную балку со сторонамиa‘и изгибающий момент M
Для балки квадратного сечения
По уравнению Эйлера-Бернулли M=σl/y/y
Z=L/у
M1 = σ1a3/6
Для балки поперечного сечения Diamond
Но М1 = М2
Прочность бетона на изгиб
Процедура оценки прочности бетона на изгиб
- Рассмотрите любую желаемую марку бетона и подготовьте неармированный образец размером 12 дюймов x 4 дюйма x 4 дюйма. Выдержите приготовленный раствор в течение 26-28 дней.
- Перед проведением испытания на изгиб дайте образцу постоять в воде при 25 ° C в течение 48 часов.
- Немедленно проведите испытание на изгиб образца, пока он находится во влажном состоянии. [Быстро после извлечения образца из воды]
- Чтобы указать положение опоры ролика, проведите контрольную линию на расстоянии 2 дюймов от обоих краев образца.
- Роликовые опоры действуют как балка с простой опорой. По оси балки прикладывается постепенная нагрузка.
- Нагрузка постоянно увеличивается до тех пор, пока напряжение в крайнем волокне балки не увеличится со скоростью 98 фунтов / кв. в / мин.
- Нагрузка прикладывается непрерывно до тех пор, пока испытуемый образец не сломается, и не будет зафиксировано максимальное значение нагрузки.
В конфигурации с 3-точечным изгибом прочность на изгиб определяется как σ = 3WL/2bd.2
Где W — сила в точке разрушения или разрушения
L — расстояние между опорами
b — ширина балки
d — толщина балки
Единица прочности на изгиб — МПа, Па и т. Д.
Прочность на изгиб почти в 0.7 раза превышает прочность бетона на сжатие.
Прочность на изгиб стали
Рассмотрим стальную балку шириной = 150 мм, глубиной = 150 мм и длиной = 700 мм, приложенная нагрузка составляет 50 кН, и найдите изгибное напряжение балки?
В конфигурации с 3-точечным изгибом напряжение при изгибе определяется как σ = 3WL/2bd.2
σ = 3*50*103*0.7/2*0.15*0.152
σ = 15.55 МПа
Прочность на изгиб алюминия
Прочность на изгиб алюминия марки 6061 составляет 299 МПа.
Прочность на изгиб древесины
В следующей таблице показана прочность на изгиб различных пород древесины.
| Тип древесины | Прочность на изгиб [МПа] |
| Ольха | 67.56 МПа |
| ясень | 103.42 МПа |
| Осина | 57.91 МПа |
| американская липа | 59.98 МПа |
| бук | 102.73 МПа |
| Береза, желтый | 114.45 МПа |
| Орех серый | 55.84 МПа |
| Вишня | 84.80 МПа |
| каштан | 59.29 МПа |
| Вяз | 81.35 МПа |
| Гикори | 139.27 МПа |
Прочность на изгиб цилиндра
Рассмотрим балку с простой опорой, у которой две равные нагрузки W / 2 действуют на расстоянии L / 3 от обоих концов.
Значение реакции в точках A и B можно рассчитать, применяя условия равновесия
ΣFx = 0, ΣFy = 0, ΣМA = 0
Для вертикального равновесия ΣFy = 0
RA +RB=Вт……….1
Принимая момент около A, момент по часовой стрелке положительный, а момент против часовой стрелки принимается как отрицательный,
Ш*Д/6 – ПB*L = WL/3
RB = Вт/2
Положив значение RB в [1] получаем,
RA = ВРB
RA = WW/2
RA = Вт/2
В соответствии с соглашением о знаках для ЮФО и ПРО
Сила сдвига при A, VA = RA = Вт/2
Сила сдвига при C, VC = RA – Вт/2
VC = Вт/2 — Вт/2 = 0
Сила сдвига в B, VB = RB = Вт/2
Для диаграммы изгибающего момента, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке воспринимается как положительный. Момент против часовой стрелки принимается как Negative.
Изгибающий момент при A = MA = 0
Изгибающий момент при C = [Вт / 2] * [L / 3] ………………………… [поскольку момент направлен против часовой стрелки, изгибающий момент становится отрицательным]
Изгибающий момент при C = MC = ВЛ/6
Изгибающий момент при D = MD = W/2*2L/3-W/2*L/3
MD = ВЛ/6
Изгибающий момент при B = 0
Пусть d = диаметр цилиндрической балки. Согласно уравнению Эйлера-Бернулли,
σ = My/л
л = π/64d4
у = d / 2
σ=1.697WL/день3
Найдите напряжение изгиба в круглой цилиндрической балке пролетом 10 м и диаметром 50 мм. Балка изготовлена из алюминия. Сравните результат с балкой квадратного сечения со стороной = 50 мм. Общая прилагаемая нагрузка составляет 70 Н.
Рассмотрим балку с простой опорой с двумя равными нагрузками W / 2 = 35 Н, действующими на расстоянии L / 3 от обоих концов.
Значение реакции в точках A и B можно рассчитать, применяя условия равновесия ΣFx = 0, ΣFy = 0, ΣМA = 0
Для вертикального равновесия ΣFy = 0
RA + RB = 70……………1
Принимая момент около A, момент по часовой стрелке положительный, а момент против часовой стрелки считается отрицательным, W * L / 6 — RB*L = WL/3
RB = Вт/2 =35
Положив значение RB в [1] получаем
RA = ВРB
RA = WW/2
RA = 70-35 = 35н
В соответствии с соглашением о знаках для ЮФО и ПРО
Сила сдвига в точке A
VA = RA = Вт/2 = 35 Н
Сила сдвига при C, VC = RA – Вт/2
VC = Вт/2 – Вт/2 = 0
Сила сдвига в B, VB = RB = -Вт/2 = -35Н
Для диаграммы изгибающего момента, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке воспринимается как положительный. Момент против часовой стрелки принимается как Negative.
Изгибающий момент при A = MA = 0
Изгибающий момент при C = [Вт / 2] * [L / 3] ………………………… [поскольку момент направлен против часовой стрелки, изгибающий момент становится отрицательным]
Изгибающий момент при C = MC = WL/6 = 70*10/6 = 125 Нм
Изгибающий момент при D = MD = W/2*2L/3-W/2*L/3
MD = ВтL/6 = 70*10/6 = 125 Нм
Изгибающий момент при B = 0
Пусть d = диаметр цилиндрической балки, согласно уравнению Эйлера-Бернулли.
σ = My/л
л=π/64d4= π/64*0.054
= 3.067 * 10-7m4
у=0.05/2=0.025 м
σ = 125*0.025/3.067*10-7=10.189 МПа
Для квадратного образца: со стороной = d = 50 мм,
σ = My/л
σ = M(d/2)/d4/ 12
σ=6M/д3
σ=6*125/0.053
σ=6МПа
Некоторые важные часто задаваемые вопросы.
В.1) Что означает высокая прочность на изгиб?
Ответ: Считается, что материал обладает высокой прочностью на изгиб, если он выдерживает высокое напряжение при изгибе или изгибе без разрушения при испытании на изгиб.
Q.2) Почему прочность на изгиб выше прочности на разрыв?
Ответ: Во время испытания на изгиб крайние волокна балки испытывают максимальное напряжение (верхнее волокно испытывает напряжение сжатия, а нижнее волокно — растягивающее напряжение). Если крайние волокна не имеют каких-либо дефектов, прочность на изгиб будет зависеть от прочности волокон, которые еще не разрушились. Однако, когда к материалу прилагается растягивающая нагрузка, все волокна испытывают одинаковое напряжение, и материал разрушится при выходе из строя самого слабого волокна, достигающего своего предельного значения прочности на разрыв. Таким образом, в большинстве случаев прочность на изгиб выше прочности материала на разрыв.
В.3) В чем разница между изгибом и изгибом?
Ответ: В случае изгибного изгиба, согласно теории простого изгиба, поперечное сечение плоскости остается плоским до и после изгиба. Создаваемый изгибающий момент действует по всему пролету балки. никакая равнодействующая сила не действует перпендикулярно поперечному сечению балки. таким образом, поперечная сила вдоль балки равна нулю, и любое индуцированное напряжение происходит исключительно из-за эффекта изгиба. При неравномерном изгибе результирующая сила действует перпендикулярно поперечному сечению балки, а изгибающий момент также изменяется по длине пролета.
Q.4) Почему важна прочность на изгиб?
Ответ: Высокая прочность на изгиб имеет решающее значение для материалов или компонентов, подверженных нагрузкам, когда к компоненту или материалу прилагается высокое напряжение. Прочность на изгиб также помогает определить признаки того, какой тип материала может использоваться для приложений высокого давления. Высокая прочность материала на изгиб также влияет на толщину стенок компонента. Высокопрочный материал обеспечивает небольшую толщину стенок. Материал, который обеспечивает высокую прочность на изгиб и высокую вязкость разрушения, позволяет изготавливать стенки с очень малой толщиной и, следовательно, идеально подходит для вариантов минимально инвазивного лечения.
Q.5) найти предел прочности на изгиб по кривой напряжения-деформации?
Ответ: Прочность на изгиб можно определить как максимальное приложенное напряжение на кривой деформации напряжения. Поглощение энергии материалом до разрушения можно оценить по площади под кривой зависимости напряжения от деформации.
Q.6) Обеспечивает ли бетон марки M30 максимальную прочность на изгиб?
Ответ: Прочность на сжатие бетона марки М30 составляет 30 МПа. Соотношение между прочностью на изгиб и прочностью на сжатие можно определить по формуле: σf = 0.7√σc
. Таким образом, максимальная прочность на изгиб бетона марки М30 составляет σf = 0.7√30 = 3.83 МПа
Q.7) Почему максимальная деформация сжатия в бетоне при испытании на изгиб составляет 0.0035, не больше или меньше, тогда как деформация разрушения в бетоне колеблется от 0.003 до 0.005?
Ответ: Для теоретического расчета максимальной деформации сжатия в бетоне при испытании на изгиб мы принимаем во внимание все допущения простой теории изгиба. Во время практических экспериментов различные факторы, такие как дефект материала, неравномерное поперечное сечение и т. Д., Влияют на деформацию сжатия в бетоне при испытании на изгиб. Таким образом, максимальная деформация сжатия в бетоне при испытании на изгиб 0.0035, не больше и не меньше, тогда как деформация разрушения в бетоне колеблется от 0.003 до 0.005.
Q.8) Если дополнительные арматурные стержни расположены на стороне сжатия железобетонной балки. Это увеличивает прочность балки на изгиб?
Ответ: Добавление дополнительных арматурных стержней обеспечивает дополнительную прочность балке на сжатие, особенно в местах возникновения положительных моментов. Арматурные стержни предназначены для предотвращения разрывов при растяжении, таких как изгибающий момент, поскольку бетон является слабым при нагрузке на растяжение. Если балка имеет большую толщину вместе с арматурными стержнями, стальные стержни ведут себя исключительно как элемент прочности на растяжение, а бетон обеспечивает прочность на сжатие.
В.9) Что произойдет с прочностью бетонной балки на изгиб, если ее размеры уменьшатся вдвое?
Ответ: для балки прямоугольного сечения,
При 3-точечном изгибе прочность на изгиб определяется по формуле
σ = 3WL/2bd2
σ = 1.5WL/бард2
Если размеры уменьшены вдвое
В = b / 2, D = d / 2
σ1 = 3WL/2BD2
σ1 = 3изн/2сб/2*д2/4
σ1 = 12WL/бод2
σ1 > о
Если размеры уменьшить вдвое, прочность на изгиб увеличивается в 8 раз для материала прямоугольного сечения.
Q.10) Что такое модуль разрыва?
Ответ: Модуль упругости при изгибе — это отношение напряжения, вызванного изгибным изгибом, к деформации во время изгибной деформации. Это свойство или способность материала сопротивляться изгибу.
Чтобы узнать о просто поддерживаемой балке (нажмите здесь.)и консольная балка (Кликните сюда.)