Как найти приведенную жесткость

схеме

1.
Приведение масс.
Значимость той или иной массы в системе
определяется величиной кинетической
энергии этой массы. Кинетическая энергия
до приведения системы, изображённой на
рис. 1.1, б, составляет

,

где J_i
– момент инерции относительно оси
вращения вала;_i– величина угловой скорости.

За центр
приведения примем вал двигателя. Это
означает, что эквивалентный вал и все
массы имеют угловую скорость, равную
скорости вала двигателя ₁.
Кинетическая энергия системы после
приведения (см. рис. 1.2, а):

.

Из
условия равенства кинетических энергий
системы до и после приведения для
приведения вращающихся масс достаточно
момент инерции приводимой детали
разделить на квадрат передаточного
отношения между центром приведения и
деталью(см. рис. 1.1, б):

, (1.1)

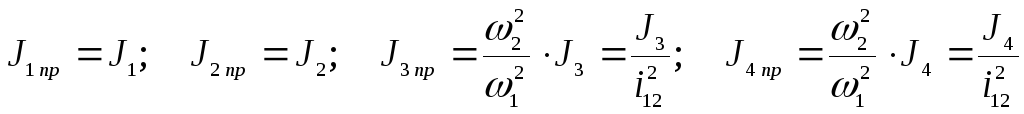
где
– передаточное отношение от центра
приведения до приводимого участка,
определяемая как отношение угловой
скорости
центра приведения к скорости приводимого
участка.

Если
требуется поступательно движущуюся
массуmгрузоподъёмного
механизма привести к вращающемуся валу,
принятому за центр приведения, то такое
приведение осуществляется следующим
образом. Кинетические энергии системы
до и после приведения определяются по
формулам:

,

где – поступательная скорость движения
массыm;_дв– угловая скорость двигателя, вал
которого принят за центр приведения.

Из
равенства кинетических энергий до и
после приведения получим

. (1.2)

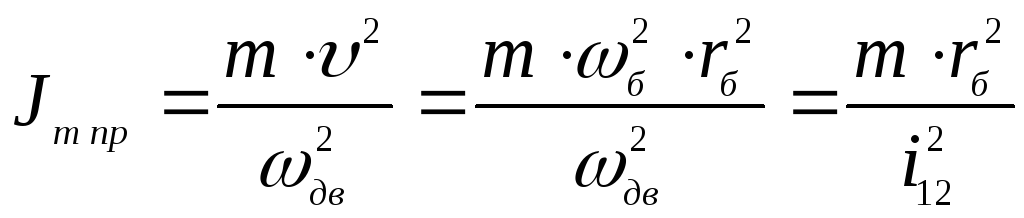
Таким
образом, при приведении к валу двигателя
поступательно движущейся со скоростью
массыmвеличина массы умножается
на квадрат радиуса барабанаr_би делится на квадрат передаточного
отношения между валом двигателя и валом
барабана
.

2.
Приведение жесткостей.В рассматриваемом
случае приведения системы (см. рис. 1.1,
б) участок 3-4, обладающей круговой
жёсткостьюС_3,4, приводится
к центру, в качестве которого взят вал
с круговой жёсткостьюС_1,2.

Потенциальная
энергия участка 3-4, подверженного
крутильным колебаниям, равна

,

где
– угол закручивания участка 3-4.

Если
этот участок получит деформацию
,
то центр приведения (вал маховикаJ₁)
повернётся за счёт деформации участка
3-4 на величину
,
являющуюсядеформациейприведенного
участка. Из условия равенства потенциальных
энергий до и после приведения

определяется
жёсткость участка 3-4, приведенная к валу
1-2:

, (1.3)

т.е. для
определения величины приведенной
жёсткости любого элемента достаточно
разделить его жёсткость на квадрат
передаточного отношения между центром
приведения и приводимым звеном.

Приведение
жёсткости каната механизма подъёма
груза, жёсткости зубчатого зацепления
к круговой жёсткости вала также
производится на основании равенства
потенциальных энергий деформации.

Так,
если жёсткость каната механизма
подъёма грузаприводится к валу
двигателя, то равенство потенциальных
энергий запишется

,

где Е_к– погонная жёсткость каната,l– длина каната;х– перемещение
поднимаемого груза за счёт деформации
каната;_дв– величина деформации вала двигателя,
вал которого принят за центр приведения.

Из
приведенного равенства получим

, (1.4)

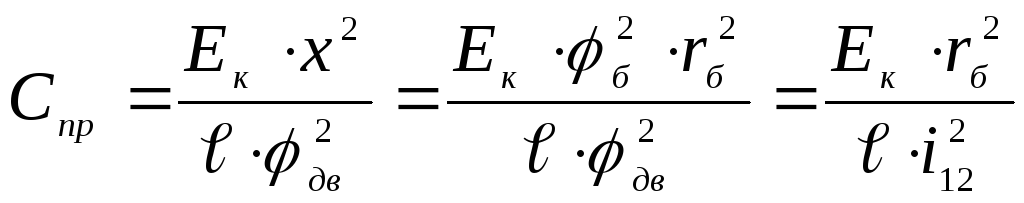
где _б– величина деформации вала барабана;r_б– радиус
барабана.

Линейная
жёсткость зубчатого зацепленияС_л
приводится сначала к круговой жёсткости
вала одной из шестерён данного зубчатого
зацепления по формуле

, (1.5)

где r_i– радиус начальной окружности шестерни,
к валу которой приводится значение
жёсткости.

Радиус
начальной окружности шестерниможно
определить из проектировочного расчёта
зубчатых передач по формуле

, (1.6)

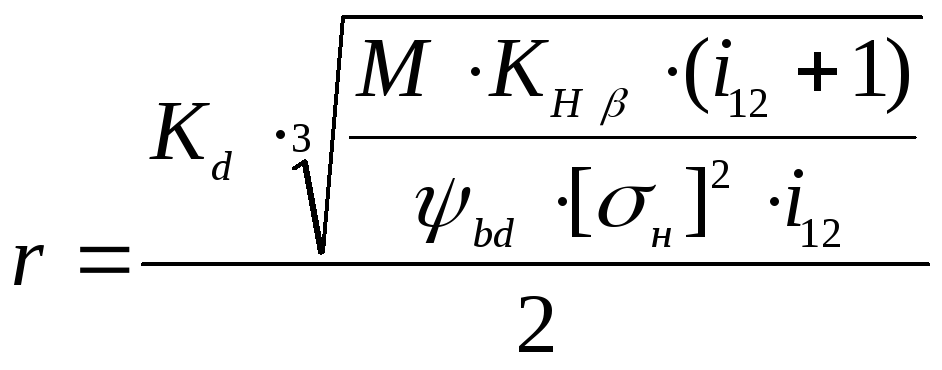
где М– крутящий момент, передаваемый
шестерней, Н^. м;

К_d–
вспомогательный коэффициент, по
рекомендациям работы1для прямозубых передачК_d= 0,77, для косозубых и шевронных передач
– 0,675;

К_–
коэффициент неравномерности распределения
нагрузки по ширине венца зубчатого
зацепления, для прямозубых передач К_= 1;

i₁₂–
передаточное число зубчатой передачи;

_bd– коэффициент ширины венца
зубчатого колеса по среднему диаметру,

;

– допускаемое контактное напряжение,
для расчёта принимаем
МПа;

Сама
же линейная жёсткость зубчатого
зацепления, зависящая от контактных
и изгибных деформаций зубьев, определяется
по формуле

, (1.7)

где – величина нагрузки пары зубьев,
отнесённой к единице ширины зуба,
Па – для стальных прямозубых колёс,
Па – для стальных косозубых колёс;b– ширина зуба, м;– угол наклона зубьев.

Аналогично
определяется линейная жёсткость
шлицевых и шпоночных соединений:

, (1.8)

где S– рабочая поверхность, передающая
нагрузку, мм²;

 – контактная жёсткость соединения,

Н/мм².

Жёсткость
крутильная всей связиопределяется
с учётом приведенных линейных жесткостей
зубчатых, шлицевых, шпоночных соединений,
жёсткости каната грузоподъёмного
механизма. Рассмотрим это на примере
(см. рис. 1.1, б) приведения линейной
жёсткости зубчатого зацепления (согласно
выражению (1.5)
)
к валу 3-4 с последующим приведением к
центру приведения системы (валу 1-2) по
общему правилу:

. (1.9)

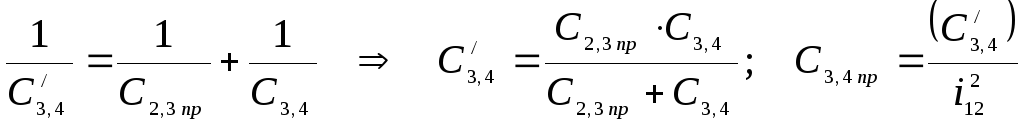
3.
Приведение сил.При переходе от
кинематической схемы машины (см. рис.
1.1, а) к эквивалентной расчётной схеме
(см. рис. 1.2, а) необходимо выполнить также
и приведение сил, так как на приведенные
массы эквивалентной расчётной схемы
должны действовать приведенные силы.
Если за центр приведения принять вал
2, то очевидно, что момент сопротивления
на рабочем органе М_с, приведенный
к валу двигателя, определится следующим
образом:

, (1.10)

где _тр– КПД трансмиссии от массы, к которой
приложена приводимая сила, до центра
приведения,

(1.11)

_зn– КПД зубчатой передачи,_зn= 0,95;_nш– КПД подшипникового узла качения,_nш= 0,98;n– количество
зубчатых передач до центра приведения;m– количество
подшипниковых опор кинематической
схемы.

Линейная
сила Р приводится к вращающемуся центру
приведения по формуле

. (1.12)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Раздел I. Растениеводство.

кооперативов — сельскохозяйственные, перерабатывающие и обслуживающие предприятия могут иметь любые организационноправовые формы и формы собственности — кооперативную, акционерную, государственную и муниципальную, смешанную. Совершенствование же Федерального закона «О сельскохозяйственной кооперации» на основе включения в него статей, разрешающих юридическим лицам быть полноправными членами производственного кооператива, позволит еще более расширить спектр многоукладности без ущемления прав сельскохозяйственных предприятий в управлении агропромышленным комплексом.

Сформированный таким образом агропромышленный комплекс России и система инженерно-технологического обеспечения в нем будет способен обеспечить конкуренцию на мировом рынке продовольствия отечественных производителей сельскохозяйственной продукции.

Получено 03.02.00.

УДК 631.33

В.В. БЕЛОВ, канд. техн. наук;

(СПбГАУ)

А.М.ВАЛГЕ, канд. техн. наук (СЗНИИМЭСХ)

ОПРЕДЕЛЕНИЕ ПРИВЕДЕННОЙ ЖЕСТКОСТИ МЕХАНИЗМА ПОДВЕСКИ РАБОЧИХ ОРГАНОВ СЕЛЬХОЗМАШИН

В статье дана формула для аналитического определения приведенной жесткости пружинного механизма подвески. Рассмотрен характер изменения приведенной жесткости. Показано, что изменение приведенной жесткости носит убывающий характер и может иметь положительный и отрицательный знаки. Для механизмов подвески с упругим звеном рекомендуется приведенная жесткость механизма, близкая к нулю.

43

ISSN 0131-5226. Сборник научных трудов СЗНИИМЭСХ. 2000. Вып. 71.

Доказано, что приведенная жесткость зависит от конструктивных параметров и положения рабочего органа, не всегда может быть параметром оптимизации при исследовании или синтезе подвески.

Проблема оптимизации упругих характеристик механизмов подвесок приобретает особую значимость ввиду возросших рабочих скоростей движения сельскохозяйственных машин. От упругих характеристик механизма подвески рабочих органов и поддержания заданных характеристик различных натяжных устройств зависит не только уровень качества выполнения технологического процесса, но и ресурс подвески, технологическая надежность.

В основном при синтезе пружинных механизмов ставят задачу определения оптимального значения приведенной жесткости подвески в предположении линейности упругих характеристик, а часть авторов — определения жесткости только самой пружины без учета конструктивных параметров механизма. Исходя из этих основных предпосылок и проводятся исследования.

Эксплуатационная практика и экспериментальные исследования показывают, что механизмы, разработанные подобным образом, не всегда имеют характеристики, отвечающие требуемым, из-за чего происходит нарушение технологического процесса. На слабонесущих почвах копирующие башмаки начинают “зарываться” в почву, а при большем натяжении пружин появляется эффект “ галопирования”.

Ввиду отсутствия аналитического метода определения приведенной жесткости механизма исследования приведенных упругих характеристик в основном проводятся экспериментальным методом, поэтому нами поставлена задача определения и исследования, в частности, приведенной жесткости механизма подвески рабочих органов сельскохозяйственных машин.

Определение приведенной жесткости механизма показано на простой схеме подвески (рис.1).

44

Раздел I. Растениеводство.

С

Рис. 1. Схема навески к определению приведенной жесткости

Используя рис.1 нами получена математическая зависимость приведенной жесткости, определяемое как соотношение приращения нагрузки на выходе к соответствующему приращению перемещения выходного звена, связанного с исполнительным рабочим органом.

Сг.

Ц2С

!з Ош ~Vi )

sln(a + у + ум )(Vl2 + l2 + 2l ,l 2cos(a + у + p+1) -Hc) co s О+n/l2 + l2 + 2l il 2cos(a + y + Pi+1) sln(a + y + О)(V1? + l2 + 2l[l2cos(a + y + o) -Hc) cos Onl l ? + l2 + 2ljl 2cos(a + y + pj)

где 11 — длина звена АО (отрезок рамы ограниченный шарниром крепления двуплечего рычага на раме и точкой крепления пружины к раме), м; l 2 — длина рычага ВО, м; l 3 — длина рычага ОС

(приложения внешней нагрузки), м; С- жесткость пружины, Н/м; a -угол, учитывающий отклонение точки крепления пружины к раме от горизонтали, град.; у- угол между рычагами АО и ВО двуплечего рычага, град.; <р, — угол, характеризующий положение звена ОС относи-

45

ISSN 0131-5226. Сборник научных трудов СЗНИИМЭСХ. 2000. Вып. 71.

тельно горизонтали, град.; Нс — свободная длина пружины, м; i — индекс переменной, целое положительное число.

Анализ представленной формулы показывает, что величина приведенной жесткости зависит от всех конструктивных параметров механизма подвески рабочих органов и является нелинейной тригонометрической трансцендентной функцией переменной (pi.

Доказано, что приведенная жесткость подвески зависит не только от всех параметров механизма подвески, но и от положения рабочего исполнительного органа — <pi.

По зависимости составлен алгоритм для ПЭВМ. Полученные нами результаты исследований приведенной жесткости представлены графически (рис. 2).

Рис. 2. Зависимость изменения приведенной жесткости СП от положения рабочего органа при различных значениях угла ВОС

Зависимости получены при постоянном значении жесткости пружины и разных значениях ZВОС между плечами двуплечего рычага, к которому приложены сила пружины и внешняя нагрузка, при условии, что величина максимального момента постоянна.

Изменение приведенной жесткости механизма уравновешивания носит для рассмотренных вариантов механизмов только убывающий характер. В крайних точках справа или слева кривые приве-

46

Раздел I. Растениеводство.

денной жесткости ассимптотически приближаются к оси ординат, ассимптотами которых являются ординаты при +900 и -900. Также надо отметить, что все кривые на рисунке пересекают ось абсцисс, значит приведенная жесткость пружинного механизма может быть равна и нулю. В то же время при пересечении оси абсцисс знак приведенной жесткости меняется с плюса на минус. Значит приведенная жесткость может быть положительной и отрицательной по знаку.

Нетрудно понять, что оптимальная рабочая зона уравновешивающего механизма подвески рабочего органа, позволяющая получить более постоянную нагрузку на копирующее устройство, находится в области точки пересечения оси абсцисс. Например, при ZВОС=510 оптимальным можно считать диапазон отклонения плеча приложения внешней нагрузки от +150 до -150, а при ZВОС =250 — от +400 до +200. При этом изменение нагрузки на копирующее устройство в рабочем диапазоне отклонения двуплечего рычага при принятых параметрах будет минимальным, так как приведенная жесткость по величине стремится к нулю. Возможно оптимальное значение приведенной жесткости механизма в зависимости от требуемой упругой характеристики может быть и в других точках. Если же требуется резко возрастающая или падающая упругая характеристика, то необходимо использовать другой подход к оптимизации механизма.

Отметим, что приведенная жесткость, не являясь постоянной величиной, может иметь одинаковые значения при разных соотношениях параметров механизма. Линейная зависимость (см. рис. 2) наблюдается только на малом участке отклонения выходного звена, поэтому допущение о линейности приведенной жесткости механизма не всегда отражает действительность.

Рассмотренные особенности изменения приведенной жесткости пружинного механизма подвески приводят к заключению, что данный показатель не всегда может быть параметром оптимизации и зависит не только от конструктивных параметров механизма, но и от положения рабочего органа относительно рамы самой машины.

Получено 25.10.99.

47

Приведенный коэффициент — жесткость

Cтраница 1

Приведенный коэффициент жесткости определяется из условия равенства величин потенциальной энергии амортизатора и эквивалентной пружины, как было показано в § 48, и в общем случае может быть нелинейной функцией перемещения у, отсчитываемого от положения статического равновесия.
 [1]

Приведенные коэффициенты жесткости могут быть определены методами сопротивления материалов. Причем для деталей малой длины ( si / sO 3) следует учитывать влияние сдвига, умножая приведенный коэффициент жесткости на коэффициент сдвига CQ, определяемый в зависимости от формы детали.
 [2]

Приведенный коэффициент жесткости подвески дан с учетом жесткости упругих элементов ее и пневматических шин.
 [3]

Приведенным коэффициентом жесткости, кинематической цепи называется коэффициент жесткости безмассовой пружины, имеющей ту же величину потенциальной энергии, что и заменяемая кинематическая цепь. Иногда приведенный коэффициент жесткости называют обобщенным, или квазиупругим.
 [4]

В этом случае приведенный коэффициент жесткости равен силе ( или моменту), вызывающей в направлении действия перемещение точки приведения, равное единице.
 [5]

В рассмотренном примере зубчатого механизма приведенный коэффициент жесткости имеет постоянную велич-и-ну, если передаточные отношения — постоянные.
 [6]

При параллельном соединении упругих звеньев приведенный коэффициент жесткости определяется из условия равенства деформаций звеньев и потенциальных энергий до и после приведения.
 [7]

Далее излагаются способы определения приведенной массы, приведенного коэффициента жесткости упругой связи и приведенной силы, знание которых необходимо для решения простейшей задачи о колебании центра приведения. После установления основных свойств нормальных функций и последовательности динамического расчета рекомендуемый метод исследования применяется к разным типам судовых конструкций — различно закрепленным балкам и пластинам, причем по ходу изложения устанавливаются способы отыскания форм и частот главных колебаний первого, второго и более высоких тонов.
 [8]

Аналогично приведенной массе или приведенному моменту инерции, приведенный коэффициент жесткости может быть или постоянным или переменным, зависящим от обобщенных координат механизма.
 [9]

Коэффициенты жесткости с, и с соответствуют коэффициенту жесткости клапанной пружины; с2 — коэффициенту жесткости коромысла; сг — приведенному коэффициенту жесткости штанги 2; c — приведенному коэффициенту жесткости участка распределительного вала; с0 — приведенной жесткости механизма. Для упрощения расчетной схемы коэффициенты демпфирования k принимают в первом приближении равными нулю.
 [10]

Таким образом, в рычажных механизмах переменными являются не толь — 3 ко приведенные силы и приведенные массы, но и приведенный коэффициент жесткости.
 [12]

& о — Коэффициенты жесткости с, и с соответствуют коэффициенту жесткости клапанной пружины; с2 — коэффициенту жесткости коромысла; с3 — приведенному коэффициенту жесткости штанги 2 с4 — приведенному коэффициенту жесткости участка распределительного вала; с0 — приведенной жесткости механизма. Для упрощения расчетной схемы коэффициенты демпфирования k принимают в первом приближении равными нулю.
 [13]

После приведения жесткостей получаем одномассовую динамическую модель ( рис. 66 6), в которой на звено приведения с массой m воздействует линейная пружина с приведенным коэффициентом жесткости са.
 [14]

Для определения кривой прогиба отбрасываем массу МЕ и прикладываем в точке Е силу Р; далее по кривой прогиба находим обычным путем приведенную массу трубопровода Мпр и приведенный коэффициент жесткости спр.
 [15]

Страницы:  

   1

   2

   3

    Приведение жесткостей выполняют по условию равенства потенциальных энергий, накапливаемых при упругой деформации звеньев приведения и приводимого  [c.86]

    Приведенные жесткости валов приведенная жесткость муфты с 2,2 = а>,2 Из,1- Если приведенная жесткость какого-либо участка на два или более порядка больше жесткости других участков, то, как правило, соответствующий участок можно считать абсолютно жестким и объединять инерционные массы, находящиеся но его концам. Например, если приведенная жесткость валов на участках 1-2 и 2 -3 очень велика, то расчетная схема приобретает вид, показанный на рис. 3.25, б. [c.87]

    Приведенные жесткости валов = [c.87]

    Рпс. 75. Схема к определению приведенной жесткости пружин [c.104]

    Найдем приведенную жесткость с р пружины, устанавливаемой на конце консоли балки (рис. 75) так, чтобы действие данной пружины было равноценно действию действительно установленной пружины жесткостью Су. Валка 3 совершает малые колебания вокруг шарнира 1 [41. [c.105]

    Приведенные жесткости валов Сщ,я = 2, ( з.4  [c.87]

    Для этих же частей оборудования в табл. П9.4 приведены значения приведенных жесткостей и приведенных масс. [c.485]

Таблица П9.4. Значения приведенных жесткостей и масс

    Приведенная жесткость узла крепления определяется по формуле [c.487]

    Координаты узлов петли ГЦК приведены в табл. 6.1, где отмечены точки, характеризующие основные размеры оборудования, узлы крепления, приведения жесткостей и масс от не рассматриваемых в расчете остальных петель я вспомогательных трубопроводов и т.п. [c.192]

    Рассмотренные ранее условия закрепления ГЦК учтены также в расчетной схеме, приведенной на рис. 6.2. В узле 4 (на уровне верхней опоры в зоне главного разъема) закреплены перемещения в горизонтальной плоскости по А и У, в узле 13 (на уровне основной несущей опоры) закреплены все степени свободы. Приведенные жесткости и массы от остальных [c.192]

    Расчет вала на виброустойчивость. Расчетные зависимости для определения виброустойчивости валов перемешивающих устройств [69], используемые в настоящей методике, основаны на известном методе расчета критических угловых скоростей вращения вала, разработанном А. Н. Крыловым [56]. Точные решения этой задачи для принятых расчетных схем весьма трудоемки и требуют применения ЭВМ. Для инженерных расчетов принят [69] приближенный способ оценки динамических прогибов роторов, основанный на методике приведения. Сущность этого метода заключается в замене вала, нагруженного распределенными и сосредоточенными массами, колебательной системой с невесомым валом, обладающей одной степенью свободы, приведенной массой /Пкр и приведенной жесткостью пр- [c.189]

    Суммарная приведенная жесткость вала [c.203]

    Поскольку приведенная жесткость вала является нелинейной функцией перемещения его центра, то для определения частоты должны быть использованы методы нелинейных колебаний. Как известно, уравнение свободных нелинейных колебаний системы без демпфирования имеет вид [c.63]

    Определяем приведенную жесткость поддерживающих упругих связей  [c.174]

    Z = Je = 1,33/0,8 = 1,66 Приведенная жесткость буферов  [c.174]

    Приведенная жесткость поддерживающих упругих связей (плоских пружин) ( 1 sin р 32 300 sin 30° [c.176]

    Отношение амплитуды колебаний Ai 2 к зазору е г = А ,. Je = = 0,018/0.0108 = 1,6 Приведенная жесткость резинометаллических блоков [т т-Лт т )] — С [c.176]

    Три слоя эпидермис, дерма и подкожная ткань соединены последовательно. Приведенную жесткость однослойной плиты Спр определяет выражение [c.188]

    В основе приведения жесткости лежит равенство потенциальных энергий биологического объекта и эквивалентной ему динамической расчетной схемы [c.204]

9.2.1. Коэффициенты жесткости и демпфирования для фундаментов на естественном основании

Основным параметром, характеризующим упругие свойства оснований фундаментов, является коэффициент упругого равномерного сжатия С_z. Его следует определять экспериментально. При отсутствии экспериментальных данных величину С_z, кН/м³, допускается определять для фундаментов с площадью подошвы А не более 200 м² по формуле

,

(9.6)

где b₀ — коэффициент, м^–1, принимаемый равным: для песков 1, для супесей и суглинков 1,2, для глин и крупноблочных грунтов 1,5; E — модуль деформации грунта, кПа, определяемый в соответствии с требованиями главы СНиП «Основания здании и сооружений. Нормы проектирования»; A — площадь подошвы фундамента, м²; А₀ = 10 м².

Модуль деформации грунта, как правило, должен определяться по результатам полевых штамповых испытаний. При отсутствии таких испытаний допускается пользоваться табличными данными.

Для фундаментов с площадью подошвы А, превышающей 200 м², значение коэффициента C_z принимается как для фундаментов с площадью подошвы A = 200 м².

Коэффициент С_z характеризует жесткость основания при поступательном вертикальном перемещении фундамента.

Помимо С_z в расчетах используются коэффициент упругого неравномерного сжатия С_φ, кН/м³ (при повороте фундамента относительно горизонтальной оси, проходящей через его подошву), упругого равномерного сдвига С_x, кН/м³ (при горизонтальном поступательном перемещении фундамента), и упругого неравномерного сдвига С_ψ, кН/м³ (при вращении относительно вертикальной оси). Их значения принимаются [1]:

(9.7)

Коэффициенты жесткости для естественных оснований фундаментов определяются по формулам:

– при вертикальных поступательных колебаниях фундамента,

k_z = C_zA;

(9.8)

– при горизонтальных поступательных колебаниях фундамента

k_x = C_xA;

(9.9)

– при вращательных колебаниях относительно горизонтальной оси, проходящей через подошву фундамента,

k_φ = C_φI_φ;

(9.10)

– при вращательных колебаниях относительно вертикальной оси, проходящей через центр тяжести подошвы фундамента,

k_ψ = C_ψI_ψ,

(9.11)

где I_φ и I_ψ — моменты инерции подошвы фундамента относительно горизонтальной и вертикальной осей.

Основной причиной, определяющей затухания колебаний фундаментов, является потеря энергии на возбуждение упругих волн в грунте, которые переносят энергию от фундамента в отдаленные от него части грунтового массива, где эта энергия постепенно поглощается за счет неупругого сопротивления грунта. Однако при описании колебаний самого фундамента учет потерь энергии за счет излучения упругих волн удобнее вести в рамках теории вязкого сопротивления, которое зависит от тех же параметров, что и жесткость естественного основания, т.е. от вида грунта, его упругих свойств и площади подошвы. Следовательно, коэффициенты демпфирования и коэффициенты жесткости для естественных оснований связаны между собой [2]. Демпфирующие свойства определяются коэффициентами относительного демпфирования ξ (доля критического затухания колебаний), определяемыми, как правило, по результатам испытаний.

Коэффициент относительного демпфирования для вертикальных колебаний ξ_z связан с коэффициентом демпфирования упруго-вязкого основания B_z в уравнении (9.4) следующим образом:

,

(9.12)

где λ_z — угловая частота свободных вертикальных колебаний установки.

При отсутствии экспериментальных данных коэффициент относительного демпфирования при вертикальных колебаниях фундамента допускается определять по формулам:

– для установившихся (гармонических) колебаний

;

(9.13)

– для неустановившихся (импульсных) колебаний

,

(9.14)

где р — среднее статическое давление, кПа, на основание под подошвой фундамента от расчетных статических нагрузок при коэффициенте перегрузки, равном 1.

Значения ξ_z, рассчитанные по формуле (9.13), примерно в 1,5 раза меньше, чем полученные по формуле (9.14). Значения ξ_z вычисляются по формуле (9.13) при определении амплитуд вынужденных установившихся колебаний и при определении темпа уменьшения амплитуд свободных колебаний фундамента в конце процесса колебаний (ориентировочно после двух-трех циклов свободных колебаний, возбужденных некоторой причиной — ударом, импульсом, начальным отклонением и т.п.). Формула (9.14) применима для оценки наибольших перемещений фундамента при свободных колебаниях под действием импульса. Меньшие значения ξ_z, вычисляемые по формуле (9.13), учитывают частичный возврат энергии колеблющемуся фундаменту упругими волнами, отразившимися от более плотных глубоких слоев грунта.

Значения коэффициентов относительного демпфирования для горизонтальных колебаний ξ_x и вращательных колебаний относительно горизонтальной ξ_φ и вертикальной ξ_ψ осей принимаются:

ξ_x = 0,6ξ_z; ξ_φ = 0,5ξ_z; ξ_ψ = 0,3ξ_z.

(9.15)

Если из опытов известны модули затухания Ф, с, колебаний фундаментов [7], то коэффициенты относительного демпфирования можно вычислить по формуле

ξ_z,x,φ,ψ = Ф_z,x,φ,ψλ_z,x,φ,ψ/2,

(9.16)

где λ_z, λ_x, λ_φ, λ_ψ — соответственно угловые чистоты свободных колебаний фундамента — вертикальных, горизонтальных и вращательных относительно горизонтальной и вертикальной осей.

9.2.2. Коэффициенты жесткости и демпфирования для свайных фундаментов. Определение приведенной массы

При определении податливости свай в вертикальном направлении принята расчетная схема в виде сжимаемого стержня в упругой винклеровой среде, препятствующей вертикальным перемещениям каждого сечения стержня (вдоль его оси); торец стержня опирается на пружину.

Ниже даны формулы для определения приведенной массы m_red свайного фундамента и приведенных коэффициентов жесткости k_φ,red, k_x,red, k_ψ,red, которые используются в расчетах вертикальных, горизонтально-вращательных и крутильных колебаний фундаментов во всех формулах вместо массы m (фундамента и машины) и коэффициентов жесткости k_z, k_φ, k_x, k_ψ.

Для вертикальных колебаний фундаментов:

;

(9.17)

;

(9.18)

; α = C^*_z/E_bt,

(9.19)

где m_r — общая масса ростверка с установленной на нем машиной, т; m_pi — масса i-й сваи, т; N — число свай; β^* = k₂[0,2 + 0,8th(6/l)]; th — тангенс гиперболический; С^*_z — коэффициент упругого равномерного сжатия грунта на уровне нижних концов свай, кН/м³, определяемый по формуле (9.6), в которой А принимается равной площади поперечного сечения сваи, а значение b₀ для забивных свай удваивается; E_bt — начальный модуль упругости бетона, кПа, принимаемый в соответствии с главой СНиП «Бетонные и железобетонные конструкции. Нормы проектирования»; l — длина свай, м; d — длина стороны поперечного сечения сваи, м; k₁ коэффициент, учитывающий упругое сопротивление грунта по боковой поверхности сваи; принимается равным 3 · 10² кПа^1/2 · м^–1/2; k₂ — коэффициент, учитывающий влияние свойств прорезаемого сваей грунта на приведенную массу свайного фундамента, принимается равным 2.

Для горизонтально-вращательных колебаний фундаментов:

m_red = m_r;

(9.20)

;

(9.21)

θ_0,red = θ_red + h²₀m_r;

(9.22)

.

(9.23)

где θ_r — момент инерции массы ростверка и машины относительно горизонтальной оси, проходящей через их общий центр перпендикулярно плоскости колебаний, т·м²; h₀ — расстояние от центра массы m_r до подошвы ростверка, м; r_i — расстояние от оси i-й сваи до оси поворота подошвы фундамента, м; k_z,red — приведенный коэффициент жесткости свайного фундамента, кН/м, определяемый по формуле (9.18).

Для горизонтальных колебаний фундаментов приведенная масса фундамента m_red определяется по формуле (9.17), как и для вертикальных колебаний, при k₂ = 2/3. Коэффициент жесткости при упругом равномерном сдвиге, кН/м, определяется по формуле

k_x,red = Nα´³E_btI/q,

(9.24)

где E_btI — жесткость поперечного сечения сваи на изгиб, кПа·м⁴; α´ — коэффициент упругой деформации системы «свая-грунт»: α´ = 1,6 α_d (здесь α_d — коэффициент деформации сваи, определяемый как и при расчете свай на статические горизонтальные нагрузки).

Значения коэффициента q вычисляются следующим образом:

– для свай, шарнирно сопряженных с низким ростверком, и для свай, защемленных в низкий ростверк, по формулам:

q = D₀;

(9.25)

q = D₀ – b²₀/C₀;

(9.26)

– для свай, шарнирно сопряженных с высоким ростверком, и для свай, защемленных в высокий ростверк, по уравнениям:

q = a₀;

(9.27)

q = a₀ – b´₀,

(9.28)

a₀ = D₀ + 2B₀l₀α´ + C₀(l₀α´)² + (l₀α´)³/3;

(9.29)

;

(9.30)

здесь D₀, В₀, С₀ — коэффициенты, зависящие от приведенной глубины погружения сваи l´ = α´l и условий опирания нижнего конца сваи; l₀ — расстояние от подошвы ростверка до поверхности грунта.

Для крутильных колебаний фундамента момент инерции массы свайного фундамента относительно вертикальной оси, проходящей через центр тяжести подошвы фундамента, определяется по формуле

;

(9.31)

Коэффициент жесткости при упругом неравномерном сдвиге вычисляется по выражению

,

(9.32)

где θ_ψ,r — момент инерции массы ростверка и машины относительно вертикальной оси, проходящей через центр тяжести подошвы фундамента, т·м²;  — расстояние от оси i-й сваи до вертикальной оси, проходящей через центр тяжести подошвы фундамента, м.