Как найти приращение в физике

§3. Изменение физической величины

Изучая физику, часто приходится использовать понятие изменения физической величины. При этом следует иметь в виду, что изменение какой-либо физической величины можно характеризовать либо её приращением, либо убылью. Приращением называется разность конечного и начального значений этой величины, в то время как убыль, напротив, представляет собой разность начального и конечного её значений.
Иными словами, убыль и приращение отличаются знаком. Мы чаще будем пользоваться понятием приращения и обозначать его в соответствии со сложившейся традицией с помощью греческой буквы «дельта»: `Delta`.
Таким образом, если этот символ стоит перед обозначением какой-либо векторной или скалярной величины, то такое выражение означает приращение соответствующей величины.
Так, выражение  `Deltavec A` означает приращение вектора A→vec A , а выражение `Delta x` — приращение скалярной величины xx. Вместе с тем во избежание недоразумений следует проявлять известную осторожность при использовании символа `Delta`. Например, убедитесь самостоятельно, что, вообще говоря,  `|DeltavecA|!=Delta|vecA|`, хотя в некоторых частных случаях возможно равенство.

Цели урока:

• Повторить, обобщить и систематизировать
  понятие приращение функции
• Закрепить навыки нахождения приращения функции
  при решении физических задач
• Раскрыть смысл понятия приращения функции в
  конкретных физических задачах

Ход урока:

Многие практические вопросы приводят к задаче
нахождения разности значений функции в двух
точках.

Алгоритм нахождения приращения функции f
при переходе от точки x к точке заключается в следующем:

1. найти значение функции f  в точке x;
2. найти значение функции f в точке ;
3. из второго значения вычесть первое.

Задача 1. Точка движется по
координатной прямой, причем ее координата x,
в момент времени равна . На сколько переместится точка за
промежуток времени 1) ; 2) ?

Решение:

Перемещение точки – это и есть приращение
функции .
Воспользуемся алгоритмом нахождения приращения
функции.

1)

2)

Ответ: 1) , 2) .

Задача 2. Угол поворота вращающегося
диска за первые секунд после начала вращения равен . Каков
физический смысл приращения функции при переходе от точки к точке ?

Решение:

Угол поворота диска в момент времени равен , а в момент
времени
равен .

Приращение функции, равное – это величина угла, на который
повернулся диск за время, равное секунд.

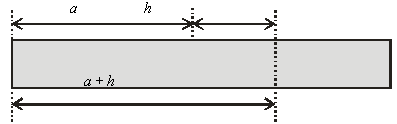
Задача 3. Масса части стержня от его
конца до точки, находящейся от этого конца на
расстоянии ,
равна . Каков
физический смысл приращения функции при переходе от
точки к
точке ?

Решение:

Значениями функции являются массы частей
стержня.

При переходе от точки к точке масса стержня меняется от значения до значения . Разность между
значениями этих масс и является приращением данной функции.

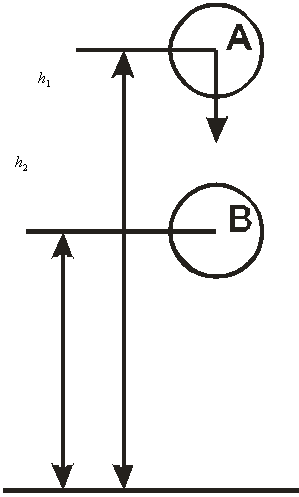
Задача 4. Тело массой перемещается под
действием силы тяжести вертикально вниз с высоты
над
поверхностью Земли до высоты . Потенциальная энергия на
высоте равна
, на высоте – . Каков физический смысл
приращения функции при перемещении тела с высоты до высоты ?

Решение:

–
приращение функции – изменение потенциальной энергии
тела при его перемещении из точки A в точку B.

– работа
силы тяжести по перемещению тела.

Методические рекомендации:

Рекомендуем из задачи 1 рассмотреть учителю 1)
пункт, самостоятельно 2) пункт. Задачи 2, 3 и 4
разобрать учителю.

Домашнее задание:

Температура стержня в точке, находящейся на
расстоянии
от его левого конца, равна . Какой физический смысл имеет
приращение функции при переходе от точки к точке ?

Тело падает с некоторой высоты над землей. В
момент падения на землю скорость его равна . С какой высоты
упало тело?

Если
тело некоторой массы m двигалось
под действием приложенных сил, и его
скорость изменилась от дото
силы совершили определеннуюработу A.

Работа
всех приложенных сил равна работе
равнодействующей силы (см.
рис. 1.19.1).

Между
изменением скорости тела и работой,
совершенной приложенными к телу силами,
существует связь. Эту связь проще всего
установить, рассматривая движение тела
вдоль прямой линии под действием
постоянной силы В
этом случае векторы
силыперемещенияскоростии
ускорениянаправлены
вдоль одной прямой, и тело совершает
прямолинейное равноускоренное движение.
Направив координатную ось вдоль прямой
движения, можно рассматриватьF, s, υ и a как
алгебраические величины (положительные
или отрицательные в зависимости от
направления соответствующего вектора).
Тогда работу силы можно записать
как A = Fs.
При равноускоренном движении
перемещение s выражается
формулой 

Отсюда
следует, что 

Это
выражение показывает, что работа,
совершенная силой (или равнодействующей
всех сил), связана с изменением квадрата
скорости (а не самой скорости).

Физическая
величина, равная половине произведения
массы тела на квадрат его скорости,
называется кинетической
энергией тела: 

Работа
приложенной к телу равнодействующей
силы равна изменению его кинетической
энергии. 

Это
утверждение называют теоремой
о кинетической энергии.
Теорема о кинетической энергии справедлива
и в общем случае, когда тело движется
под действием изменяющейся силы,
направление которой не совпадает с
направлением перемещения.

Кинетическая
энергия – это энергия движения.
Кинетическая энергия тела массой m,
движущегося со скоростью равна
работе, которую должна совершить сила,
приложенная к покоящемуся телу, чтобы
сообщить ему эту скорость:

Если
тело движется со скоростью то
для его полной остановки необходимо
совершить работу

16. Закон сохранения полной механической энергии. Закон сохранения энергии.

Соседние файлы в предмете Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
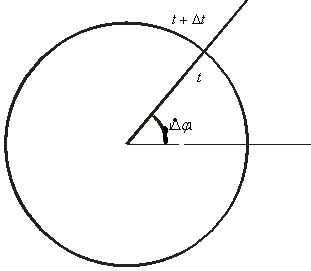
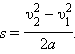
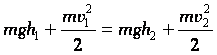