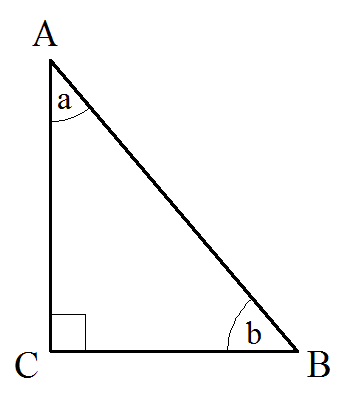
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² — b²
b = √c² — a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² — 4² = √25 — 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Как найти угол, прилежащий к катету
Две стороны треугольника, образующие его прямой угол, перпендикулярны друг дружке, что и нашло отражение в их греческом названии («катеты»), сегодня используемом повсеместно. К каждой из этих сторон примыкает по два угла, один из которых вычислять нет необходимости (прямой угол), а другой всегда является острым и рассчитать его величину можно несколькими способами.

Инструкция
Если известна величина одного из двух острых углов (β) прямоугольного треугольника, то для нахождения другого (α) больше ничего не нужно. Используйте теорему о сумме углов треугольника в евклидовой геометрии — так как она (сумма) всегда равна 180°, то рассчитайте величину недостающего угла вычитанием величины известного острого угла из 90°: α=90°-β.
Если кроме величины одного из острых углов (β) известны длины обоих катетов (А и В), то можно использовать и другой способ вычисления — с помощью тригонометрических функций. Согласно теореме синусов отношения длин каждого из катетов к синусу противолежащего угла одинаковы, поэтому синус нужного угла (α) находите делением длины прилежащего к нему катета на длину второго катета с последующим умножением результата на синус известного острого угла. Тригонометрическая функция, преобразующая значение синуса в соответствующую этому значению величину в угловых градусах, называется арксинусом — примените ее к полученному выражению и вы получите окончательную формулу: α=arcsin(sin(β)*А/В).
Если известны лишь длины обоих катетов (А и В), то их соотношения позволят получить тангенс или котангенс (в зависимости от того, что поставить в числитель) вычисляемого угла (α). Применяйте к этим соотношениям соответствующие им обратные функции: α = arctg(А/В) = arcctg(В/А).
Если известны только длина (С) гипотенузы (самой длиной стороны) и катета (В), прилежащего к вычисляемому углу (α), то отношение этих длин даст значение косинуса искомого угла. Как и для остальных тригонометрических функций, существует функция обратная косинусу (арккосинус) которая поможет из этого соотношения вывести величину угла в градусах: α=arcsin(В/С).
При тех же исходных данных, что и в предыдущем шаге, можно воспользоваться и вовсе экзотической тригонометрической функцией — секанс. Она получается делением длины гипотенузы (С) на длину прилежащего к нужному углу катета (В) — находите арксеканс от этого соотношения дли вычисления величины прилегающего к катету угла: α=arcsес(С/В).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Прилежащий катет — понятие, с которым связаны определения косинуса, тангенса и котангенса. Как определить, какой катет прямоугольного треугольника является для рассматриваемого угла прилежащим?
Само название катета — прилежащий — подсказывает его расположение в треугольнике относительно конкретного угла.
Прилежащий катет — это катет, который находится рядом с данным углом.

в треугольнике ABC
катет BC —
прилежащий к углу C.
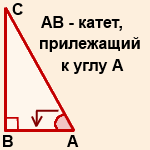
треугольнике ABC
катет, прилежащий к углу A —
это катет AB.
Маленький секрет, который помогает определить прилежащий катет:
в названии катета обязательно присутствует буква — название угла, к которому «прилежит» катет.
Вторая буква в названии прилежащего катета — «имя» прямого угла.
Смотрите:
катет AB — прилежащий к углу A, и в его названии есть буква A. Вторая буква — B — соответствует прямому углу.
катет BC — прилежащий к углу C, и в его названии есть буква C.
B — прямой угол.
Я, конечно, давно училась в школе, но почему-то мне кажется, что в вопросе Вы спутали «кислое с пресным» — так моя мама говорила.
Длина катета в прямоугольном треугольнике равна корню из разности квадрата длины гипотенузы и квадрата длины второго катета.
В данном случае понятие «прилежащий» вообще ни к чему, поскольку катет может быть прилежащим (или противолежащим) только к углу, а углы для определения длины катетов знать совсем необязательно. Обычно их (то есть углы) используют в тригонометрии для определения синусов, косинусов, тангенсов и котангенсов. Если, конечно, я ничего не путаю, так как школу закончила лет эдак 20 назад.
Расчёт катета по катету и противолежащему углу
Значащих цифр:
Введите противолежащий угол
Прямоугольный треугольник это треугольник у которого один из углов равен 90 градусов.
Прямой угол это угол 90 градусов.
Гипотенуза это противолежащая прямому углу сторона, самая длинная сторона прямоугольного треугольника.
Катеты это стороны прямоугольного треугольника прилежащие к прямому углу.
Сумма внутренних углов треугольника равна 180 градусам.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Известен катет BC и противолежащий угол a
Катет будем рассчитывать с помощью тангенса.
tg(a)=BC/AC
AC = BC / tg(a)