
Раздел 3. Решения систем линейных алгебраических уравнений (СЛАР)
Содержание
|
Абсолютная величина и норма матрицы |
2 |
|
Предел матрицы |
5 |
|
Алгебраическая проблема собственных значений |
7 |
|
Устойчивость матрицы |
15 |
|
Системы линейных алгебраических уравнений |
16 |
|
Оценка погрешности и мера обусловленности |
18 |
|
Метод Гауcса |
21 |
|
Метод Краута |
26 |
|
Метод прогонки |
33 |
|
Метод простой итерации |
38 |
|
Метод Зейделя |
42 |
|
Предметный указатель |
44 |
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Абсолютная величина и норма матрицы
Неравенство
между матрицами A = [aij] и B = [bij] одного типа означает, что
В таком смысле не всякие две матрицы можно сравнить между собой.
Абсолютной величиной (модулем) матрицы A = [aij] будем считать матрицу |A| = [|aij|], где |aij| — модули элементов матрицы A.
Если A и B — матрицы, для которых операции A + B и AB имеют смысл, то: а) |A + B| 6 |A| + |B|;
б) |AB| 6 |A| · |B|;
в) |αA| = |α| |A|, (α — число).
В частности, получаем:|Ap| 6 |A|p, (p — натуральное число).
Под нормой матрицы A = [aij] понимаем действительное число kAk, удовлетворяющее условиям:
а) kAk > 0, причем kAk = 0 тогда и только тогда, когда A = 0;
б) kαAk = |α| kAk (α — число ) и, в частности, k−Ak = kAk;
в) kA + Bk 6 kAk + kBk;
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

г) kABk 6 kAk · kBk (A и B — матрицы, для которых соответствующие операции имеют смысл). В частности, для квадратной матрицы имеем: kApk 6 kAkp, где p — натуральное число.
Отметим еще одно важное неравенство между нормами матриц A и B одинакового типа. Применяя условие в), будем иметь:
kBk = kA + (B − A)k 6 kAk + kB − Ak .
Отсюда
kA − Bk = kB − Ak > kBk − kAk .
Аналогично
kA − Bk > kAk − kBk .
Итак,
kA − Bk > kAk − kBk .
Назовем норму канонической, если дополнительно выполняются условия:
д) если A = [aij], то |aij| 6 kAk, причем для скалярной матрицы A = [a11] имеем kAk = |a11|;
е) из неравенства |A| 6 |B| (A и B — матрицы) вытекает неравенство kAk 6 kBk. В частности, kAk = k|A|k.
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

В дальнейшем для матрицы A = [aij] произвольного типа мы будем рассматривать главным образом три нормы, которые легко вычисляются:
1)kAkm = max P|aij| (m — норма);
i j
2)kAkl = max P|aij| (l — норма);
i j
|
3) kAkk |
= r |
i,j |
ai,j |
2 |
(k — норма). |
|
P |
Пример. Пусть
|
A = |
4 |
5 |
6 |
. |
|
1 |
2 |
3 |
||
|
7 |
8 |
9 |
Имеем:
kAkm = max(1 + 2 + 3, 4 + 5 + 6, 7 + 8 + 9) = max(6, 15, 24) = 24;
|
kAkl = max(1 + 4 + 7, 2 + 5 + 8, 3 |
+ 6 + 9) = max(12, 15, 18) = 18; |
||||||
|
kAkk = √ |
= |
||||||
|
12 + 22 + 32 + 42 + 52 + 62 + 72 + 82 + 92 |
|||||||
|
√ |
√ |
||||||
|
= 1 + 4 + 9 + 16 + 25 + 36 + |
49 + 64 + 81 = 285 ≈ 16, 9. |
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Предел матрицы
|
Пусть имеем последовательность матриц |
||||
|
Ak = [aij(k)] |
(k = 1, 2, . . .) |
(3.3) |
||
|
одного типа m × n (i = 1, 2, . . . , m; j = 1, 2, . . . , n). |
||||
|
Пределом последовательности матриц Ak считается матрица |
||||
|
= k→∞ |
k |
hk→∞ ij i |
(3.4) |
|
|
A |
lim A |
= lim a(k) . |
Последовательность матриц, имеющая предел, называется сходящейся.
Лемма 1 Для сходимости последовательности матриц Ak (k = 1, 2, . . .) к матрице A необходимо и достаточно, чтобы
|
kA − Akk → 0 при k → ∞, |
(3.5) |
||||||||||||||||||||||||||
|
где kAk любая коническая норма матрицы A. При этом klim kAkk = kAk. |
|||||||||||||||||||||||||||
|
→∞ |
|||||||||||||||||||||||||||
|
A |
Доказательство. Действительно, если Ak → A = |
[aij], то |
aij − aij(k) < ε при k > N(ε). Отсюда |
||||||||||||||||||||||||
|
Ak |
6 |
ε I , где I — единичная матрица размера m |
n. В силу |
свойств |
нормы имеем: |
A |
Ak |
6 |
|||||||||||||||||||
|
ε| |
I− |
при| |
× |
k − |
k |
||||||||||||||||||||||
|
k >|N|(ε), а значит, lim |
k |
A |
− |
Ak |
k |
= 0. |
|||||||||||||||||||||
|
k k |
k |
→∞ |
|||||||||||||||||||||||||
|
В другую сторону, пусть выполнено условие (3.5). Тогда при |
, имеем: |
(k) |
|||||||||||||||||||||||||
|
k > N(ε) |
aij − aij |
6 |
|||||||||||||||||||||||||
|
A |
Ak |
(k) |
= aij, то есть lim Ak = A. |
||||||||||||||||||||||||
|
k |
− |
k |
< ε и, следовательно, lim aij |
||||||||||||||||||||||||
|
k→∞ |
k→∞ |
Кроме того, если A → Ak то имеем:
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

|kAk − kAkk| 6 kA − Akk → 0 при k → ∞.
Поэтому lim kAkk = kAk.
k→∞
Вывод. Последовательность Ak → 0, где k → ∞, тогда и только тогда, когда lim kAkk = 0, где kAkk
k→∞
какая-нибудь каноническая норма.
Легко убедиться, что если lim Ak = A и lim Bk = B, то:
k→∞ k→∞
1. lim (Ak ± Bk) = A ± B;
k→∞
2. lim (AkBk) = AB;
k→∞
3. lim A−k 1 = A−1(det A 6= 0),
k→∞
подразумевая, что соответствующие операции имеют смысл. В частности, если C — матрица — такая, что возможно умножение CAk и AkC, k = 1, 2, . . ., то
|
lim CAk = CA и |
lim AkC = CA. |
|
k→∞ |
k→∞ |
Лемма 2 Для сходимости последовательности матриц Ak (k = 1, 2, . . .) необходимо и достаточно, чтобы был выполнен обобщенный критерий Коши, а именно: для всякого ε > 0 должен существовать такой номер N = N(ε), что при k > N kAk+1 − Akk 6 ε, где kk — любая каноническая норма.
•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель
Соседние файлы в папке Лекции
- #
- #
27.02.2016144.88 Кб19r1.pdf
- #
- #
27.02.2016272.57 Кб42r2.pdf
- #
27.02.2016350.47 Кб87r3.pdf
- #
- #
- #
27.02.2016226.53 Кб198r6.pdf
- #
27.02.2016155.25 Кб20r7.pdf
- #
27.02.2016248.73 Кб20r8.pdf
§ 7.
Абсолютная величина и норма матрицы
Неравенство
(1)
Между
матрицами 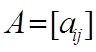
одинаковых
типов обозначает, что
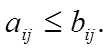
В
этом смысле не всякие две матрицы сравнимы между собой.
Под
абсолютной величиной (модулем) матрицы будем
понимать матрицу
где
– модули элементов матрицы
.
Если
и
–
матрицы, для которых операции и
имеют смысл, то:
а)
б)
в)
( — число).
В
частности, получаем:
(
— натуральное число).
Под нормой матрицы понимается действительное число
, удовлетворяющее условиям:
а) причем
тогда и только тогда, когда
=0;
б) 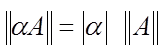
— число ) и, в частности,
;
в)
г)
( и
— матрицы, для которых соответствующие
операции имеют смысл). В частности, для квадратной матрицы имеем:
где —
натуральное число.
Отметим еще одно
важное неравенство между нормами матриц и
одинакового типа. Применяя условие в),
будем иметь:
Отсюда
Аналогично
Следовательно,
Назовем норму
канонической, если дополнительно выполнены условия:
д) если 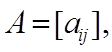
причем для скалярной матрицы 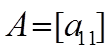
е) из неравенства 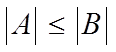
В частности, 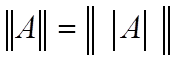
В дальнейшем для матрицы 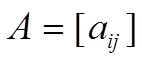
рассматривать главным образом три легко вычисляемые нормы:
1) 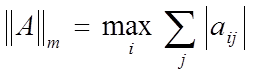
2) 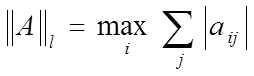
— норма);
3) 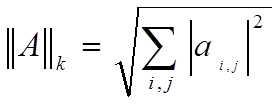
— норма).
П р и м е р. Пусть
Имеем:
§ 9. Предел матрицы
Пусть имеется последовательность матриц

oдного и того же типа 
Под пределом последовательности
матриц понимается матрица
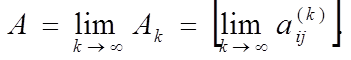
Последовательность матриц,
имеющая предел ,называется сходящейся.
Л
е м м а 1. Для сходимости последовательности матриц к матрице (к =1,2,…) к матрице А необходимо и
достаточно, чтобы
при
(3)
где любая коническая
норма матрицы А. При этом
Действительно, если
то
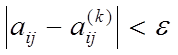
Отсюда
где
I – матрица
типа , все элементы которой равны единице.
В
силу свойств нормы имеем:
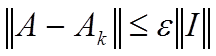
следовательно,
Обратно,
пусть выполнено условие (3). Тогда при имеем:
и,
следовательно,
т.
е.
Кроме
того, если то имеем:
Поэтому
С
л е д с т в и е. Последовательность 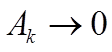
тогда и только тогда, когда
где
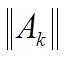
Легко
убедиться, что если
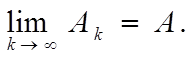
то:
a)
б)
в)
в
предложении, что соответствующие операции имеют смысл. В частности, если – постоянная матрица такая, что возможны
перемножения и
то
и
Л
е м м а 2. Для сходимости последовательности
матриц 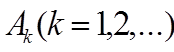
выполнен обобщенный критерий Коши, а именно: для всякого должен существовать такой номер
что при
где
— любая каноническая норма.
|
1 / 1 / 1 Регистрация: 10.12.2015 Сообщений: 91 |
|
|
1 |
|
Вычислить предел матрицы07.03.2016, 14:43. Показов 7821. Ответов 6
Нужно вычислить предел: Добавлено через 16 минут
0 |
|
4652 / 3404 / 361 Регистрация: 11.11.2010 Сообщений: 6,205 Записей в блоге: 2 |
|
|
07.03.2016, 17:25 |
2 |
|
Nickname_2015, ну проще всего, наверное, использовать представление Добавлено через 6 минут Добавлено через 5 минут
1 |
|
761 / 662 / 195 Регистрация: 24.11.2015 Сообщений: 2,158 |
|
|
07.03.2016, 17:29 |
3 |
|
По-моему, все очевидно
1 |
|
543 / 486 / 104 Регистрация: 05.05.2014 Сообщений: 1,110 |
|
|
07.03.2016, 17:35 |
4 |
|
Тут некоторая путаница. Чему равна матрица А? Она разная для разных n? Тогда как мы можем говорить о ее степени?
1 |
|
4652 / 3404 / 361 Регистрация: 11.11.2010 Сообщений: 6,205 Записей в блоге: 2 |
|
|
07.03.2016, 17:36 |
5 |
|
AGK, нет. Там ведь в степени эн.
1 |
|
543 / 486 / 104 Регистрация: 05.05.2014 Сообщений: 1,110 |
|
|
07.03.2016, 17:37 |
6 |
|
Не понимаю вообще в чем проблема В расплывчатой постановке.
1 |
|
761 / 662 / 195 Регистрация: 24.11.2015 Сообщений: 2,158 |
|
|
07.03.2016, 17:37 |
7 |
|
Решение А если имеется возведение в степень, то этот вариант приведу ниже
2 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
07.03.2016, 17:37 |
|
Помогаю со студенческими работами здесь Вычислить предел Вычислить предел Вычислить предел lim_{nrightarrowinfty }… Вычислить предел lim_{x to 0} {frac{sin 5x-sin 2x}{x}} x… Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 7 |
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Матрица в бесконечной степени
|
|
25/07/14 |
Необходимо возвести матрицу в бесконечную степень, то есть найти предел
|
|
|
|
|
ИСН |
Re: Матрица в бесконечной степени
|
||
18/05/06 |
Существует ли метод перехода к базису, в котором матрица имеет диагональный вид, для матриц nxn Да, но придётся решать уравнение n-ой степени для нахождения собственных чисел Это — эффективно. Смиритесь. Все так делают.
|
||
|
|
|||
|
Евгений Машеров |
Re: Матрица в бесконечной степени
|
||
11/03/08 |
Ну, я бы заметил, что решение уравнения n-ной степени для нахождения собственных чисел (и предварительное выписывание этого уравнения) позволяет найти собственные числа, только пользуются этим достаточно редко. Есть куда более эффективные численные методы.
|
||
|
|
|||
|
ewert |
Re: Матрица в бесконечной степени
|
||
11/05/08 |
Необходимо возвести матрицу в бесконечную степень, то есть найти предел А зачем?… Этот предел либо не существует, либо равен нулю, либо (в совсем уж частных случаях) есть некоторый проектор. Ну и какая от этого может быть польза для сельского хозяйства?… — Пт июл 25, 2014 14:37:44 — Если какое-то собственное число больше единицы — такого предела нет, равно и если есть меньше минус единицы. А если больше или меньше мнимой единицы?…
|
||
|
|
|||
|
ИСН |
Re: Матрица в бесконечной степени
|
||
18/05/06 |
Короче, так: итерационным методом находим максимальное по модулю собственное число. Если оно больше 1, то нам конец. Если меньше, то — конец матрице: она вся упадёт к 0. Если равно 1, то находим его собственные векторы, приводимся к ним и дальше как обычно.
|
||
|
|
|||
|
ewert |
Re: Матрица в бесконечной степени
|
||
11/05/08 |
Если равно 1, то находим его собственные векторы, приводимся к ним и дальше как обычно. Не так быстро. Во-первых, это не все варианты. Во-вторых, даже для единицы есть варианты.
|
||
|
|
|||
|
ИСН |
Re: Матрица в бесконечной степени
|
||
18/05/06 |
Есть, разумеется: -1 или комплексные корни с модулем 1. Тогда всё плохо, предела нет. А какие ещё варианты?
|
||
|
|
|||
|
Red_Herring |
Re: Матрица в бесконечной степени
|
||
31/01/14 |
А какие ещё варианты? Соответствующие жордановы клетки.
|
||
|
|
|||
|
Евгений Машеров |
Re: Матрица в бесконечной степени
|
||
11/03/08 |
Необходимо возвести матрицу в бесконечную степень, то есть найти предел А зачем?… Этот предел либо не существует, либо равен нулю, либо (в совсем уж частных случаях) есть некоторый проектор. Ну и какая от этого может быть польза для сельского хозяйства?… — Пт июл 25, 2014 14:37:44 — Если какое-то собственное число больше единицы — такого предела нет, равно и если есть меньше минус единицы. А если больше или меньше мнимой единицы?… Вы правы, меня что-то ограничило случаем симметричных матриц и, вследствие этого, только действительных с.з. В общем случае либо вне единичного круга (и тогда убегает), либо внутри (и тогда в ноль), либо на самом единичном круге, и если не единица, при которой предел есть, то крутимся по кругу.
|
||
|
|
|||
|
ИСН |
Re: Матрица в бесконечной степени
|
||
18/05/06 |
C небольшой натяжкой могу придумать приложение с довольно крупными матрицами, где сама природа задачи гарантирует нам наличие собственного числа 1, отсутствие больших с.ч., и следовательно — нетривиальный ответ.
|
||
|
|
|||
|
ewert |
Re: Матрица в бесконечной степени
|
||
11/05/08 |
гарантирует нам наличие собственного числа 1, отсутствие больших с.ч., и следовательно — нетривиальный ответ. и если не единица, при которой предел есть, Соответствующие жордановы клетки.
|
||
|
|
|||
|
ИСН |
Re: Матрица в бесконечной степени
|
||
18/05/06 |
Да-да, я понял. Вот и без всяких вредных клеток тоже.
|
||
|
|
|||
|
MathKir |
Re: Матрица в бесконечной степени
|
|
25/07/14 |
Всем спасибо за ответы. Попытаюсь действовать через нахождение собственных чисел.
|
|
|
|
|
Henrylee |
Re: Матрица в бесконечной степени
|
||
30/10/07 |
Еще вариант. Если (маловероятно, а вдруг?) речь идет о стохастической матрице переходов однородной цепи Маркова, то (при положительности элементов матрицы
|
||
|
|
|||
|
MathKir |
Re: Матрица в бесконечной степени
|
|
25/07/14 |
Еще вариант. Если (маловероятно, а вдруг?) речь идет о стохастической матрице переходов однородной цепи Маркова, то (при положительности элементов матрицы Речь идёт именно о стохастической матрице переходов однородной цепи Маркова) Не могли бы Вы привести упомянутую систему?
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
$begingroup$
I’m trying to learn how to show a series of matrices is convergent and find the limit. However my numerical analysis books fail to mention this and I cannot find any relevant material online! Anyway say I had
$sum_{k=0}^ infty A^K$, where A = $begin{bmatrix}frac{1}{2} & -2 & -1\0 & frac{1}{3} & 0\ 0 & 0 & -frac{1}{2}end{bmatrix}$
How would i show that the series of matrrices converges and compute its limit?
Would I use some kind of induction? Some help would be amazing, many thanks!
asked Apr 18, 2013 at 0:01
user67411user67411
3112 gold badges4 silver badges10 bronze badges
$endgroup$
2
$begingroup$
Hints:
-
How would you first write the matrix power $A^K$?
-
Once you have an expression for $A^K$, you can take the sum to each $a_{i,j}$ in your 3×3. Of course four of the terms are immediately known! Also, two of terms in the diagonal are the same, so you would be finding the sum of four expressions that are sums over $k$.
Update
So, here our sum is:
$$displaystyle sum_{k=0}^infty A^k = sum_{k=0}^infty begin{bmatrix}-frac{1}{2} & -2 & -1\0 & frac{1}{3} & 0\ 0 & 0 & -frac{1}{2}end{bmatrix}^k = sum_{k=0}^infty begin{bmatrix}(-1/2)^k & left(frac{4}{5}right) 3^{1-k} ((-3/2)^k-1) & (-1)^k 2^{1-k} k \ 0 & 3^{-k} & 0 \ 0 & 0 & (-1/2)^k)end{bmatrix}$$
Now, how do you evaluate each of these sums and do they each converge?
Update 2
You should get:
$$displaystyle sum_{k=0}^infty A^k = begin{bmatrix}frac{2}{3} & -2 & -frac{4}{9}\0 & frac{3}{2} & 0\0 & 0 & frac{2}{3}end{bmatrix}$$
I would also recommend taking this answer and seeing how the other answers apply.
answered Apr 18, 2013 at 0:17
AmzotiAmzoti
55.7k25 gold badges76 silver badges111 bronze badges
$endgroup$
10
$begingroup$
Choose any algebra norm $||.||$ and if $||A||<1$ then the geometric series
$$sum_{k=0}^infty ||A||^k$$
is convergent so the series $displaystylesum_{k=0}^infty A^k$ is normal convergent and then it’s convergent.
One possible method to calulate the limit: let $pi_A$ the minimal polynomial of $A$ and by the Euclidean division we have
$$x^k=Q(x)pi_A(x)+R_k(x)$$
with $deg(R_k)<deg(pi_A)$
and we have $$sum_{k=0}^infty A^k=sum_{k=0}^infty R_k(A)$$
and the last sum is more simple to calculate.
Added
In our case, the matrix $A$ is triangular and since $(A+frac{1}{2}I_3)(A-frac{1}{3}I_3)neq0$ so we can see easly that the minimal polynomial is
$$pi_A(x)=frac{1}{12}(3x-1)(2x+1)^2$$
hence in the Euclidean division the remainder polynomial is
$$R_k(x)=a_k x^2+b_k x+c_k$$
and we have
$$begin{align}\
left(frac{1}{3}right)^k&=a_k/9+b_k/3+c_k\
left(frac{1}{2}right)^k&=a_k/4-b_k/2+c_k\
kleft(frac{-1}{2}right)^{k-1}&=-a_k+b_k\
end{align}$$
so we solve the above system for $a_k,b_k$ and $c_k$ and finally we find
$$sum_{k=0}^infty A^k=left(sum_{k=0}^infty a_kright)A^2+left(sum_{k=0}^infty b_kright)A+left(sum_{k=0}^infty c_kright)I_3$$
answered Apr 18, 2013 at 0:17
$endgroup$
8
$begingroup$
A special solution to this problem:
You may write $A = D+N$, where $D$ is diagonal and $N$ is nilpotent in an obvious way. Then it is easy to see (either by a direct calculation or by the celebrated Cayley-Hamilton theorem) that $N^3 = O$ and thus we can simply $A^k$ as
$$ A^k = D^k + kD^{k-1}N + frac{k(k-1)}{2}D^{k-2}N^2. $$
Now both the convergence and the summation value can be easily analyzed from the knowledge on power series in $Bbb{R}$.
answered Apr 18, 2013 at 0:21
Sangchul LeeSangchul Lee
153k16 gold badges255 silver badges411 bronze badges
$endgroup$
3
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.

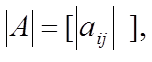
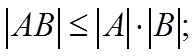
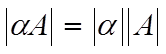
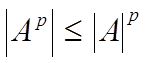
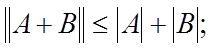
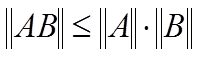
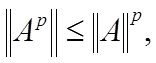
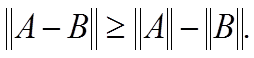
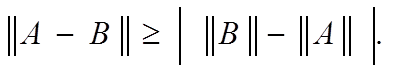
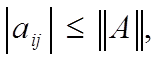
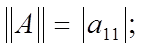
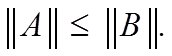
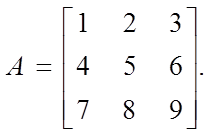
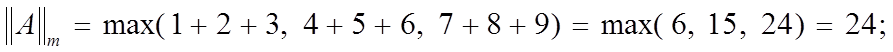
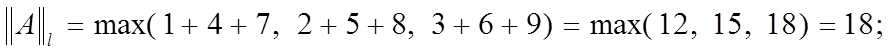
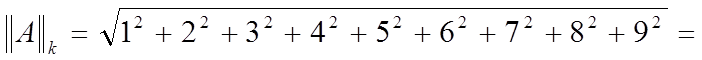
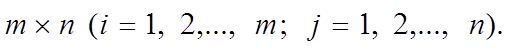
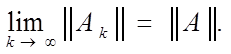
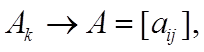
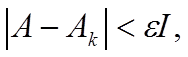
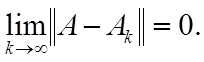
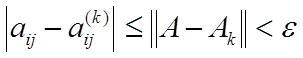
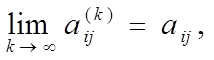
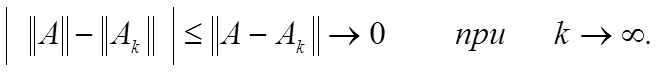
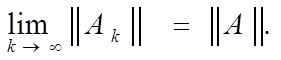
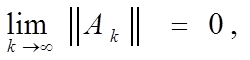
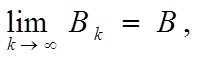
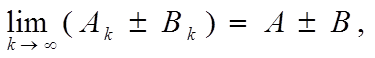
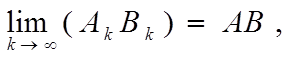
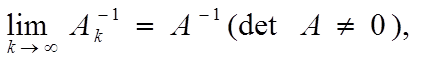
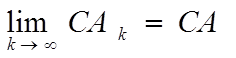
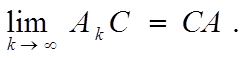



 Сообщение было отмечено Igor как решение
Сообщение было отмечено Igor как решение
 . Если матрица 2×2, то можно найти собственные векторы и перейти к базису, в котором матрица имеет диагональный вид, а потом сделать обратное преобразование. К сожалению, матрица имеет большую размерность (вообще говоря, есть множество матриц разных размерностей). Существует ли метод перехода к базису, в котором матрица имеет диагональный вид, для матриц nxn (решать уравнение n-ой степени для нахождения собственных чисел не вариант)? Или как можно эффективно решить исходную задачу?
. Если матрица 2×2, то можно найти собственные векторы и перейти к базису, в котором матрица имеет диагональный вид, а потом сделать обратное преобразование. К сожалению, матрица имеет большую размерность (вообще говоря, есть множество матриц разных размерностей). Существует ли метод перехода к базису, в котором матрица имеет диагональный вид, для матриц nxn (решать уравнение n-ой степени для нахождения собственных чисел не вариант)? Или как можно эффективно решить исходную задачу?
 для некоторого
для некоторого  ) пределом будет матрица с одинаковыми столбцами, составленными из векторов стационарного распределения упомянутой марковской цепи. Которое ищется путем решения линейной системы, т.е. очень просто.
) пределом будет матрица с одинаковыми столбцами, составленными из векторов стационарного распределения упомянутой марковской цепи. Которое ищется путем решения линейной системы, т.е. очень просто.