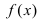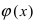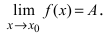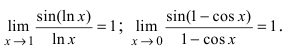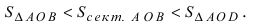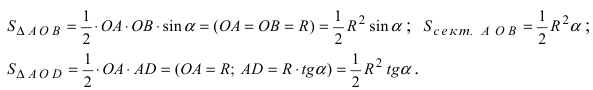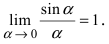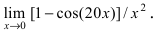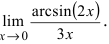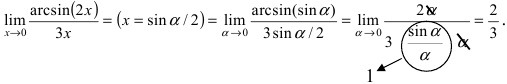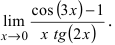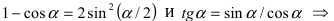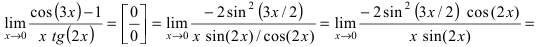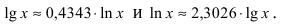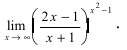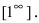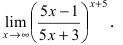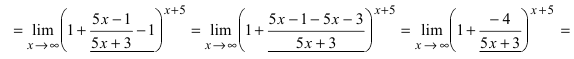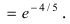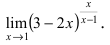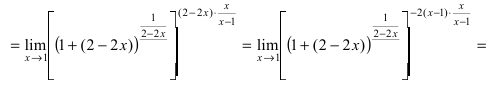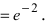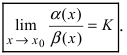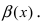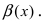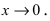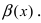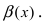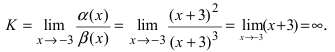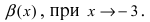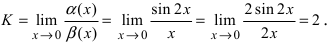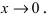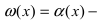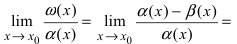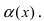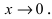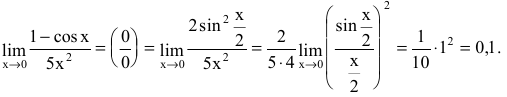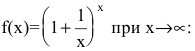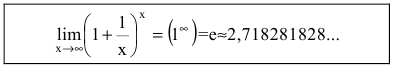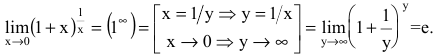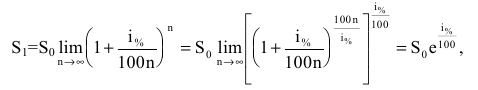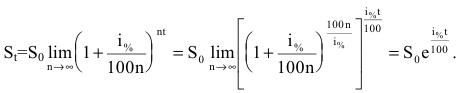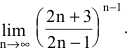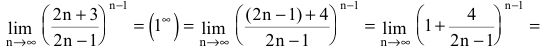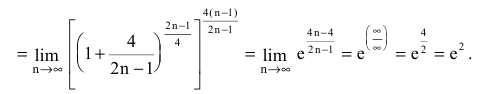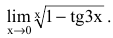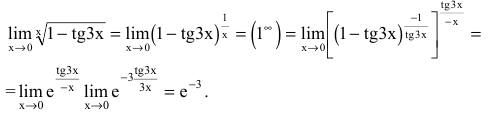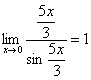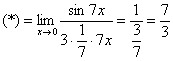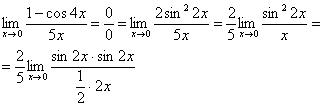Второй замечательный предел
Данная статья: «Второй замечательный предел» посвящена раскрытию в пределах неопределенностей вида:
$ bigg[frac{infty}{infty}bigg]^infty $ и $ [1]^infty $.
Так же такие неопределенности можно раскрывать с помощью логарифмирования показательно-степенной функции, но это уже другой метод решения, о котором будет освещено в другой статье.
Формула и следствия
Формула второго замечательного предела записывается следующим образом: $$ lim_{x to infty} bigg (1+frac{1}{x}bigg)^x = e, text{ где } e approx 2.718 $$
Из формулы вытекают следствия, которые очень удобно применять для решения примеров с пределами: $$ lim_{x to infty} bigg (1 + frac{k}{x} bigg)^x = e^k, text{ где } k in mathbb{R} $$ $$ lim_{x to infty} bigg (1 + frac{1}{f(x)} bigg)^{f(x)} = e $$ $$ lim_{x to 0} bigg (1 + x bigg)^frac{1}{x} = e $$
Стоить заметить, что второй замечательный предел можно применять не всегда к показательно-степенной функции, а только в случаях когда основание стремится к единице. Для этого сначала в уме вычисляют предел основания, а затем уже делают выводы. Всё это будет рассмотрено в примерах решений.
Примеры решений
Рассмотрим примеры решений с использованием прямой формулы и её следствий. Так же разберем случаи, при которых формула не нужна. Достаточно записать только готовый ответ.
| Пример 1 |
| Найти предел $ lim_{xtoinfty} bigg( frac{x+4}{x+3} bigg)^{x+3} $ |
| Решение |
|
Подставим бесконечность в предел и посмотрим на неопределенность: $$ lim_{xtoinfty} bigg( frac{x+4}{x+3} bigg)^{x+3} = bigg(frac{infty}{infty}bigg)^infty $$ Найдем предел основания: $$ lim_{xtoinfty} frac{x+4}{x+3}= lim_{xtoinfty} frac{x(1+frac{4}{x})}{x(1+frac{3}{x})} = 1 $$ Получили основание равное единице, а это значит уже можно применить второй замечательный предел. Для этого подгоним основание функции под формулу путем вычитания и прибавления единицы: $$ lim_{xtoinfty} bigg( 1 + frac{x+4}{x+3} — 1 bigg)^{x+3} = lim_{xtoinfty} bigg( 1 + frac{1}{x+3} bigg)^{x+3} = $$ Смотрим на второе следствие и записываем ответ: $$ lim_{xtoinfty} bigg( 1 + frac{1}{x+3} bigg)^{x+3} = e $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ lim_{xtoinfty} bigg( 1 + frac{1}{x+3} bigg)^{x+3} = e $$ |
| Пример 2 |
| Определить предел $ lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{x^2} $ |
| Решение |
|
Замечаем, что основание степени стремится к единице $ 1+frac{1}{x^3} to 1 $, при $ xtoinfty $, а показатель $ x^2 to infty $. Поэтому можно применить второе следствие. Но сперва, разберемся с показателем и приведем его в нужный вид — сделаем равным знаменателю основания. Для этого умножим его на $ x $ и разделим на него же. Получаем: $$ lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{x^2 cdot frac{x}{x}} = lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{frac{x^3}{x}} = $$ Уже теперь применяем формулу и получаем: $$ lim_{xtoinfty}e^ frac{1}{x} = e^{lim_{xtoinfty} frac{1}{x}} = e^0 = 1 $$ |
| Ответ |
| $$ lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{x^2} = 1 $$ |
| Пример 3 |
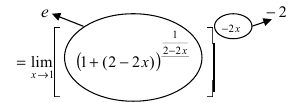
| Вычислить предел $ lim_{xto 1} (6-5x)^frac{x}{x-1} $ |
| Решение |
|
Получаем неопределенность $ 1^infty $. Для её раскрытия воспользуемся вторым замечательным пределом. Но у нас $ xto 1 $. Как быть? Выполняем замену $ y = x-1 $, тогда $ yto 0 $, при $ x to 1 $. Из замены следует, что $ x = y + 1 $. $$ lim_{xto 1} (6-5x)^frac{x}{x-1} = lim_{yto 0} (6-5(y+1))^frac{y+1}{y} = 1^infty = $$ $$ = lim_{yto 0} (1-5y)^frac{y+1}{y} = lim_{yto 0} (1+(-5y))^frac{(y+1)cdot (-5)}{-5cdot y} = $$ $$ = lim_{yto 0} e^{-5cdot (y+1)} = e^{-5} $$ |
| Ответ |
| $$ lim_{xto 1} (6-5x)^frac{x}{x-1} = e^{-5} $$ |
| Пример 4 |
| Решить предел $ lim_{xto infty} bigg (frac{3x^2+4}{3x^2-2} bigg) ^{3x} $ |
| Решение |
|
Находим предел основания и видим, что $ lim_{xtoinfty} frac{3x^2+4}{3x^2-2} = 1 $, значит можно применить второй замечательный предел. Стандартно по плану прибавляем и вычитаем единицу из основания степени: $$ lim_{xto infty} bigg (1+frac{3x^2+4}{3x^2-2}-1 bigg) ^{3x} = lim_{xto infty} bigg (1+frac{6}{3x^2-2} bigg) ^{3x} = $$ Подгоняем дробь под формулу 2-го замеч. предела: $$ = lim_{xto infty} bigg (1+frac{1}{frac{3x^2-2}{6}} bigg) ^{3x} = $$ Теперь подгоняем степень. В степени должна быть дробь равная знаменателю основания $ frac{3x^2-2}{6} $. Для этого умножим и разделим степень на неё, и продолжим решать: $$ = lim_{xto infty} bigg (1+frac{1}{frac{3x^2-2}{6}} bigg) ^{frac{3x^2-2}{6} cdot frac{6}{3x^2-2}cdot 3x} = lim_{xto infty} e^{frac{18x}{3x^2-2}} = $$ Предел, расположенный в степени при $ e $ равен: $ lim_{xto infty} frac{18x}{3x^2-2} = 0 $. Поэтому продолжая решение имеем: $$ = e^0 = 1 $$ |
| Ответ |
| $$ lim_{xto infty} bigg (frac{3x^2+4}{3x^2-2} bigg) ^{3x} = 1 $$ |
Разберем случаи, когда задача похожа на второй замечательный предел, но решается без него.
| Пример 5 |
| Найти $ lim_{xtoinfty} bigg ( frac{x+3}{3x+4} bigg )^{x+1} $ |
| Решение |
|
Начинаем с проверки равен ли предел основания единице. Имеем: $$ lim_{xtoinfty} frac{x+3}{3x+4} = frac{1}{3} $$ А это значит, что формулировка второго замечательного предела не соответствует данной задаче, так как $ frac{1}{3}ne 1 $ Продолжаем вычисление предела: $$ lim_{xtoinfty} bigg ( frac{x+3}{3x+4} bigg )^{x+1} = bigg (frac{1}{3} bigg ) ^infty = 0 $$ |
| Ответ |
| $$ lim_{xtoinfty} bigg ( frac{x+3}{3x+4} bigg )^{x+1} = 0 $$ |
| Пример 6 |
| Найти $ lim_{xtoinfty} bigg ( frac{3x+4}{x+3} bigg )^{x-5} $ |
| Решение |
|
Начинаем с проверки равен ли предел основания единице. Имеем: $$ lim_{xtoinfty} frac{3x+4}{x+3} = 3 $$ А это значит, что формулировка второго замечательного предела не соответствует данной задаче, так как $ 3 ne 1 $ Продолжаем вычисление предела: $$ lim_{xtoinfty} bigg ( frac{3x+4}{x+3} bigg )^{x-5} = 3^infty = infty $$ |
| Ответ |
| $$ lim_{xtoinfty} bigg ( frac{3x+4}{x+3} bigg )^{x-5} =infty $$ |
В статье: «Второй замечательный предел: примеры решений» была разобрана формула, её следствия и приведены частые типы задач по этой теме.
Второй замечательный предел
Обычно второй замечательный предел записывают в такой форме:
$$
begin{equation}
lim_{xtoinfty}left(1+frac{1}{x}right)^x=e
end{equation}
$$
Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $eapprox{2{,}718281828459045}$. Если сделать замену $t=frac{1}{x}$, то формулу (1) можно переписать в следующем виде:
$$
begin{equation}
lim_{tto{0}}biggl(1+tbiggr)^{frac{1}{t}}=e
end{equation}
$$
Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:
- Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
- Показатель степени (т.е. $x$ в формуле (1) или $frac{1}{t}$ в формуле (2)) должен стремиться к бесконечности.
Говорят, что второй замечательный предел раскрывает неопределенность $1^infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+infty$ или $-infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.
Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.
Пример №1
Вычислить предел $lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}$.
Решение
Сразу отметим, что основание степени (т.е. $frac{3x+1}{3x-5}$) стремится к единице:
$$
lim_{xtoinfty}frac{3x+1}{3x-5}=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{3+frac{1}{x}}{3-frac{5}{x}}
=frac{3+0}{3-0}
=1.
$$
При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $lim_{xtoinfty}(4x+7)=infty$.
Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+frac{1}{x}$, а в рассматриваемом нами примере основание степени таково: $frac{3x+1}{3x-5}$. Посему первым действием станет формальная подгонка выражения $frac{3x+1}{3x-5}$ под вид $1+frac{1}{x}$. Для начала прибавим и вычтем единицу:
$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}
=|1^infty|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
$$
Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
$$
frac{3x+1}{3x-5}-1
=frac{3x+1}{3x-5}-frac{3x-5}{3x-5}
=frac{3x+1-3x+5}{3x-5}
=frac{6}{3x-5}.
$$
Так как $frac{3x+1}{3x-5}-1=frac{6}{3x-5}$, то:
$$
lim_{xtoinfty}left(1+ frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right )^{4x+7}
$$
Продолжим «подгонку». В выражении $1+frac{1}{x}$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+frac{6}{3x-5}$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:
$$
1+frac{6}{3x-5}
=1+frac{1}{frac{3x-5}{6}}
$$
Таким образом,
$$
lim_{xtoinfty}left(1+frac{6}{3x-5}right )^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{4x+7}
$$
Итак, основание степени, т.е. $1+frac{1}{frac{3x-5}{6}}$, подогнано под вид $1+frac{1}{x}$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:
Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $frac{3x-5}{6}$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $frac{6}{3x-5}$. Итак, имеем:
$$
lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
$$
Отдельно рассмотрим предел дроби $frac{6cdot(4x+7)}{3x-5}$, расположенной в степени:
$$
lim_{xtoinfty}frac{6cdot(4x+7)}{3x-5}
=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{6cdotleft(4+frac{7}{x}right)}{3-frac{5}{x}}
=6cdotfrac{4}{3}
=8.
$$
Согласно формуле (1) имеем $lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}}=e$. Кроме того, $lim_{xtoinfty}frac{6cdot(4x+7)}{3x-5}=8$, поэтому возвращаясь к исходному пределу, получим:
$$
lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$
Полное решение без промежуточных пояснений будет иметь такой вид:
$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}=left|1^inftyright|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{4x+7}=\
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right)^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$
Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $frac{6}{3x-5}to{0}$ при $xtoinfty$, то применяя формулу (2), получим:
$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}=left|1^inftyright|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{4x+7}=\
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{6}{3x-5}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$
Ответ: $lim_{xtoinfty}left(frac{3x+1}{3x-5}right)^{4x+7}=e^8$.
Пример №2
Найти предел $lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}$.
Решение
Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $xto{1}$, т.е. $lim_{xto{1}}(7-6x)=7-6cdot1=1$. Для показателя степени, т.е. $frac{x}{3x-3}$, получаем: $lim_{xto{1}}frac{x}{3x-3}=infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела.
Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $xto{1}$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $xto{1}$, то ${x-1}to{0}$, т.е. $yto{0}$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $yto{0}$, получим:
$$
lim_{xto{1}}biggl(7-6xbiggr )^{frac{x}{3x-3}}
=left|begin{aligned}&y=x-1;;x=y+1\&yto{0}end{aligned}right|=\
=lim_{yto{0}}biggl(7-6cdot(y+1)biggr)^{frac{y+1}{3cdot(y+1)-3}}
=lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}
=lim_{yto 0}biggl(1+(-6y)biggr)^frac{y+1}{3y}
$$
Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $frac{1}{t}$, т.е. в нашем случае в показателе степени следует получить $frac{1}{-6y}$. Домножим показатель степени на выражение $frac{1}{-6y}$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $frac{-6y}{1}=-6y$:
$$
lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}=lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}cdot(-6y)cdotfrac{y+1}{3y}}
=lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
$$
Так как $lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}}=e$ и $lim_{yto{0}}(-2(y+1))=-2$, то получим:
$$
lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
=e^{-2}
=frac{1}{e^2}.
$$
Полное решение без пояснений таково:
$$
lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}
=left|begin{aligned}&y=x-1;;x=y+1\&yto{0}end{aligned}right|
=lim_{yto{0}}biggl(7-6cdot(y+1)biggr)^{frac{y+1}{3cdot(y+1)-3}}=\
=lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}
=lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}cdot(-6y)cdotfrac{y+1}{3y}}
=lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
=e^{-2}
=frac{1}{e^2}.
$$
Ответ: $lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}=frac{1}{e^2}$.
Пример №3
Найти предел $lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}$.
Решение
Так как $lim_{xto{0}}(cos{2x})=1$ и $lim_{xto{0}}frac{1}{sin^2{3x}}=infty$ (напомню, что $sin{u}to{0}$ при $uto{0}$), то мы имеем дело с неопределённостью вида $1^infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:
$$
lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}
=|1^infty|
=lim_{xto{0}}biggl(1+cos{2x}-1biggr)^{frac{1}{sin^2{3x}}}
$$
Так как $sin^2x=frac{1-cos{2x}}{2}$, то $cos{2x}-1=-2sin^2x$, поэтому:
$$
lim_{xto{0}}biggl(1+cos{2x}-1biggr)^{frac{1}{sin^2{3x}}}
=lim_{xto{0}}biggl(1+left(-2sin^2xright)biggr)^{frac{1}{-2sin^2x}cdot(-2sin^2x)cdotfrac{1}{sin^2 3x}}=\
=lim_{xto{0}}left(biggl(1+left(-2sin^2xright)biggr)^{frac{1}{-2sin^2x}}right)^{frac{-2sin^2{x}}{sin^2{3x}}}
=e^{-frac{2}{9}}.
$$
Здесь мы учли, что $lim_{xto{0}}frac{sin^2{x}}{sin^2{3x}}=frac{1}{9}$. Подробное описание того, как находить этот предел, дано в соответствующей теме.
Ответ: $lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}=e^{-frac{2}{9}}$.
Пример №4
Найти предел $lim_{xto+infty}xleft(ln(x+1)-ln{x}right)$.
Решение
Так как при $x>0$ имеем $ln(x+1)-ln{x}=lnleft(frac{x+1}{x}right)$, то:
$$
lim_{xto+infty}xleft(ln(x+1)-ln{x}right)
=lim_{xto+infty}left(xcdotlnleft(frac{x+1}{x}right)right)
$$
Раскладывая дробь $frac{x+1}{x}$ на сумму дробей $frac{x+1}{x}=1+frac{1}{x}$ получим:
$$
lim_{xto+infty}left(xcdotlnleft(frac{x+1}{x}right)right)
=lim_{xto+infty}left(xcdotlnleft(1+frac{1}{x}right)right)
=lim_{xto+infty}left(lnleft(frac{x+1}{x}right)^xright)
=ln{e}
=1.
$$
Ответ: $lim_{xto+infty}xleft(ln(x+1)-ln{x}right)=1$.
Пример №5
Найти предел $lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}$.
Решение
Так как $lim_{xto{2}}(3x-5)=6-5=1$ и $lim_{xto{2}}frac{2x}{x^2-4}=infty$, то мы имеем дело с неопределенностью вида $1^infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:
$$
lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}
=left|begin{aligned}&t=x-2;;x=t+2\&tto{0}end{aligned}right|
=lim_{tto{0}}biggl(1+3tbiggr)^{frac{2t+4}{t^2+4t}}=\
=lim_{tto{0}}biggl(1+3tbiggr)^{frac{1}{3t}cdot 3tcdotfrac{2t+4}{t^2+4t}}
=lim_{tto{0}}left(biggl(1+3tbiggr)^{frac{1}{3t}}right)^{frac{6cdot(t+2)}{t+4}}
=e^3.
$$
Можно решить данный пример и по-иному, используя замену: $t=frac{1}{x-2}$. Разумеется, ответ будет тем же:
$$
lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}
=left|begin{aligned}&t=frac{1}{x-2};;x=frac{2t+1}{t}\&ttoinftyend{aligned}right|
=lim_{ttoinfty}left(1+frac{3}{t}right)^{tcdotfrac{4t+2}{4t+1}}=\
=lim_{ttoinfty}left(1+frac{1}{frac{t}{3}}right)^{frac{t}{3}cdotfrac{3}{t}cdotfrac{tcdot(4t+2)}{4t+1}}
=lim_{ttoinfty}left(left(1+frac{1}{frac{t}{3}}right)^{frac{t}{3}}right)^{frac{6cdot(2t+1)}{4t+1}}
=e^3.
$$
Ответ: $lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}=e^3$.
Пример №6
Найти предел $lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x} $.
Решение
Выясним, к чему стремится выражение $frac{2x^2+3}{2x^2-4}$ при условии $xtoinfty$:
$$
lim_{xtoinfty}frac{2x^2+3}{2x^2-4}
=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{2+frac{3}{x^2}}{2-frac{4}{x^2}}
=frac{2+0}{2-0}=1.
$$
Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела:
$$
lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x}
=|1^infty|
=lim_{xtoinfty}left(1+frac{2x^2+3}{2x^2-4}-1right)^{3x}=\
=lim_{xtoinfty}left(1+frac{7}{2x^2-4}right)^{3x}
=lim_{xtoinfty}left(1+frac{1}{frac{2x^2-4}{7}}right)^{3x}=\
=lim_{xtoinfty}left(1+frac{1}{frac{2x^2-4}{7}}right)^{frac{2x^2-4}{7}cdotfrac{7}{2x^2-4}cdot 3x}
=lim_{xtoinfty}left(left(1+frac{1}{frac{2x^2-4}{7}}right)^{frac{2x^2-4}{7}}right)^{frac{21x}{2x^2-4}}
=e^0
=1.
$$
Ответ: $lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x}=1$.
- Первый замечательный предел
- Раскрытие неопределенностей (left[frac00right]) с тригонометрическими функциями
- Второй замечательный предел
- Раскрытие неопределенности (left[1^{infty}right])
- Примеры
п.1. Первый замечательный предел
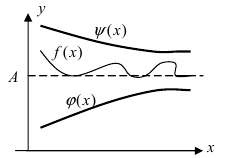
Исследуем поведение функции (f(x)=frac{sinx}{x}) вблизи (x_0=0).
Построим график.
Заполним таблицу со значениями (f(x)) непосредственно вблизи (x_0=0).
| x | -0,01 | -0,001 | -0,0001 | 0 | 0,0001 | 0,001 | 0,01 |
| sin(x)/x | 0,999983 | 0,99999983 | 0,9999999983 | [0/0] | 0,9999999983 | 0,99999983 | 0,999983 |
В самой точке 0 возникает неопределенность (left[frac00right]), но при приближении к ней с обеих сторон значение функции стремится к 1. Можем записать: $$ lim_{xrightarrow 0}frac{sinx}{x}=1 $$ Это равенство называют первым замечательным пределом.
п.2. Раскрытие неопределенностей (left[frac00right]) с тригонометрическими функциями
Из первого замечательного предела с помощью тригонометрических преобразований можно получить другие пределы: begin{gather*} lim_{xrightarrow 0}frac{tgx}{x}=1, lim_{xrightarrow 0}frac{arctgx}{x}=1\ lim_{xrightarrow 0}frac{arcsinx}{x}=1, lim_{xrightarrow 0}frac{1-cosx}{frac{x^2}{2}}=1 end{gather*} Все полученные формулы используются для раскрытия неопределенностей [0/0] при поиске пределов функций с тригонометрическими компонентами.
Например:
Найдем предел (lim_{xrightarrow 0}frac{1-cos4x}{x^2}) begin{gather*} lim_{xrightarrow 0}frac{1-cos4x}{x^2} = lim_{xrightarrow 0}frac{2sin^2 2x}{x^2}= 2lim_{xrightarrow 0}left(left(frac{sin2x}{x}right)cdotleft(frac{sin2x}{x}right)right)=\ =2cdot 4lim_{xrightarrow 0}left(left(frac{sin2x}{2x}right)cdotleft(frac{sin2x}{2x}right)right)= 8cdotlim_{xrightarrow 0}frac{sin2x}{2x}cdot lim_{xrightarrow 0}frac{sin2x}{2x}=8cdot 1cdot 1=8 end{gather*} Ответ: 8
п.3. Второй замечательный предел
Исследуем поведение функции (f(x)=left(1+frac1xright)^x) при (xrightarrowpminfty)
Построим график.
Заполним таблицу со значениями (f(x)) для больших по модулю x.
| (x) | -1000 | -100 | -10 | 10 | 100 | 1000 | 10000 |
| (left(1+frac1xright)^x) | 2,7196 | 2,7320 | 2,8680 | 2,5937 | 2,7048 | 2,7169 | 2,7181 |
На бесконечностях функция стремится к одному и тому же значению begin{gather*} e=2,7182818284\ lim_{xrightarrowinfty}left(1+frac1xright)^x=e end{gather*} Это равенство называют вторым замечательным пределом.
Число e часто называют числом Эйлера.
Бесконечность пишется без знаков, т.к. равенство справедливо как при (xrightarrow -infty), так и при (xrightarrow +infty).
п.4. Раскрытие неопределенности (left[1^{infty}right])
Если учесть, что (lim_{xrightarrowinfty}frac1x=0), тогда второй замечательный предел $$ lim_{xrightarrowinfty}left(1+frac1xright)^x=left[1^{infty}right]=e $$ дает ответ, чему равна единица в степени (infty). Поэтому его можно использовать для раскрытия неопределенностей, сводящихся к (left[1^{infty}right]).
Из второго замечательного предела с помощью преобразований для показательных и логарифмических функций можно получить другие полезные пределы: begin{gather*} lim_{xrightarrow 0}(1+x)^{frac1x}=e, lim_{xrightarrow infty}left(1+frac kxright)^x=e^k\ lim_{xrightarrow 0}frac{ln(1+x)}{x}=1, lim_{xrightarrow 0}frac{e^x-1}{x}=1 end{gather*} Для тех, кто заинтересовался, строгое доказательство замечательных пределов и их следствий можно найти в университетских учебниках по математическому анализу. Ваших знаний уже достаточно, чтобы полностью разобраться с этими вопросами.
Например:
Найдем предел (lim_{xrightarrow infty}left(frac{x+6}{x-2}right)^{3x+2})
Т.к. (lim_{xrightarrow infty}frac{x+6}{x-2}) и (lim_{xrightarrow infty}(3x+2)=infty), получаем неопределенность (left[1^{infty}right]).
Выделим целую часть из основания степени: $$ frac{x+6}{x-2}=frac{(x-2)+8}{x-2}=frac{x-2}{x-2}+frac{8}{x-2}=1+frac{8}{x-2} $$ Получаем: $$ lim_{xrightarrow infty}left(frac{x+6}{x-2}right)^{3x+2} = lim_{xrightarrow infty}left(1+frac{8}{x-2}right)^{3x+2} =left[1^{infty}right] $$ Замена переменных: (frac1t=frac{8}{x-2}, trightarrowinfty). Тогда (x=8t+2). begin{gather*} lim_{trightarrow infty}left(1+frac1tright)^{3(8t+2)+2}= lim_{trightarrow infty}left(1+frac1tright)^{24t+8} = left(lim_{trightarrow infty}left(1+frac1tright)^tright)^{24}cdot lim_{trightarrow infty}left(1+frac1tright)^8=\ =e^{24}cdot 1^8=e^{24} end{gather*} Здесь мы использовали (1^{infty}=e) и (1^8=1).
Ответ: (e^{24})
п.5. Примеры
Пример 1. Найдите значения пределов, используя первый замечательный предел:
a) ( lim_{xrightarrow 0}frac{1-cosx}{xsinx} ) begin{gather*} lim_{xrightarrow 0}frac{1-cosx}{xsinx}=left[frac00right]=lim_{xrightarrow 0}frac{2sin^2frac x2}{x^2underbrace{frac{sinx}{x}}_{=1}}=2lim_{xrightarrow 0}frac{sin^2frac x2}{x^2}=2lim_{xrightarrow 0}left(frac{sinfrac x2}{2cdotfrac x2}cdotfrac{sinfrac x2}{2cdotfrac x2}right)=\ =frac24lim_{xrightarrow 0}frac{sinfrac x2}{frac x2}cdot lim_{xrightarrow 0}frac{sinfrac x2}{frac x2}=frac12cdot 1cdot 1=frac12 end{gather*}
б) ( lim_{xrightarrow 0}frac{sin8x}{sin2x} ) begin{gather*} lim_{xrightarrow 0}frac{sin8x}{sin2x}=left[frac00right]=lim_{xrightarrow 0}frac{8xcdotoverbrace{frac{sin8x}{8x}}^{=1}}{2xcdotunderbrace{frac{sin2x}{2x}}_{=1}}=frac82=4 end{gather*}
в) ( lim_{xrightarrow 0}frac{sin(x^2-4)}{x^2-4} ) Заметим, что (lim_{xrightarrow 0}sin(x^2-4)=sin(-4)ne 0) и (lim_{xrightarrow 0}(x^2-4)=-4ne 0) $$ lim_{xrightarrow 0}frac{sin(x^2-4)}{x^2-4}neleft[frac00right] $$ Т.е., неопределенности (left[frac00right]) в этом примере нет, и он решается обычной подстановкой значения предела (x_0=0) вместо x: begin{gather*} lim_{xrightarrow 0}frac{sin(x^2-4)}{x^2-4}=frac{sin(-4)}{-4}=frac{-sin4}{-4}=frac{sin4}{4} end{gather*}
г) ( lim_{xrightarrow 2}frac{sin(x^2-4)}{x^2-4} ) А вот здесь при подстановке предела (x_0=2) получаем неопределенность (left[frac00right]). $$ lim_{xrightarrow 2}frac{sin(x^2-4)}{x^2-4}=left[frac00right] $$ Замена переменных: (t=x-2, trightarrow 0)
Тогда (x=t+2, x^2-4=(x-2)(x+2)=t(t+4)). Подставляем: begin{gather*} lim_{trightarrow 0}frac{sinleft(t(t+4)right)}{t(t+4)}=1 end{gather*} Последняя запись полностью соответствует определению первого замечательного предела с переменной (z=t(t+4), zrightarrow 0).
Внимание!
Следите, чтобы при подстановке значения предела в выражение действительно возникала неопределенность. И только тогда начинайте применять правила раскрытия неопределенностей и замечательные пределы.
Если неопределенности нет, то обычной подстановки достаточно, чтобы сразу получить ответ.
Что такое «неопределенность» — см. §37 данного справочника.
д) ( lim_{xrightarrow 0}frac{sqrt{x+3}-sqrt{3}}{sin5x} ) begin{gather*} lim_{xrightarrow 0}frac{sqrt{x+3}-sqrt{3}}{sin5x}=left[frac00right]=lim_{xrightarrow 0}frac{(sqrt{x+3}-sqrt{3})(sqrt{x+3}+sqrt{3})}{(sqrt{x+3}+sqrt{3})cdot sin5x}=\ =lim_{xrightarrow 0}frac{x+3-3}{(sqrt{x+3}+sqrt{3})cdot sin5x}= lim_{xrightarrow 0}frac{1}{(sqrt{x+3}+sqrt{3})cdotfrac{sin5x}{x}}=\ =lim_{xrightarrow 0}frac{1}{(sqrt{x+3}+sqrt{3})cdot 5cdot underbrace{frac{sin5x}{5x}}_{=1}}=frac15lim_{xrightarrow 0}frac{1}{sqrt{x+3}+sqrt{3}}=frac15cdotfrac{1}{2sqrt{3}}=frac{1}{10sqrt{3}}=frac{sqrt{3}}{30} end{gather*}
e*) ( lim_{xrightarrow 1}frac{sinpi x}{sin3pi x} ) При подстановке (x_0=1) получаем неопределенность (left[frac00right]).
Чтобы её раскрыть с помощью первого замечательного предела, нужно ввести новую переменную, которая стремится к 0.
Заметим, что: begin{gather*} sin(pi x-pi)=sinleft(pi(x-1)right)=-sinpi x\ sin(3pi x-3pi)=sinleft(3pi(x-1)right)=-sin3pi x end{gather*} Дробь можно заменить: $$ frac{sinpi x}{sin3pi x}=frac{-sinpi x}{-sin3pi x}=frac{sinleft(pi(x-1)right)}{sinleft(3pi(x-1)right)} $$ Замена переменной: (t=x-1, trightarrow 0). Получаем: begin{gather*} lim_{trightarrow 0}frac{sinpi t}{sin3pi t}=lim_{trightarrow 0}frac{pi tcdotoverbrace{frac{sinpi t}{pi t}}^{=1}}{3pi tcdotunderbrace{frac{sin3pi t}{3pi t}}_{=1}}=frac13 end{gather*} Ответ: а) (frac12); б) 4; в) (frac{sin4}{4}); г) 1; д) (frac{sqrt{3}}{30}); е) (frac 13)
Пример 2. Найдите значения пределов, используя второй замечательный предел:
a) ( lim_{xrightarrowinfty}left(1+frac{1}{3x}right)^{5x} ) $$ lim_{xrightarrowinfty}left(1+frac{1}{3x}right)^{5x}=left[1^{infty}right] $$ Замена переменной: (t=3x, trightarrowinfty). Тогда (x=frac t3). Подставляем: begin{gather*} lim_{xrightarrowinfty}left(1+frac 1tright)^{5cdotfrac t3}=left(underbrace{lim_{xrightarrowinfty}left(1+frac 1tright)^t}_{=e}right)^{frac53}=e^{frac53} end{gather*} б) ( lim_{xrightarrowinfty}left(frac{x-1}{x+4}right)^{2x} ) Предел основания степени: $$ lim_{xrightarrowinfty}frac{x-1}{x+4}=left[frac{infty}{infty}right]=lim_{xrightarrowinfty}frac{xleft(1-frac1xright)}{xleft(1+frac4xright)}=lim_{xrightarrowinfty}frac{1-frac1x}{1+frac4x}= frac{1-0}{1+0}=1 $$ Диагностируем неопределенность: $$ lim_{xrightarrowinfty}left(frac{x-1}{x+4}right)^{2x}=left[1^{infty}right] $$ Выделим целую часть из дроби: $$ frac{x-1}{x+4}=frac{(x+4)-5}{x+4}=1-frac{5}{x+4} $$ Замена: (t=-frac{(x+4)}{5}, trightarrowinfty) (знак бесконечности по условию не важен).
Тогда: (x=-5t-4). Подставляем: begin{gather*} lim_{xrightarrowinfty}left(frac{x-1}{x+4}right)^{2x}=lim_{xrightarrowinfty}left(1-frac{5}{x+4}right)^{2x}= lim_{trightarrowinfty}left(1+frac1tright)^{2cdot(-5t-4)}=\ =lim_{trightarrowinfty}left(1+frac1tright)^{-10t-8}=left(lim_{trightarrowinfty}left(1+frac1tright)^tright)^{-10}cdotlim_{trightarrowinfty}left(1+frac1tright)^{-8}=\ =e^{-10}cdot 1^{-8}=e^{-10} end{gather*}
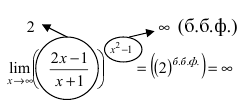
в) ( lim_{xrightarrow +infty}left(frac{2x-1}{x+4}right)^{2x} ) Предел основания степени: $$ lim_{xrightarrow +infty}frac{2x-1}{x+4}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{xleft(2-frac1xright)}{xleft(1+frac4xright)}=lim_{xrightarrow +infty}frac{2-frac1x}{1+frac4x}= frac{2-0}{1+0}=2 $$ Неопределенности здесь нет: $$ lim_{xrightarrow +infty}left(frac{2x-1}{x+4}right)^{2x}=2^{+infty}=+infty $$ Показательная функция с основанием >1 на плюс бесконечности стремится к плюс бесконечности.
г) ( lim_{xrightarrow -infty}left(frac{5x+3}{4x-1}right)^{3x-2} )
Предел основания степени: $$ lim_{xrightarrow -infty}frac{5x+3}{4x-1}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{xleft(5+frac3xright)}{xleft(4-frac1xright)}=lim_{xrightarrow -infty}frac{5+frac3x}{4-frac1x}= frac{5-0}{4+0}=frac54 $$ Неопределенности здесь нет: $$ lim_{xrightarrow -infty}left(frac{5x+3}{4x-1}right)^{3x-2}=left(frac54right)^{-infty}=left(frac45right)^{+infty}=0 $$ Показательная функция с основанием <1 на плюс бесконечности стремится к нулю.
д) ( lim_{xrightarrow 0}(1+tgx)^frac1x )
Подставляем (x_0=0) в функцию, и получаем неопределенность: $$ lim_{xrightarrow 0}(1+tgx)^frac1x=left[1^inftyright] $$ Используем следствие из второго замечательного предела: (lim_{xrightarrow 0}(1+x)^frac1x=e)
Преобразуем выражение: $$ lim_{xrightarrow 0}(1+tgx)^frac1x= lim_{xrightarrow 0}(1+tgx)^{frac{tgx}{xcdot tgx}}= lim_{xrightarrow 0}left((1+tgx)^{frac{1}{tgx}}right)^{frac{tgx}{x}} $$ Теперь используем следствие из первого замечательного предела: (lim_{xrightarrow 0}frac{tgx}{x}=1)
Тогда: $$ lim_{xrightarrow 0}(1+tgx)^{frac{1}{tgx}}= left[ begin{array}{l} t=tgx\ trightarrow 0 end{array} right] = lim_{trightarrow 0}(1+t)^frac1t=e $$ Здесь мы записали замену переменных «на ходу». Такая запись часто используется по необходимости, особенно при интегрировании.
Заметим, что если ввести понятие «эквивалентных бесконечно малых», то пример вообще решается в одну строку, т.к. (tgxsim x) при (xrightarrow 0).
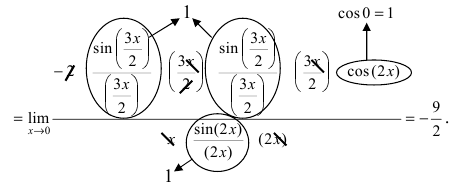
e*) ( lim_{xrightarrow 0}(cos2x)^frac{1}{sin^2 3x} )
Подставляем (x_0=0) в функцию, и получаем неопределенность: $$ lim_{xrightarrow 0}(cos2x)^frac{1}{sin^2 3x}=left[1^inftyright] $$ Используем следствие из второго замечательного предела: (lim_{xrightarrow 0}(1+x)^frac1x=e)
Преобразуем выражение: begin{gather*} lim_{xrightarrow 0}(cos2x)^frac{1}{sin^2 3x}= lim_{xrightarrow 0}(1-2sin^2 x)^frac{1}{sin^2 3x}= lim_{xrightarrow 0}left(1+(-2sin^2 x)right)^{frac{-2sin^2 x}{-2sin^2 xcdot sin^2 3x}}=\ lim_{xrightarrow 0}left((1+(-2sin^2 x))^{frac{1}{-2sin^2 x}}right)^{frac{-2sin^2x}{sin^2 3x}} end{gather*} Найдем предел для внешней степени: $$ lim_{xrightarrow 0}frac{-2sin^2x}{sin^2 3x}=left[frac00right]=-2lim_{xrightarrow 0}frac{x^2cdotleft(frac{sinx}{x}right)^2}{(3x)^2cdotleft(frac{sin3x}{3x}right)^2}= -2cdotfrac{1cdot 1}{9cdot 1}=-frac29 $$ Получаем: $$ lim_{xrightarrow 0}left((1+(-2sin^2x))^{frac{1}{-2sin^2x}}right)^{-frac29}= left[ begin{array}{l} t=-2sin^2 x\ trightarrow 0 end{array} right] = left(lim_{trightarrow 0}(1+t)^frac1tright)^{-frac29}=e^{-frac29} $$ Ответ: a) (e^{frac53}); б) (e^{-10}); в) (+infty); г) 0; д) (e); e) (e^{-frac29})
Содержание:
Замечательные пределы
Сравнение бесконечно малых функций
Признак существования предела (теорема о 2-х милиционерах)
Теорема: Если значения функции
значениями функций
Рассмотрим геометрический смысл данной теоремы (Рис. 62). Из рисунка видно, что в случае, когда функции 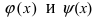
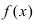
Рис. 62. Иллюстрация теоремы о “2-х милиционерах”.
Доказательство: Пусть 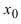
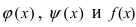
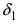
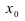
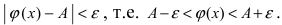
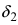
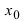
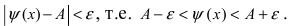
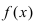
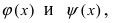
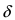
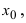
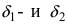
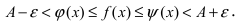
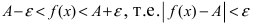
Первый замечательный предел
Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е. 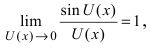
Пример:
Пределы являются первыми замечательными пределами 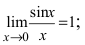
Доказательство: Для вывода этой формулы построим окружность с центром в точке О(0; 0) и радиусом R = 1. Выберем угол 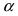
Рис. 63. Иллюстрация вывода формулы первого замечательного предела.
Из рисунка видно, что площади указанных фигу р связаны соотношением:
Вычислим эти площади
Следовательно, вышеприведенное неравенство приводится к виду 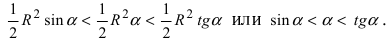
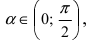
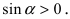
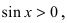
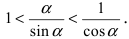
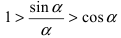
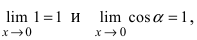
Аналогично проводится доказательство для любого значения угла
Таким образом, наличие в пределе, сводящемся к неопределенности 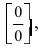
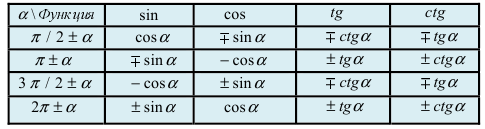
При вычислении первого замечательного предела используют следующие формулы:
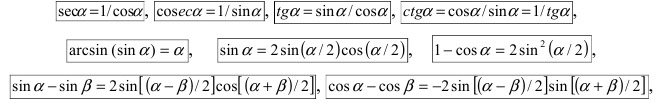
Табл. 1. Значения синуса и косинуса на интервале
Табл. 2. Формулы приведения.
Пример:
Найти
Решение:
При подстановке предельной величины переменной х имеем неопределенность 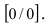
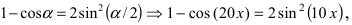
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 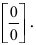
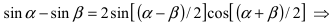
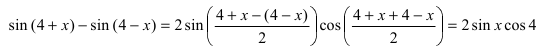
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 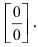
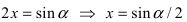
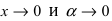
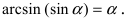
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 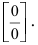
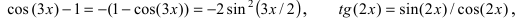
Число e и натуральные логарифмы. Второй замечательный предел
Рассмотрим логарифмическую функцию 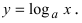
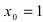
Определение: Натуральным логарифмом называется логарифм, для которого основание выбрано так, чтобы тангенс угла наклона касательной к положительному направлению оси абсцисс (Ох) был равен 1.
Основанием натурального логарифма является число 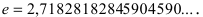
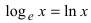
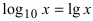
Определение: Вторым замечательным пределом называется предельное равенство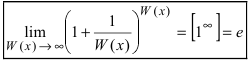
или
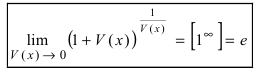
Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены 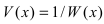
Замечание: Наличие неопределенности 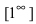
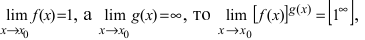
Пример:
Найти
Решение:
При подстановке предельного значения переменной х не имеем неопределенности
Пример:
Найти lim
Решение:
При подстановке предельного значения переменной х имеем неопределенность 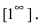
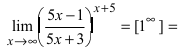
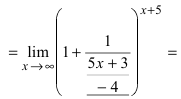
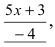
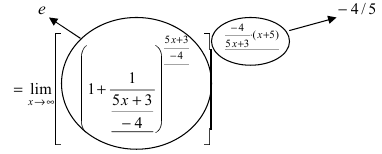
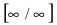
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределенность 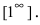
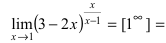
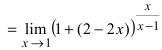
- Заказать решение задач по высшей математике
Сравнение бесконечно малых функций
Сравнить две бесконечно малые функции 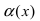
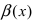
Определение: Если предел К не существует, то бесконечно малые функции 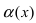
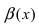
Пример:
Пусть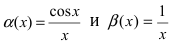
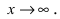
Решение:
Для доказательства вычислим предел 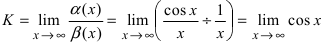
Определение: Если предел К равен нулю, то бесконечно малая функция 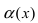
Пример:
Пусть 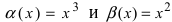
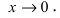
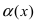
Решение:
Для доказательства вычислим предел 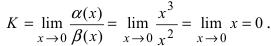
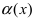
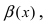
Определение: Если предел К равен 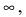
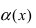
Пример:
Пусть 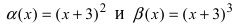
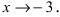
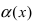
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малая функция 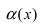
Определение: Если предел К равен конечному числу 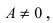
Пример:
Пусть 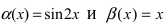
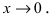
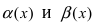
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малые функции 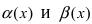
Определение: Если предел К равен 1, то бесконечно малые функции а(х) и Д(х) называются эквивалентными.
Пример:
Пусть 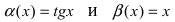
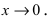
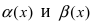
Решение:
Вычислим предел 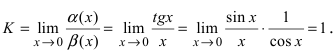

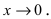
Теорема: Для того чтобы бесконечно малые функции 
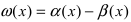

Доказательство:
1. Необходимость. Пусть бесконечно малая функция 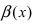
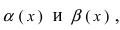
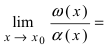
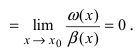
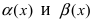
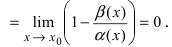
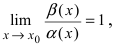
2. Достаточность. Пусть бесконечно малые функции 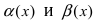
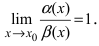
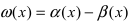
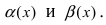
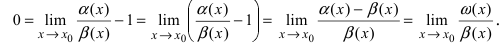
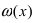
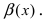
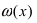
Замечание: При вычислениях одна бесконечно малая функция может быть заменена на эквивалентную бесконечно малую функцию. Например, функции 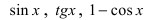
—вышмат
Замечательные пределы
Первый замечательный предел
Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:
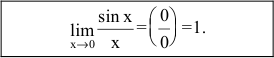
Пример №25
Найти
Решение:
Применим первый замечательный предел:
Второй замечательный предел
Числом е называется предел функции
(Для запоминания: 2<е<3; 1828 — год рождения Л.Н. Толстого) Следовательно,
Задача о непрерывном начислении процентов
Первоначальный вклад в банк составил 
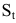
Решение:
Размер вклада будет увеличиваться ежегодно в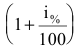
через t лет составит 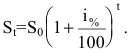
то будущая сумма составит 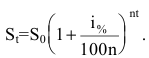
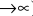
а за t лет:
Пример №26
Найти
Решение:
Т.к. 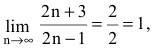
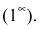
Пример №27
Найти
Решение:
Преобразуя выражение и используя непрерывность показательно-степенной функции, получим:
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
Замечательные пределы. Примеры решений
Продолжаем
наш разговор на тему Пределы
и способы их решения.
Перед изучением материалов данной
страницы настоятельно рекомендую
ознакомиться со статьей Пределы.
Примеры решений.
Из вышеуказанной статьи Вы сможете
узнать, что же такое предел, и с чем его
едят – это ОЧЕНЬ важно. Почему? Можно
не понимать, что такое определители и
успешно их решать, можно совершенно не
понимать, что такое производная и
находить их на «пятёрку». Но вот если
Вы не понимаете, что такое предел, то с
решением практических заданий придется
туго. Также не лишним будет ознакомиться
с образцами оформления решений и моими
рекомендациями по оформлению. Вся
информация изложена в простой и доступной
форме.
А для
целей данного урока нам потребуются
следующие методические материалы:Замечательные
пределы и Тригонометрические
формулы. Их можно
найти на страницеМатематические
формулы, таблицы и справочные материалы.
Лучше всего методички распечатать –
это значительно удобнее, к тому же к ним
часто придется обращаться в оффлайне.
Чем же замечательны
замечательные пределы? Замечательность
данных пределов состоит в том, что они
доказаны величайшими умами знаменитых
математиков, и благодарным потомкам не
приходиться мучаться страшными пределами
с нагромождением тригонометрических
функций, логарифмов, степеней. То есть
при нахождении пределов мы будем
пользоваться готовыми результатами,
которые доказаны теоретически.
Замечательных
пределов существует несколько, но на
практике у студентов-заочников в 95%
случаев фигурируют два замечательных
предела: Первый
замечательный предел,Второй
замечательный предел.
Следует отметить, что это исторически
сложившиеся названия, и, когда, например,
говорят о «первом замечательном пределе»,
то подразумевают под этим вполне
определенную вещь, а не какой-то случайный,
взятый с потолка предел.
Начнем.
Первый
замечательный предел
Рассмотрим
следующий предел:
(вместо
родной буквы «хэ» я буду использовать
греческую букву «альфа», это удобнее с
точки зрения подачи материала).
Согласно
нашему правилу нахождения пределов
(см. статью Пределы.
Примеры решений)
пробуем подставить ноль в функцию: в
числителе у нас получается ноль (синус
нуля равен нулю), в знаменателе, очевидно,
тоже ноль. Таким образом, мы сталкиваемся
с неопределенностью вида
,
которую, к счастью, раскрывать не нужно.
В курсе математического анализа,
доказывается, что:
Данный
математический факт носит название Первого
замечательного предела.
Нередко в
практических заданиях функции могут
быть расположены по-другому, это ничего
не меняет:
–
тот же самый первый
замечательный предел.
!
Но самостоятельно переставлять числитель
и знаменатель нельзя! Если дан предел
в виде
,
то и решать его нужно в таком же виде,
ничего не переставляя.
На
практике в качестве параметра
может
выступать не только переменная
,
но и элементарная функция, сложная
функция. Важно
лишь, чтобы она стремилась к нулю.
Примеры:
,
,
,
Здесь
,
,
,
,
и всё гуд – первый замечательный предел
применим.
А вот следующая
запись – ересь:
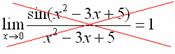
Почему?
Потому-что многочлен
не
стремится к нулю, он стремится к пятерке.
Кстати,
вопрос на засыпку, а чему равен предел
?
Ответ можно найти в конце урока.
На
практике не все так гладко, почти никогда
студенту не предложат решить халявный
предел
и
получить лёгкий зачет. Хммм… Пишу эти
строки и пришла в голову очень важная
мысль – все-таки «халявные» математические
определения и формулы вроде
лучше
помнить наизусть, это может оказать
неоценимую помощь на зачете, когда
вопрос будет решаться между «двойкой»
и «тройкой», и преподаватель решит
задать студенту какой-нибудь простой
вопрос или предложить решить простейший
пример («а может он (а) все-таки знает
чего?!»).
Переходим к
рассмотрению практических примеров:
Пример 1
Найти
предел
Если мы замечаем
в пределе синус, то это нас сразу должно
наталкивать на мысль о возможности
применения первого замечательного
предела.
Сначала
пробуем подставить 0 в выражение под
знак предела (делаем это мысленно или
на черновике):
Итак,
у нас есть неопределенность вида
,
ее обязательно
указываем в
оформлении решения. Выражение под знаком
предела у нас похоже на первый замечательный
предел, но это не совсем он, под синусом
находится
,
а в знаменателе
.
В
подобных случаях первый замечательный
предел нам нужно организовать
самостоятельно, используя искусственный
прием. Ход рассуждений может быть таким:
«под синусом у нас
,
значит, в знаменателе нам тоже нужно
получить
».
А
делается это очень просто:

То есть, знаменатель
искусственно умножается в данном случае
на 7 и делится на ту же семерку. Теперь
запись у нас приняла знакомые
очертания.
Когда задание оформляется
от руки, то первый замечательный предел
желательно пометить простым карандашом:
Что
произошло? По сути, обведенное выражение
у нас превратилось в единицу и исчезло
в произведении:
Теперь
только осталось избавиться от трехэтажности
дроби:
Готово.
Окончательный ответ:
Если не хочется
использовать пометки карандашом, то
решение можно оформить так:
“
Используем
первый замечательный предел
“
Пример 2
Найти
предел 
Опять
мы видим в пределе дробь и синус. Пробуем
подставить в числитель и знаменатель
ноль:

Действительно,
у нас неопределенность
и,
значит, нужно попытаться организовать
первый замечательный предел. На
уроке Пределы.
Примеры решений мы
рассматривали правило, что когда у нас
есть неопределенность
,
то нужно разложить числитель и знаменатель
на множители. Здесь – то же самое, степени
мы представим в виде произведения
(множителей):

Далее,
по уже знакомой схеме организовываем
первые замечательные пределы. Под
синусами у нас
,
значит, в числителе тоже нужно получить
:

Аналогично
предыдущему примеру, обводим карандашом
замечательные пределы (здесь их два), и
указываем, что они стремятся к единице:

Собственно, ответ
готов:
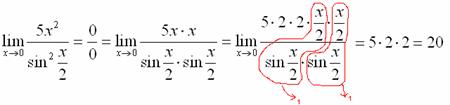
В следующих
примерах, я не буду заниматься художествами
в Пэйнте, думаю, как правильно оформлять
решение в тетради – Вам уже понятно.
Пример 3
Найти
предел
Подставляем ноль
в выражение под знаком передела:
Получена
неопределенность
,
которую нужно раскрывать. Если в пределе
есть тангенс, то почти всегда его
превращают в синус и косинус по известной
тригонометрической формуле
(кстати,
с котангенсом делают примерно то же
самое, см. методический материалГорячие
тригонометрические формулы на
странице Математические
формулы, таблицы и справочные материалы).
В данном случае:
Косинус нуля равен
единице, и от него легко избавиться (не
забываем пометить, что он стремится к
единице):
Таким образом,
если в пределе косинус является
МНОЖИТЕЛЕМ, то его, грубо говоря, нужно
превратить в единицу, которая исчезает
в произведении.
Дальше по накатанной
схеме, организуем первый замечательный
предел:

Здесь все вышло
проще, без всяких домножений и делений.
Первый замечательный предел тоже
превращается в единицу и исчезает в
произведении:

В итоге получена
бесконечность, бывает и такое.
Пример 4
Найти
предел
Пробуем подставить
ноль в числитель и знаменатель:
Получена
неопределенность
(косинус
нуля, как мы помним, равен единице)
Используем
тригонометрическую формулу
.
Возьмите на заметку! Пределы с применением
этой формулы почему-то встречаются
очень часто.
Постоянные множители
вынесем за значок предела:
Организуем первый
замечательный предел:
Здесь
у нас только один замечательный предел,
который превращается в единицу и исчезает
в произведении:
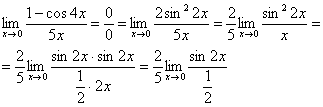
Избавимся от
трехэтажности:

Предел фактически
решен, указываем, что оставшийся синус
стремится к нулю:

Пример 5
Найти
предел
Этот пример сложнее,
попробуйте разобраться самостоятельно:

Второй
замечательный предел
В теории
математического анализа доказано, что:
Данный
факт носит название второго
замечательного предела.
Справка:
–
это иррациональное число.
В
качестве параметра
может
выступать не только переменная
,
но и сложная функция.Важно
лишь, чтобы она стремилась к бесконечности.
Пример 6
Найти
предел
Когда выражение
под знаком предела находится в степени
– это первый признак того, что нужно
попытаться применить второй замечательный
предел.
Но
сначала, как всегда, пробуем подставить
бесконечно большое число в выражение
,
по какому принципу это делается, разобрано
на уроке Пределы.
Примеры решений.
Нетрудно
заметить, что при
основание
степени
,
а показатель –
,
то есть имеется, неопределенность
вида
:
Данная
неопределенность как раз и раскрывается
с помощью второго замечательного
предела. Но, как часто бывает, второй
замечательный предел не лежит на блюдечке
с голубой каемочкой, и его нужно
искусственно организовать. Рассуждать
можно следующим образом: в данном примере
параметр
,
значит, в показателе нам тоже нужно
организовать
.
Для этого возводим основание в степень
,
и, чтобы выражение не изменилось –
возводим в степень
:
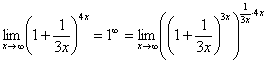
Когда задание
оформляется от руки, карандашом помечаем:
Практически
всё готово, страшная степень превратилась
в симпатичную букву
:
При
этом сам значок предела перемещаем в
показатель.

Далее, отметки
карандашом я не делаю, принцип оформления,
думаю, понятен.
Пример 7
Найти
предел
Внимание!
Предел подобного типа встречается очень
часто, пожалуйста, очень внимательно
изучите данный пример.
Пробуем подставить
бесконечно большое число в выражение,
стоящее под знаком предела:
В
результате получена неопределенность
.
Но второй замечательный предел применим
к неопределенности вида
.
Что делать? Нужно преобразовать основание
степени. Рассуждаем так: в знаменателе
у нас
,
значит, в числителе тоже нужно
организовать
:
Теперь можно
почленно разделить числитель на
знаменатель:
Вроде
бы основание стало напоминать
,
но у нас знак «минус» да и тройка какая-то
вместо единицы. Поможет следующее
ухищрение, делаем дробь трехэтажной:
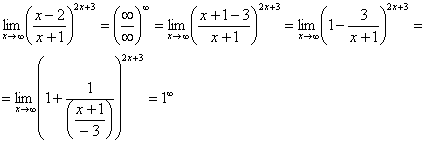
Таким
образом, основание приняло вид
,
и, более того, появилась нужная нам
неопределенность
.
Организуем второй замечательный
предел
.
Легко
заметить, что в данном примере
.
Снова исполняем наш искусственный
прием: возводим основание степени в
,
и, чтобы выражение не изменилось –
возводим в обратную дробь
:

Наконец-то
долгожданное
устроено,
с чистой совестью превращаем его в
букву
:

Но на
этом мучения не закончены, в показателе
у нас появилась неопределенность вида
,
раскрывать такую неопределенность мы
научились на уроке Пределы.
Примеры решений.
Делим числитель и знаменатель на
:

Готово.
А
сейчас мы рассмотрим модификацию второго
замечательного предела. Напомню, что
второй замечательный предел выглядит
следующим образом:
.
Однако на практике время от времени
можно встретить его «перевёртыш»,
который в общем виде записывается так:
Пример 8
Найти
предел
Сначала (мысленно
или на черновике) пробуем подставить
ноль (бесконечно малое число) в выражение,
стоящее под знаком предела:
В
результате получена знакомая
неопределенность
.
Очевидно, что в данном примере
.
С помощью знакомого искусственного
приема организуем в показателе степени
конструкцию
:
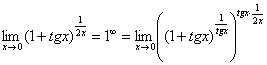
Выражение
со
спокойной душой превращаем в букву
:
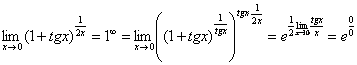
Еще
не всё, в показателе у нас появилась
неопределенность вида
.
Раскладываем тангенс на синус и косинус
(ничего не напоминает?):

Косинус нуля
стремится к единице (не забываем помечать
карандашом), поэтому он просто пропадает
в произведении:

А что
такое
и
к чему оно стремится, нужно уже знать,
иначе «двойка»!
Как видите, в
практических заданиях на вычисление
пределов нередко требуется применять
сразу несколько правил и приемов.
В 90-95% на зачете,
экзамене Вам встретится первый
замечательный предел или второй
замечательный предел. Как быть, если
попался «экзотический» замечательный
предел? (со списком всех замечательных
пределов можно ознакомиться в
соответствующей методичке). Ничего
страшного, практически все выкладки,
приёмы решения для первого замечательного
предела справедливы и для остальных
замечательных пределов. Нужно решать
их по аналогии.
Да,
так чему же равен предел
?
Если
у Вас получился ответ
,
значит в понимании высшей математики
не всё так безнадежно = ).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
08.02.20157.31 Mб91.rtf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #