Как найти предел lnx

Заказать задачи по любым предметам можно здесь от 10 минут

Пределы с логарифмами: примеры решений

Часто в контрольных работах нужно вычислить пределы с логарифмами. Такие задачи можно решить двумя способами:

1. С помощью следствия второго замечательного предела: $$ lim limits_{x to 0} frac{ln(1+f(x))}{f(x)} = 1 text{, если } f(x) to 0 $$
2. С помощью свойства бесконечно малой эквивалентной функции: $$ ln(1+f(x)) sim f(x) text{, если } f(x) to 0 $$

Оба метода решения допустимы к сдаче преподавателю на проверку. Выберите для себя самый удобный, который будете легко понимать

Содержание:

1. Предел показательно-степенной функции
2. Примеры с решением

Предел показательно-степенной функции

Показательно-степе иным и называют функции вида . Примерами таких функций могут служить и т. д.

Функция определена в области, где или где Если , то

Отсюда ясно, что показательно-степенная функция непрерывна при тех значениях х, при которых функции непрерывны, причем

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Если существуют пределы причем , то

В этом равенстве а либо число, либо , либо , либо . Остановимся теперь на особых случаях.

a) . В этом случае

Точно так же доказывается, что если то

б) Здесь

и потому Точно так же доказывается, что если

Мы опускаем разбор остальных случаев и приводим следующую таблицу значений предела

Возможно вам будут полезны данные страницы:

В случаях, соответствующих зачерненным клеткам, ответ неоднозначен и зависит от того, как именно стремятся к своим пределам. Эти случаи будут рассмотрены ниже.

Примеры с решением

Пример 1.

Вычислим предел

Решение:

Так как (см. п. 35)

то искомый предел равен

Пример 2.

Вычислим предел:

Решение:

а) Так как

то искомый предел равен 0.

б) Здесь и потому

Пример 3.

Вычислим предел:

Решение:

а) Так как

то искомый предел равен нулю. б) Здесь и потому

66. Предел п. 40 было доказано существование предела Этот предел мы обозначили буквой

Последовательность с общим членом получается, если придавать аргументу функции лишь натуральные значения. Мы покажем сейчас, что, если х стремится к бесконечности произвольным образом, предел этой функции также равен е. Иными словами, докажем, что

Для этого достаточно показать, что

Начнем с первого случая. Пусть Возьмем произвольное и обозначим целую часть через . Тогда и, следовательно, , а потому

Из неравенств следует, что

а из неравенств следует, что

Итак, мы доказали, что

где, напомним, Но

и Когда (пишут обычно ), а потому левая и правая части в (2) стремятся к е. Поэтому по теореме о пределе промежуточной функции (см. с. 80) имеем:

Рассмотрим предел . Положим

Когда и

Итак, и Значит, мы доказали равенство (1).

Если в этом равенстве положить , то получаем:

Пример 4.

Вычислим

Решение:

Имеем:

Пример 5.

Вычислим

Решение:

Имеем:

Преобразуем выражение функции, содержащейся под знаком предела, следующим образом:

и положим Вычислим

и Для вычисления первого предела введем новую переменную

Если , и мы получаем:

Вычислим второй предел:

(см. п. 35). В п. 65 мы отметили, что

Значит,

• Вычисление пределов, связанных с показательной и логарифмической функциями. Формулы (1) и (3) лежат в основе вычисления большинства пределов, связанных с показательной и логарифмической функциями.

Прологарифмировав обе части равенства (3) по основанию е, получаем

Заметим теперь, что в силу непрерывности логарифмической функции для любого а > 0 имеем: Поэтому если , то

В частности,

Итак, мы доказали, что

Это равенство означает, что при функции являются эквивалентными бесконечно малыми (см. п. 53): если

Введем новую переменную z, положив Тогда Поэтому и из формулы (4) следует, что

Мы доказали, что при функции — эквивалентные бесконечно малые: Так как, в частности, Иными словами, получаем, что

Наконец докажем, что

Для этого заметим, что , и потому Значит,

Равенство (6) означает, что

Мы доказали в этом пункте следующие соотношения эквивалентности бесконечно малых (в дополнение к тем, что были получены выше в п. 53 и 58): если , то

Пример 6.

Вычислим предел

Решение:

Так как — бесконечно малая Точно так же из . Поэтому, заменяя числитель и знаменатель дроби эквивалентными бесконечно малыми, получаем:

Итак, искомый предел равен .

Пример 7.

Вычислим предел

Решение:

Снова заменяем числитель и знаменатель эквива-лентными бесконечно малыми. Числитель запишем в виде а знаменатель — в виде . Применяя соотношение получаем:

Значит,

В п. 65 были вычислены пределы показательно-степенных функций Там остались неразобранными следующие случаи: х-»о

а) (неопределенность вида );

б) (неопределенность вида );

в) (неопределенность вида ).

Для вычисления таких пределов заменяют , т. е. на e и вычисляют предел

Тогда искомый предел равен :

Рассмотрим пределы логарифмов, которые можно найти с помощью следствия из 2-го замечательного предела.

Следствие 2-го замечательного предела:

Это следствие распространяется и на пределы логарифмов, в которых на месте x стоит некоторая функция f(x), если f(x)→0 при x→0, то есть

Рассмотрим, как находят пределы на логарифмы на примерах.

Найти предел функции:

Приводим выражени под знаком предела к такому виду, чтобы можно было применить нашу формулу (*):

так как по следствию из 2-го замечательного предела

Преобразуем выражение -1+cos x:

Продолжим

Теперь приведем предел с логарифмом к виду (*)

С пределом логарифма разобрались:

осталось убрать неопределенность 0 на 0, возникшую с появлением синуса. По 1-му замечательному пределу

Преобразовываем выражение так, чтобы применить этот замечательный предел:

Сокращаем дробь на x², имеем:

По теореме о разложении квадратного трехчлена на множители: x²-7x+10=(x-2)(x-5).

Сокращаем дробь на (x-2):

Так как при x→2  x²-7x+10→0, то

Значит, окончательный ответ

Дальше мы увидим, что пределы на логарифмы удобно находить, используя эквивалентность бесконечно малых величин.

В настоящей статье приводятся значения степенной функции, экспоненты и логарифма для некоторых специальных значений их аргументов, а также пределы некторых выражений, содержащих данные функции.

Частные значения функций

Значения степенной функции и экспоненты:

z0=1(z≠0  ,  z≠∞)  ,z^0 =1 qquad (zne 0 ;,; zne infty) ;,

z1=z  ,z^1 =z ;,

1α=1  .1^{alpha} =1 ;.

В частности,

e0=1  .e^0 =1 ;.

Значения логарифма:

ln⁡1=0  ,ln⁡e=1  ,ln 1 =0 ;,qquad ln e =1 ;,

ln⁡i=i⋅2π/4  ,ln⁡(−i)=−i⋅2π/4  ,ln⁡(−1)=i π  .ln i =icdot 2pi/4 ;,quad ln(-i) =-icdot 2pi/4 ;,quad ln(-1) =i ,pi ;.

Значения экспоненты для некоторых чисто мнимых значений аргумента могут быть получены с помощью соответствующих частных значений функций cos⁡xcos x и sin⁡xsin x (см. статью «Частные значения и пределы гиперболических и тригонометрических функций»):

ei 2πk=1(k=0,±1,±2,…)  ,e^{i ,2pi k} =1 qquad (k=0, pm 1, pm 2,…) ;,

ei π=−1  ,ei 2π/4=i  ,e−i 2π/4=−i  ,e^{i ,pi} =-1 ;,quad
e^{i ,2pi/4} =i ;,quad
e^{-i ,2pi/4} =-i ;,

ei 2π/6=12 (1+i 3)  ,ei 2π/8=2−1/2⋅(1+i)  ,ei 2π/12=12 (3+i)  .e^{i ,2pi/6} =frac{1}{2} ,bigl(1 +i ,sqrt{3}bigr) ;,
quad
e^{i ,2pi/8} =2^{-1/2}cdot(1+i) ;,
quad
e^{i ,2pi/12} =frac{1}{2},bigl(sqrt{3} +ibigr) ;.

Пределы

Пределы функций комплексной переменной

a)lim⁡z→0zα=lim⁡z→∞z−α=0(Re α>0)  ,{a )}
lim_{zto 0} z^{alpha} =lim_{zto infty} z^{-alpha} =0
qquad (mathrm{Re}, alpha >0) ;,

b)lim⁡z→0z−α=lim⁡z→∞zα=∞(Re α>0)  ;{b )}
lim_{zto 0} z^{-alpha} =lim_{zto infty} z^{alpha} =infty
qquad (mathrm{Re}, alpha >0) ;;

c)lim⁡z→0ln⁡z=lim⁡z→∞ln⁡z=∞  .{c )}
lim_{zto 0} ln z =lim_{ztoinfty} ln z =infty ;.

<<<<
При выводе формул a) и b) можно учесть соотношение (которое легко получить)

∣za+i b∣=∣z∣a e−b arg⁡z  ,|z^{a +i ,b}| =|z|^a ,e^{-b ,arg z} ;,

из которого следует

∣z∣a e−b π≤∣za+i b∣≤∣z∣a eb π  .|z|^a ,e^{-b ,pi} le |z^{a +i ,b}| le |z|^a ,e^{b ,pi} ;.

В результате определение предела функции комплексной переменной
сводится к определению предела функции действительной переменной.
>>>>

Пределы функций действительной переменной
(см. также статью «Степенная функция, экспонента и логарифм для действительных аргументов»):

lim⁡x→+∞x e−x=0  ,lim_{xto +infty} x ,e^{-x} =0 ;,

lim⁡x→+∞x−1 ln⁡x=lim⁡x→0x ln⁡x=0  .lim_{xto +infty} x^{-1} ,ln x
=lim_{xto 0} x ,ln x =0 ;.

С помощью данных формул можно также получить более общие равенства:

lim⁡x→∞xa e−b x=0(a>0;  b>0);lim_{xto infty} x^a ,e^{-b ,x} = 0
qquad (a>0;; b>0);

lim⁡x→∞x−a ln⁡x=0(a>0).lim_{xto infty} x^{-a} ,ln x = 0
qquad (a>0).

Данные равенства означают, что экспонента растет быстрее, а логарифм – медленнее, чем степень с любым положительным показателем.

Некоторые дополнительные пределы

lim⁡z→01z (eα z−1)=α  ,lim_{zto 0} frac{1}{z} ,bigl(e^{alpha ,z} -1bigr) =alpha ;,

lim⁡z→01z ln⁡(1+α z)=α  ,lim_{zto 0} frac{1}{z} ,ln(1 +alpha ,z) =alpha ;,

lim⁡z→0(1+z)α−1z=α  .lim_{zto 0} frac{(1 +z)^{alpha} -1}{z} =alpha ;.

Данные пределы следуют из формул разложения экспоненты, логрифма и степенной функции в степенные ряды.

Из второй приведенной здесь формулы также следует:

lim⁡z→∞(1+α/z)z=eα  .lim_{zto infty} bigl(1 +alpha/zbigr)^z =e^{alpha} ;.

Использование представления числа e в виде предела

В настоящем пункте рассматриваются функции действительных переменных.

Константа ee представляется в виде

e=lim⁡x→+∞(1+1/x)xe =lim_{xto +infty} (1 +1/x)^x

(см. статью «Важнейшие трансцендентные математические константы») – это так называемый второй замечательный предел.

Данная формула часто позволяет определять пределы функций, содержащих степени, без помощи правила Лопиталя.

Пример 1

Требуется доказать, что

lim⁡x→+∞(1−1/x)x=e−1  .lim_{xto +infty} (1 -1/x)^x =e^{-1} ;.

Данная формула выводится следующим образом:

lim⁡x→+∞((1−1/x)x (1+1/x)x)=lim⁡x→+∞((1−1/x2)xlim_{xto +infty} bigl((1 -1/x)^x ,(1 +1/x)^xbigr)
=lim_{xto +infty} bigl((1 -1/x^2)^x

=lim⁡x→+∞(((1−1/x2)x2)1/x=lim⁡x→+∞e1/x=e0=1  ,=lim_{xto +infty} Bigl(bigl((1 -1/x^2)^{x^2}Bigr)^{1/x}
=lim_{xto +infty} e^{1/x} =e^0 =1 ;,

откуда следует необхоимый результат.

Пример 2

Требуется доказать, что (см. последнюю формулу пункта 3)

lim⁡x→+∞(1+a/x)x=ealim_{xto +infty} (1 +a/x)^x =e^a

(a=consta =mathrm{const}).

Данная формула выводится следующим образом.

Пусть a>0a>0 (случай, когда a<0a<0 рассматривается аналогично, а случай, когда a=0a=0 – тривиален).
Введем новую переменную y=x/ay =x/a, тогда

lim⁡x→+∞(1+a/x)x=lim⁡y→+∞(1+1/y)a y=lim⁡y→+∞((1+1/y)y)a=ea  .lim_{xto +infty} (1 +a/x)^x
=lim_{yto +infty} (1 +1/y)^{a ,y}
=lim_{yto +infty} bigl((1 +1/y)^ybigr)^a
=e^a ;.

Пример 3

Требуется доказать, что

lim⁡x→±∞(x+ax+b)p x+q=ep (a−b)lim_{xto pm infty} left(frac{x +a}{x +b}right)^{p ,x +q} =e^{p ,(a-b)}

(aa, bb, pp, q=constq =mathrm{const}, p≠0pne 0).

Данная формула выводится следующим образом:
ведем новую переменную

y=x+ax+b−1  ,y =frac{x +a}{x +b} -1 ;,

тогда

x=a−by−bx =frac{a-b}{y} -b

и

lim⁡x→+∞(x+ax+b)p x+q=lim⁡y→0(1+y)p (a−b)/y+q−p blim_{xto +infty} left(frac{x +a}{x +b}right)^{p ,x +q}
=lim_{yto 0} (1 +y)^{p ,(a-b)/y +q -p ,b}

=lim⁡y→0((1+y)1/y)p (a−b)+q−p b y=ep (a−b)  .=lim_{yto 0} bigl((1 +y)^{1/y}bigr)^{p ,(a-b) +q -p ,b ,y}
=e^{p ,(a-b)} ;.

Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.

Если , то .

Логарифм крайне важная математическая величина, поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету….

Свойства логарифмов

Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что   означает, что:

.

Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.

Приведем некоторые тождества:

,

,

.

Приведем основные алгебраические выражения:

,

,

,

.

Внимание!  может существовать только при x&gt,0, x≠1, y&gt,0.

Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида первый имеет в основании число 10, и носит название десятичный логарифм. Второй называется натуральным. Основание натурального логарифма число е. Именно о нем мы и будем детально говорить в этой статье.

Обозначения:

• lg x десятичный,
• ln x натуральный.

Используя тождество   можно увидеть, что ln e = 1, как и то, что lg 10=1.

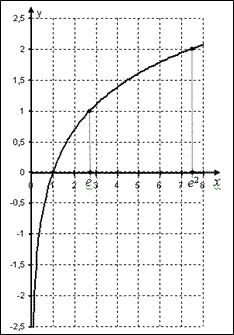
График натурального логарифма

Построим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его вручную, чтобы знать, как правильно посчитать логарифм.

Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:

х	у
1	0
е	1
е2≈7,34	2
	0,5
e-1≈0.36	-1

Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве:  . Для натурального логарифма это тождество будет выглядеть таким образом:

.

Для удобства мы можем взять пять опорных точек:

,

,

,

,

.

Как посчитать логарифмы от этих пяти значений? Очень просто, ведь:

,

,

,

,

,

.

Таким образом, подсчет натуральных логарифмов довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.

Построив по точкам график, получаем приблизительный график:

Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) все числа больше нуля.

Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма  .

Область значений (т.е. все допустимые значения функции y = ln x) все числа в интервале  .

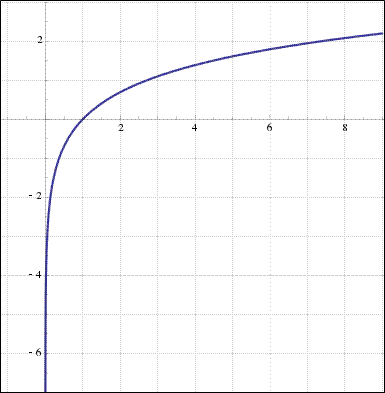
Предел натурального log

Изучая график, возникает вопрос как ведет себя функция при y&lt,0.

Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х&lt,0 не существует.

Внимание! При стремлении к нулю аргументу, функция y = ln x стремится к   (минус бесконечности).

Предел натурального log можно записать таким образом:

Это интересно! Азы геометрии: правильная пирамида — это

Формула замены основания логарифма

Иметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.

Начнем с логарифмического тождества:

.

Тогда любое число, либо переменную у можно представить в виде:

,

где х любое число (положительное согласно свойствам логарифма).

Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:

.

Воспользуемся свойством  (только вместо с у нас выражение):

Отсюда получаем универсальную формулу:

.

В частности, если z=e, то тогда:

.

Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.

Это интересно! Уравнение по трем точкам: как найти вершину параболы, формула

Решаем задачи

Для того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.

Задача 1. Необходимо решить уравнение ln x = 3.

Решение: Используя определение логарифма: если , то  , получаем:

.

Задача 2. Решите уравнение (5 + 3 * ln (x 3)) = 3.

Решение: Используя определение логарифма: если , то  , получаем:

.

Тогда:

.

.

Еще раз применим определение логарифма:

.

Таким образом:

.

Можно приближенно вычислить ответ, а можно оставить его и в таком виде.

Задача 3. Решите уравнение .

Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:

.

Перед нами квадратное уравнение. Найдем его дискриминант:

.

Первый корень уравнения:

.

Второй корень уравнения:

.

Вспоминая о том, что мы производили подстановку t = ln x, получаем:

.

Используя определение логарифма: если  , то , получаем оба корня:

.

Вспомним, что область определения: . Оба корня больше нуля, так что оба решения верны и подходят.

Внимание! Когда в логарифмических уравнениях у вас получается два корня или больше, не забывайте про область определения. Аргумент, стоящий под логарифмом никогда не может быть меньше нуля. Если одно из решений делает выражение под логарифмом меньше либо равным нулю такой корень вам не подходит, исключите его.

Интересные сведения

Логарифмы (особенно натуральные и десятичные) широко применимы почти во всех сферах деятельности.

Например, в теории простых чисел, количество простых чисел в интервале от 0 до n будет равно приблизительно:  , при этом s-ое простое число приблизительно будет равно  .

В математическом анализе, как мы уже убедились ранее, натуральные логарифмы встречаются сплошь и рядом, при этом они объединяют тригонометрические и логарифмические функции при помощи интегралов, например интеграл от тангенса:

.

В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е зачастую отражает темп роста экспоненциальных величин.

В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти натуральное число N понадобится  битов.

В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.

В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее процессы, которые математически можно описать только при помощи логарифмирования.

В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.

Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.

Натуральный логарифм Функция y=ln x ее свойства

Доказательство основного свойства натурального логарифма