Пределы с иррациональностями. Первая часть.
Пределы, содержащие иррациональности (или, попросту говоря, корни) крайне популярны у составителей типовых расчётов и контрольных работ по высшей математике. Обычно рассматриваются три группы неопределённостей:
В данной теме мы рассмотрим все три перечисленные выше группы пределов с иррациональностями. Начнём с пределов, содержащих неопределенность вида $frac{0}{0}$.
Раскрытие неопределенности $frac{0}{0}$.
Схема решения стандартных примеров такого типа обычно состоит из двух шагов:
- Избавляемся от иррациональности, вызвавшей неопределенность, домножая на так называемое «сопряжённое» выражение;
- При необходимости раскладываем выражение в числителе или знаменателе (или и там и там) на множители;
- Сокращаем множители, приводящие к неопределённости, и вычисляем искомое значение предела.
Термин «сопряжённое выражение», использованный выше, будет детально пояснён в примерах. Пока что останавливаться на нём подробно нет резона. Вообще, можно пойти иным путём, без использования сопряжённого выражения. Иногда от иррациональности может избавить удачно подобранная замена. Такие примеры редки в стандартных контрольных работах, поэтому на использование замены рассмотрим лишь один пример №6 (см. вторую часть данной темы).
Нам понадобится несколько формул, которые я запишу ниже:
$$
begin{equation}
a^2-b^2=(a-b)cdot(a+b)
end{equation}
$$
$$
begin{equation}
a^3-b^3=(a-b)cdot(a^2+ab+b^2)
end{equation}
$$
$$
begin{equation}
a^3+b^3=(a+b)cdot(a^2-ab+b^2)
end{equation}
$$
$$
begin{equation}
a^4-b^4=(a-b)cdot(a^3+a^2 b+ab^2+b^3)
end{equation}
$$
Кроме того, предполагаем, что читатель знает формулы для решения квадратных уравнений. Если $x_1$ и $x_2$ – корни квадратного трёхчлена $ax^2+bx+c$, то разложить его на множители можно по следующей формуле:
$$
begin{equation}
ax^2+bx+c=acdot(x-x_1)cdot(x-x_2)
end{equation}
$$
Формул (1)-(5) вполне хватит для решения стандартных задач, к которым мы сейчас и перейдём.
Пример №1
Найти $lim_{xto 3}frac{sqrt{7-x}-2}{x-3}$.
Решение
Найдём отдельно пределы числителя и знаменателя:
$$
begin{aligned}
& lim_{xto 3}(sqrt{7-x}-2)=sqrt{7-3}-2=sqrt{4}-2=0;\
& lim_{xto 3} (x-3)=3-3=0.
end{aligned}
$$
В заданном пределе мы имеем неопределённость вида $frac{0}{0}$. Раскрыть эту неопределённость нам мешает разность $sqrt{7-x}-2$. Для того, чтобы избавляться от подобных иррациональностей, применяют умножение на так называемое «сопряжённое выражение». Как действует такое умножение мы сейчас и рассмотрим. Умножим $sqrt{7-x}-2$ на $sqrt{7-x}+2$:
$$(sqrt{7-x}-2)(sqrt{7-x}+2)$$
Чтобы раскрыть скобки применим формулу №1, подставив в правую часть упомянутой формулы $a=sqrt{7-x}$, $b=2$:
$$(sqrt{7-x}-2)(sqrt{7-x}+2)=(sqrt{7-x})^2-2^2=7-x-4=3-x.$$
Как видите, если умножить числитель на $sqrt{7-x}+2$, то корень (т.е. иррациональность) в числителе исчезнет. Вот это выражение $sqrt{7-x}+2$ и будет сопряжённым к выражению $sqrt{7-x}-2$. Однако мы не вправе просто взять и умножить числитель на $sqrt{7-x}+2$, ибо это изменит дробь $frac{sqrt{7-x}-2}{x-3}$, стоящую под пределом. Умножать нужно одовременно и числитель и знаменатель:
$$ lim_{xto 3}frac{sqrt{7-x}-2}{x-3}= left|frac{0}{0}right|=lim_{xto 3}frac{(sqrt{7-x}-2)cdot(sqrt{7-x}+2)}{(x-3)cdot(sqrt{7-x}+2)}$$
Теперь вспомним, что $(sqrt{7-x}-2)(sqrt{7-x}+2)=3-x$ и раскроем скобки. А после раскрытия скобок и небольшого преобразования $3-x=-(x-3)$ сократим дробь на $x-3$:
$$ lim_{xto 3}frac{(sqrt{7-x}-2)cdot(sqrt{7-x}+2)}{(x-3)cdot(sqrt{7-x}+2)}=
lim_{xto 3}frac{3-x}{(x-3)cdot(sqrt{7-x}+2)}=\
=lim_{xto 3}frac{-(x-3)}{(x-3)cdot(sqrt{7-x}+2)}=
lim_{xto 3}frac{-1}{sqrt{7-x}+2}
$$
Неопределенность $frac{0}{0}$ исчезла. Сейчас можно легко получить ответ данного примера:
$$ lim_{xto 3}frac{-1}{sqrt{7-x}+2}=frac{-1}{sqrt{7-3}+2}=-frac{1}{sqrt{4}+2}=-frac{1}{4}.$$
Замечу, что сопряжённое выражение может менять свою структуру – в зависимости от того, какую именно иррациональность оно должно убрать. В примерах №4 и №5 (см. вторую часть данной темы) будет использован иной вид сопряжённого выражения.
Ответ: $lim_{xto 3}frac{sqrt{7-x}-2}{x-3}=-frac{1}{4}$.
Пример №2
Найти $lim_{xto 2}frac{3x^2-5x-2}{sqrt{x^2+5}-sqrt{7x^2-19}}$.
Решение
Запишем пределы числителя и знаменателя:
$$
begin{aligned}
& lim_{xto 2}(sqrt{x^2+5}-sqrt{7x^2-19})=sqrt{2^2+5}-sqrt{7cdot 2^2-19}=3-3=0;\
& lim_{xto 2}(3x^2-5x-2)=3cdot2^2-5cdot{2}-2=0.
end{aligned}
$$
Мы имеем дело с неопределённостью вида $frac{0}{0}$. Избавимся от иррациональности в знаменателе данной дроби. Для этого доможим и числитель и знаменатель дроби $frac{3x^2-5x-2}{sqrt{x^2+5}-sqrt{7x^2-19}}$ на выражение $sqrt{x^2+5}+sqrt{7x^2-19}$, сопряжённое к знаменателю:
$$
lim_{xto 2}frac{3x^2-5x-2}{sqrt{x^2+5}-sqrt{7x^2-19}}=left|frac{0}{0}right|=
lim_{xto 2}frac{(3x^2-5x-2)(sqrt{x^2+5}+sqrt{7x^2-19})}{(sqrt{x^2+5}-sqrt{7x^2-19})(sqrt{x^2+5}+sqrt{7x^2-19})}
$$
Вновь, как и в примере №1, нужно использовать формулу №1 для раскрытия скобок. Подставив в правую часть упомянутой формулы $a=sqrt{x^2+5}$, $b=sqrt{7x^2-19}$, получим такое выражение для знаменателя:
$$
left(sqrt{x^2+5}-sqrt{7x^2-19}right)left(sqrt{x^2+5}+sqrt{7x^2-19}right)=\
=left(sqrt{x^2+5}right)^2-left(sqrt{7x^2-19}right)^2=x^2+5-(7x^2-19)=-6x^2+24=-6cdot(x^2-4)
$$
Вернёмся к нашему пределу:
$$
lim_{xto 2}frac{(3x^2-5x-2)(sqrt{x^2+5}+sqrt{7x^2-19})}{(sqrt{x^2+5}-sqrt{7x^2-19})(sqrt{x^2+5}+sqrt{7x^2-19})}=
lim_{xto 2}frac{(3x^2-5x-2)(sqrt{x^2+5}+sqrt{7x^2-19})}{-6cdot(x^2-4)}=\
=-frac{1}{6}cdot lim_{xto 2}frac{(3x^2-5x-2)(sqrt{x^2+5}+sqrt{7x^2-19})}{x^2-4}
$$
В примере №1 практически сразу после домножения на сопряжённое выражение произошло сокращение дроби. Здесь перед сокращением придётся разложить на множители выражения $3x^2-5x-2$ и $x^2-4$, а уж потом перейти к сокращению. Чтобы разложить на множители выражение $3x^2-5x-2$ нужно использовать формулу №5. Для начала решим квадратное уравнение $3x^2-5x-2=0$:
$$
3x^2-5x-2=0\
begin{aligned}
& D=(-5)^2-4cdot3cdot(-2)=25+24=49;\
& x_1=frac{-(-5)-sqrt{49}}{2cdot3}=frac{5-7}{6}=-frac{2}{6}=-frac{1}{3};\
& x_2=frac{-(-5)+sqrt{49}}{2cdot3}=frac{5+7}{6}=frac{12}{6}=2.
end{aligned}
$$
Подставляя $x_1=-frac{1}{3}$, $x_2=2$ в формулу №5, будем иметь:
$$
3x^2-5x-2=3cdotleft(x-left( -frac{1}{3}right)right)(x-2)=3cdotleft(x+frac{1}{3}right)(x-2)=left(3cdot x+3cdotfrac{1}{3}right)(x-2)
=(3x+1)(x-2).
$$
Теперь настал черёд разложить на множители выражение $x^2-4$. Воспользуемся формулой №1, подставив в неё $a=x$, $b=2$:
$$
x^2-4=x^2-2^2=(x-2)(x+2)
$$
Используем полученные результаты. Так как $x^2-4=(x-2)(x+2)$ и $3x^2-5x-2=(3x+1)(x-2)$, то:
$$
-frac{1}{6}cdot lim_{xto 2}frac{(3x^2-5x-2)(sqrt{x^2+5}+sqrt{7x^2-19})}{x^2-4}
=-frac{1}{6}cdot lim_{xto 2}frac{(3x+1)(x-2)(sqrt{x^2+5}+sqrt{7x^2-19})}{(x-2)(x+2)}
$$
Сокращая на скобку $x-2$ получим:
$$
-frac{1}{6}cdot lim_{xto 2}frac{(3x+1)(x-2)(sqrt{x^2+5}+sqrt{7x^2-19})}{(x-2)(x+2)}
=-frac{1}{6}cdot lim_{xto 2}frac{(3x+1)(sqrt{x^2+5}+sqrt{7x^2-19})}{x+2}.
$$
Всё! Неопределённость исчезла. Ещё один шаг и мы приходим к ответу:
$$
-frac{1}{6}cdot lim_{xto 2}frac{(3x+1)(sqrt{x^2+5}+sqrt{7x^2-19})}{x+2}=\
=-frac{1}{6}cdotfrac{(3cdot 2+1)(sqrt{2^2+5}+sqrt{7cdot 2^2-19})}{2+2}=
-frac{1}{6}cdotfrac{7(3+3)}{4}=-frac{7}{4}.
$$
Ответ: $lim_{xto 2}frac{3x^2-5x-2}{sqrt{x^2+5}-sqrt{7x^2-19}}=-frac{7}{4}$.
В следующем примере рассмотрим случай, когда иррациональности будут присутствовать как в числителе, так и в знаменателе дроби.
Пример №3
Найти $lim_{xto 5}frac{sqrt{x+4}-sqrt{x^2-16}}{sqrt{x^2-3x+6}-sqrt{5x-9}}$.
Решение
Найдём пределы числителя и знаменателя:
$$
begin{aligned}
& lim_{xto 5}(sqrt{x+4}-sqrt{x^2-16})=sqrt{9}-sqrt{9}=0;\
& lim_{xto 5}(sqrt{x^2-3x+6}-sqrt{5x-9})=sqrt{16}-sqrt{16}=0.
end{aligned}
$$
Имеем неопределённость вида $frac{0}{0}$. Так как в данном случае корни наличествуют и в знаменателе, и в числителе, то дабы избавиться от неопределённости придется домножать сразу на две скобки. Во-первых, на выражение $sqrt{x+4}+sqrt{x^2-16}$, сопряжённое числителю. А во-вторых на выражение $sqrt{x^2-3x+6}-sqrt{5x-9}$, сопряжённое знаменателю.
$$
lim_{xto 5}frac{sqrt{x+4}-sqrt{x^2-16}}{sqrt{x^2-3x+6}-sqrt{5x-9}}=left|frac{0}{0}right|=\
=lim_{xto 5}frac{(sqrt{x+4}-sqrt{x^2-16})(sqrt{x+4}+sqrt{x^2-16})(sqrt{x^2-3x+6}+sqrt{5x-9})}{(sqrt{x^2-3x+6}-sqrt{5x-9})(sqrt{x^2-3x+6}+sqrt{5x-9})(sqrt{x+4}+sqrt{x^2-16})}
$$
Раскрывая скобки с помощью формулы №1, получим:
$$(sqrt{x+4}-sqrt{x^2-16})(sqrt{x+4}+sqrt{x^2-16})=\
=left(sqrt{x+4}right)^2-left(sqrt{x^2-16}right)^2=x+4-(x^2-16)=-x^2+x+20$$
$$(sqrt{x^2-3x+6}-sqrt{5x-9})(sqrt{x^2-3x+6}+sqrt{5x-9})=left(sqrt{x^2-3x+6}right)^2-left(sqrt{5x-9}right)^2=x^2-8x+15$$
Возвращаясь к рассматриваемому пределу, имеем:
$$
lim_{xto 5}frac{(sqrt{x+4}-sqrt{x^2-16})(sqrt{x+4}+sqrt{x^2-16})(sqrt{x^2-3x+6}+sqrt{5x-9})}{(sqrt{x^2-3x+6}-sqrt{5x-9})(sqrt{x^2-3x+6}+sqrt{5x-9})(sqrt{x+4}+sqrt{x^2-16})}=\
=lim_{xto 5}frac{(-x^2+x+20)(sqrt{x^2-3x+6}+sqrt{5x-9})}{(x^2-8x+15)(sqrt{x+4}+sqrt{x^2-16})}
$$
Осталось разложить на множители выражения $-x^2+x+20$ и $x^2-8x+15$. Начнем с выражения $-x^2+x+20$. Чтобы разложить его на множители требуется решить уравнение $-x^2+x+20=0$, а затем воспользоваться формулой №5:
$$
-x^2+x+20=0;\
begin{aligned}
& D=1^2-4cdot(-1)cdot 20=81;\
& x_1=frac{-1-sqrt{81}}{-2}=frac{-10}{-2}=5;\
& x_2=frac{-1+sqrt{81}}{-2}=frac{8}{-2}=-4.
end{aligned} \
-x^2+x+20=-1cdot(x-5)(x-(-4))=-(x-5)(x+4).
$$
Для выражения $x^2-8x+15$ получим:
$$
x^2-8x+15=0;\
begin{aligned}
& D=(-8)^2-4cdot 1cdot 15=4;\
& x_1=frac{-(-8)-sqrt{4}}{2}=frac{6}{2}=3;\
& x_2=frac{-(-8)+sqrt{4}}{2}=frac{10}{2}=5.
end{aligned}\
x^2+8x+15=1cdot(x-3)(x-5)=(x-3)(x-5).
$$
Подставляя полученные разожения $-x^2+x+20=-(x-5)(x+4)$ и $x^2+8x+15=(x-3)(x-5)$ в рассматриваемый предел, будем иметь:
$$
lim_{xto 5}frac{(-x^2+x+20)(sqrt{x^2-3x+6}+sqrt{5x-9})}{(x^2-8x+15)(sqrt{x+4}+sqrt{x^2-16})}=
lim_{xto 5}frac{-(x-5)(x+4)(sqrt{x^2-3x+6}+sqrt{5x-9})}{(x-3)(x-5)(sqrt{x+4}+sqrt{x^2-16})}=\
=lim_{xto 5}frac{-(x+4)(sqrt{x^2-3x+6}+sqrt{5x-9})}{(x-3)(sqrt{x+4}+sqrt{x^2-16})}=
frac{-(5+4)(sqrt{5^2-3cdot 5+6}+sqrt{5cdot 5-9})}{(5-3)(sqrt{5+4}+sqrt{5^2-16})}=-6.
$$
Ответ: $lim_{xto 5}frac{sqrt{x+4}-sqrt{x^2-16}}{sqrt{x^2-3x+6}-sqrt{5x-9}}=-6$.
В следующей (второй) части рассмотрим ещё пару примеров, в которых сопряжённое выражение будет иметь иной вид, нежели в предыдущих задачах. Главное, помните, что цель использования сопряжённого выражения – избавиться от иррациональности, вызывающей неопределённость.
Заказать задачи по любым предметам можно здесь от 10 минут
Пределы с корнями: примеры решений
Среди задач на решение пределов попадаются пределы с корнями. В результате подстановки значения $ x $ в функцию получаются неопределенности трёх видов:
- $ bigg [frac{0}{0} bigg ] $
- $ bigg [frac{infty}{infty} bigg ] $
- $ bigg [infty-infty bigg ] $
Перед тем, как приступить к решению определите тип своей задачи
Тип 1 $ bigg [frac{0}{0} bigg ] $
Для того, чтобы раскрывать такие неопределенности необходимо домножить числитель и знаменатель дроби на сопряженное к выражению содержащему корень.
| Пример 1 |
| Найти предел с корнем $$ lim limits_{x to 4} frac{x-4}{4-sqrt{x+12}} $$ |
| Решение |
|
Подставляем $ x to 4 $ в подпределельную функцию: $$ lim limits_{x to 4} frac{x-4}{4-sqrt{x+12}} = frac{0}{0} = $$ Получаем неопределенность $ [frac{0}{0}] $. Домножим числитель и знаменатель на выражение сопряженное к нему, так как он содержит корень: $ 4+sqrt{x+12} $ $$ = lim limits_{x to 4} frac{(x-4)(4+sqrt{x+12})}{(4-sqrt{x+12})(4+sqrt{x+12})} = $$ Используя формулу разности квадратов $ (a-b)(a+b) = a^2-b^2 $ приведем предел к следующему виду: $$ = lim limits_{x to 4} frac{(x-4)(4+sqrt{x+12})}{16-(x+12)} = $$ Раскрываем скобки в знаменателе и упрощаем его: $$ = lim limits_{x to 4} frac{(x-4)(4+sqrt{x+12})}{4-x} = $$ Сокращам функцию в пределе на $ x-4 $, имеем: $$ = -lim limits_{x to 4} (4+sqrt{x+12}) = -(4+sqrt{4+12}) = -8 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ lim limits_{x to 4} frac{x-4}{4-sqrt{x+12}} = -8 $$ |
Тип 2 $ bigg [frac{infty}{infty} bigg ] $
Пределы с корнем такого типа, когда $ x to infty $ вычислять нужно по-другому в отличии от предыдущего случая. Необходимо определить старшие степени выражений числителя и знаменателя. Затем вынести самую старшую из двух степеней за скобки и сократить.
| Пример 2 |
| Решить предел с корнем $$ lim limits_{x to infty} frac{x^2+5x+2}{sqrt{x+6}} $$ |
| Решение |
|
Вставляем $ x to infty $ в предел и получаем $ [frac{infty}{infty}] $. Определяем, что в числителе старшая степень это $ x^2 $, а в знаменателе $ sqrt{x} $. Выносим их за скобки: $$ lim limits_{x to infty} frac{x^2(1+frac{5x}{x^2}+frac{2}{x^2})}{x^2(sqrt{frac{x}{x^4}+frac{6}{x^4})}} = $$ Теперь выполняем сокращение: $$ = lim limits_{x to infty} frac{1+frac{5x}{x^2}+frac{2}{x^2}}{sqrt{frac{1}{x^3}+frac{6}{x^4}}} = $$ Снова подставляем $ x to infty $ в предел, имеем: $$ = frac{1 + 0 + 0}{ sqrt{0 + 0}} = lbrack frac{1}{0} rbrack = infty $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{x^2+5x+2}{sqrt{x+6}} = infty $$ |
Тип 3 $ bigg [infty-infty bigg ] $
Этот вид пределов часто попадается в дополнительных заданиях на экзамене. Ведь часто студенты не правильно вычисляют пределы такого типа. Как решать пределы с корнями данного вида? Всё просто. Необходимо умножить и разделить функцию, стоящую в пределе, на выражение сопряженное к ней.
| Пример 3 |
| Вычислить предел корня $$ lim limits_{x to infty} sqrt{x^2-3x}-x $$ |
| Решение |
|
При $ x to infty $ в пределе видим: $$ lim limits_{x to infty} sqrt{x^2-3x}-x = [infty — infty] = $$ После домножения и разделения на сопряженное имеем предел: $$ lim limits_{x to infty} frac{(sqrt{x^2-3x}-x)(sqrt{x^2-3x}+x)}{sqrt{x^2-3x}+x} = $$ Упростим числитель, используя формулу разности квадратов: $ (a-b)(a+b)=a^2-b^2 $ $$ = lim limits_{x to infty} frac{(x^2-3x)-x^2}{sqrt{x^2-3x}+x} = $$ После раскрытия скобок и упрощения получаем: $$ lim limits_{x to infty} frac{-3x}{sqrt{x^2-3x}+x} = $$ Далее выносим $ x $ за скобки и сокращаем: $$ = lim limits_{x to infty} frac{-3x}{x(sqrt{1-frac{3}{x}}+1)} = lim limits_{x to infty} frac{-3}{sqrt{1-frac{3}{x}}+1} = $$ Снова подставляем $ x to infty $ в предел и вычисляем его: $$ = frac{-3}{sqrt{1-0}+1} = -frac{3}{2} $$ |
| Ответ |
| $$ lim limits_{x to infty} sqrt{x^2-3x}-x = -frac{3}{2} $$ |
Пример 1.
Пр.
4, Пр. 2
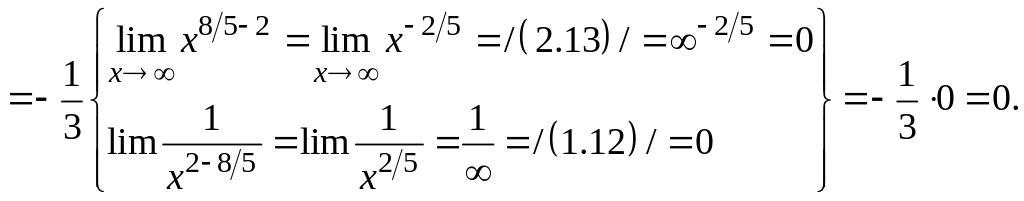
Примечание. При вычислении пределов
иррациональных выражений, дающих
неопределенности типа
или
используют введение новой переменной,
освобождающей от иррациональности, или
преобразование выражения с помощью
сопряженного ему. Например, парами
взаимно сопряженных выражений будут:
1)
и
2)
и
3)
и
которые при вычислении пределов
используются в формах:
(1.6)
(1.7)
(1.8)
Пример 2.
Пр.6
Пример 3.
Пример 4.
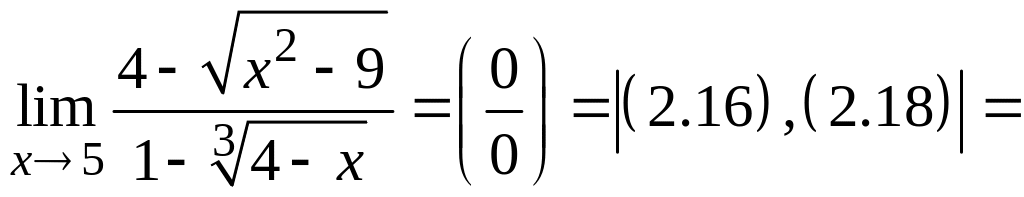
Примечание. Обратите внимание на то,
что при вычислении предела 5 из пункта
2.4.I и 3,4 настоящего пункта,
при раскрытии неопределенности
и
стараются так преобразовать выражение,
чтобы дробь можно было сократить на
множители
стремящийся к нулю.
1.3. Вычисление пределов с использованием
таблицы эквивалентных бесконечно малых
функций.
Пример 1.
Пр.2
Пр.
3
Пример 2.
EMBED Equation.DSMT4

Пример 3.
Пр. 2

Пример 4.
Пример5.
Пр.4,Пр.6
Пр.6
Пример 6.
(Пр.5)=

Пример 7.

Пример 8.
Пример 9.
не определен из-за знака
1)

2)
Пр.4
Таким образом, существуют различные
односторонние на
и на
пределы.
1.4. Указания к заданию 5.
Пример. Докажите, что
и
бесконечно малые функции одного порядка
при
Найдите значение постоянной “C”,
при котором они будут эквивалентны.
Решение.
Пр.
Пр.
Пр.3
при
1.5. Пример выполнения задания 5.
Определите порядок относительно “x”
функции
бесконечно малой при
Решение.
при
— бесконечно малая одного порядка по
отношению к
,
то сеть второго порядка относительно
“x”.
1.6. Указания к выполнению задания 7.
При исследовании функции на
непрерывность пользуются теоремой о
непрерывности элементарных функций
там, где они определены; признаком
непрерывности фуки в точке
когда
(2.19)
При наличии точек разрывов исследуют
функции в их окрестности и соответствующим
образом классифицируют.
Пример 1. Исследовать функцию на
непрерывность и построить её схематический
график, если
Решение. Сначала найдем область
определения функции

Область определения симметрична
относительно начала координат, следует
исследовать функцию на признак четности.
функция
нечетная и её график симметричен
относительно начала координат. Таким
образом, достаточно исследовать функцию
на промежутке
построить
график, а затем отобразить его симметрию
начала координат.
-
В точке
функция определена справа, поэтому
найдем лишь правосторонний предел в
ней:
— точка бесконечного разрыва (П-рода),
не входит в
-
На
получим
график
приближается к оси OX
( =0) снизу при
-
Для уточнения графика найдем дополнительную
точку
Заданная функция элементарная, и область
её непрерывности совпадает с областью
определения
— область непрерывности.
Строим график для
а затем достраиваем для

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Простое объяснение принципов решения пределов с корнями и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Основные свойства пределов с корнями
Для нахождения предела функции необходимо подставить в предел вместо Х то значение переменной, к которому стремится Х.
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Примеры решений пределов с корнями
Задание
Найти предел
Решение
Мы имеем неопределенность вида
Первый шаг – разделить числитель и знаменатель на ”х” в высшей степени. Старшая степень для числителя в данном случае равна двум.
Со знаменателем немного сложнее. Так как у нас корень, обращаем внимание только на самое ”старшее” слагаемое –
Число (4) – это константа, его тоже отбрасываем. Находим корень
Так как числитель и знаменатель оказываются одного порядка роста, предел равен конечному числу, отличному от нуля.
Видим, что функции эквивалентны на бесконечности.
Оформляем решение:
Ответ: 1
Задание
Найти предел с корнем
Решение
Подставляем
в подпредельную функцию:
Получаем неопределенность
Домножаем числитель и знаменатель на выражение, сопряженное к нему –
так как он содержит корень.
Далее, пользуясь формулой разности квадратов
и раскрывая скобки, упрощаем предел. Последний шаг – сокращение функции на
Ответ: -8
Задание
Решить предел с корнем
Решение
Подставляем
в предел и получаем неопределённость вида
Как и в предыдущих примерах, находим старшую степень для числителя и знаменателя, и выносим её за скобки.
И опять подставляем
в предел и решаем:
Ответ:
Задание
Вычислить предел корня:
Решение
Аналогично предыдущим примерам, подставляем
в предел и видим:
Находим сопряженное, в данном случае это
Как и в примере №2, пользуясь формулой разности квадратов
и раскрывая скобки, упрощаем предел:
Раскрываем скобки и упрощаем. Затем выносим х за скобки и сокращаем:
Как и в начале, подставляем в предел, получаем:
Ответ:
Задание
Вычислить предел функции
Решение
Если подставить х=1, видно, что и числитель, и знаменатель обращаются в ноль. Получаем неопределенность вида
Как и в предыдущих примерах, первым шагом находим сопряжённое –
и домножаем на него числитель и знаменатель.
Применяем правило разности квадратов
и преобразовываем предел:
Сокращаем числитель и знаменатель на (x-1) и приходим к конечному ответу:
Ответ: 6
Задание
Вычислить предел:
Решение:
Первый шаг – подставить в предел выражение
и убедиться, что выходит неопределённость вида
Шаг второй – раскрываем нашу неопределенность путём умножения числителя и знаменателя на сопряжённое выражение, в данном случае –
Далее, пользуясь формулой разности квадратов раскладываем числитель:
Подставляем х=3 в предел и вычисляем:
Ответ:
Задание
Вычислить предел
Решение
Как и в предыдущих заданиях, подставляем
и убеждаемся, что имеем дело с неопределённостью вида
Порядок действий стандартный. Избавляемся от иррациональности в знаменателе с помощью домножения числителя и знаменателя на сопряженное выражение. В данном примере сопряжённое выражение имеет вид –
Перемножаем знаменатель и сокращаем в числителе и знаменателе
Подставляем, как и ранее, х=3 и находим ответ:
Ответ: 17,8
Задание
Определить предел функции
Решение
Смотрим на функцию, подставляем
мы имеем дело с неопределённостью вида:
Начинаем работать с функциями, содержащими корень. Умножаем числитель и знаменатель на сопряжённое выражение и упрощаем предел:
После преобразований получаем ответ:
Ответ: -2
Задание
Решить предел
Решение:
Подставляя
в выражение лимита, подтверждаем догадки, что перед нами неопределённость вида
Как и раньше, первый шаг – избавиться от иррациональности с помощью домножения числителя и знаменателя на соответствующее сопряженное выражение.
Раскрываем скобки и сокращаем выражения на
Неопределённости
больше нет и ничего нам не мешает вычислить пример:
Ответ:
Задание
Вычислить предел
Решение
Оба лимита числителя и знаменателя равны нулю, значит опять неопределённость вида
Находим сопряжённое к числителю и знаменателю число:
Домножаем на полученное выражение числитель и знаменатель, раскрываем скобки и упрощаем:
Раскладываем числитель и знаменатель:
Вычисляем предел:
Ответ:
1.2. Пределы иррациональных выражений
Пример 1.
Пр.
4, Пр. 2
Примечание. При вычислении пределов
иррациональных выражений, дающих
неопределенности типа
или
используют введение новой переменной,
освобождающей от иррациональности, или
преобразование выражения с помощью
сопряженного ему. Например, парами
взаимно сопряженных выражений будут:
1)
и
2)
и
3)
и
которые при вычислении пределов
используются в формах:
(1.6)
(1.7)
(1.8)
Пример 2.
Пр.6
Пример 3.
Пример 4.
Примечание. Обратите внимание на то,
что при вычислении предела 5 из пункта
2.4.I и 3,4 настоящего пункта,
при раскрытии неопределенности
и
стараются так преобразовать выражение,
чтобы дробь можно было сократить на
множители
стремящийся к нулю.
1.
3. Вычисление пределов с использованием
таблицы эквивалентных бесконечно малых
функций.
Пример 1.
Пр.2
Пр.
3
Пример 2.
EMBED Equation.DSMT4
Пример 3.
Пр. 2
Пример 4.
Пример5.
Пр.4,Пр.6
Пр.6
Пример 6.
(Пр.5)=
Пример 7.
Пример 8.
Пример 9.
не определен из-за знака
1)
2)
Пр.4
Таким образом, существуют различные
односторонние на
и на
пределы.
1.4. Указания к заданию 5.
Пример. Докажите, что
и
бесконечно малые функции одного порядка
при
Найдите значение постоянной “C”,
при котором они будут эквивалентны.
Решение.
Пр.
Пр.
Пр.3
при
1.5. Пример выполнения задания 5.
Определите порядок относительно “x”
функции
бесконечно малой при
Решение.
при
— бесконечно малая одного порядка по
отношению к
,
то сеть второго порядка относительно
“x”.
1.6. Указания к выполнению задания 7.
При исследовании функции на
непрерывность пользуются теоремой о
непрерывности элементарных функций
там, где они определены; признаком
непрерывности фуки в точке
когда
(2.19)
При наличии точек разрывов исследуют
функции в их окрестности и соответствующим
образом классифицируют.
Пример 1. Исследовать функцию на
непрерывность и построить её схематический
график, если
Решение. Сначала найдем область
определения функции
Область определения симметрична
относительно начала координат, следует
исследовать функцию на признак четности.
функция
нечетная и её график симметричен
относительно начала координат. Таким
образом, достаточно исследовать функцию
на промежутке
построить
график, а затем отобразить его симметрию
начала координат.
-
В точке
функция определена справа, поэтому
найдем лишь правосторонний предел в
ней:
— точка бесконечного разрыва (П-рода),
не входит в
-
На
получим
график
приближается к оси OX
( =0) снизу при
-
Для уточнения графика найдем дополнительную
точку
Заданная функция элементарная, и область
её непрерывности совпадает с областью
определения
— область непрерывности.
Строим график для
а затем достраиваем для
Виды и правила раскрытия неопределенностей при вычислении пределов
|
|
||||||||||||||||||||||||||||||||||
|
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление
|
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Предел функции, суммы ряда. Ограниченность функции, замечательные пределы, односторонние и бесконечные пределы, необходимые и достаточные условия существования предела функции в точке. Правила вычисления. / / Виды и правила раскрытия неопределенностей при вычислении пределов Поделиться:
Поиск в инженерном справочнике DPVA. |
|||||||||||||||||||||||||||||||||
|
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. |
||||||||||||||||||||||||||||||||||
|
Коды баннеров проекта DPVA.ru Консультации и техническая |
Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator |
Исчисление
— Как оценить этот предел иррациональной функции?
Глядя на различные комментарии ОП, кажется, что учебники, которым он следует, не очень хорошего качества, и вместо того, чтобы предлагать пошаговый подход к ограничениям, они пытаются научить набору трюков.
Для большинства обычных предельных задач достаточно базовых правил пределов и некоторых стандартных пределов:
1) $displaystyle lim_{x to a}f(x) pm g(x) = lim_{ х to a}f(x) pm lim_{x to a}g(x)$ 9{x} — 1}{x} = 1,, lim_{x to 0}frac{log(1 + x)}{x} = 1$$
Далее мы подходим к конкретному вопросу здесь $$lim_{h to 0}frac{5}{sqrt{5h + 1} + 1}$$ Нам не нужно думать, рациональная это функция или нет, но просто заметим, что она выражение вида $f(h)/g(h)$, где $f, g$ — некоторые функции, поэтому следует применить правило 3). Ясно, что для числителя $f(h) = 5$ мы видим, что $lim_{h to 0} 5 = 5$, и нам нужно проверить, соответствует ли предел знаменателя $g(h) = sqrt{5h + 1 } + 1$ существует и не равно нулю. Если мы видим форму $g(h)$, она выглядит как сумма двух функций, и, следовательно, можно применить правило 1). Таким образом, мы можем написать
$ displaystyle begin {align} lim_ {h to 0} frac {5} { sqrt {5h + 1} + 1} & = dfrac {{ displaystyle lim_ {h to 0} 5}}{{displaystyle lim_{h to 0}{sqrt{5h + 1} + 1}}}\
& = dfrac {5} { displaystyle lim_ {h to 0} { sqrt {5h + 1} + 1 }}} \
& = dfrac {5} { displaystyle lim_ {h to 0} sqrt {5h + 1} + lim_ {h to 0} 1}} \
&= frac{5}{1 + 1} = frac{5}{2}end{aligned}$
Просто для сравнения мы пытаемся вычислить $$lim_{h to 0} frac{h}{sqrt{5h + 1} — 1}$$ Если мы будем следовать, как и раньше, мы увидим, что предел как числителя, так и знаменателя равен $0$, и, следовательно, правило 3) не может быть применено именно потому, что предел знаменателя составляет $0$.
$displaystyle begin{aligned}lim_{h to 0}frac{h}{sqrt{5h + 1} — 1} &= lim_{h to 0}frac{h}{ sqrt {5h + 1} — 1} cdot frac { sqrt {5h + 1} + 1} { sqrt {5h + 1} + 1} \
&= lim_{h to 0}frac{h{sqrt{5h + 1} + 1}}{5h}\
&= lim_{h to 0}frac{sqrt{5h + 1} + 1}{5}\
&text{(как в предыдущем примере)}\
&= frac{2}{5}end{aligned}$
Как видно из различных вопросов об ограничении на этом веб-сайте, большинство новичков в исчислении пытаются использовать такие понятия, как непрерывность, производная, L’Hospital и даже разложение в ряд для решения простые предельные проблемы (большинство ответов, приведенных здесь, также пытаются использовать эти методы). Очень жаль, что новички недооценивают силу простых правил ограничений (упомянутых выше) и переходят на концепции высокого уровня.
Можно ли представить каждое иррациональное число как (предел) бесконечной суммы рациональных чисел?
====new edit====
Благодаря ответу Люсьена я обратил внимание на то, что «представленное как бесконечная сумма последовательности рациональных чисел» может быть истолковано двояко. Это может быть просто $x = sum q_n $, где каждое $q_n$ является рациональным числом. Именно так я это интерпретировал, и именно на этой интерпретации основана остальная часть этого ответа.
Или это можно интерпретировать как $x = sum $( какое-то хорошее правило, которое дает рациональное число на основе n ). Примеры ОП относятся к этому типу и имеют прогностическое качество. Мы можем использовать их для вычисления значения действительного числа.
Согласно моей интерпретации, все иррациональные могут быть представлены таким образом (ответ ниже). По интерпретации Люсьена, они не могут. Его/Ее причина в том, что существует только счетное множество правил. Я не уверен в этом, но я считаю, что иррациональные неисчислимые делают их «произвольными» и непредсказуемыми. Но мне было бы очень трудно формализовать это.
========== конец нового редактирования ===========
Краткий ответ: Это определение действительного числа.
Длинный ответ:
Фундаментальная теорема анализа состоит в том, что существует упорядоченное поле, которое расширяет рациональные числа так, что поле обладает свойством наименьшей нижней границы. Мы определяем действительные числа как это поле.
Это означает, что по определению каждое действительное число является пределом сходящейся последовательности рациональных чисел.
Бесконечные суммы являются пределом конечных сумм. Следовательно, каждое действительное число может быть записано как бесконечная сумма рациональных чисел. Это эквивалентно определению действительного числа.
Доказательство фундаментальной теоремы довольно утомительно и долго. Это несложно, но дело в том, что вы выполняете доказательство до того, как будут определены действительные числа , и определение появится во время доказательства.
Более длинный ответ:
Теорема о фундаменте:
Шаг 1: Определить «разрез» как набор рациональных чисел со свойствами:
i) разрез не пуст.
ii) если p находится в разрезе, то каждое рациональное число меньше p находится в разрезе
iii) для любого p в разрезе можно найти большее рациональное число, которое находится в разрезе
Таким образом, разрезом могут быть все рациональные числа, меньшие, но не равные 3. Или все рациональные числа, квадраты которых меньше 2. (Первое в конечном итоге будет эквивалентно 3, а последнее в конечном итоге будет эквивалентно в $sqrt 2$
Шаг 2: Определите a < b, чтобы означать, что разрез a является подмножеством разреза b
Шаг 3: Покажите, что множество всех разрезов, назовем его R~, имеет наименьший верхний связанное свойство.
Блин. Здесь оно становится абстрактным. Свойство наименьшей верхней границы означает, что каждое ограниченное множество в универсальном множестве (например, какими будут вещественные числа, когда мы их определим) имеет четкий предел, который находится в универсальном множестве. , Пример: Q делает , а не имеют свойство наименьшей верхней границы.
Таким образом, у нас может быть множество разрезов, называемых A. Его можно ограничить сверху, что означает разрез b, такой, что все разрезы в A являются подмножествами b. (Помните, что «меньше» означает «является подмножеством»). Объединение всех разрезов в A больше или равно всем разрезам в A. Объединение само по себе является разрезом. Объединение — это наименьший разрез, который больше, чем все разрезы в A. Таким образом, объединение является наименьшей верхней гранью, а R~ обладает свойством наименьшей верхней границы.
Шаг 4: Определите разрез a «+» разрез b как разрез, который содержит суммы элементов из a плюс элементы из b.









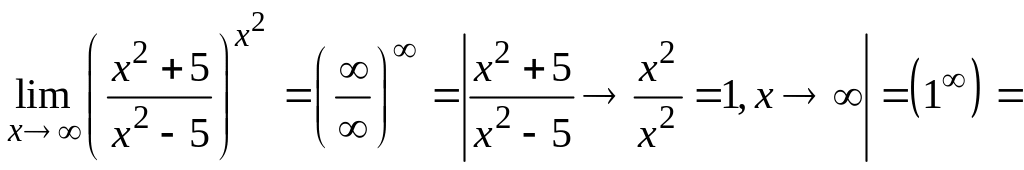



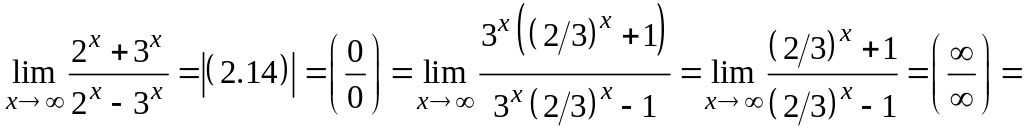







 Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
 2. Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби. В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула
2. Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби. В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула  В случае квадратных корней разность домножается на сопряженное выражение и применяется формула a2 – b2 = (a – b)(a + b) . В случае кубических корней функция домножается на неполный квадрат суммы или разности и применяется формула
В случае квадратных корней разность домножается на сопряженное выражение и применяется формула a2 – b2 = (a – b)(a + b) . В случае кубических корней функция домножается на неполный квадрат суммы или разности и применяется формула 

