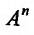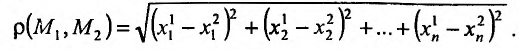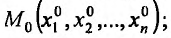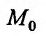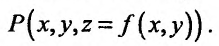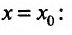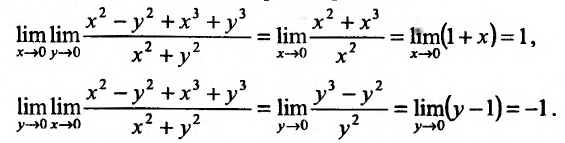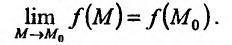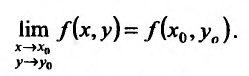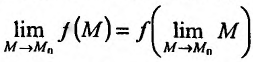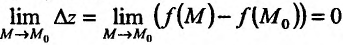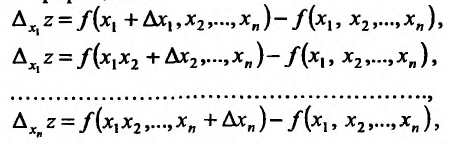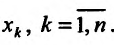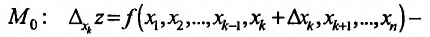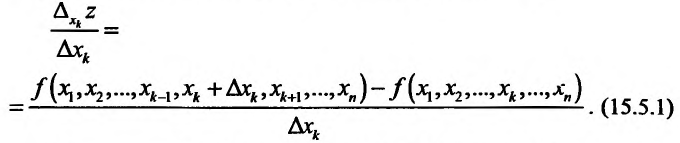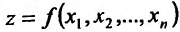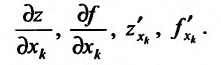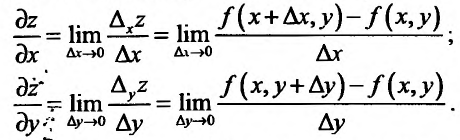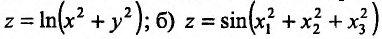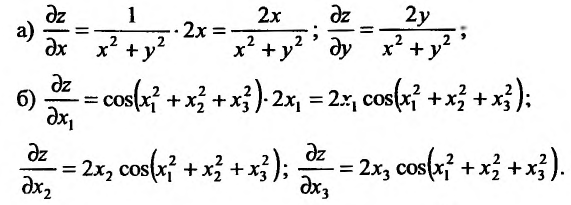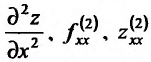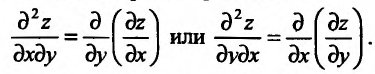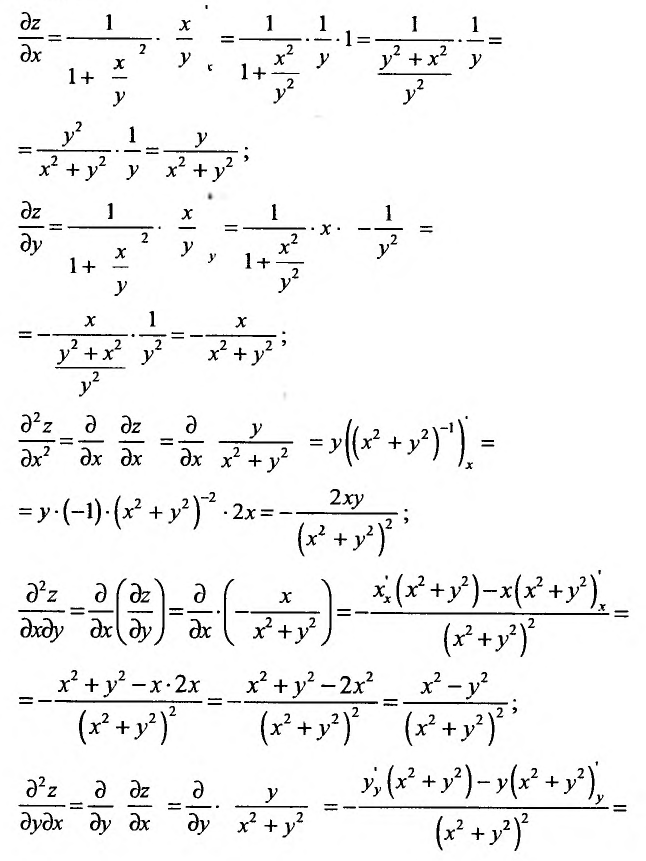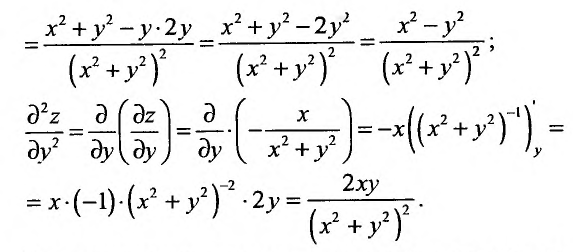Содержание:
Множества точек n-мерного евклидова пространства:
Назовем n-мерным координатным пространством и обозначим 
Координатное пространство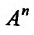 
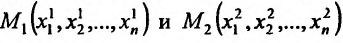
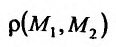
называется n-мерным евклидовым пространством и обозначается 
, если между двумя любыми точками 
пространства 
определено расстояние, обозначаемое 
и вычисляемое по формуле:
Опишем важнейшие типы множеств n-мерного евклидова пространства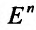 
.
Множество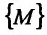 
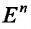
всевозможных точек М пространства 
, координаты которых удовлетворяют:
где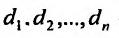 
— некоторые положительные числа, называется:
- а) открытым n-мерным шаром;
- б) замкнутым n-мерным шаром;
- в) n-мерной сферой радиуса R с центром в точке
- г) открытым n-мерным координатным параллелепипедом с центром в точке
Открытый n-мерный шар раднуса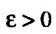 
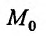
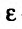
с центром в точке 
будем называть 
-окрестностью точки 
Множество {М} точек пространства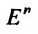
называется ограниченным, если найдется n-мерный шар, содержащий все точки этого множества.
Определение функции n переменных, двух переменных
Определение 15.2.1. Пусть задано множество точек {М} n-мерного евклидова пространства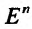 
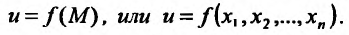
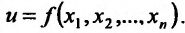
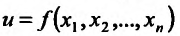
. Если каждой точке М из множества {М) ставится в соответствие по известному закону некоторое число и, то говорят, что на множестве {м} задана функция u = u(х) или 
. При этом множество {M} называют областью задания функции 
. Число u соответствующее данной точке М из множества {M}, называется частным значением функции в точке М. Совокупность {м} всех частных значений функции 
называется множеством значений этой функции.
Частным случаем функции n переменных является функция двух переменных, которую можно определить следующим образом.
Если каждой паре (х, у) значений двух независимых друг от друга переменных величин х и у. принадлежащих области D, соответствует по известному закону определенное значение величины z, то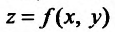 
называется функцией двух независимых переменных х и у, определенной в области D. D называется областью определения функции z = f(x, у).
Функция двух независимых переменных может быть задана:
- аналитически, то есть с помощью формул;
- при помощи таблицы, в которой указываются частные значения х и y, и соответствующие значения z;
- при помощи компьютерной программы, в которой определен алгоритм получения значений функции z для частных значений х и y
Для определения частных значений функции двух переменных должны быть заданы значения независимых переменных: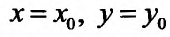 
И поэтому ясно, что функция z =f(х, у) может быть определена на всей плоскости или в некоторой ее части, то есть в некоторой области. Область определения как всякое множество может быть открытой (незамкнутой) или замкнутой.
Рассмотрим функцию 
определенную в области D на плоскости Оху и систему прямоугольных декартовых координат Oxyz. В каждой точке (x, у) восстановим перпендикуляр к плоскости Оху и на ней отложим отрезок, равный f(x,y). Тогда получим точку 
Геометрическое место точек Р, координаты которых удовлетворяют (15.2.1), называется графиком функции двух переменных. Но уравнение (15.2.1) определяет некоторую поверхность, следовательно, графиком функции двух переменных является поверхность, проектирующаяся на плоскость Оху в область определения функции.
Например, областью задания функции двух переменных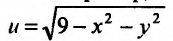 
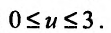
является круг радиуса 3 с центром в начале координат, а множество значений представляет собой отрезок
.
Область задания функции n переменных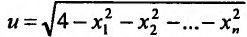 
служит n-мерный шар радиуса 2 с центром в точке O(0,0…..0). Множеством значений рассматриваемой функции является отрезок [0;2],
Из приведенных примеров, видим, что область задания функции n переменных представляет собой некоторое множество точек n-мерного евклидова пространства 
, а множество всех значений этой функции- множество одномерного евклидова пространства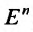 
.
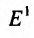
Предел функции двух переменных
Определение 15.3.1. (предел функции по Кохии) Число А называется пределом функции z = f(M) в точке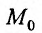 
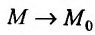
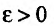
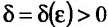
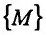
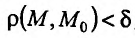
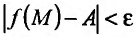
(или при 
). если для любого положительного числа 
найдется такое положительное число 
, что для любой точки М из множества 
задания этой функции, удовлетворяющей условию 
, справедливо неравенство 
.
Для обозначения предела функции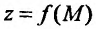 
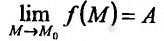
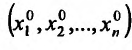
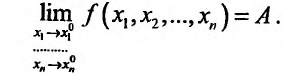
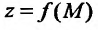
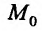
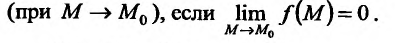
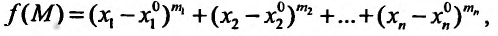
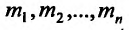
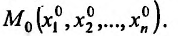
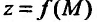
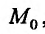
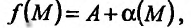
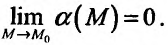
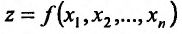
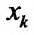
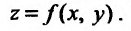
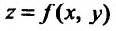
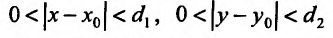
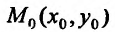
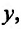
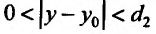
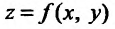
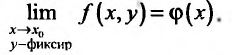
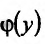
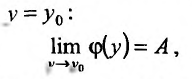
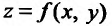
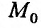
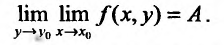
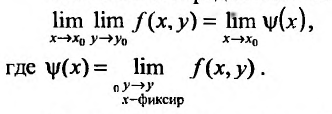
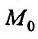
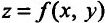
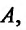
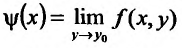
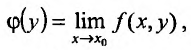
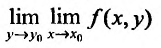
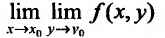
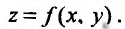
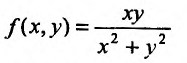
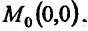
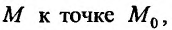
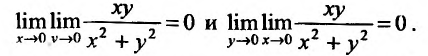
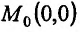
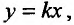
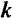
в точке используется символика: 
или если точка имеет координаты 
,тo 
Отметим, что в определении не указывается закон стремления точки М к точке Л , поэтому он может быть любым. Функция 
называется бесконечно малой в точке 
Например, функция 
где 
— положительные числа, является бесконечно малой в точке
Если функция 
имеет предел А в точке 
, то ее можно представить в виде суммы предела и бесконечно малой функции в этой точке: 
где 
Для функции 
можно определить понятие повторного предела, то есть предела по одной из переменных 
при фиксированных значениях остальных переменных. Рассмотрим повторный предел для функции двух переменных 
Пусть функция 
задана в прямоугольной окрестности 
точки 
и пусть для каждого фиксированного 
удовлетворяющего условию 
существует предел функции
одной пе ременной х в точке 
Тогда, если существует предел А функции 
в точке 
то он называется 
для функции 
в точке 
, который обозначается следующим образом:
Аналогично определяется повторный предел: 
Отметим, что если в точке 
функция 
имеет пре дел равный 
и существуют пределы 
и 
то повторные пределы 
и 
существуют и оба равны А. Однако из существования повторных пределов еще не следует существования предела функции
Так, например, функция 
не имеет предела в точке 
хотя можно указать такие законы стремления точки 
, что повторные пределы будут равны: 
Но если точка М стремится к точке
по прямой 
, то значение повторного предела будет зависеть от значения 
, что и свидетельствует об отсутствии предела рассматриваемой функции в точке (О,О).
Может оказаться, что оба повторных предела существуют, но различны. Нетрудно заметать, что для функции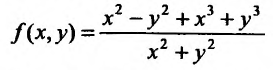 
будем иметь различные повторные пределы:
Поэтому, можно сделать вывод, что если для любого закона движения точки М к точке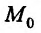 
повторные пределы существуют и они равны между собой, тогда и предел функции z = f(x, у) существует и равен этим повторным пределам.
Непрерывность функции двух переменных
Рассмотрим функцию п переменных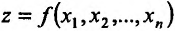 
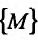
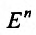
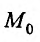
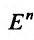
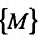
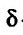
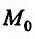
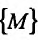
, заданную на некотором множестве 
пространства 
. Пусть 
-произвольная точка 
, принадлежащая множеству 
и такая, что в любой 
-окрестности точки 
содержатся точки множества 
.
Будем говорить, что функция z = f(М) непрерывна в точке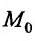 
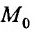
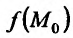
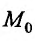
, если предел этой функции в точке 
существует и равен частному значению
. Символически непрерывность функции z = f(М) в точке 
можно записать в виде: 
В частности, для функции двух переменных: 
что поскольку 
, то условие непрерывности можно записать в виде:
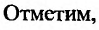
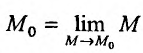
Значит, для непрерывной функции в точке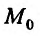 
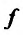
символ lim предела и символ 
характеристики функции можно менять местами.
Точки пространства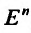 
, в которых функция z = f(м) не обладает свойством непрерывности, называются точками разрыва этой функции.
Используя определение предела функции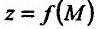 
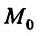
в точке 
по Коши, можно сформулировать определения непрерывности функции по Коши.
Если обозначить через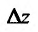 
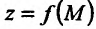
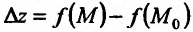
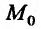
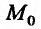
полное приращение функции 
, определяемое по формуле 
, где М произвольная точка из области задания функции, то для непрерывности функции z = f(M) в точке 
необходимо и достаточно, чтобы ее приращение представляло в точке 
бесконечно малую функцию, то есть
Аналогичным образом определяется непрерывность функции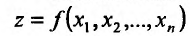 
по одной из переменных. Для этого вводятся частные приращения:
и тогда если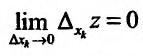 
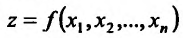
, то функция 
называется непрерывной по переменной 
Очевидно, что из условия непрерывности функции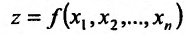 
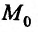
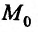
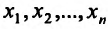
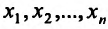
в данной точке 
вытекает непрерывность этой функции в точке 
по каждой из переменных 
. Однако, из непрерывности функции в точке 
по каждой из переменных 
не вытекает, вообще говоря, непрерывность функции в этой точке.
Для непрерывности функции n переменных справедливы многие аналогичные свойства непрерывных функций одной переменной: непрерывность сложной функции, устойчивость знака непрерывной функции, о прохождении через любое промежуточное значение, теоремы Вейрштраса и т.д.
Частные производные первого и высших порядков функции двух переменных
Пусть функция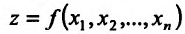 
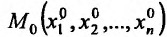
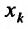
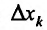
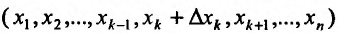
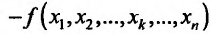
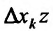
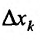
n переменных задана на множестве {м} и точка 
— внутренняя точка данного множества. Зафиксируем все аргументы, кроме 
, которому придадим произвольное приращение
, такое, чтобы точка с координатами 
находилась в области задания функции. Определим соответствующее частное приращение функции в точке 
. Составим отношение частного приращения 
к соответствующему приращению аргумента 
:
Отношение (15.5.1) представляет собой функцию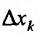 
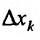
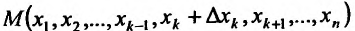
, определенную для всех отличных от нуля значений 
, для которых точка 
принадлежит области задания функции 
Определение 15.5.1. Если существует предел отношения (15.5.1) частного приращения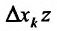 
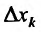
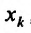
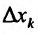
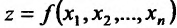
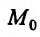
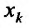
функции к соответствующему приращению 
аргумента 
, при стремлении 
к нулю, то тот предел называется частной производной функции 
в точке
по аргументу 
и обозначается одним из символов:
Таким образом,
(15.5.2)
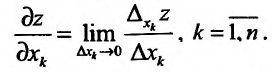
В частности, для функции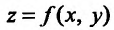 
двух переменных можно определить частные производные по х и у:
Из определения 15.5.1 следует, что частная производная функции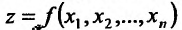 
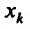
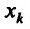
по аргументу
представляет собой обыкновенную производную функции одной переменной 
при фиксированных значениях остальных переменных. Поэтому вычисление частных производных производится с использованием правил вычислений производных функций одной переменной и таблицы производных.
- Заказать решение задач по высшей математике
Пример:
Вычислить частные производные функций:
a)
Решение:
Для вычисления частных производных воспользуемся правилами вычисления производных функции одной переменной, при этом, вычисляя частную производную по одной из переменных, другую считаем постоянной величиной.
Предположим, что частная производная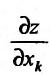 
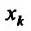
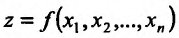
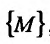
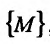
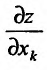
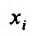
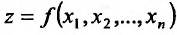
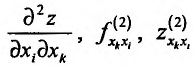
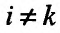
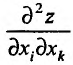
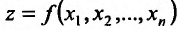
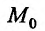
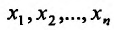
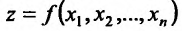
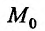
по аргументу 
функции 
, определенной на множестве 
, существует в каждой точке этого множества
. Тогда указанная частная производная представляет собой функцию n переменных, определенную на множестве {М}. Если эта функция 
имеет частную производную по аргументу 
в некоторой точке 
множества {м), то она называется частной производной второго порядка функции
в точке 
сначала по аргументу хк, а затем по аргументу х, и обозначается одним из символов: 
. При этом, если 
, то частная производная 
называется смешанной частной производной второго порядка. После того как нами введено понятие второй частной производной, последовательно вводится понятие третьей частной производной, четвертой и т.д. Частную производную функции 
П0 одному из аргументов в некоторой точке 
от частной производной (n-l)-ro порядка по аргументам 
(отдельные или даже все номера которых могут совпадать) называется частной производной n-го порядка функции 
в точке 
.
В частности для функции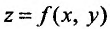 
двух переменных частные производные второго порядка определяются следующим образом.
Пусть частная производная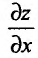 
по аргументу х функции z = f(х, у), определенной в области D. существует в каждой точке области D. В этом случае указанная частная производная представляет собой функцию двух переменных, также определенную в области D.
Тогда если эта функция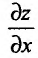 
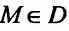
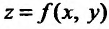
имеет частную производную по аргументу х в некоторой точке 
, то указанную частную производную по х называют второй частной производной или частной производной второго порядка функции 
в точке М по аргументу х и обозначают одним из символов: 
Аналогично определяется частная производная второго порядка по аргументу у.
Частная производная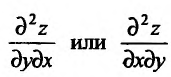 
называется смешанной производной второго порядка, т.е.
После того как введено понятие второй частной производной, можно последовательно ввести понятие третьей частной производной, затем четвертой и т.д.
Так как частная производная функции по аргументу х (у) определяется как обыкновенная производная функции одной переменной х (у)при фиксированном значении другой переменной, то методика вычисления частных производных высших порядков предполагает умение вычислять только обыкновенные производные первого порядка.
Пример:
Вычислить частные производные второго порядка функции
Решение:
Применив правило вычисления частных производных, получим: 
В рассмотренном примере смешанные частные производные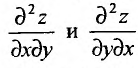 
равны друг другу. Вообще говоря, значения смешанных производных зависят от порядка, в котором производятся последовательные вычисления производных.
Достаточные условия независимости порядка вычисления производных определяются следующей теоремой.
Теорема 15.5.1. Пусть функция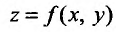 
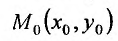
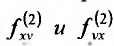
в точке
имеет непрерывные частные производные второго порядка, тогда в этой точке частные производные 
равны.
Более того имеет место такая же теорема о независимости значений любой смешанной частной производной n-го порядка от порядка, в котором производятся вычисления частных производных.
Теорема 15.5.2. Пусть функция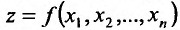 
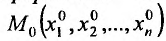
имеет непрерывные частные производные n-го порядка в точке 
Тогда в этой точке значение любой смешанной частной производной n-го порядка не зависит от порядка, в котором производится вычисление производных.
- Дифференцируемость функции нескольких переменных
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Исследование поведения функций
-
Предел функции в точке.
Начать изучение
-
Предел по множеству.
Начать изучение
-
Повторные пределы. Бесконечные пределы.
Начать изучение
Предел функции в точке.
Напомним, что окрестностью (O(x^0)) точки (x^0) в метрическом пространстве (X) называется любое множество, для которого точка (x^0) является внутренней. Проколотая окрестность (dot{O}(x^0)) получается из (O(x^0)) удалением самой точки (x^0), то есть (dot{O}(x^0)=O(x^0)backslash{x^0}).
Будем рассматривать функции (f: Mrightarrow R), где (M) есть некоторое множество, принадлежащее метрическому пространству (X). Если (X=R^n), то функция (f: Mrightarrow R) называется функцией многих переменных и обозначается обычно следующим образом:
$$
f(x)=f(x_1,ldots,x_n),quad xin M.nonumber
$$
Например, функция (displaystyle sqrt{1-x_1^2-x_2^2}) определена в единичном круге пространства (R^2) с центром в точке ((0,0)), а функция (operatorname{ln}(x_1^2+x_2^2)) определена в любой проколотой окрестности точки ((0,0)).
Определение 1.
Пусть функция (f(x)) определена в проколотой окрестности (dot{O}(x^0)) точки (x^0) метрического пространства (X). Говорят, что число (A) есть предел функции (f(x)) при (xrightarrow x_0), если (forall varepsilon > 0 exists delta > 0) такое, что для (forall xindot{O}(x^0)), удовлетворяющего условию (rho(x,x^0) < delta), выполнено неравенство (|f(x)-A| < varepsilon).
Определение 2.
Говорят, что функция (f(x)), определенная в (dot{O}(x^0)), имеет при (xrightarrow x_0) предел (A), если для любой последовательности (x^{(k)}indot{O}(x^0)) такой, что (displaystylelim_{krightarrowinfty}x^{(k)}=x^0), выполнено равенство (displaystylelim_{krightarrowinfty}f(x^{(k)})=A).
Эквивалентность двух определений предела доказывается так же, как и для функций одной переменной.
Если число (A) есть предел функции (f(x)) при (xrightarrow x_0), то будем писать
$$
A=lim_{xrightarrow x^0}f(x).nonumber
$$
Если функция двух переменных (f(x,y)) определена в (dot{O}((a,b))), a число (A) есть ее предел при ((x,y)rightarrow(a,b)), то пишут
$$
A=lim_{xrightarrow a,yrightarrow b}f(x,y)nonumber
$$
и называют иногда число (A) двойным пределом.
Аналогично, для функции (n) переменных наряду с обозначением (A=displaystylelim_{xrightarrow x^0}f(x)) будем использовать обозначение
$$
A=lim_{xrightarrow x_1^0,ldots,x_nrightarrow x_n^0}f(x_1,ldots,x_n).nonumber
$$
Лемма 1.
Пусть функции (f(x)) и (varphi(x)) определены в (dot{O}(x^0)) и (|f(x)|leq varphi(x)) в (dot{O}(x^0)). Если (displaystylelim_{xrightarrow x^0}varphi(x)=0), то и (displaystylelim_{xrightarrow x^0}f(x)=0).
Доказательство.
(circ) Так как (displaystylelim_{xrightarrow x^0}varphi(x)=0), то для любого (varepsilon > 0) найдется шар (S_{delta}(x^0)) такой, что для всех (xin S_{delta}(x^0)) выполнено неравенство (|varphi(x)| < varepsilon). Тем более для всех (xin S_{delta}(x^0)) выполнено неравенство (|f(x)| < varepsilon), то есть (displaystylelim_{xrightarrow x^0}f(x)=0). (bullet)
Пример 1.
Доказать, что (displaystylelim_{xrightarrow 0,yrightarrow 0}(x^2+y^2)^a=0), если (a > 0).
Решение.
(triangle) Возьмем любое (varepsilon > 0). Положим (delta=varepsilon^{1/(2a)}). Пусть ((x,y)in S_delta(0, 0)), тогда
$$
(x^2+y^2)^a < delta^{2a} < varepsilon,nonumber
$$
то есть
$$
lim_{xrightarrow 0,yrightarrow 0}(x^2+y^2)^a=0.nonumber
$$
Что и требовалось доказать. (blacktriangle)
Пример 2.
Показать, что (displaystyle lim_{xrightarrow 0,yrightarrow 0}frac{|x|^{alpha}|y|^{beta}}{(x^2+y^2)^{gamma}}=0), если (alpha+beta-2gamma > 0).
Решение.
(triangle) Так как
$$
|x| < sqrt{x^2+y^2},qquad |y| < sqrt{x^2+y^2},nonumber
$$
то при (x^2+y^2 > 0) имеем неравенства
$$
0leq f(x,y)=frac{vert xvert^alphavert yvert^beta}{(x^2+y^2)^gamma}leqfrac{(x^2+y^2)^{alpha/2}(x^2+y^2)^{beta/2}}{(x^2+y^2)^gamma}=\(x^2+y^2)^{(alpha+beta-2gamma)/2}=varphi(x,y).nonumber
$$
В силу примера выше (displaystylelim_{xrightarrow 0,yrightarrow 0}varphi(x,y)=0.), так как (alpha+beta-2gamma > 0). Применяя лемму 1, получаем, что
$$
lim_{xrightarrow 0,yrightarrow 0}f(x,y)=0.nonumber
$$
Что и требовалось доказать. (blacktriangle)
Пример 3.
Функция
$$
f(x,y)=frac{2xy}{x^2+y^2}label{ref1}
$$
не имеет предела при ((x,y)rightarrow (0,0)).
Решение.
(triangle) Рассмотрим последовательность точек ((x_n,y_n)=displaystyleleft(frac{1}{n},frac{1}{n}right)). Тогда (f(x_n,y_n)=1) и, следовательно, (displaystyle lim_{nrightarrowinfty}f(x_n,y_n)=1). Если же взять последовательность точек ((x_n’,y_n’)=displaystyleleft(frac{1}{n},-frac{1}{n}right)), то (displaystyle lim_{nrightarrowinfty}f(x_n’,y_n’)=-1).
Так как при любом (nin mathbb{N}) точки ((x_n,y_n)) и ((x_n’,y_n’)) не совпадают с точкой ((0,0)), а последовательности точек ((x_n,y_n)) и ((x_n’,y_n’)) сходятся к точке ((0,0)), то, используя определение 2 предела, получаем, что функция (f(x,y)) не имеет предела при ((x,y)rightarrow (0,0)). (blacktriangle)
Пример 4.
Функция
$$
f(x,y)=frac{2x^2y}{x^4+y^2}label{ref2}
$$
не имеет предела при ((x,y)rightarrow (0,0)).
Решение.
(triangle) Повторяя рассуждения примера 3, построим две последовательности точек ((x_n,y_n)=displaystyleleft(frac{1}{n},frac{1}{n}right)) и ((x_n’,y_n’)=displaystyleleft(frac{1}{n},frac{1}{n^2}right)). Так как ((x_n,y_n)rightarrow(0,0)) и ((x_n’,y_n’)rightarrow(0,0)), а (displaystylelim_{nrightarrowinfty}f(x_n,y_n)=0) и (displaystylelim_{nrightarrowinfty}f(x_n’,y_n’)=1), то двойной предел функции (f(x,y)) при ((x,y)rightarrow(0,0)) не существует. (blacktriangle)
Предел по множеству.
Предел (displaystylelim_{xrightarrow x^0}f(x)) был определен ранее для функции, заданной в (dot{O}(x^0)). Расширим определение предела, введя понятие предела по множеству.
Определение 3.
Пусть (M) есть подмножество области определения функции (f(x)), (x^0) — предельная точка множества (M). Будем говорить, что число (A) есть предел функции (f(x)) по множеству (M) при (xrightarrow x^0), если (forallvarepsilon > 0 exists delta > 0) такое, что (forall xin{dot S}_delta(x^0)cap M) выполнено неравенство (|f(x)-A| < varepsilon). В этом случае пишут
$$
A=lim_{xrightarrow x^0, xin M}f(x).nonumber
$$
Пусть функция двух переменных (f(x,y)) определена в проколотой окрестности (dot{O}(x_0,y_0)). Пределом функции (f(x,y)) в точке ((x_0,y_0)) по направлению (l=(cosalpha,sinalpha)) будем называть выражение
$$
lim_{trightarrow+0}f(x_0+tcosalpha, y_0+tsinleft(alpharight))=lim_{begin{array}{c}(x,y)rightarrow(x_0,y_0)\(x,y)indot O(x_0,y_0)cap L\end{array}}f(x,y),nonumber
$$
где (L) есть луч, выходящий из точки ((x_0,y_0)) в направлении (l).
Пример 5.
Показать, что предел функции (f(x,y)=displaystyle frac{2xy}{x^2+y^2}) в точке ((0,0)) по любому направлению (l=(cosalpha, sinalpha)) существует и равен (sin 2alpha).
Решение.
(triangle) Так как при (t > 0) выполнено равенство
$$
f(tcosalpha, tsinalpha)=2sinalphacosalpha=sin 2alpha,nonumber
$$
то
$$
lim_{trightarrow 0}f(tcosalpha, tsinalpha)=sin 2alpha.quadblacktrianglenonumber
$$
Пример 6.
Показать, что предел функции (f(x,y)=displaystyle frac{2x^2y}{x^4+y^2}) в точке ((0,0)) по любому направлению (l=(cosalpha, sinalpha)) существует и равен нулю.
Решение.
(triangle) При (t > 0) справедливо равенство
$$
f(tcosalpha, tsinalpha)=frac{2tcos^2alphasinalpha}{t^2cos^4alpha+sin^2alpha}.nonumber
$$
Если (sinalpha=0), то (f(tcosalpha, tsinalpha)=0) и, следовательно,
$$
lim_{trightarrow +0}f(tcosalpha, tsinalpha)=0.nonumber
$$
Если (sinalphaneq 0), то
$$
lim_{trightarrow +0}f(tcosalpha, tsinalpha)=0.quadblacktrianglenonumber
$$
Ясно, что из существования (displaystylelim_{xrightarrow x^0, xin M}f(x)) следует существование (displaystylelim_{xrightarrow x^0, xin M’}f(x)) для любого подмножества (M’subset M), для которого (x’) есть предельная точка. В частности, из существования двойного предела функции (f(x,y)) при ((x,y)rightarrow (x_0,y_0)) следует существование предела функции (f(x,y)) в точке ((x_0,y_0)) по любому направлению и равенство этих пределов двойному пределу функции (f(x,y)) при ((x,y)rightarrow (x_0,y_0)).
Из результатов примеров 4 и 6 следует, что из существования и равенства пределов по любому направлению в точке ((x_0,y_0)) не вытекает существование в этой точке предела функции.
Предел функции (f(x)) в точке (x^0in R^n) по направлению (l=(l_1,ldots,l_n)), где (l_1^2+ldots+l_n^2=1), определяется по аналогии со случаем функции двух переменных.
Повторные пределы. Бесконечные пределы.
Пусть функция двух переменных (f(x,y)) определена на множестве
$$
Pi={(x,y):quad 0 < |x-x_0| < a,quad 0 < |y-y_0| < b}.nonumber
$$
Пусть (forall xin (x_0-a, x_0+a), xneq x_0), существует (displaystylelim_{yrightarrow y_0}f(x,y)=g(x)), а функция (g(x)) определена в проколотой окрестности точки (x_0). Если существует (displaystylelim_{xrightarrow x_0}g(x)=lim_{xrightarrow x_0}lim_{yrightarrow y_0}f(x,y)), то этот предел называется повторным. Аналогично определяется другой повторный предел (displaystylelim_{yrightarrow y_0}lim_{xrightarrow x_0}f(x,y)).
Как показывают простые примеры, из существования двойного предела не следует существование повторных пределов, а из существования и равенства повторных пределов не следует существование двойного предела.
Так для функции (displaystyle f(x,y)=frac{2xy}{x^2+y^2}) примера 3 двойной предел при ((x,y)rightarrow (0,0)) не существует, но оба повторных предела равны нулю, так как
$$
lim_{xrightarrow0}f(x,y)=lim_{yrightarrow0}f(x,y)=0.nonumber
$$
Для функции
$$
f(x,y)=left{begin{array}{lc}xsinfrac1y,&yneq0,\0,&y=0,end{array}right.nonumber
$$
справедливо неравенство (|f(x,y)|leq|x|). В силу леммы 1 двойной предел этой функции при ((x,y)rightarrow (0,0)) равен нулю. Но при (xneq 0) не существует
$$
lim_{yrightarrow0}xsinfrac1y,nonumber
$$
а поэтому не существует и соответствующий повторный предел.
Бесконечные пределы для функций многих переменных определяются по той же схеме, что и для функций одной переменной. Например, (displaystylelim_{xrightarrow x^0}f(x)=+infty), если для любого числа (C > 0) число (delta > 0), что для всех (x) из проколотой окрестности (dot{O}(x^0)) точки (x^0) выполнено неравенство (f(x) > C).
Пример 7.
Показать, что
$$
lim_{xrightarrow +infty,yrightarrow +infty}(x^2+y^2)e^{-(x+y)}=0.nonumber
$$
Решение.
(triangle) Так как при (x > 0, y > 0) справедливо неравенство
$$
0leq (x^2+y^2)e^{-(x+y)}leq(x+y)^2e^{-(x+y)}nonumber
$$
и (displaystylelim_{trightarrow +infty}t^2e^{-t}=0), то (forall varepsilon > 0 existsdelta > 0) такое, что (forall t > delta) выполнено неравенство (t^2e^{-t} < varepsilon). Но тогда (forall x > displaystylefrac{delta}{2}) и (forall y > displaystylefrac{delta}{2}) справедливо неравенство
$$
0leq(x^2+y^2)e^{-(x+y)} < varepsilon.quadblacktrianglenonumber
$$
-
Предел и непрерывность функции нескольких переменных
Рассмотренные
выше понятия функций двух или трех
переменных можно обобщать на случай
переменных.
Определение.
Функцией
переменных
называется функция, область определения
которой принадлежит
,
а область значений – действительной
оси.
Такая функция
каждому набору переменных
из
сопоставляет единственное число
.
В дальнейшем для
определенности мы будем рассматривать
функции
переменных, но все утверждения
сформулированные для таких функции
остаются верными и для функций большего
числа переменных.
Определение.
Число
называется пределом функции
в
точке
,
если для каждого
найдется такое число
что при всех
из окрестности
,
кроме этой точки, выполняется неравенство
.
Если
предел функции
в точке
равен
,
то это обозначается в виде
.
Практически
все свойства пределов рассмотренные
нами ранее для функций одной переменной
остаются справедливыми и для пределов
функций нескольких переменных, однако
практическим нахождением таких пределов
мы заниматься не будем.
Определение.
Функция
называется непрерывной в точке
если выполняется три условия:
1)
существует
2)
существует значение функции в точке
3)
эти два числа равны между собой, т.е.
.
Практически
исследовать непрерывность функции
можно с помощью следующей теоремы.
Теорема.
Любая элементарная функция
непрерывна
во всех внутренних (т.е. не граничных)
точках своей области определения.
Пример.
Найдем все точки, в которых функция
непрерывна.
Как
было отмечено выше, эта функция определена
в замкнутом круге
.
Внутренние
точки этого круга является искомыми
точками непрерывности функции, т.е.
функция
непрерывна в открытом круге
.
Определение
понятия непрерывности в граничных
точках области определения
функции возможно, но мы этот вопрос в
курсе затрачивать не будем.
1.3 Частные приращения и частные производные
В
отличие от функций одной переменной,
функций нескольких переменных имеют
различные виды приращений. Это связано
с тем, что перемещения в плоскости
из точки
можно осуществлять по различным
направлениям.
Определение.
Частным приращением по
функции
в точке
соответствующим приращению
называется разность
.
Это
приращение по существу является
приращением функции одной переменной
полученной из функции
при постоянном значении
.
Аналогично
частным приращением по
в точке
функции
соответствующим приращению
называется разность
.
Это
приращение вычисляется при фиксированном
значении
.
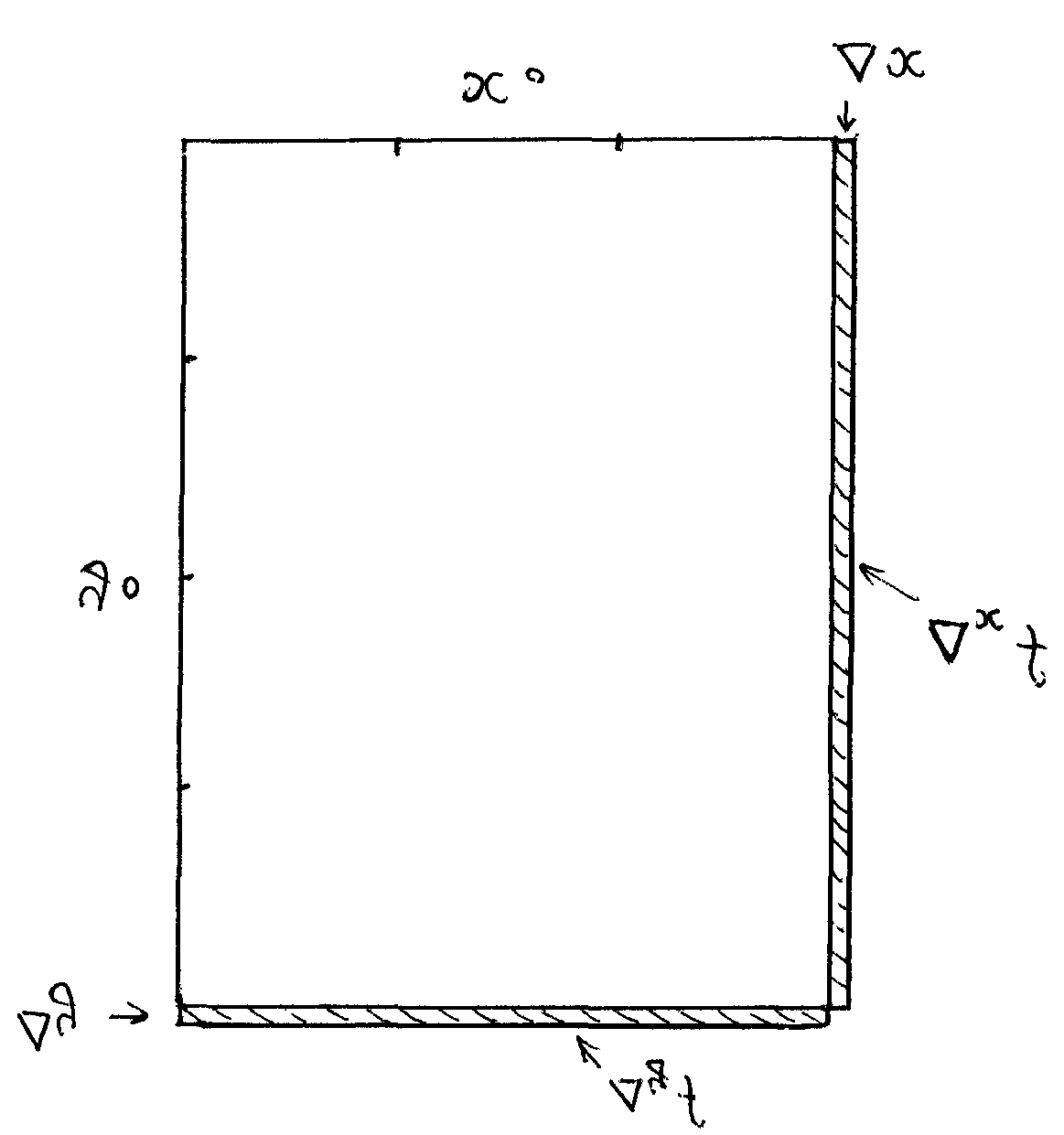
Пример.
Пусть
,
,
.
Найдем частные приращения этой функции
по
и по
.
В
данном примере при равных значениях
приращений аргументов
и
,
частные приращения функции оказались
различными. Это связано с тем, что площадь
прямоугольника со сторонами
и
при увеличении стороны
на
увеличивается на величину
,
а при увеличении стороны
на
увеличивается на
(см.рис.4).
Рис.4.
Из
того факта, что функция двух переменных
имеет два вида приращений, следует, что
для нее можно определить два вида
производных.
Определение.
Частной производной по
функции
в точке
называется предел отношения частного
приращения по
этой функции в указанной точке к
приращению
аргумента
т.е.
.
(1)
Такие
частные производные обозначаются
символами
,
,
,
.
В последних случаях круглая буква “
”
– “
”
означает слово “частная”.
Аналогично,
частная производная по
в точке
определяется с помощью предела
.
(2)
Другие
обозначения этой частной производной:
,
,
.
Частные
производные функций находятся по
известным правилам дифференцирования
функции одной переменной, при этом все
переменные, кроме той, по которой
дифференцируется функция, считаются
постоянными. Так при нахождении
переменная
принимается за постоянную, а при
нахождении
—
постоянная
.
Пример.
Найдем частные производные функции
.
,
.
Пример.
Найдем частные производные функции
трех переменных
.
;
;
.
Частные
производные функции
характеризуют скорости изменения этой
функции в случае, когда одна из переменных
фиксируется.
Пример
по экономики.
Основным
понятием теории потребления является
функция полезности
.
Эта функция выражает меру полезности
набора
,
где х- количество товара Х, у — количество
товара У. Тогда частные производные
будут соответственно называться
предельными полезностями х и у. Предельная
норма замещения
одного товара другим равна отношению
их предельных полезностей:
.
(8)
Задача
1. Найти предельную норму замещения ч
на у для функции полезности
в точке А(3,12).
Решение:
по формуле (8) получаем
Экономический
смысл предельной нормы замещения
заключается в обосновании формулы
,
где
-цена
товара Х,
—
цена товара У.
Определение.
Если у функции
имеются частные производные, то ее
частными дифференциалами называются
выражения
и
здесь
и
.
Частные
дифференциалы являются дифференциалами
функций одной переменной полученных
из функции двух переменных
при фиксированных
или
.
Примеры
из экономики.
Рассмотрим
в качестве примера функцию Кобба-Дугласа.
Величина
—
средняя производительность труда, так
как это количество продукции (в
стоимостном выражении), произведенное
одним рабочим.
Величина
—
средняя фондоотдача- количество
продукции, приходящееся на один станок.
Величина
—
средняя фондовооруженность- стоимость
фондов, приходящееся на единицу трудовых
ресурсов.
Поэтому
частная производная
называется предельной производительностью
труда, так как она равна добавочной
стоимости продукции, произведенной еще
одним дополнительным рабочим.
Аналогично,
—
предельная фондоотдача.
В
экономике часто задают вопросы: на
сколько процентов изменится выпуск
продукции, если число рабочих увеличить
на 1% или если фонды возрастут на 1%?
Ответы на такие вопросы дают понятия
эластичности функции по аргументу или
относительная производная. Найдем
эластичность выпуска продукции по труду
.
Подставляя в числитель вычисленную
выше частную производную
,
получим
.
Итак, параметр
имеет ясный экономический смысл – это
эластичность выпуска по труду.
Аналогичный
смысл имеет и параметр
— это эластичность выпуска по фондам.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #