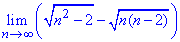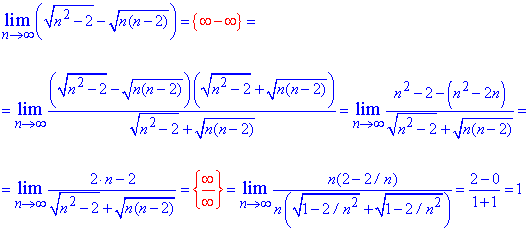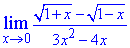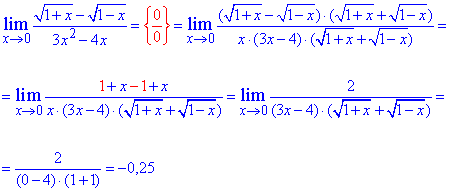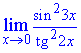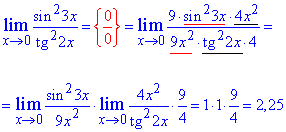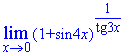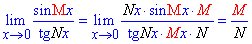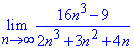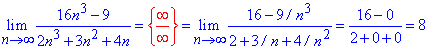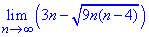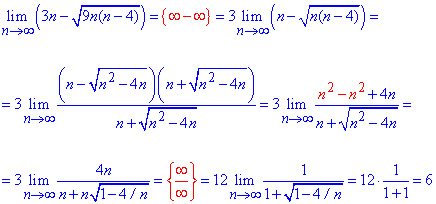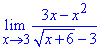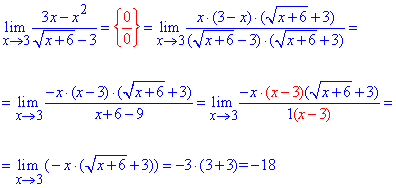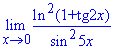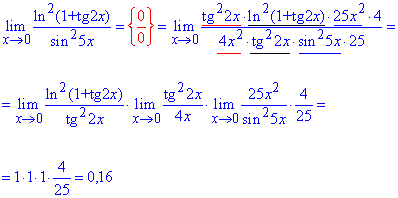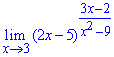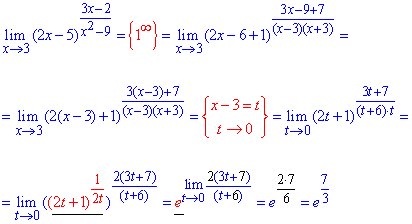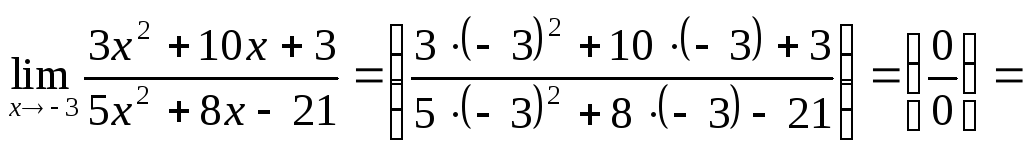Как найти предел функции дроби

6.1.1. Вычисление предела дробно — рациональной функции при

Пусть и – многочлены соответственно степеней и .

Выражение при может не представлять собой неопределённости или быть отношением двух бесконечно малых. При вычислении могут представляться следующие случаи.

А. Выражение не представляет собой неопределённости, если — не является корнем знаменателя, то есть . В этом случае используют теорему об арифметических действиях над функциями, имеющими предел в точке:

Б. Не представляет никакого труда вычисление предела и в случае, если – корень знаменателя, но не является корнем числителя, то есть , . В этом случае отношение При является бесконечно большой функцией, поэтому .

В. Если же является и корнем числителя и корнем знаменателя: , , то выражение При представляет собой неопределённость типа . В этом случае в числителе и в знаменателе можно выделить общий множитель наибольшей степени и сократить на него. Выделить такой множитель можно либо с помощью деления многочленов на «в столбик», либо путём группировки слагаемых. После сокращения на приходим либо к случаю А, либо к случаю Б.

Пример 1. Вычислить .

Решение. Число не является корнем знаменателя: (случай А), поэтому

.

Пример 2. Вычислить

Решение. Здесь ситуация такая же: число 2 не является корнем знаменателя (хотя и является корнем числителя).

Пример 3. Вычислить

Решение. В данном случае число является корнем знаменателя, но не является корнем числителя (случай Б)

Пример 4. Вычислить

Решение. В этом случае является корнем и числителя, и знаменателя, а значит выражение представляет собой неопределённость . В знаменателе следует выделить множетель . Возможно этот множитель будет входить в некоторой степени (если корни кратные). В числителе выделить такой множитель несложно:

Для того чтобы выделить такой множитель в знаменателе удобно разделить знаменатель на “в столбик”. Такое деление возможно без остатка по следствию из теоремы Безу. Действительно:

Теперь знаменатель можно представить как произведение:

Окончательно:

6.1.2 Вычисление предела дробно – рациональной функции при

Пусть при дробно-рациональная функция представляет собой неопределённость типа . Тогда при вычислении полезно учитывать, что при

Поэтому

Пример 6.

;

Пример 7.

;

Пример 8.

.

Если многочлены в числителе и знаменателе не представлены в стандартном виде, нужно внимательно отнестись к определению старшей степени. Например, выражение является многочленом третьей, а не четвёртой степени.

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

• предел обозначается значком lim;
• под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x, но не обязательно, например: “x→1″;
• затем справа дописывается сама функция, например:
  

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x→1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x→1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x→∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

• 3 – 1 = 2
• 3 – 10 = -7
• 3 – 100 = -97
• 3 – 1000 – 997 и т.д.

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

• При x = 1, y = 1² + 3 · 1 – 6 = -2
• При x = 10, y = 10² + 3 · 10 – 6 = 124
• При x = 100, y = 100² + 3 · 100 – 6 = 10294

Таким образом при “икс”, стремящемся к бесконечности, функция x² + 3x – 6 неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Решение

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

Пример: Найдем предел функции ниже.

Решение

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

В нашем случаем корнями выражения в числителе (2x² – 5x + 3 = 0) являются числа 1 и 1,5. Следовательно его можно представить в виде: 2(x-1)(x-1,5).

Знаменатель (x – 1) изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на (x – 1):

5. Остается только подставить число 1 в выражение, получившееся под пределом:

Продолжаем разбирать ответы к пределам функций и последовательностей. Примеров накопилось настолько много, что можно написать отдельную книгу — методичку по их вычислению.
В каждой публикации разжевываем методику вычислений до элементарных мелочей, при таких объяснениях каждый студент может без проблем решить подобные примеры.
Однако дальше от студентов поступают новые заказы с просьбой найти предел.
Порой нужно помочь с простыми функциями, что составляет впечатление что студенты имеют худшую подготовку, чем ученики в 11 классе, которые изучают эту тему.

Пример 11. Вычислить предел последовательности:

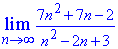
Решение: Подстановка большого номера в последовательность дает особенность вида бесконечность разделить на бесконечность. Для ее раскрытия в числителе и знаменателе дроби выделяем слагаемое, что вносит наибольший вклад. В скобках останутся константы + слагаемые, которые стремятся к нулю.

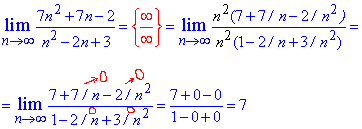
На общий множитель упрощаем, а константы дают значение предела последовательности.

Пример 12. Найти предел последовательности:

Решение: В предельном переходе имеем неопределенность вида бесконечность минус бесконечность. Функция представлена разницей корней. Чтобы избавиться от неопределенности, умножим и поделим разницу на сумму корней (сопряженное выражение). В результате придем к неопределенности бесконечность разделить на бесконечность. Чтобы ее раскрыть выносим множитель, что вносит наибольший вклад из числителя и знаменателя и сокращаем на него. Все что останется и будет пределом последовательности

Пример 13. Найти предел функции

Решение: При переменной стремящейся к нулю имеем неопределенность {0/0}. Для ее раскрытия разницу корней умножим и разделим на сопряженное выражение, чтобы в числителе образовать разность квадратов. В знаменателе имеем полином, который содержит особенность, поэтому разложим его на простые множители. После упрощений получим зависимость, предел которой легко находим методом подстановки

Пример 14. Вычислить предел

Решение: Переменная стремится к нулю, а функция задана долей синуса и тангенса в квадрате. В таких случаях нужно преобразовать выражение, чтобы в нем можно было легко выделить первый замечательный предел и его следствие. Для компенсации изменений в числитель и знаменатель записываем соответствующие константы. Далее переходим к произведению известных границ, вклад от каждой из которых равен единице.

Пример 15. Определить предел функции

Решение: При переменной стремящейся к нулю получим неопределенность вида единица в степени бесконечность. Для ее раскрытия выразим в степени множитель, который обратно пропорционален sin(4x).
Таким образом получим второй замечательный предел – экспоненту, а все что останется в показателе, даст степень экспоненты. Но здесь имеем долю sin(4x)/tan(3x), поэтому переходим к лимиту в показателе, а сам показатель сводим к первому замечательному пределу его следствии.

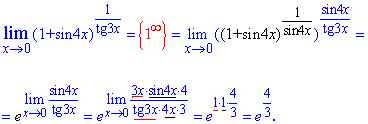
Из последнего «лимита» можно вывести простую формулу, которая может быть рассмотрена как следствие первого замечательного предела. Лимит доли тангенса к синусу (или наоборот) ровен доле их аргументов.

Пример 16. Найти предел последовательности:

Решение: Для раскрытия особенности вида бесконечность разделить на бесконечность необходимо три раза применить правило Лопиталя. Другая схема заключается в вынесении из числителя и знаменателя наибольшего множителя, и сокращении на него. В результате останутся константы и бесконечно малые функции. Последние стремятся к нулю, поэтому лимит последовательности равен

Пример 17. Вычислить предел последовательности:

Решение: Таких лимитов в предыдущих публикациях вычислено немало и суть раскрытия подобных неопределенностей заключается в умножении на сопряженное выражение – сумму корней. На это же выражение следует разделить функцию, чтобы не изменить значение лимита. В результате в числителе дроби получим разность квадратов и таким образом избавляемся от иррациональности, а предел выражения получим через оценку максимальных множителей.

Пример 18. Определить лимит функции

Решение: Когда переменная стремится к 3 имеем неопределенность вида {0/0}. Для раскрытия неопределенности в знаменателе дроби избавляемся от иррациональности умножением на сопряженное выражение, а в числителе полином раскладываем на простые множители. В результате и тат и там получаем выражение (х-3), на которое упрощаем.

Лимит функции, что осталась, вычисляем методом подстановки.

Пример 19. Найти предел функции

Решение: Предел функции в нуле дает особенность {0/0}. Ее не так просто раскрывать, как предыдущие.
Здесь следует свести выражение к первому и второму замечательному пределу и их следствиям.
Ln(1+x)/x в предельном переходе даст единицу, так же как и tan(x)/x и sin(x)/x.
Число 4/25 и будет лимитом функции.

Пример 20. Найти лимит

Решение: Предел функции в точке имеет неопределенность вида единица в степени бесконечность. Для ее раскрытия нужно преобразовать функцию под второй замечательный предел. Для этого и в скобках, и в показателе выделяем множитель, что вносит особенность (x-3) и делаем замену переменных t=x-3.
Далее переходим к экспоненте, и определяем лимит показательной функции.

Как Вы могли убедиться, задания на пределы не самые сложные в высшей математике.
Нужно знать не так много правил, чтобы без труда находить правильный ответ.

Пределы дробно-рациональных функций с квадратичными выражениями

В случае
неопределённости
следует разложить квадратичное выражение
на множители. Для этого можно

а)
воспользоваться тождеством
,
гдеи– корни уравнения,
найденные по формуле;

б)
учесть, что, когда
,
то– один из корней, и другой кореньможно найти по теореме Виета, например,
из равенства,
где;

в)
применить равенство
,
где
.

Пример 7.

(решили уравнения
ии применили 1-й способ).

Пример 8.

.

В уравнении
свободный коэффициент –10 разделили на
коэффициент, стоящий перед(число 4). Результат разделили на известный
корень 2. Получили 2-й корень.

Затем в уравнении
нашли 2-й корень из условия,
где 2 – известный корень, а 6 – свободный
коэффициент (Теорема Виета).

Пример 9.

.

Скобка
получена как,
а остальные найдены 3-м способом.

ПР6. Раскройте
неопределённость
,
разложив дробь на множители:

1) а)
; б); в);
г);

2) а)
; б); в);
г);

3) а)
; б); в);
г);

4) а)
; б); в);
г).

Пример 10.

.

Предел дробно-рациональной функции в бесконечности

Пусть дана функция
(см. стр. 16) и надо найти.
Оказывается, прився дробь ведёт себя так, как отношение
старших степеней:

.

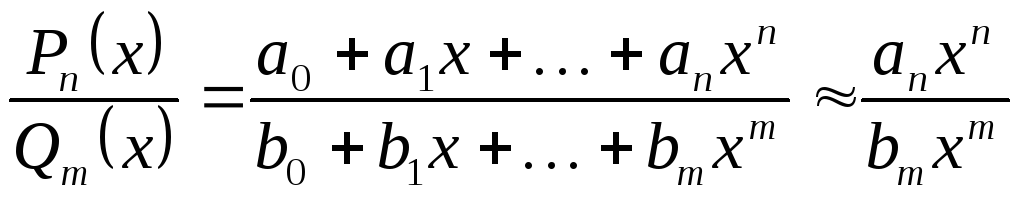
Тогда
.
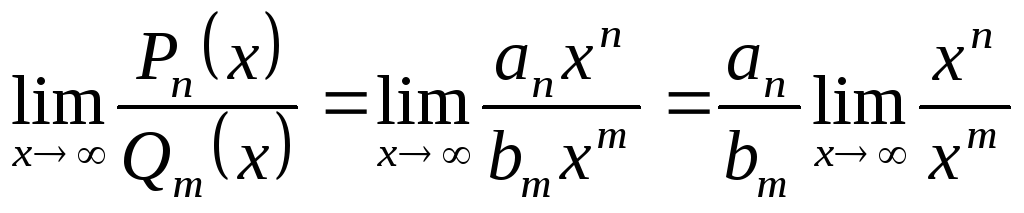
Обозначим.
Возможны 3 случая:

1)
,
тогда,
где

();

2)
,
тогда,
где

();

3)
,
тогда.

Таким образом,
предел равен

а) бесконечности,
если степень числителя больше, чем
степень знаменателя;

б) 0 в противоположном
случае;

в) отношению
старших коэффициентов, если степени
равны.

ПР7.
Найдите пределы

1) а)
; б); в); г); д);

2) а)
; б); в); г);
д);

3) а)
; б); в); г);
д);

ПР8.
Найдите пределы

1) а)
; б); в);

2) а)
; б); в);

3) а)
; б); в).

Пример 11. Оставив
в числителе и в знаменателе старшие
степени, находим

а)
;

б)
;

в)
.

Пример 12.
Оставив старшие степени, видим, что

а)
;

б)
;

в)
.

Обратите внимание,
что знак бесконечности (если таковая
получается) в ответе не указывается.
Тем не менее, если обе старшие степени
– чётные (или если обе нечётные), очевидно,
их отношение всегда положительно, что
можно учесть.

ПР9. Найдите
пределы функций
в точках,,,,,
а также при.

.

Пределы иррациональных функций

Если функция
содержит корень, подставляем, как обычно,
предельную точку. Сложности связаны с
неопределённостью
,
когда приходится умножать числитель и
знаменатель насопряжённое
выражение.

Выражения сопряжены
относительно
разности квадратов,
если их произведение превращается в
разность квадратов по формуле
.

Примеры сопряжённых выражений

а)
сопряжено с,
при этом;

б)
сопряжено с,
и тогда;

в)
сопряжено с,
поскольку

,

причём под корнем
всё остаётся без изменений;

г)
сопряжено с:

.

ПР10. Найдите
пределы иррациональных функций простой
подстановкой:

1) а)
; б); в); г);

2) а)
; б); в); г);

3) а)
; б); в); г);

4) а)
; б); в); г).

Пример 13.
Подставив указанные точки, находим
значения

а)
;

б)

.

ПР11. Раскройте
неопределённость
,
умножив числитель и знаменатель дроби
на подходящее сопряжённое выражение и
сократив одинаковые скобки:

1) а)
; б); в); г);

2) а)
; б); в); г);

3) а)
; б); в); г);

4) а)
; б); в);

г)
; д); е).

Пример 14.

.

Пример 15.

.

Пример 16.

.

ПР12. Умножьте
числитель и знаменатель на выражение,
сопряжённое к числителю, а затем – на
выражение, сопряжённое к знаменателю.
Сократив скобки, раскройте неопределённость
:

1) а)
; б); в); г);

2) а)
; б); в); г);

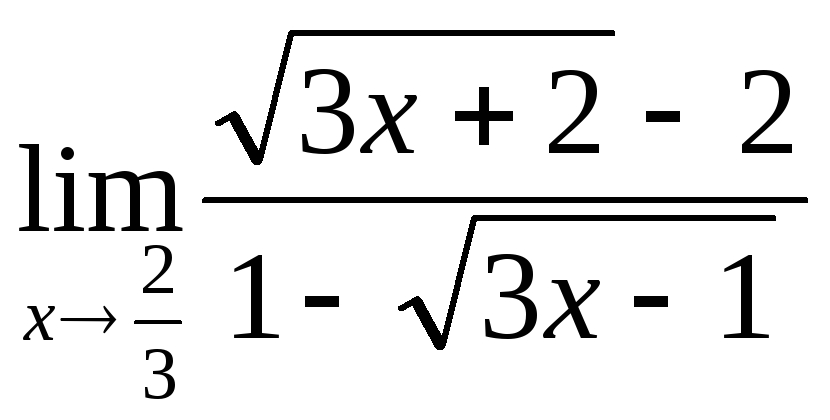
3) а)
; б); в);

4) а)
; б); в).

Пример 17.
Умножим, чтобы получить разность
квадратов:

.

Пример 18.
Так же, как в примере 17,

.

Иррациональные
пределы при
в случае неопределённостинаходят подобно рациональным, при помощи
старших степеней, а в случае неопределённостисводят её кпри помощи сопряжённого выражения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #