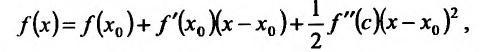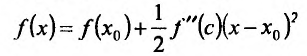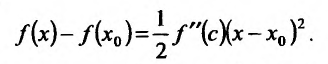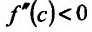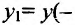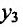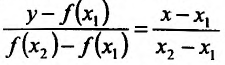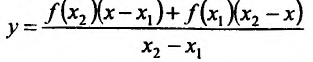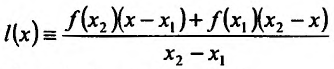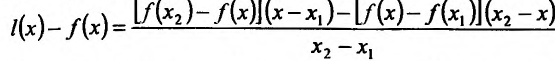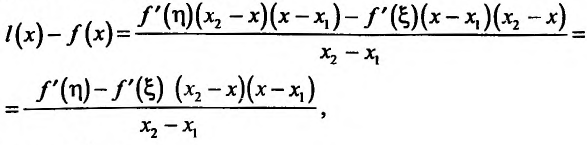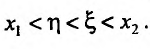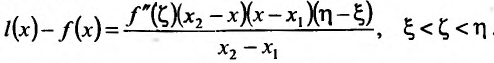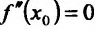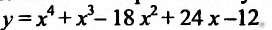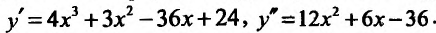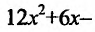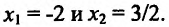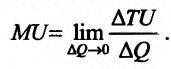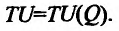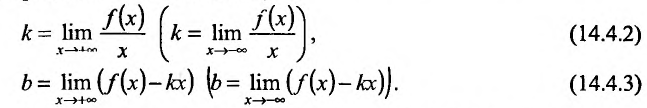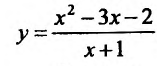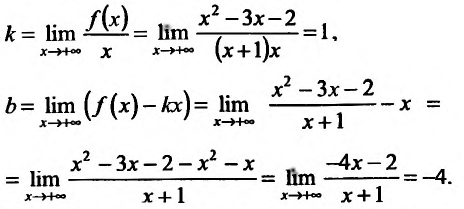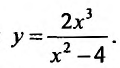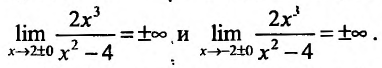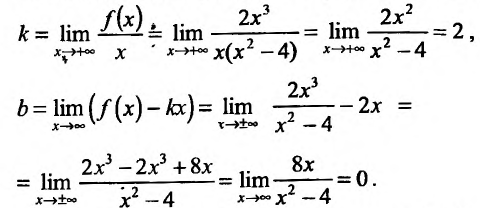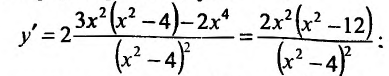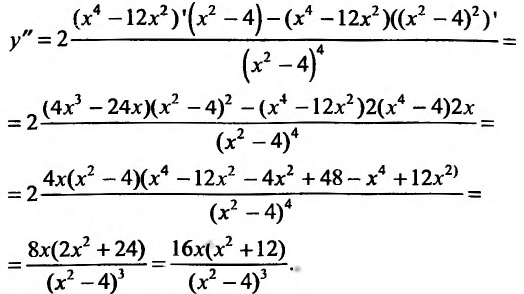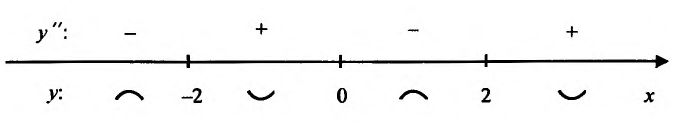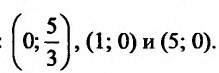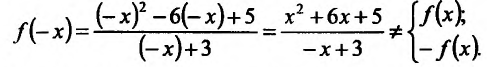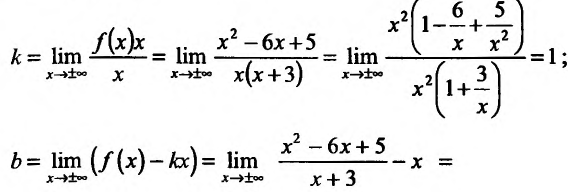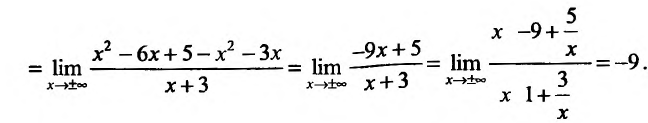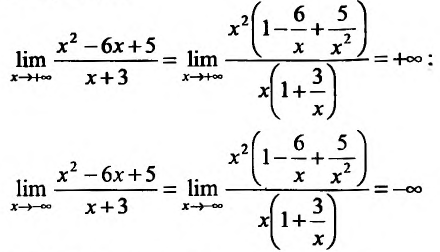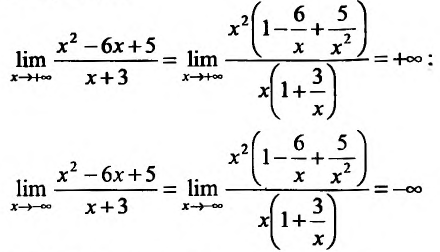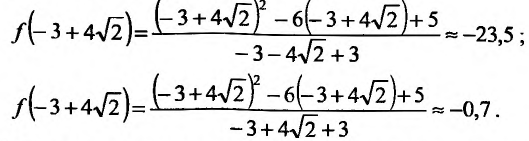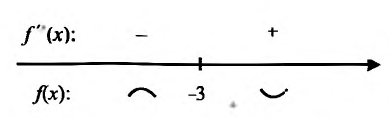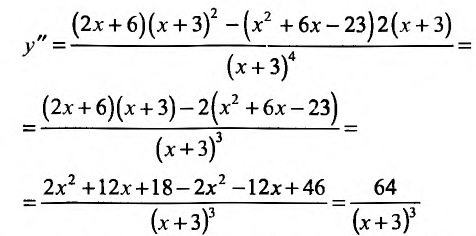Содержание:
Критерий монотонности функции:
Прежде всего, сформулируем определение монотонной функции:
- Функция f называется неубывающей (невозрастающей) на интервале (а,b), если для любых двух точек
- Функция f называется возрастающей (убывающей) на интервале (а,b), если для любых двух точек
из интервала (а, b), удовлетворяющих условию
справедливо неравенство
Неубывающие и невозрастающие функции называют монотонными функциями.
Монотонные функции
Возрастающие и убывающие функции называются строго монотонными функциями.
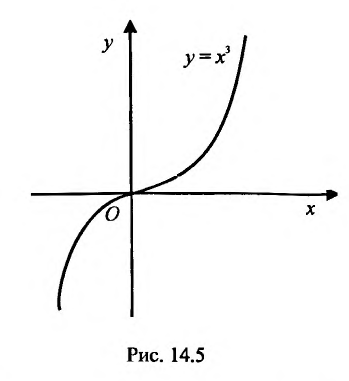
Например, функция у = х- возрастающая (строго монотонная) на всей числовой оси; функция 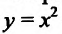
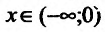
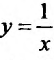
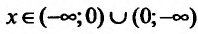
Теорема 14.1.1. (Критерий монотонности) Пусть функция 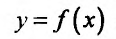
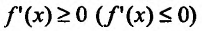
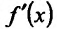
Доказательство: Пусть 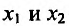
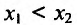
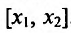
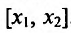
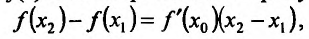
где 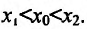
Необходимость. Пусть функция f дифференцируема на интервале (а, b) и не убывает (не возрастает) на этом интервале. Требуется доказать, что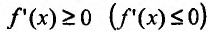
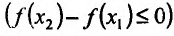
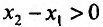
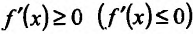
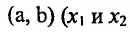
Достаточность. Пусть теперь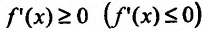
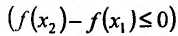
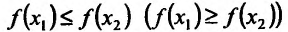
Поскольку 
Аналогично теорема доказывается и для возрастающей (убывающей) функции.
Из доказанной теоремы следует, что для определения интервалов монотонности функции нужно:
- Найти область определения функции.
- Вычислить ее производную.
- Приравнять производную к нулю; полученные нули производной разобьют область определения на интервалы, в которых производная сохраняет знак.
- Определить знак производной в каждом интервале при помощи «пробной» точки и сделать вывод.
Пример:
Найти интервалы монотонности функции
Решение:
Область определения заданной функции — вся числовая ось 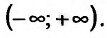
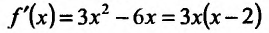
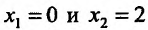
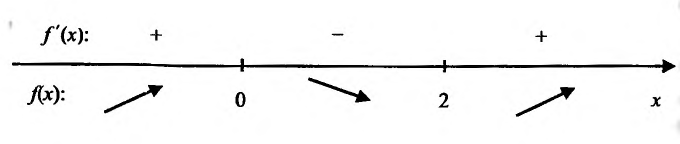
Составим схему изменения знаков производной:
Согласно теореме’ 14.1.1, данная функция возрастает при 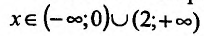
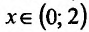
Функция 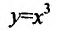
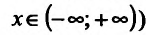
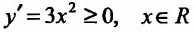
Функция 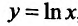
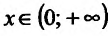
Экстремумы функций
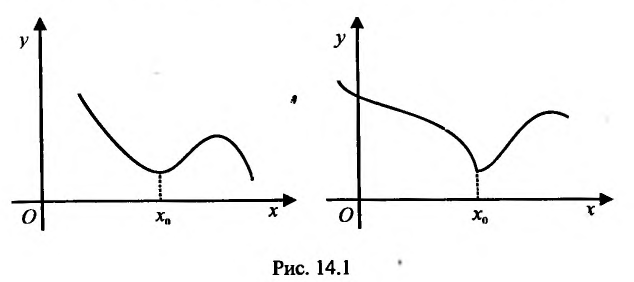
Определение 14.2.1. Пусть функция f определена в некоторой окрестности точки 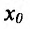
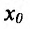
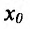
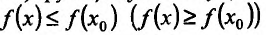
Если выполняются строгие неравенства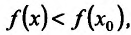
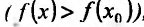
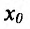
Точки максимума и минимума (строгого максимума и минимума) называются точками экстремума (строгого экстремума).
Теорема 14.2.1 .(необходимое условие экстремума) Если точка 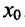
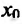
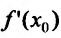
Справедливость этой теоремы следует из теоремы Ферма в силу определения точек экстремума. Действительно, если 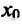
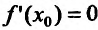
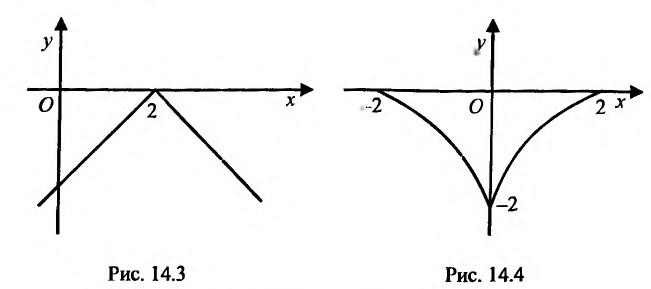
Функция может достигать экстремума также в точке, в которой производная не существует. Например, функция 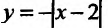
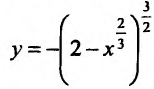
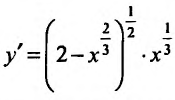
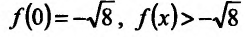
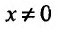
Из приведенных рассуждений следует, что точки экстремума функции нужно искать среди тех точек её области определения, где производная функции равна нулю или не существует.
Если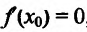
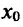
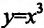
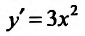
Точки области определения функции, в которых производная равна нулю, называются стационарными, а в которых производная не существует, называются критическими.
Каждая стационарная (критическая) точка — это точка возможного экстремума. Однако сделать заключение о том, что в данной стационарной (критической) точке на самом деле экстремум, можно лишь на основании дополнительного исследования, т.е. на основании достаточных условий экстремума.
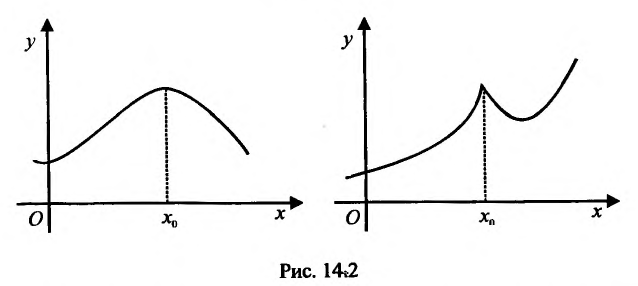
Теорема 14.2.2. (первое достаточное условие экстремума) Пусть функция f определена, дифференцируема в некоторой окрестности точки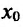
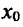
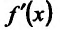
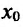
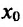
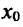
- если
на
и
на
, то точка
— точка максимума функции f(x);
- если
на
и
на
, то точка
— точка минимума функции f(x);
Если же в пределах указанной окрестности точки 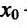
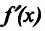
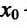
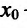
Доказательство. Докажем первое утверждение теоремы.
Предположим, что 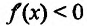
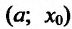
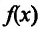
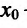
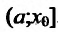
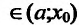
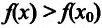
Пусть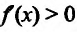
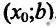
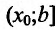
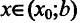
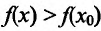
В результате получается, что при любом 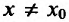
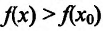
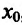
Второе утверждение теоремы доказывается аналогично.
Пример:
Найти точки экстремума функции’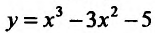
Решение:
Поскольку 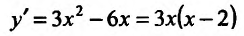
Производная функции 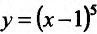
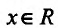
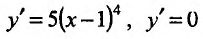
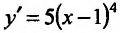
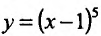
Теорема 14.2.3. (второе достаточное условие экстремума) Если функция f определена в некоторой окрестности точки 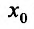
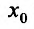

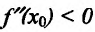
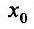
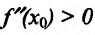
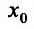
Доказательство: Поскольку функция f дважды дифференцируема в точке 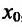
в виде:
где точка с расположена между 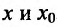
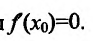
или
Поскольку 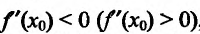
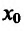
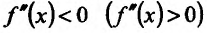
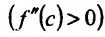
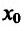
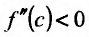
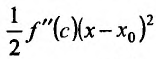
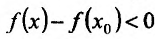
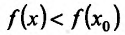
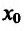
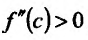
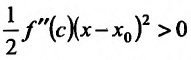
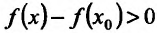
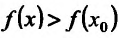
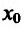
Пример:
Найти точки экстремума функции 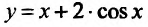
Решение:
Вычислим первую и вторую производные заданной функции: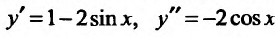
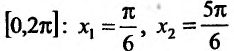
Теперь находим знак второй производной в каждой стационарной точке и определяем ее характер, используя теорему 14.2.3. Поскольку
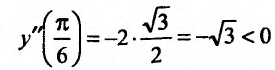
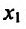
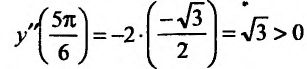
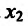
Теорема 14.2.4. (третье достаточное условие экстремума). Пусть функция f определена в некоторой окрестности точки 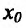
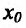
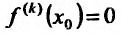
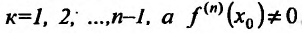
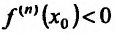
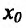
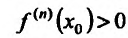
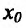
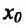
Пример:
Исследовать на экстремум функцию 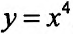
Решение:
Функция определена, непрерывна и дифференцируема на всей числовой оси. Найдем первую производную- 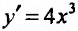
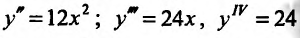
Сформулированные теоремы позволяют решать определенный круг задач. Например, требуется определить наибольшее (найме шее) значение функции f на отрезке [а, b]. Для этого следует на ней все точки, в которых производная функции либо равна нулю, ли’ не существует. Затем из этих точек выбираем те, которые принадлежат отрезку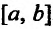
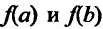
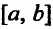
Пример:
Найти наибольшее и наименьшее значениях функции 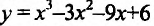
Решение:
Вычислив производную и приравняв ее к ну: 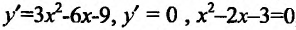
Отрезку [-2;2] принадлежит только одна точка 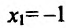
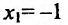
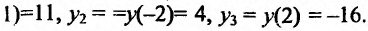
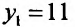
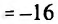
Выпуклость и точки перегиба
Пусть функция f определена на интервале (а; b) и пусть точки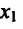
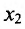
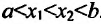
Разрешим это уравнение относительно у:
ИЛИ
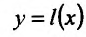
Ясно, что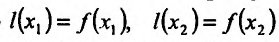
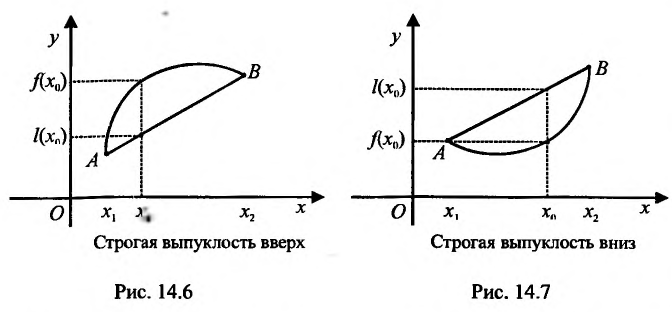
Определение 14.3.1. Функция f называется выпуклой вверх (выпуклой вниз) на интервале 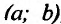
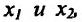
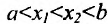
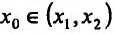
соответственно. А сам интервал называется интервалом выпуклости вверх (выпуклости вниз).
Геометрически это означает, что любая точка хорды АВ (т.е. отрезка прямой у=1(х) с концами в точках А и В) лежит не выше (не ниже) точки графика функции , соответствующей тому же значению аргумента.
Если неравенства (14.3.1) и (14.3.2) строгие, то функция f называется строго выпуклой вверх (рис. 14.6) (строго выпуклой вниз (рис. 14.7)). В этом случае любая точка хорды АВ, исключая ее концы, лежит ниже (выше) соответствующей точки графика функции
Теорема 14.3.1. (достаточное условие строгой выпуклости) Если функция f определена и дважды дифференцируема на интервале (а,b), то 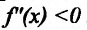
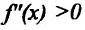
Доказательство. Пусть функция f определена и дважды непрерывно дифференцируема на интервале (а, b). Возьмем некоторые точки 
Применяя теорему Лагранжа к каждой разности, т.е. к 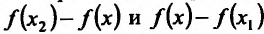
где
Снова применим теорему Лагранжа к разности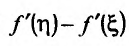
Отсюда видно, что если 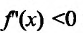
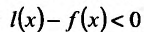
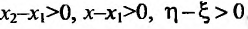
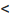

Заметим, что условие знакопостоянства второй производной не является необходимым условием. Так, функция 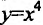
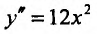
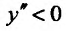
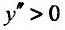
Определение 14.3.2. Пусть фунщия f определена в некоторой окрестности точки 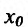
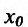
Теорема 14.3.2. (необходимое условие точки перегиба) Если функция f определена и дважды непрерывно дифференцируема на (а,b) и 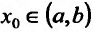
Доказательство. Пусть задана функция f, которая определена и дважды’ непрерывно дифференцируема на (а.b) и пусть точка 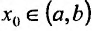
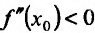
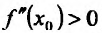
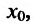
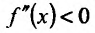
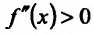
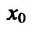
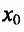
Из теоремы вытекает, что точками перегиба дважды дифференцируемой функции могут быть лишь точки, в которых вторая производная обращается в нуль либо не существует.
Сформулируем и докажем теперь достаточные условия точки перегиба.
Теорема 14.3.3. Если функция f определена и дважды дифференцируема на интервале (а,b), кроме, быть может точки 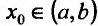
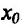
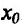
Действительно, в силу теоремы 14.3.1 точка 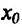
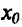
Теорема 14.3.4. Если f трижды непрерывно дифференцируема на (а,b) и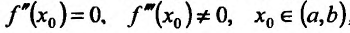
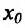
Доказательство (проведем для случая f»(x0) > 0). Так как по предположению 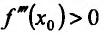
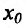
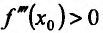
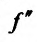
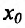
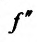
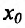
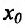
Теорема 14.3.5. Пусть функция f непрерывно дифференцируема n раз на (а,b), причем
Итак, из изложенного материала вытекает, что выпуклость вверх или вниз графика функции f зависит от знака ее второй производной. Оказывается, что и расположение графика функции относительно касательной также связано со знаком второй производной, т.е. если функция f имеет вторую производную, все значения которой имеют один и тот же знак, то все точки графика функции f лежат над (под) касательной.
Рассмотрим пример, иллюстрирующий исследование графика функции на выпуклость и точки перегиба.
Пример 14.3.1. Найти интервалы выпуклости и точки перегиба графика функции
Решение. Функция определена для всех 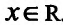
Приравняв вторую производную к нулю 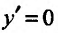
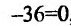
Составляет схему изменения знаков второй производной:
Следовательно, у»>0 на интервалах 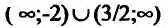
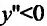
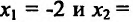
Рассмотрим пример из микроэкономики:
В количественной теории полезности предполагается, что потребитель может дать количественную оценку (в некоторых единицах измерения) полезности любого количества потребляемого им товара.
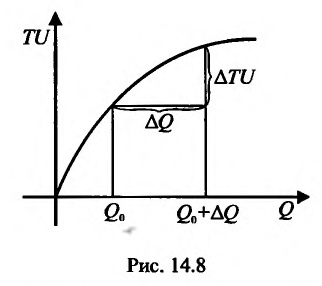
Это означает существование функции полезности TU аргумента Q -количества купленного товара. Введём понятие предельной полезности, как добавочной полезности, прибавляемой каждой последней порцией товара. Построим прямоугольную систему координат и отложим по горизонтальной оси Ох количество потребляемого товара Q, а по вертикальной оси Оу — общую полезность TU (см. рис. 14.3). Рассмотрим график функции TU = TU(Q). Точка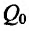
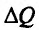
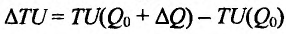
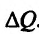
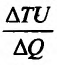
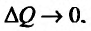
Но предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю, равен производной функции.
Следовательно, предельная полезность равна производной функции полезности TU=TU(Q). Закон убывающей предельной полезности сводится к уменьшению этой производной с ростом величины Q. Отсюда следует выпуклость графика функции
Асимптоты графика функции
Рассмотрим функцию f определенную на интервале (а;b), . Если 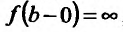
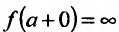
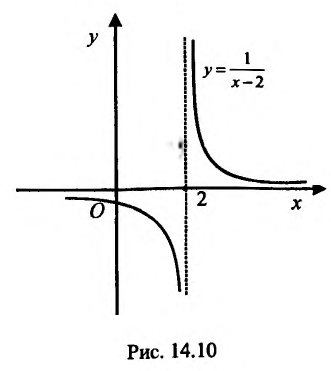
Заметим, что вертикальными асимптотами являются, как правило, нули знаменателей дробно-рациональных функций.
Если функция f определена на и для постоянных 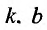
то прямая у = kх + b- называется наклонной асимптотой вправо графика функции f Если соотношение (14.4.1) выполняется и при , то прямая 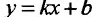
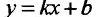
И наоборот, если пределы (14.4.2) и (14.4.3) существуют и конечны, то прямая у = kх + b- наклонная вправо (влево) асимптота графика функции f
Рассмотрим геометрический смысл асимптоты. Пусть 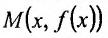
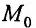
На рис. 14.9 видно, что отрезок 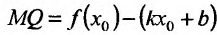
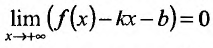
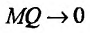
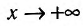
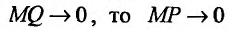
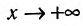
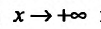
Пример:
График функции 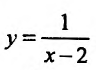
Пример:
Найти асимптоты графика функции
Решение:
Область определения функции D(f): 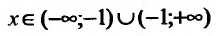
Так как значения пределов останутся такими же и при 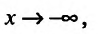
- Заказать решение задач по высшей математике
Общая схема исследования функций и построение их графиков
Под исследованием функций понимается изучение ее изменения в зависимости от изменения аргумента. Исследование функций и построение их графиков можно проводить по следующей схеме:
- Найти область определения и множество значений функции; исследовать на непрерывность, найти точки разрыва и выяснить характер точек разрыва; определить вертикальные асимптоты. Найти точки пересечения с осями координат.
- Исследовать функцию на периодичность; четность, нечетность.
- Исследовать поведение функции на границе области определения; найти асимптоты графика функции.
- Исследовать функцию на монотонность, выяснить характер экстремумов.
- Определить интервалы выпуклости графика функции, точки перегиба.
- Составить таблицу значений функции куда включаются все точки графика функции, найденные на предыдущих этапах исследования и необходимые дополнительные контрольные точки.
- Используя все полученные результаты построить график функции.
Пример:
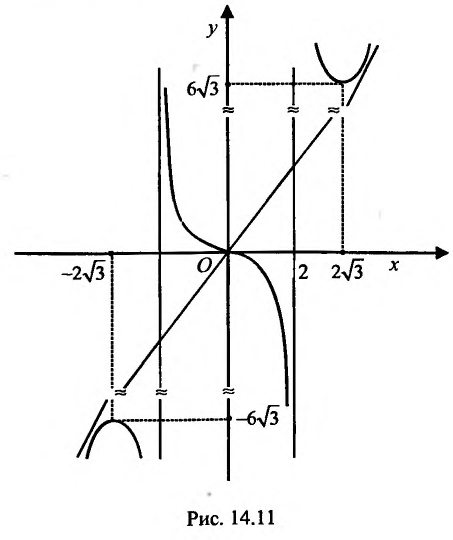
Построить график функции
Решение:
Проведем полное исследование функции по указанной схеме.
1. Функция определена и непрерывна при всех 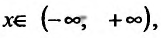
Прямые- х = ±2 являются вертикальными асимптотами, т.к.
График пересекает оси координат в точке O(0; 0).
2. Функция не периодическая. Функция не четная, т.к. выпол-
няется равенство: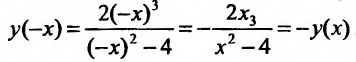
функции симметричный относительно начала координат. Поэтому достаточно провести исследование функции на полуинтервале
3. Найдем наклонную асимптоту. Для этого вычислим пределы:
Подставив значения k и b уравнение 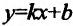
4. Для нахождения промежутков возрастания и убывания найдем первую производную:
приравняем ее к нулю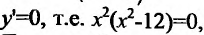
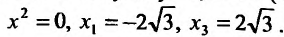

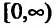
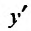
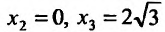
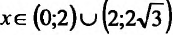
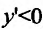
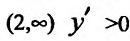
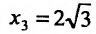
5. Для нахождения промежутков выпуклости и точек перегиба, найдем вторую производную
Вторая производная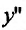
На интервале 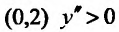
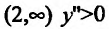
6. Используя результаты исследования и учитывая нечетность функции, строим график (рис. 14.11).
Пример:
Провести полное исследование целевой функции потребления 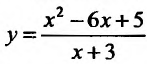
Решение:
Проведём полное и разностороннее изучение свойств функции, применив изложенную выше схему.
1) Функция определена и непрерывна для всех 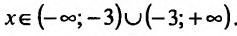
как 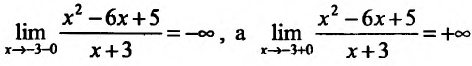
-3 является вертикальной асимптотой. Если х=0, то 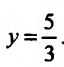
у=О, тс получим уравнение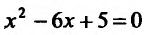
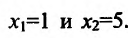
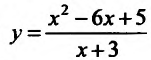
координат в точках:
2) Функция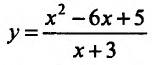
3) Исследуемая функция не является ни чётной, ни нечётной, гак как
4) Исследуем существование наклонных асимптот. Для этого вычислим пределы;
Итак, при 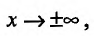
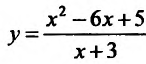
Исследуем повеление функции на границе области определения. Поведение функции в окрестности точки х = -3 исследовано. Поэтому изучим поведение функции при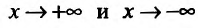
5) Первая производная
обращается в нуль в точках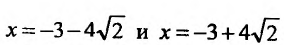
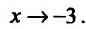
Поскольку 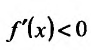
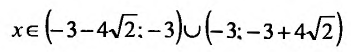
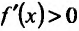
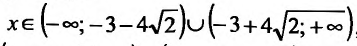
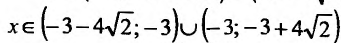
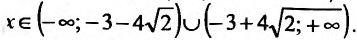
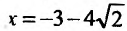
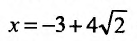
6) Вторая производная не обращается в нуль и стремится к бесконечности при 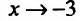
Поскольку 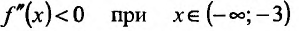
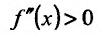
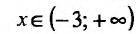
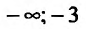
По результатам исследования строим график функции. Вначале строим систему координат; затем вертикальную и горизонтальную асимптоты; наносим точки пересечения с осями координат и точки экстремума функции. Затем строим график (рис. 14.12).
- Предел и непрерывность функции двух переменны
- Дифференцируемость функции нескольких переменных
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
Исследование функции и построение графика
На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.
Что будет дальше?
Исследование функции и построение графика
Общая схема исследования
Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены «горбы» выпуклости, где не определены значения и т.п.
А уже на основании этих «особенностей» и строится макет графика — картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).
Начнем, конечно же, с плана. Исследование функции — объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.
Алгоритм
- Найти область определения. Выделить особые точки (точки разрыва).
- Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
- Найти точки пересечения с осями координат.
- Установить, является ли функция чётной или нечётной.
- Определить, является ли функция периодической или нет (только для тригонометрических функций).
- Найти точки экстремума и интервалы монотонности.
- Найти точки перегиба и интервалы выпуклости-вогнутости.
- Найти наклонные асимптоты. Исследовать поведение на бесконечности.
- Выбрать дополнительные точки и вычислить их координаты.
- Построить график и асимптоты.
В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.
Схема исследования в формате pdf: скачать.
Полный пример решения онлайн
Лучшее спасибо — порекомендовать эту страницу
Провести полное исследование и построить график функции
$$
y(x)=frac{x^2+8}{1-x}.
$$
1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, quad Rightarrow quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-infty; 1) cup (1;+infty).
$$
2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:
Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:
Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.
Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:
Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.
Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x in (-infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x in (1; +infty)$ функция $ylt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).
4) Функция не является ни четной, ни нечетной, так как:
5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.
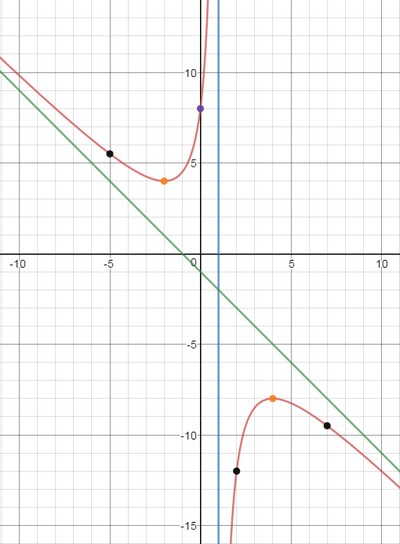
6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:
Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):
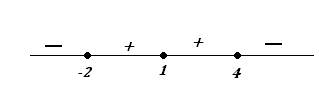
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:
При $x in (-infty; -2), (4;+infty)$ производная $y’ lt 0$, поэтому функция убывает на данных промежутках.
При $x in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.
При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).
Найдем значения функции в этих точках:
Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.
7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:
Приравняем вторую производную к нулю:
Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x in (-infty; 1)$ выполняется $y» gt 0$, то есть функция вогнутая, когда $x in (1;+infty)$ выполняется $y» lt 0$, то есть функция выпуклая.

.
Так как пределы бесконечны, горизонтальных асимптот нет.
Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:
Получили, у что функции есть одна наклонная асимптота $y=-x-1$.
9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
$$
y(-5)=5.5; quad y(2)=-12; quad y(7)=-9.5.
$$
10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):
Примеры решений по исследованию функции
Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!
Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.
$$y=frac{e^x}{x}.$$
Задача 2. Исследовать функцию и построить ее график.
$$y=-frac{1}{4}(x^3-3x^2+4).$$
Задача 3. Исследовать функцию с помощью производной и построить график.
$$y=ln frac{x+1}{x+2}.$$
Задача 4. Провести полное исследование функции и построить график.
$$y=frac{x}{sqrt{x^2+x}}.$$
Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.
$$y=frac{x^3-1}{4x^2}.$$
Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.
$$y=frac{x^3}{x^2-1}.$$
Поможем с исследованием функции: быстро, подробно
Задача 7. Проведите исследование функции с построением графика.
$$y=frac{x^3}{2(x+5)^2}.$$
Задача 8. Построить график функции $y=y(x)$, заданной параметрически
$$x=frac{t^2}{t+1}, y=frac{1}{t}-frac{t^3}{3}.$$
Задача 9. Исследовать функцию и построить ее график $r=1+tg phi$.
Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.
Задача 11. Провести полное исследование периодической функции
$y = cos 3x – 2 sin 6x$ и построить её график.
Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.
$$y=frac{4-x^3}{x^2}.$$
Задача 13. Провести полное исследование и построить график функции.
$$f(x)=frac{x}{2}-arccosfrac{2x}{1+x^2}.$$
Еще примеры исследования функции (контрольные работы)
Как построить график онлайн?
Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).
Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?
Графический калькулятор Desmos
Desmos.com
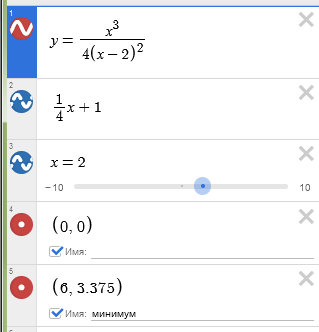
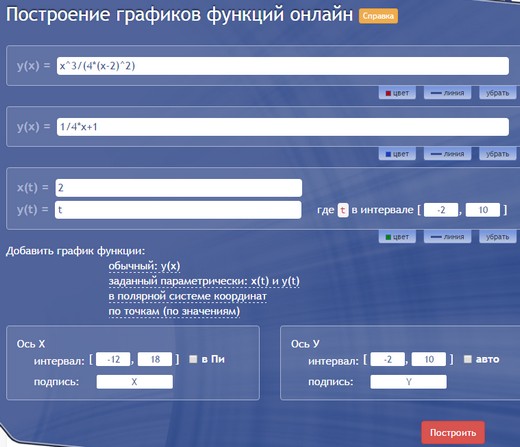
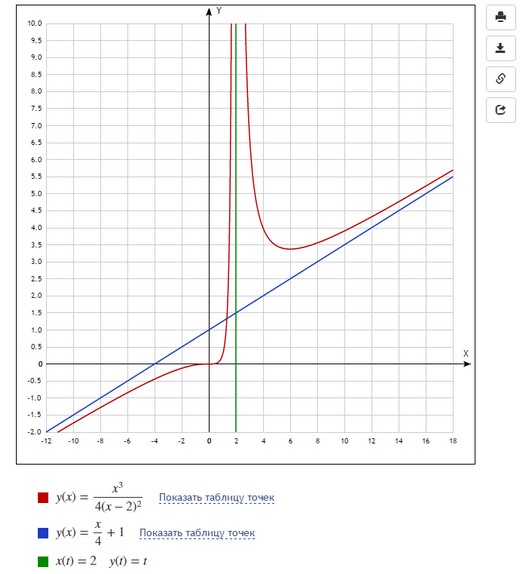
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:
При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.
Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!
Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):
Сайт для построения графиков y(x).ru
y(x).ru
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:
И такой график получается в итоге:
Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).
Другие сайты
Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:
- ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
- mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
- easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
- grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет
Больше знаний: теория и практика
Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень «съедобно» даже для полного чайника в математике: Исследование функций от Александра Емелина.
Вторая ссылка практическая, для тех, кто хочет научиться строить красивые графики в Desmos.com (см. выше описание): Полная инструкция по работе с Desmos. Эта инструкция довольно старая, с тех пор интерфейс сайта поменялся в лучшую сторону, но основы остались неизменными и помогут быстро разобраться с важными функциями сервиса.
Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.
Решебник
Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена — около 50 рублей. Может, и ваша задача уже готова? Проверьте!
Полезные видео-ролики
Вебинар по работе с Desmos.com. Это уже полноценный обзор функций сайта, на целых 36 минут. К сожалению, он на английском языке, но базовых знаний языка и внимательности достаточно, чтобы понять большую часть.
Классный старый научно-популярный фильм «Математика. Функции и графики». Объяснения на пальцах в прямом смысле слова самых основ.
Закажите полное исследование функции в МатБюро
Лучшее спасибо — порекомендовать эту страницу
§ 8.1. Исследование поведения функций одной переменной
В этом параграфе
будут сформулированы условия монотонности
и выпуклости функции, существование у
нее локальных экстремумов и наибольших
(наименьших) значений, изучено поведение
функции на бесконечности и в окрестности
точек разрыва второго рода.
8.1.1. Условия монотонности функции
Теорема 8.1.
Если функция
имеет производную на интервале
,
то справедливы
следующие утверждения.
1. Если
на интервале
то функция
возрастает(убывает)
на этом интервале.
2. Производная
на интервале
тогда и только
тогда, когда функция
не убывает(не
возрастает)
на этом интервале.
Доказательство
1. Рассмотрим
две произвольных точки
и
из интервала
и пусть
.
Так как на отрезкевыполняются условия теоремы Лагранжа,
то найдется такая точка
,
что справедливо равенство
.
(1)
Из условия теоремы
и равенства (1) следует цепочка импликаций:
на интервале
возрастает (убывает)
на интервале
.
2.
Необходимость.
Если
на интервале
,
то из формулы (1) следуют цепочки
импликаций:
на интервале
не убывает (не
возрастает) на интервале
.
Достаточность.
Пусть
теперь
не убывает (не возрастает) на интервале
.
Отсюда, если
—
произвольная точка интервалаи
,
то
.
Так как функция
дифференцируема в точке
,
то
.
■
Критическими
точками функции называют
точки, в которых производная функции
равна нулю или не существует.
Критические точки функции разбивают
область определения функции на интервалы.
В каждом таком интервале производная
сохраняет свой знак (теорема Дарбу), а
функция строго монотонна (теорема 8.1).
Примеры. Найти
интервалы убывания и возрастания функции
:
1.
.
2..
Решение
1. Функция
определена при всех значениях
.
Найдем производную и
критические точки
функции:
,
нули производной,,
являются единственными критическими
точками. Они разбивают числовую ось на
интервалы:
,
,
,
.
Определим знак производнойв каждом интервале:
,
если;
,
если
.
Отсюда следует, что на интервалах
и
функция возрастает, а на интервалах
и
— убывает.
2. Функция
определена при всех значениях
.
Найдем производную и критические точки
функции:,
в точкепроизводная не существует, а в точке
производная равна нулю. Они разбивают
числовую ось на интервалы:,
,
.
Определим знакв каждом интервале:
при
;
,
при.
Отсюда следует, что на интервалахи
функция возрастает, а на интервале
— убывает. ●
8.1.2. Локальные экстремумы функции
Пусть функция
определена в окрестности
точки
,
т.е. определена на интервале,
).
Если в точкефункция принимает наибольшее (наименьшее)
значение в окрестности,
то точкуназываютточкой
локального максимума (минимума).
Эти точки называют также точками
локального экстремума функции. Теперь
из теоремы Ферма вытекает необходимый
признак локального экстремума.
Теорема 8.2.
Функция
определена в окрестности
точки
,
и в этой точке существует производная.
Если
— точка локального экстремума функции,
т.е. точка локального максимума
или
минимума,
то
.
■
В точке локального
экстремума функция может быть не
дифференцируема. Примером такой функции
может служить функция
,
которая в точкеимеет локальный минимум, но не
дифференцируема в этой точке. Точки
локального экстремума функции являются
критическими, но обратное утверждение
в общем случае неверно. Ниже будет
доказана теорема, позволяющая установить,
когда критическая точка функции является
точкой локального экстремума.
Лемма. Функция
непрерывна на интервале
и на этом интервале имеет производную,
кроме точки.
Тогда справедливы утверждения.
1. Если
на
,
топри любом
.
2.
Если
на
,
топри любом
.
Доказательство
1.
Возьмем произвольную точку
и
.
Используя лемму Ферма, получим цепочку
импликаций:
,
.
2. Возьмем
произвольное число
и
.
Используя лемму Ферма, получим цепочку
импликаций:
,
.
■
Теорема 8.3
(достаточное
условие локального экстремума).
Функция
непрерывна на интервале
и на этом интервале имеет производную,
кроме точки.
Тогда справедливы утверждения.
1. Если
на интервале
и
на интервале
,
то точка—
точка локального минимума функции.
2. Если
на интервале
и
на интервале
,
то точка—
точка локального максимума функции.
3. Если
или
на
интервале,
то точкане является точкой локального экстремума
функции.
Доказательство
1. Из
1-го и 2-го утверждения леммы следуют
импликации:
на интервале
при любом
,
на интервале
при любом
.
Отсюда следует,
что
для всех
,
т.е. функция
имеет в точке
локальный минимум.
2.
Из 1-го и 2-го утверждения леммы следуют
импликации:
на интервале
при любом
,
на интервале
при любом
.
Отсюда следует,
что
для всех
,
т.е. функция
имеет в точке
локальный максимум.
3. Предположим,
что
на
.
Из 1-го и 2-го утверждения леммы следуют
импликации:
на интервале
при любом
,
на интервале
при любом
.
Следовательно,
не является ни наибольшим, ни наименьшим
значением функциив окрестности
,
т.е.не является точкой локального экстремума.
■
Из теоремы 8.3
следует, что
будет точкойлокального
минимума
функции
,
если знак производнойпри переходе через точку
меняется со знака – на знак +. Если же
знакв
точкеменяется со знака + на знак –, то
будет точкойлокального
максимума
функции
.
Примеры. Найти
точки локального экстремума функции
:
3.
;
4.;
5..
Решение
3. Производная
функции
равна
.
Точкаявляется единственной критической
точкой функции.
В окрестности этой точки функциянепрерывна и имеет производную. При
переходе через точкупроизводная меняет знак с – на знак +.
Из теоремы 8.3 следует, что—
точка локального минимума.
4. Производная
функции
равна
.
Точкаявляется единственной критической
точкой функции.
В окрестности этой точки функциянепрерывна и имеет всюду производную,
кроме точки.
При переходе через точкупроизводная меняет знак с – на знак +.
Из теоремы 8.3 следует, что—
точка локального минимума.
5. Производная
функции
равна
.
Точкаявляется единственной критической
точкой функции.
В окрестности этой точки функциянепрерывна и имеет всюду производную,
кроме точки.
При переходе через точкузнак производной не меняется. Из теоремы
8.3 следует, чтоне является точкой локального экстремума
функции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1. Общие понятия о поведении функций
2. Свойства монотонных функций
3. Алгоритм определения поведения функции
4. Примеры решения задач на исследование поведения функции
Общие понятия о поведении функций
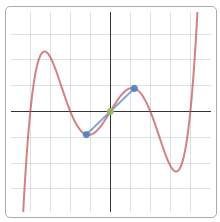
Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.
Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.
Соответственно, монотонная функция может быть возрастающая или убывающая.
Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.
Математическое выражение этого определения выглядит следующим образом:
(f(x)=↑x_1 f(x_2)).
Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.
Математическое выражение этого определения выглядит следующим образом:
(f(x)=↓x_1 f(x_2)).
Разберем примеры решения задач на изучение характера поведения функции.
Задача 1. Задана функция (y=x^3+1). Исследовать ее характер в интервале ([0;2]).
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
(y_1=0^3+1=1);
(y_2=2^3+1=9).
Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.
Задача 2. Задана функция (y={1over x}). Определить ее характер в интервале ([1;2]).
Решение: Подставим поочередно крайние значения заданного отрезка и сравним полученные значения функции.
(y_1={1over 1}=1);
(y_2={1over2}=0.5).
Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.
Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.
Не нашли то, что искали?
Попробуйте обратиться за помощью к преподавателям
Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.
Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.
Разберем задачу на исследование характера поведения функции. При данной функции (y=5) исследовать ее характер в интервале ([0;2]).
По сути эту функцию можно записать как (y=5+0∙x), подставляя крайние значения отрезка, получим:
(y_1=5+0∙0=5);
(y_2=5+0∙2=5).
То есть функция (y=5) будет постоянной.
Постоянная, не убывающая и не возрастающая функции не есть монотонные.
Свойства монотонных функций
К свойствам монотонных функций относятся такие характеристики:
- если две или больше возрастающих функций суммируются, то в результате получается тоже возрастающая функция;
- результатом произведения положительных возрастающих функций будет возрастающая функция;
- при композиции двух возрастающих функций получается также функция, которая будет возрастать;
- при положительной функции (f(x)), функция (f^n (x)) тоже будет возрастать, при условии, что (n) является натуральным числом;
- при сохранении возрастающей функцией (f(x)) своего знака, обратная ей функция будет убывать;
- при возрастающей функции (f(x)) и константе c справедливо, что функции (cf(x)) и (f(x)+c), при (c>0), будут возрастать.
Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах:
Теорема 1
При положительной производной заданной функции f^’ (x) в определенном интервале, эта функция будет возрастать в данном интервале. Существуют также обратные теоремы. Рассмотрим их определения:
Теорема 2
При отрицательной производной заданной функции f^’ (x) в определенном интервале, эта функция будет убывать в данном интервале.
Теорема 3
При заданной возрастающей функции на определенном промежутке, ее производная функция будет неотрицательна или не будет существовать в данном интервале.
Теорема 4
При заданной убывающей функции на определенном промежутке, ее производная функция будет неположительная или не будет существовать в данном интервале.
Для постоянной функции справедлива такая теорема:
Теорема 5
Если производная заданной функции f^’ (x) будет равняться нулю для всех точек заданного интервала, то заданная функция будет постоянной в этом интервале.
Алгоритм определения поведения функции
Алгоритм изучения функции на предмет возрастания или убывания выглядит следующим образом:
- для заданной функции находят производную;
- определяют стационарные или критические точки производной функции (f^’ (x)=0 или вовсе не существует);
- рассчитывают знак производной функции в каждом из интервалов;
- определяют поведение функции в каждом из интервалов.
Примеры решения задач на исследование поведения функции
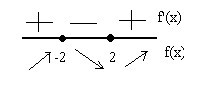
Пример 1. Дана функция следующего вида: (y=x^3-12x). Определить ее характер поведения в интервале ((-∞;+∞)).
Решение:
1. Рассчитываем производную заданной функции:
(y’=(x^3-12x)’=3x^2-12.)
2.Производная определяется на всем промежутке:
(y’=0 ⇒ 3x^2-12=0 ⇒3x^2=12 ⇒x^2=4 ⇒ x=±2,)
(x=±2) являются стационарными точками.
3. Изучаем знак производной функции при помощи числовой прямой:
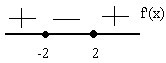
(y’ (0)=3∙0^2-12=-12);
(y’ (-3)=3∙(-3)^2-12=15);
(y’ (3)=3∙3^2-12=15).
То есть производная положительна в интервалах ( (-∞;-2]) и ([2;+∞)), и отрицательна в интервале( [-2;2]).
4. Определяем характер поведения функции:
Согласно выше рассмотренных теорем, заданная функция будет убывать в интервале ([-2;2]), и возрастать в интервалах (- (-∞;-2]) и ([2;+∞)).
Сложно разобраться самому?
Попробуйте обратиться за помощью к преподавателям
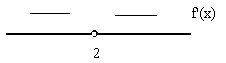
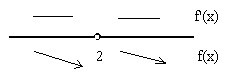
Пример 2. Дана функция следующего вида: (y={xover(x-2)}). Определить ее характер поведения в интервале(-∞;+∞).
Решение:
1. Находим производную функции:
(y’=({xover x-2})’={1∙(x-2)-x∙1over(x-2)^2} ={x-2-xover x-2^2} =-{2over(x-2)^2}) .
2. При (x=2) производная функция будет неопределенной. Стационарные точки не обнаружены.
3.Изучаем знак производной при помощи числовой прямой:
(y’ (0)=)(-{2over(0-2)^2} =)(-{2over(-2)^2} =)(-{2over(0-2)^2}) =(-{2over4}=-0,5);
(y’ (4)=-{2over(4-2)^2} =)(-{2over(2)^2} =-{2over4}=-0,5).
То есть производная функция отрицательна на определяемых участках.
4.Определяем характер поведения функции.
Согласно теореме 2, при отрицательной производной, заданная функция убывает. То есть на всем определяемом промежутке заданная функция будет убывающей.

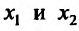
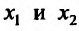 из интервала (а, b), удовлетворяющих условию
из интервала (а, b), удовлетворяющих условию 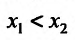 справедливо неравенство
справедливо неравенство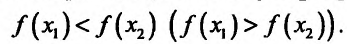 Неубывающие и невозрастающие функции называют монотонными функциями.
Неубывающие и невозрастающие функции называют монотонными функциями.
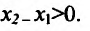
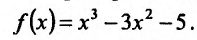
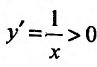
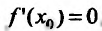
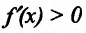 на
на 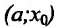 и
и 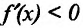 на
на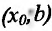 , то точка
, то точка 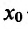 — точка максимума функции f(x);
— точка максимума функции f(x);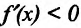 на
на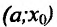 и
и 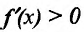 на
на 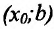 , то точка
, то точка 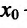 — точка минимума функции f(x);
— точка минимума функции f(x);