Как найти потери напора при трении

При течении реальной жидкости возникают силы сопротивления, обусловленные вязкими напряжениями. Эти силы производят работу, которая целиком превращается в тепловую энергию. Следовательно, при течении жидкости происходит процесс необратимого превращения части механической энергии во внутреннюю энергию. Работа сил вязкости, произведенная между двумя сечениями потока и отнесенная к единице веса движущейся жидкости, называется потерями напора hf . Потери напора

между двумя сечениями потока могут быть определены из уравнения Бернулли, cоставленного для этих сечений:

сечениях; α1 и α2 – коэффициенты неравномерности распределения скоростей в сечениях; ρ и g – плотность жидкости и ускорение силы тяжести.

Потери напора при движении жидкости складываются из потерь напора на трение hтр и потерь напора на местные сопротивленияhм:

5.1. Потери напора на трение

Потери напора на трение, или потери по длине, возникают в чистом виде в прямых трубах постоянного сечения, т. е. при равномерном течении жидкости. Для горизонтальной трубы постоянного сечения ( z1 = z2 , х1 = х2 ,

α1 = α2 ) потери напора в соответствии с выражением (1) могут быть определены по зависимости

Таким образом, при равномерном движении жидкости потери напора по длине трубы определяются разностью пьезометрических высот в сечениях.

Общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, справедливое как для ламинарного, так и для турбулентного режимов, имеет вид

где λ – коэффициент гидравлического трения.

Эта зависимость называется формулой Дарси-Вейсбаха.

33

34

только от Re, или только от /d.

На поле графика можно выделить три зоны. Первая зона – зона ламинарного режима: представлена отрезком прямой I. Здесь экспериментальные кривые λ = f (Re) , найденные для разных /d, сливаются в одну

прямую линию, совпадающую с линией I. Для этой зоны имеем следующее:

−величины Re малы, Re < 2300;

−потери на трение hтр не зависят от шероховатости трубы, а обуслов-

лены лишь трением внутри жидкости; − потери напора прямо пропорциональны скорости в первой степени:

где ν – кинематический коэффициент вязкости;

l– длина трубопровода.

−величина λ определяется формулой

Вторая зона – переходная, расположенная между вертикалями III и IY (зона, внутри которой происходит переход от турбулентного режима к ламинарному и наоборот). В связи со сложным характером движения жидкости в этой области, представить это движение на графике какими-либо определенными кривыми нет возможности. Исключение могут составить только случаи, когда ламинарный режим «затягивается» и имеет место по всей длине трубопровода (рис. 5.1, отрезок 2–3) или когда (в связи с особыми условиями движения) турбулентный режим имеет место по длине всего трубопровода (рис. 5.1, отрезок 4–5).

Вэтом случае имеют место следующие параметры:

−числа Рейнольдса лежат в пределах 2300 < Re < 20000;

35

36

37

В этой статье мы решим задачку на потерю напора в трубопроводе. Данная статья поможет вам понять, как идет сопротивление движению потока. На реальных цифрах, опишу алгоритм как это делать. Используем основные формулы.

Разберем простой пример с трубой, как видно на изображении в начале трубы насос потом идет манометр, который позволяет измерить давление жидкости в начале трубы. Через определенную длину установлен второй манометр, который позволяет измерить давление в конце трубы. Ну и в самом конце стоит кран. Эта схема достаточно проста, и я попытаюсь привести примеры. И так начнем.

Вообще существует не один способ как узнать потерю напора: Способ, когда известно давление вначале и в конце трубы, можно вычислить потерю напора по формуле: М1-М2=Давление, то есть эта разница между двумя манометрами. Допустим у нас получилось, грубо говоря 0,1 МПа, что составляет одну атмосферу. Это значит у нас потеря напора по длине составляет 0,1 МПа. Обратите внимание, мы можем указывать потерю напора по двум величинам, это по гидростатическому давлению, что составляет 0,1 МПа и по высоте напора водного столба в метрах, что составляет 10 метров. Как я не однократно говорил каждые 10 метров это одна атмосфера давления.

Существует ряд методов, как рассчитать потерю напора не имея манометров на трубах. Ученые исследователи приготовили для нашего пользования замечательные формулы и цифры, которые нам пригодятся.

Существует хорошая формула которая позволяет вычислить потерю напора по длине трубопровода.

h-потеря напора здесь она измеряется в метрах.
λ-коеффициент гидравлического трения, находится дополнительными формулами о которых опишу ниже.
L-длина трубопровода измеряется в метрах.
D-внутренний диаметр трубы, то есть диаметр потока жидкости. Должен быть вставлен в формулу в метрах.
V-скорость потока жидкости. Измеряется [Метр/секунда].
g-ускорение свободного падения равен 9,81 м/с2

А теперь поговорим о коэффициенте гидравлического трения.

Формулы нахождения этого коэффициента зависит от числа Рейнольдса и эквивалента шероховатости труб.

Напомню эту формулу (она применима только к круглым трубам):

V-Скорость потока жидкости. Измеряется [Метр/секунда].
D-Внутренний диаметр трубы, то есть диаметр потока жидкости. Должен быть вставлен в формулу в метрах.
ν-Кинематическая вязкость. Это обычно для нас готовая цифра, находится в специальных таблицах.

Далее находим формулу для нахождения коэффициента гидравлического трения по таблице:

Здесь Δ_э — Эквивалент шероховатости труб. Эта величина в таблицах указывается в милиметрах, но вы когда будете вставлять в формулу обязательно переводите в метры. Вообще не забывайте соблюдать пропорциональность единиц измерения и не смешивайте в формулах разных типа [мм] с [м].

d-внутренний диаметр трубы, то есть диаметр потока жидкости.

Также хочу подметить, что подобные величины по шероховатости бывают абсолютными и относительными или даже есть относительные коэффициенты. Поэтому когда если будете искать таблицы с величинами, то величина эта должа называться «эквивалентом шероховатости труб» и не как иначе, а то результат будет ошибочный. Эквивалент означает — средняя высота шероховатости.

В некоторых ячейках таблицы указаны две формулы, вы можете считать на любой выбранной, они почти дают одинаковый результат.

Вообще в целом, эти формулы показывают и доказывают, что при увеличении скорости или увеличении расхода, всегда увеличивается сопротивление движению потока жидкости, то есть увеличиваются потери напора. Причем увеличиваются не пропорционально, а квадратично. Это говорит о том, что единица увеличения расхода не соответствует затратам на потерю напора. То есть иметь большую скорость потока жидкости в трубе экономически не целесообразно. Поэтому бывает дешевле увеличить диаметр потока. В других статьях обязательно опишу, как посчитать, какой диаметр нам необходим.

Таблица: (Эквивалент шероховатости)

Кому интересно узнать (Эквивалент шероховатости ) для металлопластика, полипропилена и сшитого полиэтилена, то это соответствует и относится к пластмассам. То есть в таблице характеристика будет: Пластмассовые (полиэтилен, винипласт).

Так же хочу обратить внимание, на то, что со временем, на внутренних станках труб, образуется налет, что увеличивает шероховатость труб. Так что имейте ввиду что со временем потери напора только увеличиваются.

Таблица: (Кинематическая вязкость воды)

График:

Как видно из графика, что при повышении температуры кинематическая вязкость уменьшается, а это значит, что и сопротивление движению воды уменьшается. Это значит, что при потоке горячей воды, «потери напора» будут меньше чем при потоке холодной воды. Кто живет в многоквартирных домах, если обратит внимание, то скорость и напор горячей воды всегда выше чем напор холодной воды. Есть исключения, но в большинстве случаев это так. Теперь вы понимаете, почему это так.

А теперь давайте решим задачу:

Найти потерю напора по длине при движении воды по чугунной новой трубе D=500мм при расходе Q=2 м³/с, длина трубы L=900м, температура t=16°С.

Дано:
D=500мм=0.5м
Q=2 м3/с
L=900м
t=16°С
Жидкость: H2O
Найти: h-?

Видео:

Купить программу

Решение: Для начала найдем скорость потока в трубе по формуле:

V=Q/ω

Сдесь ω — площадь сечения потока. Находится по формуле:

ω=πR²=π(D²/4)=3.14*(0,5²/4)=0,19625 м²

V=Q/ω=2/0,19625=10,19 м/с

Далее находим число Рейнольдса по формуле:

Re=(V*D)/ν=(10,19*0.5)/0,00000116=4 392 241

ν=1,16*10^-6=0,00000116. Взято из таблицы. Для воды при температуре 16°С.

Δ_э=0,25мм=0,00025м. Взято из таблицы, для новой чугунной трубы.

Далее сверяемся по таблице где находим формулу по нахождению коэффициента гидравлического трения.

λ=0,11(Δ_э/D)^0,25=0,11*(0,00025/0,5)^0,25=0,01645

Далее завершаем формулой:

h=λ*(L*V²)/(D*2*g)=0,01645*(900*10,19²)/(0,5*2*9,81)=156,7 м.

Ответ: 156,7 м. = 1,567 МПа.

Также хочу обратить внимание на то, что мы в задаче рассматривали трубу которая на всей своей длине имеет горизонтальное положение.

Давайте рассмотрим пример, когда труба идет вверх под определенным углом.

В этом случае нам к обычной задаче нужно прибавить высоту(в метрах) к потери напора. Если труба будет идти на спуск в низ, то тут необходимо вичитать высоту.

Мы рассмотрели потерю напора по длине трубопровода, также существуют местные сопротивления в виде заужения и поворотов, которые тоже влияют на потерю напора. О них будет описано в других моих статьях. И я обязательно приготовлю статью о том как подобрать насос по напору, чтобы удовлетворить требования расхода жидкости, в зависимости от потерь напора. Если что-то не понятно пишите в комментарии, обязательно отвечу!

Чтобы в ручную не считать всю математику я приготовил специальную программу:

Скачать калькулятор расчетов гидравлического сопротивления.

Следующая статья: Местные гидравлические сопротивления

Все о дачном доме
        Водоснабжение
                Обучающий курс. Автоматическое водоснабжение своими руками. Для чайников.
                Неисправности скважинной автоматической системы водоснабжения.
                Водозаборные скважины
                        Ремонт скважины? Узнайте нужен ли он!
                        Где бурить скважину — снаружи или внутри?
                        В каких случаях очистка скважины не имеет смысла
                        Почему в скважинах застревают насосы и как это предотвратить
                Прокладка трубопровода от скважины до дома
                100% Защита насоса от сухого хода
        Отопление
                Обучающий курс. Водяной теплый пол своими руками. Для чайников.
                Теплый водяной пол под ламинат
        Обучающий Видеокурс: По ГИДРАВЛИЧЕСКИМ И ТЕПЛОВЫМ РАСЧЕТАМ
Водяное отопление
        Виды отопления
        Отопительные системы
        Отопительное оборудование, отопительные батареи
        Система теплых полов
                Личная статья теплых полов
                Принцип работы и схема работы теплого водяного пола
                Проектирование и монтаж теплого пола
                Водяной теплый пол своими руками
                Основные материалы для теплого водяного пола
                Технология монтажа водяного теплого пола
                Система теплых полов
                Шаг укладки и способы укладки теплого пола
                Типы водных теплых полов
        Все о теплоносителях
                Антифриз или вода?
                Виды теплоносителей (антифризов для отопления)
                Антифриз для отопления
                Как правильно разбавлять антифриз для системы отопления?
                Обнаружение и последствия протечек теплоносителей
        Как правильно выбрать отопительный котел
        Тепловой насос
                Особенности теплового насоса
                Тепловой насос принцип работы
        Запас мощности котла. Нужен ли он?
Про радиаторы отопления
        Способы подключения радиаторов. Свойства и параметры.
        Как рассчитать колличество секций радиатора?
        Рассчет тепловой мощности и количество радиаторов
        Виды радиаторов и их особенности
Автономное водоснабжение
        Схема автономного водоснабжения
        Устройство скважины Очистка скважины своими руками
Опыт сантехника
        Подключение стиральной машины
Полезные материалы
        Редуктор давления воды
        Гидроаккумулятор. Принцип работы, назначение и настройка.
        Автоматический клапан для выпуска воздуха
        Балансировочный клапан
        Перепускной клапан
        Трехходовой клапан
                Трехходовой клапан с сервоприводом ESBE
        Терморегулятор на радиатор
        Сервопривод коллекторный. Выбор и правила подключения.
        Виды водяных фильтров. Как подобрать водяной фильтр для воды.
                Обратный осмос
        Фильтр грязевик
        Обратный клапан
        Предохранительный клапан
        Смесительный узел. Принцип работы. Назначение и расчеты.
                Расчет смесительного узла CombiMix
        Гидрострелка. Принцип работы, назначение и расчеты.
        Бойлер косвенного нагрева накопительный. Принцип работы.
        Расчет пластинчатого теплообменника
                Рекомендации по подбору ПТО при проектировании объектов теплоснабжения
                О загрязнение теплообменников
        Водонагреватель косвенного нагрева воды
        Магнитный фильтр — защита от накипи
        Инфракрасные обогреватели
        Радиаторы. Свойства и виды отопительных приборов.
        Виды труб и их свойства
        Незаменимые инструменты сантехника
Интересные рассказы
        Страшная сказка о черном монтажнике
        Технологии очистки воды
        Как выбрать фильтр для очистки воды
        Поразмышляем о канализации
        Очистные сооружения сельского дома
Советы сантехнику
        Как оценить качество Вашей отопительной и водопроводной системы?
Профрекомендации
        Как подобрать насос для скважины
        Как правильно оборудовать скважину
        Водопровод на огород
        Как выбрать водонагреватель
        Пример установки оборудования для скважины
        Рекомендации по комплектации и монтажу погружных насосов
        Какой тип гидроаккумулятора водоснабжения выбрать?
        Круговорот воды в квартире
        фановая труба
        Удаление воздуха из системы отопления
Гидравлика и теплотехника
        Введение
        Что такое гидравлический расчет?
        Невязка гидравлического расчета
        Физические свойства жидкостей
        Гидростатическое давление
        Поговорим о сопротивлениях прохождении жидкости в трубах
        Режимы движения жидкости (ламинарный и турбулентный)
        Гидравлический расчет на потерю напора или как рассчитать потери давления в трубе
        Местные гидравлические сопротивления
        Профессиональный расчет диаметра трубы по формулам для водоснабжения
        Как подобрать насос по техническим параметрам
        Профессиональный расчет систем водяного отопления. Расчет теплопотерь водяного контура.
        Гидравлические потери в гофрированной трубе
        Теплотехника. Речь автора. Вступление
        Процессы теплообмена
        Тплопроводность материалов и потеря тепла через стену
        Как мы теряем тепло обычным воздухом?
        Законы теплового излучения. Лучистое тепло.
        Законы теплового излучения. Страница 2.
        Потеря тепла через окно
        Факторы теплопотерь дома
        Начни свое дело в сфере систем водоснабжения и отопления
        Вопрос по расчету гидравлики
Конструктор водяного отопления
        Диаметр трубопроводов, скорость течения и расход теплоносителя.
        Вычисляем диаметр трубы для отопления
        Расчет потерь тепла через радиатор
        Мощность радиатора отопления
        Расчет мощности радиаторов. Стандарты EN 442 и DIN 4704
        Расчет теплопотерь через ограждающие конструкции
                Найти теплопотери через чердак и узнать температуру на чердаке
        Подбираем циркуляционный насос для отопления
        Перенос тепловой энергии по трубам
        Расчет гидравлического сопротивления в системе отопления
        Распределение расхода и тепла по трубам. Абсолютные схемы.
        Расчет сложной попутной системы отопления
                Расчет отопления. Популярный миф
                Расчет отопления одной ветки по длине и КМС
                Расчет отопления. Подбор насоса и диаметров
                Расчет отопления. Двухтрубная тупиковая
                Расчет отопления. Однотрубная последовательная
                Расчет отопления. Двухтрубная попутная
        Расчет естественной циркуляции. Гравитационный напор
        Расчет гидравлического удара
        Сколько выделяется тепла трубами?
        Собираем котельную от А до Я…
        Система отопления расчет
        Онлайн калькулятор Программа расчет Теплопотерь помещения
        Гидравлический расчет трубопроводов
                История и возможности программы — введение
                Как в программе сделать расчет одной ветки
                Расчет угла КМС отвода
                Расчет КМС систем отопления и водоснабжения
                Разветвление трубопровода – расчет
                Как в программе рассчитать однотрубную систему отопления
                Как в программе рассчитать двухтрубную систему отопления
                Как в программе рассчитать расход радиатора в системе отопления
                Перерасчет мощности радиаторов
                Как в программе рассчитать двухтрубную попутную систему отопления. Петля Тихельмана
                Расчет гидравлического разделителя (гидрострелка) в программе
                Расчет комбинированной цепи систем отопления и водоснабжения
                Расчет теплопотерь через ограждающие конструкции
                Гидравлические потери в гофрированной трубе
        Гидравлический расчет в трехмерном пространстве
                Интерфейс и управление в программе
                Три закона/фактора по подбору диаметров и насосов
                Расчет водоснабжения с самовсасывающим насосом
                Расчет диаметров от центрального водоснабжения
                Расчет водоснабжения частного дома
                Расчет гидрострелки и коллектора
                Расчет Гидрострелки со множеством соединений
                Расчет двух котлов в системе отопления
                Расчет однотрубной системы отопления
                Расчет двухтрубной системы отопления
                Расчет петли Тихельмана
                Расчет двухтрубной лучевой разводки
                Расчет двухтрубной вертикальной системы отопления
                Расчет однотрубной вертикальной системы отопления
                Расчет теплого водяного пола и смесительных узлов
                Рециркуляция горячего водоснабжения
                Балансировочная настройка радиаторов
                Расчет отопления с естественной циркуляцией
                Лучевая разводка системы отопления
                Петля Тихельмана – двухтрубная попутная
                Гидравлический расчет двух котлов с гидрострелкой
                Система отопления (не Стандарт) — Другая схема обвязки
                Гидравлический расчет многопатрубковых гидрострелок
                Радиаторная смешенная система отопления — попутная с тупиков
                Терморегуляция систем отопления
        Разветвление трубопровода – расчет
        Гидравлический расчет по разветвлению трубопровода
        Расчет насоса для водоснабжения
        Расчет контуров теплого водяного пола
        Гидравлический расчет отопления. Однотрубная система
        Гидравлический расчет отопления. Двухтрубная тупиковая
        Бюджетный вариант однотрубной системы отопления частного дома
        Расчет дроссельной шайбы
        Что такое КМС?
        Расчет гравитационной системы отопления
Конструктор технических проблем
        Удлинение трубы
Требования СНиП ГОСТы
        Требования к котельному помещению
Вопрос слесарю-сантехнику
Полезные ссылки сантехнику
—
Сантехник — ОТВЕЧАЕТ!!!
Жилищно коммунальные проблемы
Монтажные работы: Проекты, схемы, чертежи, фото, описание.
Если надоело читать, можно посмотреть полезный видео сборник по системам водоснабжения и отопления

Гидравлические сопротивления и их расчет



Виды гидравлических сопротивлений

При движении жидкости в трубе между нею и стенками трубы возникают дополнительные силы сопротивлении, в результате чего частицы жидкости, прилегающие к поверхности трубы, тормозятся. Это торможение благодаря вязкости жидкости передается следующим слоям, отстоящим далее от поверхности трубы, причем скорость движения частиц по мере удаления их от оси трубы постепенно уменьшается.

Равнодействующая сил сопротивления Т направлена в сторону, противоположную движению жидкости, и параллельна направлению движения. Это и есть силы гидравлического трения (сопротивления гидравлического трения).

Для преодоления сопротивления трения и поддержания равномерного поступательного движения жидкости необходимо, чтобы на жидкость действовала сила, направленная в сторону ее движения и равная силе сопротивления, т. е. необходимо затрачивать энергию. Энергию или напор, необходимый для преодоления сил сопротивления, называют потерянной энергией или потерянным напором.
Потери напора, затрачиваемые на преодоление сопротивления трения, носят название потерь напора на трение или потерь напора по длине потока (линейные потери напора) и обозначаются обычно h_тр.

Однако трение является не единственной возможной причиной, вызывающей потери напора. Резкое изменение сечения также оказывает сопротивление движению жидкости (так называемое сопротивление формы) и вызывает потери энергии. Существуют и другие причины, вызывающие потери напора, например внезапное изменение направления движения жидкости.
Потери напора, вызываемые резким изменением конфигурации границ потока (затрачиваемые на преодоление сопротивления формы), называют местными потерями напора или потерями напора на местные сопротивления и обозначаются через h_м.

Таким образом, потери напора при движении жидкости складываются из потерь напора на трение и потерь на местные сопротивления, т. е.:

h_S = h_тр + h_м.

***

Потери напора при равномерном движении жидкости в трубах

Найдем общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, справедливое как для ламинарного, так и для турбулентного режимов.

При равномерном движении величина средней скорости и распределение скоростей по сечению остаются неизменными по всей длине трубопровода. Поэтому равномерное движение возможно лишь в трубах постоянного сечения S, так как в противном случае будет изменяться средняя скорость в соответствии с уравнением:

v = Q/S = const.

Равномерное движение имеет место в прямых трубах или в трубах с очень большим радиусом кривизны R (прямолинейное движение), так как в противном случае средняя скорость может изменяться по направлению.
Кроме того, условие неизменности характера скоростей жидкости по живому сечению можно записать в виде α = const, где α – коэффициент Кориолиса. Последнее условие может быть соблюдено лишь при достаточном удалении рассматриваемого участка потока от входа в трубу.

Если выделить на участке трубы с равномерно текущей жидкостью два произвольных сечения 1 и 2, то потери напора при перемещении жидкости между этими сечениями можно описать при помощи уравнения Бернулли:

z₁ + p₁/γ = z₂ + p₂/γ +h_тр,

где:
z₁ и z₂ – перепад высот между центрами соответствующих сечений;
p₁ и p₂ – давление жидкости в соответствующих сечениях;
γ – удельная плотность жидкости, γ = gρ;
h_тр – величина потерянной энергии (потери на трение).

Из этой формулы выразим величину потерянной энергии h_тр:

h_тр = (z₁ + p₁/γ) — (z₂ + p₂/γ).

Это выражение называют уравнением равномерного движения жидкости в трубопроводе. Если труба расположена горизонтально, т. е. перепад высот между ее сечениями отсутствует, то уравнение примет упрощенный вид:

h_тр = p₁/γ — p₂/γ = (p₁ – p₂)/γ.

***



Формула Дарси-Вейсбаха для равномерного движения жидкости в трубах

При равномерном движении жидкости в трубах потери напора на трение по длине h_л определяют по формуле Дарси-Вейсбаха, которая справедлива для круглых труб, как при турбулентном, так и при ламинарном режиме.

Эта формула устанавливает зависимость между потерями напора h_л, диаметром трубы d и средней скоростью потока жидкости v:

h_л = λv²/2gd,

где:
λ – коэффициент гидравлического трения (величина безразмерная);
g – ускорение свободного падения.

Для труб произвольного сечения в формуле Дарси-Вейсбаха используют понятие приведенного или эквивалентного диаметра сечения трубы по отношению к круглому сечению.

В некоторых случаях используют также формулу

h_л = v²l/C²R,

где:
v – средняя скорость потока в трубе или канале;
l – длина участка трубы или канала;
R – гидравлический радиус потока жидкости;
С – коэффициент Шези, связанный с коэффициентом гидравлического трения λ зависимостью: С = √(8g/λ) или λ = 8g/С². Размерность коэффициента Шези – м^1/2/с.

Для определения коэффициента гидравлического трения при различных режимах и условиях движения жидкости применяют различные способы и эмпирические зависимости, в частности, график И. И. Никурадзе, формулы П. Блазиуса, Ф. А. Шевелева (для гладких труб) и Б. Л. Шифринсона (для шероховатых труб). Все эти способы и зависимости опираются на критерий Рейнольдса Re и учитывают состояние поверхности труб.

***

Потери напора из-за местных сопротивлений

Как уже указывалось выше, местные потери напора обусловлены преодолением местных сопротивлений, создаваемых фасонными частями, арматурой и прочим оборудованием трубопроводных сетей, а также изменением направления потока жидкости (изгибы труб, колена и т. п.).
Местные сопротивления вызывают изменение величины или направления скорости движения жидкости на отдельных участках трубопровода, что связано с появлением дополнительных потерь напора.
Движение в трубопроводе при наличии местных сопротивлений является неравномерным.

Потери напора в местных сопротивлениях h_м (местные потери напора) вычисляют по формуле Вейсбаха:

h_м = ξv²/2g,

где:
v – средняя скорость в сечении, расположенном ниже по течению за местным сопротивлением;
ξ – безразмерный коэффициент местного сопротивления, определяемый для каждого вида местного сопротивления по справочным таблицам или установленным зависимостям.

Потери напора при внезапном расширении трубопровода находят по формуле Борда:

h_вн.р. = (v₁ – v₂)²2g = ξ_вн.р.1v₁²/2g = ξ_вн.р.2v₂²/2g,

где v₁ и v₂ – средние скорости течения до и после расширения.

При внезапном сужении трубопровода коэффициент местного сопротивления определяется по формуле:

h_вн.с. = (1/ε — 1)²,

где ε — коэффициент сжатия струи, определяемый, как отношение площади сечения сжатой струи в узком трубопроводе к площади сечения узкой трубы. Этот коэффициент зависит от степени сжатия потока n = S₂/S₁ и может быть найден по формуле А. Д. Альтшуля:    ε = 0,57 + 0,043/(1,1 — n).
Значение коэффициента ε при расчетах трубопроводов берут из справочных таблиц.

При резком повороте трубы круглого поперечного сечения на угол α коэффициент сопротивления можно найти по формуле:

ξ_α = ξ_90˚(1 – cos α),

где:
ξ_90˚ — значение коэффициента сопротивления для угла 90˚, которое для точных расчетов принимается по справочным таблицам, а для приближенных расчетов принимается равным ξ_90˚ = 1.

Аналогичными методами осуществляют подбор или расчет коэффициентов сопротивления для других видов местных сопротивлений – резкое или постепенное сужение (расширение) трубопровода, повороты, входы и выходы из трубы, диафрагмы, запорные устройства, сварочные швы и т. п.

Приведенные выше формулы применимы для турбулентного режима движения жидкостей с большими числами Рейнольдса, когда влияние вязкости жидкости незначительно.
При движении жидкости с малыми числами Рейнольдса (ламинарный режим) величина местных сопротивлений мало зависит от геометрических характеристик сопротивления и скорости потока, на их величину большее влияние оказывает величина числа Рейнольдса.
В таких случаях для расчета коэффициентов местных сопротивлений применима формула А. Д. Альтшуля:

ξ = А/Re + ξ_экв,

где:
А – нестесненное сечение трубопровода;
ξ_экв – значения коэффициента местного сопротивления в квадратичной области;
Re — число Рейнольдса.

Значения параметра А и некоторых местных сопротивлений приводятся в справочных таблицах и используются при практических расчетах трубопроводов, предназначенных для движения жидкостей в ламинарном режиме.

***

Трубопроводы и их гидравлический расчет



Постановка задачи

Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя. Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

Многолетний практический опыт эксплуатации систем трубопроводов показал, что трубы, имеющие круглое сечение, обладают определенными преимуществами перед трубопроводами, имеющими поперечное сечение любой другой геометрической формы:

• минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
• круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
• форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
• процесс изготовления труб круглой формы относительно простой и доступный.

Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.

Основными параметрами, характеризующими трубопровод являются:

• условный (номинальный) диаметр – D_N;
• давление номинальное – P_N;
• рабочее допустимое (избыточное) давление;
• материал трубопровода, линейное расширение, тепловое линейное расширение;
• физико-химические свойства рабочей среды;
• комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
• изоляционные материалы трубопровода.

Условный диаметр (проход) трубопровода (D_N) – это условная  безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).

Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.

Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода. Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.

Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.

Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.

Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.

Основные положения гидравлического расчета

Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.

Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний,  по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:

Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:

• ламинарный поток (Re<2300), при котором носитель-жидкость движется тонкими слоями, практически не смешивающимися друг с другом;
• переходный режим (2300<Re<4000), который характеризуется нестабильной структурой потока, когда отдельные слои жидкости перемешиваются;
• турбулентный поток (Re>4000) – устойчивый режим, при котором в каждой отдельной точке потока происходит изменение его направления и скорости, что в итоге приводит к выравниванию скорости движения потока по объему трубы.

Критерий Рейнольдса зависит от напора, с которым насос перекачивает жидкость, вязкости носителя при рабочей температуре и геометрических размеров используемой трубы (d, длина). Данный критерий является параметром подобия для течения жидкости,поэтому, используя его, можно осуществлять моделирование реального технологического процесса в уменьшенном масштабе, что удобно при проведении испытаний и экспериментов.

Проводя расчеты и вычисления по уравнениям, часть заданных неизвестных величин можно взять из специальных справочных источников. Профессор, доктор технических наук Ф. А. Шевелев разработал ряд таблиц для проведения точного расчета пропускной способности трубы. Таблицы включают значения параметров, характеризующих как сам трубопровод (размеры, материалы), так и  их взаимосвязь с физико-химическими свойствами носителя. Кроме того, в литературе приводится таблица приближенных значений скоростей движения потока жидкости, пара,газа в трубе различного сечения.

Подбор оптимального диаметра трубопровода

Определение оптимального диаметра трубопровода – это сложная производственная задача, решение которой зависит от совокупности различных взаимосвязанных условий (технико-экономические, характеристики рабочей среды и материала трубопровода, технологические параметры и т.д.). Например, повышение скорости перекачиваемого потока приводит к уменьшению диаметра трубы, обеспечивающей заданный условиями процесса расход носителя, что влечет за собой снижение затрат на материалы, удешевлению монтажа и ремонта магистрали и т.д. С другой стороны, повышение скорости потока  приводит к потере напора, что требует дополнительных энергетических и финансовых затрат на перекачку заданного объема носителя.

Значение оптимального диаметра трубопровода рассчитывается по преобразованному уравнению неразрывности потока с учетом заданного расхода носителя:

 При гидравлическом расчете расход перекачиваемой жидкости чаще всего задан условиями задачи. Значение скорости потока перекачиваемого носителя определяется, исходя из свойств заданной среды и соответствующих справочных данных (см. таблицу).

Преобразованное уравнение неразрывности потока для расчета рабочего диаметра трубы имеет вид:

Расчет падения напора и гидравлического сопротивления

Полные потери напора жидкости включают в себя потери на преодоление потоком всех препятствий: наличие насосов, дюкеров, вентилей, колен, отводов, перепадов уровня при течении потока по трубопроводу, расположенному под углом и т.д. Учитываются потери на местные сопротивления, обусловленные свойствами используемых материалов.

Другим важным фактором, влияющим на потери напора, является трение движущегося потока о стенки трубопровода, которое характеризуется коэффициентом гидравлического сопротивления.

Значение коэффициента гидравлического сопротивления λзависит от режима движения потока и шероховатости материала стенок трубопровода. Под шероховатостью понимают дефекты и неровности внутренней поверхности трубы. Она может быть абсолютной и относительной. Шероховатость различна по форме и неравномерна по площади поверхности трубы. Поэтому в расчетах используется понятие усредненной шероховатости с поправочным коэффициентом (k1). Данная характеристика для конкретного трубопровода зависит от материала, продолжительности его эксплуатации, наличия различных коррозионных дефектов и других причин. Рассмотренные выше величины являются справочными.

Количественная связь между коэффициентом трения, числом Рейнольдса и шероховатостью определяется диаграммой Муди.

Для вычисления коэффициента трения турбулентного движения потока также используется уравнение Коулбрука-Уайта, с использованием которого возможно наглядное построение графических зависимостей, по которым определяется коэффициент трения:

В расчётах используются и другие уравнения приблизительного расчета потерь напора на трение. Одним из наиболее удобных и часто используемых в этом случае считается формула Дарси-Вейсбаха. Потери напора на трение рассматриваются как функция скорости жидкости от сопротивления трубы движению жидкости, выражаемой через значение шероховатости поверхности стенок трубы: 

Потери давления по причине трения для воды рассчитывают по формуле Хазена — Вильямса:

Расчет потерь давления

Рабочее давление в трубопроводе – это на большее избыточное давление, при котором обеспечивается заданный режим технологического процесса. Минимальное и максимальное значения давления, а также физико-химические свойства рабочей среды, являются определяющими параметрами при расчёте расстояния между насосами, перекачивающими носитель, и производственной мощности.

Расчет потерь на падение давления в трубопроводе осуществляют по уравнению:

Примеры задач гидравлического расчета трубопровода с решениями

Задача 1

В аппарат с давлением 2,2 бар по горизонтальному трубопроводу с эффективным диаметром 24 мм из открытого хранилища насосом перекачивается вода. Расстояние до аппарата составляет 32 м. Расход жидкости задан – 80 м³/час. Суммарный напор составляет 20 м. Принятый коэффициент трения равен 0,028.

Рассчитайте потери напора жидкости на местные сопротивления в данном трубопроводе.

Исходные данные:

Расход Q = 80 м³/час = 80·1/3600 = 0,022 м³/с;

эффективный диаметр d = 24 мм;

длина трубы l = 32 м;

коэффициент трения λ = 0,028;

давление в аппарате Р = 2,2 бар = 2,2·10⁵ Па;

общий напор Н = 20 м.

Решение задачи:

Скорость потока движения воды в трубопроводе рассчитывается по видоизмененному уравнению:

w=(4·Q) / (π·d²) = ((4·0,022) / (3,14·[0,024]²)) = 48,66 м/с

Потери напора жидкости в трубопроводе на трение определяются по уравнению:

H_Т = (λ·l) / (d·[w²/(2·g)]) = (0,028·32) / (0,024·[48,66]²) / (2·9,81) = 0,31 м

Общие потери напора носителя рассчитываются по уравнению и составляют:

h_п = H — [(p₂-p₁)/(ρ·g)] — H_г = 20 — [(2,2-1)·10⁵)/(1000·9,81)] — 0 = 7,76 м

Потери напора на местные сопротивления определяется как разность:

7,76 — 0,31=7,45 м

Ответ: потери напора воды на местные сопротивления составляют 7,45 м.

Задача 2

По горизонтальному трубопроводу центробежным насосом транспортируется вода. Поток в трубе движется со скоростью 2,0 м/с. Общий напор составляет 8 м.

Найти минимальную длину прямого трубопровода, в центре которого установлен один вентиль. Забор воды осуществляется из открытого хранилища. Из трубы вода самотеком изливается в другую емкость. Рабочий диаметр трубопровода равен 0,1 м. Относительная шероховатость принимается равной 4·10^-5.

Исходные данные:

Скорость потока жидкости W = 2,0 м/с;

диаметр трубы d = 100 мм;

общий напор Н = 8 м;

относительная шероховатость 4·10^-5.

Решение задачи:

Согласно справочным данным в трубе диаметром 0,1 м коэффициенты местных сопротивлений для вентиля и выхода из трубы составляют соответственно 4,1 и 1.

Значение скоростного напора определяется по соотношению:

w²/(2·g) = 2,0²/(2·9,81) = 0,204 м

Потери напора воды на местные сопротивления составят:

∑ζ_МС·[w²/(2·g)] = (4,1+1)·0,204 = 1,04 м

Суммарные потери напора носителя на сопротивление трению и местные сопротивления рассчитываются по уравнению общего напора для насоса (геометрическая высота Hг по условиям задачи равна 0):

h_п = H — (p₂-p₁)/(ρ·g) — = 8 — ((1-1)·10⁵)/(1000·9,81) — 0 = 8 м

Полученное значение потери напора носителя на трение составят:

8-1,04 = 6,96 м

Рассчитаем значение числа Рейнольдса для заданных условий течения потока (динамическая вязкость воды принимается равной 1·10^-3 Па·с,  плотность воды – 1000 кг/м³):

Re = (w·d·ρ)/μ = (2,0·0,1·1000)/(1·10^-3) = 200000

Согласно рассчитанному значению Re, причем 2320 <Re< 10/e, по справочной таблице рассчитаем коэффициент трения (для режима гладкого течения):

λ = 0,316/Re^0,25 = 0,316/200000^0,25 = 0,015

Преобразуем уравнение и найдем требуемую длину трубопровода из расчетной формулы потерь напора на трение:

l = (H_об·d) / (λ·[w²/(2g)]) = (6,96·0,1) / (0,016·0,204) = 213,235 м

Ответ:требуемая длина трубопровода составит 213,235 м.

Задача 3

В производстве транспортируют воду при рабочей температуре 40°С с производственным расходом Q = 18 м³/час. Длина прямого трубопровода l = 26 м, материал — сталь. Абсолютная шероховатость (ε) принимается для стали по справочным источникам и составляет 50 мкм. Какой будет диаметр стальной трубы, если перепад давления на данном участке не превысит Δp = 0,01 мПа (ΔH = 1,2 м по воде)? Коэффициент трения принимается равным 0,026.

Исходные данные:

Расход Q = 18 м³/час = 0,005 м³/с;

длина трубопровода l=26 м;

для воды ρ = 1000 кг/м³, μ = 653,3·10^-6 Па·с (при Т = 40°С);

шероховатость стальной трубыε = 50 мкм;

коэффициент трения λ = 0,026;

Δp=0,01 МПа;

ΔH=1,2 м.

Решение задачи:

Используя форму уравнения неразрывности W=Q/F и уравнение площади потока F=(π·d²)/4 преобразуем выражение Дарси – Вейсбаха:

∆H = λ·l/d·W²/(2·g) = λ·l/d·Q²/(2·g·F²) = λ·[(l·Q²)/(2·d·g·[(π·d²)/4]²)] = =(8·l·Q²)/(g·π²)·λ/d⁵ = (8·26·0.005²)/(9,81·3,14²)· λ/d⁵ = 5,376·10^-5·λ/d⁵

Выразим диаметр:

d⁵ = (5,376·10^-5·λ)/∆H = (5,376·10^-5·0,026)/1,2 = 1,16·10^-6

d = ⁵√1,16·10^-6 = 0,065 м.

Ответ: оптимальный диаметр трубопровода составляет 0,065 м.

Задача 4

Проектируются два трубопровода для транспортировки невязкой жидкости с предполагаемой производительностью Q₁ = 18 м³/час и Q₂ = 34 м³/час. Трубы для обоих трубопроводов должны быть одного диаметра.

Определите эффективный диаметр труб d, подходящих под условия данной задачи.

Исходные данные:

Q₁ = 18 м³/час;

Q₂ = 34 м³/час.

Решение задачи:

Определим возможный интервал оптимальных диаметров для проектируемых трубопроводов, воспользовавшись преобразованным видом уравнения расхода:

d = √(4·Q)/(π·W)

Значения оптимальной скорости потока найдем из справочных табличных данных. Для невязкой жидкости скорости потока составят 1,5 – 3,0 м/с.

Для первого трубопровода с расходом Q₁ = 18 м³/час возможные диаметры составят:

d_1min = √(4·18)/(3600·3,14·1,5) = 0,065 м

d_1max = √(4·18)/(3600·3,14·3.0) = 0,046 м

Для трубопровода с расходом 18 м³/час подходят трубы с диаметром поперечного сечения от 0,046 до 0,065 м.

Аналогично определим возможные значения оптимального диаметра для второго трубопровода с расходом Q₂ = 34 м³/час:

d_2min = √(4·34)/(3600·3,14·1,5) = 0,090 м

d_2max = √(4·34)/(3600·3,14·3) = 0,063 м

Для трубопровода с расходом 34 м³/час возможные оптимальные диаметром могут быть от 0,063 до 0,090 м.

Пересечение двух диапазонов оптимальных диаметров находится в интервале от 0,063 м до 0,065 м.

Ответ: для двух трубопроводов подходят трубы диаметром 0,063–0,065 м.

Задача 5

В трубопроводе диаметром 0,15 м при температуре Т = 40°C движется поток воды производительностью 100 м³/час. Определите режим течения потока воды в трубе.

Дано:

диаметр трубы d = 0,25 м;

расход Q = 100 м³/час;

μ = 653,3·10^-6 Па·с (по таблице при Т = 40°С);

ρ = 992,2 кг/м³ (по таблице при Т = 40°С).

Решение задачи: 

Режим течения потока носителя определяется по значению числа Рейнольдса (Re). Для расчета Re определим скорость движения потока жидкости в трубе (W), используя уравнение расхода:

W = Q·4/(π·d²) = [100/3600] · [4/(3,14·0,25²)] = 0,57 м/c

Значение числа Рейнольдса определим по формуле:

Re = (ρ·W·d)/μ = (992,2·0,57·0,25) / (653,3·10^-6) = 216422

Критическое значение критерия Re_кр по справочным данным равно 4000. Полученное значение Re больше указанного критического, что говорит о турбулентном характере течения жидкости при заданных условиях.

Ответ: режим потока воды – турбулентный.

Таким образом, ламинарное и турбулентное движение представляют
два различных вида движения. Они отличаются не только характером движения
частиц, но также особенностями распределения скоростей по сечению и видом
зависимости между гидравлическим сопротивлением и скоростью.

5. ПОТЕРИ НАПОРА ПРИ ДВИЖЕНИИ ЖИДКОСТИ

При течении реальной жидкости возникают силы сопротивления,
обусловленные вязкими напряжениями. Эти силы производят работу, которая целиком
превращается в тепловую энергию. Следовательно, при течении жидкости происходит
процесс необратимого превращения части механической энергии во внутреннюю
энергию. Работа сил вязкости, произведенная между двумя сечениями потока и
отнесенная к единице веса движущейся жидкости, называется потерями напора
. Потери
напора между двумя сечениями потока могут быть определены из уравнения
Бернулли, cоставленного для этих сечений:

,     (5.1)

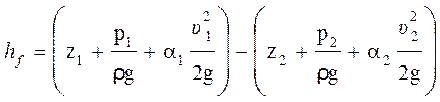
где  и  – геометрические высоты центров тяжести сечений;  и  – давления в рассматриваемых сечениях;  и  – средние скорости в сечениях;  и  – коэффициенты неравномерности распределения скоростей в
сечениях; ρ и  – плотность жидкости и ускорение силы тяжести.

Потери напора при движении жидкости складываются из потерь
напора на трение  и потерь напора на местные сопротивления :

.                                   (5.2)

5.1. Потери напора на трение

Потери напора на трение, или потери по
длине, возникают в чистом виде в прямых трубах постоянного сечения, т. е. при
равномерном течении жидкости. Для горизонтальной трубы постоянного сечения (=,  , ) потери
напора в соответствии с выражением (1) могут быть определены по зависимости

.                               (5.3)

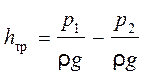
Таким образом, при
равномерном движении жидкости потери напора по длине трубы определяются
разностью пьезометрических высот в сечениях.

Общее выражение для
потерь напора на трение при равномерном движении жидкости в трубах,
справедливое как для ламинарного, так и для турбулентного режимов, имеет вид

,                             (5.4)

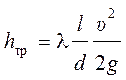
где  – коэффициент гидравлического трения.

Эта зависимость называется формулой Дарси-Вейсбаха.

5.2. Понятие шероховатости поверхности

Для грубой
количественной оценки шероховатости используется понятие средней высоты
выступов. Эта высота, измеряемая в линейных единицах, называется абсолютной
шероховатостью и обозначается обычно буквой Δ.

При одной и той же величине абсолютной
шероховатости влияние ее на величину гидравлических сопротивлений различно в
зависимости от диаметра трубы. Поэтому вводится понятие относительной
шероховатости, измеряемой отношением абсолютной шероховатости к диаметру
трубы, т. е. Δ/d.

Кроме того, даже при одной и той же абсолютной шероховатости
и одинаковом диаметре трубы из разного материала могут иметь совершенно
различное сопротивление в зависимости от формы выступов, густоты и характера их
расположения и т. д. Учесть это влияние непосредственными измерениями
практически невозможно. В связи с этим в практику гидравлических расчетов было
введено представление об эквивалентной разнозернистой шероховатости Δ_э. Под эквивалентной
шероховатостью понимают такую высоту
выступов шероховатости, сложенной из песчинок одинакового размера, которая дает
одинаковую с заданной шероховатостью величину коэффициента гидравлического
трения λ.

5.3. Коэффициент гидравлического трения

При ламинарном движении расчетная зависимость для  может быть
получена чисто теоретическим путем. Ввиду сложности турбулентного течения и
трудности его теоретического исследования до сих пор не создано достаточно
строгой и точной теории этого течения. Поэтому при турбулентном течении  находится
по различным эмпирическим формулам, предлагаемым разными авторами. Расчетные
формулы для  предусматривают
зависимость этого коэффициента в общем случае только от шероховатости стенок
русла и от числа Рейнольдса. Первые систематические опыты для выявления
характера зависимости  от числа Рейнольдса Re и относительной
шероховатости D/d, были проведены Никурадзе в гладких латунных трубах
и  трубах с искусственной равнозернистой шероховатостью. Результаты опытов
Никурадзе представил в виде особого графика (рис. 5.1). На нем изображен ряд
кривых, соответствующих различной величине относительной шероховатости D/d, (D – высота выступов
шероховатости, d – диаметр трубы) и две «опорные» прямые: прямая
ламинарного режима I, построенная по уравнению 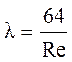, и прямая II,
построенная по уравнению Блазиуса .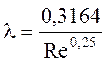

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.