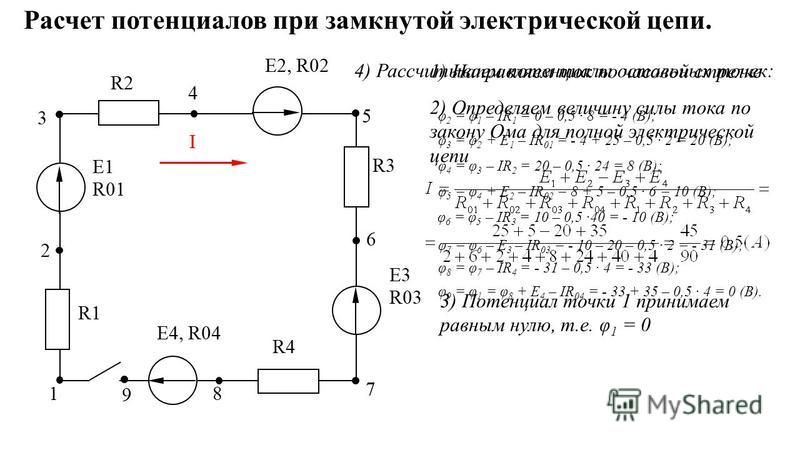
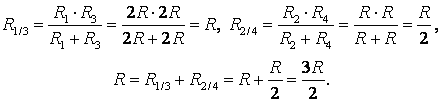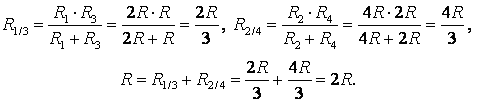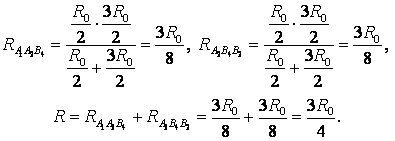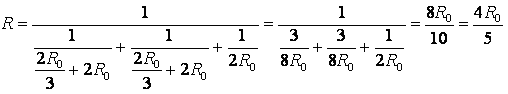Измерение потенциалов точек электрической цепи и построение потенциальной диаграммы
Электротехника
Электротехника
Страницы работы
7
страниц
(Word-файл)
Посмотреть все страницы
Скачать файл
Фрагмент текста работы
любой ветви схемы можно найти по закону Ома для
участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома,
необходимо знать потенциалы узлов схемы. Метод расчета электрических цепей, в
котором за неизвестные принимают потенциалы узлов схемы, называют методом
узловых потенциалов.
Допустим, что в схеме n узлов.
Так как любая (одна) точка схемы может быть заземлена без изменения
токораспределения в схеме, то один из узлов схемы можно мысленно заземлить, т.
е. принять потенциал его равным нулю. При этом число неизвестных уменьшается с n до n-1.
Число неизвестных в методе узловых потенциалов равно
числу уравнений, которые необходимо составить для схемы по первому закону
Кирхгофа. Метод узловых потенциалов, как и метод контурных токов, — один из
основных расчетных приемов. В том случае, когда число узлов без единицы меньше
числа независимых контуров в схеме, данный метод является более экономичным,
чем метод контурных токов.
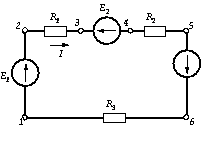
Вывод основных расчетных уравнений проведем применительно
к схеме рис. 2, в которой три узла. Если узел 3 мысленно заземлить, т. е.
принять =0, то необходимо определить потенциалы
только двух узлов:,.
Запишем уравнения по первому закону Кирхгофа для
независимых узлов, причем токи, направленные к узлу берем со знаком минус, а от
узла – со знаком плюс.
Для первого узла ,
Для второго узла .
Рис. 2. Схема для
расчета по методу узловых потенциалов
Запишем токи по закону Ома:
, , , ,
, .
Подставим токи в уравнения по первому закону Кирхгофа:
,
.
Перепишем уравнения:
,
;
,
;
,
, где ,
, , ,
,
,
G11— сумма проводимостей
ветвей, сходящихся в первом узле,
G12— сумма проводимостей
ветвей, соединяющих первый и второй узлы, взятая со знаком минус,
G21— сумма проводимостей
ветвей, соединяющих первый и второй узлы, взятая со знаком минус,
G11— сумма проводимостей
ветвей, сходящихся во втором узле,
I11— узловой ток первого
узла,
I22 — узловой ток второго
узла.
Запишем уравнения в матричной форме:
,
, , .
Решим эти уравнения относительно искомых потенциалов и
выразим токи ветвей, используя закон Ома.
После нахождения токов ветвей любым методом всегда
делается проверка по первому закону Кирхгофа.
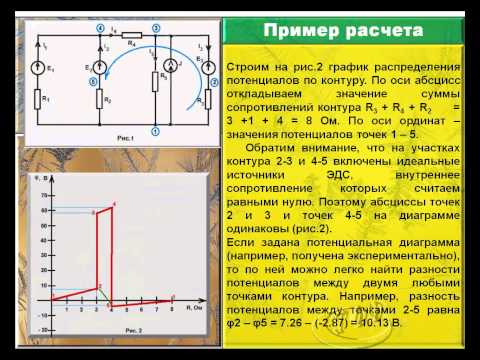
Потенциальная диаграмма.
Под потенциальной диаграммой понимают график
распределения потенциала вдоль какого-либо участка цепи или замкнутого контура.
По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо
произвольной точки, по оси ординат – потенциалы. Каждой точке участка цепи или
замкнутого контура соответствует своя точка на потенциальной диаграмме.
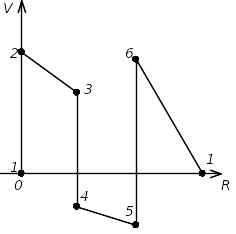
Построим потенциальную диаграмму для контура на рис.3. Пусть R1=10 Ом, R2=5 Ом, R3=15
Ом, E1=20 В, E2=10 В, I=1A.
Рис.3. Контур для
построения потенциальной диаграммы
,
,
,
,
,
.
Построим график.
Рис. 4. Потенциальная
диаграмма для контура на рис.3.
Таблица 1. Исходные
данные
|
Схема |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
E1 |
E2 |
|
|
Рис. |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
В |
В |
|
|
Вариант 1 |
5 |
15 |
10 |
25 |
20 |
10 |
30 |
100 |
60 |
|
Вариант 2 |
6 |
4 |
6 |
3 |
2 |
5 |
6 |
35 |
25 |
|
Вариант 3 |
7 |
5 |
1 |
6 |
4 |
2 |
6 |
10 |
30 |
|
Вариант 4 |
8 |
3 |
6 |
9 |
10 |
6 |
8 |
55 |
40 |
|
Вариант 5 |
5 |
6 |
6 |
8 |
8 |
10 |
12 |
70 |
45 |
|
Вариант 6 |
6 |
4 |
2 |
4 |
5 |
6 |
3 |
15 |
35 |
|
Вариант 7 |
7 |
1 |
2 |
5 |
1 |
3 |
3 |
10 |
15 |
|
Вариант 8 |
8 |
25 |
50 |
15 |
25 |
20 |
30 |
150 |
75 |
Порядок выполнения работы:
1.
схему. Записать данные.
2. Найти токи
ветвей методом контурных токов.
3. Сделать
проверку по первому закону Кирхгофа.
4. Найти токи
ветвей методом узловых потенциалов.
5. Рассчитанные
токи занести в таблицу 2.
Таблица
2
|
I1,A |
I2,A |
I3,A |
I4,A |
I5,A |
I6,A |
|
|
расчет |
||||||
|
эксперимент |
6.
7. Потенциалы точек отмеченных на схеме занести в таблицу
3.
Таблица 3
|
A, B |
B, B |
C, B |
D, B |
F, B |
|
|
расчет |
|||||
|
эксперимент |
8.
схему в программе Electronics Workbench.
9. Измерить
токи во всех ветвях. Для чего в каждую ветвь включить амперметр. Результаты
измерений занести в таблицу 2.
10. Заземлить узел, который
заземляли при расчете по методу узловых потенциалов.
11. Измерить потенциалы точек,
отмеченных на схеме. Результаты занести в таблицу 3.
12. Построить потенциальную
диаграмму заданного контура.
13. Сравнить измеренные данные с
расчетными.
14. Сделать вывод.
Содержание отчета:
1. Тема,
цель, приборы и оборудование.
2. Схема
заданной цепи. Исходные данные.
3. Расчет по
методу контурных токов и методу узловых потенциалов.
4. Заполненная
таблица 2.
5. Проверка
по первому закону Кирхгофа.
6. Баланс
мощностей.
7. Заполненная
таблица 3.
8. Токи
ветвей и потенциалы узлов цепи, измеренные в программе Electronics Workbench .
9. Потенциальная
диаграмма.
10. Вывод.
Вопросы на защиту:
1.
метода контурных токов.
2. Суть
метода узловых потенциалов.
3. Какой
используется закон Кирхгофа для составления уравнений по методу контурных
токов? Сформулировать его.
4. Какой
используется закон Кирхгофа для составления уравнений по методу узловых
потенциалов? Сформулировать его.
5. Как
называется сопротивление R11? Как оно
находится?
6. Как
называется сопротивление R12? Как оно
находится?
7. Что такое
Е11 в матричной записи уравнений по методу контурных токов?
8. Как
находится собственная проводимость узла по методу узловых потенциалов?
9. Матричная
форма записи уравнений по методу узловых потенциалов.
10. Как строится потенциальная
диаграмма контура сложной цепи
Похожие материалы
Информация о работе
Скачать файл
РАСЧЕТ ПОТЕНЦИАЛОВ ТОЧЕК ЦЕПИ — Мегаобучалка
Чтобы найти ток в цепи с несколькими источниками надо:
1) Сложить все Е, направленные в одну сторону;
2) Вычесть все Е, направленные в другую сторону
3) Разделить на сумму всех сопротивлений цепи
Ток течет в сторону большей суммы Е.
Пусть Е1 > Е2, тогда
Если ток и ЭДС совпадают по направлению, то источник работает в режиме генератора, если нет, то в режиме потребителя.
Е1 — генератор; Е2— потребитель
Потенциалом точки цепи называется напряжение между данной точкой и заземлённой.
φ0 = 0
При переходе через источник в режиме генератора потенциал повышается на величину ЭДС минус падение напряжения внутри источника.
φА = φ0 + Е1 — I∙Ri1
При переходе через резистор потенциал понижается на величину падения напряжений в нём:
φВ = φА — I∙R
При переходе через источник в режиме потребителя потенциал понижается на величину ЭДС и на величину падения напряжения внутри источника.
φ0 = φB — E2 — I∙Ri2
Потенциальная диаграмма — это график зависимости потенциалов точек цепи от величины сопротивления цепи.
Рассмотрим построение потенциальной диаграммы на конкретном примере. Одну точку цепи заземляем. Расставляем точки вдоль направления тока. При расчете снова должен получиться равным нулю
Пример решения задачи:
Дано:
Е1 = 25 B
Е2 = 35 В
Е3 = 18 В
Ri1 = 2 Ом
Ri2 = 1 Ом
Ri3 =2 Ом
R1 = 12 Ом
R2 = 5 Ом
R3 = 14 Ом
R4 = 6 Ом
1) Рассчитаем ток в цепи и определяем его направление:
A
2) Рассчитаем потенциалы точек:
φ0 = 0
φ1 = φ0 — I∙R1 = 0 — 12 = -12 B
φ2 = φ1 + Е1 — I∙Ri1 = -12 + 25 — 2 = 11 B
φ3 = φ2 — I∙R2 = 11 — 5 = 6 B
φ4 = φ3 + E2 — I∙Ri2 = 6 + 35 — 1 = 40 B
φ5 = φ4 — E3 — I∙Ri3 = 40 — 18 — 2 = 20 B
φ6 = φ5 — I∙R3 = 20 — 14 = 6 B
φ0 = φ6 — I∙R4 = 6 — 6 = 0
Вывод: При переходе через резистор потенциал понижается плавно, через источник в режиме генератора резко увеличивается, а в режиме потребителя резко уменьшается.
Тестовые задания:
| Задание | Варианты ответов |
| 1.Являются ли напряжение между данной точкой цепи и заземленной потенциалом точки этой цепи? | Да; Нет. |
| 2. Источник работает в режиме генератора если… | а) ЭДС и ток направлены в разные стороны; б) ЭДС и ток направлены в одну сторону. |
РАБОТА ИСТОЧНИКА НА НАГРУЗКУ С ПЕРЕМЕННЫМ СОПРОТИВЛЕНИЕМ.
Построение зависимостей I, U, η = F(R).
Пусть сопротивление нагрузки изменяется от Rкз=0 до Rxx= . Рассмотрим величину тока в трех режимах короткое замыкание, холостой ход и согласованный режим.
1) Iкз = =
2) Iхх =
3)
Вывод 1: с ростом величины сопротивления ток в цепи уменьшается;
Вывод 2: ток максимальный в режиме короткого замыкания;
Рассмотрим величину напряжения в трех режимах
1) Uкз=
2)
3)
Вывод 1: с ростом величины сопротивления напряжение на зажимах источника растет;
Вывод 2: напряжение максимально в режиме Х.
Рассмотрим величину К.П.Д. в трех режимах
Вывод: η стремиться к 1 в режиме Х.Х., но использовать на практике этот режим невозможно, так как цепь разомкнута.
Построение зависимостей Pu, Pн = F(R)
Рассмотрим величину мощности источника в трех режимах
Pu = E∙I = E∙
Вывод: мощность источника максимальна в режиме короткого замыкания.
Рассмотрим величину мощности нагрузки в трех режимах
Исследуя функцию Pн = f(R) на экстремум доказано, что максимальная мощность выделяется в нагрузке при согласованном режиме. Поэтому линии связи и другие устройства работают в этом режиме. И хотя η = 50%, но в слаботочных цепях это не имеет значения.
Тестовые задания:
| Задание | Режим работы | Варианты ответов |
4. Укажите при каких режимах работы перечисленные в ответах величины максимальны. Укажите при каких режимах работы перечисленные в ответах величины максимальны.
|
1) режим холостого хода; 2) режим короткого замыкания; 3) согласованный режим. |
а) мощность источника; б) ток цепи; в) мощность нагрузки напряжение на зажимах источника. |
Калькулятор электрического потенциала
Автор Purnima Singh, PhD
Отзыв Стивена Вудинга
Последнее обновление: 02 февраля 2023 г.
Содержание:
- Разность электрических потенциалов
- Что такое электрический потенциал? – Определение электрического потенциала
- Формула электрического потенциала
- Как рассчитать электрический потенциал?
- Как пользоваться калькулятором электрического потенциала
- Единицы измерения электрического потенциала
- Размерная формула электрического потенциала
- Часто задаваемые вопросы
Используйте калькулятор электрического потенциала, чтобы определить электрический потенциал в точке либо за счет одиночного точечного заряда, либо за счет системы точечных зарядов.
Если вы хотите рассчитать электрическое поле, создаваемое точечным зарядом, воспользуйтесь калькулятором электрического поля.
Продолжайте читать эту статью, чтобы узнать:
- Что такое электрический потенциал?
- Какая связь между электрическим потенциалом и электрической потенциальной энергией?
- Как рассчитать электрический потенциал?
- Что такое единица электрического потенциала?
Разность электрических потенциалов
Чтобы понять идею разности электрических потенциалов, рассмотрим некоторое распределение заряда. Это распределение заряда создаст электрическое поле. Теперь, если мы хотим переместить небольшой заряд qqq между любыми двумя точками в этом поле, необходимо совершить некоторую работу против кулоновской силы (вы можете использовать наш калькулятор закона Кулона, чтобы определить эту силу).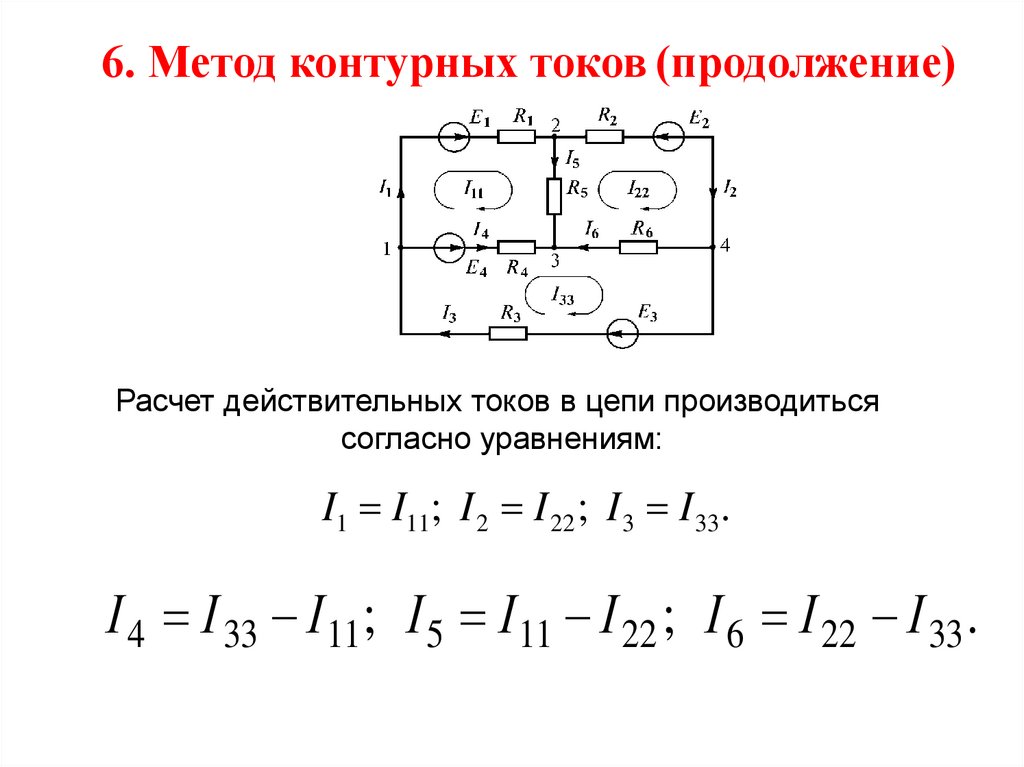
Если мы рассмотрим две произвольные точки, скажем A и B, то выполненная работа (WABW_{AB}WAB) и изменение потенциальной энергии (ΔUDelta UΔU) при перемещении заряда (qqq) из A в B можно записать как:
- WAB=ΔU=(VA−VB)qW_{AB} = Delta U = (V_A — V_B)qWAB=ΔU=(VA−VB)q …… (1)
, где VAV_AVA и VBV_BVB — электрические потенциалы в точках A и B соответственно (мы объясним, что это значит, в следующем разделе).
Если величина qqq равна единице (мы называем положительный заряд единичной величины пробным зарядом), уравнение меняется на:
- ΔV=(VA−VB)=WABq Delta V = (V_A — V_B) = frac{W_{AB}}{q}ΔV=(VA−VB)=qWAB …. .. (2)
Используя приведенное выше уравнение, мы можем определить разность электрических потенциалов (ΔVDelta VΔV) между двумя точками (B и A) как работу, выполненную для перемещения пробного заряда из A в B против электростатической силы .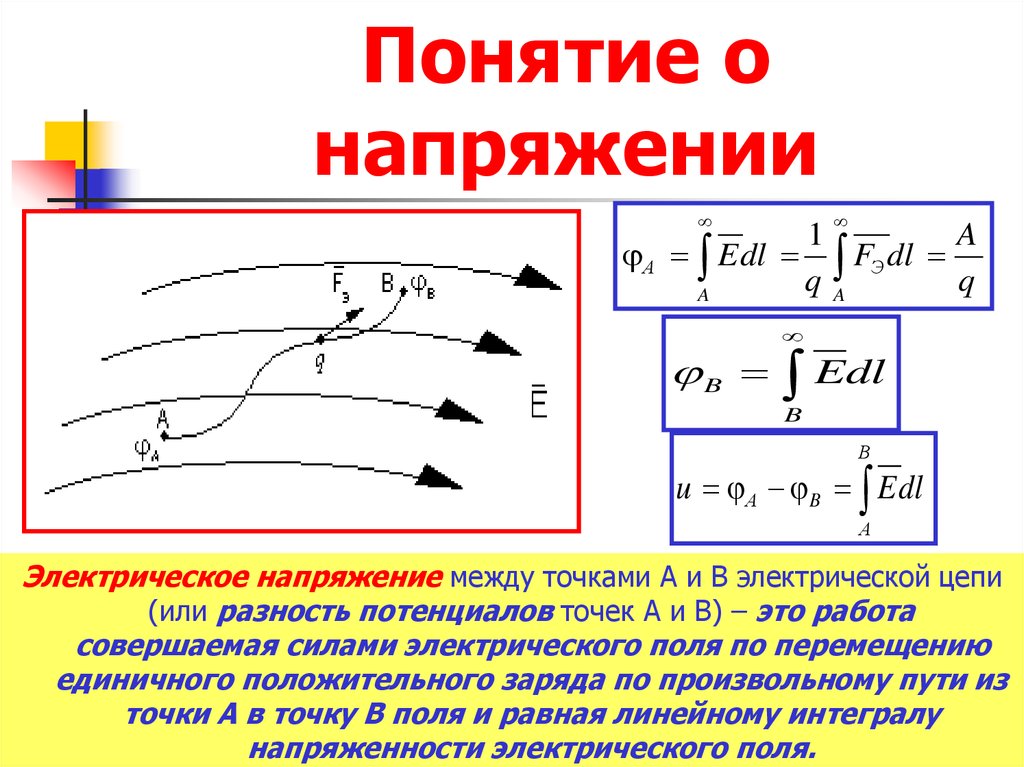
Помните, что потенциальную электрическую энергию нельзя рассчитать по стандартной формуле потенциальной энергии E=mghE=mghE=mgh.
Что такое электрический потенциал? – Определение электрического потенциала
Если мы возьмем одну из точек в предыдущем разделе, скажем, точку A, находящуюся в бесконечности, и выберем потенциал на бесконечности равным нулю, мы можем изменить формулу разности электрических потенциалов (уравнение 2) следующим образом:
- VB=W ∞Бк V_B = frac{W_{infty B}}{q}VB=qW∞B
Следовательно, мы можем определить электрический потенциал в любой точке как количество работы, выполненной при перемещении пробного заряда из бесконечности в эту точку .
Мы также можем определить электрический потенциал как электрическую потенциальную энергию на единицу заряда, т.е.:
- V=ΔUq V = frac{Delta U}{q}V=qΔU
Итак, вы видите, что электрический потенциал и электрическая потенциальная энергия — это не одно и то же.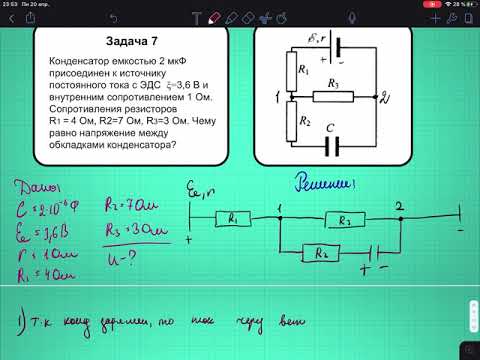
Формула электрического потенциала
Для расчета электрического потенциала в любой точке A от одного точечного заряда (см. рис. 1) воспользуемся формулой:
В=кквscriptsize
V = k frac{q}{r}V=krq
где:
- qqq — электростатический заряд;
- rrr — расстояние между точкой А и точечным зарядом; и
- k=14πϵ0k = frac{1}{4 pi epsilon_0}k=4πϵ01 — постоянная Кулона.
Рис. 1: Электрический потенциал точечного заряда.
Заметим, что когда заряд qqq положителен, электрический потенциал положителен. Когда заряд qqq отрицателен, электрический потенциал отрицателен.
Теперь рассмотрим случай, когда имеются четыре точечных заряда: q1q_1q1, q2q_2q2, q3q_3q3 и q4q_4q4 (см. рис. 2). Потенциал в точке A от заряда q1q_1q1 равен:
V1=kq1r1scriptsize
V_1 = k frac{q_1}{r_1}V1=kr1q1
Рис. 2: Электрический потенциал, обусловленный системой точечных зарядов.
Мы можем написать аналогичные выражения для потенциала в точке A от других зарядов:
V2=kq2r2V3=kq3r3V4=kq4r4scriptsize
начать{выравнивать*}
V_2 &= k frac{q_2}{r_2} \ \
V_3 &= k frac{q_3}{r_3} \ \
V_4 &= k frac{q_4}{r_4}
end{align*}V2V3V4=kr2q2=kr3q3=kr4q4
Чтобы получить результирующий потенциал в точке A, воспользуемся принципом суперпозиции, т.
V=V1+V2+V3+V4V=k(q1r1+q2r2+q3r3+q4r4)размер сценария
начать{выравнивать*}
V &= V_1 + V_2 + V_3 + V_4 \ \
V &= k left (frac{q_1}{r_1} + frac{q_2}{r_2} + frac{q_3}{r_3} + frac{q_4}{r_4}right ) \
end{align*}VV=V1+V2+V3+V4=k(r1q1+r2q2+r3q3+r4q4)
Для системы nnn точечных зарядов результирующий потенциал можно записать в виде: кирискриптсайз
начать{выравнивать*}
V &= V_1 + V_2 + V_3 + …. +V_n \ \
V &= k left (frac{q_1}{r_1} + frac{q_2}{r_2} + frac{q_3}{r_3} + …. +frac{q_n}{r_n}right ) \\
V & = k sum frac{q_i}{r_i}
end{align*}VVV=V1+V2+V3+….+Vn=k(r1q1+r2q2+r3q3+…. +rnqn)=k∑riqi 94 rm В3,6×104 В.
Как пользоваться калькулятором электрического потенциала
Теперь посмотрим, как можно решить ту же задачу с помощью нашего калькулятора электрического потенциала:
-
В раскрывающемся меню выберите электрический потенциал за счет точечного заряда .
-
Введите значение электрического заряда , т. е. 4e−074e-074e−07 и расстояние между точечным зарядом и точкой наблюдения (10 см10 rm см10 см). 94 rm В3,595×104 В.
Единицы электрического потенциала
Единицей электрического потенциала СИ является вольт (В) . Мы можем сказать, что электрический потенциал в точке равен 1 В , если 1 Дж работы совершается при переносе положительного заряда 1 Кл из бесконечности в эту точку против электростатической силы.
Единицей измерения разности потенциалов также является вольт. Возможно, вы более знакомы с напряжением, а не с термином «разность потенциалов». Например, когда мы говорим о 3 В , мы просто имеем в виду, что разность потенциалов между двумя его клеммами составляет 3 В .
💡 Наш калькулятор емкости аккумулятора — это удобный инструмент, который поможет вам узнать, сколько энергии хранится в вашем аккумуляторе.
Размерная формула электрического потенциала
Чтобы написать размерную формулу электрического потенциала (или разности электрических потенциалов), мы сначала напишем уравнение для электрического потенциала:
- V=Wq V = frac{W}{q} V=qW 9{-1}]V=[AT][M1L2T−2]=[M1L2T−3A−1]
Часто задаваемые вопросы
Как рассчитать электрический потенциал точечного заряда?
Для расчета электрического потенциала точечного заряда (q) на расстоянии (r) следуйте приведенным инструкциям:
-
Умножить заряд q на постоянную Кулона .
-
Разделить значение из шаг 1 на расстояние р.
-
Поздравляю! Вы вычислили электрический потенциал точечного заряда.
Может ли электрический потенциал быть отрицательным?
Да , электрический потенциал может быть отрицательным.
Электростатический потенциал в точке из-за положительного заряда положителен. Если заряд отрицательный, электрический потенциал также отрицателен.
Что такое разность электрических потенциалов?
Разность электрических потенциалов между двумя точками A и B определяется как работа, совершаемая для перемещения единичного положительного заряда из A в B . Единицей разности потенциалов в системе СИ является вольт (В).
Является ли электрический потенциал скалярной или векторной величиной?
Электрический потенциал является скалярной величиной , поскольку он не имеет направления.
Какова единица измерения электрического потенциала?
Электрический потенциал – электрическая потенциальная энергия на единицу заряда. Единицей электрической потенциальной энергии в системе СИ является джоуль (Дж), а единицы заряда — кулон (Кл). Следовательно, единицей электрического потенциала СИ является Дж/Кл, т. е. вольт (В) .
Чему равен электрический потенциал заряда в точке, удаленной на бесконечность?
Ноль . Электрический потенциал в точке
P, обусловленный зарядомq, обратно пропорционален расстоянию между ними. Следовательно, когда расстояние бесконечно, электрический потенциал равен нулю.Пурнима Сингх, доктор философии
Я хочу вычислить…..
Электрический потенциал
Заряд (q)
Расстояние (r)
Электрический потенциал (В)
Ознакомьтесь с 40 похожими калькуляторами электромагнетизма 🧲
Ускорение частицы в электрическом полеВатт переменного токаЕмкость… еще 37
3.3 Расчеты электрического потенциала – введение в электричество, магнетизм и электрические цепи
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Расчет потенциала точечного заряда
- Расчет потенциала системы множественных точечных зарядов
- Описать электрический диполь
- Определить дипольный момент
- Расчет потенциала непрерывного распределения заряда
Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи.
Кроме того, сферические распределения заряда (например, заряд на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть.
Мы можем использовать исчисление, чтобы найти работу, необходимую для перемещения пробного заряда с большого расстояния на расстояние от точечного заряда. Отмечая связь между работой и потенциалом, как и в предыдущем разделе, мы можем получить следующий результат.
ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
В ТОЧЕЧНЫЙ ЗАРЯД
Электрический потенциал точечного заряда определяется как
(3.3.1)
где постоянная, равная .
Потенциал на бесконечности выбран равным нулю. Таким образом, для точечного заряда уменьшается с расстоянием, тогда как для точечного заряда уменьшается с квадратом расстояния:
Напомним, что электрический потенциал — скаляр и не имеет направления, тогда как электрическое поле — вектор.
Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов, принимая во внимание величину и направление. Это согласуется с тем фактом, что тесно связано с энергией, скаляром, тогда как тесно связано с силой, вектором.
ПРИМЕР 3.3.1
Какое напряжение создает небольшой заряд на металлическом шаре?
Заряды статического электричества обычно находятся в диапазоне от нанокулонов () до микрокулонов (). Каково напряжение вдали от центра твердого металлического шара диаметром, имеющего статический заряд?
Стратегия
Как мы обсуждали в разделе «Электрические заряды и поля», заряд на металлическом шаре распространяется равномерно и создает поле, похожее на поле точечного заряда, расположенного в его центре. Таким образом, мы можем найти напряжение, используя уравнение.
Решение
Подставляя известные значения в выражение для потенциала точечного заряда, получаем
Значение
Отрицательное значение напряжения означает, что положительный заряд будет притягиваться с большего расстояния, поскольку потенциал ниже (более отрицательный), чем на больших расстояниях.
И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
ПРИМЕР 3.3.2
Что такое избыточный заряд генератора Ван де Граафа?
Демонстрационный генератор Ван де Граафа имеет металлическую сферу диаметром, которая создает напряжение вблизи ее поверхности (рис. 3.3.1). Какой избыточный заряд находится на шаре? (Предположим, что каждое числовое значение здесь показано с тремя значащими цифрами.)
(рис. 3.3.1)
Рисунок 3.3.1 Напряжение этого демонстрационного генератора Ван де Граафа измеряется между заряженной сферой и землей. Потенциал Земли принимается равным нулю в качестве эталона. Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре.
Стратегия
Потенциал на поверхности такой же, как и у точечного заряда в центре сферы вдали. (Радиус сферы равен .) Таким образом, мы можем определить избыточный заряд, используя уравнение
Решение
Решение для и ввод известных значений дает
Значение
Это относительно небольшая зарядка, но выдает довольно большое напряжение.
У нас есть еще одно указание на то, что трудно хранить изолированные заряды.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 3.8
Каков потенциал внутри металлической сферы в Примере 3.3.1?
Напряжения в обоих этих примерах можно измерить с помощью измерителя, который сравнивает измеренный потенциал с потенциалом земли. Потенциал земли часто принимается равным нулю (вместо того, чтобы принимать потенциал на бесконечности равным нулю). Важна именно разность потенциалов между двумя точками, и очень часто неявно предполагается, что какая-то точка отсчета, например Земля или очень удаленная точка, имеет нулевой потенциал. Как отмечалось ранее, это аналогично уровню моря при рассмотрении потенциальной энергии гравитации.
Системы многоточечных зарядов
Как электрическое поле подчиняется принципу суперпозиции, так и электрический потенциал. Рассмотрим систему, состоящую из зарядов . Каков чистый электрический потенциал в точке пространства от этих зарядов? Каждый из этих зарядов является исходным зарядом, который создает свой собственный электрический потенциал в точке , независимо от того, какие другие изменения могут происходить.
Пусть — электрические потенциалы при , создаваемые зарядами соответственно. Тогда суммарный электрический потенциал в этой точке равен сумме этих отдельных электрических потенциалов. Это легко показать, рассчитав потенциальную энергию пробного заряда, когда вы перенесете пробный заряд из точки отсчета на бесконечности в точку:
Обратите внимание, что электрический потенциал следует тому же принципу суперпозиции, что и электрическое поле и электрическая потенциальная энергия. Чтобы показать это более явно, обратите внимание, что тестовый заряд в точке пространства находится на расстоянии от зарядов, зафиксированных в пространстве выше, как показано на рисунке 3.3.2. Используя нашу формулу потенциала точечного заряда для каждого из этих (предполагаемых точечными) зарядов, находим, что
(3.3.2)
Следовательно, электрическая потенциальная энергия пробного заряда равна
, который аналогичен работе по вводу пробного заряда в систему, описанной в первом разделе главы.
(рис. 3.3.2)
Рисунок 3.3.2 Обозначение прямых расстояний от зарядов до точки пространства.
Электрический диполь
Электрический диполь – это система двух равных, но противоположных зарядов, находящихся на фиксированном расстоянии друг от друга. Эта система используется для моделирования многих систем реального мира, включая атомные и молекулярные взаимодействия. Одной из таких систем является молекула воды при определенных обстоятельствах. Эти обстоятельства встречаются внутри микроволновой печи, где электрические поля переменного направления заставляют молекулы воды менять ориентацию. Эта вибрация аналогична теплу на молекулярном уровне.
ПРИМЕР 3.3.3
Электрический потенциал диполя
Рассмотрим диполь на Рисунке 3.3.3 с величиной заряда и расстоянием разделения . Каков потенциал в следующих местах в космосе? (а) ; (б) ; (с) .
(рис. 3.3.3)
Рисунок 3.
3.3 Общая схема электрического диполя и обозначения расстояний от отдельных зарядов до точки в пространстве.
Стратегия
Применить к каждой из этих трех точек.
Решение
а.
б.
в.
Значение
Обратите внимание, что оценка потенциала значительно проще, чем электрического поля, поскольку потенциал является скаляром, а не вектором.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 3.9
Какой потенциал на -оси? -ось?
Теперь рассмотрим частный случай, когда расстояние точки от диполя много больше, чем расстояние между зарядами в диполе, ; например, когда нас интересует электрический потенциал поляризованной молекулы, такой как молекула воды. Это не так далеко (бесконечность), чтобы мы могли просто считать потенциал равным нулю, но расстояние достаточно велико, чтобы мы могли упростить наши вычисления по сравнению с предыдущим примером.
Начнем с того, что на рис. 3.3.4 потенциал представлен как
.
где
(рис. 3.3.4)
Рисунок 3.3.4 Общая схема электрического диполя и обозначения расстояний от отдельных зарядов до точки в пространстве.
Это по-прежнему точная формула. Чтобы воспользоваться тем, что , мы перепишем радиусы в терминах полярных координат, с и . Это дает нам
Мы можем упростить это выражение, вытащив из корня,
, а затем умножить скобки на
.
Последний член в корне достаточно мал, чтобы им можно было пренебречь (помните, что и, следовательно, чрезвычайно мал, фактически равен нулю до уровня, который мы, вероятно, будем измерять), оставляя нам
Использование биномиального приближения (стандартный результат математики рядов, когда небольшое)
и подставив это в нашу формулу для , мы получим
Это может быть записано более удобно, если мы определим новую величину, электрический дипольный момент ,
(3.
3.3)
, где эти векторы указывают от отрицательного заряда к положительному. Обратите внимание, что это имеет величину . Эта величина позволяет нам записать потенциал в точке из-за диполя в начале координат как
.
(3.3.4)
Схема применения этой формулы показана на Рисунке 3.3.5.
(рис. 3.3.5)
Рисунок 3.3.5 Геометрия приложения потенциала диполя.
Существуют также моменты более высокого порядка для квадруполей, октуполей и т. д. Вы увидите их на следующих уроках.
Возможность непрерывного распределения заряда
Мы много работали с точечными зарядами, но как насчет непрерывного распределения заряда? Напомним из уравнения 3.3.2, что
Мы можем рассматривать непрерывное распределение заряда как набор бесконечно малых отдельных точек. Это дает интеграл
(3.3.5)
для потенциала в точке . Обратите внимание, что это расстояние от каждой отдельной точки распределения заряда до точки .
Как мы видели в разделе «Электрические заряды и поля», бесконечно малые заряды равны
, где – линейная плотность заряда, – заряд на единицу площади и – заряд на единицу объема.
ПРИМЕР 3.3.4
Потенциал линии заряда
Найдите электрический потенциал однородно заряженного непроводящего провода с линейной плотностью (кулон/метр) и длиной в точке, лежащей на линии, которая делит провод на две равные части.
Стратегия
Для постановки задачи мы выбираем декартовы координаты таким образом, чтобы максимально использовать симметрию в задаче. Поместим начало координат в центр провода и ориентируем -ось вдоль провода так, чтобы концы провода находились в точках . Точка поля находится в -плоскости, и поскольку выбор осей зависит от нас, мы выбираем -ось для прохождения через точку поля, как показано на рисунке 3.3.6.
(рис. 3.3.6)
Рисунок 3.3.6 Мы хотим рассчитать электрический потенциал линии заряда.
Решение
Рассмотрим небольшой элемент распределения заряда между и . Заряд в этой ячейке равен , а расстояние от ячейки до точки поля равно . Таким образом, потенциал становится равным
.
Значение
Обратите внимание, что это было проще, чем эквивалентная задача для электрического поля, из-за использования скалярных величин. Напомним, что мы ожидаем, что нулевой уровень потенциала будет на бесконечности, когда у нас конечный заряд. Чтобы исследовать это, мы берем предел вышеуказанного потенциала по мере приближения к бесконечности; в этом случае члены внутри натурального логарифма стремятся к единице, и, следовательно, потенциал приближается к нулю в этом пределе. Обратите внимание, что мы могли бы решить эту задачу эквивалентно в цилиндрических координатах; единственный эффект будет состоять в том, чтобы заменить на и на .
ПРИМЕР 3.3.5
Потенциал из-за кольца заряда
Кольцо имеет однородную плотность заряда с единицами кулонов на единицу дугового метра.
Найти электрический потенциал в точке на оси, проходящей через центр кольца.
Стратегия
Используем ту же процедуру, что и для заряженного провода. Отличие здесь в том, что заряд распределяется по окружности. Мы делим окружность на бесконечно малые элементы в виде дуг на окружности и используем цилиндрические координаты, показанные на рис. 3.3.7.
(рис. 3.3.7)
Рисунок 3.3.7 Мы хотим рассчитать электрический потенциал из-за кольца заряда.
Решение
Общий элемент дуги между и имеет длину и поэтому содержит заряд, равный . Элемент находится на расстоянии от , и поэтому потенциал равен
Значение
Этот результат ожидаем, поскольку все элементы кольца находятся на одинаковом расстоянии от точки . Чистый потенциал при является потенциалом полного заряда, расположенного на общем расстоянии, .
ПРИМЕР 3.3.6
Потенциал за счет однородного диска заряда
Диск радиусом имеет однородную плотность заряда в единицах кулон-метр в квадрате.
Найти электрический потенциал в любой точке оси, проходящей через центр диска.
Стратегия
Мы делим диск на кольцеобразные ячейки и используем результат для кольца, полученный в предыдущем примере, затем интегрируем по в дополнение к . Это показано на Рисунке 3.3.8.
(рис. 3.3.8)
Рисунок 3.3.8 Мы хотим рассчитать электрический потенциал заряженного диска.
Решение
Ячейка бесконечно малой ширины между цилиндрическими координатами и изображенная на рис. 3.3.8 будет представлять собой кольцо зарядов, электрический потенциал которого в точке поля имеет следующее выражение
где
Суперпозиция потенциалов всех бесконечно малых колец, составляющих диск, дает суммарный потенциал в точке. Это достигается путем интеграции from to :
Значение
Основная процедура для диска состоит в том, чтобы сначала интегрировать , а затем . Это было продемонстрировано для однородной (постоянной) плотности заряда.
Часто плотность заряда зависит от , и тогда последний интеграл будет давать разные результаты.
ПРИМЕР 3.3.7
Потенциал из-за бесконечного заряженного провода
Найдите электрический потенциал бесконечно длинного однородно заряженного провода.
Стратегия
Поскольку мы уже рассчитали потенциал провода конечной длины в примере 3.2.4, мы можем задаться вопросом, сработает ли наш предыдущий результат:
Однако этот предел не существует, потому что аргумент логарифма принимает вид , поэтому этот способ нахождения бесконечной проволоки не работает. Причину этой проблемы можно проследить в том, что заряды не локализованы в каком-то пространстве, а продолжаются на бесконечность в направлении провода. Следовательно, наше (негласное) предположение о том, что нулевой потенциал должен находиться на бесконечном расстоянии от провода, больше не имеет силы.
Чтобы избежать этой трудности при вычислении пределов, давайте воспользуемся определением потенциала путем интегрирования по электрическому полю из предыдущего раздела и значением электрического поля из этой конфигурации заряда из предыдущей главы.
Решение
Используем интеграл
, где — конечное расстояние от линии заряда, как показано на рис. 3.3.9.
(рис. 3.3.9)
Рисунок 3.3.9 Точки интереса для расчета потенциала бесконечной линии заряда.
В этой настройке мы используем и для получения
Теперь, если мы определим опорный потенциал при , это упрощается до
Обратите внимание, что эта форма потенциала вполне пригодна для использования; оно находится в бесконечности и не определено в бесконечности, поэтому мы не можем использовать последнее в качестве ссылки.
Значение
Хотя прямой расчет потенциала может быть весьма удобным, мы только что обнаружили систему, для которой эта стратегия не работает. В таких случаях возвращение к определению потенциала с точки зрения электрического поля может предложить путь вперед.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 3.10
Чему равен потенциал на оси неоднородного кольца заряда, где плотность заряда ?
Цитаты Кандела
Контент под лицензией CC, конкретное указание авторства
- Загрузите бесплатно по адресу http://cnx.
-
Понятие электрического потенциала является одним из важных основ теории электростатики и электродинамики. Понимание его сущности является необходимым условием для дальнейшего изучения этих разделов физики.
Содержание
- 1 Что такое электрический потенциал
- 2 Свойства потенциала
- 3 Разность потенциалов
- 4 Эквипотенциальные поверхности
Что такое электрический потенциал
Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.
Здесь и далее k=((1/4)*π* ε0* ε), где ε0 — электрическая постоянная (8,85*10-12 Ф/м), а ε – диэлектрическая постоянная среды.
Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:
φ=W/q,
где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:
- эта работа будет равна убыли потенциальной энергии заряда (A=W2-W1);
- работа не зависит от траектории перемещения заряда.
В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.
Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.
Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.
Свойства потенциала
Среди важных свойств потенциала надо отметить следующие:
- если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), где r – расстояние от соответствующего заряда то рассматриваемой точки.
Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:
- p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
- r – расстояние до диполя;
- ά – угол между плечом диполя и радиус-вектором r.
Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.
Разность потенциалов
Если две точки обладают определённым потенциалом, и если они не равны, то говорят о том, что между двумя точками существует разность потенциалов. Разность потенциалов возникает между точками:
- потенциал которых определяется зарядами разных знаков;
- точкой с потенциалом от заряда любого знака и точкой с нулевым потенциалом;
- точками, имеющими потенциал равного знака, но отличающимися по модулю.
То есть, разность потенциалов не зависит от выбора системы координат. Можно провести аналогию с бассейнами с водой, расположенными на разной высоте относительно нулевой отметки (например, уровня моря).
Вода каждого бассейна имеет определенную потенциальную энергию, но если соединить два любых бассейна трубкой, то в каждой из них возникнет поток воды, расход которой определяется не только размерами трубки, но и разностью потенциальных энергий в гравитационном поле Земли (то есть, разностью высот). Абсолютное значение потенциальных энергий значения в данном случае не имеет.
Точно так же, если соединить проводником две точки с разным потенциалом, по нему потечёт электрический ток, определяемый не только сопротивлением проводника, но и разностью потенциалов (но не их абсолютным значением). Продолжая аналогию с водой, можно сказать, что вода в верхнем бассейне скоро закончится, и если не найдется той силы, которая переместит воду обратно наверх (например, насоса), то и поток очень быстро прекратится.
Так и в электрической цепи – чтобы поддерживать разность потенциалов на определенном уровне, потребуется сила, переносящая заряды (точнее, носители зарядов) к точке с наибольшим потенциалом. Такая сила называется электродвижущей силой и сокращенно обозначается ЭДС. ЭДС может носить различную природу – электрохимическую, электромагнитную и т.п.
На практике имеет значение в основном разность потенциалов между начальной и конечной точками траектории движения носителей зарядов. В этом случае эту разность называют напряжением, и оно в СИ также измеряется в вольтах. О напряжении в 1 Вольт можно говорить, если поле совершает работу в 1 Джоуль при перемещении заряда в 1 Кулон из одной точки в другую, то есть 1В=1Дж/1Кл, и Дж/Кл также может являться единицей измерения разности потенциалов.
Эквипотенциальные поверхности
Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.
Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.
Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.
И
зменение
потенциалов в электрической цепи можно
наглядно изобразить в виде потенциальной
диаграммы.
Рис. 3.
П
Рис. 3
отенциальная диаграмма представляет
собой график изменения потенциала при
обходе цепи, построенный в прямоугольной
системе координат, в которой по оси
абсцисс откладывают в определенном
масштабе сопротивления участков цепи,
а по оси ординат – потенциалы
соответствующих точек.
Пример:
Принимаем
потенциал точки 1 равным нулю V1=0.
Потенциалы точек цепи находим согласно
равенствам.
V2=V1+E1
V3=V2+IR1
V4=V3–E2
V5=V4–IR2
V6=V5+E3
V1=V6–IR3
Если
направление ЭДС совпадает с направлением
обхода, то при расчёте потенциалов точек
записывается со знаком «+», как Е1
и Е3; если не совпадает – «–», как
Е2.
Для
падений напряжений другое правило: если
ток в пассивном элементе направлении
встречно обходу контура, то падение
напряжения записывается со знаком «+»,
если совпадает по направлению, то знак
«–».
В
еличина
тока проводимости определяется
алгебраической суммой ЭДС всех источников,
делённой на полное сопротивление цепи:
Рис. 4.
Если
при расчёте результат получился
положительным, то ток совпадает с
произвольно выбранным направлением
обхода. Если же результат получился
отрицательным, то ток имеет направление
противоположное выбранному.
Строим
потенциальную диаграмму по точкам.
Так как
внутренне сопротивление ЭДС приняты
равным нулю, то при переходе через эти
элементы потенциалы изменяются скачком.
Пример:
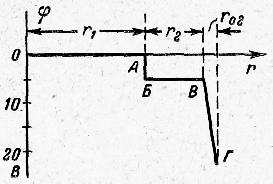
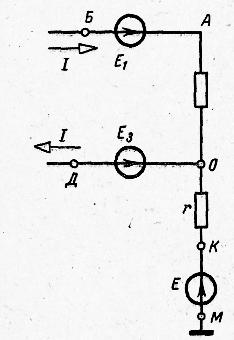
Условие задачи
В электрической цепи (рис. 5) Е1
= 5 В, Е2 = 18 В, Е3
= 8 В, r1
=500 Ом, r2 = 250
Ом, r3 = 700 Ом, r01
= 50 0м. Внутренними сопротивлениями
первого и третьего источников пренебрегаем.
Вычислить потенциалы всех точек,
обозначенных на схеме, напряжение между
точками А и Д и построить
потенциальную диаграмму.
Р
ис.
5.
Решение задачи
1. Потенциал точки электрической цепи.
Напряжение между двумя точками
электрической цепи определяется как
разность потенциалов двух точек. Это
же положение используется при определении
потенциалов точек электрической цепи.
Так, например, между точками А и О
(рис. 5), где действует некоторое напряжение
Uао
, разность
потенциалов (этих точек)
Выбором для одной (любой) точки цепи
значения равным нулю, примем для точки
О (рис. 5) потенциал
.
При этом для точки А потенциал
Таким образом, потенциал какой-либо
точки (А) цепи равен напряжению (UА0)
между этой точкой (А) и другой (О), для
которой потенциал принят равным нулю.
2. План решения задачи.
Чтобы воспользоваться выражениями для
разности потенциалов (
)
и для потенциала одной точки (
),
нужно знать ток цепи. С его вычисления
и начнем решение задачи.
Кроме того, следует для одной точки цепи
принять потенциал, равный нулю. Это уже
выполнено: выражение для
записано при условии
= 0. Точку с нулевым потенциалом (точка
О, рис. 5) иногда присоединяют к заземляющему
установку проводу или к корпусу прибора
и в последнем случае (при присоединении
к корпусу) обозначают, как показано на
рис. 5.
Имея точку с нулевым потенциалом и
напряжения всех участков цепи, определим
потенциалы точек цепи.
3. Вычисление тока.
В неразветвленной цепи с несколькими
э. д. с., ток равен отношению алгебраической
суммы всех э.д.с. к сумме всех сопротивлений,
цепи. В рассматриваемой схеме две э.
д. с. (Е1 и Е2)
действуют в одном направлении (по
направлению движения часовой стрелки)
и их сумма Е’ = Е1 + Е2
= 5 + 18 = 23 В. Одна э. д. с. Е3
= 8 В действует против направления
движения часовой стрелки, т. е. навстречу
суммарной э.д.с. Е’. Поскольку Е’ >
Е3, то направление тока
совпадает с направлением э. д. с. Е’, т.
е. ток направлен по движению часовой
стрелки (рис. 5).
4. Вычисление потенциалов точек
электрической цепи.
Для точки О (рис. 5) выбран потенциал
=
0. При этом условии, как было показано,
потенциал точки А
Потенциал точки А оказался
положительным и
.
так как ток в сопротивлении направлен
от точки большего потенциала к точке
меньшего потенциала (ток I
на рис. 5 направлен от А к О). Это правило
используется и дальше для участков БВ
и ГД, содержащих только сопротивления.
Для определения потенциала другой точки
цепи, например Б, воспользуемся уже
вычисленным потенциалом
В и известным напряжением на зажимах
участка АБ. Так как источник с э. д.
с. Е1 не имеет внутреннего
сопротивления, то потенциал его зажима
(точка Б на рис. 5) всегда (при любом
токе) меньше потенциала зажима «+» (точки
А на рис. 5) на величину э. д. с. или
равного ему напряжения UАБ
= 5 В. Поэтому
.
Зная потенциал
= 0, вычислим теперь потенциал
следующей точки В. Так как ток в
сопротивлении r2
направлен от точки В к точке Б,
то потенциал точки В больше
потенциала точки Б на величину
падения напряжения в сопротивлении r2:
.
На участке ВГ изменение потенциала
обусловлено двумя причинами: действием
э. д. с. Е2 и падением
напряжения на сопротивлении r02.
Электродвижущая сила Е2
вызывает уменьшение потенциала точки
Г (точка Г является зажимом «–»
источника, а точка Д – зажимом «+»).
Падение напряжения на внутреннем
сопротивлении источника (r02I)
вызывает увеличение потенциала точки
Г, так как ток направлен от точки Г
к точке В. Поэтому
.
Для участка ГД
.
В целях проверки расчетов найдем
потенциал точки О, используя известный
потенциал
=
8 В и учитывая, что
(см.
направление стрелки э. д. с. Е3
на рис. 5):
Если бы мы обходили цепь в обратном
направлении, т. е. двигались по направлению
тока в цепи, то на всех внешних и внутренних
сопротивлениях потенциалы увеличивались
бы на величину падения напряжения.
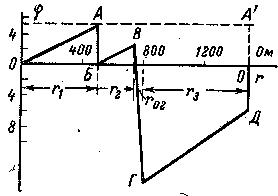
5. Построение потенциальной диаграммы.
По полученным значениям потенциалов
различных точек цепи построим потенциальную
диаграмму (рис.6).
По оси х или r
откладываются величины сопротивлений
всех участков (r1
r2 ,
r02 , r3).
Они расположены одно за другим в той
же последовательности, как и в рассмотренной
цепи (рис. 6). Участок цепи АБ (рис.
6), сопротивление которого равно нулю,
изображается на оси r
(рис.6) точкой.
Так как ось r представляет
собой как бы линейную развертку
сопротивлений замкнутого контура, то
в начале и в конце на оси r
оказывается одна и та же точка О.
Рис.
6.
По оси у или
отложены величины потенциалов точек с
учетом их знака: положительные потенциалы
вверх, а отрицательные вниз от оси г.
Рис. 6 . Потенциальная диаграмма
цепи по рис..5 .
Рассмотрим построение диаграммы
для нескольких участков цепи. Так,
например, для участка ОА были получены
потенциалы крайних точек
= 0 и
=
5 В.
Это означает, что на участке ОА (рис.
5) потенциал возрастает от 0 до 5В, это
изображено линией ОА на рис. 5.
На участке АБ, где сопротивление
равно нулю, линия потенциала (рис.5)
параллельна оси φ. Участок БВ цепи
аналогичен участку ОА, так как и тот
и другой содержат только сопротивления.
Если учитывать, что по их сопротивлениям
(r1 и r2)
проходит один и тот же ток I,
то линии ОА и БВ (рис. 5) параллельны.
Так же построены другие отрезки
потенциальной диаграммы.
6. Вычисление напряжения Uад
.
При помощи потенциальной диаграммы или
величин потенциалов точек цепи легко
определить напряжение между заданными
точками. Так, например,
.
Это же напряжение можно определить
графически, как показано на диаграмме
(рис. 6, отрезок АД).
Дополнительные вопросы к задаче
-
Как повлияет на вид потенциальной
диаграммы выбор другой точки с нулевым
потенциалом?
Разности потенциалов (напряжения) на
участках цепи не изменятся, так как
определяются только величинами э. д.
с., сопротивлений и тока (не зависят от
выбора точки нулевого потенциала).
Действительно, если принять
=
0 (рис. 7), что равносильно перемещению
оси г в точку А (рис. 7, пунктирная
прямая АА’), то потенциалы всех точек
уменьшатся на
= 5 В, а разности потенциалов останутся
прежними. Итак, выбор другой точки
нулевого потенциала проводник перемещению
оси r.
-
Можно ли выбрать потенциал, равный нулю
(заземлить), одновременно у нескольких
точек цепи?
В общем случае потенциал только одной
точки можно выбрать любым, в частности
равным нулю (заземлить).
В нашем случае можно, кроме точки О,
также заземлить точку Б, не нарушив
режим цепи, так как потенциал
=
0. При равных потенциалах точек Б
и О между ними отсутствует напряжение,
а следовательно, не будет тока в корпусе
прибора или в земле.
3. Изменится ли режим цепи, если замкнуть
проводником точки О и Б (рис.5 )?
Так как потенциалы точек О и Б
равны, то между этими точками напряжение
UОБ = 0 и
в проводнике ОБ тока не будет.
Следовательно, проводник ОБ не
внесет никаких изменений в режим работы
цепи.
Полученный результат можно объяснить
иначе. После включения проводника ОБ
цепь (рис.5) становится двухконтурной.
Токи внешних ветвей правого и левого
контура равны (в этом читатель может
легко убедиться самостоятельно) и
одинаково направлены относительно
узловых точек О и Б. При этом ток
в ветви ОБ (рис.5) равен нулю (1-й закон
Кирхгофа).
4. Как вычислить потенциалы при разомкнутом
ключе?
При разомкнутом ключе К, (рис.5) ток
I = 0. При этом имеем
два незамкнутых участка цепи: ОАБВГ
и ОДГ’. Принимая
,
получаем для первого участка:

Вычислим потенциалы участка ОДГ
(рис. 5):
Рис.
7.
По полученным данным на рис. 7 построена
потенциальная диаграмма участка ОАБВГ.
Аналогично можно построить потенциальную
диаграмму другой ветви (ОДГ). Диаграммы
этих участков независимы друг от друга.
Результаты вычислений показывают, что
изменение потенциалов разомкнутой цепи
происходит только в местах где включены
источники.
Рис.
8.
5. Как повлияет диаграмма разомкнутой
цепи.
На потенциалы цепи (рис. 
между точкой О и корпусом участка ОМ?
Учитывая, что в незамкнутом участке
цепи ОМ (рис. 
э. д. с. Е = 10 В, а потенциал φМ
= 0, получаем:
При расчете потенциалов замкнутого
контура ОАБДО (рис. 
=
10 В вместо нуля. В остальном порядок
расчета ничем не отличается от
рассмотренного в задаче. Потенциалы
всех точек увеличатся на 10 В.
6. Как используются на практике
потенциальные диаграммы?
Ко многим электронным приборам,
используемым в радиотехнике, автоматике,
технике связи, придаются таблицы
потенциалов, которые облегчают их ремонт
и наладку. Такими таблицами, в частности,
снабжается большинство электронных
устройств, используемых в быту.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
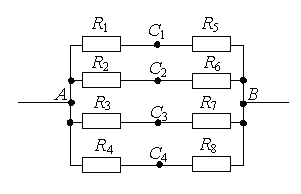
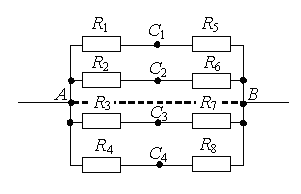
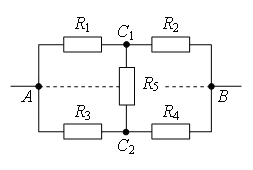
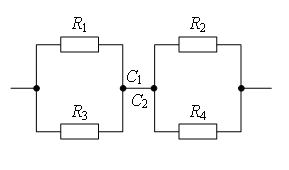
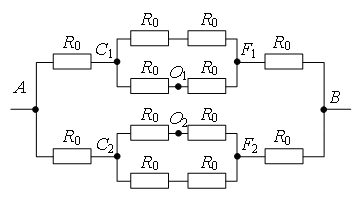
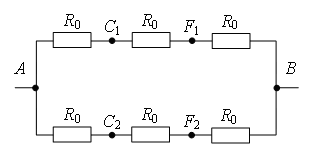
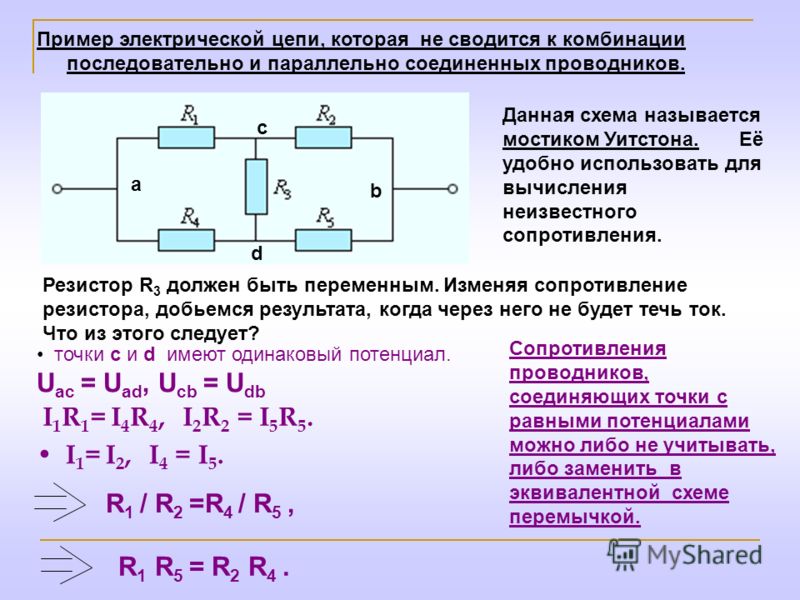
В литературе описано несколько методов преобразования электрических цепей [1; 2; 3]. В этих статьях описаны и методы упрощения схем, имеющих точки равного потенциала. Но при решении подобных задач авторы обычно пишут так: «Из симметрии ветвей цепи видно, что точки В и D имеют равные потенциалы» [2], хотя эта видимость не совсем очевидна.
Рассмотрим способы нахождения точек одинакового потенциала более подробно. Пусть нам дана электрическая цепь, состоящая из сопротивлений R1, R2, …, R8 (рис. 1 а). Проведем через точки подключения цепи прямую АВ (рис. 1 б).
1 способ. Если схема содержит проводники с одинаковым сопротивлением, расположенные симметрично относительно определенной оси или плоскости, то концы этих проводников имеют одинаковый потенциал. При этом точки будут симметричными относительно прямой АВ, если равны сопротивления участков цепи между данными точками и любыми точками этой прямой.
Используя этой признак, можно сделать вывод, что точки С1 и С2 (рис. 1 б) будут симметричны относительно прямой АВ, если R1 = R2 (сопротивления между точкой А и С1 и между точкой А и С2 равны) и R5 = R6 (сопротивления между точкой В и С1 и между точкой В и С2 равны). Аналогично, точки С3 и С4 будут симметричны относительно прямой АВ, если R3 = R4 и R7 = R8.
а.
б.
Рис. 1.
2 способ. Точки имеют одинаковый потенциал, если равны отношения сопротивлений между данными точками и точками подключения.
Например, точки С1 и С2 (рис. 1 а) имеют одинаковый потенциал, если . Аналогично, точки С3 и С4 имеют одинаковый потенциал, если
.
Покажем на примерах, как можно использовать эти способы для преобразования электрических цепей.
Метод объединения равнопотенциальных узлов:точки с одинаковыми потенциалами можно соединять в узлы.
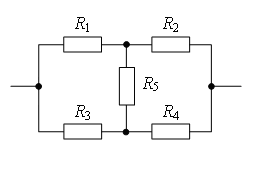
Пример 1. Определите сопротивление электрической цепи (рис. 2), если: а) R1 = R3 = 2R, R2 = R4 = R, R5 = 3R; б) R1 = R4 = 2R, R2 = 4R, R3 = R, R5 = 5R.
Рис. 2.
а) Если провести через точки подключения прямую АВ (рис. 3 а), то равны сопротивления участков АС1 и АС2 (R1 = R3), и равны сопротивления участков ВС1 и ВС2 (R2 = R4). Следовательно, точки С1 и С2 симметричны относительно прямой АВ и имеют равные потенциалы.
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 3, б). Резисторы R1 и R3 соединены параллельно, и резисторы R2 и R4 – параллельно, участки 1/3 и 2/4 последовательно. Следовательно,
б) Если провести прямую АВ (рис. 3 а), то сопротивления участков АС1 и АС2 не равны , следовательно, точки С1 и С2 не симметричны относительно прямой АВ. НО точки С1 и С2имеют равные потенциалы, т.к.
.
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 3 б). Резисторы R1 и R3 соединены параллельно, и резисторы R2 и R4 – параллельно, участки 1/3 и 2/4 последовательно. Следовательно,
а
б
Рис. 3.
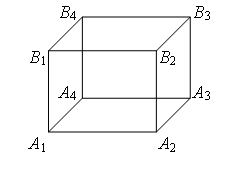
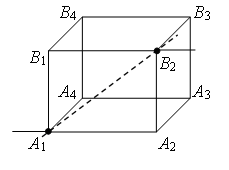
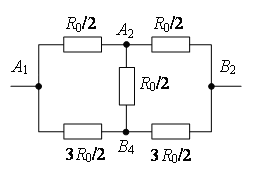
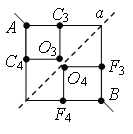
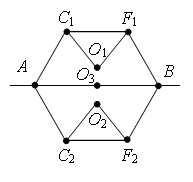
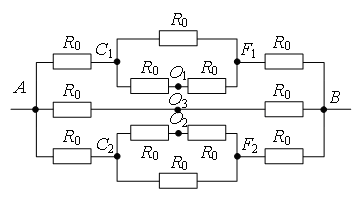
Пример 2. Найдите сопротивление проволочного куба между точками А1 и В3 (рис. 4). Сопротивление каждого ребра R0.
Рис. 4.
Рис. 5.
Проведем через точки подключения прямую А1В3 (рис. 5). Равны сопротивления (равны длины – ребра) участков А1В1, А1А2 и А1А4, и равны сопротивления (равны длины – диагонали) участков В3В1, В3А2 и В3А4. Следовательно точки В1, А2 и А4 симметричны относительно прямой А1В3 и имеют равные потенциалы. Равны сопротивления участков А1А3, А1В2 и А1В4, и равны сопротивления участков В3А3, В3В2 и В3В4. Следовательно точки А3, В2 и В4 симметричны относительно прямой А1В3 и имеют равные потенциалы.
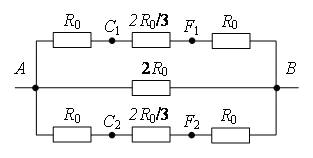
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 6). Три резистора R0 соединены параллельно между точками А1 и А2 (В1, А4), шесть резисторов R0 – параллельно между точками А2 (В1, А4) и А3 (В2, В4), три резистора R0 – параллельно между точками А3 (В2, В4) и В3, участки между этими точками соединены последовательно. Следовательно,
.
Рис. 6.
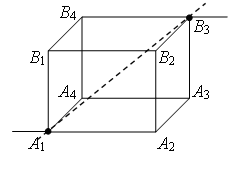
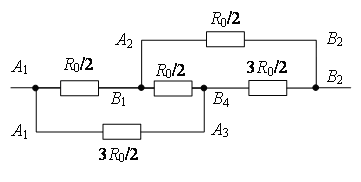
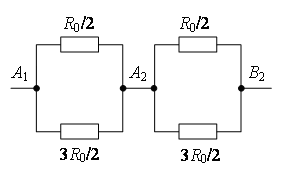
Пример 3. Найдите сопротивление проволочного куба между точками А1 и В2 (рис. 4). Сопротивление каждого ребра R0.
Проведем через точки подключения прямую А1В2 (рис. 7 а). Равны сопротивления (равны длины – ребра) участков А1В1, А1А2, и равны сопротивления (равны длины – ребра) участков В2В1, В2А2. Следовательно точки В1 и А2 симметричны относительно прямой А1В2 и имеют равные потенциалы. Равны сопротивления участков А1А3 и А1В4, и равны сопротивления участков В2А3 и В2В4. Следовательно, точки А3 и В4А1 симметричны относительно прямой В2 и имеют равные потенциалы.
Точки с одинаковыми потенциалами можно соединять в узлы (рис. 7 б). Используя рекуррентный метод, схему можно упростить (рис. 7 в или г).
Точки А2 и В4имеют равные потенциалы, т.к. . Точки с одинаковыми потенциалами можно соединять в узлы (рис. 7 д). Резисторы на участке А1А2 соединены параллельно, и резисторы на участке А2В2 – параллельно, а эти участки соединены последовательно. Следовательно,
а
б
в
г
д
Рис. 7.
Если возможно объединение двух равнопотенциальных узлов, то возможен и обратный переход.
Метод разделения узлов: узел схемы можно разделить на два или несколько узлов, если получившиеся при этом узлы имеют одинаковые потенциалы.
Обязательным условием при этом является проверка получившихся при разделении узлов на равенство потенциалов (симметричность или пропорциональность сопротивлений).
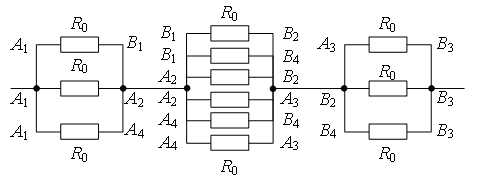
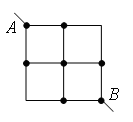
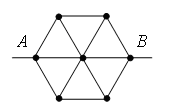
Пример 4. Найдите сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. 
Рис. 8.
Разделим узел в середине каркаса на два узла О1 и О2 так, как показано на рис. 9 а. Это можно сделать, так как точки О1 и О2 имеют равные потенциалы: равны сопротивления участков AO1, AO2, и равны сопротивления участков BO1, BO2. Перерисуем схему в стандартный вид (рис. 9 б). Используя рекуррентный метод, схему можно упростить (рис. 9 в), т.к. сопротивление участка C1F1 равно , аналогично
. Тогда общее сопротивление цепи равно
.
Обратите внимание. С точки зрения геометрии точки О3 и О4 симметричны относительно прямой а (рис. 9 г), но потенциалы этих точек не равны, т.к. сопротивления участков АО3 и АО4 не равны, а отношения сопротивлений участков АО3 и АО4 не равны отношению сопротивлений участков ВО3 и ВО4.
а
б
в
г
Рис. 9.
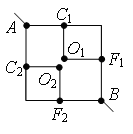
Пример 5. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. 10) сопротивлением R0 каждый.
Рис. 10.
Разделим узел в середине каркаса на три узла О1, О2 и О3 так, как показано на рис. 11 а. Это можно сделать, так как точки О1, О2 и О3 имеют равные потенциалы: равны сопротивления участков AO1 и BO1, участков AO2 и BO2, и участков AO3 и BO3, следовательно, отношения сопротивления этих участков равны.
Перерисуем схему в стандартный вид (рис. 11, б). Используя рекуррентный метод, схему можно упростить (рис. 11 в), т.к. сопротивление участка C1F1 равно , аналогично
, сопротивление
. Тогда общее сопротивление цепи равно
а
б
в
Рис. 11.
Литература
- Зильберман А. Расчет электрических цепей // Квант. – 1988. – № 8. – С. 30-34.
- Петросян В.Г., Долгополова Л.В., Лихицкая И.В. Методы расчета резисторных схем постоянного тока // Физика. – 2002. – № 14, 18, 22.
- Хацет А. Методы расчета эквивалентных сопротивлений // Квант. – 1972. – № 2. – С. 54-59.



 Электростатический потенциал в точке из-за положительного заряда положителен. Если заряд отрицательный, электрический потенциал также отрицателен.
Электростатический потенциал в точке из-за положительного заряда положителен. Если заряд отрицательный, электрический потенциал также отрицателен. 
 Кроме того, сферические распределения заряда (например, заряд на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть.
Кроме того, сферические распределения заряда (например, заряд на металлическом шаре) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть.  Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов, принимая во внимание величину и направление. Это согласуется с тем фактом, что тесно связано с энергией, скаляром, тогда как тесно связано с силой, вектором.
Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля в виде векторов, принимая во внимание величину и направление. Это согласуется с тем фактом, что тесно связано с энергией, скаляром, тогда как тесно связано с силой, вектором.  И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось. 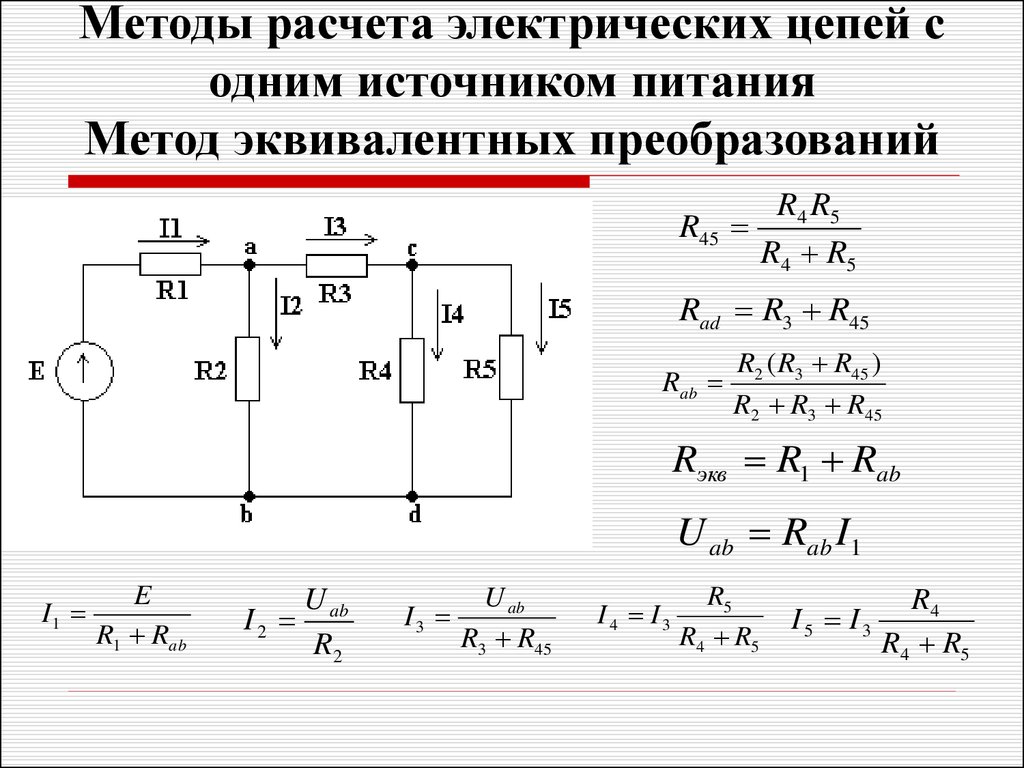 У нас есть еще одно указание на то, что трудно хранить изолированные заряды.
У нас есть еще одно указание на то, что трудно хранить изолированные заряды.  Пусть — электрические потенциалы при , создаваемые зарядами соответственно. Тогда суммарный электрический потенциал в этой точке равен сумме этих отдельных электрических потенциалов. Это легко показать, рассчитав потенциальную энергию пробного заряда, когда вы перенесете пробный заряд из точки отсчета на бесконечности в точку:
Пусть — электрические потенциалы при , создаваемые зарядами соответственно. Тогда суммарный электрический потенциал в этой точке равен сумме этих отдельных электрических потенциалов. Это легко показать, рассчитав потенциальную энергию пробного заряда, когда вы перенесете пробный заряд из точки отсчета на бесконечности в точку: 
 3.3 Общая схема электрического диполя и обозначения расстояний от отдельных зарядов до точки в пространстве.
3.3 Общая схема электрического диполя и обозначения расстояний от отдельных зарядов до точки в пространстве.
 3.3)
3.3)  Как мы видели в разделе «Электрические заряды и поля», бесконечно малые заряды равны
Как мы видели в разделе «Электрические заряды и поля», бесконечно малые заряды равны 
 Найти электрический потенциал в точке на оси, проходящей через центр кольца.
Найти электрический потенциал в точке на оси, проходящей через центр кольца.  Найти электрический потенциал в любой точке оси, проходящей через центр диска.
Найти электрический потенциал в любой точке оси, проходящей через центр диска.  Часто плотность заряда зависит от , и тогда последний интеграл будет давать разные результаты.
Часто плотность заряда зависит от , и тогда последний интеграл будет давать разные результаты.