Как найти потенциал поля созданного диполем

Потенциал электрического диполя

Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.

Два равных по величине и противоположных по знаку точечных заряда Q, находящиеся на расстоянии r друг от друга, называются электрическим диполем. Силовые линии и эквипотенциальные поверхности диполя показаны в предыдущей публикации на рис. 24.3.
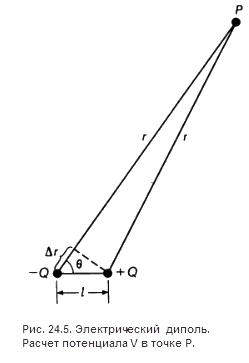
Рассчитаем электрический потенциал, создаваемый диполем в произвольной точке Р (рис. 24.5). Потенциал V представляет собой сумму потенциалов, создаваемых каждым из зарядов:

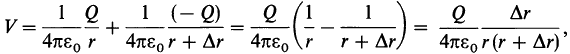
где r — расстояние от точки Р до положительного заряда, а r + Δr — до отрицательного заряда. Выражение упростится, если рассматривать точки, расстояние которых до диполя гораздо больше расстояния между зарядами, когда r значительно больше l . Как видно из рисунка, в этом случае Δr ≈ lcosθ;

тогда r будет значительно больше Δr = lcosθ, и в знаменателе величиной Δr можно пренебречь по сравнению с r. Такого рода приближения часто оказываются полезными и позволяют получить простое выражение для потенциала

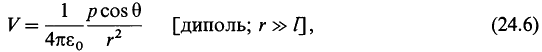
где р = Ql — дипольный момент. При 0° < θ < 90° потенциал V положителен, при 90° < 0 < 180° потенциал
отрицателен (поскольку отрицательно значение cosθ). Это разумно, поскольку в первом случае точка Р ближе к положительному заряду, а во втором-к отрицательному. При 0 = 90° потенциал равен нулю (cos 90° = 0) в соответствии с результатом примера 24.4. Из (24.6) мы видим, что потенциал убывает как квадрат расстояния до диполя, в то время как потенциал точечного заряда убывает как первая степень расстояния [см. (24.5)].
Это неудивительно: на больших расстояниях от диполя заряды кажутся столь близкими друг к другу, что взаимно нейтрализуются.

Во многих молекулах, в целом электрически нейтральных, электроны проводят больше времени у одного атома, чем у другого, что эквивалентно разделению зарядов. Такие молекулы обладают дипольным моментом и называются полярными.

Зная напряженность электрического поля, создаваемого данным распределением зарядов, можно рассчитать разность потенциалов между любыми двумя точками, пользуясь формулой (24.4). Но нередко поле Е неизвестно и его сложно рассчитать. Потенциал любого распределения
зарядов можно получить иным и часто более простым способом, вычисляя потенциалы, создаваемые каждым точечным зарядом
и затем суммируя их.
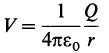
Если имеется n точечных зарядов, то потенциал в некоторой точке c равен

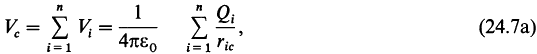
где r_ic — расстояние от i-го заряда Q_i до точки c.
Такой подход использовался в примере 24.4 Джанколи для случая диполя (разд. 24.6). Если распределение зарядов можно считать непрерывным, тогда:

где r — расстояние от элемента заряда dq до точки, в которой определяется V.

Альтернативные статьи:
Постоянный ток, Переменный ток.

Диполь
есть система, состоящая из двух равных
по модулю и противоположных по знаку
зарядов. Вектор I,
проведенный от отрицательного к
положительному заряду, называется
плечом диполя.

Электрический
момент диполя

,

где
– заряд диполя.

Электрический
дипольный момент молекулы принято
выражать в единицах атомного масштаба
– дебай (D) = 3,33∙10^-30Кл∙м.

Диполь
называется точечным, если расстояние
rот центра диполя до
точки, в которой рассматривается действие
диполя, много больше плеча диполя.

Напряженность
поля точечного диполя:

а)
на оси диполя

,
или

;

б)
на перпендикуляре к оси диполя

,
или

;

в)
в общем случае

,
или

,

где
─ угол между радиусом-векторомrи электрическим дипольным моментомр
(рис. 2.1).

Потенциал поля диполя

.

Потенциальная энергия
диполя в электростатическом поле

.

Механический момент,
действующий на диполь с электрическим
дипольным моментом
,
помещенный в однородное электрическое
поле с напряженностью,

или

,

где
– угол между направлением векторови.

Сила F,
действующая на диполь в неоднородном
электростатическом поле, обладающем
осевой (вдоль осих)
симметрией,

,

где
─ величина, характеризующая степень
неоднородности электростатического
поля вдоль оси х;– угол между векторамии.

Примеры решения задач

Пример
1.
Диполь с электрическим моментом
находится в однородном электрическом
поле напряженностью.
Вектор электрического моментасоставляет уголс направлением силовых линий поля.
Определить работуA
внешних сил, совершенную при повороте
диполя на угол
.

Решение.
Из исходного положения
(рис. 2.2, а)
диполь можно повернуть на угол
,
вращая его по часовой стрелкедо
угла
(рис. 2.2, б),
или
против часовой стрелки до угла
(рис. 2.2,в).

В
первом случае диполь будет поворачиваться
под действием сил поля. Следовательно,
работа внешних сил при этом отрицательна.
Во втором случае поворот может быть
произведен только под действием внешних
сил и работа внешних сил при этом
положительна.

Работу,
совершаемую при повороте диполя, можно
вычислить двумя способами: 1) непосредственно
интегрированием выражения элементарной
работы; 2) с помощью соотношения между
работой и изменением потенциальной
энергии диполя в электрическом поле.

а
б
в

Рис.
2.2

1-й
способ. Элементарная работа при
повороте диполя на угол:

,

а
полная работа при повороте на угол от
до:

.

Произведя
интегрирование, получим

. (2.1)

Работа
внешних сил при повороте диполя по
часовой стрелке

,

против
часовой стрелки

.

2-й
способ. Работа А внешних сил связана
с изменением потенциальной энергии
соотношением

,

где

─ потенциальные энергии системы
соответственно в начальном и конечном
состояниях. Так как потенциальная
энергия диполя в электрическом поле
выражается формулой,то

, (2.2)

что
совпадает с формулой (2.1), полученной
первым способом.

Пример
2.Три точечных заряда
,
,
,
образуют электрически нейтральную
систему, причем
.
Заряды расположены в вершинах
равностороннего треугольника. Определить
максимальные значения напряженностии потенциалаполя, создаваемого этой системой зарядов,
на расстоянииот центра треугольника, длина стороны
которого.

Решение.Нейтральную систему, состоящую из трех
точечных зарядов, можно представить в
виде диполя. Действительно, «центр
тяжести» зарядов
и
лежит на середине отрезка прямой,
соединяющей эти заряды (рис. 2.3). В этой
точке можно считать сосредоточенным
заряд.
А так как система зарядов нейтральная
(),
то

.

Так
как расстояние между зарядами Q₃
и Q
много меньше расстояния r
(рис. 2.4), то систему этих двух зарядов
можно считать диполем с электрическим
моментом,где

─
плечо диполя. Электрическиймомент
диполя

.

Тот
же результат можно получить другим
способом. Систему из трех зарядов
представим как два диполя с электрическими
моментами (рис. 2.5), равными по модулю:;.
Электрический момент системы зарядов
найдем как векторную суммуи,
и.Как
это следует из рис. 2.5, имеем.Так
как,то

,

что
совпадает с найденным ранее значением.

Напряженность
и потенциалполя диполя выражаются формулами

;

,

где─ угол между радиусом-вектороми электрическим дипольным моментом
(рис. 2.1).

Напряженность
и потенциал будут иметь максимальные
значения при
= 0, следовательно,

;

.

Так
как,то

;
.

Вычисления
дают следующие значения:

;
.

Задачи

201.
Вычислить электрический момент р диполя,
если его заряд,.
(Ответ:50
нКл∙м).

202.
Расстояние
между зарядамиидиполя равно 12 см. Найти напряженность
Е и потенциалполя, созданного диполем в точке,
удаленной накак от первого, так и от второго заряда.(Ответ:

;).

203.
Диполь с электрическим моментомобразован двумя точечными зарядамии.
Найти напряженностьE
и потенциал
электрического поля в точкеA
(рис. 2.6), находящейся на расстоянии
от центра диполя. (Ответ:

;

).

204.
Электрический момент диполя
.
Определить напряженность Е и потенциалполя, созданного в точкеA
(рис. 2.6), находящейся на расстоянии
от
центра диполя. (Ответ:;

).

205.
Определить напряженность E
и потенциал
поля, создаваемого диполем с электрическим
моментомна расстоянииот центра диполя, в направлении,
составляющем уголс вектором электрического момента.(Ответ:
;).

206.
Диполь с электрическим моментом
равномерно вращается с частотойотносительно оси, проходящей через
центр диполя и перпендикулярной его
плечу. Точка С находится на расстоянииот центра диполя и лежит в плоскости
вращения диполя. Вывести закон изменения
потенциала как функцию времени в точке
С. Принять, что в начальный момент времени
потенциал в точке С.
Построить график зависимости.
(Ответ:
;;).

207.
Диполь с электрическим моментом
равномерно вращается с угловой скоростьюотносительно оси, проходящей через
центр диполя и перпендикулярной его
плечу. Определить среднюю потенциальную
энергиюзаряда,
находящегося на расстояниии лежащего в плоскости вращения, завремя,
равное
полупериоду
(от
до).
В начальный момент времени считать.
(Ответ:).

208.
Два диполя с электрическими моментами
инаходятся на расстояниидруг от друга. Найти силу их взаимодействия,
если оси диполей лежат на одной прямой.

(Ответ:
).

209.
Два диполя с электрическими моментами
инаходятся
на расстояниидруг от друга, так что оси диполей лежат
на одной прямой. Вычислить взаимную
потенциальную энергию диполей,
соответствующую их устойчивому
равновесию. (Ответ:

).

210.
Диполь с электрическим моментомприкреплен к упругой нити (рис. 2.7). Когда
в пространстве, где находится диполь,
было создано электрическое поле
напряженностью,
перпендикулярно плечу диполя и нити,
диполь повернулся на угол.
Определить момент силы М, который
вызывает закручивание нити на 1
рад.
(Ответ:

).

211.
Диполь с электрическим моментом
прикреплен
к упругой нити (рис. 2.7). Когда в пространстве,
где находится диполь, было создано
электрическое поленапряженностью

,
перпендикулярно плечу диполя и нити,
диполь повернулся на малый угол.
Определить момент силы М, который
вызывает закручивание нити на 1
рад.
(Ответ:
).

212.
Диполь с электрическим моментом
находится в однородном электрическом
поле напряженностью.
Вектор электрического момента составляет
уголс
линиями поля. Какова потенциальная
энергия П поля? Считать,
когда вектор электрического момента
диполя перпендикулярен линиям поля.
(Ответ:
).

213.
Диполь с электрическим моментом
свободно
устанавливается в однородном электрическом
поле напряженностью.
Вычислить работу А, необходимую для
того, чтобы повернуть диполь на угол.
(Ответ:

).

214.
Диполь с электрическим моментом
свободно установился в однородном
электрическом поле напряженностью.
Определить изменение потенциальной
энергиидиполя при повороте его на угол.
(Ответ:
).

215.
Перпендикулярно плечу диполя с
электрическим моментом
возбуждено однородное электрическое
поле напряженностью.
Под действием сил поля диполь начинает
поворачиваться относительно оси,
проходящей через его центр. Найти угловую
скоростьдиполя в момент прохождения им положения
равновесия. Момент инерции диполя
относительно оси, перпендикулярной
плечу ипроходящей
через его центр.
(Ответ: ;).

216.
Диполь с электрическим моментом
свободно
установился в однородном электрическом
поле напряженностью.
Диполь повернули на малый угол и
предоставили самому себе. Определить
частоту собственных колебаний диполя
в электрическом поле. Момент инерции
диполя относительно оси, проходящей
через его центр.
(Ответ:
).

217.
Диполь с электрическим моментом
находится в неоднородном электрическом
поле. Степень неоднородности поля
характеризуется величиной,
взятой в направлении оси диполя. Вычислить
силуF,
действующую на диполь в этом направлении.
(Ответ:
).

218.
Диполь с электрическим моментом
установился вдоль силовой линии в поле
точечного зарядана расстоянииот него. Определить для этой точки
величину,
характеризующую степень неоднородности
поля в направлении силовой линии и силуF,
действующую на диполь.
(Ответ:

;
).

219.
Диполь с электрическим моментом
установился
вдоль силовой линии в поле, созданном
бесконечной прямой нитью, заряженной
бесконечной прямой нитью, заряженной
с линейной плотностьюна
расстоянииот нее. Определить в этой точке величину,
характеризующую степень неоднородности
поля в направлении силовой линии и силуF,
действующую на диполь.(Ответ:
;).

220.
Диполь с электрическим моментом
образован
двумя точечными зарядамии.
Найти напряженность Е и потенциалэлектрического поля в точке В (рис. 2.6),
находящихся на расстоянииот центра диполя.
(Ответ:
;

).

221.
Электрический момент диполя
.
Определить напряженность Е и потенциалполя, созданного в точке В (рис. 3.6),
находящейся на расстоянииот центра диполя. (Ответ:
;

).

222.
Определить напряженность Е и потенциал
поля, создаваемого диполем с электрическим
моментомна расстоянииот центра диполя, в направлении,
составляющем уголс
вектором электрического момента.
(Ответ:
;).

223.
Диполь с электрическим моментом
равномерно вращается с угловой скоростьюотносительно
оси, проходящей через центр диполя и
перпендикулярной его плечу. Определить
среднюю потенциальную энергиюзаряда,
находящегося на расстояниии лежащего в плоскости вращения, в
течение времени.В
начальный момент времени считать
.
(Ответ:
).

224.
Диполь с электрическим моментом
свободно устанавливается в однородном
электрическом поле напряженностью.
Вычислить работу А, необходимую для
того, чтобы повернуть диполь на угол.
(Ответ:
).

225.
Диполь с электрическим моментом
свободно установился в однородном
электрическом поле напряженностью.
Определить изменение потенциальной
энергиидиполя при повороте его на угол.
(Ответ:

).

226.
Молекула HF
обладает электрическим моментом
.
Межъядерное расстояние
.
Найти заряд
такого диполя и объяснить, почему
найденное значениесущественно отличается от значения
элементарного заряда.
(Ответ:

).

227.
Точечный заряд
находится на расстоянииот точечного диполя с электрическим
моментом.
Определить потенциальную энергию П и
силуF
их взаимодействия в случае, когда
точечный заряд находится на оси диполя.
(Ответ:

;).

228.
Точечный заряд
находится на расстоянииот точечного диполя с электрическим
моментом.
Определить потенциальную энергию П и
силуF
их взаимодействия в случае, когда
точечный заряд находится на перпендикуляре
к оси диполя. (Ответ:
;).

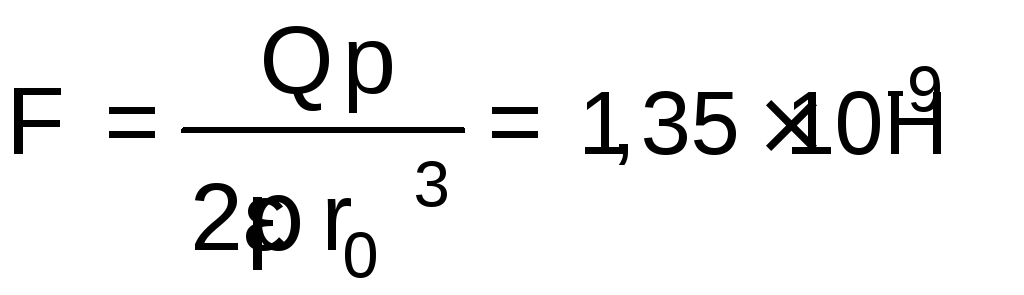
2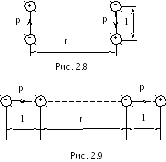29.
Два диполя (рис. 2.8) с электрическими
моментаминаходятся на расстояниидруг от друга
(─ плечо диполя). Определить потенциальную
энергию П взаимодействия диполей.
(Ответ:

).

230.
Два одинаково ориентированных диполя
(рис. 2.9) с электрическими моментами
находятся на расстояниидруг от друга
(─ плечо диполя). Определить потенциальную
энергию П и силуF
взаимодействия диполей.
(Ответ:
;).

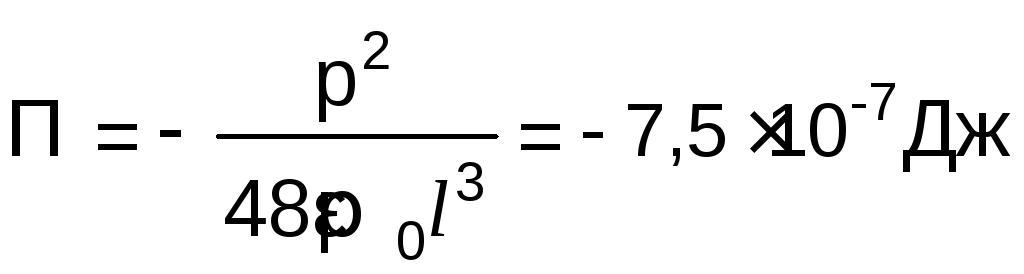
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание книги

Предыдующая страница

§9. Электрическое поле и его свойства

9.12 Электрический диполь.

Часто возникает необходимость найти характеристики электрического поля, создаваемого системой зарядов, локализованных в небольшой области пространства. Примером такой системы зарядов могут служить атомы и молекулы, состоящие из электрически заряженных ядер и электронов. Если требуется найти поле на расстояниях, которые значительно больше размеров области расположения частиц, то нет необходимости пользоваться точными, но громоздкими формулами, достаточно ограничится более простыми приближенными выражениями.

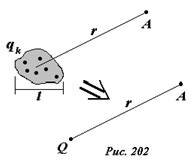
Пусть электрическое поле создается набором точечных зарядов q_k (k = 1,2…N), расположенных в пределах небольшой области пространства, характерные размеры которой обозначим l (Рис. 202). Для расчета характеристик электрического поля, в некоторой точке A, находящейся на расстоянии r, значительно превышающем l, все заряды системы можно «объединить» и рассматривать систему зарядов как точечный заряд Q, величина которого равна сумме зарядов исходной системы

(~Q = q_1 + q_2 + ldots + q_N) . (1)

Этот заряд можно мысленно расположить в любой точке области расположения системы зарядов q_k (k = 1,2…N), так как при l << r, изменение положения в пределах малой области незначительно повлияет на изменение поля в рассматриваемой точке.

В рамках такого приближения напряженность и потенциал электрического поля определяются по известным формулам

(~E = frac{Q}{4 pi varepsilon_0 r^2} ; varphi = frac{Q}{4 pi varepsilon_0 r}) . (2)

Если суммарный заряд системы равен нулю, то указной приближение является слишком грубым, приводящим к выводу об отсутствии электрического поля.

Более точное приближение можно получить, если мысленно собрать отдельно положительные и отрицательные заряды рассматриваемой системы. Если их «центры» смещены друг относительно друга, то электрическое поле такой системы может быть описано как поле двух точечных зарядов, равных по величине и противоположных по знаку, смещенных друг относительно друга. Более точную характеристику системы зарядов в этом приближении мы дадим немного позднее, после изучения свойств электрического диполя.

Электрическим диполем называется система, состоящая из двух точечных зарядов одинаковых по величине и противоположных по знаку, расположенных на малом расстоянии друг от друга.

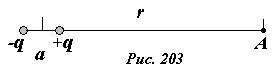
Рассчитаем характеристики электрического поля, создаваемого диполем, состоящего из двух точечных зарядов +q и —q, расположенных на расстоянии a друг от друга (Рис. 203). Сначала найдем потенциал и напряженность электрического поля диполя на его оси, то есть на прямой, проходящей через оба заряда. Пусть точка A, находится на расстоянии r от центра диполя, причем будем считать, что r >> a. В соответствии с принципом суперпозиции потенциал поля в данной точке описывается выражением

(~varphi = frac{q}{4 pi varepsilon_0 left (r — frac{a}{2}right )} — frac{q}{4 pi varepsilon_0 left (r + frac{a}{2}right )} = frac{q}{4 pi varepsilon_0} frac{a}{r^2 — left (frac{a}{2}right )^2} approx frac{qa}{4 pi varepsilon_0 r^2}) . (3)

На последнем шаге мы пренебрегли вторым малой величиной (~left (frac{a}{2}right )^2) по сравнению с r² . Величину вектора напряженности электрического поля также можно вычислить на основании принципа суперпозиции

(~E = frac{q}{4 pi varepsilon_0 left (r — frac{a}{2}right )^2} — frac{q}{4 pi varepsilon_0 left (r + frac{a}{2}right )^2} = frac{q}{4 pi varepsilon_0} frac{2ar}{left (r^2 — left (frac{a}{2}right )^2right )^2} approx frac{qa}{2 pi varepsilon_0 r^3}) . (4)

Напряженность поля можно вычислить, используя соотношение между потенциалом и напряженностью поля (~E_x = -frac{Delta varphi}{Delta x}) . В данном случае вектор напряженности направлен вдоль оси диполя, поэтому его модуль рассчитывается следующим образом

(~E = -frac{Delta varphi}{Delta r} = -frac{varphi(r + Delta r) — varphi(r)}{Delta r} = frac{qa}{4 pi varepsilon_0} frac{1}{Delta r} left ( frac{1}{(r + Delta r)^2} — frac{1}{r^2} right ) = -frac{qa}{4 pi varepsilon_0} frac{1}{Delta r} frac{-2rDelta r -(Delta r)^2}{r^2(r + Delta r)^2} approx frac{qa}{2 pi varepsilon_0 r^3}) . (5)

Обратите внимание, что поле диполя ослабевает быстрее поля точечного заряда, так потенциал поля диполя убывает обратно пропорционально квадрату расстояния, а напряженность поля — обратно пропорционально кубу расстояния.

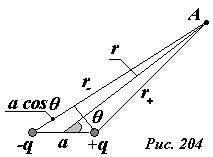
Аналогичным, но более громоздким, способом можно найти потенциал и напряженность поля диполя в произвольной точке, положение которой определим с помощью полярных координат: расстояния до центра диполя r и угла θ (Рис. 204). По принципу суперпозиции потенциал поля в точке A равен

(~varphi = frac{q}{4 pi varepsilon_0 r_+} — frac{q}{4 pi varepsilon_0 r_-} = frac{q}{4 pi varepsilon_0} frac{r_- — r_+}{r_-r_+}) . (6)

Учитывая, что r >> a, формулу (6) можно упростить с помощью приближений (~r_-r_+ approx r^2 ; r_- — r_+ approx a cos theta) , в этом случае получаем

(~varphi = frac{qa cos theta}{4 pi varepsilon_0 r^2}) .

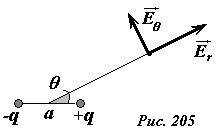
Вектор напряженности электрического поля (~vec E) удобно разложить на две составляющие: радиальную (~vec E_r) , направленную вдоль прямой, соединяющей данную точку с центром диполя, и перпендикулярную ей (~vec E_{theta}) (рис. 205). При таком разложении каждая компонента направлена вдоль направления изменения каждой из координат точки наблюдения, поэтому может быть найдена из соотношения, связывающего напряженность поля и изменение потенциала.

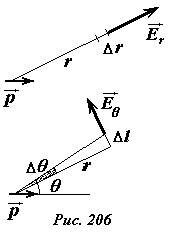
Для того, чтобы найти компоненты вектора напряженности поля, запишем отношение изменения потенциала, при смещении точки наблюдения в направлении соответствующих векторов (Рис. 206).

Радиальная составляющая тогда выразится соотношением

(~E_r = -frac{Delta varphi}{Delta r} = -frac{varphi(r + Delta r) — varphi(r)}{Delta r} = frac{qa cos theta}{4 pi varepsilon_0} frac{1}{Delta r} left ( frac{1}{(r + Delta r)^2} — frac{1}{r^2} right ) = frac{qa cos theta}{4 pi varepsilon_0} frac{1}{Delta r} frac{2rDelta r + (Delta r)^2}{r^2(r + Delta r)^2} approx frac{qa cos theta}{2 pi varepsilon_0 r^3}) .

Для расчета перпендикулярной составляющей следует учесть, что величина малого смещения в перпендикулярном направлении выражается через изменение угла следующим образом (~Delta l = r Delta theta) . Поэтому величина этой компоненты поля равна

(~E_{theta} = -frac{Delta varphi}{r Delta theta} = -frac{varphi(theta + Delta theta) — varphi(theta)}{r Delta theta} = -frac{qa}{4 pi varepsilon_0 r^3} frac{cos (theta + Delta theta) — cos theta}{Delta theta} = frac{qa sin theta}{4 pi varepsilon_0 r^3} frac{sin Delta theta}{Delta theta} approx frac{qa sin theta}{4 pi varepsilon_0 r^3}) .

При выводе последнего соотношения использована тригонометрическая формула для разности косинусов и приближенное соотношение, справедливое при малых Δθ : sin Δθ ≈ Δθ.

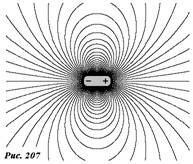
Полученные соотношения полностью определяют поле диполя в произвольной точке и позволяют построить картину силовых линий этого поля (рис. 207).

Теперь обратим внимание, что во всех формулах, определяющих потенциал и напряженность поля диполя, фигурирует только произведение величины одного из зарядов диполя на расстояние между зарядами. Поэтому именно это произведение является полной характеристикой электрических свойств и называется дипольным моментом системы. Так как диполь является системой двух точечных зарядов, то он обладает осевой симметрией, осью которой является прямая, проходящая через заряды. Следовательно, для задания полной характеристики диполя следует указать и ориентацию оси диполя. Проще всего это сделать, задавая вектор дипольного момента, величина которого равна дипольному моменту, а направление совпадает с осью диполя

(~vec p = q vec a) , (7)

где (~vec a) — вектор, соединяющий отрицательный и положительный заряды диполя ^[1]. Такая характеристика диполя весьма удобна и позволяет во многих случая упрощать формулы, придавая им векторный вид. Так, например, потенциал поля диполя в произвольной точке, описываемый формулой (6), может быть записан в векторной форме

(~varphi = frac{vec p cdot vec r}{4 pi varepsilon_0 r^3}) . (8)

После введения векторной характеристики диполя, его дипольного момента, появляется возможность использовать еще одну упрощающую модель – точечный диполь: систему зарядов, геометрическими размерами которой можно пренебречь, но обладающей дипольным моментом ^[2].

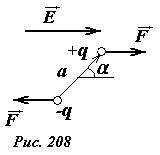
Рассмотрим поведение диполя в электрическом поле. Пусть два точечных заряда, находящиеся на фиксированном расстоянии друг от друга, помещены в однородное электрическое поле. Со стороны поля на заряды действуют силы F = ±qE, равные по величине и противоположные по направлению. Суммарная сила, действующая на диполь равна нулю, однако эти силы приложены к различным точкам, поэтому суммарный момент этих отличен от нуля, а равен

(~M = Fa sin alpha = qEa sin alpha = pE sin alpha) , (9)

где α — угол меду вектором напряженности поля и вектором дипольного момента. Наличие момента силы, приводит к тому, что дипольный момент системы стремится повернуться по направлению вектора напряженности электрического поля.

Обратите внимание, что и момент силы, действующий на диполь, полностью определяется его дипольным моментом. Как мы показали ранее, если сумма сил, действующих на систему, равна нулю, то суммарный момент сил не зависит от оси, относительно которой этот момент рассчитывается. Положению равновесия диполя соответствуют как направление по полю α = 0, так и против него α = π, однако легко показать, что первое положение равновесия устойчиво, а второе нет.

Если электрический диполь находится в неоднородном электрическом поле, то силы, действующие на заряды диполя различны, поэтому результирующая сила отлична от нуля.

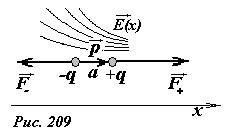
Для упрощения, будем считать, что ось диполя совпадает с направлением вектора напряженности внешнего электрического поля. Совместим ось системы координат с направлением вектора напряженности (Рис. 209). Результирующая сила, действующая на диполь, равна векторной сумме сил, действующих на заряды диполя,

(~F = F_+ — F_- = q(E(x+a) — E(x)) = qa frac{Delta E}{Delta x}) . (10)

Здесь E(x) — напряженность поля в точке расположения отрицательного заряда, E(x + a) — напряженность в точке положительного заряда. Так как расстояние между зарядами мало, разность напряженностей представлена как произведение скорости изменения напряженности на размер диполя. Таким образом, в неоднородном поле, на диполь действует сила, направлена в сторону возрастания поля, или диполь втягивается в область более сильного поля.

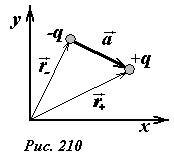
В заключение вернемся к строгому определению дипольного момента произвольной системы зарядов. Вектор дипольного момента, системы, состоящей из двух зарядов (Рис. 210), может быть записан в виде

(~vec p = q vec a = q(vec r_+ — vec r_-) = (+q)vec r_+ — (-q)vec r_-) .

Если теперь пронумеровать заряды, то эта формула приобретает вид

(~vec p = (+q)vec r_+ — (-q)vec r_- = q_1 vec r_1 + q_2 vec r_2) ,

где величины зарядов понимаются в алгебраическом смысле, с учетом их знаков. Последняя формула допускает очевидное обобщение (обоснованием которого является принцип суперпозиции) на систему произвольного числа зарядов

(~vec p = q_1 vec r_1 + q_2 vec r_2 + q_3 vec r_3 + ldots = sum_{k} {q_k vec r_k}) . (11)

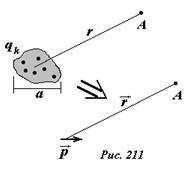
Эта формула определяет дипольный момент произвольной системы зарядов, с ее помощью произвольная система зарядов может быть заменена на точечный диполь (Рис. 211). Положение диполя внутри области расположения зарядов произвольно, естественно, если электрическое поле рассматривается на расстояниях значительно превышающих размеры системы.

Задания для самостоятельной работы.

1. Докажите, что для произвольной системы зарядов, алгебраическая сумма которых равна нулю, дипольный момент, определяемый по формуле (11), не зависит от выбора системы отсчета.
2. Определите «центры» положительных и отрицательных зарядов системы, по формулам аналогичным, формулам для координат центра масс системы. Если все положительный и все отрицательные заряды собрать в своих «центрах», то получим диполь, состоящий из двух зарядов. Покажите, что его дипольный момент совпадает с дипольным моментом, рассчитанным по формуле (11).
3. Получите двумя способами формулу, выражающую силу взаимодействия точечного диполя и точечного заряда, находящегося на оси диполя: во-первых, найдите силу, действующую на точечный заряд со стороны диполя; во-вторых, найдите силу, действующую на диполь со стороны точечного заряда; в-третьих, убедитесь, что эти силы равны по модулю и противоположны по направлению.

Примечания

1. ↑ Направление вектора дипольного момента, в принципе можно задать и противоположным, но исторически сложилось задание направления дипольного момента от отрицательного к положительному заряду. При таком определении силовые линии как бы являются продолжением вектора дипольного момента.
2. ↑ Очередная, абсурдная на первый взгляд, но удобная абстракция – материальная точка, имеющая два заряда, разнесенных в пространстве.

Следующая страница