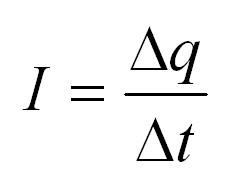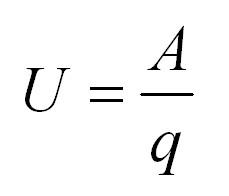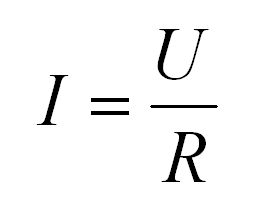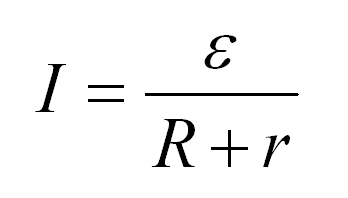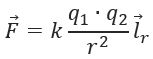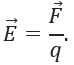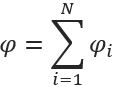Как найти потенциал через силу тока

Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.

Основные понятия закона Ома

Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.

Сила тока I

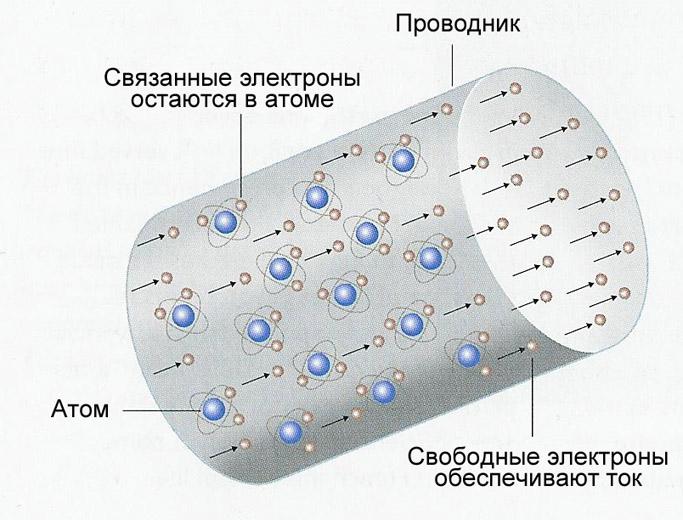
Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10^-19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.

Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах.

Напряжение U, или разность потенциалов

Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.

Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.

Сопротивление R

Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.

Формулировка и объяснение закона Ома

Закон немецкого учителя Георга Ома очень прост. Он гласит:

Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.

Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря «участок цепи» мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.

Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.

Пусть  у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.

Закон запишется в следующем виде:

Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.

Кстати, о том, что такое что такое ЭДС, читайте в нашей отдельной статье.

Как понять закон Ома?

Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.

Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе.  Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.

Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)

Сила тока прямо пропорциональна напряжению.

Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.

Сила тока обратно пропорциональна сопротивлению.

Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.

В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.

В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.

Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего студенческого сервиса. А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!

Разность потенциалов и сложение при соединение выводов нескольких источников питания

Потенциал простыми словами

Степень электризации тела характеризует величину, называемую электрическим потенциалом или просто потенциалом тела. Электризация — это процесс сообщения телу электрического заряда путем переноса с другого тела. При этом нарушается электрическая нейтральность обоих тел. Тело, заряженное положительно, станет обладать положительным потенциалом, а тело, заряженное отрицательно, — отрицательным потенциалом. Как пример, электризация эбонитовой палочки при трении о мех.

Разность потенциалов — это разность уровней электрических зарядов двух тел. Разность потенциалов также можно получить и между различными частями (точками) одного и того же тела под влиянием электростатической или электромагнитной индукции.

Электростатическая индукция — явление наведения собственного электростатического поля при действии на тело внешнего электрического поля. Явление обусловлено перераспределением зарядов внутри проводящих тел, а также поляризацией внутренних микроструктур у непроводящих тел.

Электромагнитная индукция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении магнитного поля во времени или при движении материальной среды в магнитном поле.

Далее мы будем рассматривать потенциалы только между различными частями (точками) одного и того же тела при воздействии на него магнитного поля. То есть будем анализировать разность потенциалов на выводах генератора переменного и постоянного тока.

Получение разности потенциалов на выводах генератора

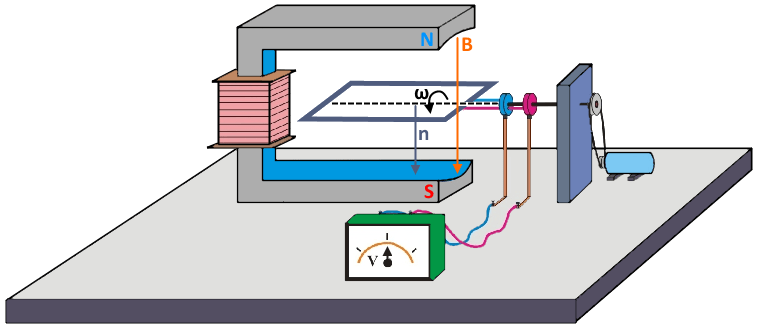
В основе практически всех генераторов тока лежит проводящая рамка, вращающаяся в магнитном поле. В этой рамке может быть много витков. Для примера упрощенно можно рассмотреть рамку, состоящую из одного витка.

При вращении рамки два ее участка постоянно пересекают силовые линии магнитного поля. При этом, когда один участок движется в одну сторону, второй движется в другую. Что происходит при этом? Под действием магнитного поля силы Лоренца перемещают электроны от одного конца (1) рамки к концу (2), потом обратно и далее уже от конца (2) к концу (1). Все это происходит за один оборот рамки. А так как рамка вращается постоянно, то на концах мы имеем переменную разность потенциалов (переменную ЭДС электромагнитной индукции).

Более подробно на данном вопросе останавливаться не будем, и далее перейдем непосредственно к основной теме — сложению и разности потенциалов.

Разность потенциалов на примере электрической цепи

Рассмотрим электрическую цепь состоящую из генератора постоянного тока, резистора (нагрузки) и соединительных проводов.

Начнем с генератора. В предыдущем пункте мы кратко рассмотрели принцип работы генератора переменного тока. Чем же отличается генератор переменного тока? Не будем углубляться в конструктивные особенности, а отметим лишь главное — на одном выводе генератора (источника) постоянного тока всегда имеется избыток электронов (отрицательный потенциал), на другом — недостаток электронов (избыток положительных зарядов, положительный потенциал).

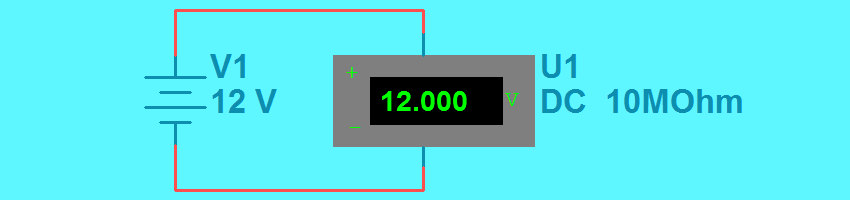
Возьмем для примера 12 вольтовый источник постоянного тока и наглядно поэкспериментируем с ним в программе Multisim:

На схеме к плюсу источника тока подключен плюс вольтметра, а к минусу источника — минус вольтметра. Вольтметр показывает напряжение между выводами источника тока. В данном случае напряжение 12 Вольт численно равно ЭДС, так как внутреннее сопротивление мы приняли равным 0 Ом. Далее мы рассмотрим пример с внутренним сопротивлением источника питания. Пока же остановимся на напряжении. Как известно, напряжение — это разность потенциалов. Если разность потенциалов 12 Вольт, то какие же потенциалы на выводах источника? Так как в источнике постоянного тока определенное количество отрицательных зарядов (электронов) скапливается на минусовом выводе, то естественно на плюсовом выводе остается такое же количество положительных зарядов. Соответственно потенциал на плюсе источника +6 Вольт, на минусе -6 Вольт, а разность потенциалов равна +6-(-6) = +12 Вольт. Почему мы отнимаем от +6? Все просто — несмотря на то, что электроны движутся от минуса к плюсу, направление тока принято брать от плюса к минусу.

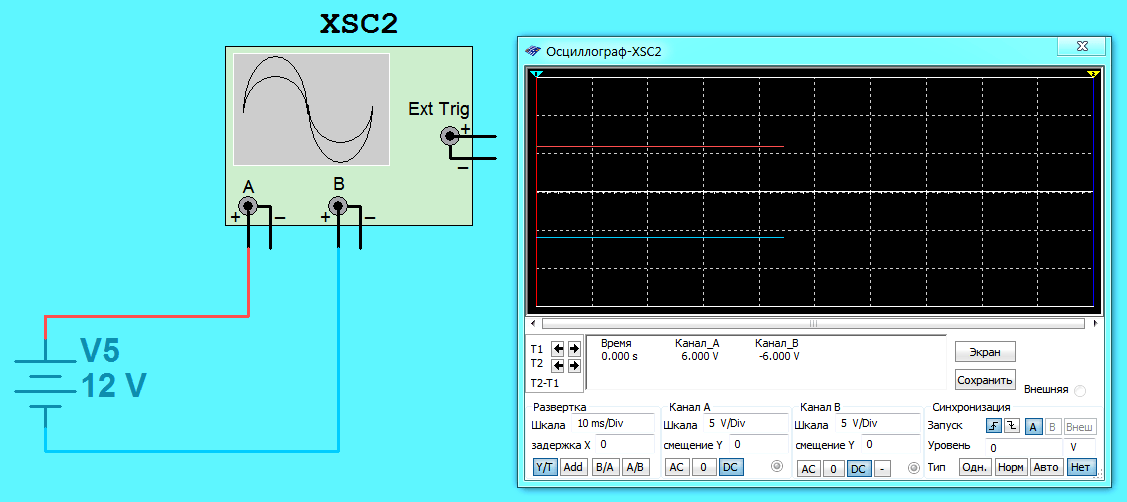
Покажем наглядно потенциалы на выводах генератора (источника) постоянного тока:

Мы подключили к плюсу источника тока канал A осциллографа, а к минусу — канал B. На экране осциллографа два графика (красная и синяя прямая), которые показывают, что потенциал на плюсовом выводе не изменяется и равен +6 Вольт, на минусовом -6 Вольт.

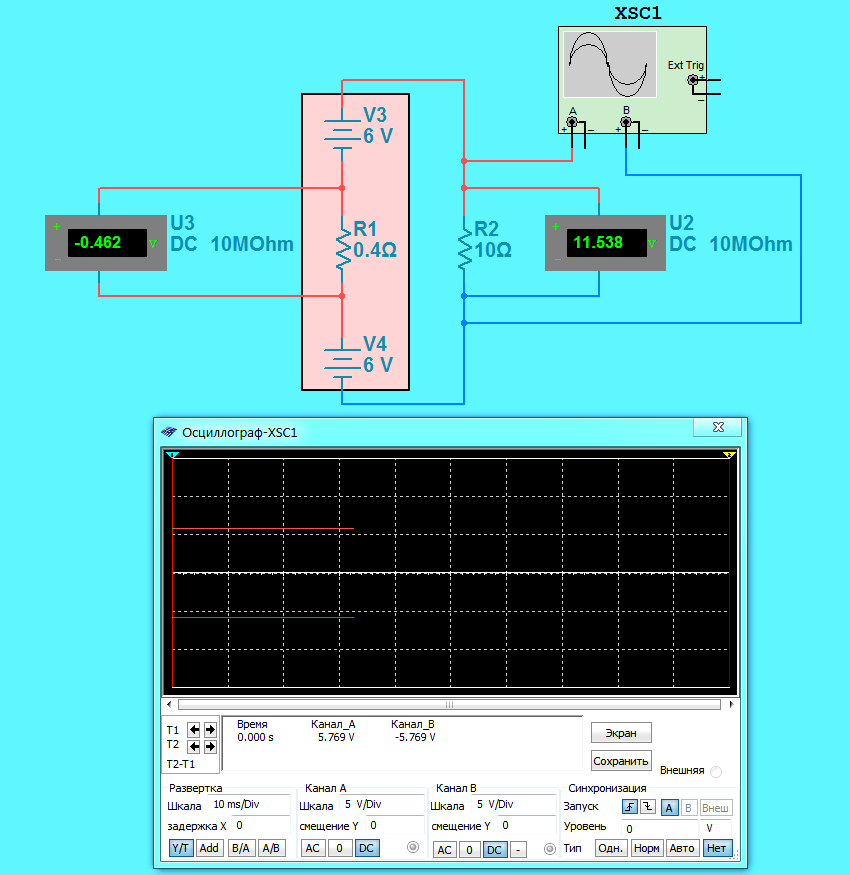
Теперь добавим в цепь резистор (нагрузку) и проанализируем распределение потенциалов на выводах источника с учетом его внутреннего сопротивления:

Как видно из схемы потенциалы на выводах источника вместо +6 и — 6 уменьшились до +5,769 и -5,769 Вольт. То есть напряжение на выводах уже не равно ЭДС. Происходит это за счет падения напряжения на внутреннем сопротивлении источника питания. В нашем случае падение напряжения равно +0,462 Вольт (на схеме оно со знаком минус, так как не соблюдена полярность подключения вольтметра). Если прибавить его к напряжению на выводах источника, то получим ЭДС источника тока: +0,462+(+5,769-(-5,769)) = 0,462+11,538 = 12 Вольт.

Остановимся чуть подробнее на этой схеме и разберемся, что произошло при добавлении в цепь нагрузки (резистора 10 Ом):

• В первую очередь, цепь замкнулась и по ней потек ток.
• В цепи находятся два последовательно соединенных резистора. Один резистор — это нагрузка во внешней цепи, второй резистор — внутреннее сопротивление источника питания (он находится во внутренней цепи и мы его как бы не видим, но он есть).
• По правилу последовательного соединения сумма внутреннего сопротивления и сопротивления нагрузки во внешней цепи дает общее сопротивление Rобщ = 0,4+10 = 10,4 Ом.
• Так как ЭДС определяется по формуле E = I×Rобщ, то нетрудно найти силу тока в цепи I = E/Rобщ = 12/10, 4 = 1,154 А.
• Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
• Зная силу тока в цепи нетрудно определить напряжения на каждом резисторе по формуле Uрез = I×Rрез. Получаем напряжение (падение напряжения) на внутреннем сопротивлении источника 0,462 Вольт и напряжение на резисторе внешней цепи 11,538 Вольт. Суммарно эти напряжения равны значению ЭДС источника тока.

Подведем итог по разности потенциалов на выводах источника постоянного тока. Любой источник (батарея, генератор) обладает некоторым внутренним сопротивлением (иногда для удобства его значением пренебрегают, то есть приравнивают его к нулю). До тех пор, пока к источнику питания не подключена внешняя нагрузка (когда цепь замыкается и по ней течет ток), разность потенциалов (напряжение) численно равно значению ЭДС. Как только цепь замыкается через нагрузку, разность потенциалов (напряжение) на выводах источника питания уже не равно ЭДС. Оно уменьшается на значение падения напряжения на внутреннем сопротивлении источника питания.

Сложение потенциалов

Теперь рассмотрим довольно интересный вопрос — сложение потенциалов при соединении выводов нескольких источников питания.

Возьмем для начала две батарейки с ЭДС 6 Вольт. Если их соединить последовательно (плюс одной батарейки с минусом другой), то ЭДС такой батареи удвоится и будет равно 12 Вольт. Потенциал в точке соединения будет 0 Вольт, а потенциалы на оставшихся выводах +6 и -6 Вольт. Это самый простой пример, так как две батарейки имеют одинаковую ЭДС и соединены разноименными полюсами.

Все становится намного сложнее, когда мы соединяем батарейки с разными ЭДС. Да, суммарное ЭДС батареи складывается из ЭДС двух батареек. Но распределение потенциалов имеет некоторую особенность. Рассмотрим это на примерах: 

Сначала мы соединили две 6 вольтовые батарейки (минус одной с плюсом другой). На осциллографе точка соединения имеет потенциал 0 Вольт, а оставшиеся выводы +6 и -6 Вольт. Суммарное ЭДС такой батареи +6-(-6) = 12 Вольт.

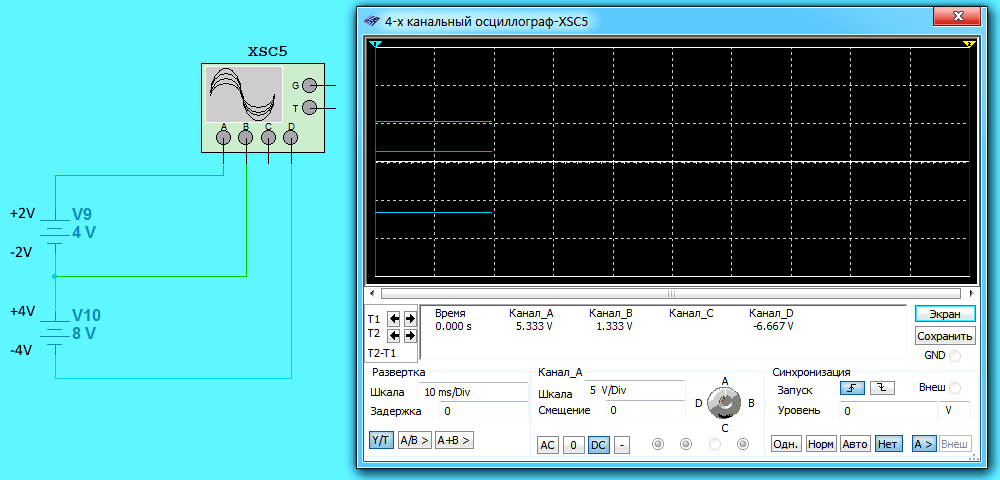
Ниже на схеме тоже батарея с ЭДС 12 Вольт. Однако ЭДС одной батарейки 4 Вольт, а другой 8 Вольт. Здесь самое интересное — распределение потенциалов. Можно было бы предположить, что потенциал в точке соединения равен -2+4 = 6 Вольт (сложили потенциал на минусе одной батарейки с потенциалом на плюсе другой). Исходя из этого потенциалы на выводах самой батареи (батарея — это соединенные вместе несколько батареек (гальванических элементов)) стали бы +10 Вольт и -2 Вольт, что в сумме тоже дает общую ЭДС 12 Вольт. Но как ни странно осциллограф показывает в точке соединения потенциал +1,333 Вольт, а на выводах батареи +5,333 и -6,667 Вольт. Как же так получилось? Давайте разбираться.

Поможет нам математика. Рассмотрим следующую схему и составим систему уравнений:

1. a-x = 2a’ (разность получившихся потенциалов после соединения равна удвоенному значению потенциала (ЭДС) на одном из выводов до соединения в батарею; a — потенциал на выводе батарейки после соединения в батарею; a’ — потенциал на выводе батарейки до соединения в батарею).
2. x-b = -2b’ (разность получившихся потенциалов после соединения равна удвоенному значению потенциала (ЭДС) на одном из выводов до соединения в батарею; со знаком минус, так как удваивается потенциал отрицательного вывода; b — потенциал на выводе батарейки после соединения в батарею; b’ — потенциал на выводе батарейки до соединения в батарею).
3. x = -a+(-b) (потенциал в точке соединения равен сумме потенциалов; a и b взяты со знаком минус, так как складываются потенциалы противоположных им выводов).

Выразим из первого уравнения a: a = 2a’+x. Выразим из второго уравнения b: b = x+2b’. Подставим все это в третье уравнение: x = -2a’-x-x-2b’; 3x = -2(a’+b’); x = (-2/3)×(a’+b’) = -(a’+b’)/1,5.

Простыми словами, чтобы сложить потенциалы в точке соединения двух источников питания, нужно сложить потенциалы соединяемых выводов, а затем полученное значение разделить на 1,5. Причем это правило справедливо для любых комбинаций соединения (-и+, -и-, +и+).

Закрепим материал наглядными примерами из программы и самостоятельным расчетом по формуле:

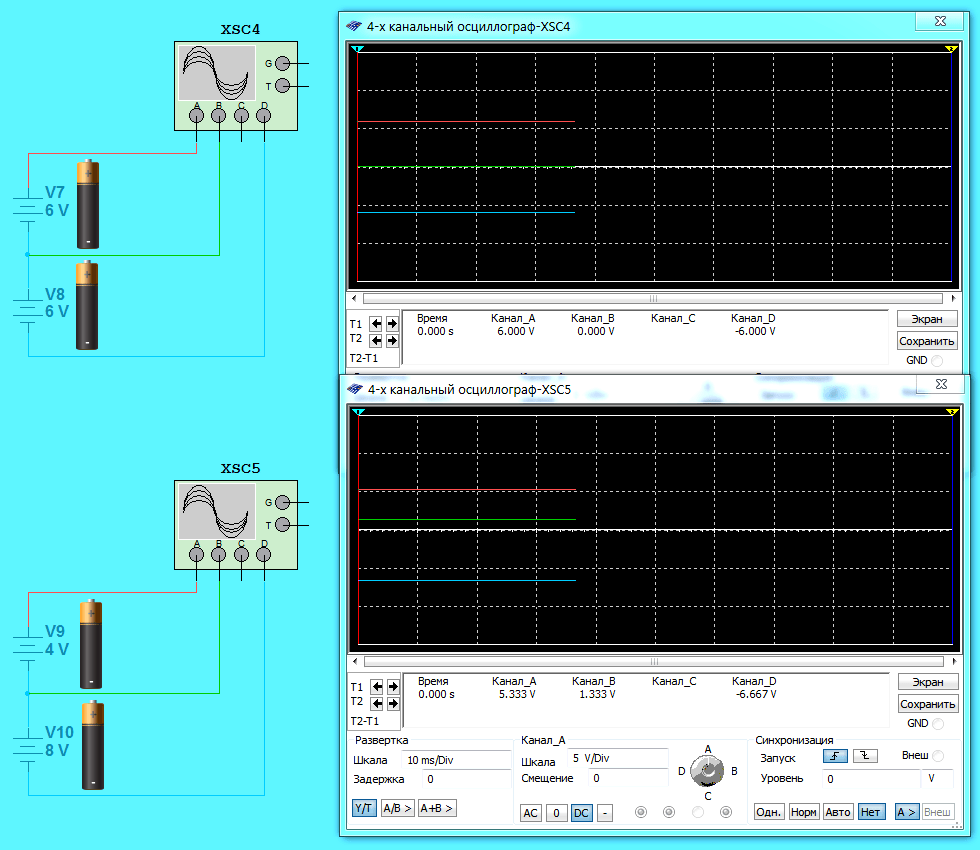
На первой схеме пример, который уже рассматривался. Здесь минус одной батарейки соединяется с плюсом другой батарейки. ЭДС первой батарейки 4 Вольт (соответственно потенциалы на выводах +2 и -2 Вольт). ЭДС второй батарейки 8 Вольт (соответственно потенциалы на выводах +4 и -4 Вольт). Воспользуемся правилом и определим потенциал в точке соединения. Сначала складываем потенциалы -2+(+4) = +2 Вольт. Затем это значение делим на 1,5. Получаем +2/1,5 = +1,333333333333333 Вольт. То же самое показывает осциллограф (канал B).

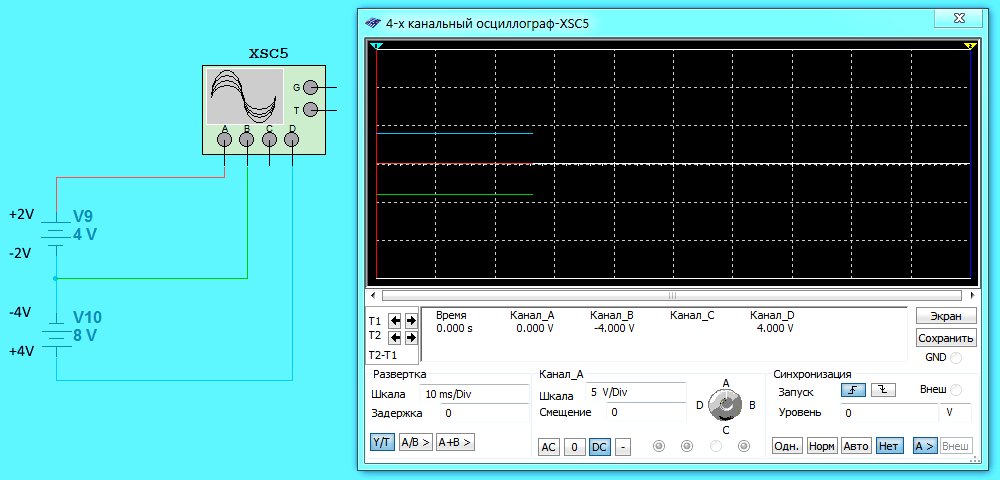
На второй схеме минус одной батарейки соединяется с минусом другой батарейки. ЭДС первой батарейки 4 Вольт (соответственно потенциалы на выводах +2 и -2 Вольт). ЭДС второй батарейки 8 Вольт (соответственно потенциалы на выводах +4 и -4 Вольт). Воспользуемся правилом и определим потенциал в точке соединения. Сначала складываем потенциалы -2+(-4) = -6 Вольт. Затем это значение делим на 1,5. Получаем -6/1,5 = -4 Вольт. То же самое показывает осциллограф (канал B).

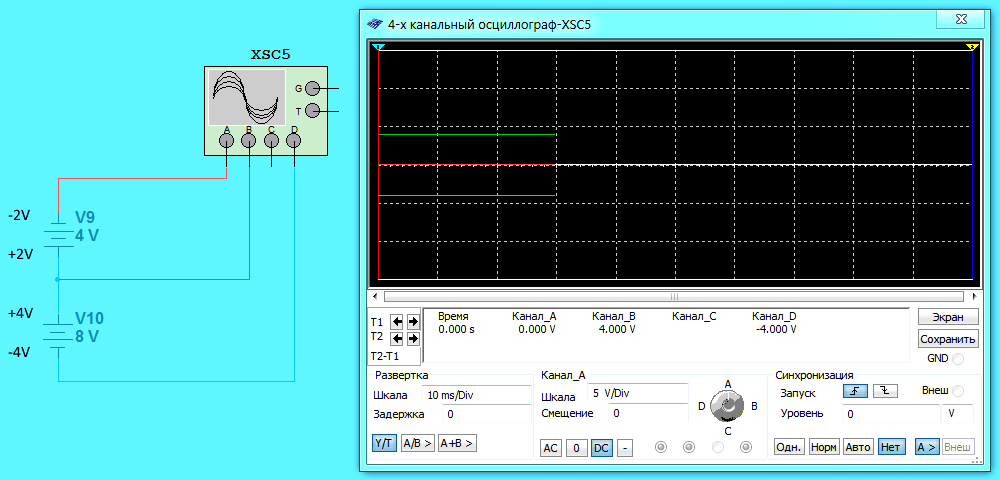
На третьей схеме плюс одной батарейки соединяется с плюсом другой батарейки. ЭДС первой батарейки 4 Вольт (соответственно потенциалы на выводах +2 и -2 Вольт). ЭДС второй батарейки 8 Вольт (соответственно потенциалы на выводах +4 и -4 Вольт). Воспользуемся правилом и определим потенциал в точке соединения. Сначала складываем потенциалы +2+(+4) = +6 Вольт. Затем это значение делим на 1,5. Получаем +6/1,5 = +4 Вольт. То же самое показывает осциллограф (канал B).

Подведем итог. Разность потенциалов показывает напряжение между двумя точками (выводами). Сумма же потенциалов нужна для определения потенциала в точке соединения нескольких источников питания. Мы рассмотрели сумму потенциалов в точке при соединении двух источников питания. Но в цепи может быть и более двух последовательно соединенных источников питания, и здесь с распределением потенциалов также имеет свои особенности (в данном обзоре не рассматривалась такая схема). Может возникнуть вопрос — а зачем вообще нужно это сложение потенциалов? Ответ будет в одной из следующих публикаций, где будут рассмотрены особенности при переходе со звезды на треугольник.

Любой физический объект в окружающем нас мире состоит из огромного количества элементарных частиц, обладающих зарядами. Элементарная частица протон имеет элементарный электрический заряд, которому приписывают (условно) положительный знак, элементарная частица электрон имеет элементарный отрицательный заряд.

Содержание:

• • Электрический заряд
  • Напряженность
  • Потенциал, напряжение
•  

• ---

Электрический заряд

Под электрическим зарядом понимают физическую величину, которая характеризует способность тел (объектов) вступать в электрическое взаимодействие. Электрический заряд обозначается через q (иногда для обозначения используют заглавную букву Q) и в Международной системе единиц (СИ) измеряется в Кулонах, [Кл].

Электрический заряд – дискретная величина, кратная элементарному электрическому заряду одного электрона (по модулю) e = 1,60217*10^-9 Кл.

где N – целое число.

С физической точки зрения 1 кулон [Кл] соответствует электрическому заряду, проходящему через поперечное сечение проводника при силе тока 1 Ампер  за 1 секунду.

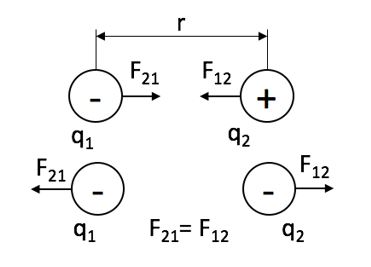
Заряды существуют в двух видах: положительные (+) и отрицательные (-). Одноименные заряды отталкиваются, а разноименные – притягиваются.

Сила взаимодействия зарядов направлена вдоль прямой, соединяющей их, пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния между ними (рисунок 1).

где k – коэффициент пропорциональности, зависящий от выбора системы единиц; 

– единичный вектор, направленный вдоль прямой, соединяющей заряды q₁ и q₂.

Силу взаимодействия двух зарядов принято называть кулоновской силой в честь ученого-физика Шарля Кулона, обнаружевшего ее существование.

Если объект (система) не обменивается зарядами с окружающей средой, его называют электрически изолированным. В такой системе сумма электрических зарядов (положительных и отрицательных) не меняется со временем, то есть наблюдается закон сохранения заряда.

Большинство тел в природе электрически нейтральны, так как содержат заряды обоих типов в одинаковом количестве. Положительные и отрицательные заряды попарно нейтрализуют действие друг друга. Для перехода тела в заряженное состояние необходимо пространственно перераспределить в нем заряды, сконцентрировав одноименные заряды в одной  области тела. Это возможно сделать, например, при помощи трения или взаимодействия с другим заряженным объектом (рисунок 2).

Электрический заряд порождает в окружающем его пространстве непрерывную материю, называемую электрическим полем. Благодаря электрическому полю заряды имеют возможность  взаимодействовать между собой. В электротехнике электрическое поле характеризуется двумя величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика).

Напряженность электрического поля

Напряженность электрического поля – это векторная физическая количественная характеристика электрического поля. Ее величина показывает силу, которая действует на пробный точечный единичный положительный заряд, помещенный в некоторую точку электрического поля.

Под точечным зарядом понимают упрощенную модель положительного заряда, в которой его формой и размером можно пренебречь.

Вектор напряженности по направлению совпадает с вектором силы , с которой электрическое поле действует на положительный точечный заряд, помещенный в заданную точку поля (рисунок 3).

Величина напряженности поля в точке А определяется согласно формуле

где r – расстояние от заряда q до точки А, k – коэффициент пропорциональности, зависящий от выбора системы единиц.

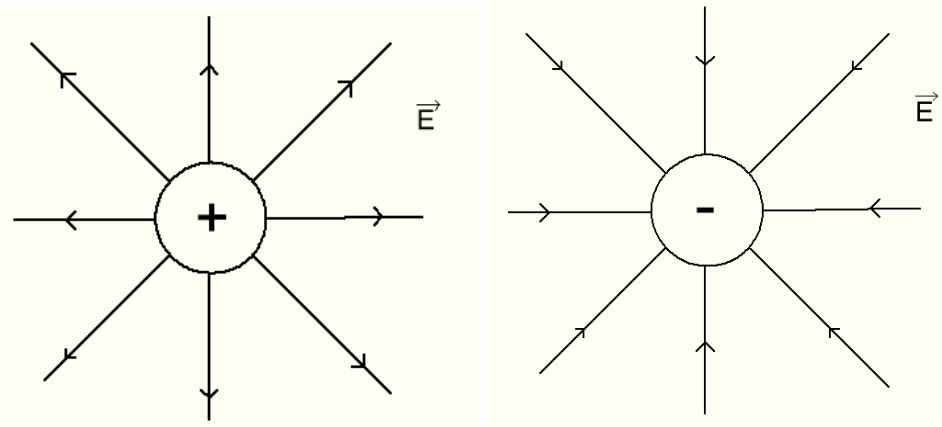
Электрическое поле графически изображается линиями напряженности электрического поля, которые условно принято обозначать исходящими из положительно заряженных элементов и входящими в отрицательно заряженные заряды (рисунок 4).

Рис. 4. Распределение линий напряженности для изолированных (а) и взаимодействующих (б) зарядов

Потенциал, напряжение

Физическую величину, равную отношению потенциальной энергии W электрического заряда в электростатическом поле к величине самого заряда q, называют потенциалом φ электрического поля

Потенциал – это скалярная величина, которая показывает, какую работу способно затратить поле, чтобы переместить единичный пробный положительный заряд в бесконечно удалённую точку. Единицей измерения электрического потенциала является вольт, [В].

При этом важно отметить, что работа сил электростатического поля при перемещении заряда из одной точки электрического поля в другую не зависит от формы траектории перемещения, а зависит только от начального и конечного положения заряда, а также от его величины.

Если имеется некоторая система, состоящая из N точечных зарядов, то потенциал ее электрического поля φ будет равен алгебраической сумме потенциалов полей каждого входящего в него заряда, то есть

Напряжение электрического поля – это разность потенциалов между двумя точками этого поля (рисунок 5).
Напряжение (U) — это работа (А) совершаемая силой поля по перемещению заряженных частиц между двумя точками поля.

U = A/q  [Дж/Кл] или [В]

Напряжение является относительной величиной, то есть всегда определяется относительно некоторого уровня. Нулевой уровень выбирается произвольно и не влияет на итоговое значение напряжения, так как соответствует разности потенциалов в двух точках (то есть изменению потенциальной энергии). Для простоты расчетов в качестве нулевого уровня в большинстве случаев принимают потенциал заземленного проводника или земли.
Как уже было отмечено ранее электрическое напряжение – это разность потенциалов двух точек, следовательно его значение определяется по формуле

В системе СИ за единицу измерения напряжения принимается вольт, [В]. Физически величина напряжения, равная 1 вольту, соответствует работе 1 джоуль при перемещении заряда в 1 кулон.

Понятие электрического потенциала является одним из важных основ теории электростатики и электродинамики. Понимание его сущности является необходимым условием для дальнейшего изучения этих разделов физики.

Что такое электрический потенциал

Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.

Здесь и далее k=((1/4)*π* ε₀* ε), где ε_{0 —} электрическая постоянная (8,85*10^-12 Ф/м), а ε – диэлектрическая постоянная среды.

Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:

φ=W/q,

где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:

• эта работа будет равна убыли потенциальной энергии заряда (A=W₂-W₁);
• работа не зависит от траектории перемещения заряда.

В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.

Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.

Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.

Свойства потенциала

Среди важных свойств потенциала надо отметить следующие:

• если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ₁+φ₂+φ₃+φ₄+φ₅+…+φ_n;
• если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q₁/r₁+q₂/r₂+q₃/r₃+…+q_n/r_n), где r – расстояние от соответствующего заряда то рассматриваемой точки.

Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r², где:

• p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
• r – расстояние до диполя;
• ά – угол между плечом диполя и радиус-вектором r.

Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r².

Разность потенциалов

Если две точки обладают определённым потенциалом, и если они не равны, то говорят о том, что между двумя точками существует разность потенциалов. Разность потенциалов возникает между точками:

• потенциал которых определяется зарядами разных знаков;
• точкой с потенциалом от заряда любого знака и точкой с нулевым потенциалом;
• точками, имеющими потенциал равного знака, но отличающимися по модулю.

То есть, разность потенциалов не зависит от выбора системы координат. Можно провести аналогию с бассейнами с водой, расположенными на разной высоте относительно нулевой отметки (например, уровня моря).

Вода каждого бассейна имеет определенную потенциальную энергию, но если соединить два любых бассейна трубкой, то в каждой из них возникнет поток воды, расход которой определяется не только размерами трубки, но и разностью потенциальных энергий в гравитационном поле Земли (то есть, разностью высот). Абсолютное значение потенциальных энергий значения в данном случае не имеет.

Точно так же, если соединить проводником две точки с разным потенциалом, по нему потечёт электрический ток, определяемый не только сопротивлением проводника, но и разностью потенциалов (но не их абсолютным значением). Продолжая аналогию с водой, можно сказать, что вода в верхнем бассейне скоро закончится, и если не найдется той силы, которая переместит воду обратно наверх (например, насоса), то и поток очень быстро прекратится.

Так и в электрической цепи – чтобы поддерживать разность потенциалов на определенном уровне, потребуется сила, переносящая заряды (точнее, носители зарядов) к точке с наибольшим потенциалом. Такая сила называется электродвижущей силой и сокращенно обозначается ЭДС. ЭДС может носить различную природу – электрохимическую, электромагнитную и т.п.

На практике имеет значение в основном разность потенциалов между начальной и конечной точками траектории движения носителей зарядов. В этом случае эту разность называют напряжением, и оно в СИ также измеряется в вольтах. О напряжении в 1 Вольт можно говорить, если поле совершает работу в 1 Джоуль при перемещении заряда в 1 Кулон из одной точки в другую, то есть 1В=1Дж/1Кл, и Дж/Кл также может являться единицей измерения разности потенциалов.

Эквипотенциальные поверхности

Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.

Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.

Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.