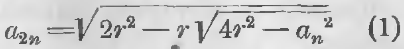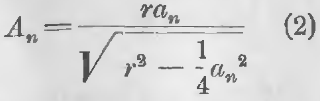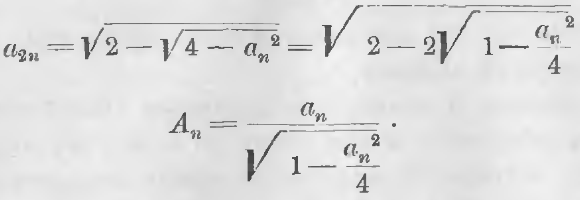Метод пределов. Определение длины окружности
При рассмотрении каждого вопроса встречаются количества постоянные и переменные.
Постоянные количества. Количества, не изменяющие своей величины при рассмотрении какого-нибудь вопроса, называются постоянными.
Переменные количества. Количества, могущие изменить свою величину, называются переменными.
Если дан круг, то радиус этого круга величина постоянная, хорды же круга, проходящие через какую-нибудь точку, лежащую на окружности, являются величинами переменными.
Точно также с увеличением числа сторон правильного описанного многоугольника апофемы их остаются величинами постоянными, а периметры величинами переменными.
Переменные величины изменяются в каких-нибудь пределах.
Приближающаяся величина. Когда переменная величина при своем изменении увеличиваясь или уменьшаясь приближается к некоторой постоянной величине так, что разность между ней и постоянной величиной может быть сделана менее всякой данной величины, ее называют величиной приближающейся.
Постоянная величина, к которой приближается переменная величина, называется ее пределом.
Предел. Пределом называется такая постоянная величина, к которой приближается другая переменная величина увеличиваясь или уменьшаясь, но никогда ее не достигая, хотя разность может быть сделана менее всякой данной величины.
Метод пределов. Совокупность свойств, которыми обладают величины приближающиеся и их пределы, и применение этих свойств к решению различных вопросов называют методом пределов.
Из самого определения предела вытекают следующие свойства предела:
-
Предел есть величина постоянная.
-
Приближающаяся величина всегда более или менее предела.
-
Разность между приближающейся величиной и ее пределом может быть сделана меньше всякой данной величины.
Сумма углов правильного многоугольника, имеющего n сторон, выражается формулой:
S = 2d (n — 2) = 2nd — 4d
Величина каждого угла будет
A = S/n = 2d — (4d)/n
Эта величина A есть величина переменная. Она изменяется с увеличением n числа сторон правильного многоугольника.
В этом выражении количество 2d обладает всеми тремя свойствами предела:
-
Во первых количество 2d есть величина постоянная.
-
Во вторых приближающаяся величина A всегда меньше 2d и
-
наконец разность (4d)/n с увеличением n может быть сделана менее всякой данной величины.
С увеличением числа сторон правильного многоугольника величина его каждого угла A, увеличиваясь все более и более, приближается к двум прямым, а два прямых есть предел, к которому стремится эта величина.
Если в уравнении X = K + α количество α может быть сделано менее всякой данной величины, а K есть величина постоянная, то X есть величина приближающаяся, а K есть ее предел.
Предел обозначают словом lim. (limite) или пред. (предел), поставленными перед величиной приближающейся.
Таким образом пишут
K = lim X = lim (K + α)
Из этого соотношения видно, что
lim α = 0.
Бесконечно-малая величина есть величина переменная, имеющая своим пределом нуль.
В методе пределов имеют значение следующие теоремы.
Теорема 129. Если две приближающиеся величины равны, то и пределы их равны.
Дано. Пусть X и Y две приближающиеся величины, A и B их пределы, так что
X = A + α, Y = B + β
Переменные величины α и β могут быть сделаны менее всякой данной величины.
Доказательство. Из того, что две приближающиеся величины X и Y равны, вытекает равенство X = Y или
A + α = B + β (a)
Здесь могут иметь место следующие три предположения:
A > B, A < B и A = B
1. Если бы имело место неравенство A > B, то разность A — B была бы равна некоторой конечной постоянной величине k.
A — B = k = β — α
Так как β и α могут беспредельно уменьшаться, то никак нельзя допустить, чтобы разность β — α равнялась постоянной конечной величине k, следовательно, неравенство A > B невозможно.
2. Точно также неравенство A < B ведет к разности
B — A = l
где l постоянная конечная величина.
Из равенства (a) вытекает равенство
B — A = α — β = l
Это неравенство точно также невозможно, следовательно, невозможно и предположение A < B.
Итак остается справедливым только равенство: A = B (ЧТД).
Теорема 130. Отношение величин приближающихся равно отношению их пределов.
Даны две приближающиеся величины
X = A + α и Y = B + β
Требуется доказать, что X/Y = A/B.
Доказательство. Отношение двух приближающихся величин будет
X/Y = (A + α) / (B + β)
Обозначим конечную величину этого отношения через l, тогда
(A + α) / (B + β) = l
откуда
A + α = Bl + Bβ (1)
A + α есть приближающаяся величина, имеющая своим пределом A; Bl + Bβ есть приближающаяся величина, имеющая своим пределом величину Bl.
На основании предыдущей теоремы равенство (1) ведет к равенству
A = Bl
Следовательно, l = A/B откуда
(A + α) / (B + β) = A/B (ЧТД).
Теорема 131. Внешняя ломаная больше выпуклой кривой, находящейся внутри ломаной.
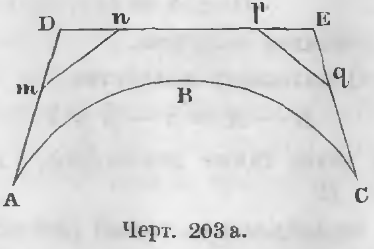
Доказательство. Если бы кривая ABC не была меньше всякой внешней ломаной (черт. 203 а), то существовала бы такая внешняя ломаная, которая была бы меньше всякой другой внешней ломаной, а следовательно и меньше кривой ABC.
Пусть ADEC будет такая ломаная.
В этом случае можно всегда провести так отрезки mn, pq, чтобы они не пересекали кривой ABC, тогда образуется новая ломаная AmnpqC, которая меньше ADEC, ибо
mn < mD + Dn
pq < pE + Eq
Прибавив к этим неравенствам величины Am, np, qC, получим:
mn + pq + Am + np + qC < mD + Dn + pE + Eq + Am + np + qC
или AmnpqC < ADEC.
Таким образом предположение, что существует внешняя ломаная меньше кривой, не имеет места.
Отсюда вытекает следствие: периметр описанного многоугольника больше окружности.
Теорема 132. Разность между периметром одноименного описанного и вписанного многоугольника при удвоении числа сторон может быть сделана меньше всякой данной величины.
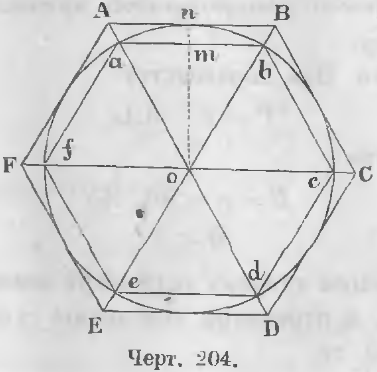
Обозначив через P и p периметры описанного и вписанного многоугольника, имеющего n сторон (черт. 204), мы знаем, что
P/p = OA/Oa
откуда
(P — p)/p = (OA — Oa)/Oa, (P — p)/p = Aa/Oa, P — p = (Aa/Oa)p (a)
Периметр всякого многоугольника больше периметра многоугольника, заключающегося внутри, следовательно, периметр p меньше периметра описанного квадрата.
Периметр описанного квадрата равен 8 · Oa (8 радиусам), следовательно, p < 8 · Oa.
Вставив вместо p во вторую часть равенства (a) величину 8 · Oa, мы ее увеличим, следовательно,
P — p < 8 · Oa · (Aa/Oa) или
P — p < 8Aa
При удвоении числа сторон длина отрезка Aa может быть сделана меньше всякой данной величины, ибо с удвоением числа сторон угол AOB, а следовательно, и угол AOn уменьшаются, и наклонная AO приближается к перпендикуляру nO так, что разность между косвенной и перпендикуляром может быть сделана меньше всякой данной величины.
Теорема 133. С увеличением числа сторон периметры описанного и вписанного многоугольников приближаются к одному и тому же пределу.
Доказательство. Из неравенства
P — p < 8Aa
вытекает равенство
P — p = 8g · Aa
где g < 1.
С удвоением числа сторон периметр описанного многоугольника уменьшается, а периметр вписанного увеличивается. Так как предел Aa равен 0, то предел (P — p) = 0. Откуда пред. P = пред. p, или lim P = lim p (ЧТД).
Теорема 134. Окружность есть предел периметров многоугольников вписанных и описанных.
При удвоении числа сторон периметр правильного описанного многоугольника уменьшается, а периметр вписанного увеличивается. При этом периметр описанного многоугольника больше, а вписанного меньше окружности. Так как разность между периметрами описанного и вписанного многоугольников может быть сделана меньше всякой данной величины, то и подавно с постепенным удвоением числа сторон разность между периметрами правильных многоугольников описанных и окружностью, а также между окружностью и периметрами вписанных правильных многоугольников может быть сделана меньше всякой данной величины, следовательно:
Окружность есть предел периметров вписанных и описанных многоугольников.
Теорема 135. Окружности пропорциональны радиусам.
Доказательство. Обозначим длины двух окружностей через O и O’, их радиусы через R и R’.
Впишем в обе окружности правильные многоугольники, имеющие n сторон. Обозначив их периметры через Pn и Pn‘, мы имеем равенство
Pn/Pn‘ = R/R’
Так как
Pn = O — α
Pn‘ = O — β
то предыдущее равенство дает
(O — α)/(O — β) = R/R’
С последовательным увеличением числа сторон разности α и β между окружностями и периметрами вписанных многоугольников могут быть сделаны меньше всякой данной величины, следовательно, разности O — α, O’ — β являются величинами приближающимися, а величины O и O’ их пределы. На основании теоремы 130 имеем равенство (O — α)/(O’ — β) = O/O’, откуда
O/O’ = R/R’
На основании равенств
O/R = O’/R’ или O/2R = O’/2R’
вытекает следствие: отношение каждой окружности к своему диаметру есть величина постоянная.
Это постоянное отношение окружности к диаметру называют буквой π.
Из равенства
O/2R = π
вытекает равенство
O = 2πR
Длина окружности равна радиусу, умноженному на 2π.
Здесь длина выражается в тех же единицах, в каких выражается радиус.
Отвлеченное количество π есть величина несоизмеримая.
Приближенная величина его 22/7 дана Архимедом. Она выражает истинную величину π с точностью до 0,01.
Меций, живший в конце 16-го столетия, нашел для π приближенную величину 355/113 = 3,141592 с точностью до 0,000001.
Это отношение легко помнить, если его представить в виде
1/π = 113 ÷ 355.
Длина дуги, имеющей n градусов. Окружность имеет 360°. Длина окружности радиуса R выражается формулой 2πR. Длина одного градуса будет величина (2πR)/360.
Обозначив через s длину дуги, имеющей n градусов, имеем:
s = (2πRn)/360 (a)
Формула (a) связывает три величины: n число градусов дуги, s ее длину и R радиус круга. Она дает возможность определить одну из них по двум другим.
Определение величины π
Формула, выражающая длину окружности,
O = 2πR
принимает для R = 1 вид
O = 2π
откуда видно, что 2π выражает длину окружности, описанной радиусом равным единице.
Для определения π вычисляют периметры правильных многоугольников вписанного и описанного с одинаковым числом сторон. Длина окружности заключается между периметрами этих многоугольников. Она меньше периметров описанных и больше периметров вписанных многоугольников. Разность между периметрами укажет в каких пределах заключается погрешность в определении окружности, а следовательно и в определении π.
Чтобы убавить эту погрешность в определении π, последовательно вычисляют периметры многоугольников с удвоенным числом сторон.
Разность между периметрами их будет все меньше и меньше, а следовательно, увеличивается и точность, с какой можно определить π.
Обозначив длину стороны правильных многоугольников, имеющих n сторон, вписанного через an, описанного через An и радиуса через r, мы для определения длины стороны вписанного многоугольника с удвоенным числом сторон пользуется формулой:
а для определения стороны описанного многоугольника по стороне вписанного формулой:
Обозначив через Pn и pn периметры описанного и вписанного правильного многоугольника, имеем:
Pn = nAn, pn = nan
Приближенная величина π удовлетворяет неравенствам:
π > (nan)/2, π < (nAn)/2
в которых an и An вычислены для окружности с радиусом равным 1, следовательно, в формулах, их определяющих принимают r = 1.
Формулы (1) и (2) для r = 1 принимают вид:
Предположив, что n = 6, мы для a6 стороны правильного вписанного шестиугольника при r = 1 имеем:
a6 = 1
откуда
Умножая эти величины на число сторон, имеем следующую таблицу периметров правильных вписанных и описанных многоугольников соответствующего числа сторон, вычисленных с точностью до 6 десятичных знаков
Из этой таблицы видно, что разность между периметрами правильных многоугольников вписанного и описанного все уменьшается.
Для 96-угольника она уже меньше 0,01, а для многоугольника, имеющего 3072 стороны, она меньше 0,00001.
Архимед остановился на вычислении стороны 96-угольника и дал приближенную величину π с точностью до 0,01. Меций дал для π величину π = 355/113 = 3,1415920 с точностью до 0,000001.
Математика
При рассмотрении каждого вопроса встречаются количества постоянные и переменные.
Постоянные количества. Количества, не изменяющие своей величины при рассмотрении какого-нибудь вопроса, называются постоянными.
Переменные количества. Количества, могущие изменить свою величину, называются переменными.
Если дан круг, то радиус этого круга величина постоянная, хорды же круга, проходящие через какую-нибудь точку, лежащую на окружности, являются величинами переменными.
Точно также с увеличением числа сторон правильного описанного многоугольника апофемы их остаются величинами постоянными, а периметры величинами переменными.
Переменные величины изменяются в каких-нибудь пределах.
Приближающаяся величина. Когда переменная величина при своем изменении увеличиваясь или уменьшаясь приближается к некоторой постоянной величине так, что разность между ней и постоянной величиной может быть сделана менее всякой данной величины, ее называют величиной приближающейся.
Постоянная величина, к которой приближается переменная величина, называется ее пределом.
Предел. Пределом называется такая постоянная величина, к которой приближается другая переменная величина увеличиваясь или уменьшаясь, но никогда ее не достигая, хотя разность может быть сделана менее всякой данной величины.
Метод пределов. Совокупность свойств, которыми обладают величины приближающиеся и их пределы, и применение этих свойств к решению различных вопросов называют методом пределов.
Из самого определения предела вытекают следующие свойства предела:
Предел есть величина постоянная.
Приближающаяся величина всегда более или менее предела.
Разность между приближающейся величиной и ее пределом может быть сделана меньше всякой данной величины.
Сумма углов правильного многоугольника, имеющего n сторон, выражается формулой:
S = 2d (n — 2) = 2nd — 4d
Величина каждого угла будет
Эта величина A есть величина переменная. Она изменяется с увеличением n числа сторон правильного многоугольника.
В этом выражении количество 2d обладает всеми тремя свойствами предела:
Во первых количество 2d есть величина постоянная.
Во вторых приближающаяся величина A всегда меньше 2d и
наконец разность (4d)/n с увеличением n может быть сделана менее всякой данной величины.
С увеличением числа сторон правильного многоугольника величина его каждого угла A, увеличиваясь все более и более, приближается к двум прямым, а два прямых есть предел, к которому стремится эта величина.
Если в уравнении X = K + α количество α может быть сделано менее всякой данной величины, а K есть величина постоянная, то X есть величина приближающаяся, а K есть ее предел.
Предел обозначают словом lim. (limite) или пред. (предел), поставленными перед величиной приближающейся.
Таким образом пишут
K = lim X = lim (K + α)
Из этого соотношения видно, что
Бесконечно-малая величина есть величина переменная, имеющая своим пределом нуль.
В методе пределов имеют значение следующие теоремы.
Теорема 129. Если две приближающиеся величины равны, то и пределы их равны.
Дано. Пусть X и Y две приближающиеся величины, A и B их пределы, так что
X = A + α, Y = B + β
Переменные величины α и β могут быть сделаны менее всякой данной величины.
Доказательство. Из того, что две приближающиеся величины X и Y равны, вытекает равенство X = Y или
Здесь могут иметь место следующие три предположения:
A > B, A B, то разность A — B была бы равна некоторой конечной постоянной величине k.
Так как β и α могут беспредельно уменьшаться, то никак нельзя допустить, чтобы разность β — α равнялась постоянной конечной величине k, следовательно, неравенство A > B невозможно.
2. Точно также неравенство A · Oa (8 радиусам), следовательно, p · Oa.
Вставив вместо p во вторую часть равенства (a) величину 8 · Oa, мы ее увеличим, следовательно,
Зависимость длины окружности и радиуса
Формула длины окружности через радиус или диаметр
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Диаметр окружности — отрезок, соединяющий две любые точки расположенные на линии окружности и проходящий через её центр. Диаметр, в два раза больше радиуса
r — радиус окружности
D — диаметр окружности
Формула длины окружности через радиус или диаметр, (L):
Длина окружности
О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r — радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π — математическая константа, примерно равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Как посчитать длину окружности
Онлайн калькулятор
Как посчитать длину окружности зная диаметр
Какая длина у окружности если
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d , где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r , где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅ √ S /π , где π ≈ 3.14
Пример
Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.
Радиус — что это такое и как найти радиус окружности
Через длину стороны
Формула для нахождения длины окружности через радиус:
, где r — радиус окружности.
Найти радиус круга, зная окружность
Окружность круга P
Результат
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
Длина диаметра равна удвоенной длине радиуса.
Вычисление радиуса
Радиус можно посчитать разными способами.
Если известен диаметр
Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.
Если известна длина окружности круга
Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:
Означает данное значение отношение длины окружности к диаметру той же окружности.
Если известна площадь круга
Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:
В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.
Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.
Способ расчета радиуса круга:
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14
Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Как посчитать радиус зная длину окружности
Чему равен радиус (r) если длина окружности C?
Формула
r = C /2π , где π ≈ 3.14
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
Радиус, который перпендикулярен хорде, делит ее на две равные части.
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.
По площади сектора и центральному углу
- Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем
В случае, когда величина α выражена в в радианах , получаем
Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Центральный угол, вписанный угол и их свойства
Связанные определения
- Центральный угол в окружности — это угол , образованный двумя радиусами.
- Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .
В случае, когда величина α выражена в градусах , справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах , справедлива пропорция
из которой вытекает равенство:
Уравнение окружности
r 2 = ( x – a ) 2 + ( y – b ) 2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:
| < | x = a + r cos t |
| y = b + r sin t |
Углы между двумя хордами
Случай 1: два секущие пересекаются внутри окружности.
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Основные свойства касательных к окружности
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
Обобщения
Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Площадь круга, онлайн расчет
Как найти площадь круга по формуле через радиус либо диаметр круга.
Площадь круга, онлайн расчет
Вместо заключения
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.
Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.
http://b4.cooksy.ru/articles/zavisimost-dliny-okruzhnosti-i-radiusa
http://exceltut.ru/radius-chto-eto-takoe-i-kak-najti-radius-okruzhnosti/
Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое.
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Также круг можно определить как часть плоскости, ограниченную окружностью.
Отношение длины окружности к её диаметру одинаково для всех окружностей. Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: π = 3.14159…
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина. Наш онлайн калькулятор вычисляет периметр круга по значению длины его радиуса.
Формула для вычисления длины окружности
$S = 2 pi r$, где:
r — радиус окружности
Остались вопросы?
Здесь вы найдете ответы.
Периметр круга – что это такое?
Периметр круга, также называемый длиной окружности, представляет собой
число, получаемое в результате умножения его радиуса на два Пи, либо путем
перемножения между собой его диаметра и числа Пи. Формула, используемая
для расчета периметра круга, представлена в следующем виде:
L = d*π = 2*r*π.
Расшифровка обозначений:
d — диаметр круга,
r — его радиус,
π — это величина, которая является константой, выражающей отношение длины
окружности к ее диаметру. Ее значение постоянно равно 3,14.
Каким способом производится вычисление периметра круга?
Под определением «расчет периметра круга» подразумевается процедура,
направленная на установление длины окружности, ограничивающей его. В
случае, когда длина радиуса круга является известной величиной, длина
окружности может быть вычислена с применением приведенной ниже формулы:
l=2*π*r,
в ней радиус круга обозначен как r.
Под радиусом окружности подразумевается отрезок, который соединяет центр
окружности с любой из множества точек, находящихся на ней.
Значение длины окружности также может быть вычислено, если диаметр круга
известен. С этой целью нужно произвести умножение ее диаметра (d) на число
Пи (π). В этом случае следует пользоваться формулой:
l=πd.
Если раскрывать такое понятие, как «диаметр окружности», то стоит
отметить, что им является отрезок, проходящий через ее центр и соединяющий
две любые точки этой окружности.
Число Пи (π) является математической постоянной, рассчитываемой как
отношение длины окружности к величине ее диаметра. Оно равно 3,14.
В квадрат, длина стороны которого равна 20 см, вписан круг. Как вычислить
периметр данного круга?
Периметр круга представлен величиной, равной длине окружности, которая
ограничивает его. Это значит, что данная величина может быть рассчитана по
формуле:
P = L = d*π.
В описанном в задании случае сторона квадрата, в который вписан круг,
выступает в роли его диаметра. Это дает основания для расчета периметра
круга следующим образом:
P = 20 * 3,14 = 62,8 см.
Ответ: Периметр круга, который вписан в квадрат, имеющий сторону 20 см,
равен 62,8 см.
Периметр круга равен 30 π. Как можно вычислить длину его окружности?
Длина окружности представляет собой произведение, полученное в результате
умножения ее диаметра (D) на число Пи (π): L = π*D = 30*π. В данном случае
длина окружности – это ее периметр. Из этого следует, что диаметр
окружности D равен 30.
Известно, что длина одного круга равна 3,6 дм. Каким образом можно
определить длину второго круга, если известно то, что диаметр первого круга
в три раза меньше диаметра второго?
Решение поставленной задачи следует начинать с расчета длины первого
круга. Для этого число Пи, равное 3,14, нужно умножить на два, а затем
полученное значение также умножить на длину радиуса круга. Формула,
используемая при этом, выглядит так:
L=2пR.
Принимая во внимание тот факт, что диаметр второго круга в три раза
превышает диаметр первого из них, то можно с уверенностью говорить о том,
что его радиус также будет троекратно превышать радиус первого круга. Это
означает, что формула, применяемая для расчета длины второго круга, будет
выглядеть так:
L=2п*3R
2п*3R/2пR=3.
Подставив в формулу величины, приведенные в задании, можно получить
следующий результат:
3,6*3=10,8 дм.
Ответ: Длина второго круга равна 10,8 дм.
Каким образом можно высчитать длину круга, если известно, что его площадь
составляет 25 дм.кв?
В задании указано, что площадь круга составляет 25 дм.кв. Это значит, что
произведение числа Пи и радиуса круга, возведенного в квадрат, равно 25
дм.кв. Из этого следует, что радиус данного круга равен величине,
полученной в результате деления 5 на квадратный корень из числа Пи (r =
5/√π). На основании этого можно сделать вывод о том, что длина круга может
быть высчитана по следующей формуле:
L = 2πr = 10√π дм.
В результате получается число, приблизительно равное 17,72 дм.
Ответ: Длина круга равна примерно 17,72 дм.
Как высчитать диаметр круга, длина которого равна 40 Пи см?
Формула, которая предназначена для расчета длины круга выглядит так:
L = πD.
По сути, это произведение числа Пи и диаметра круга.
В случае, который описан в задании, длина круга равна 40 Пи см, а это
значит следующее:
πD = 40π.
Число Пи сокращается в обеих частях получившегося уравнения, и в итоге
получается, что диаметр круга равен 40 см:
D = 40 cм.
Каким образом следует рассчитывать площадь круга, если известно, что его
длина составляет 19,1 м?
Располагая информацией о длине круга, можно вычислить его радиус. Это
можно сделать на основании приведенной ниже формулы:
r = L/(2*π) = 19,1:(2*3,14)=3 м.
Таким образом удалось установить, что радиус круга равен 3 м.
Теперь, зная длину радиуса круга, можно произвести расчет его площади по
формуле:
π*r2 = 3,14*3*3 = 28,26 м².
Ответ: Площадь круга равна 28,26 м. кв.
Величина длины круга известна. Она составляет 26 см. Как можно рассчитать
его площадь и диаметр?
При расчете таких показателей, как площадь и диаметр круга, следует
использовать его длину. Она обозначается как с и равна 26 см. Согласно
формуле вычисления длины круга, она равна произведению 2 Пи и радиуса
круга, либо Пи и его диаметра (с=2πr или c=πd). Исходя из этого, диаметр
круга можно найти путем деления длины круга на число Пи:
d=c/π
В данном случае d=26/3,14=8,28 см.
Теперь, когда все необходимые для вычисления площади круга параметры
известны, можно перейти непосредственно к ее расчету:
S=2πr²=2*3,14*8,28*8,28=53,7 см².
Как выглядит формула, используемая для расчета длины окружности по радиусу?
В целях выполнения вычисления длины окружности по радиусу (r) следует
произвести умножение величины, выражающей его значение, на два Пи. При
этом используется следующая формула:
P=2πr.
Чему равна длина окружности, диаметр которой 4 м?
При расчете длины окружности используется формула, которая имеет следующий
вид:
L = π*D.
Согласно данной формуле, для того чтобы вычислить, чему равна длина
окружности, необходимо произвести умножение ее диаметра на число Пи,
равное 3,14.
Подставляя в приведенную выше формулу числа, указанные в задании, можно
произвести расчет длины окружности, которая будет равна:
3,14*4 = 12,56 м.
Ответ: Длина окружности диаметром в 4 м равна 12,56 м.
Какому числу будет равна длина окружности круга при условии, что его площадь
равна Пи м. кв?
Площадь круга высчитывается при помощи формулы:
S=πR².
В данном конкретном случае указано, что площадь равна Пи м. кв. (S=π).
Исходя из вышеизложенного, можно произвести расчет величины радиуса,
которая будет равна отношению корня квадратного из числа Пи и числа Пи:
R=√π/π=1.
Теперь можно приступить к вычислению непосредственно длины окружности,
используя следующую формулу:
C = 2πR = 2π⋅1 = 2π.
Ответ: Длина окружности круга площадью Пи кв. м равна 2 Пи.
Чему будет равна длина круга диаметром 16 см?
При расчете длины круга следует брать за основу формулу, которая
предполагает умножения числа Пи, равного 3,14, на диаметр окружности
круга. Если говорить о конкретном случае, упомянутом в задании, то расчет
длины окружности будет выглядеть следующим образом:
L=16 см*3,14=50,24 см.
Ответ: Длина круга, диаметр которого равен 16 см, составляет 50,24 см.
Диаметр круга составляет 5,8 дм. Какому числу будет равна длина этого круга?
Длина окружности рассчитывается с применением формулы, составными
элементами которой являются диаметр (d) и число ПИ, равное 3,14. Для
вычисления длины окружности упомянутые величины следует перемножить:
L=π*d=3,14*5,8=18,212 дм.
Ответ: Круг диаметром 5,8 дм имеет длину окружности, равную 18,212 дм.
Известно, что круг имеет диаметр 18 м. Как вычислить длину этого круга по
диаметру?
Если диаметр круга является известной величиной, то ее вполне достаточно,
для того чтобы произвести расчет длины данного круга. С этой целью следует
использовать формулу, приведенную ниже:
l = 2πr = πd.
Если подставить в данную формулу величины, заданные в вопросе, то можно
получить следующий результат:
l = 3,14*18 = 56,52 м.
Ответ: Длина круга, диаметр которого равен 18 м, составляет 56,52 м.
На этом уроке мы рассмотрим одни из самых древнейших геометрических фигур: окружность и круг.
Эта информация доступна зарегистрированным пользователям
Определим, какими элементами характеризуются круг и окружность, в чем сходство и различие этих фигур.
Узнаем, как рассчитать длину окружности и площадь круга.
Мы часто встречаем такие понятия, как окружность и круг.
Давайте попробуем разобраться, что называют окружностью, а что кругом.
Окружность — это замкнутая плоская кривая, все точки которой удалены на одинаковые расстояния от заданной точки, называемой центром окружности.
Центр окружности— это точка, которая находится на одинаковом расстоянии (равноудаленная) от любой точки окружности, ее обозначают обычно заглавной буквой О.
По сути, окружность — это изогнутая линия. Наглядно представить данную геометрическую фигуру можно, обведя стакан или блюдце карандашом, — оставшийся нарисованный след и будет окружностью.
Круг — это часть плоскости, ограниченная окружностью. Можно также сказать что это часть плоскости, которая находится внутри линии окружности.
Круг — плоская фигура, ее можно получить, закрасив окружность или вырезав его из бумаги по контуру окружности.
Эта информация доступна зарегистрированным пользователям
Свои имена окружность и круг приобрели не сразу.
В древние времена специальных названий для этих фигур не существовало. Люди пытались описать различные геометрические формы, сравнивая объекты. Например, говоря про что-то круглое, говорили: «такой, как солнце» или «такой, как орех» и т.п.
Только в Древней Греции окружность и круг приобрели себе свои названия.
Круг всегда привлекал к себе внимание как самая простая фигура из кривых, но самая загадочная.
Эта информация доступна зарегистрированным пользователям
В живой и неживой природе круги и окружности встречаются как на макроуровнях, так и на микроуровнях. Например, движение электронов вокруг атомного ядра; вращение планет вокруг солнца; распространение волн на воде от упавшего груза; образование солнечного и лунного гало; срез дерева; зрачок глаза у человека и многое другое.
Эта информация доступна зарегистрированным пользователям
Рассмотрим подробней элементы, характерные для окружности.
Радиус окружности— это отрезок, соединяющий центр окружности и любую другую точку, расположенную на линии окружности.
С латинского радиус (radius)- луч, спица колеса. Радиус не сразу приобрел себе такое название.
Слово радиус впервые встречается в 1569 году у французского ученого П. Рамуса, а общепризнанным становится к концу XVII века.
Радиус обозначается маленькой латинской буквой (r) или заглавной (R).
Эта информация доступна зарегистрированным пользователям
В окружности можно провести столько же радиусов, сколько точек имеет линия окружности; все эти радиусы равны.
Диаметр — это отрезок прямой, проходящий через центр окружности и соединяющий две точки на этой окружности.
Диаметр в переводе с греческого (diametros) — поперечник.
Обычно диаметр обозначают латинской маленькой буквой d или заглавной D.
По величине диаметр равен двум радиусам, лежащим на одной прямой.
Эта информация доступна зарегистрированным пользователям
d = 2r
Следовательно, радиус- это половина диаметра.
r = d: 2
Пример 1
Радиус окружности равен 6 см.
Чему равен диаметр окружности?
Дано:
r = 6 см
Найти:
d — ?
Решение:
d = 2r
d = 2r= 2*6 = 12 (см) диаметр окружности
Ответ: d= 12 см
Пример 2
Диаметр окружности равен 12 см.
Чему равен радиус окружности?
Дано:
d = 12 см
Найти:
r — ?
Решение:
r = d : 2
r = 12 : 2 = 6 (см) радиус окружности
Ответ: r = 6 см
Эта информация доступна зарегистрированным пользователям
Важно отметить, что все рассмотренные элементы окружности одинаковы и для круга.
Эта информация доступна зарегистрированным пользователям
Давайте выясним, что такое длина окружности и как ее определить.
Представьте, что окружность обернута нитью.
Если разрезать эту нить в некоторой точке и размотать ее, то длина нитки будет равна длине окружности.
Обычно длина окружности обозначается заглавной буквой С
Эта информация доступна зарегистрированным пользователям
Длина окружности (С) зависит от длины ее диаметра (d)
Эта информация доступна зарегистрированным пользователям
Обратите внимание на рисунок.
Вы можете заметить, что чем больше диаметр, тем больше длина окружности.
Из этого следует, что длина окружности прямо пропорционально зависит от диаметра окружности.
А значит, для любых окружностей отношение длины окружности (С) к длине диаметра (d) является числом постоянным.
Это число (коэффициент пропорциональности) обозначают греческой буквой (mathbf{pi}), читается «пи».
Зная, что:
С— это длина окружности
d— диаметр окружности
запишем отношение (mathbf{C div d = pi})
отсюда следует, что длина окружности равна
(mathbf{C = pi d})
Так как диаметр окружности вдвое больше радиуса d = 2r, получим еще одну формулу для вычисления длины окружности
(mathbf{C = pi 2r = 2pi r})
Эта информация доступна зарегистрированным пользователям
Выясним, чему равна постоянная величина — число (mathbf{pi})
Число (mathbf{pi})- это иррациональное число, т.е. число, которое представлено в виде бесконечной непериодической десятичной дроби.
Эта информация доступна зарегистрированным пользователям
Мы с вами не будем оперировать настолько точными данными.
Для вычислений и решения задач нам будет хватать округления числа (mathbf{ pi}) до сотых.
И будем принимать число (mathbf{ pi}) приблизительно равным 3,14.
Эта информация доступна зарегистрированным пользователям
Число (mathbf{ pi}) используют во многих математических и физических формулах.
Площадь круга
Так как круг — это часть плоскости, то одной из его характеристик является площадь.
Площадь круга равна произведению квадрата радиуса на число (mathbf{ pi}).
Эта информация доступна зарегистрированным пользователям
Где S— это площадь круга
r— радиус круга
(mathbf{ pi}) — постоянная величина
Так как (mathbf{r = frac {d}{2} = frac {1}{2}d}), то получаем еще одну формулу для определения площади круга
(mathbf{S = pi (frac{1}{2} d)^2 = frac {1}{4} pi d^2})
Эта информация доступна зарегистрированным пользователям
Рассмотрим примеры решения задач
Задача 1
Найдите длину окружности, если ее радиус равен 4 см.
Число (mathbf{{pi}}) округлите до сотых.
Дано:
r = 4 см
(mathbf{{pi} approx 3,14})
Найти:
Длину окружности С — ?
Решение:
(mathbf{C = 2{pi}r})
Подставив в формулу известные значения радиуса и постоянной (mathbf{pi}), получим:
(mathbf{C = 2{cdot}3,14{cdot}4=25,12})(см) длина окружности
Ответ: (mathbf{C=25,12})(см)
Задача 2
Длина окружности надувного бассейна 15,7м.
Найдите диаметр этого бассейна.
Число (mathbf{pi}) округлите до сотых.
Дано:
C = 15,7 м
(mathbf{piapprox 3,14})
Найти:
Диаметр d — ?
Решение:
(mathbf{C = pi d})
(mathbf{d = frac {c}{pi}})
Подставив в формулу известные значения длины окружности и постоянной (mathbf{pi}), получим:
(mathbf{d = frac {15,7}{3,14}}=5) (м) диаметр бассейна
Ответ: (mathbf{d = 5}) (м)
Задача 3
Диаметр окружности равен 6 см.
Найдите площадь круга, ограниченного этой окружностью.
Значение числа (mathbf{pi}) округлить до сотых.
Дано:
d = 6 cм
(mathbf{{pi} approx 3,14})
Найти:
Площадь круга S — ?
Решение:
(mathbf{S = frac {1}{4}{pi}d^2})
Подставим в формулу известные значения диаметра окружности и постоянной , получим:
(mathbf{S = frac {1}{4}{cdot}3,14{cdot}6^2 = frac {3,14{cdot}36}{4} } = 3,14{cdot}9=28,26) (cм2) площадь круга
Ответ: (mathbf{S = 28,26}) (см2)
Задача 4
Вычислите площадь полукруга, если радиус круга равен 5 см.
Значение (mathbf{pi }) округлить до целых.
Дано:
r = 5 cм
(mathbf{{pi} approx 3})
Найти:
Площадь полукруга Sп — ?
Решение:
Площадь круга найдем по формуле:
(mathbf{S = {pi} r^2})
Площадь полукруга будет равна половине площади всего круга.
Следовательно, формула для расчета площади полукруга получится вида:
(mathbf{S_п = frac{pi r^2}{2}})
Подставим в формулу известные значения радиуса круга и постоянной (mathbf{pi}), получим:
(mathbf{S_п = frac{3 cdot 25}{2} =37,5}) (cм2) площадь полукруга
Ответ: (mathbf{S_п =37,5}) (см2)
Задача 5
Найдите площадь круга, если известна длина окружности С.
Дано:
Длина окружности С
Найти:
Площадь круга S — ?
Решение:
Длина окружности выражается формулой:
(mathbf{C = 2{pi}r})
Выразим неизвестный радиус окружности через длину окружности:
(mathbf{r = frac{C}{2{pi}}})
Площадь круга определяем по формуле:
(mathbf{S ={pi}r^2})
Подставим, полученные выражения для радиуса окружности, в формулу площади круга, получим:
(mathbf{S ={pi}(frac{C}{2{pi}})^2 = {pi}frac {C^2}{4{pi}^2} = frac{{pi}C^2}{4{pi}^2}})
Сократим полученную дробь:
(mathbf{S=frac{C^2}{4{pi}}})площадь круга
Ответ: (mathbf{S=frac{C^2}{4{pi}}})
Эта информация доступна зарегистрированным пользователям
Взгляните на изображение:
Окружность — это геометрическая фигура, которая состоит из всех точек плоскости. Точки эти расположены на заданном расстоянии от неё.
Круг — это геометрическая фигура, которая состоит из всех точек плоскости, расположенных на расстоянии не больше заданного от данной точки.
Для изображения окружности нужно задать:
- Центр окружности — некоторую точку на плоскости;
- Определённое расстояние от центра до точки, лежащей на окружности — его называют радиусом.
Также существует диаметр — это отрезок, который проходит через центр окружности и соединяет две точки, которые лежат на окружности. Диаметр равен двум радиусам.
Изучим рисунок:
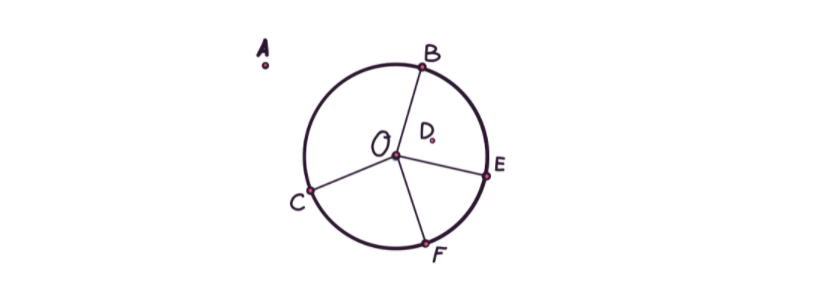
Центр окружности — точка O.
Во внутренней области окружности лежит точка D.
У окружности несколько радиусов: OC, OB, OE, OF.
Диаметра не проведён.
И последняя точка — A. Она расположена во внешней области окружности.
Ещё одно понятие, с которым нам надо познакомиться, — хорда. Так называется отрезок, соединяющий две точки окружности.
Взгляните на рисунок:

Для нахождения длины окружности существует специальная формула.
C = 2πr
где С — длина окружности;
π — отношение длины окружности к длине её диаметр; математическая постоянная, которая приблизительно равна (≈) 3,14;
r — радиус окружности.

С = 2π * 5;
С = 10π
Также существует формула для нахождения площади круга.
Площадь круга с радиусом r равна произведению числа π на длину радиуса в квадрате:
S = π*r*r
Найдём площадь круга с радиусом 4 см.
S = π * 4*4;
S = 16π
Как Вы могли заметить, математическую величину π мы не представляли в виде 3,14 и не умножали её на число. В этом нет нужды, так как величина постоянная.
Тема изучена, формула площади круга и длины окружности изучена — теперь можно и
попрактиковаться!
- Найдите длину окружности, если её радиус равен 5 см.
- Найдите площадь круга, если его радиус равен 7 см.
Также Ваш ребёнок может изучить тему “Длина окружности и площадь круга” под руководством квалифицированного педагога школы World of Math. Первое занятие — бесплатное! Записаться на него Вы можете здесь.