Введение
Постоя́нная Ха́ббла — коэффициент, входящий в закон Хаббла, который связывает расстояние до внегалактического объекта (галактики, квазара) со скоростью его удаления. Имеет размерность, обратную времени (H = 2,3×10-18 с-1), но выражается обычно в км/с на мегапарсек.
Наиболее надёжная оценка на 2010 год составляет 
Страница: 0
en: Hubble’s law
de: Hubble-Konstante
Примечания
- ↑ Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Sky Maps, Systematic Errors, and Basic Results
См.также
- Закон Хаббла
Ссылки
- Ю.Н.Ефремов, Постоянная Хаббла
- G.A. Tammann, B. Reindl, Cosmic Expansion and Ho: A Retro- and Pro-Spective Note
- G.A. Tammann, The Ups and Downs of the Hubble Constant
Литература
|
Выделить Постоянная Хаббла и найти в:
|
|
|
- Страница 0 — краткая статья
- Страница 1 — энциклопедическая статья
- Разное — на страницах: 2 , 3 , 4 , 5
- Прошу вносить вашу информацию в «Постоянная Хаббла 1», чтобы сохранить ее
Комментарии читателей:
Для статьи
An analogy for explaining the Hubble’s law, using raisins in bread in place of galaxies. If a raisin that is twice as further away from a place as another raisin, then the farther raisin would move away twice as fast.
Hubble’s law, also known as the Hubble–Lemaître law,[1] is the observation in physical cosmology that galaxies are moving away from Earth at speeds proportional to their distance. In other words, the farther they are, the faster they are moving away from Earth. The velocity of the galaxies has been determined by their redshift, a shift of the light they emit toward the red end of the visible spectrum.
Hubble’s law is considered the first observational basis for the expansion of the universe, and today it serves as one of the pieces of evidence most often cited in support of the Big Bang model.[2][3]
The motion of astronomical objects due solely to this expansion is known as the Hubble flow.[4] It is described by the equation v = H0D, with H0 the constant of proportionality—the Hubble constant—between the «proper distance» D to a galaxy, which can change over time, unlike the comoving distance, and its speed of separation v, i.e. the derivative of proper distance with respect to the cosmological time coordinate. (See Comoving and proper distances § Uses of the proper distance for some discussion of the subtleties of this definition of «velocity».)
The Hubble constant is most frequently quoted in (km/s)/Mpc, thus giving the speed in km/s of a galaxy 1 megaparsec (3.09×1019 km) away, and its value is about 70 (km/s)/Mpc. However, crossing out units reveals that H0 is a unit of frequency (SI unit: s−1) and the reciprocal of H0 is known as the Hubble time. The Hubble constant can also be interpreted as the relative rate of expansion. In this form H0 = 7%/Gyr, meaning that at the current rate of expansion it takes a billion years for an unbound structure to grow by 7%.
Although widely attributed to Edwin Hubble,[5][6][7] the notion of the universe expanding at a calculable rate was first derived from general relativity equations in 1922 by Alexander Friedmann. Friedmann published a set of equations, now known as the Friedmann equations, showing that the universe might be expanding, and presenting the expansion speed if that were the case.[8] Then Georges Lemaître, in a 1927 article, independently derived that the universe might be expanding, observed the proportionality between recessional velocity of, and distance to, distant bodies, and suggested an estimated value for the proportionality constant; this constant, when Edwin Hubble confirmed the existence of cosmic expansion and determined a more accurate value for it two years later, came to be known by his name as the Hubble constant.[2][9][10][11][12] Hubble inferred the recession velocity of the objects from their redshifts, many of which were earlier measured and related to velocity by Vesto Slipher in 1917.[13][14][15] Though the Hubble constant H0 is constant at any given moment in time, the Hubble parameter H, of which the Hubble constant is the current value, varies with time, so the term constant is sometimes thought of as somewhat of a misnomer.[16][17]
Discovery[edit]
Three steps to the Hubble constant[18]
A decade before Hubble made his observations, a number of physicists and mathematicians had established a consistent theory of an expanding universe by using Einstein field equations of general relativity. Applying the most general principles to the nature of the universe yielded a dynamic solution that conflicted with the then-prevalent notion of a static universe.
Slipher’s observations[edit]
In 1912, Vesto M. Slipher measured the first Doppler shift of a «spiral nebula» (the obsolete term for spiral galaxies) and soon discovered that almost all such nebulae were receding from Earth. He did not grasp the cosmological implications of this fact, and indeed at the time it was highly controversial whether or not these nebulae were «island universes» outside our Milky Way.[19][20]
FLRW equations[edit]
In 1922, Alexander Friedmann derived his Friedmann equations from Einstein field equations, showing that the universe might expand at a rate calculable by the equations.[21] The parameter used by Friedmann is known today as the scale factor and can be considered as a scale invariant form of the proportionality constant of Hubble’s law. Georges Lemaître independently found a similar solution in his 1927 paper discussed in the following section. The Friedmann equations are derived by inserting the metric for a homogeneous and isotropic universe into Einstein’s field equations for a fluid with a given density and pressure. This idea of an expanding spacetime would eventually lead to the Big Bang and Steady State theories of cosmology.
Lemaître’s equation[edit]
In 1927, two years before Hubble published his own article, the Belgian priest and astronomer Georges Lemaître was the first to publish research deriving what is now known as Hubble’s law. According to the Canadian astronomer Sidney van den Bergh, «the 1927 discovery of the expansion of the universe by Lemaître was published in French in a low-impact journal. In the 1931 high-impact English translation of this article, a critical equation was changed by omitting reference to what is now known as the Hubble constant.»[22] It is now known that the alterations in the translated paper were carried out by Lemaître himself.[10][23]
Shape of the universe[edit]
Before the advent of modern cosmology, there was considerable talk about the size and shape of the universe. In 1920, the Shapley–Curtis debate took place between Harlow Shapley and Heber D. Curtis over this issue. Shapley argued for a small universe the size of the Milky Way galaxy, and Curtis argued that the universe was much larger. The issue was resolved in the coming decade with Hubble’s improved observations.
Cepheid variable stars outside the Milky Way[edit]
Edwin Hubble did most of his professional astronomical observing work at Mount Wilson Observatory,[24] home to the world’s most powerful telescope at the time. His observations of Cepheid variable stars in «spiral nebulae» enabled him to calculate the distances to these objects. Surprisingly, these objects were discovered to be at distances which placed them well outside the Milky Way. They continued to be called nebulae, and it was only gradually that the term galaxies replaced it.
Combining redshifts with distance measurements[edit]
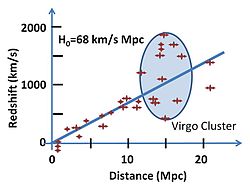
Fit of redshift velocities to Hubble’s law.[25] Various estimates for the Hubble constant exist. The HST Key H0 Group fitted type Ia supernovae for redshifts between 0.01 and 0.1 to find that H0 = 71 ± 2 (statistical) ± 6 (systematic) km⋅s−1⋅Mpc−1,[26] while Sandage et al. find H0 = 62.3 ± 1.3 (statistical) ± 5 (systematic) km⋅s−1⋅Mpc−1.[27]
The parameters that appear in Hubble’s law, velocities and distances, are not directly measured. In reality we determine, say, a supernova brightness, which provides information about its distance, and the redshift z = ∆λ/λ of its spectrum of radiation. Hubble correlated brightness and parameter z.
Combining his measurements of galaxy distances with Vesto Slipher and Milton Humason’s measurements of the redshifts associated with the galaxies, Hubble discovered a rough proportionality between redshift of an object and its distance. Though there was considerable scatter (now known to be caused by peculiar velocities—the ‘Hubble flow’ is used to refer to the region of space far enough out that the recession velocity is larger than local peculiar velocities), Hubble was able to plot a trend line from the 46 galaxies he studied and obtain a value for the Hubble constant of 500 (km/s)/Mpc (much higher than the currently accepted value due to errors in his distance calibrations; see cosmic distance ladder for details).
At the time of discovery and development of Hubble’s law, it was acceptable to explain redshift phenomenon as a Doppler shift in the context of special relativity, and use the Doppler formula to associate redshift z with velocity. Today, in the context of general relativity, velocity between distant objects depends on the choice of coordinates used, and therefore, the redshift can be equally described as a Doppler shift or a cosmological shift (or gravitational) due to the expanding space, or some combination of the two.[28]
Hubble diagram[edit]
Hubble’s law can be easily depicted in a «Hubble diagram» in which the velocity (assumed approximately proportional to the redshift) of an object is plotted with respect to its distance from the observer.[29] A straight line of positive slope on this diagram is the visual depiction of Hubble’s law.
Cosmological constant abandoned[edit]
After Hubble’s discovery was published, Albert Einstein abandoned his work on the cosmological constant, which he had designed to modify his equations of general relativity to allow them to produce a static solution, which he thought was the correct state of the universe. The Einstein equations in their simplest form model generated either an expanding or contracting universe, so Einstein’s cosmological constant was artificially created to counter the expansion or contraction to get a perfect static and flat universe.[30] After Hubble’s discovery that the universe was, in fact, expanding, Einstein called his faulty assumption that the universe is static his «biggest mistake».[30] On its own, general relativity could predict the expansion of the universe, which (through observations such as the bending of light by large masses, or the precession of the orbit of Mercury) could be experimentally observed and compared to his theoretical calculations using particular solutions of the equations he had originally formulated.
In 1931, Einstein made a trip to Mount Wilson Observatory to thank Hubble for providing the observational basis for modern cosmology.[31]
The cosmological constant has regained attention in recent decades as a hypothetical explanation for dark energy.[32]
Interpretation[edit]
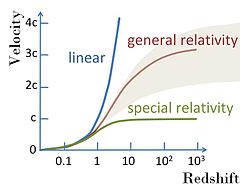
A variety of possible recessional velocity vs. redshift functions including the simple linear relation v = cz; a variety of possible shapes from theories related to general relativity; and a curve that does not permit speeds faster than light in accordance with special relativity. All curves are linear at low redshifts. See Davis and Lineweaver.[33]
The discovery of the linear relationship between redshift and distance, coupled with a supposed linear relation between recessional velocity and redshift, yields a straightforward mathematical expression for Hubble’s law as follows:
where
Hubble’s law is considered a fundamental relation between recessional velocity and distance. However, the relation between recessional velocity and redshift depends on the cosmological model adopted and is not established except for small redshifts.
For distances D larger than the radius of the Hubble sphere rHS , objects recede at a rate faster than the speed of light (See Uses of the proper distance for a discussion of the significance of this):
Since the Hubble «constant» is a constant only in space, not in time, the radius of the Hubble sphere may increase or decrease over various time intervals. The subscript ‘0’ indicates the value of the Hubble constant today.[25] Current evidence suggests that the expansion of the universe is accelerating (see Accelerating universe), meaning that for any given galaxy, the recession velocity dD/dt is increasing over time as the galaxy moves to greater and greater distances; however, the Hubble parameter is actually thought to be decreasing with time, meaning that if we were to look at some fixed distance D and watch a series of different galaxies pass that distance, later galaxies would pass that distance at a smaller velocity than earlier ones.[34]
Redshift velocity and recessional velocity[edit]
Redshift can be measured by determining the wavelength of a known transition, such as hydrogen α-lines for distant quasars, and finding the fractional shift compared to a stationary reference. Thus, redshift is a quantity unambiguous for experimental observation. The relation of redshift to recessional velocity is another matter. For an extensive discussion, see Harrison.[35]
Redshift velocity[edit]
The redshift z is often described as a redshift velocity, which is the recessional velocity that would produce the same redshift if it were caused by a linear Doppler effect (which, however, is not the case, as the shift is caused in part by a cosmological expansion of space, and because the velocities involved are too large to use a non-relativistic formula for Doppler shift). This redshift velocity can easily exceed the speed of light.[36] In other words, to determine the redshift velocity vrs, the relation:
is used.[37][38] That is, there is no fundamental difference between redshift velocity and redshift: they are rigidly proportional, and not related by any theoretical reasoning. The motivation behind the «redshift velocity» terminology is that the redshift velocity agrees with the velocity from a low-velocity simplification of the so-called Fizeau–Doppler formula.[39]
Here, λo, λe are the observed and emitted wavelengths respectively. The «redshift velocity» vrs is not so simply related to real velocity at larger velocities, however, and this terminology leads to confusion if interpreted as a real velocity. Next, the connection between redshift or redshift velocity and recessional velocity is discussed. This discussion is based on Sartori.[40]
Recessional velocity[edit]
Suppose R(t) is called the scale factor of the universe, and increases as the universe expands in a manner that depends upon the cosmological model selected. Its meaning is that all measured proper distances D(t) between co-moving points increase proportionally to R. (The co-moving points are not moving relative to each other except as a result of the expansion of space.) In other words:
[41]
where t0 is some reference time. If light is emitted from a galaxy at time te and received by us at t0, it is redshifted due to the expansion of space, and this redshift z is simply:
Suppose a galaxy is at distance D, and this distance changes with time at a rate dtD. We call this rate of recession the «recession velocity» vr:
We now define the Hubble constant as
and discover the Hubble law:
From this perspective, Hubble’s law is a fundamental relation between (i) the recessional velocity contributed by the expansion of space and (ii) the distance to an object; the connection between redshift and distance is a crutch used to connect Hubble’s law with observations. This law can be related to redshift z approximately by making a Taylor series expansion:
If the distance is not too large, all other complications of the model become small corrections, and the time interval is simply the distance divided by the speed of light:
or
According to this approach, the relation cz = vr is an approximation valid at low redshifts, to be replaced by a relation at large redshifts that is model-dependent. See velocity-redshift figure.
Observability of parameters[edit]
Strictly speaking, neither v nor D in the formula are directly observable, because they are properties now of a galaxy, whereas our observations refer to the galaxy in the past, at the time that the light we currently see left it.
For relatively nearby galaxies (redshift z much less than unity), v and D will not have changed much, and v can be estimated using the formula 
For distant galaxies, v (or D) cannot be calculated from z without specifying a detailed model for how H changes with time. The redshift is not even directly related to the recession velocity at the time the light set out, but it does have a simple interpretation: (1 + z) is the factor by which the universe has expanded while the photon was travelling towards the observer.
Expansion velocity vs. relative velocity[edit]
In using Hubble’s law to determine distances, only the velocity due to the expansion of the universe can be used. Since gravitationally interacting galaxies move relative to each other independent of the expansion of the universe,[42] these relative velocities, called peculiar velocities, need to be accounted for in the application of Hubble’s law.
The Finger of God effect is one result of this phenomenon. In systems that are gravitationally bound, such as galaxies or our planetary system, the expansion of space is a much weaker effect than the attractive force of gravity.
Time-dependence of Hubble parameter[edit]
The parameter 

Another common source of confusion is that the accelerating universe does not imply that the Hubble parameter is actually increasing with time; since 


On defining the dimensionless deceleration parameter
, it follows that
From this it is seen that the Hubble parameter is decreasing with time, unless 
However, in the standard Lambda cold dark matter model (Lambda-CDM or ΛCDM model), 

Idealized Hubble’s law[edit]
The mathematical derivation of an idealized Hubble’s law for a uniformly expanding universe is a fairly elementary theorem of geometry in 3-dimensional Cartesian/Newtonian coordinate space, which, considered as a metric space, is entirely homogeneous and isotropic (properties do not vary with location or direction). Simply stated the theorem is this:
Any two points which are moving away from the origin, each along straight lines and with speed proportional to distance from the origin, will be moving away from each other with a speed proportional to their distance apart.
In fact, this applies to non-Cartesian spaces as long as they are locally homogeneous and isotropic, specifically to the negatively and positively curved spaces frequently considered as cosmological models (see shape of the universe).
An observation stemming from this theorem is that seeing objects recede from us on Earth is not an indication that Earth is near to a center from which the expansion is occurring, but rather that every observer in an expanding universe will see objects receding from them.
Ultimate fate and age of the universe[edit]
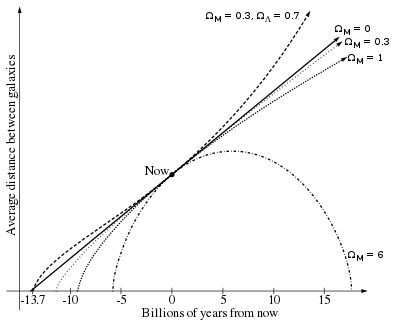
The age and ultimate fate of the universe can be determined by measuring the Hubble constant today and extrapolating with the observed value of the deceleration parameter, uniquely characterized by values of density parameters (ΩM for matter and ΩΛ for dark energy). A «closed universe» with ΩM > 1 and ΩΛ = 0 comes to an end in a Big Crunch and is considerably younger than its Hubble age. An «open universe» with ΩM ≤ 1 and ΩΛ = 0 expands forever and has an age that is closer to its Hubble age. For the accelerating universe with nonzero ΩΛ that we inhabit, the age of the universe is coincidentally very close to the Hubble age.
The value of the Hubble parameter changes over time, either increasing or decreasing depending on the value of the so-called deceleration parameter 
In a universe with a deceleration parameter equal to zero, it follows that H = 1/t, where t is the time since the Big Bang. A non-zero, time-dependent value of 
It was long thought that q was positive, indicating that the expansion is slowing down due to gravitational attraction. This would imply an age of the universe less than 1/H (which is about 14 billion years). For instance, a value for q of 1/2 (once favoured by most theorists) would give the age of the universe as 2/(3H). The discovery in 1998 that q is apparently negative means that the universe could actually be older than 1/H. However, estimates of the age of the universe are very close to 1/H.
Olbers’ paradox[edit]
The expansion of space summarized by the Big Bang interpretation of Hubble’s law is relevant to the old conundrum known as Olbers’ paradox: If the universe were infinite in size, static, and filled with a uniform distribution of stars, then every line of sight in the sky would end on a star, and the sky would be as bright as the surface of a star. However, the night sky is largely dark.[43][44]
Since the 17th century, astronomers and other thinkers have proposed many possible ways to resolve this paradox, but the currently accepted resolution depends in part on the Big Bang theory, and in part on the Hubble expansion: In a universe that exists for a finite amount of time, only the light of a finite number of stars has had enough time to reach us, and the paradox is resolved. Additionally, in an expanding universe, distant objects recede from us, which causes the light emanated from them to be redshifted and diminished in brightness by the time we see it.[43][44]
Dimensionless Hubble constant[edit]
Instead of working with Hubble’s constant, a common practice is to introduce the dimensionless Hubble constant, usually denoted by h and commonly referred to as «little h»,[45] then to write Hubble’s constant H0 as h × 100 km⋅s−1⋅Mpc−1, all the relative uncertainty of the true value of H0 being then relegated to h.[46] The dimensionless Hubble constant is often used when giving distances that are calculated from redshift z using the formula d ≈ c/H0 × z. Since H0 is not precisely known, the distance is expressed as:
In other words, one calculates 2998×z and one gives the units as 

Occasionally a reference value other than 100 may be chosen, in which case a subscript is presented after h to avoid confusion; e.g. h70 denotes 

This should not be confused with the dimensionless value of Hubble’s constant, usually expressed in terms of Planck units, obtained by multiplying H0 by 1.75 × 10−63 (from definitions of parsec and tP), for example for H0 = 70, a Planck unit version of 1.2 × 10−61 is obtained.
Acceleration of the expansion[edit]
A value for 
Derivation of the Hubble parameter[edit]
Start with the Friedmann equation:
where 



Matter-dominated universe (with a cosmological constant)[edit]
If the universe is matter-dominated, then the mass density of the universe 
where 

therefore:
Also, by definition,
where the subscript nought refers to the values today, and 


Matter- and dark energy-dominated universe[edit]
If the universe is both matter-dominated and dark energy-dominated, then the above equation for the Hubble parameter will also be a function of the equation of state of dark energy. So now:
where 

If w is constant, then
implying:
Therefore, for dark energy with a constant equation of state w, 

If the dark energy derives from a cosmological constant such as that introduced by Einstein, it can be shown that 


and
If dark energy does not have a constant equation-of-state w, then
and to solve this, 

[49]
Other ingredients have been formulated recently.[50][51][52]
Units derived from the Hubble constant[edit]
Hubble time[edit]
The Hubble constant 
This is slightly different from the age of the universe, which is approximately 13.8 billion years. The Hubble time is the age it would have had if the expansion had been linear, and it is different from the real age of the universe because the expansion is not linear; it depends on the energy content of the universe (see § Derivation of the Hubble parameter).
We currently appear to be approaching a period where the expansion of the universe is exponential due to the increasing dominance of vacuum energy. In this regime, the Hubble parameter is constant, and the universe grows by a factor e each Hubble time:
Likewise, the generally accepted value of 2.27 Es−1 means that (at the current rate) the universe would grow by a factor of 
Over long periods of time, the dynamics are complicated by general relativity, dark energy, inflation, etc., as explained above.
Hubble length[edit]
The Hubble length or Hubble distance is a unit of distance in cosmology, defined as 

Hubble volume[edit]
The Hubble volume is sometimes defined as a volume of the universe with a comoving size of 


Determining the Hubble constant[edit]
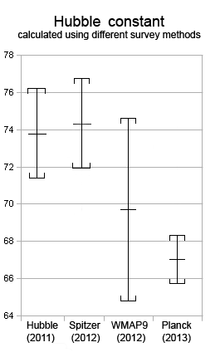
Value of the Hubble constant, including measurement uncertainty for recent surveys[54]
The value of the Hubble constant is estimated by measuring the redshift of distant galaxies and then determining the distances to them by some other method than Hubble’s law. This approach forms part of the cosmic distance ladder for measuring distances to extragalactic objects. Uncertainties in the physical assumptions used to determine these distances have caused varying estimates of the Hubble constant.[2]
Hubble tension[edit]
Multiple methods have been used to determine the Hubble constant. «Late universe» measurements using calibrated distance ladder techniques have converged on a value of approximately 73 (km/s)/Mpc. Since 2000, «early universe» techniques based on measurements of the cosmic microwave background have become available, and these agree on a value near 67.7 (km/s)/Mpc. (This is accounting for the change in the expansion rate since the early universe, so is comparable to the first number.) As techniques have improved, the estimated measurement uncertainties have shrunk, but the range of measured values has not, to the point that the disagreement is now highly statistically significant. This discrepancy is called the Hubble tension.[55][56]
In December 2021, National Geographic reported that the cause of the Hubble tension discrepancy is not known.[57] However, if the cosmological principle fails (see «Violations of the cosmological principle» in the «Lambda-CDM model» article), then the existing interpretations of the Hubble constant and the Hubble tension have to be revised, which might resolve the Hubble tension.[58]
One possibility is that the Hubble tension is caused by the KBC Void, as measuring galactic supernovae inside a void is predicted by some authors to yield a larger local value for the Hubble constant than cosmological measures of the Hubble constant.[59] However, other work has found no evidence for this in observations, finding the scale of the claimed underdensity to be incompatible with observations which extend beyond its radius.[60] Important deficiencies were subsequently pointed out in this analysis, leaving open the possibility that the Hubble tension is indeed caused by outflow from the KBC Void.[61]
Another possibility is that the Hubble tension calls for new physics beyond the ΛCDM model.[56] Moritz Haslbauer and collaborators have proposed modified Newtonian dynamics as a possible solution to the Hubble tension,[61] while Marc Kamionkowski and collaborators have proposed an early dark energy model as a possible solution to the Hubble tension.[62]
Others have suggested that at least a portion of the tension could be a result of underestimation of uncertainties in data.[63][64]
Earlier measurement and discussion approaches[edit]
The observations of astronomer Walter Baade led him to define distinct «populations» for stars (Population I and Population II). The same observations led him to discover that there are two types of Cepheid variable stars. Using this discovery, he recalculated the size of the known universe, doubling the previous calculation made by Hubble in 1929.[65][66][67] He announced this finding to considerable astonishment at the 1952 meeting of the International Astronomical Union in Rome.
For most of the second half of the 20th century, the value of 
The value of the Hubble constant was the topic of a long and rather bitter controversy between Gérard de Vaucouleurs, who claimed the value was around 100, and Allan Sandage, who claimed the value was near 50.[68] In one demonstration of vitriol shared between the parties, when Sandage and Gustav Andreas Tammann (Sandage’s research colleague) formally acknowledged the shortcomings of confirming the systematic error of their method in 1975, Vaucouleurs responded “It is unfortunate that this sober warning was so soon forgotten and ignored by most astronomers and textbook writers”.[69] In 1996, a debate moderated by John Bahcall between Sidney van den Bergh and Gustav Tammann was held in similar fashion to the earlier Shapley–Curtis debate over these two competing values.
This previously wide variance in estimates was partially resolved with the introduction of the ΛCDM model of the universe in the late 1990s. With the ΛCDM model observations of high-redshift clusters at X-ray and microwave wavelengths using the Sunyaev–Zel’dovich effect, measurements of anisotropies in the cosmic microwave background radiation, and optical surveys all gave a value of around 70 for the constant.[citation needed]
21st century measurements[edit]
Landscape of H0 measurements around 2021 with Planck (2018) and SH0ES (2020) values highlighted in pink and cyan respectively.[56]
More recent measurements from the Planck mission published in 2018 indicate a lower value of 67.66±0.42 (km/s)/Mpc, although, even more recently, in March 2019, a higher value of 74.03±1.42 (km/s)/Mpc has been determined using an improved procedure involving the Hubble Space Telescope.[70] The two measurements disagree at the 4.4σ level, beyond a plausible level of chance.[71] The resolution to this disagreement is an ongoing area of active research.[72]
In October 2018, scientists presented a new third way (two earlier methods, one based on redshifts and another on the cosmic distance ladder, gave results that do not agree), using information from gravitational wave events (especially those involving the merger of neutron stars, like GW170817), of determining the Hubble constant.[73][74]
In July 2019, astronomers reported that a new method to determine the Hubble constant, and resolve the discrepancy of earlier methods, has been proposed based on the mergers of pairs of neutron stars, following the detection of the neutron star merger of GW170817, an event known as a dark siren.[75][76] Their measurement of the Hubble constant is 73.3+5.3
−5.0 (km/s)/Mpc.[77]
Also in July 2019, astronomers reported another new method, using data from the Hubble Space Telescope and based on distances to red giant stars calculated using the tip of the red-giant branch (TRGB) distance indicator. Their measurement of the Hubble constant is 69.8+1.9
−1.9 (km/s)/Mpc.[78][79][80]
In February 2020, the Megamaser Cosmology Project published independent results that confirmed the distance ladder results and differed from the early-universe results at a statistical significance level of 95%.[81] In July 2020, measurements of the cosmic background radiation by the Atacama Cosmology Telescope predict that the Universe should be expanding more slowly than is currently observed.[82]
Estimated values of the Hubble constant, 2001–2020. Estimates in black represent calibrated distance ladder measurements which tend to cluster around 73 (km/s)/Mpc; red represents early universe CMB/BAO measurements with ΛCDM parameters which show good agreement on a figure near 67 (km/s)/Mpc, while blue are other techniques, whose uncertainties are not yet small enough to decide between the two.
| Date published | Hubble constant (km/s)/Mpc |
Observer | Citation | Remarks / methodology |
|---|---|---|---|---|
| 2023-05-11 | 66.6+4.1 −3.3 |
P. L. Kelly et al. | [83] | Timing delay of gravitationally lensed images of Supernova Refsdal. Independent of cosmic distance ladder or the CMB. |
| 2022-12-12 | 68.3±1.5 | SPT-3G | [84] | CMB TT/TE/EE power spectrum. Less than 1σ discrepancy with planck. (Preprint) |
| 2022-02-08 | 73.4+0.99 −1.22 |
Pantheon+ | [85] | SN Ia distance ladder (+SH0ES) |
| 2022-06-17 | 75.4+3.8 −3.7 |
T. de Jaeger et al. | [86] | Use Type II supernovae as standardisable candles to obtain an independent measurement of the Hubble constant—13 SNe II with host-galaxy distances measured from Cepheid variables, the tip of the red giant branch, and geometric distance (NGC 4258)— |
| 2021-12-08 | 73.04±1.04 | SH0ES | [87] | Cepheids-SN Ia distance ladder (HST+Gaia EDR3+»Pantheon+»). 5σ discrepancy with planck. |
| 2021-09-17 | 69.8±1.7 | W. Freedman | [88] | Tip of the red-giant branch (TRGB) distance indicator (HST+Gaia EDR3) |
| 2020-12-16 | 72.1±2.0 | Hubble Space Telescope and Gaia EDR3 | [89] | Combining earlier work on red giant stars, using the tip of the red-giant branch (TRGB) distance indicator, with parallax measurements of Omega Centauri from Gaia EDR3. |
| 2020-12-15 | 73.2±1.3 | Hubble Space Telescope and Gaia EDR3 | [90] | Combination of HST photometry and Gaia EDR3 parallaxes for Milky Way Cepheids, reducing the uncertainty in calibration of Cepheid luminosities to 1.0%. Overall uncertainty in the value for  is 1.8%, which is expected to be reduced to 1.3% with a larger sample of type Ia supernovae in galaxies that are known Cepheid hosts. Continuation of a collaboration known as Supernovae, is 1.8%, which is expected to be reduced to 1.3% with a larger sample of type Ia supernovae in galaxies that are known Cepheid hosts. Continuation of a collaboration known as Supernovae,  , for the Equation of State of Dark Energy (SHoES). , for the Equation of State of Dark Energy (SHoES).
|
| 2020-12-04 | 73.5±5.3 | E. J. Baxter, B. D. Sherwin | [91] | Gravitational lensing in the CMB is used to estimate  without referring to the sound horizon scale, providing an alternative method to analyze the Planck data. without referring to the sound horizon scale, providing an alternative method to analyze the Planck data.
|
| 2020-11-25 | 71.8+3.9 −3.3 |
P. Denzel et al. | [92] | Eight quadruply lensed galaxy systems are used to determine  to a precision of 5%, in agreement with both «early» and «late» universe estimates. Independent of distance ladders and the cosmic microwave background. to a precision of 5%, in agreement with both «early» and «late» universe estimates. Independent of distance ladders and the cosmic microwave background.
|
| 2020-11-07 | 67.4 ± 1.0 | T. Sedgwick et al. | [93] | Derived from 88 0.02 <  < 0.05 Type Ia supernovae used as standard candle distance indicators. The < 0.05 Type Ia supernovae used as standard candle distance indicators. The  estimate is corrected for the effects of peculiar velocities in the supernova environments, as estimated from the galaxy density field. The result assumes Ωm = 0.3, ΩΛ = 0.7 and a sound horizon of 149.3 Mpc, a value taken from Anderson et al. (2014).[94] estimate is corrected for the effects of peculiar velocities in the supernova environments, as estimated from the galaxy density field. The result assumes Ωm = 0.3, ΩΛ = 0.7 and a sound horizon of 149.3 Mpc, a value taken from Anderson et al. (2014).[94]
|
| 2020-09-29 | 67.6+4.3 −4.2 |
S. Mukherjee et al. | [95] | Gravitational waves, assuming that the transient ZTF19abanrh found by the Zwicky Transient Facility is the optical counterpart to GW190521. Independent of distance ladders and the cosmic microwave background. |
| 2020-06-18 | 75.8+5.2 −4.9 |
T. de Jaeger et al. | [96] | Use Type II supernovae as standardisable candles to obtain an independent measurement of the Hubble constant—7 SNe II with host-galaxy distances measured from Cepheid variables or the tip of the red giant branch— |
| 2020-02-26 | 73.9±3.0 | Megamaser Cosmology Project | [81] | Geometric distance measurements to megamaser-hosting galaxies. Independent of distance ladders and the cosmic microwave background. |
| 2019-10-14 | 74.2+2.7 −3.0 |
STRIDES | [97] | Modelling the mass distribution & time delay of the lensed quasar DES J0408-5354. |
| 2019-09-12 | 76.8±2.6 | SHARP/H0LiCOW | [98] | Modelling three galactically lensed objects and their lenses using ground-based adaptive optics and the Hubble Space Telescope. |
| 2019-08-20 | 73.3+1.36 −1.35 |
K. Dutta et al. | [99] | This  is obtained analysing low-redshift cosmological data within ΛCDM model. The datasets used are type-Ia supernovae, baryon acoustic oscillations, time-delay measurements using strong-lensing, is obtained analysing low-redshift cosmological data within ΛCDM model. The datasets used are type-Ia supernovae, baryon acoustic oscillations, time-delay measurements using strong-lensing,  measurements using cosmic chronometers and growth measurements from large scale structure observations. measurements using cosmic chronometers and growth measurements from large scale structure observations.
|
| 2019-08-15 | 73.5±1.4 | M. J. Reid, D. W. Pesce, A. G. Riess | [100] | Measuring the distance to Messier 106 using its supermassive black hole, combined with measurements of eclipsing binaries in the Large Magellanic Cloud |
| 2019-07-16 | 69.8±1.9 | Hubble Space Telescope | [78][79][80] | Distances to red giant stars are calculated using the tip of the red-giant branch (TRGB) distance indicator. |
| 2019-07-10 | 73.3+1.7 −1.8 |
H0LiCOW collaboration | [101] | Updated observations of multiply imaged quasars, now using six quasars, independent of the cosmic distance ladder and independent of the cosmic microwave background measurements. |
| 2019-07-08 | 70.3+5.3 −5.0 |
LIGO and Virgo detectors | [77] | Uses radio counterpart of GW170817, combined with earlier gravitational wave (GW) and electromagnetic (EM) data. |
| 2019-03-28 | 68.0+4.2 −4.1 |
Fermi-LAT | [102] | Gamma ray attenuation due to extragalactic light. Independent of the cosmic distance ladder and the cosmic microwave background. |
| 2019-03-18 | 74.03±1.42 | Hubble Space Telescope | [71] | Precision HST photometry of Cepheids in the Large Magellanic Cloud (LMC) reduce the uncertainty in the distance to the LMC from 2.5% to 1.3%. The revision increases the tension with CMB measurements to the 4.4σ level (P=99.999% for Gaussian errors), raising the discrepancy beyond a plausible level of chance. Continuation of a collaboration known as Supernovae,  , for the Equation of State of Dark Energy (SHoES). , for the Equation of State of Dark Energy (SHoES).
|
| 2019-02-08 | 67.78+0.91 −0.87 |
Joseph Ryan et al. | [103] | Quasar angular size and baryon acoustic oscillations, assuming a flat ΛCDM model. Alternative models result in different (generally lower) values for the Hubble constant. |
| 2018-11-06 | 67.77±1.30 | Dark Energy Survey | [104] | Supernova measurements using the inverse distance ladder method based on baryon acoustic oscillations. |
| 2018-09-05 | 72.5+2.1 −2.3 |
H0LiCOW collaboration | [105] | Observations of multiply imaged quasars, independent of the cosmic distance ladder and independent of the cosmic microwave background measurements. |
| 2018-07-18 | 67.66±0.42 | Planck Mission | [106] | Final Planck 2018 results. |
| 2018-04-27 | 73.52±1.62 | Hubble Space Telescope and Gaia | [107][108] | Additional HST photometry of galactic Cepheids with early Gaia parallax measurements. The revised value increases tension with CMB measurements at the 3.8σ level. Continuation of the SHoES collaboration. |
| 2018-02-22 | 73.45±1.66 | Hubble Space Telescope | [109][110] | Parallax measurements of galactic Cepheids for enhanced calibration of the distance ladder; the value suggests a discrepancy with CMB measurements at the 3.7σ level. The uncertainty is expected to be reduced to below 1% with the final release of the Gaia catalog. SHoES collaboration. |
| 2017-10-16 | 70.0+12.0 −8.0 |
The LIGO Scientific Collaboration and The Virgo Collaboration | [111] | Standard siren measurement independent of normal «standard candle» techniques; the gravitational wave analysis of a binary neutron star (BNS) merger GW170817 directly estimated the luminosity distance out to cosmological scales. An estimate of fifty similar detections in the next decade may arbitrate tension of other methodologies.[112] Detection and analysis of a neutron star-black hole merger (NSBH) may provide greater precision than BNS could allow.[113] |
| 2016-11-22 | 71.9+2.4 −3.0 |
Hubble Space Telescope | [114] | Uses time delays between multiple images of distant variable sources produced by strong gravitational lensing. Collaboration known as  Lenses in COSMOGRAIL’s Wellspring (H0LiCOW). Lenses in COSMOGRAIL’s Wellspring (H0LiCOW).
|
| 2016-08-04 | 76.2+3.4 −2.7 |
Cosmicflows-3 | [115] | Comparing redshift to other distance methods, including Tully–Fisher, Cepheid variable, and Type Ia supernovae. A restrictive estimate from the data implies a more precise value of 75±2. |
| 2016-07-13 | 67.6+0.7 −0.6 |
SDSS-III Baryon Oscillation Spectroscopic Survey (BOSS) | [116] | Baryon acoustic oscillations. An extended survey (eBOSS) began in 2014 and is expected to run through 2020. The extended survey is designed to explore the time when the universe was transitioning away from the deceleration effects of gravity from 3 to 8 billion years after the Big Bang.[117] |
| 2016-05-17 | 73.24±1.74 | Hubble Space Telescope | [118] | Type Ia supernova, the uncertainty is expected to go down by a factor of more than two with upcoming Gaia measurements and other improvements. SHoES collaboration. |
| 2015-02 | 67.74±0.46 | Planck Mission | [119][120] | Results from an analysis of Planck‘s full mission were made public on 1 December 2014 at a conference in Ferrara, Italy. A full set of papers detailing the mission results were released in February 2015. |
| 2013-10-01 | 74.4±3.0 | Cosmicflows-2 | [121] | Comparing redshift to other distance methods, including Tully–Fisher, Cepheid variable, and Type Ia supernovae. |
| 2013-03-21 | 67.80±0.77 | Planck Mission | [54][122][123][124][125] | The ESA Planck Surveyor was launched in May 2009. Over a four-year period, it performed a significantly more detailed investigation of cosmic microwave radiation than earlier investigations using HEMT radiometers and bolometer technology to measure the CMB at a smaller scale than WMAP. On 21 March 2013, the European-led research team behind the Planck cosmology probe released the mission’s data including a new CMB all-sky map and their determination of the Hubble constant. |
| 2012-12-20 | 69.32±0.80 | WMAP (9 years), combined with other measurements | [126] | |
| 2010 | 70.4+1.3 −1.4 |
WMAP (7 years), combined with other measurements | [127] | These values arise from fitting a combination of WMAP and other cosmological data to the simplest version of the ΛCDM model. If the data are fit with more general versions, H0 tends to be smaller and more uncertain: typically around 67±4 (km/s)/Mpc although some models allow values near 63 (km/s)/Mpc.[128] |
| 2010 | 71.0±2.5 | WMAP only (7 years). | [127] | |
| 2009-02 | 70.5±1.3 | WMAP (5 years), combined with other measurements | [129] | |
| 2009-02 | 71.9+2.6 −2.7 |
WMAP only (5 years) | [129] | |
| 2007 | 70.4+1.5 −1.6 |
WMAP (3 years), combined with other measurements | [130] | |
| 2006-08 | 76.9+10.7 −8.7 |
Chandra X-ray Observatory | [131] | Combined Sunyaev–Zeldovich effect and Chandra X-ray observations of galaxy clusters. Adjusted uncertainty in table from Planck Collaboration 2013.[132] |
| 2003 | 72 ± 5 | WMAP (First year) only | .[133] | |
| 2001-05 | 72±8 | Hubble Space Telescope Key Project | [26] | This project established the most precise optical determination, consistent with a measurement of H0 based upon Sunyaev–Zel’dovich effect observations of many galaxy clusters having a similar accuracy. |
| before 1996 | 50–90 (est.) | [68] | ||
| 1994 | 67 ± 7 | Supernova 1a Light Curve Shapes | [134] | Determined relationship between luminosity of SN 1a’s and their Light Curve Shapes. Riess et al used this ratio of the light curve of SN 1972E and the Cepheid distance to NGC 5253 to determine the constant. |
| mid 1970’s | 100 ± 10 | Gérard de Vaucouleurs | [69] | De Vaucouleurs believed he had improved the accuracy of Hubble’s constant from Sandage’s because he used 5x more primary indicators, 10x more calibration methods, 2x more secondary indicators, and 3x as many galaxy data points to derive his 100 ± 10. |
| early 1970s | ≈ 55 (est.) | Allan Sandage and Gustav Tammann | [135] | |
| 1958 | 75 (est.) | Allan Sandage | [136] | This was the first good estimate of H0, but it would be decades before a consensus was achieved. |
| 1956 | 180 | Humason, Mayall and Sandage | [135] | |
| 1929 | 500 | Edwin Hubble, Hooker telescope | [137][135][138] | |
| 1927 | 625 | Georges Lemaître | [139] | First measurement and interpretation as a sign of the expansion of the universe |
See also[edit]
- Accelerating expansion of the universe
- Cosmology
- Dark matter
- List of scientists whose names are used in physical constants
- Tests of general relativity
References[edit]
- ^ «IAU members vote to recommend renaming the Hubble law as the Hubble–Lemaître law» (Press release). IAU. 29 October 2018. Retrieved 2018-10-29.
- ^ a b c Overbye, Dennis (20 February 2017). «Cosmos Controversy: The Universe Is Expanding, but How Fast?». New York Times. Retrieved 21 February 2017.
- ^
Coles, P., ed. (2001). Routledge Critical Dictionary of the New Cosmology. Routledge. p. 202. ISBN 978-0-203-16457-0. - ^
«Hubble Flow». The Swinburne Astronomy Online Encyclopedia of Astronomy. Swinburne University of Technology. Retrieved 2013-05-14. - ^
van den Bergh, S. (2011). «The Curious Case of Lemaitre’s Equation No. 24». Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195. Bibcode:2011JRASC.105..151V. - ^
Nussbaumer, H.; Bieri, L. (2011). «Who discovered the expanding universe?». The Observatory. 131 (6): 394–398. arXiv:1107.2281. Bibcode:2011Obs…131..394N. - ^
Way, M.J. (2013). «Dismantling Hubble’s Legacy?». ASP Conference Proceedings. 471: 97–132. arXiv:1301.7294. Bibcode:2013ASPC..471…97W. - ^ Friedman, A. (December 1922). «Über die Krümmung des Raumes». Zeitschrift für Physik. 10 (1): 377–386. Bibcode:1922ZPhy…10..377F. doi:10.1007/BF01332580. S2CID 125190902.. (English translation in Friedman, A. (December 1999). «On the Curvature of Space». General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995.)
- ^
Lemaître, G. (1927). «Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques». Annales de la Société Scientifique de Bruxelles A. 47: 49–59. Bibcode:1927ASSB…47…49L. Partially translated in Lemaître, G. (1931). «Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae». Monthly Notices of the Royal Astronomical Society. 91 (5): 483–490. Bibcode:1931MNRAS..91..483L. doi:10.1093/mnras/91.5.483. - ^ a b
Livio, M. (2011). «Lost in translation: Mystery of the missing text solved». Nature. 479 (7372): 171–3. Bibcode:2011Natur.479..171L. doi:10.1038/479171a. PMID 22071745. S2CID 203468083. - ^
Livio, M.; Riess, A. (2013). «Measuring the Hubble constant». Physics Today. 66 (10): 41. Bibcode:2013PhT….66j..41L. doi:10.1063/PT.3.2148. - ^ Hubble, E. (1929). «A relation between distance and radial velocity among extra-galactic nebulae». Proceedings of the National Academy of Sciences. 15 (3): 168–73. Bibcode:1929PNAS…15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.
- ^ Slipher, V.M. (1917). «Radial velocity observations of spiral nebulae». The Observatory. 40: 304–306. Bibcode:1917Obs….40..304S.
- ^ Longair, M. S. (2006). The Cosmic Century. Cambridge University Press. p. 109. ISBN 978-0-521-47436-8.
- ^ Nussbaumer, Harry (2013). ‘Slipher’s redshifts as support for de Sitter’s model and the discovery of the dynamic universe’ In Origins of the Expanding Universe: 1912-1932. Astronomical Society of the Pacific. pp. 25–38. arXiv:1303.1814.
- ^ Overbye, Dennis (25 February 2019). «Have Dark Forces Been Messing With the Cosmos? – Axions? Phantom energy? Astrophysicists scramble to patch a hole in the universe, rewriting cosmic history in the process». The New York Times. Retrieved 26 February 2019.
- ^ O’Raifeartaigh, Cormac (2013). The Contribution of V.M. Slipher to the discovery of the expanding universe in ‘Origins of the Expanding Universe’. Astronomical Society of the Pacific. pp. 49–62. arXiv:1212.5499.
- ^ «Three steps to the Hubble constant». www.spacetelescope.org. Retrieved 26 February 2018.
- ^
Slipher, V. M. (1913). «The Radial Velocity of the Andromeda Nebula». Lowell Observatory Bulletin. 1 (8): 56–57. Bibcode:1913LowOB…2…56S. - ^
Slipher, V. M. (1915). «Spectrographic Observations of Nebulae». Popular Astronomy. 23: 21–24. Bibcode:1915PA…..23…21S. - ^
Friedman, A. (1922). «Über die Krümmung des Raumes». Zeitschrift für Physik. 10 (1): 377–386. Bibcode:1922ZPhy…10..377F. doi:10.1007/BF01332580. S2CID 125190902. Translated in
Friedmann, A. (1999). «On the Curvature of Space». General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995. - ^ van den Bergh, Sydney (2011). «The Curious Case of Lemaître’s Equation No. 24». Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195. Bibcode:2011JRASC.105..151V.
- ^ Block, David (2012). ‘Georges Lemaitre and Stigler’s law of eponymy’ in Georges Lemaître: Life, Science and Legacy (Holder and Mitton ed.). Springer. pp. 89–96.
- ^ Sandage, Allan (December 1989). «Edwin Hubble 1889-1953». Journal of the Royal Astronomical Society of Canada. 83 (6): 351–362.
- ^ a b Keel, W. C. (2007). The Road to Galaxy Formation (2nd ed.). Springer. pp. 7–8. ISBN 978-3-540-72534-3.
- ^ a b
Freedman, W. L.; et al. (2001). «Final results from the Hubble Space Telescope Key Project to measure the Hubble constant». The Astrophysical Journal. 553 (1): 47–72. arXiv:astro-ph/0012376. Bibcode:2001ApJ…553…47F. doi:10.1086/320638. S2CID 119097691. - ^
Weinberg, S. (2008). Cosmology. Oxford University Press. p. 28. ISBN 978-0-19-852682-7. - ^
Bunn, E. F. (2009). «The kinematic origin of the cosmological redshift». American Journal of Physics. 77 (8): 688–694. arXiv:0808.1081. Bibcode:2009AmJPh..77..688B. doi:10.1119/1.3129103. S2CID 1365918. - ^
Kirshner, R. P. (2003). «Hubble’s diagram and cosmic expansion». Proceedings of the National Academy of Sciences. 101 (1): 8–13. Bibcode:2003PNAS..101….8K. doi:10.1073/pnas.2536799100. PMC 314128. PMID 14695886. - ^ a b
«What is a Cosmological Constant?». Goddard Space Flight Center. Retrieved 2013-10-17. - ^
Isaacson, W. (2007). Einstein: His Life and Universe. Simon & Schuster. p. 354. ISBN 978-0-7432-6473-0. - ^
«Einstein’s Biggest Blunder? Dark Energy May Be Consistent With Cosmological Constant». Science Daily. 28 November 2007. Retrieved 2013-06-02. - ^
Davis, T. M.; Lineweaver, C. H. (2001). «Superluminal Recessional Velocities». AIP Conference Proceedings. 555: 348–351. arXiv:astro-ph/0011070. Bibcode:2001AIPC..555..348D. CiteSeerX 10.1.1.254.1810. doi:10.1063/1.1363540. S2CID 118876362. - ^ «Is the universe expanding faster than the speed of light?». Ask an Astronomer at Cornell University. Archived from the original on 23 November 2003. Retrieved 5 June 2015.
- ^ Harrison, E. (1992). «The redshift-distance and velocity-distance laws». The Astrophysical Journal. 403: 28–31. Bibcode:1993ApJ…403…28H. doi:10.1086/172179.
- ^
Madsen, M. S. (1995). The Dynamic Cosmos. CRC Press. p. 35. ISBN 978-0-412-62300-4. - ^ Dekel, A.; Ostriker, J. P. (1999). Formation of Structure in the Universe. Cambridge University Press. p. 164. ISBN 978-0-521-58632-0.
- ^ Padmanabhan, T. (1993). Structure formation in the universe. Cambridge University Press. p. 58. ISBN 978-0-521-42486-8.
- ^
Sartori, L. (1996). Understanding Relativity. University of California Press. p. 163, Appendix 5B. ISBN 978-0-520-20029-6. - ^ Sartori, L. (1996). Understanding Relativity. University of California Press. pp. 304–305. ISBN 978-0-520-20029-6.
- ^ «Introduction to Cosmology», Matts Roos
- ^ Scharping, Nathaniel (18 October 2017). «Gravitational Waves Show How Fast The Universe is Expanding». Astronomy. Retrieved 18 October 2017.
- ^ a b Chase, S. I.; Baez, J. C. (2004). «Olbers’ Paradox». The Original Usenet Physics FAQ. Retrieved 2013-10-17.
- ^ a b Asimov, I. (1974). «The Black of Night». Asimov on Astronomy. Doubleday. ISBN 978-0-385-04111-9.
- ^ Croton, Darren J. (14 October 2013). «Damn You, Little h! (Or, Real-World Applications of the Hubble Constant Using Observed and Simulated Data)». Publications of the Astronomical Society of Australia. 30. arXiv:1308.4150. Bibcode:2013PASA…30…52C. doi:10.1017/pasa.2013.31. S2CID 119257465. Retrieved 8 December 2021.
- ^
Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton University Press. - ^
Perlmutter, S. (2003). «Supernovae, Dark Energy, and the Accelerating Universe» (PDF). Physics Today. 56 (4): 53–60. Bibcode:2003PhT….56d..53P. CiteSeerX 10.1.1.77.7990. doi:10.1063/1.1580050. Archived (PDF) from the original on 2022-10-09. - ^ Carroll, Sean (2004). Spacetime and Geometry: An Introduction to General Relativity (illustrated ed.). San Francisco: Addison-Wesley. p. 328. ISBN 978-0-8053-8732-2.
- ^
Heneka, C.; Amendola, L. (2018). «General modified gravity with 21cm intensity mapping: simulations and forecast». Journal of Cosmology and Astroparticle Physics. 85 (8): 084032. arXiv:1108.5697. Bibcode:2012PhRvD..85h4032T. doi:10.1103/PhysRevD.85.084032. S2CID 73716828. - ^
Tawfik, A.; Harko, T. (2012). «Quark-hadron phase transitions in the viscous early universe». Physical Review D. 85 (8): 084032. arXiv:1108.5697. Bibcode:2012PhRvD..85h4032T. doi:10.1103/PhysRevD.85.084032. S2CID 73716828. - ^
Tawfik, A. (2011). «The Hubble parameter in the early universe with viscous QCD matter and finite cosmological constant». Annalen der Physik. 523 (5): 423–434. arXiv:1102.2626. Bibcode:2011AnP…523..423T. doi:10.1002/andp.201100038. S2CID 118500485. - ^
Tawfik, A.; Wahba, M.; Mansour, H.; Harko, T. (2011). «Viscous quark-gluon plasma in the early universe». Annalen der Physik. 523 (3): 194–207. arXiv:1001.2814. Bibcode:2011AnP…523..194T. doi:10.1002/andp.201000052. S2CID 119271582. - ^ Hawley, John F.; Holcomb, Katherine A. (2005). Foundations of modern cosmology (2nd ed.). Oxford [u.a.]: Oxford Univ. Press. p. 304. ISBN 978-0-19-853096-1.
- ^ a b
Bucher, P. A. R.; et al. (Planck Collaboration) (2013). «Planck 2013 results. I. Overview of products and scientific Results». Astronomy & Astrophysics. 571: A1. arXiv:1303.5062. Bibcode:2014A&A…571A…1P. doi:10.1051/0004-6361/201321529. S2CID 218716838. - ^ Mann, Adam (26 August 2019). «One Number Shows Something Is Fundamentally Wrong with Our Conception of the Universe — This fight has universal implications». Live Science. Retrieved 26 August 2019.
- ^ a b c di Valentino, Eleonora; et al. (2021). «In the realm of the Hubble tension—a review of solutions». Classical and Quantum Gravity. 38 (15): 153001. arXiv:2103.01183. Bibcode:2021CQGra..38o3001D. doi:10.1088/1361-6382/ac086d. S2CID 232092525.
- ^ Gresko, Michael (17 December 2021). «The universe is expanding faster than it should be». National Geographic. Retrieved 21 December 2021.
- ^ Elcio Abdalla; Guillermo Franco Abellán; et al. (11 Mar 2022), «Cosmology Intertwined: A Review of the Particle Physics, Astrophysics, and Cosmology Associated with the Cosmological Tensions and Anomalies», Journal of High Energy Astrophysics, 34: 49, arXiv:2203.06142v1, Bibcode:2022JHEAp..34…49A, doi:10.1016/j.jheap.2022.04.002, S2CID 247411131
- ^ Shanks, T; Hogarth, L M; Metcalfe, N (2019-03-21). «Gaia Cepheid parallaxes and ‘Local Hole’ relieve H 0 tension». Monthly Notices of the Royal Astronomical Society: Letters. 484 (1): L64–L68. arXiv:1810.02595. Bibcode:2019MNRAS.484L..64S. doi:10.1093/mnrasl/sly239. ISSN 1745-3925.
- ^ Kenworthy, W. D’Arcy; Scolnic, Dan; Riess, Adam (2019-04-24). «The Local Perspective on the Hubble Tension: Local Structure Does Not Impact Measurement of the Hubble Constant». The Astrophysical Journal. 875 (2): 145. arXiv:1901.08681. Bibcode:2019ApJ…875..145K. doi:10.3847/1538-4357/ab0ebf. ISSN 1538-4357. S2CID 119095484.
- ^ a b Haslbauer, M; Banik, I; Kroupa, P (2020-12-21). «The KBC void and Hubble tension contradict LCDM on a Gpc scale — Milgromian dynamics as a possible solution». Monthly Notices of the Royal Astronomical Society. 499 (2): 2845–2883. arXiv:2009.11292. Bibcode:2020MNRAS.499.2845H. doi:10.1093/mnras/staa2348. ISSN 0035-8711.
- ^ Poulin, Vivian; Smith, Tristan L.; Karwal, Tanvi; Kamionkowski, Marc (2019-06-04). «Early Dark Energy can Resolve the Hubble Tension». Physical Review Letters. 122 (22): 221301. arXiv:1811.04083. Bibcode:2019PhRvL.122v1301P. doi:10.1103/PhysRevLett.122.221301. PMID 31283280. S2CID 119233243.
| - ^ Rameez, Mohamed; Sarkar, Subir (15 July 2021). «Is there really a Hubble tension?». Classical and Quantum Gravity. 38 (15): 154005. arXiv:1911.06456. Bibcode:2021CQGra..38o4005R. doi:10.1088/1361-6382/ac0f39. ISSN 0264-9381. S2CID 208075753.
- ^ Singh, Ritesh (28 October 2021). «Evidence for possible systematic underestimation of uncertainties in extragalactic distances and its cosmological implications». Astrophysics and Space Science. 366 (10): 99. arXiv:2111.07872. Bibcode:2021Ap&SS.366…99S. doi:10.1007/s10509-021-04006-5. ISSN 1572-946X. S2CID 240179422.
- ^ Baade W (1944) The resolution of Messier 32, NGC 205, and the central region of the Andromeda nebula. ApJ 100 137-146
- ^ Baade W (1956) The period-luminosity relation of the Cepheids. PASP 68 5-16
- ^ Allen, Nick. «Section 2: The Great Debate and the Great Mistake: Shapley, Hubble, Baade». The Cepheid Distance Scale: A History. Archived from the original on 10 December 2007. Retrieved 19 November 2011.
- ^ a b
Overbye, D. (1999). «Prologue». Lonely Hearts of the Cosmos (2nd ed.). HarperCollins. p. 1ff. ISBN 978-0-316-64896-7. - ^ a b de Vaucouleurs, G. (1982). The cosmic distance scale and the Hubble constant. Mount Stromlo and Siding Spring Observatories, Australian National University.
- ^ Ananthaswamy, Anil (22 March 2019). «Best-Yet Measurements Deepen Cosmological Crisis». Scientific American. Retrieved 23 March 2019.
- ^ a b Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan (18 March 2019). «Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LambdaCDM». The Astrophysical Journal. 876 (1): 85. arXiv:1903.07603. Bibcode:2019ApJ…876…85R. doi:10.3847/1538-4357/ab1422. S2CID 85528549.
- ^ Millea, Marius; Knox, Lloyd (2019-08-10). «The Hubble Hunter’s Guide». arXiv:1908.03663v1 [astro-ph.CO].
- ^ Lerner, Louise (22 October 2018). «Gravitational waves could soon provide measure of universe’s expansion». Phys.org. Retrieved 22 October 2018.
- ^ Chen, Hsin-Yu; Fishbach, Maya; Holz, Daniel E. (17 October 2018). «A two per cent Hubble constant measurement from standard sirens within five years». Nature. 562 (7728): 545–547. arXiv:1712.06531. Bibcode:2018Natur.562..545C. doi:10.1038/s41586-018-0606-0. PMID 30333628. S2CID 52987203.
- ^ National Radio Astronomy Observatory (8 July 2019). «New method may resolve difficulty in measuring universe’s expansion — Neutron star mergers can provide new ‘cosmic ruler’«. EurekAlert!. Retrieved 8 July 2019.
- ^ Finley, Dave (8 July 2019). «New Method May Resolve Difficulty in Measuring Universe’s Expansion». National Radio Astronomy Observatory. Retrieved 8 July 2019.
- ^ a b Hotokezaka, K.; et al. (8 July 2019). «A Hubble constant measurement from superluminal motion of the jet in GW170817». Nature Astronomy. 3 (10): 940–944. arXiv:1806.10596. Bibcode:2019NatAs…3..940H. doi:10.1038/s41550-019-0820-1. S2CID 119547153.
- ^ a b Carnegie Institution of Science (16 July 2019). «New measurement of universe’s expansion rate is ‘stuck in the middle’ — Red giant stars observed by Hubble Space Telescope used to make an entirely new measurement of how fast the universe is expanding». EurekAlert!. Retrieved 16 July 2019.
- ^ a b Sokol, Joshua (19 July 2019). «Debate intensifies over speed of expanding universe». Science. doi:10.1126/science.aay8123. S2CID 200021863. Retrieved 20 July 2019.
- ^ a b Wendy L. Freedman; Madore, Barry F.; Hatt, Dylan; Hoyt, Taylor J.; et al. (2019). «The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch». The Astrophysical Journal. 882 (1): 34. arXiv:1907.05922. Bibcode:2019ApJ…882…34F. doi:10.3847/1538-4357/ab2f73. S2CID 196623652.
- ^ a b Pesce, D. W.; Braatz, J. A.; Reid, M. J.; Riess, A. G.; et al. (26 February 2020). «The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints». The Astrophysical Journal. 891 (1): L1. arXiv:2001.09213. Bibcode:2020ApJ…891L…1P. doi:10.3847/2041-8213/ab75f0. S2CID 210920444.
- ^ Castelvecchi, Davide (2020-07-15). «Mystery over Universe’s expansion deepens with fresh data». Nature. 583 (7817): 500–501. Bibcode:2020Natur.583..500C. doi:10.1038/d41586-020-02126-6. PMID 32669728. S2CID 220583383.
- ^ Kelly, P. L.; Rodney, S.; Treu, T.; Oguri, M.; Chen, W.; Zitri, A.; et al. (2023-05-11). «Constraints on the Hubble constant from Supernova Refsdal’s reappearance». Science. doi:10.1126/science.abh1322.
- ^ Balkenhol, L.; Dutcher, D.; Mancini, A. Spurio; Doussot, A.; Benabed, K.; Galli, S.; Ade, P. A. R.; Anderson, A. J.; Ansarinejad, B.; Archipley, M.; Bender, A. N.; Benson, B. A.; Bianchini, F.; Bleem, L. E.; Bouchet, F. R. (2022-12-14). «A Measurement of the CMB Temperature Power Spectrum and Constraints on Cosmology from the SPT-3G 2018 TT/TE/EE Data Set». arXiv:2212.05642 [astro-ph.CO].
- ^ Brout, Dillon; Scolnic, Dan; Popovic, Brodie; Riess, Adam G.; Zuntz, Joe; Kessler, Rick; Carr, Anthony; Davis, Tamara M.; Hinton, Samuel; Jones, David; Kenworthy, W. D’Arcy (2022-02-08). «The Pantheon+ Analysis: Cosmological Constraints». The Astrophysical Journal. 938 (2): 110. arXiv:2202.04077. Bibcode:2022ApJ…938..110B. doi:10.3847/1538-4357/ac8e04. S2CID 246679941.
- ^ de Jaeger, T.; Galbany, L.; Riess, A. G.; Stahl, Ben E.; et al. (17 June 2022). «A 5 per cent measurement of the Hubble–Lemaître constant from Type II supernovae». MNRAS. 514 (3): 4620–4628. arXiv:2203.08974.
- ^ Riess, Adam G.; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan; Brout, Dillon; Casertano, Stefano; Jones, David O.; Murakami, Yukei; Breuval, Louise; Brink, Thomas G.; Filippenko, Alexei V. (2021-12-08). «A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team». The Astrophysical Journal. 934 (1). arXiv:2112.04510. Bibcode:2022ApJ…934L…7R. doi:10.3847/2041-8213/ac5c5b. S2CID 245005861.
- ^ Freedman, Wendy L. (2021-09-01). «Measurements of the Hubble Constant: Tensions in Perspective*». The Astrophysical Journal. 919 (1): 16. arXiv:2106.15656. Bibcode:2021ApJ…919…16F. doi:10.3847/1538-4357/ac0e95. ISSN 0004-637X. S2CID 235683396.
- ^ Soltis, J.; Casertano, S.; Riess, A. G. (2021). «The Parallax of Omega Centauri Measured from Gaia EDR3 and a Direct, Geometric Calibration of the Tip of the Red Giant Branch and the Hubble Constant». The Astrophysical Journal. 908 (1): L5. arXiv:2012.09196. Bibcode:2021ApJ…908L…5S. doi:10.3847/2041-8213/abdbad. S2CID 229297709.
- ^ Riess, A. G.; Casertano, S.; Yuan, W.; Bowers, J. B.; et al. (2021). «Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with LambdaCDM». The Astrophysical Journal. 908 (1): L6. arXiv:2012.08534. Bibcode:2021ApJ…908L…6R. doi:10.3847/2041-8213/abdbaf. S2CID 229213131.
- ^ Baxter, E. J.; Sherwin, B. D. (February 2021). «Determining the Hubble constant without the sound horizon scale: measurements from CMB lensing». Monthly Notices of the Royal Astronomical Society. 501 (2): 1823–1835. arXiv:2007.04007. Bibcode:2021MNRAS.501.1823B. doi:10.1093/mnras/staa3706. S2CID 220404332.
- ^ Denzel, P.; Coles, J. P.; Saha, P.; Williams, L. L. R. (February 2021). «The Hubble constant from eight time-delay galaxy lenses». Monthly Notices of the Royal Astronomical Society. 501 (1): 784–801. arXiv:2007.14398. Bibcode:2021MNRAS.501..784D. doi:10.1093/mnras/staa3603. S2CID 220845622.
- ^ Sedgwick, Thomas M; Collins, Chris A; Baldry, Ivan K; James, Philip A (2020-11-07). «The effects of peculiar velocities in SN Ia environments on the local H0 measurement». Monthly Notices of the Royal Astronomical Society. 500 (3): 3728–3742. arXiv:1911.03155. doi:10.1093/mnras/staa3456. ISSN 0035-8711.
- ^ Anderson, Lauren; Aubourg, Éric; Bailey, Stephen; Beutler, Florian; Bhardwaj, Vaishali; Blanton, Michael; Bolton, Adam S.; Brinkmann, J.; Brownstein, Joel R.; Burden, Angela; Chuang, Chia-Hsun (2014-04-21). «The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples». Monthly Notices of the Royal Astronomical Society. 441 (1): 24–62. doi:10.1093/mnras/stu523. hdl:2445/101758. ISSN 1365-2966.
- ^ Mukherjee, S.; Ghosh, A.; Graham, M. J.; Karathanasis, C.; et al. (29 September 2020). «First measurement of the Hubble parameter from bright binary black hole GW190521». arXiv:2009.14199 [astro-ph.CO].
- ^ de Jaeger, T.; Stahl, B.; Zheng, W.; Filippenko, A.V.; et al. (18 June 2020). «A measurement of the Hubble constant from Type II supernovae». MNRAS. 496 (3): 3402–3411. arXiv:2006.03412. doi:10.1093/mnras/staa1801.
- ^ Shajib, A. J.; Birrer, S.; Treu, T.; Agnello, A.; et al. (14 October 2019). «STRIDES: A 3.9 per cent measurement of the Hubble constant from the strongly lensed system DES J0408-5354». Monthly Notices of the Royal Astronomical Society. arXiv:1910.06306. doi:10.1093/mnras/staa828. S2CID 204509190.
- ^ Chen, G.C.-F.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; et al. (12 September 2019). «A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging». Monthly Notices of the Royal Astronomical Society. 490 (2): 1743–1773. arXiv:1907.02533. Bibcode:2019MNRAS.490.1743C. doi:10.1093/mnras/stz2547. S2CID 195820422.
- ^ Dutta, Koushik; Roy, Anirban; Ruchika, Ruchika; Sen, Anjan A.; Sheikh-Jabbari, M. M. (20 August 2019). «Cosmology With Low-Redshift Observations: No Signal For New Physics». Phys. Rev. D. 100 (10): 103501. arXiv:1908.07267. Bibcode:2019PhRvD.100j3501D. doi:10.1103/PhysRevD.100.103501. S2CID 201107151.
- ^ Reid, M. J.; Pesce, D. W.; Riess, A. G. (15 August 2019). «An Improved Distance to NGC 4258 and its Implications for the Hubble Constant». The Astrophysical Journal. 886 (2): L27. arXiv:1908.05625. Bibcode:2019ApJ…886L..27R. doi:10.3847/2041-8213/ab552d. S2CID 199668809.
- ^ Kenneth C. Wong (2020). «H0LiCOW XIII. A 2.4% measurement of H0 from lensed quasars: 5.3σ tension between early and late-Universe probes». Monthly Notices of the Royal Astronomical Society. arXiv:1907.04869. doi:10.1093/mnras/stz3094. S2CID 195886279.
- ^ Domínguez, Alberto; et al. (28 March 2019). «A new measurement of the Hubble constant and matter content of the Universe using extragalactic background light γ-ray attenuation». The Astrophysical Journal. 885 (2): 137. arXiv:1903.12097. Bibcode:2019ApJ…885..137D. doi:10.3847/1538-4357/ab4a0e. S2CID 85543845.
- ^ Ryan, Joseph; Chen, Yun; Ratra, Bharat (8 February 2019). «Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature». Monthly Notices of the Royal Astronomical Society. 488 (3): 3844–3856. arXiv:1902.03196. Bibcode:2019MNRAS.488.3844R. doi:10.1093/mnras/stz1966. S2CID 119226802.
- ^ Macaulay, E; et al. (DES collaboration) (2018). «First Cosmological Results using Type Ia Supernovae from the Dark Energy Survey: Measurement of the Hubble Constant». Monthly Notices of the Royal Astronomical Society. 486 (2): 2184–2196. arXiv:1811.02376. doi:10.1093/mnras/stz978. S2CID 119310644.
- ^ Birrer, S; Treu, T; Rusu, C. E; Bonvin, V; et al. (2018). «H0LiCOW — IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant». Monthly Notices of the Royal Astronomical Society. 484 (4): 4726–4753. arXiv:1809.01274. Bibcode:2019MNRAS.484.4726B. doi:10.1093/mnras/stz200. S2CID 119053798.
- ^ Planck Collaboration; Aghanim, N.; et al. (2018). «Planck 2018 results. VI. Cosmological parameters». arXiv:1807.06209. Bibcode:2018arXiv180706209P.
- ^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; et al. (2018). «Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant». The Astrophysical Journal. 861 (2): 126. arXiv:1804.10655. Bibcode:2018ApJ…861..126R. doi:10.3847/1538-4357/aac82e. ISSN 0004-637X. S2CID 55643027.
- ^ Devlin, Hannah (10 May 2018). «The answer to life, the universe and everything might be 73. Or 67». the Guardian. Retrieved 13 May 2018.
- ^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; et al. (22 February 2018). «New parallaxes of galactic Cepheids from spatially scanning the Hubble Space Telescope: Implications for the Hubble constant» (PDF). The Astrophysical Journal. 855 (2): 136. arXiv:1801.01120. Bibcode:2018ApJ…855..136R. doi:10.3847/1538-4357/aaadb7. S2CID 67808349. Archived (PDF) from the original on 2022-10-09. Retrieved 23 February 2018.
- ^ Weaver, Donna; Villard, Ray; Hille, Karl (22 February 2018). «Improved Hubble Yardstick Gives Fresh Evidence for New Physics in the Universe». NASA. Retrieved 24 February 2018.
- ^ The LIGO Scientific Collaboration and The Virgo Collaboration; The 1M2H Collaboration; The Dark Energy Camera GW-EM Collaboration and the DES Collaboration; The DLT40 Collaboration; et al. (2017-10-16). «A gravitational-wave standard siren measurement of the Hubble constant» (PDF). Nature. 551 (7678): 85–88. arXiv:1710.05835. Bibcode:2017Natur.551…85A. doi:10.1038/nature24471. ISSN 1476-4687. PMID 29094696. S2CID 205261622. Archived (PDF) from the original on 2022-10-09.
- ^ Feeney, Stephen M; Peiris, Hiranya V; Williamson, Andrew R; Nissanke, Samaya M; et al. (2019). «Prospects for resolving the Hubble constant tension with standard sirens». Physical Review Letters. 122 (6): 061105. arXiv:1802.03404. Bibcode:2019PhRvL.122f1105F. doi:10.1103/PhysRevLett.122.061105. hdl:2066/201510. PMID 30822066. S2CID 73493934.
- ^ Vitale, Salvatore; Chen, Hsin-Yu (12 July 2018). «Measuring the Hubble Constant with Neutron Star Black Hole Mergers». Physical Review Letters. 121 (2): 021303. arXiv:1804.07337. Bibcode:2018PhRvL.121b1303V. doi:10.1103/PhysRevLett.121.021303. hdl:1721.1/117110. PMID 30085719. S2CID 51940146.
- ^ Bonvin, Vivien; Courbin, Frédéric; Suyu, Sherry H.; et al. (2016-11-22). «H0LiCOW – V. New COSMOGRAIL time delays of HE 0435−1223: H0 to 3.8 per cent precision from strong lensing in a flat ΛCDM model». MNRAS. 465 (4): 4914–4930. arXiv:1607.01790. Bibcode:2017MNRAS.465.4914B. doi:10.1093/mnras/stw3006. S2CID 109934944.
- ^ Tully, R. Brent; Courtois, Hélène M.; Sorce, Jenny G. (3 August 2016). «COSMICFLOWS-3». The Astronomical Journal. 152 (2): 50. arXiv:1605.01765. Bibcode:2016AJ….152…50T. doi:10.3847/0004-6256/152/2/50. S2CID 250737862.
- ^ Grieb, Jan N.; Sánchez, Ariel G.; Salazar-Albornoz, Salvador (2016-07-13). «The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological implications of the Fourier space wedges of the final sample». Monthly Notices of the Royal Astronomical Society. 467 (2): stw3384. arXiv:1607.03143. Bibcode:2017MNRAS.467.2085G. doi:10.1093/mnras/stw3384. S2CID 55888085.
- ^ «The Extended Baryon Oscillation Spectroscopic Survey (eBOSS)». SDSS. Retrieved 13 May 2018.
- ^ Riess, Adam G.; Macri, Lucas M.; Hoffmann, Samantha L.; Scolnic, Dan; et al. (2016-04-05). «A 2.4% Determination of the Local Value of the Hubble Constant». The Astrophysical Journal. 826 (1): 56. arXiv:1604.01424. Bibcode:2016ApJ…826…56R. doi:10.3847/0004-637X/826/1/56. S2CID 118630031.
- ^ «Planck Publications: Planck 2015 Results». European Space Agency. February 2015. Retrieved 9 February 2015.
- ^ Cowen, Ron; Castelvecchi, Davide (2 December 2014). «European probe shoots down dark-matter claims». Nature. doi:10.1038/nature.2014.16462. Retrieved 6 December 2014.
- ^ Tully, R. Brent; Courtois, Helene M.; Dolphin, Andrew E.; Fisher, J. Richard; et al. (5 September 2013). «Cosmicflows-2: The Data». The Astronomical Journal. 146 (4): 86. arXiv:1307.7213. Bibcode:2013AJ….146…86T. doi:10.1088/0004-6256/146/4/86. ISSN 0004-6256. S2CID 118494842.
- ^
«Planck reveals an almost perfect universe». ESA. 21 March 2013. Retrieved 2013-03-21. - ^
«Planck Mission Brings Universe Into Sharp Focus». JPL. 21 March 2013. Retrieved 2013-03-21. - ^
Overbye, D. (21 March 2013). «An infant universe, born before we knew». New York Times. Retrieved 2013-03-21. - ^ Boyle, A. (21 March 2013). «Planck probe’s cosmic ‘baby picture’ revises universe’s vital statistics». NBC News. Archived from the original on 2013-03-23. Retrieved 2013-03-21.
- ^
Bennett, C. L.; et al. (2013). «Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Final maps and results». The Astrophysical Journal Supplement Series. 208 (2): 20. arXiv:1212.5225. Bibcode:2013ApJS..208…20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232. - ^ a b
Jarosik, N.; et al. (2011). «Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Sky maps, systematic errors, and basic results». The Astrophysical Journal Supplement Series. 192 (2): 14. arXiv:1001.4744. Bibcode:2011ApJS..192…14J. doi:10.1088/0067-0049/192/2/14. S2CID 46171526. - ^ Results for H0 and other cosmological parameters obtained by fitting a variety of models to several combinations of WMAP and other data are available at the NASA’s LAMBDA website Archived 2014-07-09 at the Wayback Machine.
- ^ a b Hinshaw, G.; et al. (WMAP Collaboration) (2009). «Five-year Wilkinson Microwave Anisotropy Probe observations: Data processing, sky maps, and basic results». The Astrophysical Journal Supplement. 180 (2): 225–245. arXiv:0803.0732. Bibcode:2009ApJS..180..225H. doi:10.1088/0067-0049/180/2/225. S2CID 3629998.
- ^
Spergel, D. N.; et al. (WMAP Collaboration) (2007). «Three-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for cosmology». The Astrophysical Journal Supplement Series. 170 (2): 377–408. arXiv:astro-ph/0603449. Bibcode:2007ApJS..170..377S. doi:10.1086/513700. S2CID 1386346. - ^
Bonamente, M.; Joy, M. K.; Laroque, S. J.; Carlstrom, J. E.; et al. (2006). «Determination of the cosmic distance scale from Sunyaev–Zel’dovich effect and Chandra X‐ray measurements of high‐redshift galaxy clusters». The Astrophysical Journal. 647 (1): 25. arXiv:astro-ph/0512349. Bibcode:2006ApJ…647…25B. doi:10.1086/505291. S2CID 15723115. - ^ Planck Collaboration (2013). «Planck 2013 results. XVI. Cosmological parameters». Astronomy & Astrophysics. 571: A16. arXiv:1303.5076. Bibcode:2014A&A…571A..16P. doi:10.1051/0004-6361/201321591. S2CID 118349591.
- ^ Spergel, D.N. (September 2003). «First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters». The Astrophysical Journal Supplement Series. 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226. S2CID 10794058.
- ^ Riess, Adam G. (January 1995). «Using SN Ia Light Curve Shapes to Measure The Hubble Constant». The Astrophysical Journal. 438 (L17). arXiv:astro-ph/9410054. doi:10.1086/187704. S2CID 118938423.
- ^ a b c John P. Huchra (2008). «The Hubble Constant». Harvard Center for Astrophysics.
- ^
Sandage, A. R. (1958). «Current problems in the extragalactic distance scale». The Astrophysical Journal. 127 (3): 513–526. Bibcode:1958ApJ…127..513S. doi:10.1086/146483. - ^ Edwin Hubble, A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae, Proceedings of the National Academy of Sciences, vol. 15, no. 3, pp. 168-173, March 1929
- ^ «Hubble’s Constant». Skywise Unlimited — Western Washington University.
- ^ Lemaître, Georges (1927). «Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques». Annales de la Société Scientifique de Bruxelles (in French). A47: 49–59. Bibcode:1927ASSB…47…49L.
Bibliography[edit]
- Hubble, E. P. (1937). The Observational Approach to Cosmology. Clarendon Press. LCCN 38011865.
- Kutner, M. (2003). Astronomy: A Physical Perspective. Cambridge University Press. ISBN 978-0-521-52927-3.
- Liddle, A. R. (2003). An Introduction to Modern Cosmology (2nd ed.). John Wiley & Sons. ISBN 978-0-470-84835-7.
Further reading[edit]
- Freedman, W. L.; Madore, B. F. (2010). «The Hubble Constant». Annual Review of Astronomy and Astrophysics. 48: 673–710. arXiv:1004.1856. Bibcode:2010ARA&A..48..673F. doi:10.1146/annurev-astro-082708-101829. S2CID 119263173.
External links[edit]
- NASA’s WMAP — Big Bang Expansion: the Hubble Constant
- The Hubble Key Project
- The Hubble Diagram Project
- Coming to terms with different Hubble Constants (Forbes; 3 May 2019)
- Merrifield, Michael (2009). «Hubble Constant». Sixty Symbols. Brady Haran for the University of Nottingham.
В начале 20-го века было сделано несколько значительных открытий, продвинувших астрономическую науку на принципиально новый уровень. Кроме теорий Эйнштейна, ученые получили в свое распоряжение закон Хаббла, с помощью которого стало возможным оценить расстояния между галактиками. В 20-х годах американец Эдвин Хаббл сопоставил линейное соотношение между доступными на тот момент галактическими скоростями и расстоянием до них.
Оглавление
- 1 История открытия
- 2 Общие сведения
- 3 Оценка постоянной Хаббла и ее физический смысл
- 4 Применение в астрономии
История открытия
На протяжении некоторого времени Хаббл наблюдал за туманностью в созвездии Андромеды. Имея в распоряжении стодюймовый рефлектор, астроном получил достаточно данных, чтобы дать этому скоплению космических объектов статус системы звезд. Одновременно таким же образом была классифицирована в качестве галактики и туманность из созвездия Треугольник. Благодаря открытиям Хаббла, изменился взгляд ученого сообщества на структуру космоса. Вселенная на глазах превратилась из хаотически раскиданных звезд, покрывающих небо, в организованное пространство, состоящее из отдельных галактик. Расширенные пределы окружающего мира привели к открытию одного из основных законов космологической теории, работа над которым велась в период с 1913 по 1929 годы.
Общие сведения
Основываясь на научных трудах Ж. Леметра, Э. Хаббл обратил внимание на свойства светимости цефеид. Эти небесные тела обладают периодичностью в интенсивности излучения. Такая особенность позволяет с достаточной достоверностью определить их удаление от наблюдателя. Взяв за основу соотношение степени светимости цефеид, по отношению к периоду времени, Хаббл смог измерить расстояние до некоторых из них.
Проверенный способ стал основой для объективной оценки времени, потраченного Вселенной на процесс расширения. Вычисления по формуле Хаббла производятся с участием постоянной величины, известной еще, как коэффициент пропорциональности ( H_0 ):
[ H_0 = 67,80pm0,77 (км/с)/Мпк ]
Постоянная величина полученного Хабблом коэффициента составляет примерное значение в 500 км/сек. на каждый милипарсек (Мпк). Однако в 20-е годы прошлого века еще не было известно о поправке на поглощение света, которая была открыта позже. По этой причине, сейчас «постоянная Хаббла» составляет ( 67,80pm0,77 км/с ) за 1 Мпк. Совсем недавно ученым удалось установить, что у каждой галактики имеется собственная скорость вращения, которая прибавляется к общей скорости группы, состоящей из этих космических объектов. Кроме того, всеобщее движение галактик в пространстве оказывает воздействие на всю его динамику, изменяющуюся по мере расширения и разлета Вселенной.
Для закона Хаббла характерно сопоставление расстояния от Земли, до космического объекта, со скоростью его удаления от пункта наблюдения. Значение постоянной при этом определяет среднюю скорость, с которой движутся галактики при расширении Вселенной. Таким образом, галактика, расстояние до которой составляет 100 Мпк, движется со скоростью 7 тысяч км/сек. В то же время, галактический объект, находящийся на расстоянии в 10 Мпк, удаляется от наблюдателя со скорость в 700 км/сек. Закон Хаббла был неоднократно проверен на просторах далекого космоса, где его справедливость неизменно подтверждалась. Однако, в условиях расширения Вселенной, любые постоянные значения могут подвергаться корректировкам. Относительность постоянства любых величин в космосе может быть актуальной только для определенного этапа эволюции галактики, поэтому астрономы иногда называют постоянную Хаббла — переменной.
Оценка постоянной Хаббла и ее физический смысл
После того, как Хаббл понял, что туманность Андромеды представляет собой отдельную галактику, для него стала ясной картина смещения линий спектра, в соседних с ней космических образованиях того же ряда. Явлению сдвига спектра в сторону красного цвета астроном дал характеристику проявления эффекта Доплера. Открытие содержало информацию о постоянном удалении галактик в сторону, противоположную Земле. Скорость расширения прямо пропорциональна расстоянию от космических объектов до нашей планеты, что говорит об увеличении центробежных сил на самых дальних рубежах видимого пространства Вселенной.
Если попытаться мысленно пройти данный процесс в обратном направлении, то можно прийти к начальной точке, из которой космическое пространство начало расширяться. Теоретически, Вселенная могла возникнуть из бесконечно малой крошки протоматерии, в которой она была сконцентрирована настолько, насколько смогла затем расшириться до сегодняшних объемов. Из этого закона, выдвинутого Хабблом, следует вывод, что любая галактика должна иметь отправную точку своего развития во времени. Так была выдвинута основная гипотеза о Большом взрыве, положившем начало эволюционному развитию Вселенной. Уже на протяжении почти 100 лет, эта теория считается наиболее вероятной среди астрофизиков. Открытый Хабблом закон позволяет также оценить примерный возраст галактик, которые удаляются от Земли с примерно одинаковой скоростью. По мнению ученого, наша Вселенная могла возникнуть 13,8 миллиардов лет назад.
Применение в астрономии
Благодаря открытию Хабблом красных спектральных смещений, в астрономии появилось доказательство динамичной и постоянно расширяющейся Вселенной. Ученый создал закон, согласно которому стало очевидным, что в космическом пространстве существует какая-то структурная субстанция, влияющая на распространение галактик в разные стороны. Если бы космические образования двигались только по инерции Большого взрыва и повинуясь гравитации, то можно было бы со временем наблюдать их замедление. Поскольку галактики продолжают разбегаться с ускорением, то на них действует некая разгоняющая сила, получившая определение темной энергии.
Пользуясь законом Хаббла, можно с достаточной точностью определять расстояния от Земли до самых дальних квазаров и галактик.
Зако́н Ха́ббла (закон всеобщего разбегания галактик) — эмпирический закон, связывающий красное смещение галактик и расстояние до них линейным образом[1]:
где z — красное смещение галактики, D — расстояние до неё, H0 — коэффициент пропорциональности, называемый постоянной Хаббла. При малом значении z выполняется приближённое равенство cz=Vr, где Vr — скорость галактики вдоль луча зрения наблюдателя, c — скорость света. В этом случае закон принимает классический вид:
С помощью этого закона можно рассчитать так называемый Хаббловский возраст Вселенной:
Этот возраст является характерным временем расширения Вселенной на данный момент и с точностью до множителя 2 соответствует возрасту Вселенной, рассчитываемому по стандартной космологической модели Фридмана.
С другой стороны, если подставить в формулу красного смещения 

Содержание
- 1 История открытия
- 2 Теоретическая интерпретация
- 3 Оценка постоянной Хаббла и её физический смысл
- 4 Возможная нелинейность закона
- 5 См. также
- 6 Примечания
- 7 Ссылки
История открытия[править | править вики-текст]
В 1913—1914 годах американский астроном Весто Слайфер установил, что Туманность Андромеды и ещё более десятка небесных объектов движутся относительно Солнечной системы с огромными скоростями (порядка 1000 км/сек). Это означало, что все они находится за пределами Галактики (ранее многие астрономы полагали, что туманности представляют собой формирующиеся в нашей Галактике планетные системы). Другой важный результат: все исследованные Слайфером туманности, кроме трех, удалялись от Солнечной системы. В 1917—1922 годах Слайфер получил дополнительные данные, подтвердившие, что скорость почти всех внегалактических туманностей направлена прочь от Солнца. Артур Эддингтон на основе обсуждавшихся в те годы космологических моделей Общей теории относительности предположил, что этот факт отражает общий природный закон: Вселенная расширяется, и чем дальше от нас астрономический объект, тем больше его относительная скорость.
Вид закона для расширения Вселенной был установлен экспериментально для галактик бельгийским учёным Жоржем Леметром в 1927[2], а позже — знаменитым Э. Хабблом в 1929 с помощью 100-дюймового телескопа, который разрешает ближайшие галактики на звезды. Среди них были цефеиды, используя зависимость «период-светимость» которых, Хаббл измерил расстояние до них, а также красное смещение галактик, позволяющее определить их радиальную скорость.
Полученный Хабблом коэффициент пропорциональности составлял около 500 км/с на мегапарсек. Современное значение составляет 67,80 ± 0,77 (км/с) на мегапарсек[3]. Столь существенную разницу обеспечивают два фактора: отсутствие поправки нуль-пункта зависимости «период-светимость» на поглощение (которое тогда ещё не было открыто) и существенный вклад собственных скоростей в общую скорость для местной группы галактик[4].
Теоретическая интерпретация[править | править вики-текст]
С точки зрения классической механики, закон Хаббла можно наглядно объяснить следующим образом. Когда-то давно Вселенная образовалась в результате Большого взрыва. В момент взрыва различные частицы материи (осколки) получили различные скорости. Те из них, которые получили бо́льшие скорости, соответственно успели к настоящему моменту улететь дальше, чем те, которые получили меньшие скорости. Если провести численный расчёт, то окажется, что зависимость расстояния от скорости оказывается линейной. Кроме того, получается, что эта зависимость одна и та же для всех точек пространства, то есть, по наблюдениям за разлетающимися осколками нельзя найти точку взрыва: с точки зрения каждого осколка, именно он находится в центре. Однако, несмотря на такую наглядность, следует помнить, что расширение Вселенной должно описываться не классической механикой, а общей теорией относительности.
| Космология |

|
| Изучаемые объекты и процессы |
|
| Наблюдаемые процессы |
|
| Теоретические изыскания |
|
Первое замечание касается того, учитывается ли при наблюдениях тот факт, что из-за того, что свет идёт от галактик миллионы лет, мы наблюдаем их в прошлом. В результате, поскольку они удаляются от нас, в настоящий момент они должны находиться уже дальше. Вопрос: для какого из двух расстояний определена зависимость Хаббла? Ответ: до середины XX века это не имело значения. Из графика Хаббла видно, что наибольшие скорости галактик, рассмотренных Хабблом, составили до 1000 км/с. В принципе это большая скорость, но за время движения света от них до Земли они всё равно успели сдвинуться лишь на незначительный процент общего расстояния.
Второе замечание заключается в том, что расширение Вселенной не является простым разлётом галактик в пустом пространстве. Оно заключается в динамическом изменении самого пространства. Непонимание этого факта часто заставляет делать неверные заключения авторов даже серьёзной литературы. Например, часто говорят, что скорость убегания галактик не должна превышать скорость света и потому на тех расстояниях, где это должно наблюдаться, должны наблюдаться и отклонения от закона Хаббла. Это не так: согласно общей теории относительности, должны существовать и наблюдаться галактики, убегающие быстрее света[5].
За несколько лет до экспериментального открытия закона Хаббла Александр Фридман вывел теоретически решения уравнения Эйнштейна для всей Вселенной, и в результате было получено, что если распределение вещества в ней в среднем равномерно, то она должна или сжиматься, или расширяться, причём в последнем случае должен наблюдаться линейный закон между расстоянием и скоростью убегания. Эта особенность решений Фридмана была сразу же отождествлена с явлением, открытым Хабблом.
В соответствии с этой (общепринятой) моделью космологическое красное смещение нельзя интерпретировать как Эффект Доплера, так как получаемая из наблюдаемого z по формулам этого эффекта скорость не соответствует (лишь приближённо равна) никакой скорости в смысле изменения космологического расстояния между галактиками. Галактики неподвижны (за исключением пекулярных собственных скоростей), а расширяется пространство, что и вызывает расширение волнового пакета. (См. в статье Космологическое красное смещение). Соотношение
является приближённым, в то время как равенство
где 
Оценка постоянной Хаббла и её физический смысл[править | править вики-текст]
В процессе расширения, если оно происходит равномерно, постоянная Хаббла должна уменьшаться, и индекс «0» при её обозначении указывает на то, что величина Н0 относится к современной эпохе. Величина, обратная постоянной Хаббла, должна быть в таком случае равна времени, прошедшему с момента начала расширения, то есть возрасту Вселенной.
Значение Н0 определяется по наблюдениям галактик, расстояния до которых измерены без помощи красного смещения (прежде всего, по ярчайшим звёздам или цефеидам). Большинство независимых оценок Н0 дают для этого параметра значение 70—80 км/с на мегапарсек. Это означает, что галактики, находящиеся на расстоянии 100 мегапарсек, удаляются от нас со скоростью 7000—8000 км/с. В настоящее время (2014) наиболее надёжной (хотя и модельно зависимой) считается оценка Н0 = (67,80 ± 0,77) (км/c)/Мпк[3].
Проблема оценки Н0 осложняется тем, что, помимо космологических скоростей, обусловленных расширением Вселенной, галактики ещё обладают собственными (пекулярными) скоростями, которые могут составлять несколько сотен км/с (для членов массивных скоплений галактик — более 1000 км/с). Это приводит к тому, что закон Хаббла плохо выполняется или совсем не выполняется для объектов, находящихся на расстоянии ближе 10—15 млн св. лет, то есть как раз для тех галактик, расстояния до которых наиболее надёжно определяются без красного смещения.
Закон Хаббла плохо выполняется и для галактик на очень больших расстояниях (в миллиарды световых лет), которым соответствует величина z > 1. Расстояния до объектов с таким большим красным смещением теряют однозначность, поскольку зависят от принимаемой модели Вселенной и от того, к какому моменту времени они отнесены. В качестве меры расстояния в этом случае обычно используется только красное смещение.
Возможная нелинейность закона[править | править вики-текст]
В наше время наблюдениями, говорящими в пользу существования тёмной энергии, были, по-видимому, обнаружены отклонения от линейного закона Хаббла (как связи наблюдаемого красного смещения с расстоянием). Было обнаружено, что, по-видимому, наша Вселенная расширяется с ускорением.[6] Этот факт не отменяет закона Хаббла, если его понимать как зависимость от расстояния в данный конкретный момент времени, то есть если учесть, что далёкие объекты мы наблюдаем в прошлом.
См. также[править | править вики-текст]
- Космологическое красное смещение
- Расширение Вселенной
- Космологический принцип
- Объём Хаббла
Примечания[править | править вики-текст]
- ↑ Adam G. Riess, Lucas Macri, Stefano Casertano, Megan Sosey, Hubert Lampeitl, Henry C. Ferguson, Alexei V. Filippenko, Saurabh W. Jha, Weidong Li, Ryan Chornock, and Devdeep Sarkar. A Redetermination of the Hubble Constant with the Hubble Space Telescope from a Differential Distance Ladder.
- ↑ Edwin Hubble in translation trouble : Nature News
- ↑ 1 2 P. A. R. Ade et al. (Planck Collaboration) (22 March 2013). «Planck 2013 results. I. Overview of products and scientific results». Astronomy and Astrophysics 1303: 5062. DOI:10.1051/0004-6361/201321529. Bibcode:2013arXiv1303.5062P.
- ↑ Ю. Н. Ефремов. Постоянная Хаббла. Архивировано из первоисточника 11 августа 2011.
- ↑ Попов С. Б., кандидат физико-математических наук, Топоренский А. В., кандидат физико-математических наук. За горизонтом вселенских событий. Архивировано из первоисточника 24 августа 2011.
- ↑ K. Nakamura et al., Review of Particle Properties J. Phys. G 37, 075021 (2010): K.A. Olive, J.A.Peacock. Chapter 19. Big-Bang cosmology.
Ссылки[править | править вики-текст]
- Космология
- G.A. Tammann, B. Reindl, Cosmic Expansion and Ho: A Retro- and Pro-Spective Note
- G.A. Tammann, The Ups and Downs of the Hubble Constant.
- Вселенная может оказаться больше и старше. CompuLenta.ru.