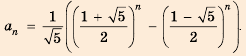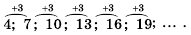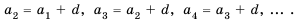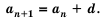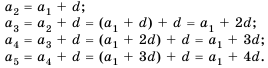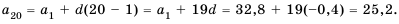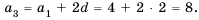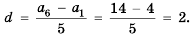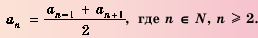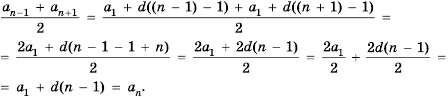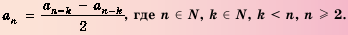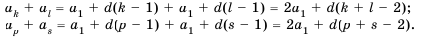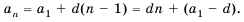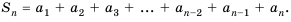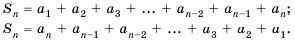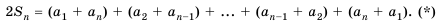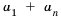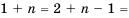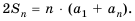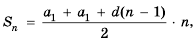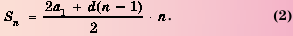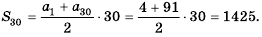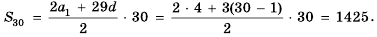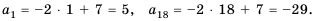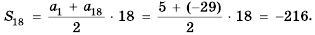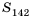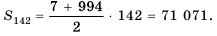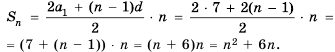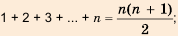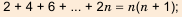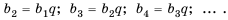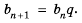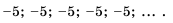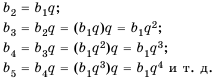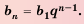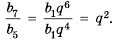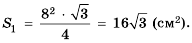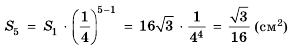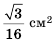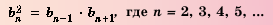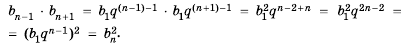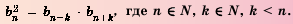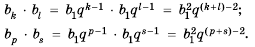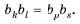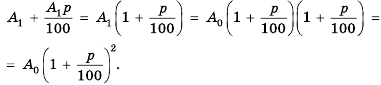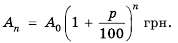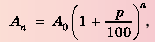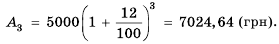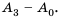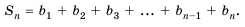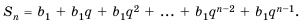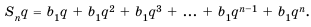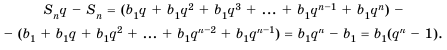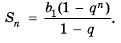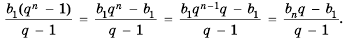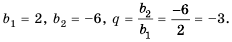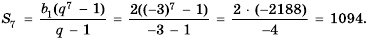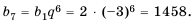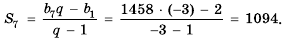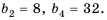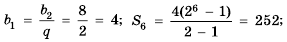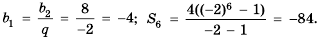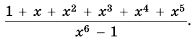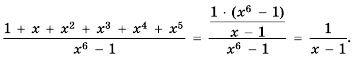Пусть известно, что
в последовательности каждый член, начиная со второго, равен квадрату
предыдущего.
ПРИМЕР:
Чтобы задать последовательность
2; 4; 16;
256; … ,
достаточно указать первый её член. Таким образом, эта
последовательность задаётся двумя условиями:
– первый член равен
2,
– каждый член, начиная со второго, равен квадрату
предшествующего.
Если последовательность обозначить через (an),
то эти условия запишутся так:
a1 = 2; an+1 = an2.
ПРИМЕР:
Рассмотрим последовательность (bn),
первый член которой равен единице, второй – двум, а каждый член, начиная с
третьего, равен сумме двух предыдущих членов:
b1 = 1; b2 = 2;
bn+2 = bn + bn+1.
Зная первые два члена
b1 и b2
последовательности (bn) и формулу
bn+2 = bn + bn+1,
можно найти любой член последовательности:
b3 = 1 + 2 = 3;
b4 = 2 + 3 = 5;
b5 = 3 + 5 = 8 и т. д.
Значит, последовательность (bn) задана.
Рекуррентный способ задания последовательности состоит
в том, что задаётся первый член последовательности (или несколько членов) и правило, по которому определяется следующий
член последовательности по известным его предыдущим членом (или несколькими членами).
Формула, которая устанавливает
соотношение n-го члена последовательности его предыдущим членом, называется
рекуррентным соотношением.
ПРИМЕР:
Пусть задано
u1 = 1, u2 = 3,
а рекуррентное соотношение
имеет вид
un = 2un—1 + un-2 (n ≥ 3).
Тогда получим последовательность
u1 = 1, u2 = 3,
u3 = 2×3 + 1 = 7,
u4 = 2×7 + 3 = 17, … ,
или
1, 3, 7, 17,
…
ПРИМЕР:
Пусть первый член
последовательности (сn) равен
12,
а каждый следующий, начиная со второго, получается вычитанием из предыдущего
члена числа 5, т. е.
с1 = 12; сn+1 = сn – 5.
Тогда
с2 = с1 – 5 = 7,
с3 = с2 – 5 = 2,
с4 = с3 – 5 = –3 и т. д.
- Задания к уроку 3
Другие уроки:
- Урок 1. Понятие последовательности
- Урок 2. Способы задания последовательностей
- Урок 4. Определение арифметической прогрессии
- Урок 5. Формула n-го члена арифметической прогрессии
- Урок 6. Формула суммы n первых членов арифметической прогрессии
- Урок 7. Определение геометрической прогрессии
- Урок 8. Формула n-го члена геометрической прогрессии
- Урок 9. Формула суммы n первых членов геометрической прогрессии
Содержание
- Рекуррентные соотношения и уравнения
- Как решать рекуррентные соотношения?
- Метод производящих функций
- Метод характеристических функций
- Решение для последовательности чисел Фибоначчи
- Способ 1. Производящяя функция
- Способ 2. Характеристическое уравнение
- Примеры решений
- Решение рекуррентных соотношений
- Содержание
- Определения [ править ]
- Метод производящих функций [ править ]
- Примеры [ править ]
- [math]1[/math] пример [ править ]
- [math]2[/math] пример: числа Фибоначчи [ править ]
- [math]3[/math] пример [ править ]
- [math]4[/math] пример [ править ]
Рекуррентные соотношения и уравнения
В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.
Как решать рекуррентные соотношения?
Для решения рекуррентных соотношений применяют один из двух основных способов:
- Метод производящих функций
- Метод характеристического уравнения
В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.
Метод производящих функций
- Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен $k$) $$a_ <0>= …, \ a_ <1>= …, \ a_ = …, \ … \ a_ = …, ngeqslant k$$
- Домножить каждую строчку на $z$ в соответствующей степени $z^ cdot a_$ и сложить все выражения для $n ge 0$. В левой части получится сумма $displaystylesum_^ <infty>a_nz^n$ — это производящая функция, назовем ее $G(z)$. Правую часть преобразовать так, чтобы она превратилась в выражение, включающее $G(z)$.
- Решить полученное уравнение относительно $G(z)$.
- Разложить $G(z)$ в степенной ряд, тогда коэффициент при $z_n$ будет искомым выражением для $a_n$.
Метод характеристических функций
Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:
- Записать соответствующее однородное рекуррентное уравнение (РУ): $$ p_ a_ + p_a_ + . + p_n a_n =f to \ to p_ a_ + p_a_ + . + p_n a_n =0. $$
- Выписать для него характеристическое уравнение и найти его корни $lambda_i$ $$ p_ lambda^ + p_lambda^ + . + p_lambda + p_n =0. $$
- Выписать согласно полученным корням $lambda_1, . lambda_k$ общее решение однородного рекуррентного соотношения (подробнее теорию см. по ссылке [1] ниже). $$ C_1 lambda_1^n +. +C_k lambda_k^n , mbox < для случая различных простых корней>, $$ $$ C_1 lambda_1^n + C_2 nlambda_1^n +. +C_m n^m lambda_1^n+. +C_k lambda_k^n mbox < для случая корня >, lambda_1 , < кратности >, m. $$
- Подобрать частное решение неоднородного рекуррентного соотношения по виду правой части (особенно удобно для правых частей вида $mu^n*P(n)$, $P(n)$ — многочлен от $n$).
- Представить общее решение неоднородного РУ как сумму общего решения соответствующего однородного РУ и частного решения неоднородного РУ.
- Подставить начальные условия $a_0, a_1, . a_$ и получить значения констант $C_1, . C_k$.
Решение для последовательности чисел Фибоначчи
Последовательность чисел Фибоначи — это последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:
$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 , . $$
Числа Фибоначчи растут быстро: $f_<10>=55$, $f_<20>=6765$, а $f_<100>=354224848179261915075$.
Общая формула данной рекуррентной последовательности имеет вид6
Способ 1. Производящяя функция
Начинаем с второго шага алгоритма, домножаем на $z^n$:
$$begin 1cdot f_0 &= &0cdot 1,\ zcdot f_1 &= &1cdot z,\ zcdot f_n & = &(f_+f_)cdot z^n, quad ngeq2.\ end $$
Складываем все строчки:
На третьем шаге алгоритма приводим все суммы к замкнутому виду:
откуда выводим искомое выражение для производящей функции:
Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:
Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:
Рассмотрим первую дробь и поделим в ней числитель и знаменатель на $z_1$:
Аналогично (но с делением на $z_2$) действуем со второй дробью:
Преобразуем данное выражение, используя то, что
$$1/z_1=-z_2, quad 1/z_2 = -z_1, quad z_1-z_2=sqrt <5>$$ $$f_n=frac<1><sqrt<5>>left( biggl( frac<1+sqrt<5>> <2>biggr)^n — biggl( frac<1-sqrt<5>> <2>biggr)^n right). $$
Способ 2. Характеристическое уравнение
Запишем характеристический многочлен для $f_n=f_+f_$, и найдем его корни:
Тогда общее решение однородного рекуррентного уравнения имеет вид:
Осталось найти значения произвольных постоянных $C_1, C_2$ из начальных условий $f_0=0, f_1=1$.
Решая систему, найдем
Итоговое выражение для последовательности чисел Фибоначчи:
Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.
Примеры решений
Задача 1. Решить рекуррентное соотношение $f(n+2)=-6f(n+1)+7f(n)+n-3$ с начальными условиями $f(0)=2$ и $f(1)=4$, сделать проверку
Задача 2. Решить рекуррентное соотношение $f(n+2)=-2f(n+1)+3f(n)-3^n$ с начальными условиями $f(0)=1$, $f(1)=3$ и сделать проверку
Задача 3. 1. Решить рекуррентное соотношение $f(n+2) =-5f(n+1) -4f(n) + 3n^2$ с начальными условиями $f(0) = 2$, $f(1) = 3$.
2. Проверить, удовлетворяет ли найденное решение начальным условиям и обращает ли оно рекуррентное соотношение в справедливое тождество.
Задача 4. Найти последовательность $$, удовлетворяющую рекуррентному соотношению $a_ + 4 a_ + 3 a_ = 0$ и начальным условиям $a_1=2$, $a_2=4$.
Источник
Решение рекуррентных соотношений
Содержание
Определения [ править ]
| Определение: |
| Рекуррентная формула (англ. recurrence relation) — формула вида [math]a_n=f(n, a_, a_, dots, a_ ) [/math] , выражающая каждый следующий член последовательности [math]a_n[/math] через [math]p[/math] предыдущих членов и номер члена последовательности [math]n[/math] , вместе с заданными первыми p членами, где [math]p[/math] — порядок рекуррентного соотношения. |
Для рекуррентного соотношения, которому удовлетворяет последовательность [math] < a_n >[/math] мы часто хотим получить выражение для [math]a_n[/math] . Например, для рекуррентного соотношения, задающего числа Фибоначчи:
[math] F_0 = 0,qquad F_1 = 1,qquad F_ = F_ + F_, quad ngeqslant 2, quad nin Z[/math]
[math]a_n[/math] член может быть записан следующим образом: [math]a_n=dfrac<1><sqrt<5>>left( biggl( dfrac<1+sqrt<5>> <2>biggr)^n — biggl( dfrac<1-sqrt<5>> <2>biggr)^n right).[/math]
Для этого можно использовать метод производящих функций (англ. generating function method).
Метод производящих функций [ править ]
Алгоритм получения выражения для чисел [math]a_[/math] , удовлетворяющих рекуррентному соотношению, с помощью производящих функций cостоит из [math]4[/math] шагов.
- Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен [math]k[/math] ): [math]a_ <0>= …, \ a_ <1>= …, \ a_ = …, \ … \ a_ = …, ngeqslant k[/math]
- Домножить каждую строчку на [math]z[/math] в соответствующей степени ( [math]z^ cdot a_ = … cdot z^[/math] ) и сложить все выражения, многоточие надо рассматривать как множество из выражений, где [math]n in [k, +infty)[/math] . В левой части получится сумма [math]displaystylesum_^ <infty>a_nz^n[/math] — это производящая функция, назовем ее [math]G(z)[/math] . Правую часть преобразовать так, чтобы она превратилась в выражение, включающее [math]G(z)[/math] .
- Решить полученное уравнение, получив для [math]G(z)[/math] выражение в замкнутом виде.
- Разложить [math]G(z)[/math] в степенной ряд, коэффициент при [math]z_n[/math] будет искомым выражением для [math]a_n[/math] .
Примеры [ править ]
[math]1[/math] пример [ править ]
Производящие функции позволяют решать рекуррентные соотношение механически по одному и тому же алгоритму. Рассмотрим общую схему на простом примере, который позволит продемонстрировать базовые приёмы работы.
Задано линейное однородное рекуррентное соотношение порядка [math]2[/math] с постоянными коэффициентами:
[math]begin a_0&<>=<>&0,\ a_1&<>=<>&1,\ a_n&<>=<>&5a_-6a_, quad ngeqslant2.\ end [/math]
Порядок соотношения — это его «глубина», то есть количество предшествующих элементов, требуемых для вычисления элемента с номером [math]n[/math] . В данном случае порядок равен [math]2[/math] , так как для вычисления [math]a_n[/math] требуется знать [math]a_[/math] и [math]a_[/math] .
Будем искать производящую функцию последовательности в виде
[math] G(z)=displaystylesum_^ <infty>a_nz^n = a_0+a_1z+a_2z^2+cdots, [/math]
с этой целью умножим верхнюю строчку в записи рекуррентного соотношения на [math]z^0[/math] , следующую — на [math]z^1[/math] и последнюю — на [math]z^n[/math] :
[math]begin 1cdot a_0&<>=<>&0cdot 1,\ zcdot a_1&<>=<>&1cdot z,\ z^ncdot a_n&<>=<>&(5a_-6a_)cdot z^n, quad ngeqslant2.\ end [/math]
Теперь сложим все уравнения для всех значений [math]n[/math] :
[math] underbrace^<infty>a_nz^n>_ <=>z+5displaystylesum_^<infty>a_z^n-6displaystylesum_^<infty>a_z^n. [/math]
Левая часть уравнения в точности равна [math]G(z)[/math] , а в правой части есть суммы, очень похожие на функцию [math]G(z)[/math] , но не равные ей. Эти суммы нужно привести к виду [math]G(z)[/math] . Начнём с первой:
[math] displaystylesum_^<infty>a_z^n stackrel<(1)><=>zdisplaystylesum_^<infty>a_z^ stackrel<(2)> <=>zdisplaystylesum_^<infty>a_z^n stackrel<(3)> <=>zbiggr( underbrace< displaystylesum_^<infty>a_z^n+a_0>_ — a_0biggr)=z(G(z)-a_0) stackrel<(4)> <=>z G(z). [/math]
Равенство [math](1)[/math] получатся вынесением [math]z[/math] в первой степени за знак суммы, это необходимо, чтобы уровнять степень переменной [math]z[/math] и индекс переменной a внутри суммы. Действие [math](2)[/math] — изменение индекса суммирования, которое позволяет избавиться от [math]n-1[/math] . Равенство [math](3)[/math] получается, если прибавить и снова отнять значение [math]a_0[/math] , чтобы получить полную сумму от [math]n=0[/math] до [math]∞[/math] . Равенство [math](4)[/math] справедливо в силу того, что [math]a_0=0[/math] .
Аналогичные манипуляции со второй суммой дают нам выражение
[math] displaystylesum_^<infty>a_z^n = z^2displaystylesum_^<infty>a_z^ = z^2displaystylesum_^<infty>a_z^=z^2G(z). [/math]
Теперь наше исходное уравнение для производящей функции принимает вид:
[math] G(z) = z + 5zG(z) -6z^2G(z), [/math]
откуда получаем производящую функцию последовательности в замкнутом виде:
[math] G(z) = dfrac<1-5z+6z^2>. [/math]
Отыскав производящую функцию в замкнутом виде, её нужно снова разложить в ряд. Это можно сделать разными способами, но самый простой из них — разбить всю дробь на простые дроби и применить формулу для разложения [math]dfrac<1><1-z>[/math] . Итак, разложим знаменатель функции на множители:
[math] G(z) = dfrac <1-5z+6z^2>= dfrac<(1-3z)(1-2z)>. [/math]
Теперь разобьём дробь на сумму простых дробей:
[math] dfrac <(1-3z)(1-2z)>= dfrac<1> <1-3z>— dfrac<1><1-2z>. [/math]
Из этого разложения следует, что
[math] dfrac<1><1-3z>= displaystylesum_^<infty>(3z)^n quadmbox< и >quad dfrac<1><1-2z>= displaystylesum_^<infty>(2z)^n. [/math]
Таким образом,
[math] G(z) = displaystylesum_^<infty>3^nz^n — displaystylesum_^<infty>2^nz^n = displaystylesum_^<infty>(3^n-2^n)z^n. [/math]
С другой стороны, мы искали [math]G(z)[/math] в виде
[math] G(z)=displaystylesum_^ <infty>a_nz^n, [/math]
поэтому, в силу равенства рядов, [math]a_n=3^n-2^n[/math] (для [math]ngeqslant 0[/math] ).
[math]2[/math] пример: числа Фибоначчи [ править ]
Рассмотрим рекуррентное соотношение для чисел Фибоначчи:
[math]begin f_0&<>=<>&0,\ f_1&<>=<>&1,\ f_n&<>=<>&f_+f_, quad ngeqslant2.\ end [/math]
Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг:
[math]begin 1cdot f_0&<>=<>&0cdot 1,\ zcdot f_1&<>=<>&1cdot z,\ z^ncdot f_n&<>=<>&(f_+f_)cdot z^n, quad ngeqslant2.\ end [/math]
Складываем все строчки:
[math] f_0 + f_1 z + displaystylesum_^<infty>f_nz^n = z + displaystylesum_^<infty>f_z^n+displaystylesum_^<infty>f_z^n. [/math]
Третий шаг алгоритма требует привести все суммы к замкнутому виду:
[math]begin G(z) &<>=<>& z + zdisplaystylesum_^<infty>f_z^+z^2displaystylesum_^<infty>f_z^, \ G(z) &<>=<>& z + zdisplaystylesum_^<infty>f_z^n+z^2displaystylesum_^<infty>f_z^n, \ G(z)&<>=<>& displaystyle z + z(G(z)-f_0)+z^2G(z),\ G(z)&<>=<>& displaystyle z + zG(z)+z^2G(z),\ end [/math]
откуда получаем замкнутое выражение для производящей функции:
[math] G(z) = dfrac<1-z-z^2>. [/math]
Осталось разложить её в ряд (чего требует четвёртый шаг алгоритма). С этой целью нужно разложить знаменатель на множители. Найдем корни уравнения:
[math]displaylines< 1-z-z^2 = 0 cr z_1=-dfrac<1-sqrt<5>><2>, z_2=-dfrac<1+sqrt<5>><2>. > [/math]
Нам известно разложение следующей рациональной функции:
[math] dfrac<1> <1-z>= displaystylesum_^<infty>z^n = 1 + z + z^2 + z^3 + cdots. [/math]
Рассмотрим первую дробь и поделим в ней числитель и знаменатель на [math]z_1[/math] :
[math] dfrac = dfrac1dfrac<1><1-dfrac> = dfrac1displaystylesum_^<infty>dfrac. [/math]
Аналогично (но с делением на [math]z_2[/math] ) поступим со второй дробью:
[math] dfrac = dfrac1dfrac1<1-dfrac> = dfrac1displaystylesum_^<infty>dfrac. [/math]
Данное выражение можно упростить, если обратить внимание на то, что [math]1/z_1=-z_2[/math] , [math]1/z_2=-z_1[/math] и [math]z_1-z_2=√5[/math] . Подставим [math]z_1[/math] и [math]z_2[/math] в предыдущее выражение:
[math] f_n=dfrac<1><sqrt<5>>left( biggl( dfrac<1+sqrt<5>> <2>biggr)^n — biggl( dfrac<1-sqrt<5>> <2>biggr)^n right). [/math]
[math]3[/math] пример [ править ]
Найдём производящую функцию для последовательности квадратов чисел Фибоначчи: $1, 1, 4, 9, 25, ldots, f_k^2,ldots$.
По определению последовательности Фибоначчи выполняется:
[math] left< begin f_ = f_ + f_n \ f_ = f_ — f_n end right. [/math]
Возведя в квадрат и сложив, получим:
[math] begin f_^2 + f_^2 = 2f_^2 + 2f_n^2, \ f_^2 = 2f_^2 + 2f_n^2 — f_^2, \ f_^2 = 2f_^2 + 2f_^2 — f_^2.\ end [/math]
Обозначим рассматриваемую последовательность [math]A[/math] , а её члены [math]a_n[/math] , тогда:
[math]a_n = 2a_ + 2a_ — a_[/math]
Рекуррентное соотношение:
[math] begin a_0 = f_0^2 = 1 \ a_1 = f_1^2 = 1 \ a_2 = f_2^2 = 4 \ a_n = 2a_ + 2a_ — a_, quad ngeqslant3.\ end [/math]
Приведём суммы к замкнутому виду:
[math] begin A(z) = displaystylesum_^<infty>a_nz^n = 1 + z + 4z^2 + displaystylesum_^<infty>(2a_ + 2a_ — a_)z^n, \ A(z) = 1 + z + 4z^2 + 2displaystylesum_^<infty>a_z^n + 2displaystylesum_^<infty>a_z^n — displaystylesum_^<infty>a_z^n, \ A(z) = 1 + z + 4z^2 + 2zdisplaystylesum_^<infty>a_nz^n + 2z^2displaystylesum_^<infty>a_nz^n — z^3displaystylesum_^<infty>a_nz^n, \ A(z) = 1 + z + 4z^2 + 2z(A(z) — 1 — z) + 2z^2(A(z) — 1) — z^3A(z), \ A(z) = 1 + z + 4z^2 + 2zA(z) — 2z — 2z^2 + 2z^2A(z) — 2z^2 — z^3A(z), \ A(z)(1 — 2z — 2z^2 + z^3) = 1 + z + 4z^2 — 2z — 2z^2 — 2z^2 = 1 — z, \ end [/math]
откуда получаем замкнутое выражение для производящей функции:
[math]G(z) = dfrac<1 — z><1 — 2z 2z^2 + z^3>.[/math]
[math]4[/math] пример [ править ]
Рассмотрим следующее рекуррентное соотношение:
[math]begin a_0&<>=<>&1,\ a_1&<>=<>&2,\ a_n&<>=<>&6a_-8a_+n, quad ngeqslant2.\ end [/math]
Следующие действия аналогичны тем, которые мы делали для чисел Фибоначчи:
[math]begin displaystyle a_0 + a_1 z + displaystylesum_^<infty> &<>=<>& 1+2z+6displaystylesum_^<infty>>-8displaystylesum_^<infty>>+displaystylesum_^<infty>nz^n, \ G(z) &<>=<>& 1+2z+6zdisplaystylesum_^<infty>>>-8z^2displaystylesum_^<infty>>>+displaystylesum_^<infty>nz^n, \ G(z) &<>=<>& 1+2z+6zdisplaystylesum_^<infty>>>-8z^2displaystylesum_^<infty>>>+displaystylesum_^<infty>nz^n, \ G(z) &<>=<> & 1+ 2z + 6z(G(z)-a_0)-8z^2G(z) + displaystylesum_^<infty>nz^n.\ G(z) &<>=<> & 1 — 4z + 6zG(z)-8z^2G(z) + displaystylesum_^<infty>nz^n.\ end [/math]
Вспомним, что
[math] (z^n)’ = nz^, [/math]
поэтому
[math] displaystylesum_^<infty>nz^n=zdisplaystylesum_^<infty>nz^=zdisplaystylesum_^<infty>(z^n)’=zbiggl(displaystylesum_^<infty>z^nbiggr)’. [/math]
Последняя сумма может быть свёрнута:
[math] displaystylesum_^<infty>z^n=displaystylesum_^<infty>z^n-1-z=dfrac<1><1-z>-1-z=dfrac<1-z>. [/math]
Подставив свёрнутое выражение обратно, имеем,
[math] zbiggl(displaystylesum_^<infty>z^nbiggr)’ = z biggl(dfrac<1-z>biggr)’=dfrac<(1-z)^2>. [/math]
Таким образом, наше последнее уравнение примет вид
[math] G(z) = 1 -4z + 6zG(z)-8z^2G(z) + dfrac<(1-z)^2>.\ [/math]
Это уравнение для производящей функции. Из него выражаем [math]G(z)[/math] :
[math] G(z) = dfrac<1-6z+11z^2-5z^3><(1-6z+8z^2)(1-z)^2>. [/math]
Дальше мы знаем что делать со всеми этими дробями, кроме, разве лишь, первой. Рассмотрим её (без множителя) подробнее:
[math] dfrac<1> <(1-z)^2>=(1-z)^ <-2>=displaystylesum_^<infty>binom<-2>(-z)^n=displaystylesum_^<infty>(-1)^nbinom<1>(-z)^n =displaystylesum_^<infty>(n+1)z^n. [/math]
Источник
Числовая последовательность
- Формулы числовых последовательностей
- Задание последовательностей описанием
- Рекуррентные формулы числовых последовательностей
- Свойства числовых последовательностей
- Примеры
п.1. Формулы числовых последовательностей
Запишем несколько первых чётных чисел и пронумеруем их:
2n
2
4
6
8
10
12
14
16
18
Этот ряд бесконечен, но, глядя на таблицу, его легко задать формулой: begin{gather*} mathrm{y_n = 2n, n in mathbb{N}} end{gather*}
Теперь, пользуясь формулой, для любого порядкового номера n мы сможем найти соответствующее чётное число.
Функцию натурального аргумента (mathrm{y_n=f(n), ninmathbb{N}}) называют числовой последовательностью.
Значения y1, y2, …, yn,… называют членами последовательности.
В символе yn число n называют индексом последовательности.
Для обозначения членов последовательности и их индексов можно использовать разные буквы: x1, x2, …, xm,…; a1, a2, …, ak,…; A1, A2, …, As,… и т.д.
Числовую последовательность как частный случай функции можно задавать аналитически (формулой), описанием (словесно), рекуррентно, графически и т.д.
Первые три способа используются чаще других.
Например:
Найти 1й, 3й и 4й члены последовательности, заданной формулой (mathrm{y_n=frac{n-1}{n+1}}) $$ mathrm{ y_1=frac{1-1}{1+1}=0, y_3=frac{3-1}{3+1}=frac12, y_4=frac{4-1}{4+1}=frac35 } $$
п.2. Задание последовательностей описанием
Последовательность, заданную формулой yn=2n, можно задать описанием как «последовательность чётных чисел».
Последовательность, заданную формулой (mathrm{y_n=frac{n-1}{n+1}}), можно задать описанием как «последовательность дробей, числитель которых на 1 меньше индекса, а знаменатель на 1 больше индекса последовательности».
Кроме того, существуют такие последовательности, которые можно задать только описанием.
Например:
1. Последовательность простых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
2. Последовательность десятичных приближений числа (mathrm{sqrt{3}}) по недостатку:
1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,7302050; 1,73020508,…
п.3. Рекуррентные формулы числовых последовательностей
Важнейшим классом числовых последовательностей, которые широко используются в алгоритмах вычислительной математики, являются рекуррентные отношения (от латинского слова recurrere – возвращаться).
Рекуррентной формулой называют правило, по которому можно найти n-й член последовательности, если известны значения её предыдущих членов.
Например:
Найти y5, если y1 = 1, yn = 2yn-1 + 1
Проводим последовательные вычисления:
y2 = 2y1 + 1 = 3, y3 = 2y2 + 1 = 7, y4 = 2y3 + 1 = 15, y5 = 2y4 + 1 = 31
Интересно, что, если присмотреться, эту последовательность можно также задать аналитически: yn = 2n – 1.
п.4. Свойства числовых последовательностей
Числовую последовательность называют возрастающей, если каждый её член, начиная со второго, больше предыдущего:
y1 < y2 < y3 < … < yn < …
Например:
Последовательность квадратов натуральных чисел yn = n2 возрастающая:
1 < 4 < 9 < … < n2 < …
Числовую последовательность называют убывающей, если каждый её член, начиная со второго, меньше предыдущего:
y1 > y2 > y3 > … > yn > …
Например:
Последовательность дробей с индексом в знаменателе (mathrm{y_n=frac1n}) – убывающая: $$ 1gtfrac12gtfrac13gt…gtfrac1ngt… $$
Числовую последовательность называют ограниченной сверху, если существует такое число M, что для любого члена последовательности выполняется неравенство
yn ≤ M
Например:
Последовательность отрицательных дробей с индексом в знаменателе (mathrm{y_n=-frac1n}) ограничена сверху числом M = 0: $$ -1lt 0, -frac12lt 0, -frac13lt 0,.., -frac1nlt 0, … $$
Числовую последовательность называют ограниченной снизу, если существует такое число M, что для любого члена последовательности выполняется неравенство
yn ≥ M
Например:
Последовательность дробей с индексом в знаменателе (mathrm{y_n=frac1n}) ограничена снизу числом M = 0: $$ -1gt 0, frac12gt 0, frac13gt 0,.., frac1ngt 0, … $$
Числовую последовательность называют ограниченной, если она ограничена сверху и снизу, т.е. существуют такие числа M и K, что для любого члена последовательности выполняется неравенство
M ≤ yn ≤ K или M ≥ yn ≥ K
Например:
Последовательность дробей с индексом в знаменателе (mathrm{y_n=frac1n}) ограничена: $$ 1gt frac12gt frac13gt … gt frac1ngt … gt 0 $$ Верхней границей является M = 1, нижней границей K = 0.
Числовую последовательность называют стационарной, если для любого члена последовательности выполняется равенство
yn = C
где C — некоторое число.
Например:
Последовательность (mathrm{y_1=1, y_n=y^2_{n-1} — 4y_{n-1}+4}) стационарна, т.к. begin{gather*} mathrm{ y_2=1-4+4=1, y_3=1-4+4=1,…}\ mathrm{ y_n=1, forall nin mathbb{N}} end{gather*}
п.5. Примеры
Пример 1. Найдите первые 4 члена последовательности, заданной формулой
a) (mathrm{y_n=frac{n^2+1}{2n-1}})
yn
$$ mathrm{ frac{1^2+1}{2-1}=2 } $$
$$ mathrm{ frac{2^2+1}{4-1}=frac53=1frac23 } $$
$$ mathrm{ frac{3^2+1}{6-1}=2 } $$
$$ mathrm{ frac{4^2+1}{8-1}=frac{17}{7}=2frac37 } $$
б) (mathrm{y_n=frac{2^n}{n^2}})
yn
$$ mathrm{ frac{2^1}{1^2}=2 } $$
$$ mathrm{ frac{2^2}{2^2}=1 } $$
$$ mathrm{ frac{2^3}{3^2}=frac89 } $$
$$ mathrm{ frac{2^4}{4^2}=1 } $$
Пример 2. Найдите первые 4 члена последовательности, заданной рекуррентной формулой
a) y1 = 3, yn = 3yn – 1
yn
3
3 · 3 – 1 = 8
3 · 8 – 1 = 23
3 · 23 – 1 = 68
б) y1 = 1, y2 = 2, yn = 2yn-1 + yn-2
yn
1
2
2 · 2 + 1 = 5
2 · 5 + 2 = 12
Пример 3*. Укажите какую-либо формулу для n-го члена числовой последовательности
а) 3, 5, 7, 9, …
Это – последовательность нечётных чисел, для которой:
yn = 2n + 1
б) 5, -5, 5, -5,…
Это – знакопеременная последовательность, для которой модуль всегда равен 5, а знак меняется. Изменение знака можно записать как степень (–1). Учитывая, что нечётные члены последовательности положительные, а чётные – отрицательные, получаем:
yn = (–1)n+1 · 5
в) (mathrm{frac{1}{1cdot 2}, frac{1}{2cdot 3}, frac{1}{3cdot 4},…})
Это – последовательность дробей, у которых в знаменателе произведение текущего индекса n на следующий индекс (n + 1):
(mathrm{y_n=frac{1}{n(n+1)}})
г) 2, 5, 10, 17, 26, 37, …
Заметим, что
5 — 2 = 3, 10 — 5 = 5, 17 — 10 = 7, 26 — 17 = 9, …
Каждый последующий член отличается от предыдущего на возрастающее нечётное число. Можем записать рекуррентную формулу:
y1 = 2, yn = yn-1 + (2n –1)
Пример 4*. Пифагор изучал последовательность «треугольных» чисел, которые можно задать следующими геометрическими фигурами:

Задайте эту последовательность 1) рекуррентной формулой; 2) аналитической формулой.
1) Запишем последовательность в явном виде, как это следует из чертежа: $$ mathrm{ y_1=1, y_2=underbrace{1}_{y_1}+2=3, y_3=underbrace{1+2}_{y_2}+3=6, y_4=underbrace{1+2+3}_{y_3}+4=10 } $$ Отсюда получаем следующую рекуррентную формулу: y1 = 1, yn = yn-1 + n
2) Для произвольного члена последовательности:
yn = 1 + 2 + 3 + … + (n — 2) + (n — 1) + n
Найдём эту сумму. Для этого запишем выражение наоборот:
yn = n + (n — 1) + (n — 2) + … + 3 + 2 + 1
И найдём сумму: begin{gather*} mathrm{ y_n+y_n=2y_n=(1+2+3+…+(n-2)+(n-1)+n)+ }\ mathrm{ +(n+(n-1)+(n-2)+…+3+2+1)= }\ mathrm{ =(1+n)+underbrace{(2+n-1)}_{=n+1}+ underbrace{3+n-2}_{=n+1}+…+underbrace{n-2+3}_{=n+1}+underbrace{n-1+2}_{=n+1}+(n+1)= }\ mathrm{ =n(n+1) } end{gather*} Получаем: (mathrm{2y_n=n(n+1)Rightarrow y_n=frac{n(n+1)}{2}}) – искомая аналитическая формула.
Ответ: 1) y1 = 1, yn = yn-1 + 2; 2) (mathrm{y_n=frac{n(n+1)}{2}})
Рекуррентная
последовательность. Из курса математики
известно понятие рекуррентной
последовательности. Это понятие вводится
так: пусть известно k
чисел a1,
…, аk.
Эти числа являются первыми числами
числовой последовательности. Следующие
элементы данной последовательности
вычисляются так:
Здесь F—
функция от k
аргументов. Формула
вида
называется
рекуррентной формулой. Величина k
называется глубиной рекурсии.
Другими
словами, можно сказать, что рекуррентная
последовательность — это бесконечный
ряд чисел, каждое из которых, за исключением
k
начальных, выражается через предыдущие.
Примерами рекуррентных
последовательностей являются
арифметическая (1) и геометрическая (2)
прогрессии:
Рекуррентная формула
для указанной арифметической прогрессии:
Рекуррентная формула
для данной геометрической прогрессии:
Глубина рекурсии в
обоих случаях равна единице (такую
зависимость еще называют одношаговой
рекурсией). В целом рекуррентная
последовательность описывается
совокупностью начальных значений и
рекуррентной формулы. Все это можно
объединить в одну ветвящуюся формулу.
Для арифметической прогрессии:
Для геометрической
прогрессии:
Следующая числовая
последовательность известна в математике
под названием чисел Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
…
Начиная
с третьего элемента каждое число равно
сумме значений двух предыдущих, т. е.
это рекуррентная последовательность
с глубиной равной 2 (двухшаговая рекурсия).
Опишем ее в
ветвящейся форме:
Введение
представления о рекуррентных
последовательностях позволяет по-новому
взглянуть на некоторые уже известные
нам задачи. Например, факториал целого
числа п! можно рассматривать как значение
n-го
элемента следующего ряда чисел:
Рекуррентное описание
такой последовательности выглядит
следующим образом:
Программирование
вычислений рекуррентных последовательностей.
С рекуррентными последовательностями
связаны задачи такого рода:
1) вычислить
заданный (n-й)
элемент последовательности;
2)
математически обработать определенную
часть последовательности (например,
вычислить сумму или произведение первых
n
членов);
3) подсчитать
количество элементов на заданном отрезке
последовательности, удовлетворяющих
определенным свойствам;
4) определить номер
первого элемента, удовлетворяющего
определенному условию;
5) вычислить и
сохранить в памяти заданное количество
элементов последовательности.
Данный перечень
задач не претендует на полноту, но
наиболее часто встречающиеся типы он
охватывает. В четырех первых задачах
не требуется одновременно хранить в
памяти множество элементов числового
ряда. В таком случае его элементы могут
получаться последовательно в одной
переменной, сменяя друг друга.
Пример
1. Вычислить n-й
элемент арифметической прогрессии (1).
Var M,I: 0..Maxint;
A: Real;
Begin
Write(‘N=’);
ReadLn(N);
A:=l;
For I: =2 To N Do
A:=A+2;
WriteLn(‘A(‘,N:l,’)=’,A:6:0)
End.
Рекуррентная формула
ai = ai-1 + 2 перешла в оператор А := А + 2.
Пример 2. Просуммировать
первые п элементов геометрической
прогрессии (2) (не пользуясь формулой
для суммы первых n членов прогрессии).
Var N,1: 0..Maxint;
A,S: Real;
Begin
Write(‘N=’); ReadLn(N);
A:=l;
S:=A;
For I: =2 To N Do
Begin
A:=2*A;
S:=S+A
End;
WriteLn(‘Сумма
равна’,S:6:0)
End.
При вычислении
рекуррентной последовательности с
глубиной 2 уже нельзя обойтись одной
переменной. Это видно из следующего
примера.
Пример 3. Вывести на
печать первые п (п ≥ 3) чисел Фибоначчи.
Подсчитать, сколько среди них четных
чисел.
Var N,I,K,F,F1,F2: 0..Maxint;
Begin
Fl:=l; F2:=l;
K:=0;
WriteLn(‘F(l)=’,Fl,’F(2)=’,F2);
For I:=3 To N Do
Begin
F:=F1+F2;
WriteLn(‘F(‘,I:l,’)=’,F);
If Not Odd(F) Then K:=K+1;
F1:=F2; F2:=F
End;
WriteLn(‘Количество
четных чисел в последовательности
равно’,К)
End.
Понадобились три
переменные для последовательного
вычисления двухшаговой рекурсии,
поскольку для нахождения очередного
элемента необходимо помнить значения
двух предыдущих.
Пример 4. Для заданного
вещественного х и малой величины ε
(например, ε = 0,000001) вычислить сумму ряда
включив в нее только
слагаемые, превышающие ε. Известно, что
сумма такого бесконечного ряда имеет
конечное значение, равное еx, где е =
2,71828… — основание натурального логарифма.
Поскольку элементы этого ряда представляют
собой убывающую последовательность
чисел, стремящуюся к нулю, то суммирование
нужно производить до первого слагаемого,
по абсолютной величине не превышающего
ε.
Если слагаемые в
этом выражении обозначить следующим
образом:
то обобщенная формула
для i-го элемента будет следующей:
Нетрудно увидеть,
что между элементами данной
последовательности имеется рекуррентная
зависимость. Ее можно найти интуитивно,
но можно и вывести формально. Правда,
для этого нужно догадаться, что рекурсия
— одношаговая, и что каждый следующий
элемент получается путем умножения
предыдущего на некоторый множитель,
т.е.
Используя обобщенную
формулу, имеем:
Отсюда:
Действительно:
Следовательно,
данная рекуррентная последовательность
может быть описана следующим образом:
И наконец, приведем
программу, решающую поставленную задачу.
Var A,X,S,Eps: Real;
I: Integer;
Begin
Write(‘X =’); ReadLn(X);
Write(‘Epsilon =’); ReadLn(Eps);
A:=l; S:=0; I:=0;
While Abs(A)>Eps Do
Begin
S:=S+A;
I:=I+1;
A:=A*X/I
End;
WriteLn(‘Сумма
ряда
равна’,
S:10:4)
End.
Как и прежде, значения
одношаговой рекуррентной последовательности
вычисляются в одной переменной.
Каждое повторное
выполнение цикла в этой программе
приближает значение S к искомому (уточняет
значащие цифры в его записи). Такой
вычислительный процесс в математике
называется итерационным процессом.
Соответственно, циклы, реализующие
итерационный вычислительный процесс,
называются итерационными циклами. Для
их организации используются операторы
While или Repeat.
Пример 5. Для заданного
натурального N и вещественного х (х >
0) вычислить значение выражения:
В этом случае
рекуррентность не столь очевидна.
Попробуем найти ее методом индукции.
Будем считать, что искомое выражение
есть N-й элемент последовательности
следующего вида:
Отсюда видна связь:
Теперь поставленная
задача решается очень просто:
Var A,X: Real; I,N: Integer;
Begin
Write(‘X=’); ReadLn(X);
Write(‘N=’); ReadLn(N);
A:= Sqrt(X);
For I:=2 To N Do
A:=Sqrt(X+A);
WriteLn(‘Ответ:’,А)
End.
К решению всех
перечисленных выше задач можно подойти
иначе.
Вспомним о рекурсивно
определенных подпрограммах. Посмотрите
на описание арифметической прогрессии
в форме рекуррентной последовательности.
Из него непосредственно вытекает способ
определения функции для вычисления
заданного элемента прогрессии.
Сделаем это для
общего случая, определив арифметическую
прогрессию с первым членом а0 и разностью
d:
Соответствующая
подпрограмма-функция выглядит так:
Function Progres(АО,D:
Real;I: Integer): Real;
Begin
If I=1
Then Progres:=AO
Else Progres:=Progres(A0,D,I-1)+D
End;
Следующая программа
выводит на экран первые 20 чисел Фибоначчи,
значения которых вычисляет рекурсивная
функция Fibon.
Var К:
Byte;
Function Fibon(N: Integer):
Integer;
Begin
If (N=1) Or (N=2)
Then Fibon:=1
Else Fibon:=Fibon(N-1)+Fibon(N-2)
End;
Begin
For K:=l To 20 Do
WriteLn(Fibon(K))
End.
Необходимо
отметить, что использование рекурсивных
функций ведет к замедлению счета. Кроме
того, можно столкнуться с проблемой
нехватки длины стека, в котором
запоминается «маршрут» рекурсивных
обращений.
Рекуррентные
последовательности часто используются
для решения разного рода эволюционных
задач, т.е. задач, в которых прослеживается
какой-то процесс, развивающийся во
времени. Рассмотрим такую задачу.
Пример 6. В ходе
лечебного голодания масса пациента за
30 дней снизилась с 96 до 70 кг. Было
установлено, что ежедневные потери
массы пропорциональны массе тела.
Вычислить, чему была равна масса пациента
через k дней после начала голодания для
k = 1, 2, …, 29.
Обозначим массу
пациента в i-й день через рi (i = 0, 1, 2, …,
30). Из условия задачи известно, что р0 =
96 кг, p30 = 70 кг.
Пусть К— коэффициент
пропорциональности убывания массы за
один день. Тогда
Получаем
последовательность, описываемую
следующей рекуррентной формулой:
Однако нам неизвестен
коэффициент К. Его можно найти, используя
условие p30 = 70.
Для этого будем
делать обратные подстановки:
Далее программирование
становится тривиальным.
Var I: Byte; P,Q: Real;
Begin
P:=96;
Q:=Exp(l/30*Ln(70/96));
For I:=l To 29 Do
Begin
P:=Q*P;
WriteLn(I,’-й
день-‘,Р:5:3,’кг’)
End
End.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Числовые последовательности
Термин «последовательность» используют, когда говорят о расположении учеников в шеренге, очередности дней недели, расположении команд в турнирной таблице и т. п. В этом параграфе мы выясним, что такое числовая последовательность, в частности, что такое арифметическая и геометрическая прогрессии, каковы их свойства, научимся использовать свойства упомянутых прогрессий при решении прикладных задач.
- 1; 1; 2; 3; 5; 8;… — последовательность
- 2; 5; 8; 11; 14;… — арифметическая прогрессия (каждое число, начиная со второго, на 3 больше предыдущего)
- 2; 6; 18:54; 162:. . — геометрическая прогрессия (каждое число, начиная со второго, в три раза больше предыдущего)
Рассмотрим несколько примеров.
Пример:
Один подсолнух за лето «выпивает» в среднем 250 л воды. Сколько воды «выпьют» за лето 1 ,2 ,3 ,4 ,5 подсолнухов?
Решение:
Во второй строке получили несколько чисел, записанных в определенном порядке, говорят, получим последовательность чисел: 250; 500; 750: 1000; 1250, в которой на первом месте стоит число 250, на втором — 500, на пятом — 1250. В этом примере каждому натуральному числу от 1 до 5 включительно соответствует одного число из указанной последовательности. Итак, имеем функцию, областью определения которой является множество чисел 1.2.3.4.5.
Пример:
3аписать в порядке возрастания натуральные числа запись которых оканчивается цифрой 2.
Решение:
Получим последовательность чисел 2; 12; 22; 32; 42; …. в которой на первом месте стоит число 2, на втором — 12. на третьем — 22 и т. д.
В этом примере каждому натуральному числу 
Определение:
Последовательностью называют функцию, заданную на множестве всех или первых 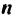
Числа образующие последовательность. называют членами последовательности. Если последовательность имеет конечное число членов, тогда ее называют конечной последовательностью (пример 1). Если последовательность имеет бесконечное число членов, то ее называют бесконечной последовательностью (пример 2), а в записи это показывают многоточием после последнего записанною члена последовательности.
Приведем еще примеры последовательностей:
- 4; 8; 12; 16;… — последовательность натуральных чисел, кратных 4;
— последовательность правильных дробей с числителем 1;
- -1: -2 ; -3 ; -4 ;… — последовательность отрицательных целых чисел;
- 0.1; 1.1; 2.1: 3,1 — последовательность, состоящая из четырех членов;
- 7 :7 ; 7 :7 :… — последовательность, все члены которой равны 7.
- Четвертая последовательность конечная, остальные — бесконечные.
В общем случае члены последовательности, как правило, обозначают маленькими буквами с индексами внизу. Каждый индекс указывает порядковый номер члена последовательности. Например, первый член последовательности обозначают 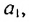
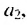
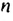
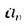
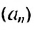
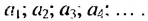
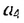
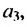
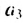
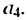
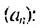
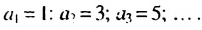
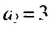
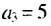
Способы задании последовательностей
Чтобы задать последовательность, нужно указать способ, при помощи которого можно найти любой ее член. Существуют различные способы задания последовательностей.
1. Последовательность можно задать описанием способа определения ее членов. Например, пусть задана последовательность, членами которой являются делители числа 15, записанные в порядке возрастания. Эту последовательность, описанную словами, можно записать так; 1 ; 3; 5: 15.
2. Конечную последовательность можно задать, перечислив ее члены. Например,
3. Последовательность можно задать таблицей, в которой напротив каждого члена последовательности указывают его порядковый номер. Например.
4. Последовательность можно задать формулой, по которой можно найти любой член последовательности, зная его номер. Например, последовательность натуральных чисел, кратных 3, можно задать формулой 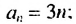
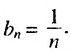
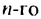
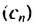
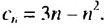
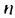
Поэтому 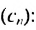
5. Последовательность можно задать так: сначала указать первый или несколько первых членов последовательности, а потом — условие, по которому можно определить любой член последовательности, зная предыдущие. Такой способ задания последовательности называют рекуррентным. Например, найдем несколько членов последовательности 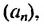
Условия, определяющие эту последовательность, можно записать так: 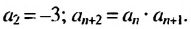
Рассмотренные выше последовательности являются числовыми последовательностями, так как их элементами являются числа. Существуют и другие последовательности. Например, последовательность передач на канале телевидения, последовательность футбольных команд в турнирной таблице и т. п.
В дальнейшем будем рассматривать только числовые последовательности.
Пример:
Записать шесть первых членов последовательности натуральных чисел, которые при делении на 3 дают остаток 2.
Решение:
Первым натуральным числом, которое при делении па 3 дает остаток 2, является число 2. Следующим является число 5 — оно на 3 больше 2, дальше 8 — на 3 больше 5 и т. д. Поэтому получим: 2; 5; 8; I I ; 14; 17.
Ответ. 2 ;5 ;8 ; 11; 14; 17
Пример:
Записать формулу 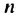
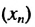
Решение:
Первым натуральным числом, которое больше 8 и при делении на 9 дает остаток 7, является число 16. Его можно записать так: 16 = 9 •1 + 7 . Вторым будет число 25, которое можно записать гак: 25 = 9 • 2 + 7, третьим — 34 = 9 • 3 + 7 и т. д. Тогда формула 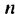
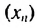
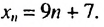
Пример:
Последовательность задана формулой 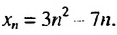
Решение:
Число 6 будет членом этой последовательности, если найдется такой номер 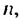
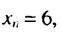
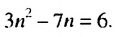
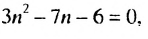
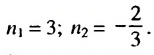
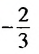
Ответ. Да.
Пример:
Записать три первых члена последовательности 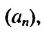
Решение:
При 
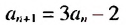
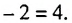
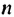
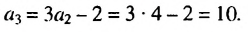
Арифметическая прогрессия и ее свойства
Среди числовых последовательностей важную роль играют последовательности, которые называют арифметической и геометрической прогрессиями.
Пример:
Группа туристов поднималась на гору в течение 4 ч. За первый час туристы прошли 2,5 км, а та каждый следующий — на 0,5 км меньше, чем за предыдущий. Какой путь проходили туристы за каждый час движения?
Решение:
За первый час туристы прошли 2.5 км. за второй — 2,5 — 0,5 = 2 (км), за третий — 2 — 0,5 = 1,5 (км), за четвертый — 1 км. Получили конечную последовательность чисел: 2,5; 2; 1,5; 1, в которой каждый последующий член, начиная со второю, равен предыдущему, сложенному с одним и тем же числом -0.5.
Пример:
3аписать последовательность натуральных чисел, которые при делении на 3 дают остаток 1.
Решение:
Получим: 1;4 ;7 ; 10; 13; 16; 19; 22 ;…. В этой последовательности любой член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом 3. Каждая из рассмотренных последовательностей является примером арифметической прогрессии.
Определение:
Арифметической прогрессией называют последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Это число называют разностью арифметической прогрессии и обозначают буквой d (d — начальная буква латинского слова differentia — разность). Итак, если имеется арифметическая прогрессия 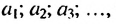
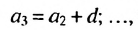
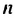
Из определения арифметической прогрессии следует, что разность между любым ее членом, начиная со второго, и предыдущим членом равна одному и тому же числу — разности d, то есть 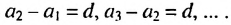
Верно и наоборот: если в некоторой числовой последовательности разность между любым ее членом, начиная со второго, и предыдущим членом равна одному и тому же числу, то такая последовательность является арифметической прогрессией.
Арифметические прогрессии могут быть конечными (пример 1) и бесконечными (пример 2).
Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность. Тогда каждый последующий член можно вычислить по предыдущему по рекуррентной формуле 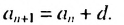
Рассмотрим свойства арифметической прогрессии.
1. В арифметической прогрессии 1; 3; 5: 7; 9 ;… каждый член, начиная со второго, является средним арифметическим двух соседних с ним членов:
Покажем, что такое свойство имеет любая арифметическая прогрессия. Пусть имеется арифметическая прогрессия 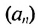
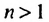
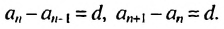
Свойство 1. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух соседних с ним членов. С этим свойством арифметической прогрессии и связано ее название.
2. Рассмотрим конечную арифметическую прогрессию 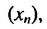
Сумма любых двух членов арифметической прогрессии, равноотстоящих от ее крайних членов, равна сумме крайних членов.
Используем эти соображения для произвольной конечной арифметической прогрессии 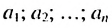
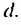
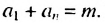
Свойство 2. Сумма любых двух членов конечной арифметической прогрессии, равноотстоящих от ее крайних членов, равна сумме крайних членов этой прогрессии.
Пример:
Найти разность и третий член арифметической прогрессии
Решение:
В этой прогрессии 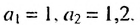
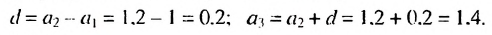
Пример:
Является ли последовательность чисел 3: 0: -3 : -6 ; -9 арифметической прогрессией?
Решение:
Обозначим члены заданной последовательности:
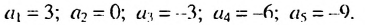
Так как полученные разности равны одному и тому же числу — 3, то эта последовательность является арифметической прогрессией.
Пример:
Между числами 7 и 15 вставить такое число, чтобы все три числа образовали арифметическую прогрессию.
Решение:
Пусть 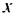
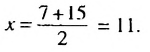
Формула n-го члена арифметической прогрессии
Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность, а последующие члены можно найти по формуле
Например, найдем несколько первых членов арифметической прогрессии, в которой 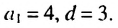
Далее можно найти 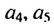
Чтобы найти член этой прогрессии с большим порядковым номером, например, 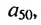
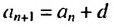
По определению арифметической прогрессии получим:
Замечаем, что в этих формулах коэффициент при d на 1 меньше порядкового номера искомого члена прогрессии. Так, 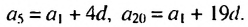
Полученную формулу называют формулой 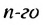
Пример:
Найти девятый член арифметической прогрессии
Решение:
Имеем: 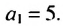
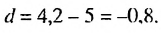
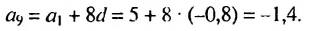
Пример:
Найти первый член арифметической прогрессии 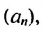
Решение:
Используя формулу 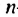
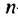
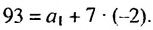
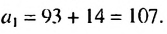
Пример:
Является ли число 181 членом арифметической прогрессии, в которой
Решение:
Число 181 будет членом прогрессии, если существует такое натуральное число 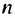
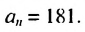
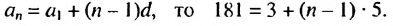
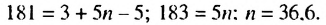
Пример:
Найти первый член и разность арифметической прогрессии 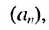
Решение:
По условию имеем: 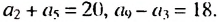
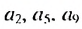
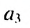
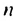
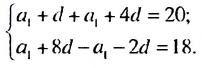
Ответ. 2.5;3 .
Формула суммы первых п членов арифметической прогрессии
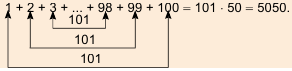
Пример:
Найти сумму натуральных чисел от 1 до 100 включительно.
Решение:
Запишем суму 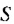
Суммы пар чисел, расположенных друг под другом в правых частях этих равенств, равны одному и тому же числу 101; таких нар 100. Поэтому
Отсюда
Итак, сумма всех натуральных чисел от 1 до 100 включительно равна 5050. Отметим, что последовательность натуральных чисел I; 2; …; 99: 100 является арифметической прогрессией 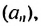
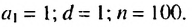
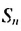
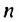
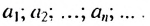
Сложим почленно эта равенства, получим:
По свойству 2 арифметической прогрессии сумма каждых двух членов, взятых в скобки, равна 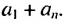
Отсюда
Если в этой формуле вместо 
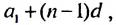
Итак,
Формулы (1) и (2) называют формулами суммы первых 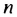
Пример:
Найти сумму первых девяти членов арифметической прогрессии
Решение:
1-й способ. Имеем: 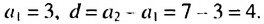
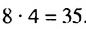
2-й способ. Зная, что 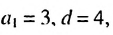
Ответ. 171.
Пример:
Найти сумму нечетных натуральных чисел, не превышающих 71.
Решение:
Нечетные натуральные числа образуют арифметическую прогрессию 1; 3: 5;……. в которой 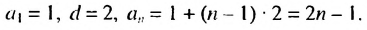
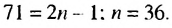
Ответ. 1296.
Пример:
Найти сумму натуральных чисел не больше 105, которые при делении на 9 дают остаток 1.
Решение:
Натуральные числа, которые при делении на 9 дают остаток 1, образуют арифметическую прогрессию 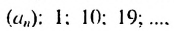
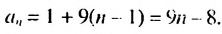
Следовательно, нужно искать сумму первых двенадцати членов прогрессии. Имеем: 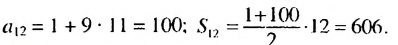
Пример:
Найти первый член арифметической прогрессии 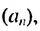
Решение:
По условию имеем: 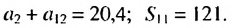
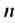
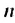
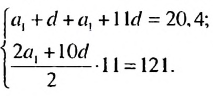
Ответ. 15.
Пример:
Сколько нужно взять первых членов арифметическом прогрессии 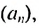
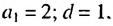
Решение:
Используя формулу суммы первых 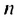
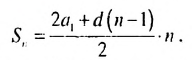
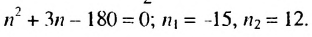
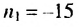
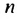
Геометрическая прогрессия и ее свойства
В благоприятных условиях некоторые бактерии размножаются так, что их количество удваивайся каждые 30 минут. Поэтому, если первоначально была одна бактерия, то их будет:
- через 0,5 ч 2
- через I ч 4
- через 1,5 ч 8
- через 2 ч 16
- …………………..
Во втором столбце получили последовательность чисел: 2: 4; 8; 16; каждый член которой, начиная со второго, равен предыдущему, умноженному на число 2. Такая последовательность является примером геометрической прогрессии.
Определение:
Геометрической прогрессией называют последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
Это число называют знаменателем геометрической прогрессии и обозначают буквой q (начальная буква французского слова qwoti — частное). Итак, если имеем геометрическую прогрессию 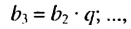
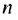
Из определения геометрической прогрессии следует, что частное от деления любого ее члена, начиная со второго, на предыдущий член равно одному и тому же числу — знаменателю то есть: 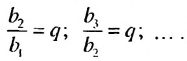
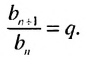
Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель. Тогда каждый последующий член по предыдущему можно вычислить по рекуррентной формуле
В таблице прицелены примеры геометрических прогрессий для некоторых значений
Рассмотрим свойства геометрической прогрессии.
1. В геометрической прогрессии 1; 3: 9, 27; 81;… квадрат каждого члена, начиная со второго, равен произведению двух соседних с ним членов:
Покажем, что такое свойство имеет любая геометрическая прогрессия. Пусть имеется геометрическая прогрессия 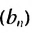
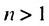
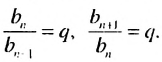
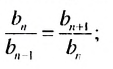
Свойство 1
Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних с ним членов.
Если все члены геометрической прогрсссии являются положительными числами, то из равенства 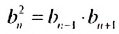
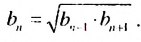
2. Рассмотрим конечную геометрическую прогрессию 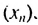
Видим, что произведения членов профессии, равноотстоящих от ее крайних членов, одинаковы и равны произведению крайних членов.
Используем эти соображения для произвольной конечной геометрической прогрессии 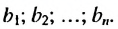
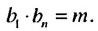
Свойство 2
Произведение любых двух членов конечной геометрической прогрессии, равноотстоящих от ее крайних членов, равно произведению крайних членов.
Пример:
Найти знаменатель и третий член геометрической npoгpеcсии
Решение:
В этой прогрессии 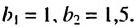
Ответ. 1,5; 2,25.
Пример:
Доказать, что последовательность 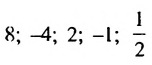
Решение:
Обозначим члены последовательности: 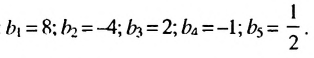
Так как полученные частные равны одному и тому же числу 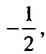
Пример:
Найти второй член геометрической прогрессии:
Решение:
Согласно свойству 1 геометрической прогрессии 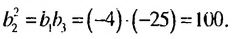
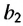
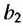
Формула n-го члена геометрической прогрессии
Чтобы задать геометричсскую прогрессию 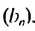
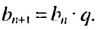
Далее можно найти 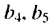
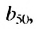
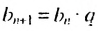
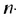
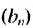
Замечаем, что в этих формулах показатель степени числа q на единицу меньше порядкового номера искомого члена прогрессии. Так, 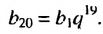
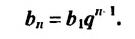
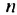
Пример:
Найти шестой член геометрической прогрессии
Решение:
Имеем: 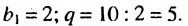
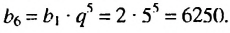
Пример:
Найти первый член геометрической прогрессии 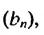
Решение:
Используя формулу 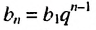
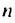
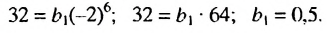
Пример:
Найти знаменатель геометрической прогрессии 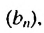
Решение:
Используя формулу 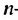
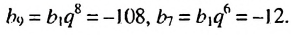
Ответ. -3 или 3.
Формула суммы первых n членов геометрической прогрессии
Пусть 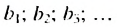
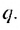
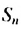
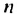
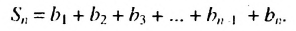
Умножив обе части этого равенства на q получим:
Пo определению геометрической прогрессии: 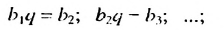
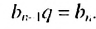
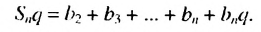
Вычтем почленно из равенства (1) равенство (2), получим:
Если 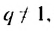
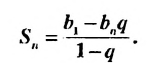
Учитывая, что 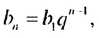
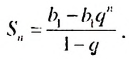
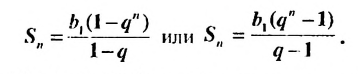
Формулы (3) и (4) называют формулами суммы первых 
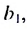
Пример:
Найти сумму восьми первых членов геометрической прогрессии
Решение:
Имеем : 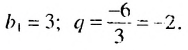
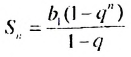
Ответ. -255.
Пример:
Найти первый член геометрической прогрессии 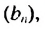
Решение:
Так как 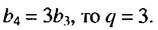
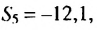
Ответ. -0,1.
Сумма бесконечной геометрической прогрессии, в которой [q] меньше 1
Сумма бесконечной геометрической прогрессии, в которой
Пусть стороны прямоугольника 
Найдем площадь этою прямоугольника иначе. Отрезком MN. соединяющим середины противоположных сторон ВС и 
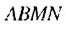
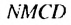
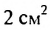
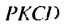
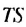
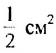
Найдем сумму площадей прямоугольников 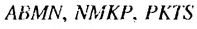
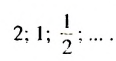
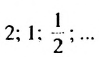
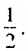
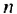
Если число 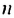
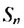
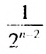
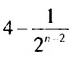
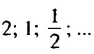
Итак, сумма площадей прямоугольников ABMN, NMKP, PKTS и т. д. равна 4 см2, то есть равна площади прямоугольника ABCD. Обобщим рассмотренный пример. Пусть 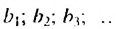
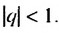
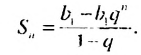
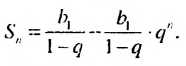
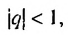
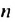
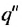
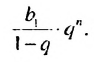
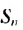
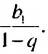
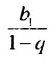
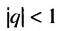
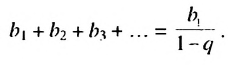
Полученную формулу называют формулой суммы бесконечной геометрической прогрессии, в которой
Пример:
Найти сумму бесконечной геометрической прогрессии 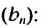
Решение:
По условию 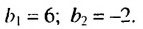
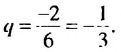
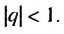
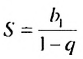
Ответ. 4,5.
Решение задач, связанных с арифметической и геометрической прогрессиями
Вычисление сумм
Изучая арифметическую и геометрическую прогрессии, мы вычисляли суммы первых 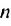
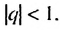
Пример 1. Найти сумму
Решение:
Обозначим эту сумму через 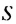
В первых скобках записана сумма членов арифметической прогрессии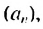
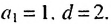
Итак, в первых скобках записана сумма первых семи членов арифметической прогрессии. Во вторых скобках записана сумма первых семи членов геометрической прогрессии 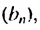
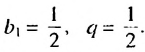
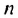
Ответ:
Обращение бесконечных периодических десятичных дробей в обыкновенную дробь
Рассмотрим пример.
Пример:
Записать число 0,(7) в виде обыкновенной дроби.
Решение:
Бесконечную десятичную дробь 0,(7) = 0,777… запишем в виде такой суммы: 0,(7) = 0.7 + 0,07 + 0,007 + …. Слагаемые 0,7; 0,07; 0.007;… — члены бесконечной геометрической прогрессии с первым членом 0,7 и знаменателем 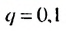
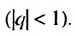
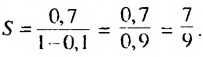
Ответ:
Решение уравнении
Рассмотрим пример.
Пример:
Решить уравнение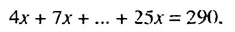
Решение:
Запишем уравнение так:
В скобках записана сумма первых членов арифметической прогрессии. в которой 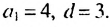
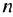
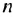
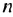
Итак, в скобках записана сумма первых 8 членов арифметической прогрессии. Тогда получим:
Ответ. 2,5.
Пример:
Записать число 3.1(23) в виде обыкновенной дроби.
Решение:
Число 3.1(23) = 3,12323… запишем в виде такой суммы:
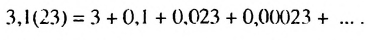
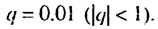
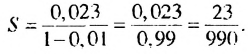
Ответ:
Пример:
Решить уравнение:
Решение:
Запишем уравнение в виде:
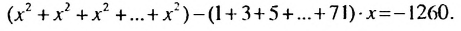
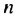
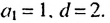
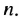
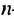
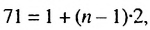
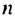
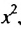
Ответ. 1; 35.
Пример:
Найти сумму
Решение:
Обозначим данную сумму через S. Записав слагаемые в виде 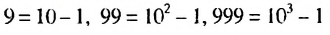
В скобках записана сумма первых 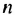
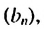
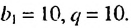
Ответ.
ИНТЕРЕСНО ЗНАТЬ
Слово «прогрессия» происходит от латинского слона «prcigrcssio» и значит «движение вперед» (как и слово «прогресс»). Впервые этот термин встречается в работах римского ученого Боэция (V -V I в.). Прогрессии как частные виды числовых последовательностей встречаются в папирусах II тысячелетия до н. э. Первые задачи на прогрессии, дошедшие до нас, связаны с хозяйственной деятельностью, а именно — с распределением продуктов, разделом наследства и т. п. Древнейшей задачей на прогрессии считают задачу из египетского папируса Ахмеса Райнда о распределении 100 мер хлеба между пятью людьми так, чтобы второй получил на столько больше первого, на сколько третий получил больше второго и т. д. В этой задаче речь идет об арифметической прогрессии, сумма первых пяти членов которой равна 100. В одной из задач этого папируса представлена формула первого члена арифметической прогрессии, которую в современной символике записывают так:
где а — первый член, 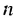
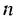
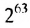
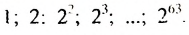
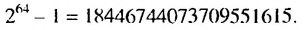
————
Числовые последовательности
♦ Множество чисел в котором каждое число имеет свой номер 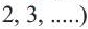
♦ Числа, образующие последовательность, называются соответственно первым, вторым, третьим, четвертым и т.д. членами последовательности. Члены последовательности, обычно обозначаются буквами, индекс буквы показывает порядковый номер члена. Например, первый член 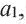
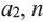
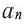
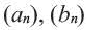
♦ Последовательности бывают конечные и бесконечные. Например, множество двузначных чисел может быть примером конечной последовательности. А последовательность натуральных чисел — бесконечна.
♦ Обычно последовательность задают с помощью формулы определящей функцию 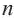
Например: 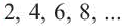
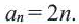
Наблюдается взаимосвязь многих природных явлений с последовательностью Фибоначчи.
Фибоначчи родился в итальянском городе Пиза: Его произведение «Книга вычислений» (Liber Abaci) оказала огромное влияние на распространение математических знаний в Европе, служила учебником — справочником европейских ученых. Особенно неоценима его роль в быстром распространении в Европе индийско-арабской десятичной системы. В то время в Европе при записи и вычислениях пользовались Римскими цифрами. В этом произведении Фибоначчи также уделил большое внимание задаче о размножении кроликов, которая дает последовательность чисел 1,1, 2, 3, 5, 8, 13, 21,… Для членов этого ряда (при 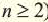
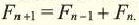
Рекуррентный и экспилитический способы задания последовательности
Формула, выражающая любой член последовательности, начиная с некоторого, через один или несколько предыдущих членов называется рекуррентной формулой, (от латинского слова recirro — возвращаться). Например, в последовательности 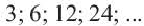
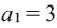
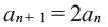
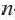
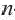
Например,
Арифметическая прогрессия, рекуррентное правило
Определение. Числовая последовательность, в которой каждый член, начиная со второго равен предыдущему, сложенному с одним и тем же для данной последовательности числом называется арифметической прогрессией. То есть арифметическая прогрессия — это такая последовательность, в которой 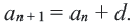
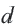
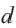
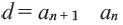
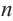
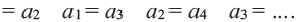
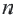
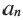
Пример 1. Определите, какие из последовательностей являются арифметической прогрессией.
а) 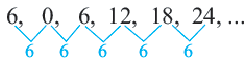
b) 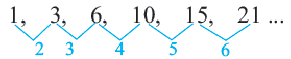
Разность арифметической прогрессии может быть положительным, отрицательным числом или нулем. При 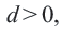
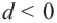
Пример 2. а) При 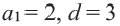
b) При условии 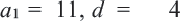
При 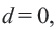
Формула n-го члена арифметической прогрессии
Каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же для данной последовательности числом. Согласно этому правилу:
По этому правилу можно записать:
Формула 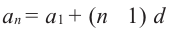
Пример 1. В арифметической прогрессии 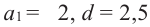
Отметим, что 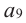
Вообще, 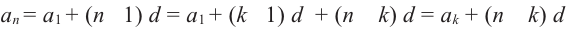
Отсюда, получаем формулу для разности прогресии:
Пример 2. В арифметической прогрессии
Решение:
Замечание. Переписав формулу 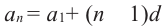
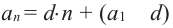
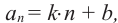
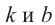
Арифметическая прогрессия и среднее арифметическое
Свойство. Любой член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов.
Действительно, из 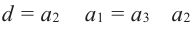
Так как в общем случае, 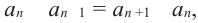
Это свойство можно обобщить таким образом. Каждый член арифметической прогрессии (начиная со второго) равен среднему арифметическому равноудаленных от него членов:
Это свойство поясняет причину названия арифметической прогрессии. Верно и обратное. Если любой член последовательности, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то эта последовательность является арифметической прогрессией.
В конечной арифметической прогрессии сумма членов, расположенных на одинаковом расстоянии от концов, равна сумме крайних членов.
В общем, если
Сумма n-первых членов арифметической прогрессии
Обозначим через 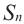
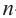
Попарные суммы 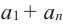
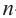
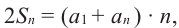
Сумма 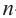
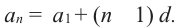
Пример 1. Найдите сумму 12-ти первых членов арифметической прогрессии заданной формулой 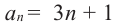
Решение:
Пример 2. Найдите сумму 10-ти первых членов арифметической прогрессии 3; 5; 13;… .
Решение.
Пример 3. В зале заседаний 30 рядов. В первом ряду 24 места, а в каждом следующем ряду на одно место больше, чем в предыдущем. Сколько всего мест в зале?
Решение:
В последнем ряду: 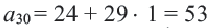
Пример 4. Сколько членов арифметической прогрессии 5; 7; 9… нужно сложить, чтобы получить 320 ?
Решение:
Так как количество членов не может быть отрицательным, то сумма 16-ти первых членов этой прогрессии равна 320. Перепишем сумму первых 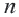
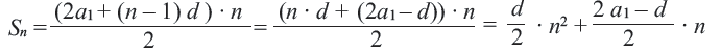
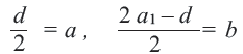
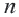
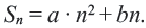
Пример 5. Найдем первый член и разность арифметической прогрессии, сумма 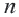
Решение:
Внимание! При решении некоторых задач для определения 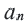
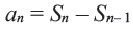
Члены геометрической прогрессии, рекуррентное правило
Определение. Геометрической прогрессией называется числовая последовательность, члены которой отличны от нуля, а каждый член, начиная со второго, равен предыдущего члену, умноженному на одно и то же, не равное нулю, число. То есть если для любого натурального числа 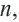
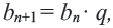
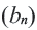
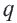
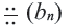
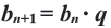
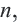
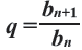
Пример 1. а) Если 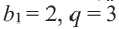
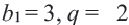
Пример 2. Какая из данных числовых последовательностей геометрическая прогрессия?
а) 4, 12, 22, 34, 48; b) 625, 125, 25, 5, 1.
Отношение каждого члена геометрической прогрессии на предыдущий всегда остается постоянной. Проверим это условие для обеих прогрессий.
а)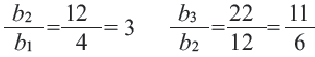
b)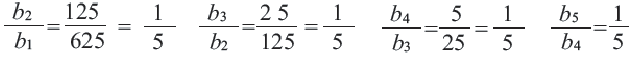
Формула n-го члена геометрической прогрессии
Вообще, чтобы в геометрической прогрессии найти 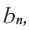
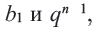
Это выражение называется формулой 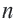
Пример 1. Если в геометрической прогрессии 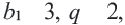
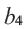
Указание. Можно было бы вычислить следующем способом
Вообще, справедливо равенство,
Пример 2. Найдем 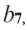
Решение: 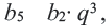
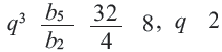
Заключение: Если известны какие-либо два члена, то можно задать геометрическую прогрессию, 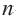
Если перемножить почленно эти 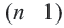
Сократив одинаковые члены в левой и правой частях, получим формулу
Заключение: Записав 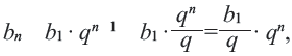
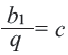
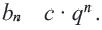
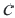
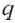
Члены геометрической прогрессии и среднее геометрическое
В геометрической профессии с положительными членами, начиная со второго, каждый член равен среднему геометрическому соседних с ним членов. Это свойство поясняет причину названия геометрической прогрессии. Например, в последовательности, 2, 6, 18, 54, 162,… число 18 является средним геометрическим 6 и 54. Среднее геометрическое-можно ясно увидеть, записывая отношения, выражающие знаменатель профессии. Из определения геометрической прогрессии получатся равенства:

Взяв попарно эти равенства, получим: 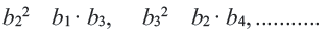
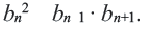
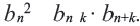
Еще одно свойство членов геометрической профессии: Если 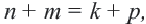
Сумма n-первых членов геометрической прогрессии
Обозначим через 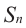
При 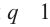
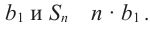
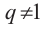
Умножим обе части (1 )-го равенства на 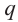
Отнимем от (2)-го равенства (1)-е. Получим:
Отсюда S
(3)-я формула называется формулой 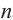
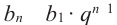
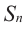
Пример. В геометрической прогрессии 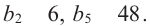
Решение. 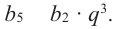
Из формулы 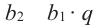
Тогда
Сумма бесконечной геометрической прогрессии при
Если число членов геометрической прогрессии бесконечно, то ее называют бесконечной геометрической профессией. Преобразуем формулу суммы 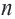
Если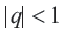
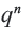
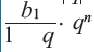
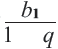
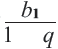
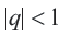
Если обозначить эту сумму через 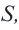
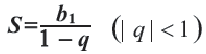
Пример. Примените формулу суммы бесконечной геометрической профессии в преобразовании периодической дроби 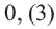
Так как 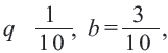
Геометрические преобразования. Движение
Параллельный перенос
При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и тоже расстояние и фигура переходит в фигуру конгруэнтную себе. Треугольник 
В координатной плоскости каждая точка данного треугольника 
Применяя формулу расстояния между двумя точками, получим: 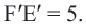
При параллельном переносе фигуры произвольная точка 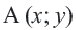
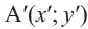
На координатной плоскости при параллельном переносе перемещение по осям координат направо и наверх выражаегся положительными, налево и вниз отрицательными единицами. Это определяется числами 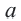
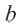
Действительно, при параллельном переносе произвольные точки 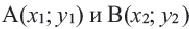
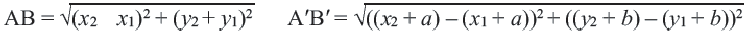
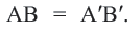
Координаты середины отрезка
Координаты середины отрезка 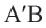
Значит, диагонали четырехугольника 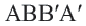
- Заказать решение задач по высшей математике
Параллельный перенос и векторы
Каждый параллельный перенос определяет один вектор. То есть при параллельном переносе перемещение всех точек фигуры выполняется по одному вектору. Выражение параллельного переноса вектором упрощает запись. Компоненты вектора 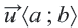
На картине изображен параллельный перенос 
Длина вектора
Движение и конгруэнтные фигуры
Пусть каждой точке фигуры 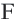
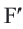
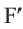
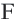
Теорема. При движении отрезок преобразуется в отрезок.
Доказательство. Пусть при движении концы отрезка 
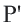
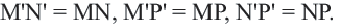
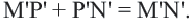
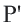
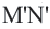
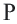
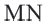
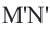
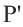
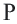
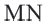
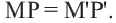
Следствие. При движении каждая сторона треугольника переходит в конгруэнтный отрезок, и поэтому по признаку 
Теорема. Осевая симметрия (отражение) есть движение.
На рисунке изображено отражение отрезка 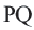
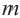
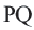
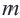
Докажем теорему для первого случая:
Текстовое доказательство
В этом случае точки 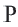
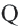
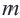
Из определения отражения следует, что, так как отрезок 
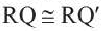
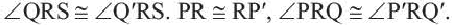
——
Числовые последовательности
В этой лекции вы:
Пример №356
Запишем в порядке возрастания четные натуральные числа: 2; 4; 6; 8; 10; … .
Получим последовательность четных натуральных чисел. На первом месте в ней число 2, на втором — число 4, на пятом — 10. Если и далее записывать четные натуральные числа, то, например, на десятом месте окажется число 20, на сотом — число 200. Вообще, для любого натурального числа 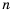
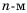
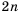
Числа, образующие последовательность, называют соответственно первым, вторым, третьим, четвертым и т. д. членами последовательности. Члены последовательности принято обозначать буквами с индексами, указывающими порядковый номер члена последовательности. Например: 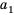
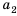
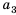
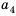
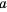
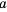
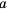
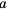
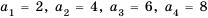
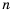
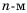
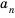
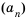
Рассмотрим два соседних члена последовательности с номерами 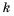
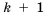
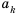
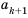
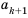
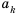
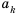
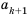
Поскольку в последовательности четных натуральных чисел на 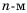
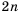
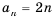

Эта последовательность содержит бесконечное число членов. Такую последовательность называют бесконечной. В записи бесконечной последовательности после перечисления нескольких ее первых членов ставят многоточие. Если же последовательность содержит конечное число членов, то ее называют конечной.
Пример №357
Последовательность двузначных натуральных чисел 10; 11; 12; …; 98; 99 является конечной. Она содержит 90 членов и может быть задана формулой 
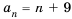
Зная формулу 
Пример №358
Последовательность задана формулой 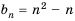
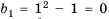
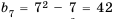
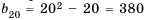
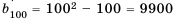
Формула 
Пример №359
Конечную последовательность можно задать перечислением ее членов. Например, 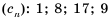
Пример №360
Последовательность можно задать описанием ее членов. Например, последовательность натуральных делителей числа 18, записанных в порядке возрастания, выглядит так: 1; 2; 3; 6; 9; 18.
Пример №361
Конечную последовательность можно задать и в виде таблицы. Например:
Последовательность можно задавать, указав первый или несколько первых членов последовательности, а затем — формулу, позволяющую найти остальные члены последовательности через предыдущие. Такую формулу называют рекуррентной, а способ задания последовательности — рекуррентным.
Пример №362
Пусть первый член последовательности 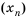
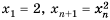
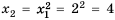
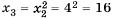
Получим последовательность: 2; 4; 16; 256; 65 536; … .
Пример №363
Найдем третий, четвертый и пятый члены последовательности 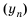
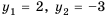
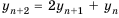
Получим:
Последовательности, рассмотренные выше, являются числовыми последовательностями, так как состоят из чисел. Иногда рассматривают последовательности, членами которых являются выражения, функции и т. п. В дальнейшем будем рассматривать только числовые последовательности.

- 1, 2, 3, 4, 5,… — последовательность натуральных чисел;
- 2, 4, 6, 8, 10,… — последовательность четных чисел;
- 1, 3, 5, 7, 9,… — последовательность нечетных чисел;
- 1,4,9,16,25,… — последовательность квадратов натуральных чисел;
- 2, 3, 5, 7, 11,… — последовательность простых чисел;
— последовательность чисел, обратных натуральным.
Для всех этих последовательностей, кроме пятой, можно записать формулу 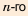
Одной из наиболее известных является числовая последовательность, которую называют последовательностью Фибоначчи в честь итальянца Л. Пизанского (Фибоначчи) (ок. 1170 — ок. 1250). Он первым рассмотрел последовательность чисел, два первых члена которой — единицы и каждый член которой, начиная с третьего, равен сумме двух предыдущих:
1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144 ….
Лишь несколько веков спустя была найдена формула 
Арифметическая прогрессия, ее свойства. формула n-го члена арифметической прогрессии
Рассмотрим числовую последовательность, первый член которой равен 4, а каждый следующий, начиная со второго, равен предыдущему, сложенному с числом 3:
Такую последовательность называют арифметической прогрессией.
Последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом, называют арифметической прогрессией.
Это число называют разностью арифметической прогрессии и обозначают буквой 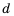
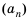
Таким образом, для любого натурального 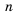
Тогда: 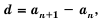
разность арифметической прогрессии можно найти, если от любого члена прогрессии, начиная со второго, отнять предыдущий.
Пусть первый член арифметической прогрессии равен 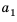
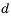
Заметим, что в каждой из полученных формул коэффициент у разности 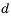
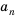
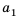
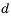

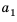
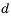
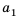
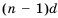
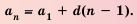

Рассмотрим несколько примеров применения этой формулы.
Пример №364
Последовательность 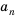
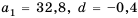
Решение:
Ответ. 25,2.
Пример №365
Принадлежит ли арифметической прогрессии 7; 10; 13; … число: 1) 82; 2) 102?
Решение:
В данной прогрессии 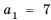
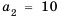
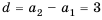

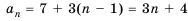
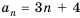
1) Допустим, число 82 является членом прогрессии 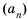
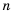
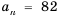
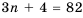
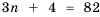
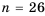
Следовательно, число 82 является двадцать шестым членом арифметической прогрессии, то есть 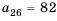
2) Рассуждая аналогично, имеем: 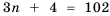
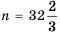
Полученное число 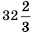
Ответ. 1) Да; 2) нет.
Пример №366
Кубики сложены рядами так, что в верхнем ряду 4 кубика, а в каждом следующем ниже ряду — на одно и то же количество кубиков больше, чем в предыдущем. Известно, что в шестом ряду 14 кубиков. Сколько кубиков в третьем ряду?
Решение:
Так как в каждом следующем ряду на одно и то же количество кубиков больше, чем в предыдущем, то числа, равные количеству кубиков в рядах, образуют арифметическую прогрессию, в которой 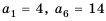
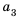
Для начала найдем разность 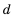
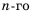
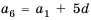
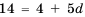
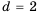
Теперь, зная значение 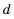
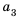
Следовательно, в третьем ряду 8 кубиков.
Заметим, что найти 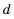
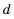
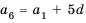
Ответ. 8 кубиков.
Докажем несколько важных свойств арифметической прогрессии.
1. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух соседних с ним членов, то есть
Доказательство: Используем формулу 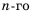
По одной из версий именно с этим свойством арифметической прогрессии связано ее название.
2. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух равноудаленных от него членов, то есть
Свойство доказывается аналогично предыдущему свойству.
3. Если 
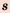
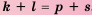

Доказательство: Используем формулу 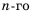
Но 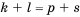
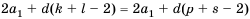
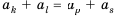
4. Любую арифметическую прогрессию можно задать формулой 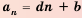
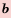
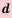
Доказательство: По формуле 
Обозначив 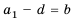
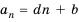
5. Последовательность 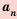
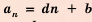
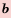
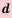
Доказательство: Рассмотрим разность 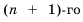
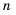
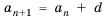
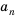
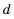


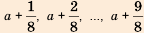
Задачи на арифметические прогрессии есть и в древнекитайском трактате «Математика в девяти книгах».
Первые из дошедших до нас задач на прогрессии связаны с запросами хозяйственной жизни и общественной практики, как, например, распределение продуктов, деление наследства и т. п.
У древних греков теория арифметических прогрессий была связана с так называемой непрерывной арифметической пропорцией:
Здесь числа 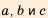
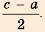
Сумма n первых членов арифметической прогрессии
Рассмотрим 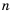
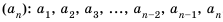
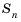
Найдем формулу для вычисления этой суммы. Запишем эту сумму дважды, разместив в первом случае слагаемые в порядке возрастания их номеров, а во втором — в порядке убывания:
Теперь сложим эти равенства почленно и получим:
Но по свойству 3 из предыдущего параграфа: 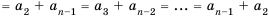
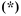
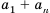

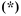
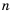
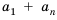
Разделив обе части этого равенства на 2, получим формулу суммы 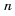
Если в формуле 
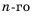
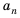
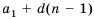
или
Получили еще одну формулу для вычисления суммы п первых членов арифметической прогрессии, которой удобно пользоваться, если известны первый член и разность прогрессии.
Применим формулы 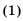
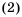
Пример №367
Найти сумму тридцати первых членов арифметической прогрессии 4; 7; 10; … .
Решение:
1-й способ. Так как 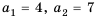
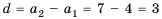
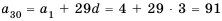
Тогда по формуле 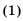
2-й способ. Так как 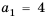
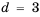
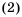
Ответ. 1425.
Пример №368
Найти сумму восемнадцати первых членов последовательности 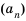
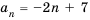
Решение:
Поскольку последовательность задана формулой 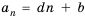
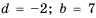
Имеем:
Найдем 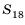
Ответ. -216.
Пример №369
Найти сумму всех натуральных чисел, кратных числу 7 и не превышающих 999.
Решение:
Натуральные числа, кратные числу 7, образуют арифметическую прогрессию: 7; 14; 21; 28; …, которую можно задать формулой 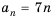
Найдем, сколько членов этой прогрессии не превышают числа 999. Для этого решим неравенство 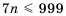
что 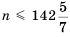
Следовательно, 142 члена прогрессии не превышают 999. Найдем их сумму, то есть
Имеем: 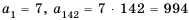
Ответ. 71 071.
Пример №370
Из двух точек, расстояние между которыми 100 м, одновременно навстречу друг другу начинают двигаться два объекта. Первый движется равномерно со скоростью 9 м/с, а второй за первую секунду проходит 7 м, а за каждую следующую на 2 м больше, чем за предыдущую. Через сколько секунд они встретятся?
Решение:
Пусть объекты встретятся через 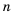
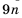
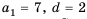
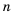
По условию 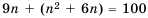
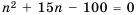
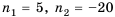
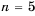
Ответ. 5 с.

1)
2)
3) 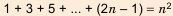
С вычислением суммы арифметической прогрессии связана интересная история, произошедшая с выдающимся немецким математиком Карлом Гауссом (1777-1855), который, еще учась в школе, проявил чрезвычайные математические способности. Однажды учитель предложил ученикам найти сумму ста первых натуральных чисел. Юный Гаусс мгновенно получил результат. Он заметил, что значения сумм 1 + 100, 2 + 99, 3 + 98, … одинаковы, а количество таких сумм равно 50:
Геометрическая прогрессия, ее свойства. формула n-го члена геометрической прогрессии
Рассмотрим числовую последовательность, первый член которой равен 3, а каждый следующий, начиная со второго, равен предыдущему, умноженному на число 2:
Такую последовательность называют геометрической прогрессией.
Геометрической прогрессией называют последовательность отличных от нуля чисел, каждое из которых, начиная со второго, равно предыдущему, умноженному на одно и то же число.
Это число называют знаменателем геометрической прогрессии и обозначают буквой 
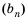
Следовательно, для любого натурального 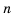
Тогда 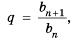
знаменатель геометрической прогрессии можно найти, ли любой член прогрессии, начиная со второго, разделить на предыдущий.
Заметим, что поскольку члены геометрической прогрессии отличны от нуля, то и знаменатель 
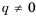
Если 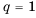
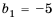
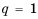
Заметим, что полученную последовательность можно также считать и арифметической прогрессией, первый член которой равен -5, а разность равна нулю.
Пусть первый член геометрической прогрессии равен 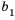

Заметим, что в каждой из полученных формул показатель степени числа 
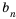
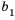


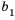

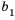
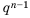
Получили формулу 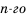
Рассмотрим несколько примеров применения этой формулы.
Пример №371
Последовательность 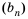
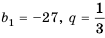
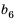
Решение:
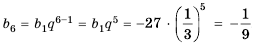
Ответ. 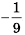
Пример №372
Найти знаменатель 
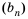
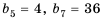
Решение:
1-й способ. 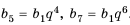
При этом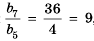
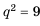
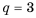
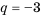
2-й способ. 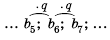
Так как 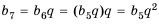
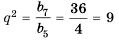
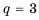
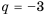
Ответ. 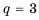
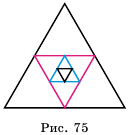
Пример №373
Дан равносторонний треугольник со стороной 8 см. Середины его сторон являются вершинами второго треугольника, а середины сторон второго являются вершинами третьего и т. д. (рис. 75). Найти площадь пятого треугольника, построенного по тому же принципу.
Решение:
Пусть 
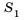
Поскольку стороны каждого следующего треугольника являются средними линиями предыдущего, то длина стороны каждого следующего треугольника будет вдвое меньше длины стороны предыдущего. Тогда сторона второго треугольника равна 4 см, а его площадь 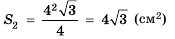
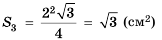
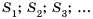
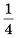
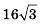
Ответ.
Докажем некоторые важные свойства геометрической прогрессии.
1. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних с ним членов, то есть
Доказательство. Воспользуемся формулой 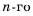
Если все члены геометрической прогрессии являются положительными числами, то 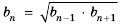
По одной из версий именно с этим свойством геометрической прогрессии и связано ее название.
2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух равноудаленных от него членов, то есть
Свойство доказывается аналогично предыдущему свойству.
3. Если 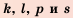

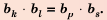
Доказательство: Воспользуемся формулой 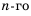
Нo 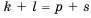
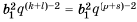

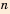
В своей работе «Псаммит» Архимед впервые сопоставил арифметическую и геометрическую прогрессии:
и указал на связь между ними, например: 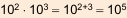
У древних греков теория геометрических прогрессий была связана с так называемой непрерывной геометрической пропорцией:
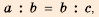
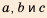
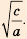
Формула сложных процентов
Бухгалтерам и работникам банков часто приходится решать задачи на проценты. Рассмотрим задачу о начислении процентного дохода. С экономической точки зрения процентный доход можно считать вознаграждением, которое платит лицо или учреждение (заемщик) за пользование в течение определенного времени определенной суммой средств, полученных от другого лица или учреждения (кредитора). Размер этого вознаграждения зависит от суммы средств и срока пользования ими.
Пример №374
Вкладчик открыл в банке депозит в размере 10 ООО грн под 11 % годовых (то есть банк обязан выплатить процентный доход в размере 11 % в год от начальной суммы вклада). Какой процентный доход получит вкладчик через год?
Решение:
11 % = 0,11, поэтому вкладчик получит 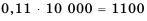
Ответ. 1100 грн.
Если вкладчик решил держать средства в банке более года, не добавляя новых средств и не забирая вложенных, то определить сумму средств на счету вкладчика через несколько лет можно с помощью формулы сложных процентов.
Пусть вкладчик положил в банк 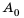
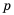
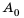
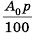
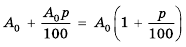
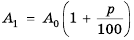
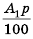
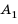
Рассуждая аналогично и применяя формулу 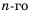
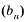
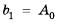
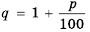
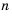
Таким образом,
начальный капитал 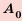
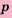
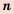
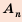
которую называют формулой сложных процентов.
Пример №375
Вкладчик открыл в банке депозит на 5000 грн под 12 % годовых. Сколько средств будет на счету вкладчика через 3 года? Какой процентный доход получит вкладчик через 3 года?
Решение:
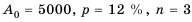
Процентный доход можно найти как разность
Таким образом, 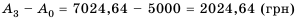
Ответ. 7024,64 грн, 2024,64 грн.
По формуле сложных процентов можно решать и другие задачи, не связанные с наращиванием капитала.
Пример №376
Население города составляет 30 000 жителей. Каждый год количество населения уменьшается на 0,2 %. Сколько жителей будет в этом городе через 10 лет?
Решение:
Так как население города ежегодно уменьшается на один и тот же процент, и это процент от количества населения каждого предыдущего года, а не от начального количества жителей, то можно воспользоваться формулой сложных процентов.
Имеем, 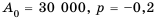
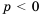
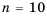
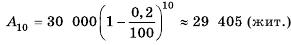
Ответ. 29 405 жителей.
Сумма n первых членов геометрической прогрессии
Рассмотрим 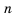
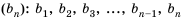
Обозначим через 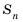
Найдем формулу для вычисления этой суммы. Имеем (учитывая формулу 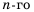
Умножим обе части этого равенства на 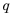
Вычтем почленно из этого равенства предыдущее:
Таким образом, 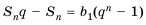
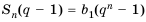
Если 
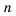
Если 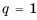
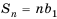
Заметим, что полученную формулу 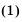
Так как 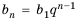
Таким образом,
Получили еще одну формулу для вычисления суммы 
Пример №377
Найти сумму первых семи членов геометрической прогрессии 2; -6; 18; … .
Решение:
1-й способ. По условию:
Тогда по формуле 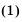
2-й способ. Известно, что 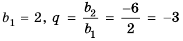
По формуле 
Ответ. 1094.
Пример №378
Найти сумму первых шести членов геометрической прогрессии 
Решение:
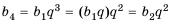
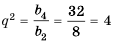
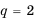
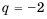
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи:
1) если 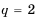
2) если 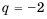
Ответ. 252 или -84.
Пример №379
Сократить дробь
Решение:
Слагаемые в числителе дроби являются последовательными членами геометрической прогрессии 1, 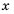
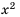
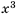
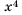
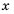
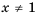
Найдем сумму всех шести членов этой прогрессии по формуле 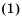
Ответ. 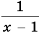

Царь удивился, что изобретатель пожелал столь мало, и приказал придворным математикам подсчитать необходимое количество зерен. Каково же было изумление царя, когда он узнал, что не сможет выдать обещанную награду, так как необходимое число зерен равно
Чтобы получить столько зерен, потребовалось бы собрать урожай с площади, в 2000 раз превышающей всю поверхность Земли. А для хранения такого урожая понадобился бы амбар, который при высоте 4 м и ширине 10 м тянулся бы на 300 000 000 км, то есть вдвое дальше, чем от Земли до Солнца.
- Предел числовой последовательности
- Предел и непрерывность числовой функции одной переменной
- Функции, их свойства и графики
- Параллельность в пространстве
- Рациональные выражения
- Квадратные корни
- Квадратные уравнения
- Неравенства

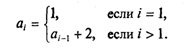
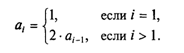
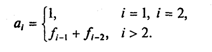
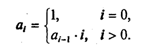
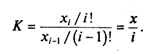
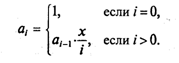
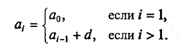
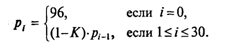
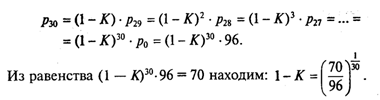


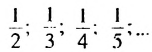 — последовательность правильных дробей с числителем 1;
— последовательность правильных дробей с числителем 1;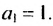
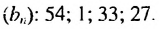

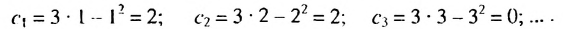
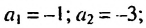
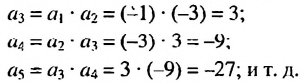
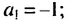
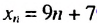
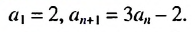
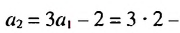
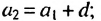
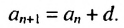
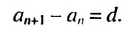

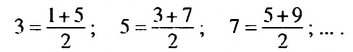
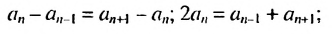
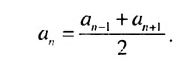
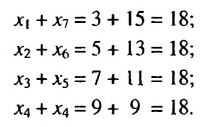
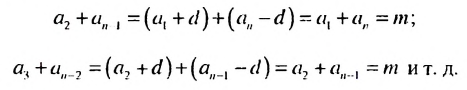
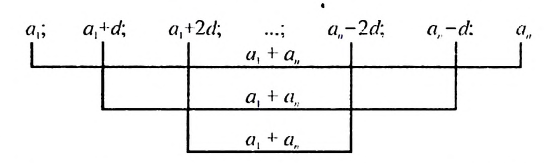
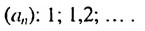
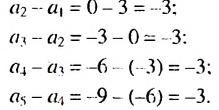
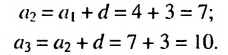
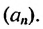
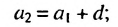
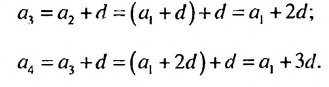
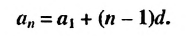
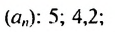
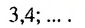
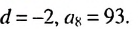
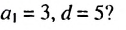
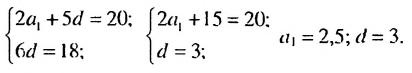
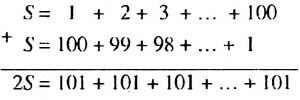
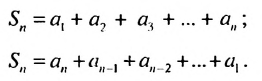
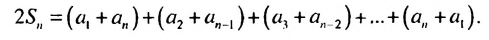
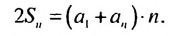

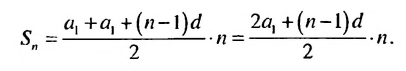
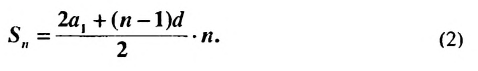
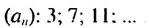
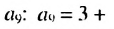
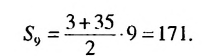
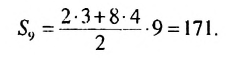
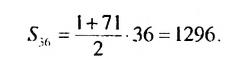
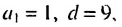
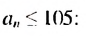
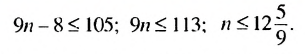
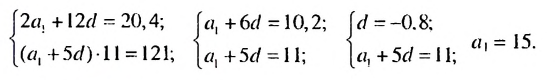
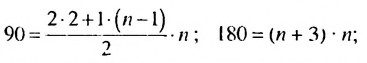
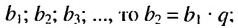
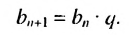
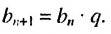
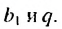

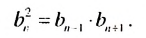
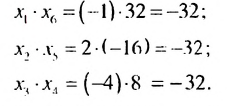
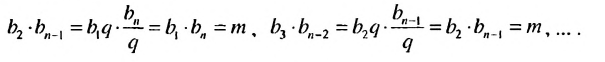
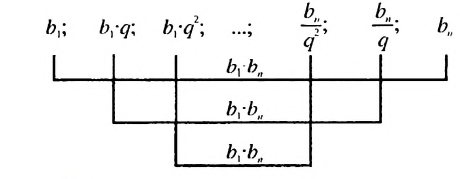
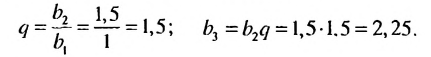
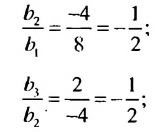
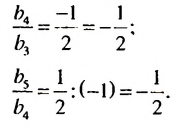
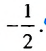
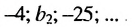
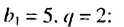
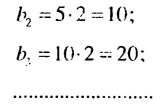
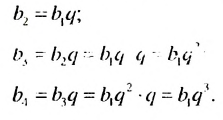
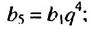
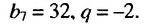
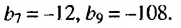
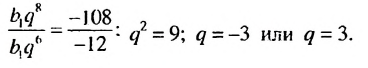
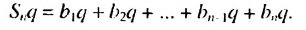
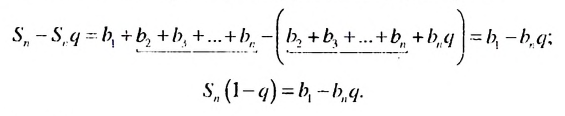
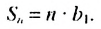
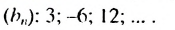
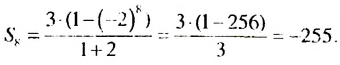
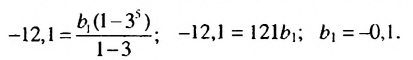
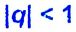
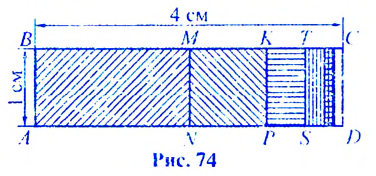
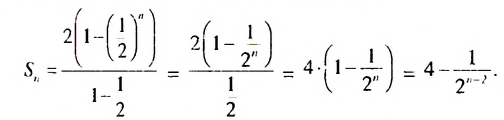
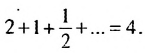
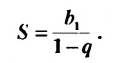
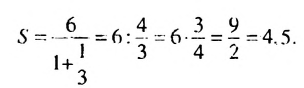
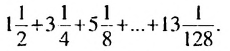
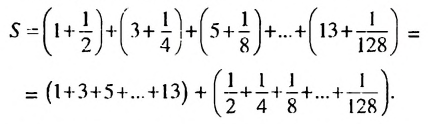
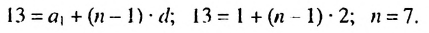
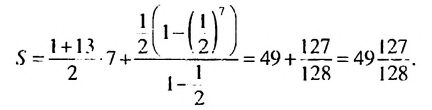
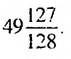
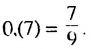
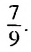
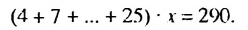
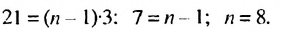
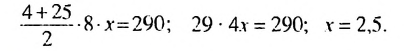
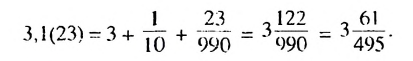
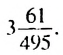
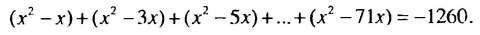
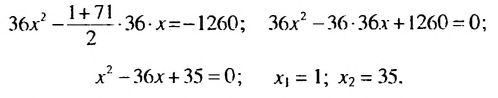
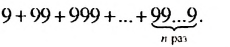
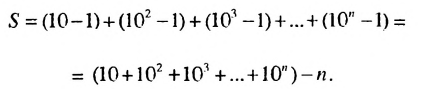
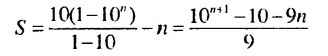
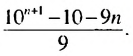
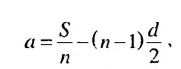
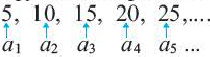
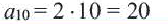

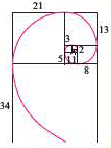
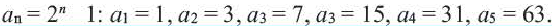
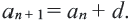
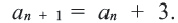
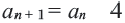
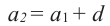
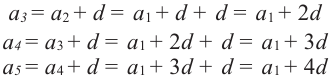
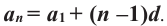
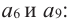
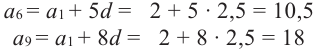
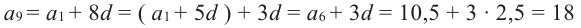
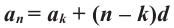
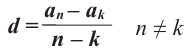
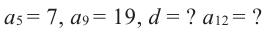
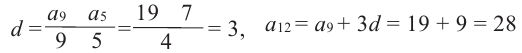
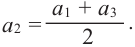
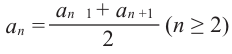
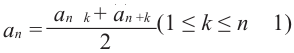
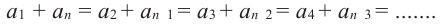
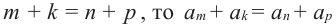
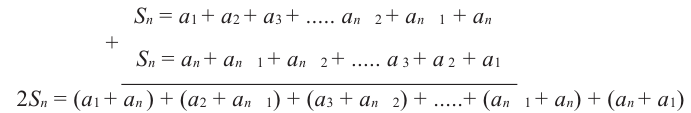
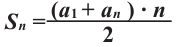
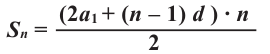

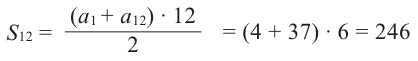
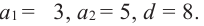
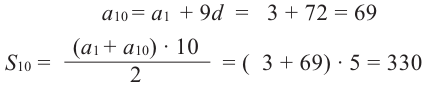
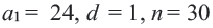
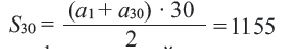
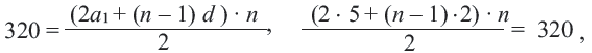
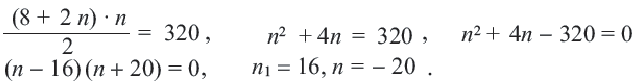
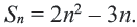
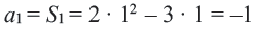
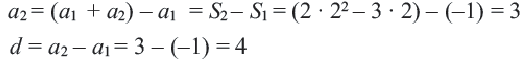
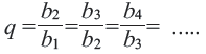
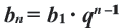

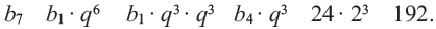
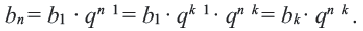
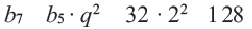
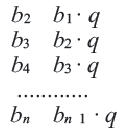
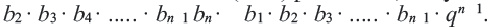
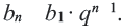

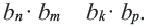
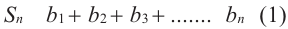
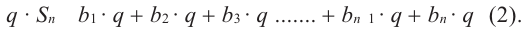
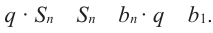
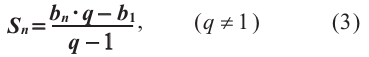
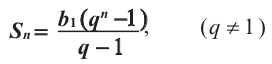
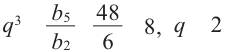
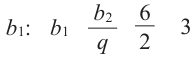
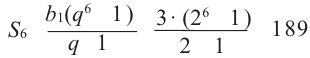

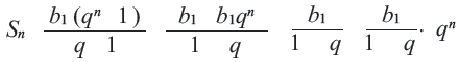

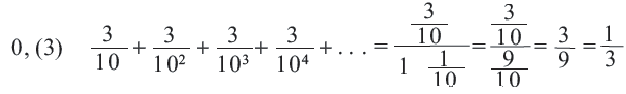
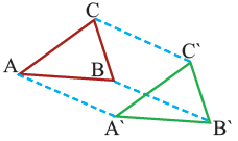
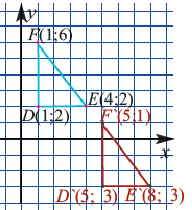
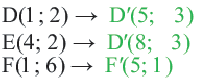
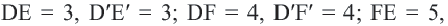

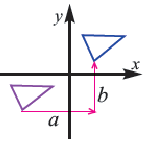
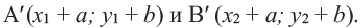
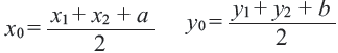
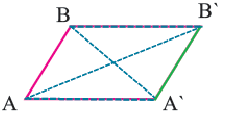
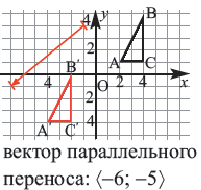
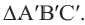
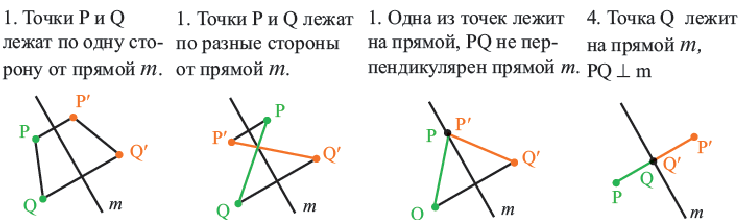
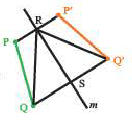

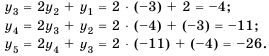
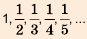 — последовательность чисел, обратных натуральным.
— последовательность чисел, обратных натуральным.